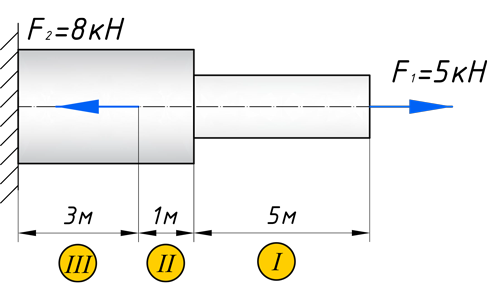
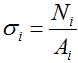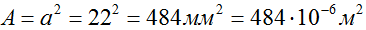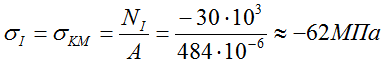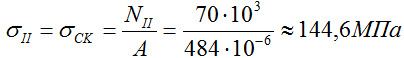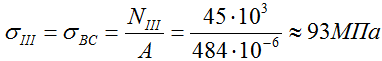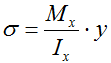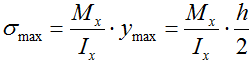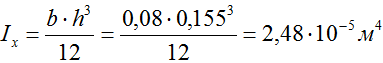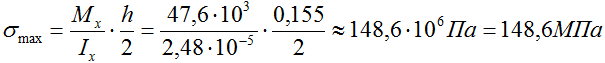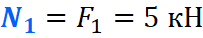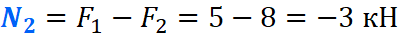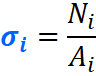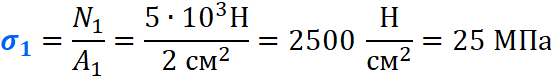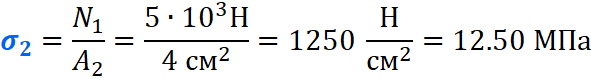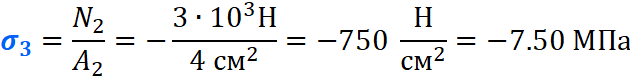Товарищи как найти сигму в задаче по сопромату, на тему : “расчет стержневой системы”?
Пользователь удален
Ученик
(135),
закрыт
16 лет назад
??
Наталья
Просветленный
(42156)
16 лет назад
спроси у омеги
Леонид Серёжкин
Мастер
(1801)
16 лет назад
сигма которая всмысле напряжение??? У всех сигма разное может означать.
Что вообще за глупый вопрос? открой учебник или лекции свои!
Олег Демидов
Мастер
(1303)
16 лет назад
Элементарно!! ! Пэ дэлить на Эф!! ! Или проще говоря, действующее усилие на площадь поперечного сечения!
Похожие вопросы
Зачем нужен предел текучести?
Предел текучести — механическая характеристика материала, характеризующая напряжение, при котором деформации продолжают расти без увеличения нагрузки. С помощью этого параметра рассчитываются допустимые напряжения для пластичных материалов.
Что такое предел текучести как определить?
Условным пределом текучести называется напряжение, при котором остаточная (пластическая) деформация составляет 0,2%. Это значение используется для высокопрочных болтов (например, кл. пр. 8.8), которые при напряжении демонстрируют непрерывный сдвиг между упругой и пластической деформацией.
Чем выше предел текучести?
Чем выше показатель предела текучести стали, тем дольше сталь способна находиться в напряженном состоянии и противостоять стационарным и динамическим нагрузкам.
Как найти предел упругости?
Предел упругости принято определять величиной напряжения при допускаемой малой деформации и, соответственно, измерять в паскалях. где σy — предел упругости[Па], FY [Н]— нагрузка, S0 [м2]— площадь образца при допускаемой остаточной деформации. У большинства тел предел упругости и предел пропорциональности совпадают.
Что показывает предел прочности?
Предел прочности — это максимальное механическое напряжение, выше которого происходит разрушение материала, подвергаемого деформации; предел прочности при растяжении обозначается σВ и измеряется в килограммах силы на квадратный сантиметр (кгс/см2), а также указывается в мегапаскалях (МПа).
Что характеризует относительное удлинение?
Пластичность характеризует относительное удлинение σ и относительное сужение ψ (его называют поперечным сужением). Удлинение — это характеристика пластичности металла, оцениваемая по увеличению длины образца из этого металла при растяжении.
Величина предела текучести материала ττ=G/2π. , где G — модуль сдвига, как раз и определяющий устойчивость связей между атомами.
Что называется площадкой текучести?
площадка текучести — Напряжение в материале обычно меньшее, чем максимальное напряжение, при котором увеличение деформации происходит без увеличения напряжения.
На значение предела текучести металла влияют самые разные факторов, например: толщина образца, режим термообработки, наличие тех или иных примесей и легирующих элементов, микроструктура, тип и дефекты кристаллической решётки и др. Предел текучести металлов сильно меняется с изменением температуры.
В чем измеряется предел прочности?
Предел прочности — это максимальное механическое напряжение, выше которого происходит разрушение материала, подвергаемого деформации; предел прочности при растяжении обозначается σВ и измеряется в килограммах силы на квадратный сантиметр (кгс/см2), а также указывается в мегапаскалях (МПа).
[2] Под условным пределом текучести обычно подразумевают такое напряжение, при котором остаточная деформация составляет 0,2%. Таким образом обычно условный предел текучести при растяжении обозначается σ0,2. Выделяют также условный предел текучести при изгибе и условный предел текучести при кручении.
Что значит прочность на сжатие?
Прочность на сжатие — одна из основных характеристик показателей бетона. Именно по ней определяется класс бетона, который обозначается буквой «В». … Например, обозначение показателя бетона В25 означает, что бетон выдерживает давление в 25 мегапаскалей согласно СНиП 2.03.01-84.
Что такое предел прочности при изгибе?
2.2. Предел прочности при изгибе — максимум, рассчитанный при натяжении поверхности при изгибе, которому подвергается испытуемый образец до разрыва.
Что характеризует относительное удлинение при разрыве?
Относительное удлинение при разрыве характеризует изменение первоначальной длины пленки при растяжении до момента разрыва. Модуль упругости при растяжении характеризует степень жесткости материала.
Характеристиками пластичности металла являются относительное удлинение δ = ∆l/l и относительное сужение ψ = (F0 — Fk)/F0, где F0 — первоначальная площадь сечения образца; Fk — минимальная площадь сечения образца после разрушения. Чем больше величины этих характеристик, тем пластичнее материал.
Как определить предел пропорциональности?
Предел пропорциональности σ пц = Fпц / А0 – это наибольшее напряжение, до которого справедлив закон Гука.
Какая характеристика пластичности зависит от длины образца?
Удлинение — это характеристика пластичности металла, оцениваемая по увеличению длины образца из этого металла при растяжении. Относительное сужение — это характеристика пластичности металла, оцениваемая по относительному уменьшению площади поперечного сечения растягиваемого образца.
Пределом текучести называют механическую характеристику материала, характеризующую напряжение, при котором деформации продолжают расти без увеличения нагрузки.
Обозначение σт
Единица измерения – Паскаль [Па] либо кратные [МПа].
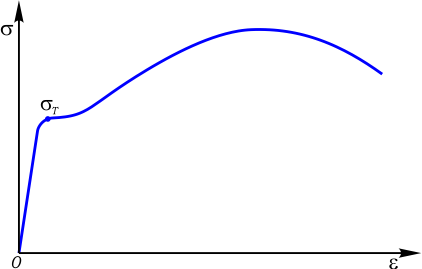
На диаграмме напряжений (рис. 1) предел текучести стали обозначается точкой, в которой начинается практически горизонтальный участок диаграммы, называемый площадкой текучести.
Рис. 1. Предел текучести
Это важный параметр, с помощью которого рассчитываются допустимые напряжения для пластичных материалов.
После прохождения предела текучести в металле образца начинают происходить необратимые изменения, перестраивается кристаллическая решетка металла, появляются значительные пластические деформации. При этом металл самоупрочняется, об этом говорит то, что после площадки текучести деформации растут при возрастающем значении растягивающей силы.
Условный предел текучести
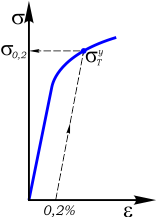
В случаях, когда на диаграмме напряжений нет выраженной площадки текучести, определяют так называемый условный предел текучести σ0,2. Это величина напряжений, при которых относительные остаточные деформации равны 0,2%.
Рис. 2. Условный предел текучести
Для его определения (рис. 2) вдоль оси ε откладывается значение равное 0,2%, откуда проводится луч параллельный начальному участку диаграммы напряжений.
Точка пересечения луча с линией диаграммы есть условный предел текучести для данного материала.
Предел прочности >
Предел пропорциональности >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения

σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение “xср” вместо “μ”.
Разница между формулами S и σ (“n” и “n–1”)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с “n–1”),
- полностью все данные – используется формула σ (с “n”).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 – μ = 15 – 20 = -5
x2 – μ = 26 – 20 = 6
x3 – μ = 15 – 20 = -5
x4 – μ = 24 – 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 – μ)² = (-5)² = 25
(x2 – μ)² = 6² = 36
(x3 – μ)² = (-5)² = 25
(x4 – μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi – μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:

S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле “=СТАНДОТКЛОНА(“
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
iSopromat.ru
Пример решения задачи на построение эпюры нормальных напряжений σ при растяжении и сжатии стального стержня квадратного сечения.
Задача
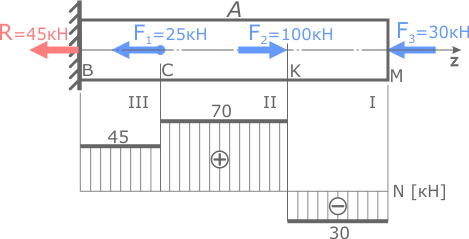
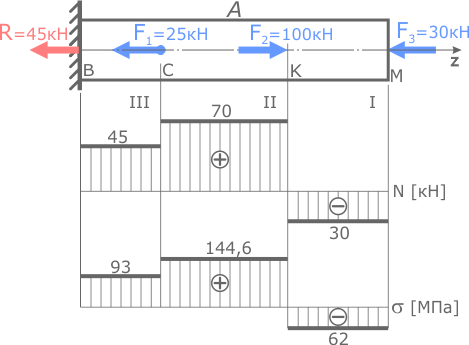
Построить эпюру нормальных напряжений для стержня постоянного сечения, нагруженного продольными силами.
Решение
Предыдущие пункты решения задачи:
т.е. напряжения в рассматриваемом сечении определяются отношением соответствующей величины внутренней силы к площади поперечного сечения стержня.
Площадь поперечного сечения стержня постоянна по всей его длине, и составляет
Очевидно, что в пределах участка стержня, на котором внутренняя сила и площадь постоянны, напряжения так же будут иметь одинаковую величину.
Здесь, при одинаковой площади, внутренние силы различаются на трех силовых участках. Соответственно на этих участках нормальные напряжения тоже будут отличаться.
Знак напряжений зависит от знака соответствующей внутренней продольной силы.
Значения внутренних сил принимаются с построенной ранее эпюры N.
Расчет напряжений
Нормальные напряжения на I силовом участке (KM)
По этим данным строим эпюру нормальных напряжений.
По построенной эпюре видно, что напряжения не превышают заданных допустимых значений, следовательно, рассчитанные размеры стержня обеспечивают его прочность.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
iSopromat.ru
Пример решения задачи на построение эпюры нормальных напряжений σ при изгибе стальной балки прямоугольного сечения.
Задача
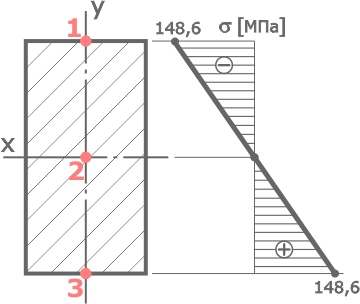
Построить эпюру распределения нормальных напряжений для подобранного ранее прямоугольного сечения двухопорной балки с размерами h=155мм и b=80мм.
Пример решения
Предыдущие пункты решения задачи:
Рассмотрим пример построения эпюры распределения нормальных напряжений в опасном сечении балки.
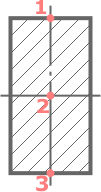
Прямоугольное сечение имеет три характерных точки:
Для построения эпюры достаточно найти значения в любых двух точках, потому что при изгибе нормальная составляющая полных напряжений по высоте сечения меняется линейно.
где Ix – осевой момент инерции сечения,
y – расстояние от оси х проходящей через центр тяжести сечения до точки в которой рассчитывается напряжение.
Очевидно, что на самой оси x (точка №2) где координата y=0 напряжения отсутствуют.
Наибольшие значения нормальных напряжений будут на максимальном удалении от оси x, то есть при ymax=h/2 (в точках 1 и 3).
При изгибе верхний и нижний слой балки испытывают продольную деформацию разных знаков.
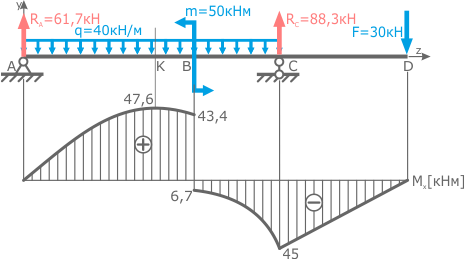
Знаки напряжений в точках 1 и 3 определяются по построенной ранее эпюре изгибающих моментов Mx.
В данном случае по ней видно, что в опасном сечении балки эпюра моментов имеет положительное значение (+47,6 кНм), что согласно правила знаков при изгибе говорит о том, что в рассматриваемом месте балки сжимаются верхние слои (нижние соответственно растягиваются).
Поэтому в соответствии с правилом знаков для напряжений, нормальные напряжения в верхней точке 1 будут отрицательны (потому что сжатие), а в точке 3 – положительны (растяжение) или σ т1=-148,6МПа, σ т3=148,6МПа.
По полученным данным строим эпюру
Как видно по построенной эпюре, нормальные напряжения не превышают заданных допустимых значений, что говорит о том, что размеры прямоугольного сечения были подобраны верно, и прочность балки обеспечена.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Построение эпюр при растяжении и сжатии: продольных сил и нормальных напряжений для ступенчатого стержня (бруса)
Автор: Константин Вавилов · Опубликовано 23.11.2017 · Обновлено 14.03.2021
Приветствую, друзья! Сегодня дебютирует наш курс – «сопромат для чайников», Вы находитесь на сайте проекта SoproMats, который связан с сопроматом и не только. На этой страничке будет выложен первый урок из заявленного экспресс курса, который связан с таким простейшим видом деформации как растяжение (сжатие). В частности, будем учиться строить эпюры для бруса (стержня), который загружен растягивающей и сжимающей силой. Как правило, такое домашнее задание, одним из первых, дают всем студентам, которые начинают знакомиться с сопроматом. После изучения материалов данного урока вы научитесь строить следующие эпюры: продольных сил и нормальных напряжений. Не пугайтесь мудреных названий, на самом деле все эти эпюры строятся очень просто. Что же давайте приступим к изучению!
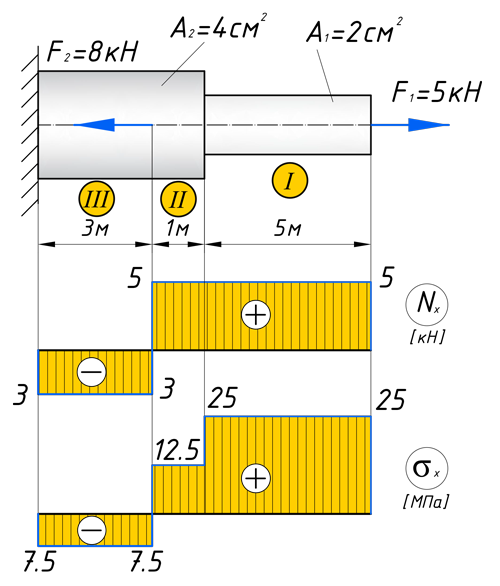
Построение эпюры продольных сил
Так как это курс для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику. Если вы хотите более детально изучить рассматриваемые здесь вопросы, то могу предложить Вам другие материалы нашего сайта. Например, что касается данного блока статьи, то у нас есть материалы про продольную силу, где представлено полное досье на данный внутренний силовой фактор: что эта за сила, зачем нужна и т.д. Но если Вам некогда залазить в эти дебри, и хотите по-быстрому освоить продольную силу, то оставайтесь здесь, сейчас покажу как строится первая эпюра!
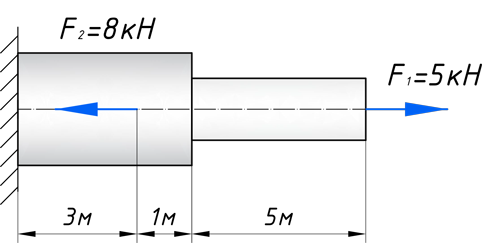
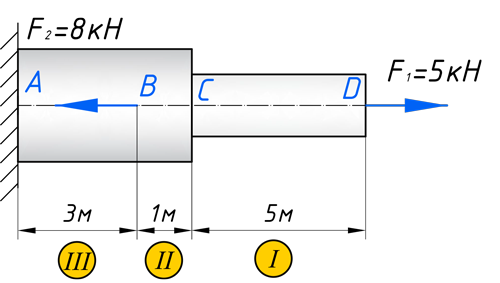
Кстати, вот объект нашего сегодняшнего исследования:
Чтобы построить эпюру продольных сил, нужно разбить наш брус на несколько участков, на которых эта эпюра будет иметь постоянное значение. Конкретно, для продольной эпюры, границами участков служат те точки, где прикладываются силы. То бишь, для нашего примера, нужно рассмотреть всего 2 участка:
Важно! На эпюру продольных сил, никак не влияет форма бруса, в отличие от других эпюр, которые будем дальше рассчитывать и строить.
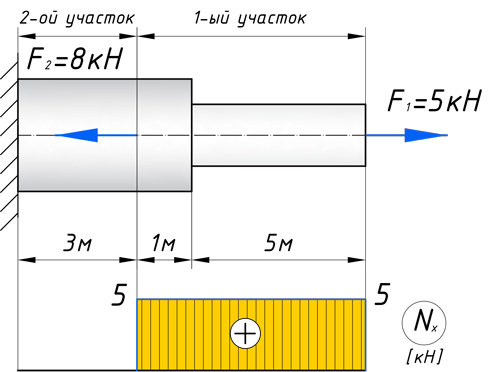
На первом участке сила F1 растягивает брус на величину 5кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике. Эпюры в сопромате, принято штриховать перпендикулярно нулевой линии, а также для продольных сил, на эпюрах проставляются знаки:
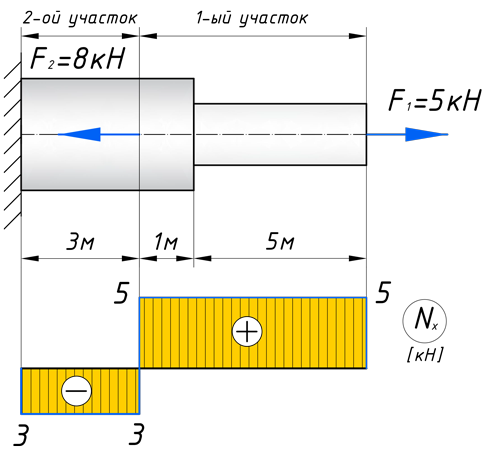
На втором же участке, сила F2 сжимает брус, тем самым в уравнение продольных сил, она пойдет с минусом:
Откладываем полученное значение на эпюре:
Вот так, достаточно просто, строится эта эпюра!
Построение эпюры нормальных напряжений
Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:
То бишь, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.
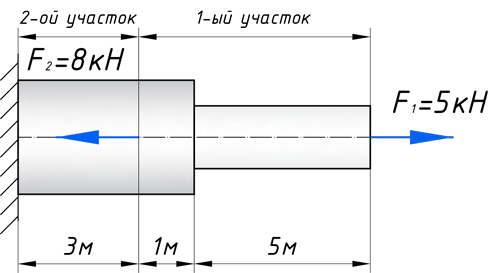
Для того чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:
Зададим брусу на первом участке (I) площадь поперечного сечения A1=2 см 2 , а вторая ступень бруса, допустим, будет иметь площадь A2=4 см 2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию. Также в задачах, часто, просят определить эти площади из условия прочности, с учетом допустимого напряжения, обязательно сделаю статью про это.
Вычисляем напряжения на каждом участке:
По полученным значениям строим эпюру нормальных напряжений:
Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие). В рамках статьи, была рассмотрена достаточно простая расчетная схема, если Вы хотите развить свои навыки по построению эпюр, то приглашаю Вас на страничку про различные эпюры, где можно найти примеры расчета более сложных брусьев с распределенными нагрузками, где о каждой эпюре подготовлена отдельная статья.
Если Вам понравилась статья, расскажите о ней своим друзьям, подписывайтесь на наши социальные сети, где публикуется информация о новых статьях проекта. Также, там можно задать любой интересующий Вас вопрос о сопромате и не только.
Источник
Построение эпюры перемещений



Построение эпюры нормальных напряжений
Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:
То бишь, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.
Для того, чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:
Зададим брусу на первом участке (I) площадь поперечного сечения A1=2 см 2 , а вторая ступень бруса, допустим, будет иметь площадь A2=4 см 2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию.
Вычисляем напряжения на каждом участке:
По полученным значениям строим эпюру нормальных напряжений:
Построение эпюры перемещений
Самое время перейти к последней эпюре, которая называется эпюрой осевых перемещений поперечных сечений. Для краткости, ее еще называют просто эпюрой перемещений. Для расчета данного графика, пользуются следующей формулой:
Эта формула, является следствием закона Гука. Также ее можно записать как:
Сейчас покажу как ею пользоваться. Все характерные сечения бруса назовем буквами английского алфавита, чтобы потом в решении, было удобно ссылаться на них:
Традиционно расчет перемещений начинают с жестко защемленного торца. Так как сечение в заделке, не имеет возможности перемещаться, то и в решение записываем, что перемещение этого сечения равно нулю:
Далее, для построения эпюры нужно вычислить перемещения в характерных сечениях, которые находятся на границах участков (B, C и D). Этого будет достаточно, так как в пределах участков, эпюра будет меняться по линейному закону. Исключениями могут быть участки, на которых действует распределенная нагрузка, но это тема отдельной статьи.
Приступаем к расчету перемещения сечения B. По формуле, оно будет равно площади эпюры σ, на третьем участке, деленной на модуль упругости — E. При этом, обязательно, учитываем знак эпюры:
Для других сечений, перемещения будут вычисляться аналогичным образом:
ВАЖНО! Вы, наверное, заметили, что для каждого последующего сечения, в расчетах учитывается перемещение предыдущего. Это обязательно необходимо делать.
По полученным значениям, откладываем эпюру перемещений
Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие).
Эпюры построения смотри ниже.
Решить задачу(домашняя работа)
Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений, а также максимальное удлинение.
Принять А=200 мм², А1=400мм 2 ,l=2м, а=4м,в=3м,с=2м,Е=2 ·10 5 МПа.
Источник