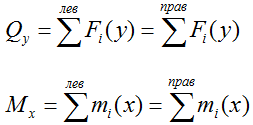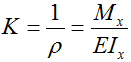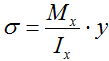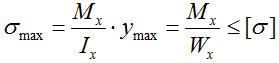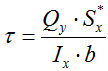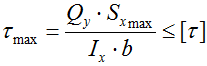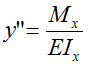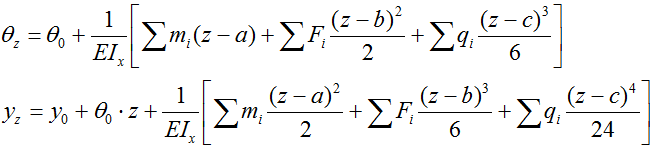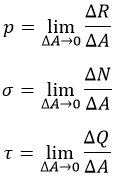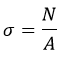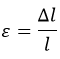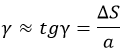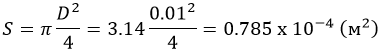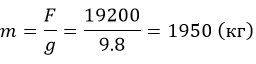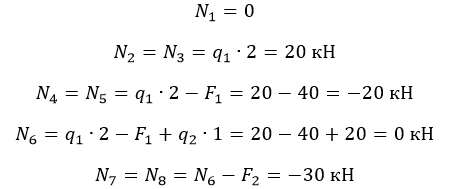Подборка формул для расчета балок и рам на изгиб и решения задач сопротивления материалов по расчету внутренних сил, напряжений, деформаций и перемещений при изгибе.
Обозначения:
σ — нормальные напряжения,
τ — касательные напряжения,
Qy – внутренняя поперечная сила,
Mx – внутренний изгибающий момент,
Ix – осевой момент инерции сечения балки,
Wx – осевой момент сопротивления сечения,
A — площадь поперечного сечения,
[σ], [τ] – соответствующие допустимые напряжения,
E – модуль упругости I рода (модуль Юнга),
y — расстояние от оси x до рассматриваемой точки сечения балки.
Расчет внутренних поперечных сил и изгибающих моментов
Формула кривизны балки в заданном сечении
Расчет нормальных напряжений в произвольной точке сечения балки при изгибе
Условие прочности по нормальным напряжениям при изгибе (проверочный расчет)
Осевые моменты инерции I и сопротивления W
Касательные напряжения в произвольной точке сечения при изгибе определяются по формуле Журавского:
Здесь:
Sx* — статический момент относительно оси x отсеченной части сечения
b — ширина сечения на уровне рассматриваемой точки
Другие видео
Условие прочности балки по касательным напряжениям
Дифференциальное уравнение линии изогнутой оси балки
Уравнения метода начальных параметров (МНП)
θz, yz — соответственно угол наклона и прогиб сечения балки на расстоянии z от начала координат,
θ0, y0 — соответственно угол наклона и прогиб сечения балки в начале координат,
m, F, q — соответственно все изгибающие моменты, сосредоточенные силы и распределенные нагрузки приложенные к балке,
a, b — расстояние от начала координат до сечений где приложены моменты и силы соответственно,
c — расстояние от начала координат до начала распределенной нагрузки q.
Пример расчета перемещений в балке методом начальных параметров >
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Товарищи как найти сигму в задаче по сопромату, на тему : “расчет стержневой системы”?
Пользователь удален
Ученик
(135),
закрыт
16 лет назад
??
Наталья
Просветленный
(42156)
16 лет назад
спроси у омеги
Леонид Серёжкин
Мастер
(1801)
16 лет назад
сигма которая всмысле напряжение??? У всех сигма разное может означать.
Что вообще за глупый вопрос? открой учебник или лекции свои!
Олег Демидов
Мастер
(1303)
16 лет назад
Элементарно!! ! Пэ дэлить на Эф!! ! Или проще говоря, действующее усилие на площадь поперечного сечения!
Похожие вопросы
В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:
Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
| А | – площадь сечения (иногда обозначается как F), см2 |
| E | – модуль продольной упругости, МПа (кгс/см2) |
| G | – модуль сдвига, МПа |
 |
– Коэффициент поперечной деформации Пуассона, иногда обозначают μ (мю) |
| Jx, Jy | – осевые моменты инерции относительно осей х и у (см4) |
| Jmax, Jmin | – осевые моменты инерции относительно главных осей |
| Jp | – полярный момент инерции, (см4) |
| Sx, Sx | – статические моменты инерции относительно осей x,y |
| ix, iy | – радиус инерции |
| imax, imin | – радиус инерции относительно главных осей |
| Wx, Wy | – Момент сопротивления относительно осей x и y |
| F | – внешняя сила (часто обозначают буквой “P” ) |
| q | – распределенная нагрузка |
| M | – внешний момент, действующий на элемент конструкции (изгибающий или крутящий), кН·м |
| Mx, My | – изгибающий момент, действующий на элемент конструкции относительно осей x и y |
| N | – продольная сила |
| Q (Qx, Qy) | – поперечная сила |
| Mk или T | – крутящий момент |
| σ | – нормальное напряжение (сигма) |
| [σ] | – допускаемое нормальное напряжение |
| σпред | – предельное нормальное напряжение |
 |
– касательное напряжение (тау) |
[ ] ] |
– допускаемое касательное напряжение |
| L, l | – длина стержня (балки, бруса) |
| ΔL, Δl | – абсолютная деформация |
| ε | – поперечная деформация |
| λ | – гибкость стержня (лямбда, lambda ) |
 |
– угловые деформации (углы сдвига); |
| φ | – угол поворота оси стержня (балки) при изгибе, рад. |
| θ | – угол закручивания стержня (вала) при кручении, рад. |
| α | – коэффициент линейного температурного расширения, 1/град |
Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».
На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.
Что такое сопромат
Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.
Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.
Основные задачи по сопротивлению материалов
Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.
Требования
Перечислены далеко не все, но для статики и базовой программы хватит:
-
Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.
-
Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.
-
Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.
Материал и силы
Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:
-
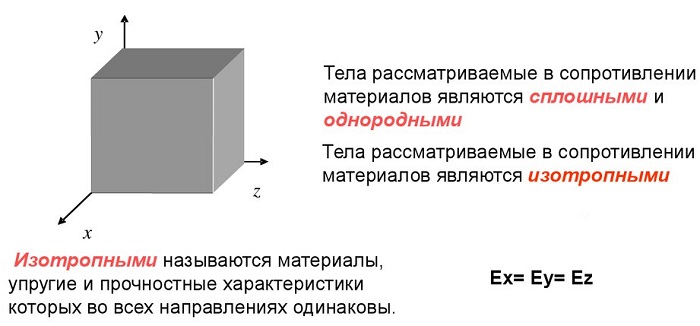
материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;
-
свойства не зависят от направления;
-
образец восстанавливает начальные параметры при снятии нагрузки;
-
поперечные сечения не меняются при деформации;
-
в удаленных от места нагрузки местах усилие распределяется равно по сечению;
-
результат воздействия нагрузок равен сумме последствий от каждой;
-
деформации не влияют на точки приложения сил;
-
отсутствуют изначальные внутренние напряжения.
Схемы
Служат для создания возможности расчета реальных конструкций:
-
тело – объект с практически одинаковыми «длина х ширина х высота»;
-
брус (балка, стержень, вал) – характеризуется значительной длиной.
На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):
Рис. 1. Опоры с воспринимаемыми реакциями:
а) шарнирно-подвижная;
б) шарнирно-неподвижная;
в) жесткая заделка (защемление).
Силы в сопромате
Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».
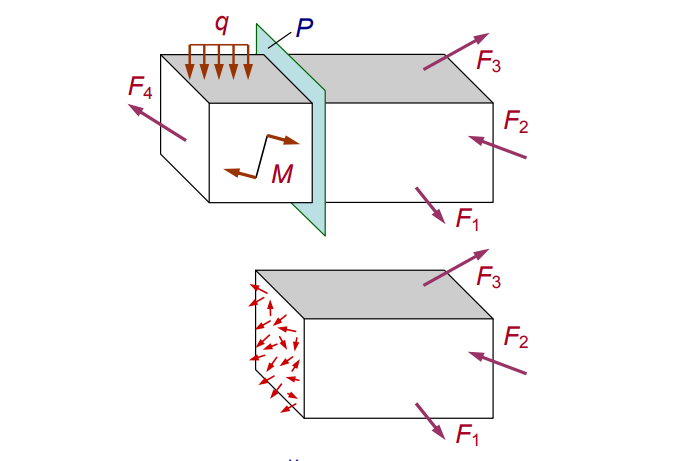
Разделим нагруженное тело виртуальным сечением P (см. рис. 2).
Рис. 2
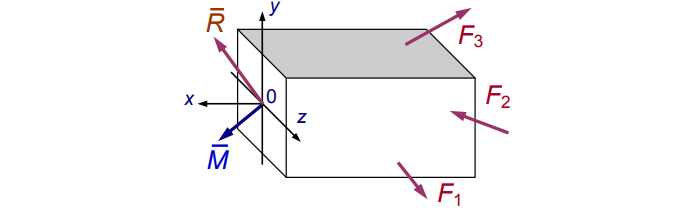
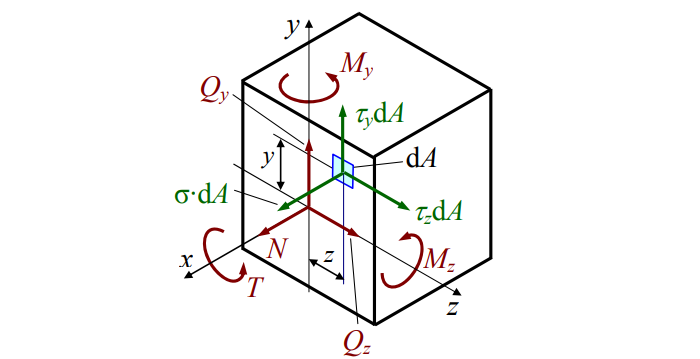
Заменим хаос равнодействующей R и моментом M (см. рис. 3):
Рис. 3
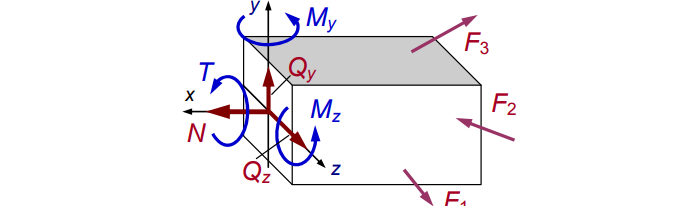
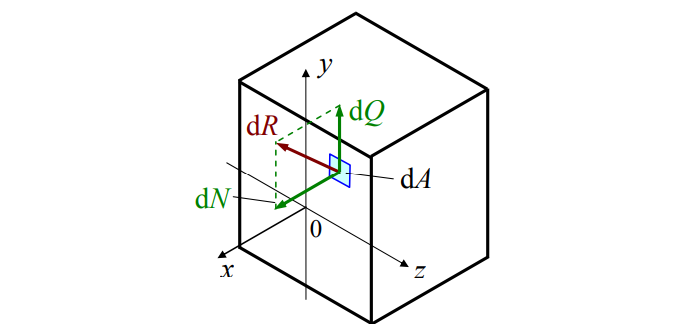
Распределив по осям, получим картину нагрузки сечения (см. рис. 4):
Рис. 4
Нагрузки и деформации, изучаемые в сопромате
Изучим несколько принятых терминов.
Напряжения
В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:
Элементарные усилия таковы:
-
σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;
-
τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;
-
p – полное напряжение.
Просуммировав элементы, получим:
Здесь:
-
N – нормальная сила;
-
A – площадь сечения.
В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).
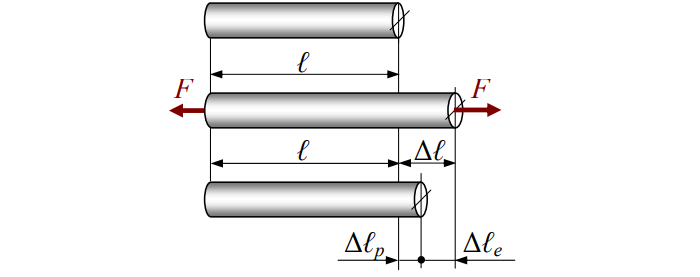
Деформации
Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет.
Полная деформация будет равна:
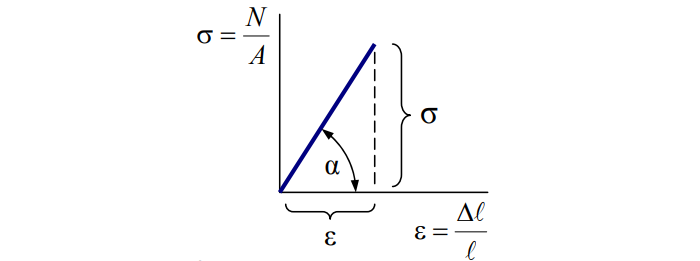
Деформация относительная обозначается «ε» и рассчитывается так:
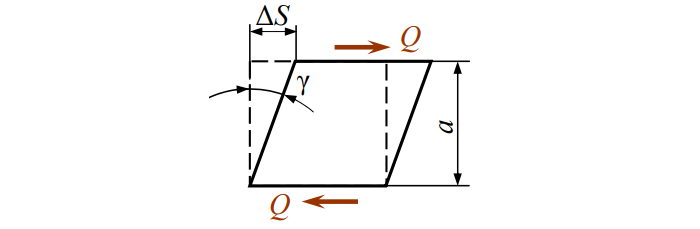
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:
Здесь γ – относительный сдвиг.
Виды нагрузки
Перечислены основные.
-
Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).
-
Кручение – действует момент. Обычно рассчитываются передающие усилия валы.
-
Изгиб – воздействие направлено на искривление.
Основные формулы
Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:
E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 106 Па.
Сопротивление материала прямо пропорционально деформации:
Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.
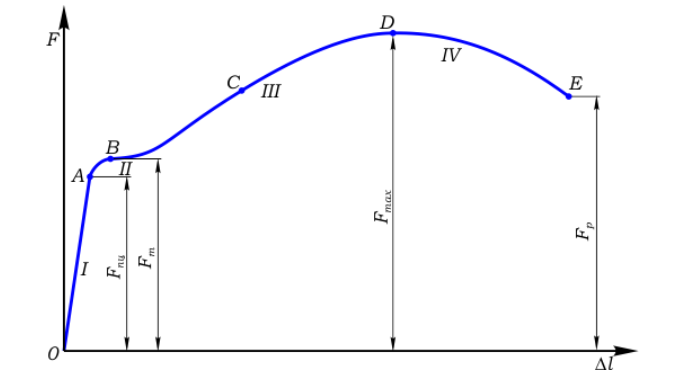
Реальная диаграмма
Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:
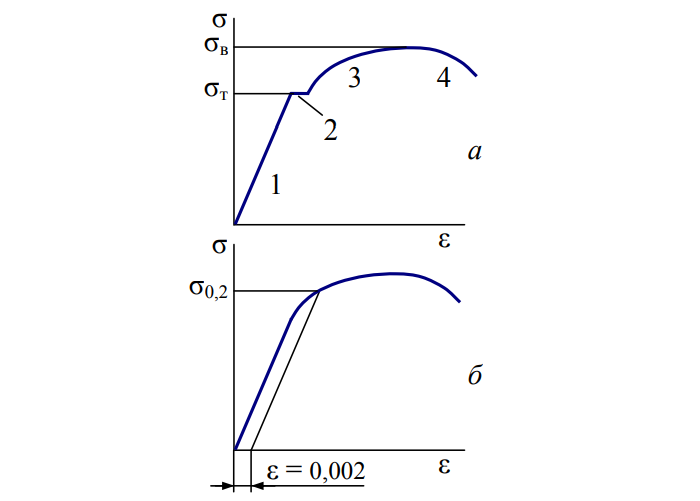
Принимаемые схемы:
График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.
Расчеты обычно ведут по σт (а) и σ0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.
Пример решения задачи
Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?
Решение.
σ0,2 для стали 45 равна 245 МПа (из ГОСТ).
Площадь сечения прутка:
Допустимая сила тяжести:
Для получения веса следует разделить на ускорение свободного падения g:
Ответ: необходимо подвесить груз массой 1950 кг.
Как найти опасное сечение
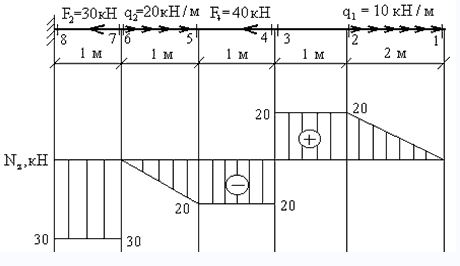
Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца.
Усилие положительно, если направлено на растяжение.
На схеме показано, что:
-
на участке (7 – 8) действует сжатие 30 кН;
-
на (2 – 3) – растяжение 20 кН.
Зачем и кому нужен сопромат
Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.
Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».
Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.