Среднее квадратичное отклонение двух, трех, четырех и более чисел. Оно же стандартное отклонение, среднеквадратическое отклонение, среднеквадратичное отклонение, средняя квадратическая, стандартный разброс — показатель рассеивания значений случайной величины относительно её математического ожидания в теории вероятностей и статистике.
Как правило перечисленные термины равны квадратному корню дисперсии.
Пример вычисления стандартного отклонения по следующим формулам:
Вычислим среднюю оценку ученика: 2; 4; 5; 6; 8.
Cредняя оценка будет равна:
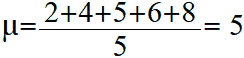
Вычисляем квадраты отклонений оценок от их средней оценки:
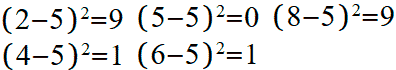
Вычислим среднее арифметическое (дисперсию) этих значений:
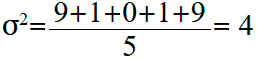
Стандартное отклонение равно квадратному корню дисперсии:
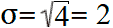
Эта формула справедлива только если эти пять значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки пяти случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 5 нужно было бы поставить n − 1 = 4:
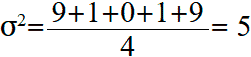
Тогда стандартное отклонение будет равняться:
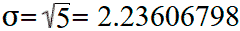
Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Среднее квадратичное отклонение
Среднее квадратичное отклонение — это показатель рассеивания значений случайной величины относительно её математического ожидания.
Обозначается символом σ (греческая буква «сигма»).
Среднеквадратичное отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки
среднего арифметического,
при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
Чтобы найти среднеквадратичное отклонение, нужно взять квадратный корень из дисперсии:

Другими словами, среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.
Данный онлайн калькулятор поможет вычислить среднее квадратичное отклонение ряда значений.
Вводите каждое новое число в отдельную ячейку. Для добавления ячейки нажмите на кнопку со знаком «+».
Поделиться страницей в социальных сетях:
Среднеквадратическое отклонение
begin{align}
& sigma=sqrt{frac{1}{n}sum_{i=1}^N (x_i-bar{x})^2} \
end{align}
Стандартное отклонение
begin{align}
& s=sqrt{frac{n}{n-1}sigma^2}=sqrt{frac{1}{n-1}sum_{i=1}^N (x_i-bar{x})^2} \
end{align}
begin{align}
& где sigma^2-дисперсия; x_i-i-ый элемент выборки; n-объем выборки; bar{x}-среднее арифметическое выборки. \
end{align}
Калькулятор вычислит среднеквадратическое отклонение, а также стандартное отклонение и среднее арифметическое. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
количество чисел
стандартное отклонение калькулятор
Среднеквадратическое отклонение (СО) - это показатель рассеяния значений во множестве данных относительно их математического ожидания. Обозначается также как СО. Символом среднеквадратического отклонения является σ(сигма). Можно также сказать, что это показатель изменчивости или дисперсии в этом множестве данных. Находите математическое ожидание, дисперсию, среднеквадратическое отклонение данных чисел с помощью этих бесплатных арифметических онлайн-калькуляторов среднеквадратического отклонения.
Среднеквадратическое отклонение калькулятор
Для Рассчитать среднее значение, дисперсия, стандартное отклонение :
Введите все цифры, разделенные запятыми ‘,’.
E.g: 13,23,12,44,55
дисперсия(стандартное отклонение)
население стандартное отклонение
дисперсия(население стандартное отклонение)
Среднеквадратическое отклонение (СО) - это показатель рассеяния значений во множестве данных относительно их математического ожидания. Обозначается также как СО. Символом среднеквадратического отклонения является σ(сигма). Можно также сказать, что это показатель изменчивости или дисперсии в этом множестве данных. Находите математическое ожидание, дисперсию, среднеквадратическое отклонение данных чисел с помощью этих бесплатных арифметических онлайн-калькуляторов среднеквадратического отклонения.
формула :
означать :
Средняя = сумма значений X / N (количество значений)
дисперсия :
дисперсия = s2
Среднеквадратическое отклонение :

население Среднеквадратическое отклонение :

пример:
Рассмотрим множество X цифр 5,10,15,20,25
шаг 1 :
Средняя = сумма значений X / N (количество значений)
= (5+10+15+20+25) / 5
= 75 / 5
= 15
шаг 2 :
Чтобы найти дисперсию,
Вычесть среднее из каждого из значений,
5-15 = -10
10-15 = -5
15-15 = 0
20-15 = 5
25-15 = 10
Теперь квадрат все ответы вы получили от вычитания.
(-10)2 = 100
(-5)2 = 25
(0)2 = 0
(5)2 = 25
(10)2 = 100
Добавить все квадраты чисел,
100 + 25 + 0 + 25 + 100 = 250
Разделите сумму квадратов (n-1)
250 / (5-1) = 250 / 4 = 62.5
Отсюда Разница = 62.5
шаг 3 :
Чтобы найти стандартное отклонение, найти квадратный корень из дисперсии,
√62.5 = 7.905
Следовательно Стандартное отклонение является 7.905
Чтобы найти минимальное и максимальное стандартное отклонение,
Минимальная CO = среднее – CO
= 15 – 7.905
= 7.094
Максимальная CO = среднее + CO
=15 + 7.905
= 22.906
шаг 4 :
Чтобы найти стандартный население отклонение,
Разделите сумму квадратов найденных на шаге 2 по n
250 / 5 = 50
Найти квадратный корень 50, √50 = 7.07
Этот инструмент поможет вам динамически вычислять статистические проблемы. Расчет среднее значение, дисперсия, стандартное отклонение легче.
Standard Deviation Calculator
Standard deviation is a measure of spread of numbers in a set of data from its mean value. Use our online standard deviation calculator to find the mean, variance and arithmetic standard deviation of the given numbers.
Enter all the numbers separated by comma ‘,’.
E.g: 13,23,12,44,55
Variance(Standard deviation)
Population Standard deviation
Variance(Population Standard deviation)
Standard deviation is a measure of spread of numbers in a set of data from its mean value. Use our online standard deviation calculator to find the mean, variance and arithmetic standard deviation of the given numbers.
Code to add this calci to your website 

Formula :
Mean :
Mean = Sum of X values / N(Number of Values)
Variance :
Variance = s2
Sample Standard Deviation :

Population SD :

In statistics, Standard Deviation (SD) is the measure of ‘Dispersement’ of the numbers in a set of data from its mean value. This is represented using the symbol σ (sigma). The formula for the Standard Deviation is square root of the Variance. Here is a free online arithmetic standard deviation calculator to help you solve your statistical questions. This can also be used as a measure of variability or volatility for the given set of data. Enter the set of values in the online SD calculator to calculate the mean, standard deviation, variance and population standard deviation.
Example:
Consider a set X = {5,10,15,20,25}
Step 1 :
Mean = Sum of X values / N(Number of values)
= (5+10+15+20+25) / 5
= 75 / 5
= 15
Hence Mean = 15
Step 2 :
To find the variance,
Subtract the mean from each of the x values,
5-15 = -10
10-15 = -5
15-15 = 0
20-15 = 5
25-15 = 10
Now square all the answers you have got from subtraction.
(-10)2 = 100
(-5)2 = 25
(0)2 = 0
(5)2 = 25
(10)2 = 100
Add all the Squared numbers,
100 + 25 + 0 + 25 + 100 = 250
Divide the sum of squares by (n-1)
250 / (5-1) = 250 / 4 = 62.5
Hence Variance = 62.5
Step 3 :
Find the square root of variance,
√62.5 = 7.905
Hence Standard deviation is 7.905
To find minimum and maximum SD,
Minimum SD = Mean – SD
= 15 – 7.905
= 7.094
Maximum SD = Mean + SD
=15 + 7.905
= 22.906
Step 4 :
To find the population SD,
Divide the sum of squares found in step 2 by n
250 / 5 = 50
Find the square root of 50, √50 = 7.07
Related Calculators:
- Population Confidence Interval
- Hypothesis Testing Calculator For Population Mean
- Sample Size Calculator
- Mean Squared Error, Sum Of Squared Error Calculator
- Mean Median Mode Range Calculator
- Geometric Mean Calculator
