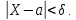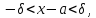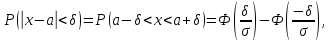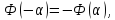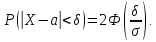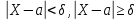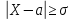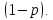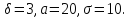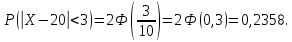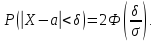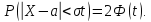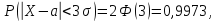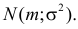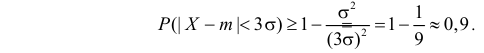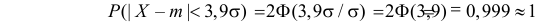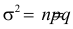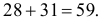Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы – случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.
Часто
требуется вычислить вероятность того,
что отклонение нормально распределенной
случайной величины
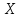
абсолютной величине меньше заданного
положительного числа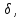
требуется найти вероятность осуществления
неравенства
Перейдем
к двойному неравенству
так
как
то
События,
состоящие в осуществление неравенств
противоположные.
Поэтому,
если вероятность осуществления
неравенства
равна
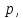
равна
Рассмотрим
пример.
Случайная величина

нормально. Математическое ожидание и
среднее квадратическое отклонение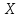
равны 20 и 10. Найти вероятность того, что
отклонение по абсолютной величине будет
меньше трех.
По
условию
Тогда
Правило
трех сигм.
Преобразуем
формулу
Пусть
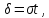
Если
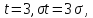
т.е.
вероятность того, что отклонение по
абсолютной величине будет меньше
утроенного среднего квадратического
отклонения, равна 0,9973. Другими
словами, вероятность того, что абсолютная
величина отклонения превысит утроенное
среднее квадратическое отклонение,
очень мала, а именно 0,0027.
В
этом и состоит правило
трех сигм:
если случайная величина распределена
нормально, то абсолютная величина ее
отклонения от математического ожидания
не превосходит утроенного среднего
квадратического отклонения.
На
практике применяют правило трех сигм
в случаях: если распределение изучаемой
случайной величины неизвестно, но
условие, указанное в приведенном правиле,
выполняется, то есть основание
предполагать, что изучаемая случайная
величина распределена нормально; в
противном случае, случайная величина
не распределена нормально.
Контрольные
вопросы
1.
Сформулировать понятие потока событий.
2.
Записать аналитически и изобразить
графически нормальный, равномерный и
показательный законы распределения.
3.
В чем состоит смысл правила трех сигм?
Лекция
№48. Закон больших чисел
48.1.
Закон больших чисел и его практическое
значение.
48.2.
Центральная предельная теорема Ляпунова.
48.3.
Применение закона больших чисел и
центральной предельной теоремы.
48.1. Закон больших чисел и его практическое значение
Нельзя
заранее уверенно предвидеть, какое из
возможных значений примет случайная
величина в итоге испытания; это зависит
от многих случайных причин, учесть
которые невозможно. Вряд ли можно
установить закономерности поведения
и суммы достаточно большого числа
случайных величин. На самом деле это не
так. При некоторых сравнительно широких
условиях суммарное поведение достаточно
большого числа случайных величин почти
утрачивает случайный характер и
становится закономерным.
Для
практики очень важно знание условий,
при выполнении которых совокупное
действие очень многих случайных причин
приводит к результату, почти не зависящему
от случая, так как позволяет предвидеть
ход явлений. Эти условия указываются в
теоремах, носящих название закона
больших чисел (теоремы Чебышева и
Бернулли).
Нормально
распределенные случайные величины
широко распространены на практике. Чем
это объясняется?
Ответ
дал А.М. Ляпунов. Если случайная величина
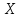
собой сумму очень большого числа взаимно
независимых случайных величин, влияние
каждой из которых на всю сумму ничтожно
мало, то
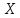
распределение, близкое к нормальному.
В
практической деятельности большое
значение имеют события с вероятностями,
близкими к единице или нулю. Отсюда
становится ясным, что одной из основных
задач теории вероятностей должно быть
установление закономерностей, происходящих
с вероятностями, близкими к единице,
при этом особую роль должны играть
закономерности, возникающие в результате
наложения большого числа независимых
или слабо зависимых случайных факторов.
Закон больших чисел является одним из
таких предложений теории вероятностей.
Под
законом больших
чисел понимают всю
совокупность предложений, утверждающих
с вероятностью, близкой к единице, что
наступит некоторое событие, зависящее
от неограниченного числа случайных
событий, каждое из которых оказывает
на него лишь незначительное влияние.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
Правило «трех сигм» в теории вероятности – определение и вычисление с примерами решения
Правило «трех сигм»:
Пусть случайная величина X имеет закон распределения
т.е. отклонения, большие 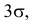
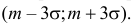
Поэтому правилом «трех сигм» иногда пользуются не печалясь о том, что случайная величина вовсе не имеет нормального закона распределения.
Замечание. Последние годы все чаще предпочитают брать не 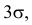
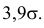
(Величина 0,999 впечатляет больше, нежели 0,997!)
Пример:
Монета подброшена 100 раз. Герб выпал 30 раз. Можно ли считать, что монета было симметричной?
Решение. Подбрасывание монеты можно считать независимым опытом, число которых 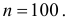
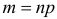
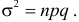
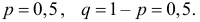
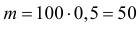
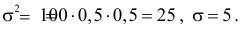
Ответ. При симметричной монете такой результат практически невозможен.
Пример:
Некто утверждает, что он экстрасенс. Для проверки был проделан следующий опыт. Взято пять карточек с рисунками простейших геометрических фигур. Испытатель выбирает карточку наугад, а испытуемый, находясь в соседней комнате, пытается определить, руководствуясь сверхчувственным восприятием, какая карточка выбрана экспериментатором. Карточки перемешиваются. Затем опыт повторяется. Так проделали 100 раз. Оказалось, что в 28 случаях испытуемый правильно назвал карточку. Есть ли основания считать, что имело место сверхчувственное восприятие?
Решение. Естественно предположить, что 28 совпадений произошли случайно. Вероятность угадать нужную карточку равна 1/5. Угадывание каждой карточки можно считать независимым опытом. Так как опытов много (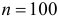
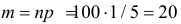
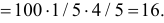
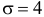
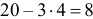
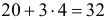
Замечание. Предположим, что экстрасенс все-таки настаивает на своем сверхчуственном восприятии. Серию опытов повторили. Совпадений оказалось 31. В этом случае всего опытов 
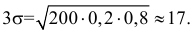
Такое число совпадений при простом угадывании практически невозможно. Это может послужить поводом для тщательной проверки условий эксперимента (подавляющее большинство так называемых экстрасенсов – откровенные жулики). Или следует настоять на лабораторном обследовании экстрасенса (от чего экстрасенсы всячески уклоняются, их стихия – работа на публику).
- Производящие функции
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Функции случайных величин
- Центральная предельная теорема
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
Из данной статьи вы узнаете:
-
Что такое доверительный интервал?
-
Как его самостоятельно рассчитать в Excel? Инструкция с пошаговым описанием и файл с примером!
-
В чем суть правила 3-х сигм?
-
Как можно применить эти знания на практике?
В наше время из-за переизбытка информации, связанного с большим ассортиментом товаров, направлений продаж, сотрудников, направлений деятельности и т.д., бывает трудно выделить главное, на что, в первую очередь, стоит обратить внимание и приложить усилия для управления. Определение доверительного интервала и анализ выхода за его границы фактических значений — методика, которая поможет вам выделить ситуации, влияющие на изменение тенденций. Вы сможете развивать позитивные факторы и снизить влияние негативных. Данная технология применяется во многих известных мировых компаниях.
Существуют так называемые “оповещения”, которые информируют руководителей о том, что очередное значение в определенном направлении вышло за доверительный интервал. Что это означает? Это сигнал, что произошло какое-то нестандартное событие, которое, возможно, изменит существующую тенденцию в данном направлении. Это сигнал к тому, чтобы разобраться в ситуации и понять, что на неё повлияло.
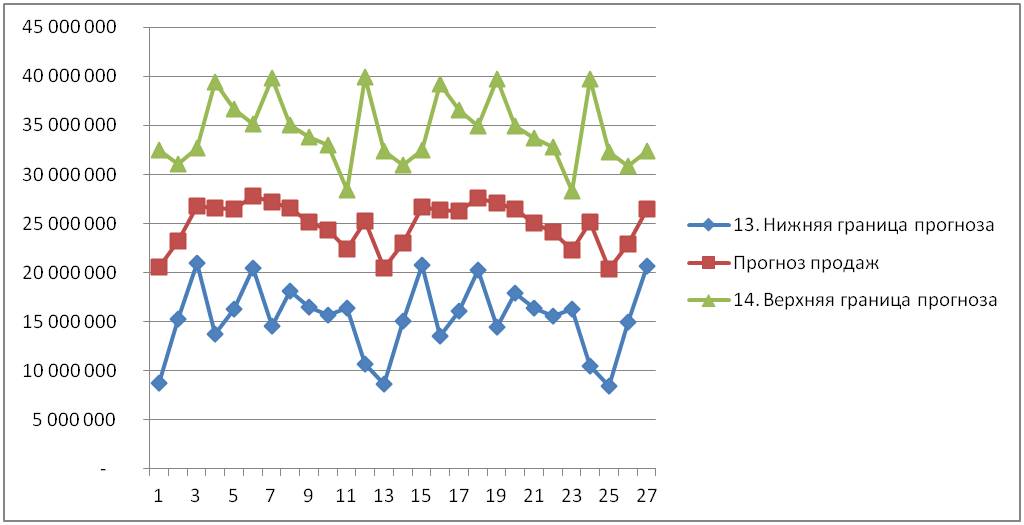
Например, рассмотрим несколько ситуаций. Мы рассчитали прогноз продаж с границами прогноза по 100 товарным позициям на 2011 год по месяцам и в марте фактические продажи:
- По «Подсолнечному маслу» пробили верхнюю границу прогноза и не попали в доверительный интервал.
- По «Сухим дрожжам» вышли за нижнюю границу прогноза.
- По «Овсяным Кашам» пробили верхнюю границу.
По остальным товарам фактические продажи оказались в рамках заданных границ прогноза. Т.е. их продажи оказались в рамках ожиданий. Итак, мы выделили 3 товара, которые вышли за границы, и начали разбираться, что же повлияло на выход за границы:
- По «Подсолнечному маслу» мы вошли в новую торговую сеть, которая дала нам дополнительный объем продаж, что привело к выходу за верхнюю границу. Для этого товара стоит пересчитать прогноз до конца года с учетом прогноза продаж в данную сеть.
- По «Сухим дрожжам» машина застряла на таможне, и образовался дефицит в рамках 5 дней, что повлияло на снижение продаж и выход за нижнюю границу. Возможно, стоит разобраться, что послужило причиной и постараться не повторять данную ситуацию.
- По «Овсяным Кашам» было запущено мероприятие по стимулированию сбыта, которое дало значительный прирост продаж и привело к выходу за границы прогноза.
Мы выделили 3 фактора, которые повлияли на выход за границы прогноза. В жизни их может быть гораздо больше.Для повышения точности прогнозирования и планирования факторы, которые приводят к тому, что фактические продажи могут выйти за границы прогноза, стоит выделить и строить прогнозы и планы по ним отдельно. А затем учитывать их влияние на основной прогноз продаж. Также можно регулярно оценивать влияние данных факторов и менять ситуацию к лучшему за счет уменьшения влияния негативных и увеличения влияния позитивных факторов.
С помощью доверительного интервала мы можем:
- Выделить направления, на которые стоит обратить внимание, т.к. в этих направлениях произошли события, которые могут повлиять на изменение тенденции.
- Определить факторы, которые реально влияют на изменение ситуации.
- Принять взвешенное решение (например, о закупках, при планировании и т.д.).
Теперь рассмотрим, что такое доверительный интервал и как его рассчитать в Excel на примере.
Что такое доверительный интервал?
Доверительный интервал – это границы прогноза (верхняя и нижняя), в рамки которых с заданной вероятностью (сигма) попадут фактические значения.
Т.е. мы рассчитываем прогноз — это наш основной ориентир, но мы понимаем, что фактические значения вряд ли на 100% будут равны нашему прогнозу. И возникает вопрос, в какие границы могут попасть фактические значения, если существующая тенденция сохранится? И на этот вопрос нам поможет ответить расчет доверительного интервала, т.е. – верхней и нижней границы прогноза.
Что такое заданная вероятность сигма?
При расчете доверительного интервала мы можем задать вероятность попадания фактических значений в заданные границы прогноза. Как это сделать? Для этого мы задаем значение сигма и, если сигма будет равна:
-
3 сигма — то, вероятность попадания очередного фактического значения в доверительный интервал составят 99,7%, или 300 к 1, или существует 0,3% вероятности выхода за границы.
-
2 сигма — то, вероятность попадания очередного значения в границы составляет ≈ 95,5 %, т.е. шансы примерно 20 к 1, или существует 4,5% вероятности выхода за границы.
-
1 сигма — то, вероятность ≈ 68,3%, т.е. шансы примерно 2 к 1, или существует 31,7% вероятность того, что очередное значение выйдет за пределы доверительного интервала.
Мы сформулировали правило 3 сигм, которое гласит, что вероятность попадания очередного случайного значения в доверительный интервал с заданным значением три сигма составляет 99.7%.
Великим русским математиком Чебышевым была доказана теорема о том, что существует 10% вероятность выхода за границы прогноза с заданным значением три сигма. Т.е. вероятность попадания в доверительный интервал 3 сигма составит минимум 90%, в то время как попытка рассчитать прогноз и его границы «на глазок» чревата куда более существенными ошибками.
Как самостоятельно рассчитать доверительный интервал в Excel?
Расчет доверительного интервала в Excel (т.е. верхней и нижней границы прогноза) рассмотрим на примере. У нас есть временной ряд — продажи по месяцам за 5 лет. См. Вложенный файл.
Для расчета границ прогноза рассчитаем:
- Прогноз продаж (см. статью «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонностью»).
- Сигма – среднеквадратическое отклонение модели прогноза от фактических значений.
- Три сигма.
- Доверительный интервал.
1. Прогноз продаж.
О том, «как рассчитать прогноз продаж с учетом роста и с сезонностью» подробно описано в данной статье. Поэтому для тех, кто еще не изучал данный материал и не знает, как самостоятельно рассчитать прогноз продаж по месяцам с учетом роста и сезонности, рекомендуем для понимания последующих действий изучить данную статью, а затем перейти к дальнейшему изучению данного материала.
2. Для определения сигма рассчитаем среднеквадратическое отклонение модели прогноза от фактических значений.
Для расчета сигма рассчитаем среднеквадратическое отклонение для каждого месяца.
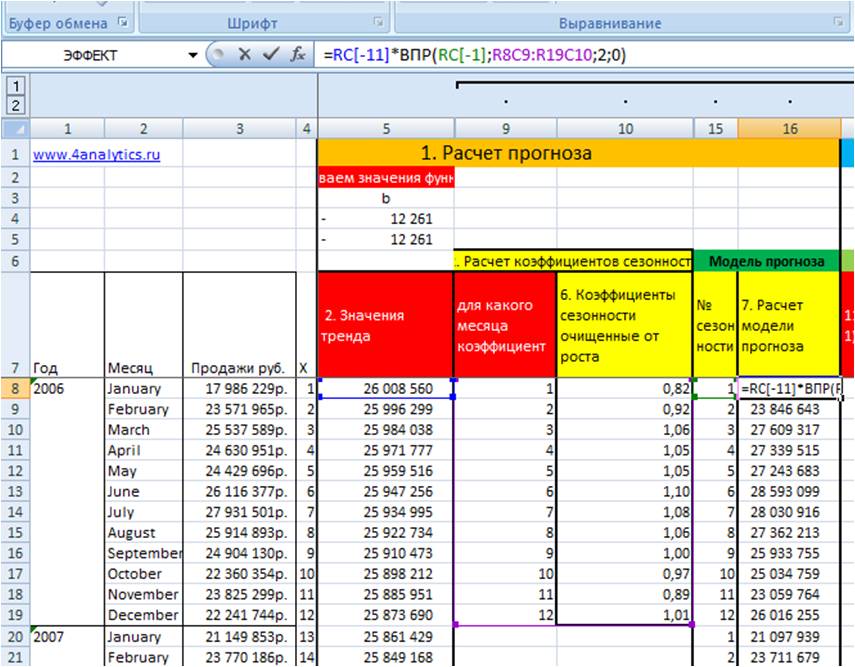
1. Для этого на 7-м шаге во вложенном файле рассчитаем значения прогнозной модели, в нашем случае это прогноз с линейным трендом и сезонностью.
Значение модели = Значение тренда умножим на коэффициент сезонности соответствующего месяца.
В Excel введем формулу:
=RC[-11] (ссылка на тренд)*ВПР(RC[-1];R8C9:R19C10;2;0)(формула ВПР со ссылкой на коэффициент сезонности соответствующего месяца)
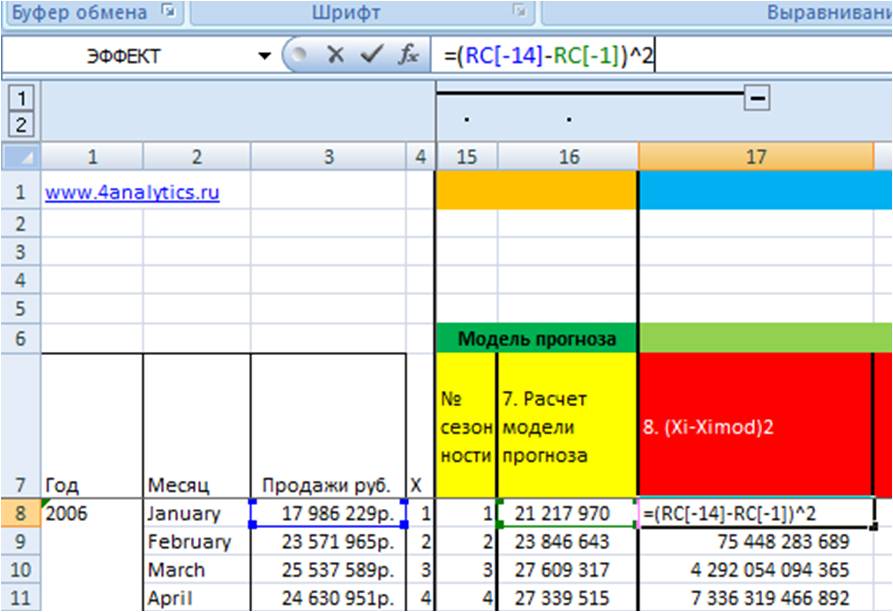
2. Рассчитаем квадрат разницы фактических значений и прогнозной модели (Xi-Ximod)^2 (8 этап во вложенном файле)
=(RC[-14](данные во временном ряду) — RC[-1](значение модели))^2(в квадрате)
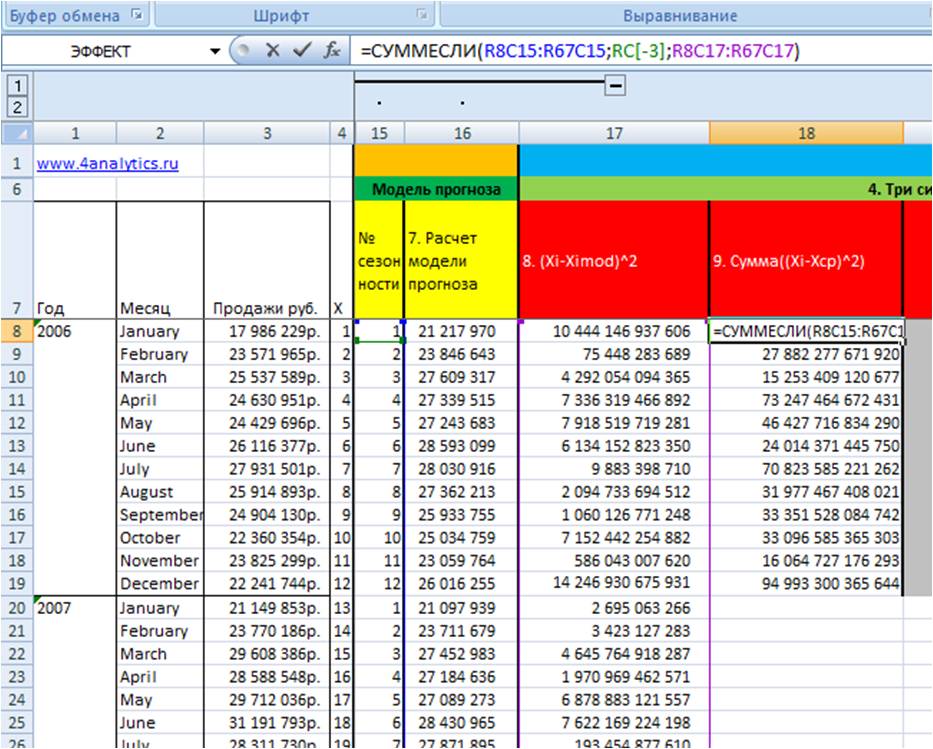
3. Просуммируем для каждого месяца значения отклонений из 8 этапа Сумма((Xi-Ximod)^2), т.е. просуммируем январи, феврали… для каждого года.
Для этого воспользуемся формулой =СУММЕСЛИ()
=СУММЕСЛИ(массив с номерами периодов внутри цикла (для месяцев от 1 до 12);ссылка на номер периода в цикле; ссылка на массив с квадратами разницы исходных данных и значений периодов)
(9 этап во вложенном файле)
4. Рассчитаем среднеквадратическое отклонение для каждого периода в цикле от 1 до 12 (10 этап во вложенном файле).
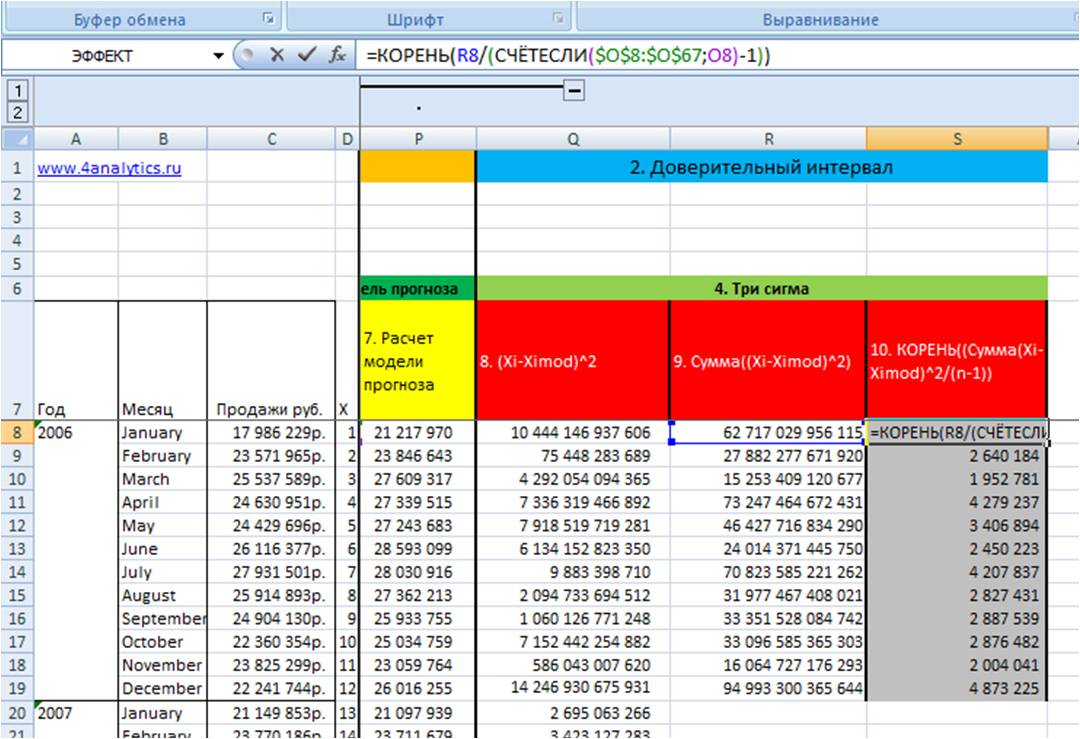
Для этого из значения рассчитанного на 9 этапе мы извлекаем корень и делим на количество периодов в этом цикле минус 1 = КОРЕНЬ((Сумма(Xi-Ximod)^2/(n-1))
Воспользуемся формулами в Excel =КОРЕНЬ(R8 (ссылка на (Сумма(Xi-Ximod)^2)/(СЧЁТЕСЛИ($O$8:$O$67 (ссылка на массив с номерами цикла); O8 (ссылка на конкретный номер цикла, которые считаем в массиве))-1))
С помощью формулы Excel = СЧЁТЕСЛИ мы считаем количество n
Рассчитав среднеквадратическое отклонение фактических данных от модели прогноза, мы получили значение сигма для каждого месяца — этап 10 во вложенном файле.
3. Рассчитаем 3 сигма.
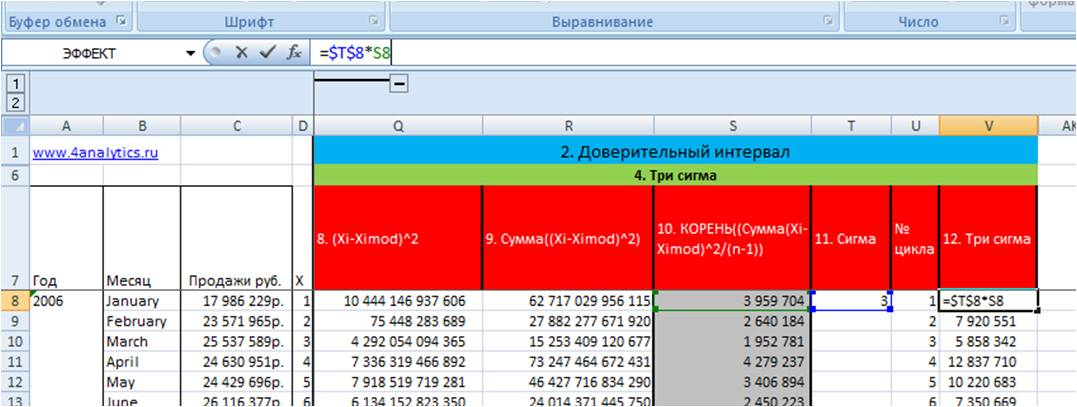
На 11 этапе задаем количество сигм — в нашем примере «3» (11 этап во вложенном файле):
Также удобные для практики значения сигма:
1,64 сигма — 10% вероятность выхода за предел (1 шанс из 10);
1,96 сигма — 5% вероятность выхода за пределы (1 шанс из 20);
2,6 сигма — 1% вероятность выхода за пределы (1 шанс из 100).
5) Рассчитываем три сигма, для этого мы значения «сигма» для каждого месяца умножаем на «3».
3.Определяем доверительный интервал.
- Верхняя граница прогноза — прогноз продаж с учетом роста и сезонности + (плюс) 3 сигма;
- Нижняя граница прогноза — прогноз продаж с учетом роста и сезонности – (минус) 3 сигма;
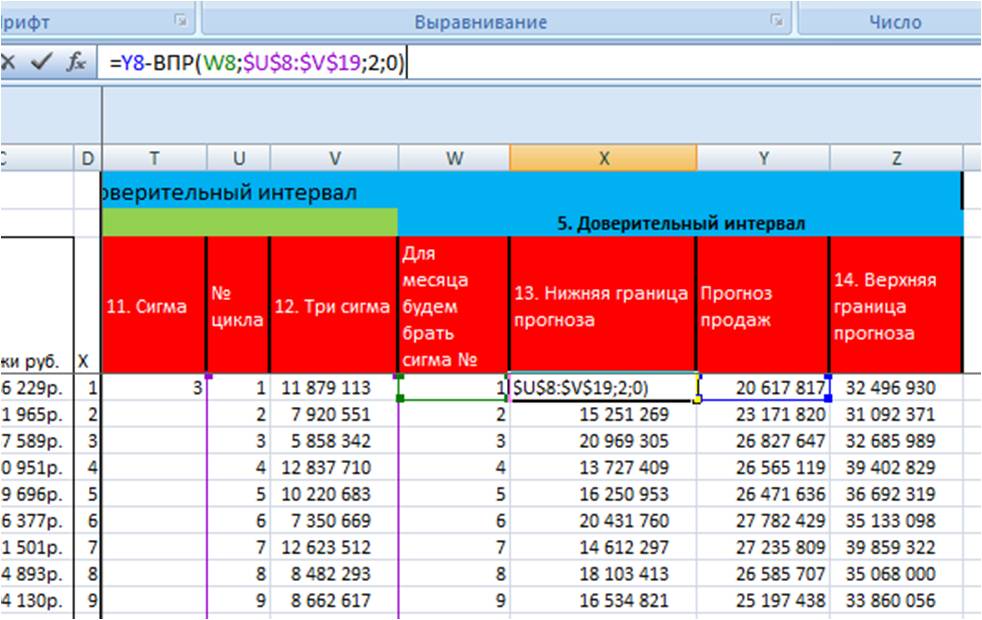
Для удобства расчета доверительного интервала на длительный период (см. вложенный файл) воспользуемся формулой Excel =Y8+ВПР(W8;$U$8:$V$19;2;0), где
Y8 — прогноз продаж;
W8 — номер месяца, для которого будем брать значение 3-х сигма;
$U$8:$V$19 — таблица, из которой с помощью функции =ВПР извлекаем значение 3-х сигма, соответствующее данному месяцу, фиксируем ссылку на таблицу с помощью F4, подробнее в статье “Как зафиксировать ссылку в Excel”.
Т.е. Верхняя граница прогноза = «прогноз продаж» + «3 сигма» (в примере, ВПР(номер месяца; таблица со значениями 3-х сигма; столбец, из которого извлекаем значение сигма равное номеру месяца в соответствующей строке;0)).
Нижняя граница прогноза = «прогноз продаж» минус «3 сигма».
Итак, мы рассчитали доверительный интервал в Excel.
Теперь у нас есть прогноз и диапазон с границами в пределах, которого с заданной вероятностью сигма попадут фактические значения.
В данной статье мы рассмотрели, что такое сигма и правило трёх сигм, как определить доверительный интервал и для чего вы можете использовать данную методику на практике.
Вы можете скачать файл с примером расчета 3-х сигма и границ прогноза
Точных вам прогнозов и успехов!
Чем Forecast4AC PRO может вам помочь при расчете доверительного интервала?:
-
Forecast4AC PRO автоматически рассчитает верхнюю или нижнюю границы прогноза для более чем 1000 временных рядов одновременно;
-
Возможность анализа границ прогноза в сравнении с прогнозом, трендом и фактическими продажами на графике одним нажатием клавиши;
+ В программе Forcast4AC PRO есть возможность задать значение сигма от 1 до 3.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite – автоматический расчет прогноза в Excel.
- 4analytics – ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition – BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO – прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Правило трех сигм
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Напомним для начала следующие факты:
Вспомним формулу для нахождения вероятности того, что отклонение, распределенной по нормальному закону непрерывной случайной величины $X$, от математического ожидания $a$ по абсолютной величине (то есть по модулю) будет меньше $delta $:
среднее
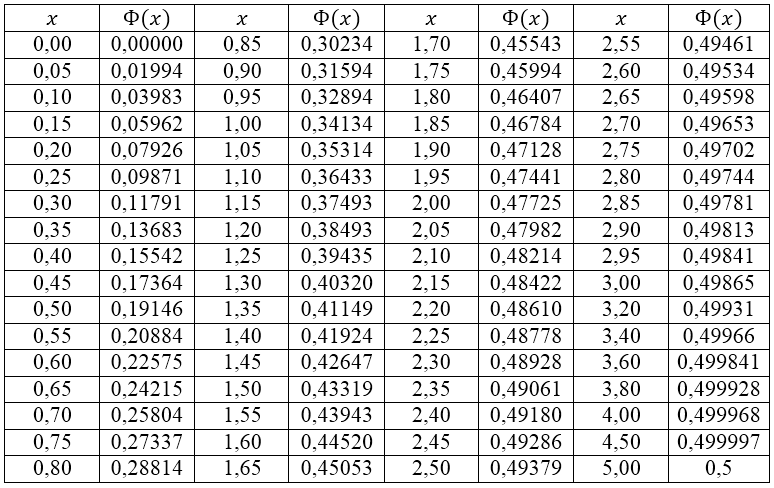
Напомним таблицу нахождения значений интегральной функции (таблица 1)
Рисунок 1. Значения интегральной функции $Ф(x)$.
Теперь найдем, чему будет равна вероятность того, что отклонение, распределенной по нормальному закону непрерывной случайной величины $X$, от математического ожидания $a$ по абсолютной величине (то есть по модулю) будет меньше $3sigma $, то есть:
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
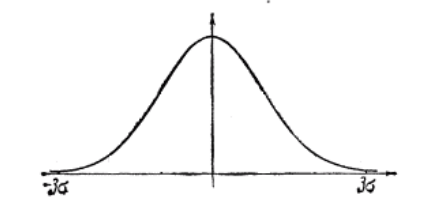
Геометрически этот факт можно представить следующим образом:
Рисунок 2.
Из всего вышесказанного сформулируем следующее правило:
Правило трёх сигм: Если непрерывная случайная величина $X$ распределена по нормальному закону, то абсолютная величина её отклонения от математического ожидания $a$ не превосходит утроенного значения среднего квадратического отклонения $sigma $.
Примеры решения задач на применение правила трех сигм
Пример 1
Длина изготавливаемого стержня подчинена нормальному закону распределения. Математическое ожидание $a=1$ м, а среднее математическое отклонение $sigma =0,01$ м. Найти границы, пределах которых гарантируется длина стержня.
Решение.
Для решения задачи воспользуемся правилом трех сигм:
[Pleft(|X-a|
Пример 2
Текущая цена на молоко подчинена нормальному закону распределения. Математическое ожидание $a=25$ рублей, а среднее математическое отклонение $sigma =1$ рубль. Найти границы, в которых будет находиться текущая цена нам молоко.
Решение.
Для решения задачи воспользуемся правилом трех сигм:
[Pleft(|X-a|Так как случайная величина (цена) распределена по нормальному закону, то
[Pleft(left|X-25right|Ответ: (22,28).
Пример 3
На заводе изготавливают шурупы для ноутбуков. Размер диаметра шурупа распределен по нормальному закону распределения с математическим ожиданием $a=0,2 $см и средним квадратическим отклонением $sigma =0,02$ мм. В каких границах можно практически 100% гарантировать размер шурупа?
Решение.
Вначале приведем все величины к одному измерению:
$a=0,2 $см$=2$ мм.
Так как случайная величина подчинена нормальному закону распределения, то мы можем применить правило трех сигм:
[Pleft(left|X-2right|Ответ: (1,94, 2,06)
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 20.02.2023