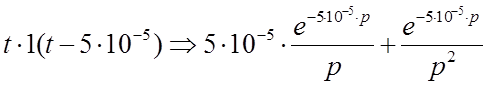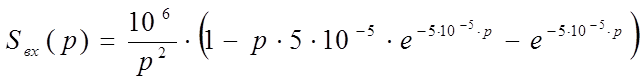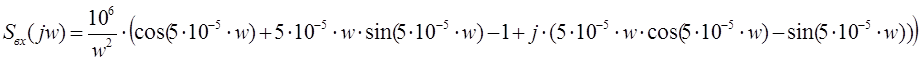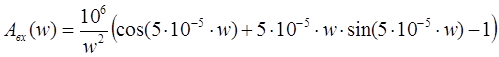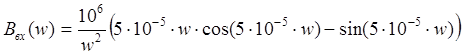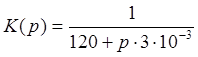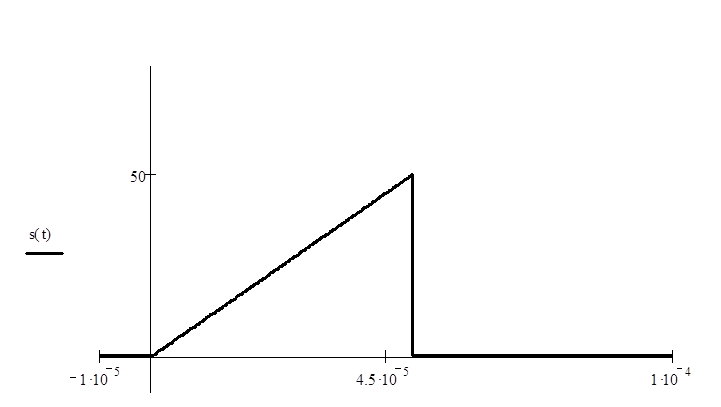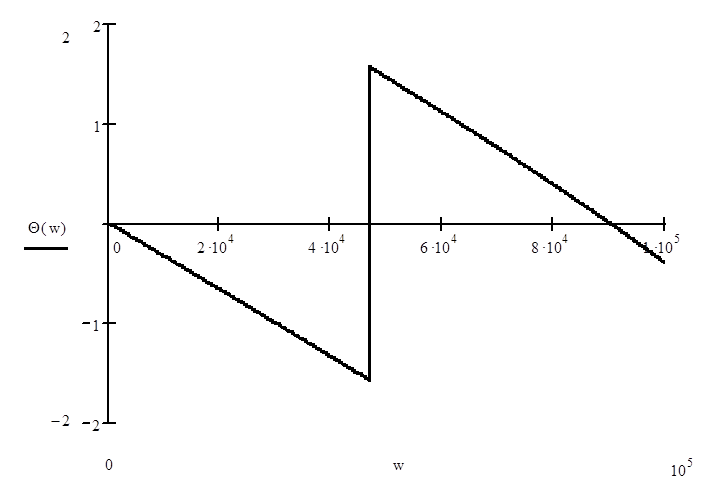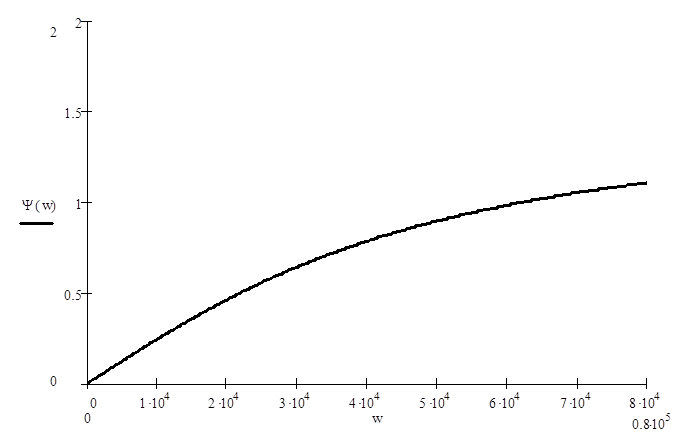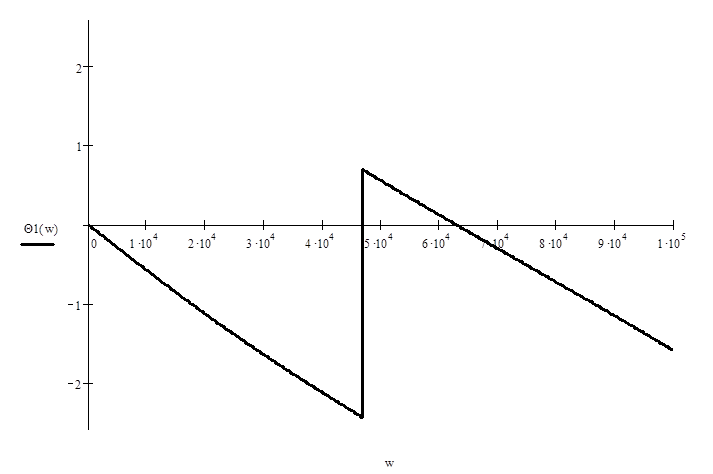Как найти сигнал по изображению - Сайт, где вы сможете решить свои вопросы

Преобразование Лапласа и его свойства

Основные определения

Свойства преобразования Лапласа

Запаздывание оригинала

Дифференцирование оригинала

Интегрирование оригинала

Дифференцирование изображения

Интегрирование изображения

Умножение изображений (теорема Бореля)

Дифференцирование свертки (интеграл Дюамеля)

Теорема о связи “начальных” и “конечных” значений оригинала и изображения

Нахождение изображения по оригиналу

Нахождение изображений функций, заданных графиком

Нахождение изображений периодических функций

Нахождение оригинала по изображению

Применение таблицы и свойств преобразования Лапласа

Преобразование Лапласа и его свойства

Основные определения

Свойства преобразования Лапласа

Запаздывание оригинала

Дифференцирование оригинала

Интегрирование оригинала

Дифференцирование изображения

Интегрирование изображения

Умножение изображений (теорема Бореля)

Дифференцирование свертки (интеграл Дюамеля)

Теорема о связи “начальных” и “конечных” значений оригинала и изображения

Нахождение изображения по оригиналу

Нахождение изображений функций, заданных графиком

Нахождение изображений периодических функций

Нахождение оригинала по изображению

Применение таблицы и свойств преобразования Лапласа

5.4.1. Классический метод

5.4.2. Временной метод

5.4.3. Спектральный метод

5.4.4. Операторный метод

5.4.1. Классический метод

5.4.2. Временной метод

5.4.3. Спектральный метод

5.4.4. Операторный метод

Вам также может понравиться

Как найти зарегистрированного одноклассника

Не работает смарт тв на телевизоре самсунг как исправить

Как найти фургон для мамы гта 5

Добавить комментарий Отменить ответ

5.4.1. Классический метод

5.4.2. Временной метод

5.4.3. Спектральный метод

5.4.4. Операторный метод

Основной задачей анализа является определение реакции (выходного) сигнала цепи при действии на её входе сигнала известной формы. При этом, входной сигнал может быть описан как во временной, так и в частотной области. В связи с этим различают следующие методы анализа: классический, временной (или метод интеграла наложения), спектральный и операторный. Выбор того или иного метода зависит от структуры цепи, вида воздействующего на неё сигнала, формы представления (временная или частотная) входного сигнала.

Классический метод основывается на решении дифференциального уравнения вида (5.16), описывающего линейную цепь. Решение этого уравнения представляет собой сумму двух слагаемых

, (5.19)

где первое слагаемое представляет собой общее решение однородного дифференциального уравнения

, (5.20)

а второе слагаемое – частотное решение (5.16) при , где – правая часть уравнения (5.16). Физически – свободная составляющая полного отклика (выходного сигнала), представляет собой реакцию цепи на отключение(или включение) входного сигнала и характеризует переходные процессы в цепи. Второе слагаемое – вынужденная составляющая, является реакцией цепи после окончания переходных процессов и характеризует установившейся(стационарный) режим преобразования цепью входного сигнала. Обычно, классический метод используется для изучения переходных процессов, что приводит к необходимости решения уравнения (5.20). Общее решение однородного уравнения (5.20) имеет вид

, (5.21)

где , ,…, – постоянные коэффициенты, определяемые начальными условиями,

, ,…, – корни характеристического уравнения:

. (5.22)

Это уравнение имеет ровно n корней, при этом корни могут быть либо вещественными, либо комплексными, что определяет характер переходных процессов. Что же касается , то если входной сигнал является постоянным или периодическим, то после окончания переходных процессов выходной сигнал принимает форму входного сигнала. Так, если представляет собой гармонический сигнал, то также будет гармоническим, отличаясь от входного сигнала амплитудой и начальной фазой.

В качестве примера рассмотрим, что собой представляет отклик RC-цепи (рис. 5.3,8) на входной сигнал вида .

Дифференциальное уравнение цепи (5.15) перепишем в виде

где – постоянная времени.

Поскольку дифференциальное уравнение имеет порядок n=1, решение однородного уравнения

согласно (5.21), запишется в виде

где – корень характеристического уравнения

откуда следует . Тогда

До поступления входного сигнала ёмкость С разряжена. В момент поступления входного сигнала (скачка) ёмкость не может мгновенно зарядиться до , это произойдёт по мере перехода к установившемуся режиму. Очевидно в установившемся режиме

Таким образом, суммарный выходной сигнал

Коэффициент найдём из начальных условий. Начальными условиями при исследовании линейных цепей называют значения токов в индуктивностях и напряжений на емкостях в момент времени . Так как в этот момент времени , то можно записать

Откуда следует . Тогда окончательно суммарный выходной сигнал

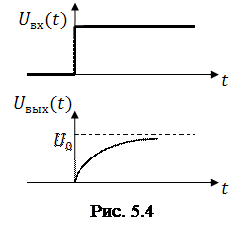
На рис. 5.4. изображены эпюры напряжений на входе и выходе исследуемой RC-цепи.

Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( – функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы.

Выберем в качестве элементарного сигнала – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом

Очевидно, выходной сигнал

Так как оператор не зависит от времени, его можно внести под знак интеграла. Тогда, с учётом (5.5)

. (5.23)

Если момент появления входного сигнала , то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид

. (5.24)

Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента и заканчивая текущим моментом времени . Роль весовой функции выполняет импульсная характеристика цепи.

Выражение (5.24) носит название интеграла Дюамеля. Это выражение было получено в предположении, что входной сигнал представлен в виде суммы элементарных сигналов вида – функций. Если входной сигнал представить в виде (1.15) комбинаций сигналов вида единичного скачка, то можно получить другие формы интеграла Дюамеля, в частности

. (5.25)

Здесь – переходная характеристика цепи.

Итак, для использования метода интеграла наложения необходимо знать импульсную характеристику или переходную характеристику . Эти характеристики можно определить несколькими способами. Прямой (непосредственный способ состоит в решении дифференциального уравнения (5.20) в предположении, что входной сигнал является очень коротким импульсом(для определения импульсной характеристики) или сигналом вида единичного скачка( для определения переходной характеристики).

В выше приведённом примере было решено дифференциальное уравнение и найден отклик RC-цепи на воздействие сигнала

Очевидно, форма отклика не изменится, если входной сигнал будет единичным скачком, при этом масштаб отклика изменится в раз. Тогда выходной сигнал

, (5.26)

поскольку реакция цепи на единичный скачок является переходной характеристикой. В соответствии с (5.7) определяется импульсная характеристика

(5.27)

Второй способ определения импульсной или переходной характеристики, назовём его косвенным, состоит в использовании однозначного соответствия между импульсной характеристикой и комплексным коэффициентом передачи.

При рассмотрении характеристик линейной цепи было получено соотношение (5.10), связывающее спектральные характеристики входного и выходного сигнала с комплексным коэффициентом передачи цепи. Это соотношение лежит в основе спектрального анализа. Если задачей анализа является определение частотных характеристик выходного сигнала, то при известных и использование (5.10) полностью решает эту задачу. В ряде случаев сигнал представлен во временной области и требует найти отклик цепи как функцию времени. При этом использование метода интеграла наложения может быть затруднено сложностью нахождения импульсной характеристики цепи. В то же время комплексный коэффициент передачи найти достаточно просто. Тогда спектральный метод анализа сводится к следующим операциям:

– для входного сигнала прямым преобразованием Фурье находится комплексный спектр ;

– определяется комплексный коэффициент передачи цепи ;

– в соответствии с (5.10) определяется комплексный спектр выходного сигнала ;

– обратным преобразованием Фурье вычисляется форма сигнала на выходе цепи.

Итак, важнейшим условием использования спектрального метода является знание комплексного коэффициента передачи исследуемой цепи. Найти комплексный коэффициент передачи можно, используя методы теории цепей (метод узловых потенциалов или метод контурных токов). Если известно аналитическое описание цепи дифференциальным уравнением (5.16), то комплексный коэффициент передачи находится в соответствии с (5.18). Наконец, цепь можно представить в виде делителя напряжения, элементами которого являются комплексные сопротивления

; ; .

Проиллюстрируем последний подход на примере уже рассматривавшейся выше RC-цепи. Если представить цепь как делитель напряжения, то выходной сигнал представляет собой напряжение на ёмкости С. Тогда, если комплексный ток, протекающий в цепи, то

и комплексный коэффициент передачи

что совпадает с результатом, полученным в подразделе 5.3.

Операторный метод является обобщением спектрального метода. В основе метода лежит преобразование Лапласа. Рассмотрим некоторый сигнал , определённый на интервале времени (0, ). Умножим этот сигнал на и полученный новый сигнал подвергнем преобразованию Фурье

Обозначая через , получим

. (5.28)

Выражение (5.28) называется односторонним преобразованием Лапласа функции . При этом, называют оригиналом, а изображением.

Нетрудно убедиться, что при выражение (5.28) преобразуется к виду

что соответствует преобразованию Фурье. Таким образом если преобразование Фурье представляет собой спектральное разложение сигнала по гармоническим составляющим , то преобразование Лапласа – разложение сигнала по экспоненциально – косинусным составляющим . Действительно, представим

Здесь использована формула Эйлера

С другой стороны

где .

Тогда окончательно

представляет собой экспоненциально – косинусную функцию.

Переход от изображения к оригиналу осуществляется при помощи обратного преобразования Лапласа

. (5.29)

Для значительной части функций широко используемых при описании оригиналов были рассчитаны изображения по Лапласу. Некоторая часть оригиналов и изображений приведена в таблице 5.1.

Поскольку преобразование Лапласа является обобщением преобразования Фурье, то оно обладает теми же свойствами, что и преобразование Фурье. Остановимся на некоторых из них, которые будем использовать в дальнейшем. Пару преобразований (прямое и обратное) будем обозначать следующим образом

1. Линейность преобразований Лапласа

(5.30)

2. Свойство временного сдвига

(5.31)

3. Операция дифференцирования

; (5.32)

4. Операция интегрирования

. (5.33)

Применим к обеим частям уравнения (5.16) прямое преобразования Лапласа. Тогда с учётом (5.32), получим

(5.34)

откуда следует

. (5.35)

Это отношение называется передаточной функцией цепи или её операторным коэффициентом. Таким образом, передаточная функция является оператором преобразования линейной цепью в базисе экспоненциально – косинусных сигналов.

Сравним выражение комплексного коэффициента передачи (5.18) с выражением (5.35). Из этого сравнения следует, что комплексный коэффициент передачи является частным случаем при , т.е.

(5.36)

Таким образом, если известна передаточная функция цепи, то операторный метод поиска отклика цепи состоит в следующем:

– находится изображение по Лапласу входного сигнала

; (5.37)

– находится изображение выходного сигнала как произведение

; (5.38)

– определяется оригинал выходного сигнала

. (5.39)

Установим связь между временными характеристиками и передаточной функцией. Произведя в (5.12) замену на , получим

Таким образом, передаточная функция и импульсная характеристика связаны между собой преобразованием Лапласа

Что касается переходной характеристики, то применяя к (5.8) преобразование Лапласа и учитывая (5.33), получим

В заключение отметим, что операторный метод позволяет сводить линейные дифференциальные уравнения вида (5.16) к алгебраическим уравнениям (5.34), что позволяет в ряде случаев упростить анализ цепей. Помимо этого, учитывая широкое распространение таблиц преобразований Лапласа для большого числа функций, можно исключить громоздкие вычисления, непосредственно обращаясь к этим таблицам.

Рассмотрим применение операторного метода на примере анализа определения отклика RC-цепи на входной сигнал вида . Эта задача была решена классическими временными методами. Спектральным методом был найден комплексным коэффициент передачи. Заменив в выражении для цепи на , получим передаточную функцию цепи

Следуя операторному методу найдём изображение по Лапласу входного сигнала, воспользовавшись при этом таблицей 5.1

Далее, в соответствии с (5.38), определим изображение выходного сигнала

И наконец, по таблице 5.1 (позиция 5) находим оригинал

что совпадает с полученными ранее результатами.

Источник

величинах легко пересчитываются к конкретным значениям параметров. Для этого достаточно умножить нормированные величины на их базисные значения, произведя денормирование.

3.3.Контрольные вопросы

1.Что называют переменными состояния?

2.Какие способы составления уравнений состояния Вы знаете?

3.Каковы преимущества метода переменных состояния по сравнению

сдругими методами анализа во временной области?

4.Что такое передаточная функция цепи и какие способы расчета передаточных функций Вы знаете?

5.Что такое переходная и импульсная характеристики цепи и какова их связь с передаточной функцией?

6.Почему полюсы передаточной функции пассивной цепи расположены в левой полуплоскости?

7.Как найти сигнал по изображению U (s) = (1+ e−πs )/(s2 +1)?

8.Как найти изображение сигнала

u(t) = 2e−3tδ1(t) + 4e−3t(t−2)δ1(t − 2)?

9.Как по изображению U (s) = (2s2 + s +1) / (s3 + s2 ) определить на-

чальное значение оригинала u(0 +) и начальное значение его производной u′(0 +) ?

10. Как по известным полюсам s1,2 = −2, s3,4 = ± j2 изображения сиг-

нала записать его общую форму во времени?

11.Как проверить предельные значения АЧХ и ФЧХ исследуемой цепи при ω → 0 и ω → ∞ исходя из свойств цепи?

12.Каково условие неискаженной передачи сигнала через цепь? Удовлетворяет ли Ваша цепь этому условию?

13.Как изменится амплитудный спектр апериодического сигнала при изменении его длительности; амплитуды?

14.Какова связь спектра одиночного сигнала со спектром периодической последовательности этих сигналов?

15.Как влияет скважность периодического сигнала на спектр?

3.4.Типовой пример

Для цепи, изображенной на рис. 3.3, выполним задания курсовой работы. Параметры ветвей R1 = R2 = R3 = Rн = 1 Ом, С = 1 Ф, L = 0,5 Гн.

Rн

Рис. 3.3

1. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях

Дано u0 (t) =U0 =10B; i0 (t) = I0δ1(t) =10δ1(t) A. Выполнить п. 1 задания к курсовой работе. Переменными состояния следует принять iL (t) и uC (t). Для формирования уравнений состояния заменим в исходной цепи для t > 0 все L-элементы источниками тока с токами iL (t) и все С-элемен- ты – источниками напряжения с напряжениями uC (t). Тогда цепь будет иметь вид, показанный на рис. 3.4.

R1	1	R2	2	iL
3
		iC		uL

u0		uC	R3	i0	RH

Рис. 3.4

В полученной цепи одним из методов анализа R-цепей найдем напряжение uL (t) введенного источника тока и ток iC (t) – источника напряжения. Воспользуемся методом узловых напряжений [1,2]. Примем четвертый узел базисным, считая U(4) = 0. Тогда напряжение первого узла определяется сразу u(1) = uC (t). Для определения неизвестных u(2) и u(3) за-

пишем уравнения узловых напряжений для 2-го и 3-го узлов:

+ G22u(2) + G23u(3) = i(2);

(3.1)

+ G32u(2) + G33u(3) = i(3).

Определим коэффициенты уравнений и правые части:

G =

= 2; G =

=1; G = −

= −1;

G = G = 0; G = 0; i

= −i

(t); i

= I

+ i (t).

(

(3)

Систему уравнений (3.1) перепишем в следующем виде:

−u

(t) + 2u

= −i

(t);

(2)

= I

+ i

(t),

(3)

отсюда u

= 0,5u

(t) − 0,5i

(t);

= I

+ i

(t).

(2)

(3)

Напряжение u

(t) введенного источника тока:

(t) = u

− u

= 0,5u

(t) −1,5i (t) −10.

(3.2)

(2)

(3)

Ток i

(t) введенного источника напряжения:

− u (t)

(t) − u

(t)

(t) = i

+ i

(2)

= −1,5u

(t)

− 0,5i

(t) +

10. (3.3)

Так как

/ dt = u

(t) / L , то, разделив (3.2) на L, получим первое

уравнение состояния; учитывая, что du

(t) / dt = i

(t)

/ C, разделив (3.3)

на С, получим второе уравнение состояния:

diL

= u

(t) − 3i

(t) −

20,

(3.4)

duC

= −1,5u

(t)

− 0,5i

(t) +10.

Найдем

точное

решение

этих

уравнений. Определим

независимые

предначальные условия, рассмотрев установившийся режим в исходной

цепи для t < 0: u	(0 −) = 6 B, i	L	(0 −) = 2 A.
C
Для определения частот собственных колебаний алгебраизируем
уравнения состояния (3.4):
		( p + 3)i	L	− u	= −20,
					C	(3.5)
			+ ( p +1,5)u
		=10,
	0,5i	L
					C

причем в системе (3.5) p = d / dt. Характеристическое уравнение получим, приравнивая нулю главный определитель системы (3.5):

( p) = ( p + 3)( p +1,5)+ 0,5 = p2 + 4,5p + 5 = 0.

(3.6)

Из (3.6) частоты собственных колебаний p1 = −2, p2 = −2,5. Общий вид точных решений уравнений состояния:

(t)

= i

+ i

= i

A e−2t

+ A e−2,5t

;

Lв

Lсв

Lв

(3.7)

(t) = u

+ u

= u

A e−2t

+ A e−2,5t.

Cв

Cсв

Cв

Вынужденные составляющие

iLв = ILв = const, uCв =UCв = const оп-

ределим из уравнений состояния (3.4):

0 =UCв − 3ILв − 20;

= −1,5UCв − 0,5ILв +10;

отсюда

ILв = −4A, UCв = 8B. Для определения постоянных интегрирова-

ния найдем начальные значения производных из уравнений (3.4):

i′ (

0 +) = u

(

0 +) − 3i

(0 +) − 20 = 6 − 6 − 20 = −20;

u′ (0 +) = −1,5u

(0 +) − 0,5i

(0 +) +10 = −9 −1+10 = 0.

На основании решений (3.7) при t = 0+ составим уравнения, необхо-

димые для определения постоянных интегрирования А1 и А2:

(

0 +) = −4 + A + A = 2;

(3.8)

i′

(

0 +) = −2A

−

2,5A = −20,

а затем – систему для определения А3 и А4:

(0 +) = 8 + A + A = 6;

(3.9)

u′

(0 +) = −2A

− 2,5A

После отыскания из систем (3.8), (3.9) постоянных интегрирования

получим точные решения уравнений состояния:

(t) = −4 −10e−2t +16e−2,5t;

(t) = 8 −10e−2t + 8e−2,5t.

Для численного решения уравнений состояния воспользуемся алго-

ритмом Эйлера:

[(n +1)h]= i

(nh) + h

diL

= i

(nh)

+ h u

(nh) − 3i

(nh) − 20 ;

t=nh

duC

[(

n +

)

]

(

)

= u

(

)

+ h

−1,5u

(

)

− 0,5i

(

)

+10 ,

h = u

+ h

t=nh

где h – шаг расчета, n = 0, 1, 2, 3,…. Взяв, например, h = 0,1 с, получим:

iL [(n +1)h] = 0,7iL (nh) + 0,1uC (nh) − 2;

uC [(n +1)h]= −0,05iL (nh) + 0,85uC (nh) +1.

На рис. 3.5 а, б построены графики точного (кривая 1) и численного (кривая 2) решений. Как видно, для uC (t) точное и численное решения в принятом масштабе практически совпадают.

2.Анализ цепи операторным методом при апериодическом воздействии

Дано: в цепи рис. 3.3 i0 (t) = 0; u0 (t) задано графиком рис. 3.6, а, где

Um =10B, tи = 5c. Независимые предначальные условия нулевые. Требуется выполнить п. 2 задания.

Применяя метод пропорциональных величин к операторной схеме замещения, построенной на основании схемы рис. 3.3, находим функцию передачи HU (s) =Uн (s) /U0 (s) =1/ (s2 + 4,5s + 5).

Полюсы функции передачи являются корнями уравнения s2 + 4,5s +

+5 = 0, откуда s1 = –2; s2 = –2,5. Они являются корнями характеристиче-

ского уравнения (частотами собственных колебаний цепи). Конечных нулей функция передачи не имеет.

iL							uC
	2

									8
	1


										6
		0		1		2
					t, c



									4
–1



										2
–2


			2
–3

							0		1		2
			1						t, c




–4
						a					б
								Рис. 3.5

Импульсная характеристика

	h(t) = L	−1 H	(s) = 2e−2t	− 2e−2,5t.
			U
Переходная характеристика
h	(t) = L −1 H	(s)	/ s = 0,2 − e−2t + 0,8e−2,5t.
1		U

Графики h(t) и h1(t) показаны на рис. 3.6, б.

h1, h

0,2

0,1

0,5

1,0

1,5

2,0

t, c

Рис. 3.6

Изображение заданного входного напряжения

(s) =

−

−st

−

−5s

Изображение выходного напряжения

(s)

= H

(s)U

(s) =

−

10e−5s

s(s2 + 4,5s + 5) s(s2 + 4,5s + 5)

Оригинал выходного напряжения

(t) = (2 −10e−2t + 8e−2,5t

)δ

(t)

− (2 −10e−2(t−5)

+ 8e−2,5(t−5) )δ

(t − 5).

1 2

4 5

Рис. 3.7

На рис. 3.7 построены графики входного u0 (t) и выходного uн (t) напряжений.

3. Качественный анализ цепи частотным методом при апериодическом воздействии

По условиям п. 2 задания требуется выполнить п. 3. Обобщенная частотная, т. е. амплитудно-фазовая, характеристика

Амплитудно-частотная характеристика

HU ( jω) =1/ (5 − ω2 )2 + (4,5ω)2 =1/ ω4 +10,25ω2 + 25.

Фазочастотная характеристика

Φн (ω) = −arctg 4,5ω / (5 − ω

) .

Графики АФХ, АЧХ и ФЧХ показаны на рис. 3.8, а, б соответственно.

Полоса

пропускания,

определенная

по

графику

HU ( jω)

Δω

1,5c−1.

0,707

Спектральная плотность входного напряжения

( jω)

= U

(s)

= A (ω)e jα0(ω),

s= jω

где

A (ω) – амплитудный, α

(ω) – фазовый спектры воздействия;

U0 ( jω)

(1− e− jωtu )=

sin2,5ω e− j2,5ω

(3.10)

jω

Из выражения (3.10) следует, что амплитудный спектр

A (ω) =

sin 2,5ω

фазовый спектр

α0 (ω) = −2,5ω, если sin2,5ω > 0;

−2,5ω + π, если sin2,5ω < 0.

jImH(jω)

ω = ∞

			0,1
ω = 5



	ω = 3

	ω = 2,5

		ω = 2		ω = 1

ω = 1,5

			\|H(jω)\|

		0,2

	0,14

	0,1

							Δω

		ω = 0

0,2				0		1		2	3		4		5	6
ReH(jω)								ω, с–1

			Фн(ω)


	ω = 0,5				1			2		3		4		5	6
											ω

−π

Рис. 3.8

Графики спектров A0 (ω) и α0 (ω) показаны на рис. 3.9. Ширина спектра, определенная по графику по 10%-му критерию, Δω0 3,4c−1.

А0				α (ω)
				0
50
				0
25				1	2	3 ω, c–1

				–π
0	1	2	3	4 ω

∆ω0

Рис. 3.9

Сопоставляя спектры входного сигнала (рис. 3.9) с частотными характеристиками цепи (рис. 3.8, б), можно установить, что существенная часть амплитудного спектра входного сигнала укладывается в полосу пропускания, а фазочастотная характеристика в этой полосе близка к линейной. Поэтому при прохождении через цепь входной сигнал будет сравнительно мало искажен. Поскольку при ω → ∞ АЧХ равна нулю, можно ожидать

увеличения длительности переднего и заднего фронтов выходного импуль-
са по сравнению с входным. Этот качественный вывод подтверждается
точным расчетом в п. 2 (см. рис. 3.7).
			4. Анализ цепи частотным методом
			при периодическом воздействии
	Цепь, подлежащая анализу, задана в п. 2. Периодическое напряжение
u (t)	задано графиком рис. 3.10, а, где U	m	=10B, t	и	= 5c, T = 2t =10c.
0							и
Требуется выполнить задание п. 4.
		u0
		Um
Ak	0	tи				t

10	A0	T	a	Akн
	8	A1			2 A0
	6					A1
	4		A3	A5	1			A3
	2						A5
	0	ω1	3ω1	5ω1 ω	0	ω1	3ω1	5ω1 ω

αk				αkн

	0			ω					ω

	π	α1	α3	α5	− π	α1
−	2			α3
2				−π
						α5


		б				в
				Рис. 3.10

Для разложения в ряд Фурье периодической последовательности им-

пульсов найдем комплексные амплитуды гармоник ряда:

A =	2	U	( jω)	,

k	T 0		ω=kω1

где ω1 = 2π/T = 0,2π – частота первой гармоники, k = 0, 1, 2, … U0(jω) определено в (3.10).

В примере получим

A	=		20	sin	kπ	e− jkπ/2	= A exp( jα	).
		k
k						k
		kπ		2

Значения Ak и αk приведены в табл. 3.5; на рис. 3.10, б построены дискретные амплитудный и фазовый спектры.

					Таблица 3.5

k	Ak	αk	k	Ak	αk
0	10	–	4	0	–
1	6,366	–π/2	5	1,273	–π/2
2	0	–	6	0	–
3	2,122	–π/2	7	0,909	–π/2

Таким образом, в соответствии с шириной спектра аппроксимирующий отрезок ряда Фурье u0a (t), описывающего периодическое воздействие u0 (t), имеет вид

		A	n					π
u0a	=	0	+ ∑ Ak cos(kω1t + αk ) = 5 + 6,366cos	0,2πt −		+

	2	k=1					2
				π	π
			+2,122cos 0,6πt −		+1,273cos πt −		.

				2	2

Амплитуды и начальные фазы гармоник выходного напряжения

Akн = HU ( jkω1) Ak; αkн = Φн (kω1)+ αk (kω1),

т. е. необходимо вычислить значения АЧХ и ФЧХ функции передачи для требуемых частот kω1; k = 0, 1, 2, … . Результаты всех вычислений сведены в табл. 3.6.

					Таблица 3.6

k	kω1,c−1	HU ( jkω1)	Φн (kω1),рад	Akн,В	αkн,рад

0	0	0,2	–	2	–
1	0,2π	0,185	–0,55	1,178	–2,12
2	0,6π	0,116	–1,4	0,246	–2,97
3	π	0,067	–1,9	0,085	–3,47

Дискретные амплитудный и фазовый спектры выходного сигнала построены на рис. 3.10, в.

Пренебрегая пятой гармоникой, имеем

() A0н n ( )

нt + ∑ Akн cos kω1t + αkн =

2 k=1

=1+1,178 cos(0,2πt − 2,12) + 0,246 cos(0,6πt − 2,97).u

Соседние файлы в предмете Теоретические основы электротехники

#
09.02.201511.97 Mб46TOE-Spravochnik.djvu
#
#
#
#
#
#
#
#
#

Источник

I Задание: С
помощью спектрального метода проанализировать изменение формы сигнала,
проходящего через линейную цепь.

Операторный метод анализа:

1.
Определение изображения входного
сигнала S_вх(t)÷S_вх(p).

2.
Замена АЧХ и ФЧХ цепи Z(w) и
Ψ(w) на операторное изображение K(p).

3.
Определение изображения выходного
сигнала S_вых(p)=K(p)S_вх(p).

4.
Определение выходного отклика цепи
S_вых(t) ÷S_вых(p).

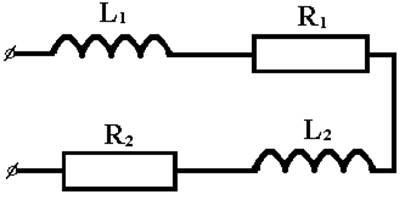
R₁=0.02 кОм; R₂=0.1 кОм

L₁=1мГн; L₂=2мГн

-входной
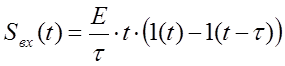
сигнал (рис. 1).

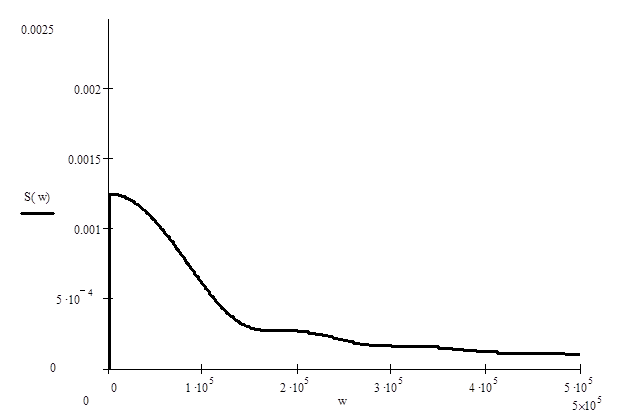
II 1). Найдем форму спектральной плотности входного сигнала:

Используя
таблицу преобразования Лапласа, находим изображение входного сигнала S_вх(p):

;

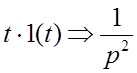
Отсюда:

Для
того чтобы найти модуль и фазу спектра входного сигнала, заменим p
на jw.

– амплитуда спектра входного сигнала (рис.
2).

– фаза спектра входного сигнала (рис. 3).

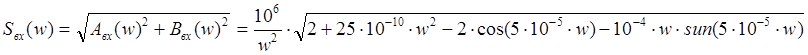
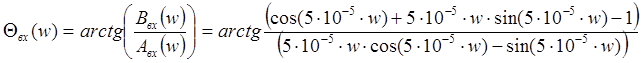
2).
На основе цепи найдем переходную характеристику:

Найдем переходную характеристику цепи K(p), она равна 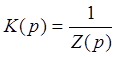, где Z(p) – комплексное сопротивление цепи.

отсюда

Найдем
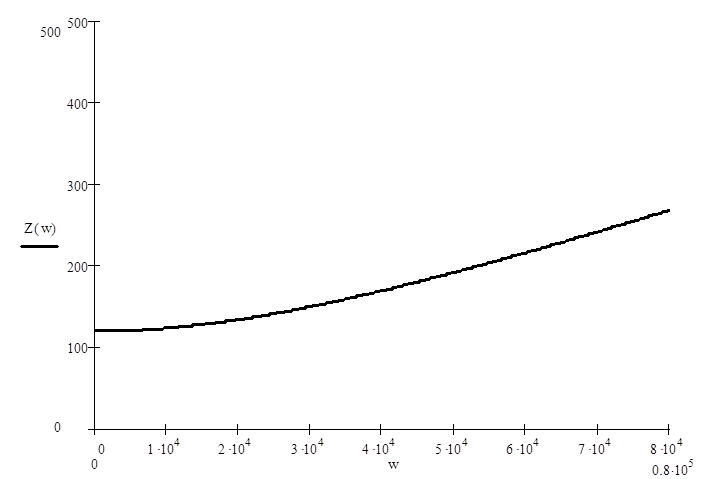
АЧХ и ФЧХ цепи:

АЧХ
– (рис. 4).

ФЧХ
– (рис. 5).

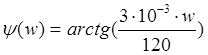
3).
Найдем форму спектральной плотности выходного сигнала: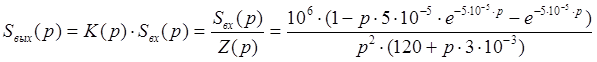 для того чтобы найти
модуль спектра выходного сигнала поделим модуль спектра входного сигнала на
модуль сопротивления цепи:

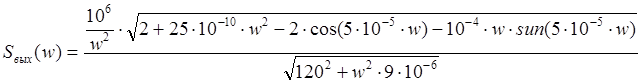
– модуль спектра выходного сигнала (рис.
6).

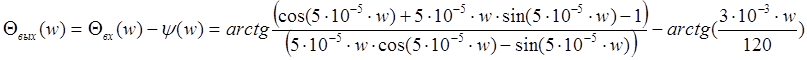
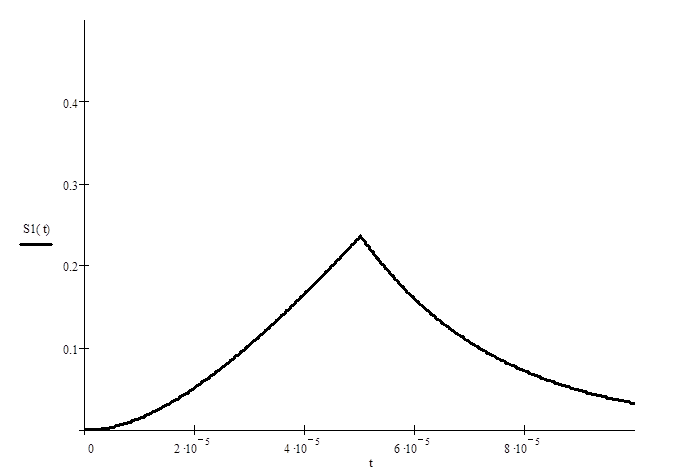
– фаза спектра выходного сигнала (рис. 7).

4).
Имея S_вых(w)
найдем S_вых(t):

Используя
таблицу обратных преобразований Лапласа по изображению

найдем оригинал.

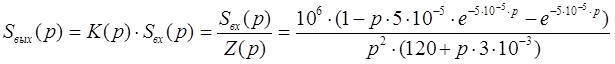
S_вых(t) – отклик цепи на входное воздействие S_вх(t) (рис. 8).

III Графики

Рис.
1
Входной сигнал.

Рис. 2 Амплитуда
спектра входного сигнала.

Рис. 3 Фаза спектра
входного сигнала.

Рис. 4 АЧХ цепи.

Рис. 5 ФЧХ цепи.

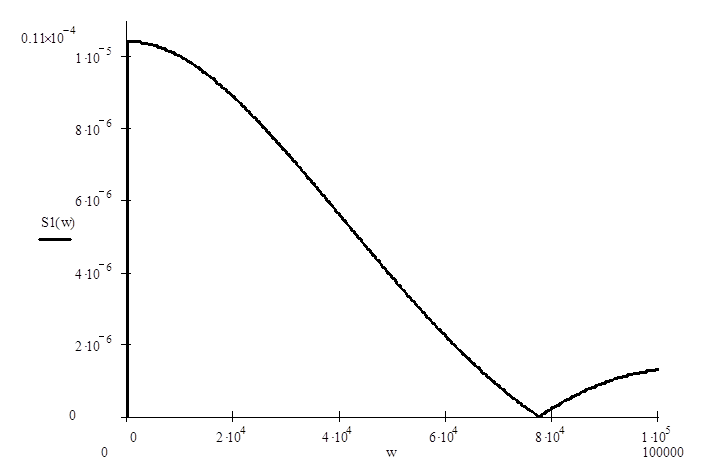
Рис. 6
Амплитуда спектра выходного сигнала.

Рис. 7 Фаза
спектра выходного сигнала.

Рис. 8 Выходной
сигнал.

Источник

Главная

Статьи

» ТОЭ » ИДЗ

В6. Задача 1.4.6. Найти изображение указанного сигнала

Условие задачи

В вариантах 1—8 найти изображение указанного сигнала (из представленных на рис. 1.5). Сигнал: F_m = 9; t₁₂ = 0; t₁₃ = 3; t₁₄ = 5.

Решение задачи

Категория: ИДЗ | Добавил: Creator (27.11.2016)

Просмотров: 3783 | Теги: сигнал, цепь, изображение
| Рейтинг: 0.0/0

Всего комментариев: 0

Войдите:

avatar

Источник

1. Оригинал — это комплекснозначная функция f(t) действительного аргумента , которая удовлетворяет следующим условиям:

а) f(t)=0 при t<0 ;

б) на любом конечном отрезке [a;b]in[0;+infty) функция f(t) имеет не более чем конечное число точек разрыва первого рода;

в) f(t)f(t) имеет ограниченный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные M>0 и sigmageqslant0 , что $|f(t)|<M,e^{sigma t}$ при t>0 .

Замечания 5.1

1. Величина sigma_0=infsigma называется показателем роста функции f(t) . Для любой ограниченной функции, являющейся оригиналом, можно принять sigma_0=0 .

2. Обозначим $f(+0)= limlimits_{tto+0} f(t),~ f(+infty)= limlimits_{tto+infty} f(t)$ , если пределы существуют и конечны.

3. Совокупность всех оригиналов называется пространством оригиналов.

4. В точке t_0 разрыва первого рода функция имеет конечные односторонние пределы: $limlimits_{tto t_0+0} f(t),~ limlimits_{tto t_0-0} f(t)$ .

Пример 5.1

2. Изображение функции f(t) — функция F(p) комплексного переменного , определяемая равенством

$F(p)= intlimits_{0}^{+infty} e^{-pt}f(t),dt,.$

(5.1)

Область существования этой функции определяется областью сходимости интеграла Лапласа, стоящего в правой части равенства (5.1). Исследование интeгpaлa позволяет определить эту область и установить свойства функции F(p) . Имеет место следующее утверждение.

Утверждение 5.1. Если функция f(t) , является оригиналом, то интеграл Лапласа сходится абсолютно в области $operatorname{Re}p=sigma> sigma_0$ (рис. 5.1) , где sigma_0 — показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмножестве $operatorname{Re}p=sigma geqslant a>sigma_0$ , интеграл сходится равномерно и определяет аналитическую функцию F(p) .

Рис. 5.1.

Замечания 5.2

1. Утверждение 5.1 аналогично свойствам степенных рядов, сходящихся в круге и равномерно сходящихся внутри этого круга, где сумма ряда является аналитической функцией.

2. Свойство аналитичности изображения имеет важное значение в теории и практике применения преобразования Лапласа, так как позволяет использовать в пространстве изображений методы теории аналитических функций, в частности разложения функций в ряды и теорию вычетов.

3. Совокупность всех изображений F(p) называется пространством изображений.

4. Переход, определяющий изображение F(p) по оригиналу f(t) , называется преобразованием Лапласа:

$F(p)= Lbigl[f(t)bigr]= intlimits_{0}^{+infty} e^{-pt}f(t),dt,.$

(5.2)

Запись F(p)=L[f(t)] означает, что оригиналу f(t) соответствует изображение F(p) .

5. Оригинал по изображению находится с помощью обратного преобразования Лапласа по формуле обращения

$f(t)=L^{-1}bigl[F(p)bigr]= frac{1}{2pi i} intlimits_{sigma-iinfty}^{sigma+iinfty} e^{pt}F(p),dp,,$

(5.3)

где путь интегрирования — любая прямая operatorname{Re}p=sigma , параллельная мнимой оси и лежащая правее прямой $operatorname{Re}p=sigma_0$ (рис. 5.1).

Непосредственное применение формулы обращения часто затруднительно. Поэтому на практике пользуются методами, изложенными ранее.

Замечания 5.3

1. Для преобразования Лапласа используются различные обозначения, на пример f(t)risingdotseq F(p) и F(p)fallingdotseq f(t) , что означает: оригиналу f(t) соответствует изображение F(p) и изображению F(p) соответствует оригинал f(t) . В некоторых учебниках вместо аргумента применяется , то есть F(s)=L[f(t)] и $L^{-1}[F(s)]=f(t)$ .

2. Для компактной записи оригиналов используется единичная ступенчатая функция boldsymbol{1}(t-tau)colon

$boldsymbol{1}(t-tau)= begin{cases}1,& t>tau,\ 0,& t leqslant tau,end{cases}$

(5.4)

Рис. 5.2.

где tau — точка приложения (рис. 5.2). Так как во многих практических задачах аргумент имеет смысл текущего времени, то tau также называется моментом приложения единичной ступенчатой функции. В системах автоматического регулирования и управления функция boldsymbol{1}(t-tau) рассматривается как типовой входной сигнал.

При tau=0 функция boldsymbol{1}(t-tau) является функцией Хевисайда:

$boldsymbol{1}(t)= begin{cases}1,& t>0,\ 0,& t leqslant 0.end{cases}$

(5.5)

Тогда, если функция f(t) удовлетворяет условиям “б”, “в” в определении оригинала (п. 1), но не удовлетворяет условию “а”, то функция f(t)cdot boldsymbol{1}(t) будет оригиналом, так как

$f(t)cdotboldsymbol{1}(t)= begin{cases}f(t),& t>0,\ 0,& tleqslant0. end{cases}$

Далее под заданной с помощью аналитической формулы функцией f(t) , там, где это не вызывает недоразумений, будем понимать произведение этой функции на функцию Хевисайда, а множитель boldsymbol{1}(t) опускать.

3. Функции F(p) , являющиеся изображениями, удовлетворяют необходимому условию: если F(p) есть изображение, то F(p)to0 при operatorname{Re}p=sigmato+infty . Поэтому функции $F_1(p)=1,~ F_2(p)=p,~ F_3(p)=sin p,~ F_4(p)= frac{p}{p-1}$ не являются изображениями. Однако в практических задачах функции типа и другие встречаются. Это требует расширения понятий оригинала и изображения.

Класс оригиналов можно расширить, включив в него функции, которые могут быть не ограничены в окрестности некоторых конечных точек, но такие, что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой полуплоскости $operatorname{Re}p>sigma_0$ . К числу таких обобщенных оригиналов относятся степенная функция $f(t)=t^{mu}$ при mu>-1,~ln t и некоторые другие.

4. Во всякой точке t_0 , являющейся точкой разрыва функции f(t) , правая часть формулы (5.3) равна $frac{1}{2}bigl[f(t_0-0)+f(t_0+0)bigr]$ .

Примеры 5.2-5.3

Пример 5.2. Найти изображение единичной функции Хевисайда f(t)= boldsymbol{1}(t) .

Решение. Так как функция boldsymbol{1}(t) ограничена, то в качестве показателя роста можно положить sigma_0=0 . По формуле (5.2) имеем

$F(p)= L[boldsymbol{1}(t)]= intlimits_{0}^{+infty} boldsymbol{1}(t) e^{-pt},dt=left.{-frac{1}{p},e^{-pt}}right|_{0}^{+infty}= frac{1}{p},.$

так как из равенства $|e^{-pt}|= e^{operatorname{Re}(-pt)}= e^{-t operatorname{Re}p}= e^{-sigma t}$ следует, что $limlimits_{tto+infty} e^{-pt}=0$ при $operatorname{Re}p= sigma>sigma_0=0$ .

Пример 5.3. Найти изображение функции $f(t)=e^{at}$ , где — действительное число.

Решение. Показателем роста можно считать sigma_0=a . По формуле (5.2)

$F(p)= intlimits_{0}^{+infty} e^{at}e^{-pt},dt= intlimits_{0}^{+infty} e^{(a-p)t},dt= left.{frac{e^{(a-p)t}}{a-p}}right|_{0}^{+infty}=-frac{1}{a-p}=frac{1}{p-a},.$

так как из равенства $|e^{(a-p)t}|= e^{-t(operatorname{Re}p-a)}= e^{-t(sigma-a)}$ следует, что $limlimits_{tto+infty} e^{(a-p)t}=0$ при operatorname{Re}p=sigma>a .

Будем предполагать, что рассматриваемые далее функции f(t),f_1(t),ldots,f_n(t) являются оригиналами. Соответствующие им изображения (при $operatorname{Re}p> sigma_i,~ i=0,1,ldots,n$ ) обозначим F(p),F_1(p),ldots,F_n(p) .

1. Линейность. Если f_1(t),ldots,f_n(t) — оригиналы, то для любых комплексных чисел c_i,~ i=1,2,ldots,n , функция $textstyle{f(t)= sumlimits_{k=1}^{n} c_kf_k(t)}$ также является оригиналом и справедливо равенство $textstyle{L!left[ sumlimits_{k=1}^{n} c_kf_k(t)right]= sumlimits_{k=1}^{n}c_k L[f_k(t)]}$

$L bigl[c_1f_1(t)+ldots+ c_nf_n(t)bigr]= c_1F_1(p)+ldots+ c_nF_n(p),quad operatorname{Re}p>max{sigma_1,ldots,sigma_n}.$

(5.6)

Заметим, что для функции $textstyle{f(t)= sumlimits_{k=1}^{n} c_kf_k(t)}$ существенно, что все слагаемыс являются оригиналами, так как, например, функция $f(t)=frac{e^{t}-1}{t}$ является оригиналом, а слагаемые $f_1(t)=frac{e^t}{t}$ и $f_2(t)=-frac{1}{t}$ не являются.

Справедливо и обратное утверждение: если F_1(p),ldots,F_n(p) — изображения, то

$L^{-1} bigl[c_1F_1(p)+ldots+ c_nF_n(p)bigr]= c_1f_1(t)+ldots+ c_nf_n(t).$

Здесь также важно, что слагаемые функции c_1F_1(p)+ldots+ c_nF_n(p) являются изображениями, поскольку из того, что F(p)= c_1F_1(p)+ldots+ c_nF_n(p) — изображение, не следует, что F_1(p)+ldots+ F_n(p) — изображения. Например, функция $F(p)= ln frac{p-1}{p}$ является изображением, а слагаемые F_1(p)= ln(p-1) и F_2(p)=-ln p не являются.

Примеры 5.4-5.5

Пример 5.4. Найти изображение функции $f(t)=3+2e^{-t}$ .

Решение. Из примера 5.2 имеем $L[boldsymbol{1}(t)]= frac{1}{p}$ , а из примера 5.3 при a=-1 имеем $L[e^{-t}]= frac{1}{p+1}$ . Тогда согласно свойству линейности для оригинала $f(t)=3cdotboldsymbol{1}(t)+2cdot e^{-t}$ получаем $F(p)= 3cdot frac{1}{p}+2cdot frac{1}{p+1}$ .

Пример 5.5. Найти изображение функции f(t)=cos t .

Решение. Используя формулу Эйлера (2.11), получаем $f(t)=cos t=frac{e^{it}+e^{-it}}{2}= frac{1}{2},e^{it}+frac{1}{2},e^{-it}$ .

Из примера 5.3 при a=i и a=-i следует: $L[e^{it}]= frac{1}{p-i},,~ L[e^{-it}]=frac{1}{p+i}$ . Тогда по свойству линейности

$L[cos t]= frac{1}{2}L[e^{it}]+frac{1}{2}L[e^{-it}]= frac{1}{2}cdot frac{1}{p-i}+ frac{1}{2}cdot frac{1}{p+i}= frac{p+i+p-i}{2(p^2+1)}= frac{p}{p^2+1},.$

2. Подобие (теорема подобия). Для любого a>0 из F(p)=L[f(t)] следует

$L bigl[f(at)bigr]= frac{1}{a},F! left(frac{p}{a}right)!,quad operatorname{Re}p>asigma_0,$

(5.7)

и обратно: $L^{-1} bigl[F(ap)bigr]= frac{1}{a},f! left(frac{t}{a}right)$ .

Пример 5.6

Найти изображение функции f(t)=cos at .

Решение. Из примера 5.5 следует, что $L[cos t]= frac{p}{p^2+1}$ . Тогда по теореме подобия

$L[cos at]= frac{1}{a}cdot frac{p!!not{phantom{|}},a}{(p!!not{phantom{|}}, a)^2+1}= frac{p}{p^2+a^2},.$

3. Смещение (теорема смещения). При любом комплексном из F(p)= L[f(t)] следует

$L bigl[e^{at}f(t)bigr]= F(p-a),quad operatorname{Re}(p-a)>sigma_0,$

(5.8)

то есть умножению оригинала на $e^{at}$ соответствует смещение изображения на .

Пример 5.7

Найти изображение функции $f(t)=e^{at}cos bt$ .

Решение. Из примера 5.6 следует $L[cos bt]=frac{p}{p^2+a^2}$ . Тогда по теореме смещения $L[e^{at}cos bt]= frac{p-a}{(p-a)^2+b^2}$ .

Рис. 5.3.

4. Запаздывание (теорема запаздывания). Для любого tau>0 из F(p)=L[f(t)] следует

$Lbigl[f(t-tau)bigr]= e^{-ptau}cdot F(p),quad operatorname{Re}p>sigma_0,$

(5.9)

где f(t-tau)=f(t-tau)cdot boldsymbol{1}(t-tau) (рис. 5.3), т.е. запаздыванию оригинала на tau>0 соответствует умножение изображения на $e^{-ptau}$ .

Примеры 5.8-5.10

Пример 5.8. Найти изображение функции f(t)=cos(t-3)cdot boldsymbol{1}(t-3)= cos(t-3) .

Решение. В примере 5.5 получено $L[cos t]=frac{p}{p^2+1}$ . По теореме запаздывания при tau=3 имеем $L[cos(t-3)]= frac{e^{-3p}cdot p}{p^2+1}$ .

Пример 5.9. Найти оригиналы по изображениям: a) $F(p)=frac{(p-1)e^{-4p}}{(p-1)^2+4}$ ; б) $F(p)=frac{e^{-p}}{p^2}$ .

а) Из примера 5.7 следует, что при a=1,~b=2 изображению $frac{p-1}{(p-1)^2+4}$ соответствует оригинал e^tcos2t . Тогда по теореме запаздывания при tau=4 имеем

$f(t)= L^{-1}[F(p)]= e^{t-4}cos(t-4)cdot boldsymbol{1}(t-4).$

б) По формуле 3 из табл. 5.1 $L^{-1}!left[frac{1}{p^2}right]=t$ .По теореме запаздывания при tau=1 получаем $f(t)=L^{-1}[F(p)]= (t-1)cdot boldsymbol{1} (t-1)$ . Заметим, что для похожего, но отличного от полученного, оригинала f(t)=t-1 (его можно записать в виде (t-1)cdot boldsymbol{1}(t) ) изображение имеет вид $F(p)=frac{1}{p^2}-frac{1}{p}ne frac{e^{-p}}{p^2}$ .

рис. 5.4.

Пример 5.10. Найти изображение функции $delta_h(t)= begin{cases}frac{1}{h},& 0<tleqslant h,\ 0,& t<0,,t>h,end{cases}$ , график которой представлен на рис. 5.4.

С учетом (5.4) представим функцию delta_h(t) в виде $delta_h(t)= frac{boldsymbol{1}(t)-boldsymbol{1}(t-h)}{h}$ .

Из примера 5.2 имеем $L[boldsymbol{1}(t)]=frac{1}{p}$ . Применяя свойства линейности и запаздывания, получаем

$Lbigl[delta_h(t)bigr]= frac{1}{h}Lbigl[boldsymbol{1}(t)bigr]-frac{1}{h}Lbigl[boldsymbol{1}(t-h)bigr]= frac{1}{h}cdot frac{1}{p}-frac{1}{h}cdot frac{1}{p},e^{-ph}= frac{1-e^{-ph}}{ph},.$

Заметим, что, находя предел при hto0 в последнем выражении, можно получить изображение δ-функции $delta(t)= limlimits_{hto0} delta_h(t)colon$

$Lbigl[delta(t)bigr]= limlimits_{hto0} frac{1-e^{-ph}}{ph}= limlimits_{hto0} frac{p,e^{-ph}}{p}=1.$

Замечание 5.4. Дельта-функция часто встречается в инженерных приложениях как идеализация импульса конечной длительности. В теории автоматического регулирования и управления δ-функция вместе с единичной ступенчатой являются типовыми входными воздействиями.

Очевидно, изображение дельта-функции не удовлетворяет необходимому условию (п.2 замечаний 5.3). Этот факт свидетельствует о практическом требовании расширения понятия оригинала. Дельта-функция относится к обобщенным функциям и задается соотношением

$intlimits_{a}^{b} f(t)delta(t-tau),dt= begin{cases}f(tau+0),& a leqslant tau<b,\ 0,& tau<a,, taugeqslant b.end{cases}$

(5.10)

5. Если функции $f(t),f'(t),ldots,f^{(n)}(t)$ являются оригиналами и F(p)=L[f(t)] , то

$begin{aligned}& L[f'(t)]= pF(p)-f(+0),\ & L[f''(t)]= p^2F(p)-pf(+0)-f'(+0),\ & quadvdots\ & L[f^{(n)}(t)]= p^nF(p)-p^{n-1}f(+0)-ldots-f^{(n-1)}(+0), end{aligned}$

(5.11)

где $f^{i}(+0)= limlimits_{tto+0} f^{(i)}(t),~ i=0,1,2,ldots,n-1$ .

Примеры 5.11-5.12

Пример 5.11. Найти изображение f'(t) , если $f(t)=e^{-t}cos3t$ .

Решение. Из примера 5.7 следует, что при a=-1,~b=3 имеем $L[e^{-t}cos3t]= frac{p+1}{(p+1)^2+9}$ .

Найдем $f(+0)=limlimits_{tto+0}e^{-t}cos3t=1$ . Согласно (5.11) $L[f'(t)]= pcdot frac{p+1}{(p+1)^2+9}-1$ .

Пример 5.12. Найти изображение выражения x''+3x'+2x+1 с начальными условиями x(+0)=1,~x'(+0)=4 .

Решение. Пусть X(p)=L[x(t)] , тогда L[x'(t)]= pX(p)-1;~ L[x''(t)]= p^2X(p)-pcdot1-4 . В примере 5.2 получено L[boldsymbol{1}(t)]=1!!not{phantom{|}},p . Используя свойство линейности, имеем

$begin{aligned}L[x''+3x'+2x+1]&= L[x'']+3L[x']+2L[x]+L[1]=\ &=p^2X(p)-p-4+3pX(p)-3+2X(p)+frac{1}{p}=\ &=(p^2+3p+2)X(p)-p-7+frac{1}{p},.end{aligned}$

Если функция f(t) является оригиналом и F(p)=L[f(t)] , то

$textstyle{L! left[intlimits_{0}^{t} f(tau),dtauright]= dfrac{F(p)}{p},quad operatorname{Re}p>sigma_0,}$

(5.12)

т.е. интегрированию оригинала соответствует деление изображения на .

Пример 5.13

Найти изображение интеграла $textstyle{intlimits_{0}^{t} f(tau),dtau}$ от функции f(t)=cos t .

Решение. Из примера 5.6 следует, что $L[cos t]=frac{p}{p^2+1}=F(p)$ . Тогда

$LBiggl[intlimits_{0}^{t} costau,dtauBiggr]= L[sin t]= frac{p}{p(p^2+1)}= frac{1}{p^2+1}$ , то есть $L[sin t]= frac{1}{p^2+1}$ .

Если функция f(t) является оригиналом и F(p)=L[f(t)] . то

$Lbigl[(-1)^nt^nf(t)bigr]= F^{(n)}(p).$

(5.13)

Примеры 5.14-5.15

Если функция $frac{f(t)}{t}$ является оригиналом, то из F(p)=L[f(t)] следует

$L! left[frac{f(t)}{t}right]= intlimits_{p}^{infty} F(z),dz,.$

(5.14)

Пример 5.16

Найти изображение функции $frac{sin t}{t}$ .

Решение. Функция $frac{sin t}{t}$ является оригиналом, так как $left|frac{sin t}{t}right|<1$ (условие “в”) и точка t=0 является точкой разрыва первого рода (условие “б”). Из примера 5.13 следует $L[sin t]=frac{1}{p^2+1}=F(p)$ .

Отсюда $L! left[frac{sin t}{t}right]= intlimits_{p}^{+infty} frac{dz}{z^2+1}= Bigl.{operatorname{arctg}z}Bigr|_{p}^{+infty}=frac{pi}{2}-operatorname{arctg}p.$ .

Из F_1(p)=L[f_1(t)] и F_2(p)=L[f_2(t)] следует

Lbigl[f_1(t)ast f_2(t)bigr]= F_1(p)cdot F_2(p),

(5.15)

т.е. свертке оригиналов соответствует произведение изображений. Функция f_1(t)ast f_2(t) определяется формулой

$f_1(t)ast f_2(t)= intlimits_{0}^{t} f_1(tau)f_2(t-tau),dtau= intlimits_{0}^{t} f_1(t-tau)f_2(tau),dtau$

(5.16)

и называется сверткой оригиналов f_1(t) и f_2(t) .

Пример 5.17

Найти оригинал, соответствующий изображению $F(p)= frac{p}{(p^2+1)^2}$ .

Решение. Представим F(p) в виде произведения изображений: $F(p)= F_1(p)cdot F_2(p)= frac{1}{p^2+2}cdot frac{p}{p^2+1}$ .

Из примеров 5.6 и 5.13 следует $f_1(t)=L^{-1}! left[frac{1}{p^2+2}right]=sin t,~ f_2(t)=L^{-1}! left[frac{p}{p^2+2}right]=cos t$ .

Согласно (5.15),(5.16) получаем искомый оригинал:

$begin{aligned}L^{-1}! left[frac{p}{(p^2+1)^2}right]&= f_1(t)ast f_2(t)= intlimits_{0}^{t} sintaucos(t-tau),tau= frac{1}{2} intlimits_{0}^{t} bigl[sin t+sin(2tau-t)bigr]dtau=\ &=left.{frac{1}{2}! left(sin tcdottau-frac{1}{2}cos(2tau-t)right) }right|_{0}^{t}= frac{1}{2}! left(tsin t-frac{1}{2}cos t+frac{1}{2}cos(-t)right)= frac{t}{2}sin t.end{aligned}$

10. Согласно свойствам 9 и 5 найдем преобразование Лапласа от производной свертки двух функций:

$Lleft{bigl[f_1(t)ast f_2(t)bigr]'right}= pF_1(p)cdot F_2(p).$

С другой стороны,

$bigl[f_1(t)ast f_2(t)bigr]'= frac{d}{dt} intlimits_{0}^{t} f_1(tau) f_2(t-tau),dtau= f_2(0)f_1(t)+ intlimits_{0}^{t} f'_2(tau) f_1(t-tau),dtau$

или, применяя правило дифференцирования интеграла, зависящего от параметра, имеем

$bigl[f_1(t)ast f_2(t)bigr]'= frac{d}{dt} intlimits_{0}^{t} f_1(t-tau)f_2(tau),dtau= f_1(0)f_2(t)+intlimits_{0}^{t} f'_1(tau)f_2(t-tau),dtau,.$

Здесь при дифференцировании интеграла, зависящего от параметра, применялась формула Лейбница, которая для общего случая имеет вид

$frac{d}{dlambda} intlimits_{u(lambda)}^{v(lambda)}f(x,lambda),dx= f bigl(v(lambda),lambdabigr)frac{dv}{dlambda}-f bigl(u(lambda),lambdabigr)frac{du}{dlambda}+ intlimits_{u(lambda)}^{v(lambda)} frac{partial}{partiallambda}f(x,lambda),dx,.$

Объединяя полученные результаты, можно записать:

$begin{aligned}L^{-1} bigl[pF_1(p)F_2(p)bigr]&= f_1(0)f_2(0)+ f'_1ast f_2= f_2(0)f_1(t)+ f'_2ast f_1=\ &=f_1(0)f_2(0)+ intlimits_{0}^{t}f'_1(tau)f_2(t-tau),dtau= f_2(0)f_1(t)+ intlimits_{0}^{t} f'_2(tau) f_1(t-tau),dtau,.end{aligned}$

(5.17)

Формула (5.17) называется интегралом Дюамеля. Интеграл Дюамеля применяется для решения дифференциальных уравнений.

Пример 5.18

Найти оригиналы, соответствующие изображениям: a) $F(p)= frac{p}{(p-1)(p-2)}$ ; б) $F(p)= frac{p^3}{(p^2+1)(p^2+4)}$ .

Решение. а) Заметим, что здесь нельзя непосредственно воспользоваться теоре мой Бореля, так как в произведении $F(p)=frac{p}{p-1}cdot frac{1}{p-2}$ множитель $F_1(p)= frac{p}{p-1}$ не является изображением (не выполняется необходимое условие).

Представим изображение в виде произведения $F(p)=pcdotfrac{1}{p-1}cdot frac{1}{p-2}$ . Из примера 5.3 вытекает

$f_1(t)=L^{-1}bigl[F_1(p)bigr]= L^{-1}!left[frac{1}{p-1}right]= e^t;qquad f_2(t)= L^{-1} bigl[F_2(p)bigr]= L^{-1}! left[frac{1}{p-2}right]=e^{2t}.$

Тогда по формуле (5.17) имеем

$L^{-1} bigl[F(p)bigr]= f_1(0)f_2(t)+ f'_1ast f_2= 1cdot e^{2t}+ intlimits_{0}^{t} e^{tau}cdot e^{2(t-tau)},dtau= e^{2t}+ e^{2t} intlimits_{0}^{t} e^{-tau},dtau=-e^{t}+2e^{2t}.$

Можно решить этот пример с помощью теоремы Бореля, представив изображение в виде

$F(p)= frac{p}{(p-1)(p-2)}= frac{p-1+1}{(p-1)(p-2)}= frac{1}{p-2}+ frac{1}{p-1}cdot frac{1}{p-2},.$

Тогда, используя свойство линейности и теорему Бореля, получаем

$L^{-1}bigl[F(p)bigr]= e^{2t}+e^{t}ast e^{2t}= e^{2t}+ intlimits_{0}^{t} e^{2tau}cdot e^{t-tau},dtau= e^{2t}+ e^{t} intlimits_{0}^{t} e^{tau},dtau= e^{2t}+e^{t}(e^{t}-1)= 2e^{2t}-e^{t}.$

б) Представим изображение в виде произведения:

$F(p)= frac{p^3}{(p^2+1)(p^2+4)}= pcdot frac{p}{p^2+1}cdot frac{p}{p^2+1}= pcdot F_1(p)cdot F_2(p).$

Из примера 5.6 при a=1 и a=2 следует

$L^{-1}! left[frac{p}{p^2+1}right]=cos t=f_1(t),qquad L^{-1}! left[frac{p}{p^2+ 4}right]= cos2t= f_2(t).$

Тогда по формуле (5.17) получаем

$begin{aligned}f(t)&= L^{-1} bigl[F(p)bigr]= f_1(0)f_2(t)+ f'_1ast f_2= cos2t-intlimits_{0}^{t} sintaucos[2(t-tau)],dtau=\ &=cos2t-frac{1}{2} intlimits_{0}^{t} bigl[sin(3tau-2t)+sin(2t-tau)bigr]dtau=\ &=cos2t+ left.{frac{1}{6}cos(3tau-2t)}right|_{0}^{t}-left.{frac{1}{2} cos(2t-tau)}right|_{0}^{t}= frac{4}{3}cos2t-frac{1}{3}cos t,.end{aligned}$

Начальное значение оригинала находится по формуле

$f(+0)= limlimits_{ptoinfty} pF(p).$

(5.18)

Если существует конечный предел $limlimits_{tto+infty} f(t)= f(+infty)$ , то

$f(+infty)= limlimits_{pto0} pF(p).$

(5.19)

Из соотношений (5.18),(5.19) следует, что для нахождения начальных и конечных значений оригинала не требуется знания оригинала, а достаточно иметь соответствующее изображение. На практике соотношение (5.19) применяется, например, для нахождения установившегося значения выходного сигнала в системах автоматического регулирования.

Пример 5.19

Найти начальное и конечное значения оригинала, которому соответствует изображение $F(p)= frac{p+1}{(p+1)^2+9}$ .

Решение. Согласно (5.18) и (5.19) имеем

$f(+0)= limlimits_{ptoinfty} frac{p(p+1)}{(p+1)^2+9}=1;qquad f(+infty)= limlimits_{pto0} frac{p(p+1)}{(p+1)^2+9}=0.$

С другой стороны, из примера 5.7 следует, что

$f(t)= L^{-1}! left[frac{p+1}{(p+1)^2+9}right]=e^{-t}cos3t,,$

поэтому легко убедиться в правильности полученного результата.

Полученные решения примеров 5.2–5.17 позволяют сформировать таблицу преобразования Лапласа. Табл. 5.1 является фрагментом более полных таблиц, используемых далее при решении примеров и задач.

Для нахождения изображения требуется применить свойства преобразования Лапласа Так, чтобы к функции или ее составляющим можно было применить результаты, содержащиеся в табл. 5.1.

Таблица 5.1. Таблица основных преобразований Лапласа

Посмотреть

Пример 5.21

Найти изображения функций:

a) $f(t)=t,e^{2t}sin3t$ ; б) $f(t)=frac{2}{t}(1-cos t)$ ;

в) $f(t)=begin{cases}cos[4(t-2)],&t>3,\ 0,&t leqslant 2;end{cases}$ ; г) $f(t)= begin{cases}e^{-3t}cos[4(t-2)],& t>2,\ 0,& t leqslant 2;end{cases}$ ;

д) $f(t)= frac{1}{2}(t-2)^2e^{-(t-2)}boldsymbol{1}(t-2)$ ; е) $f(t)= e^{2t}+ boldsymbol{1}(t-1)+ boldsymbol{1}(t-4)sin[3(t-4)]$ ;

ж) $intlimits_{0}^{t} frac{operatorname{sh}tau}{tau},dtau$ ; з) f(t)= cos(4t-8) .

Решение

а) Согласно формуле 12 из табл. 5.1 $L bigl[e^{2t}sin3tbigr]= frac{3}{(p-2)^2+9}$ . По свойству дифференцирования изображения (формула (5.13) при n=1 ):

L bigl[(-1)tf(t)bigr]=F'(p) или L bigl[tf(t)bigr]=-F'(p) .

Поэтому $Lbigl[t,e^{2t}sin3tbigr]=-left[frac{3}{(p-2)^2+9}right]'=-frac{-2(p-2)cdot3}{bigl[(p-2)^2+9bigr]^2}= frac{6(p-2)}{bigl[(p-2)^2+9bigr]^2}$ .

Можно решать иначе, используя формулу 10 из табл. 5.1 при а = 3 и свойство смещения при a=2colon

$L bigl[tsin3tbigr]= frac{6p}{(p^2+9)^2}$ и $L bigl[t,e^{2t}sin3tbigr]= frac{6(p-2)}{bigl[(p-2)^2+9bigr]^2}$ .

б) Применим свойства линейности и интегрирования изображения. Так как $L[1-cos t]=frac{1}{p}-frac{p}{p^2+1}$ в силу формул 1 и 9 из табл. 5.1 , то согласно (5.14)

$L! left[frac{2}{t}(1-cos t)right]= 2 intlimits_{p}^{+infty}! left(frac{1}{z}-frac{z}{z^2+1}right)!dz= ldots= lnfrac{p^2+1}{p^2},.$

в) По формуле 9 из табл. 5.1 $L[cos4t]= frac{p}{p^2+16}$ . Функцию fit) можно записать, используя единичную ступенчатую функцию: f(t)= cos[4(t-2)]cdot boldsymbol{1}(t-2) . Поэтому для нахождения изображения следует применить теорему запаздывания (5.9) к оригиналу cos4t при tau=2colon

$L bigl[cos[4(t-2)]bigr]= e^{-2p}cdot frac{p}{p^2+16},.$

г) Согласно теореме смещения (5.8) и с учетом результата п. “в” имеем

$L bigl[e^{-3t}cos[4(t-2)]bigr]= e^{-2(p+3)}cdot frac{p+3}{(p+3)^2+16}$ , так как a=-3 .

д) По теореме запаздывания (5.9) при tau=2 и по формуле 7 из табл. 5.1 при a=2,~ b=-1 получаем

$L! left[frac{1}{2}(t-2)^2e^{-(t-2)} boldsymbol{1}(t-2)right]= e^{-2p}cdot L! left[frac{1}{2},t^2e^{-t}right]= e^{-2p}cdot frac{1}{2}cdot frac{2!}{(p+1)^3}= frac{e^{-2p}}{(p+1)^3},.$

е) Используя свойства линейности, запаздывания и формулы 6,1,8 из табл. 5.1, получаем

$F(p)= frac{1}{p-2}+ frac{1}{p},e^{-p}+ e^{-4p}cdot frac{3}{p^2+9},.$

ж) По формуле 19 из табл. 5.1 находим $L[operatorname{sh}t]=frac{1}{p^2-1}$ . По свойству интегрирования изображения (формула (5.14)):

$L! left[frac{operatorname{sh}t}{t}right]= intlimits_{p}^{+infty} frac{dz}{z^2-1}= left.{frac{1}{2}ln frac{z-1}{z+1}}right|_{p}^{+infty}= ldots=-frac{1}{2} ln frac{p-1}{p+1}= frac{1}{2}ln frac{p+1}{p-1},.$

По свойству интегрирования оригинала (5.12): $L Biggl[intlimits_{0}^{t} frac{operatorname{sh}tau}{tau},dtauBiggr]= frac{1}{2p}ln frac{p+1}{p-1}$ .

з) Используем формулу косинуса разности и запишем оригинал в виде суммы:

f(t)= cos(4t-8)= cos4tcos8+sin4tsin8

По свойству линейности получаем:

$L bigl[cos(4t-8)bigr]= cos8cdot frac{p}{p^2+16}+ sin8cdot frac{4}{p^2+16}= frac{pcos8+4sin8}{p^2+16},.$

Заметим, что здесь f(t)=f(t)cdot boldsymbol{1}(t) и результаты пп. “в” и “з” различны так как оригиналами являются разные функции.

При решении прикладных задач оригинал часто задан графиком. Это может быть, например, входной сигнал, действующий на систему автоматической регулирования. В этом случае рекомендуется сначала записать аналитическое выражение оригинала с помощью единичной ступенчатой функции (5.4), привести полученное выражение к виду, удобному для применения табл. 5.1 и свойстве преобразования Лапласа.

Пример 5.22

Найти изображения функций, заданных графиками на рис. 5.5.

Решение.

рис. 5.5.

а) Представим функцию в виде f(t)=(1-t)cdot boldsymbol{1}(t-1)=-(t-1)cdot boldsymbol{1}(t-1) .

По формуле 3 из табл.5.1 и теореме запаздывания (формула (5.9) при tau=1 )

$F(p)=-frac{1}{p^2}cdot e^{-p}.$

б) Запишем функцию в виде f(t)=(1-t) bigl[boldsymbol{1}(t)+boldsymbol{1}(t-1)bigr]=(1-t)cdot boldsymbol{1}(t)+ (t-1)cdot boldsymbol{1}(t-1) .

По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем $F(p)=frac{1}{p}-frac{1}{p^2}+frac{e^{-p}}{p^2}$ .

в) Запишем изображенную функцию в виде f(t)=-tcdot boldsymbol{1}(t-1)= (-t+1-1)cdot boldsymbol{1}(t-1)=-(t-1)cdot boldsymbol{1}(t-1)-boldsymbol{1}(t-1) .

По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем $F(p)=-frac{e^{-p}}{p^2}-frac{e^{-p}}{p}$ .

г) Представим функцию в виде

$begin{aligned}f(t)&= (t-1)cdot bigl[boldsymbol{1}(t-1)-boldsymbol{1}(t-2)bigr]+ (3-t)cdot bigl[boldsymbol{1}(t-2)-boldsymbol{1}(t-3)bigr]=\ &=(t-1)cdot boldsymbol{1}(t-1)-2(t-2)cdot boldsymbol{1}(t-2)+ (t-3)cdot boldsymbol{1}(t-3). end{aligned}$

По формулам 3 из табл. 5.1 и (5.6), (5.9) имеем $F(p)= frac{e^{-p}}{p^2}-frac{2e^{-2p}}{p^2}+frac{e^{-3p}}{p^2}$ .

д) Запишем функцию в форме

$begin{aligned}f(t)&= t bigl[boldsymbol{1}(t)-boldsymbol{1}(t-1)bigr]+ bigl[boldsymbol{1}(t-1)-boldsymbol{1}(t-2)bigr]+ (3-t)cdot bigl[boldsymbol{1}(t-2)-boldsymbol{1}(t-3)bigr]=\[2pt] &=tcdotboldsymbol{1}(t)-(t-1)cdot boldsymbol{1}(t-1)-boldsymbol{1}(t-1)+boldsymbol{1}(t-1)-boldsymbol{1}(t-2),+\ &quad+(2-t)cdot boldsymbol{1}(t-2)+ boldsymbol{1}(t-2)-(3-t)cdot boldsymbol{1}(t-3)=\[2pt] &=tcdot boldsymbol{1}(t)-(t-1)cdot boldsymbol{1}(t-1)-(t-2)cdot boldsymbol{1}(t-2)+ (t-3)cdot boldsymbol{1}(t-3). end{aligned}$

По формулам З из табл. 5.1 и (5.6), (5.9) $F(p)=frac{1}{p^2}-frac{e^{-p}}{p^2}-frac{e^{-2p}}{p^2}+frac{e^{-3p}}{p^2}$ .

е) Представим изображенную функцию в виде

$begin{aligned}f(t)&= (1-t) bigl[boldsymbol{1}(t)-boldsymbol{1}(t-1)bigr]-1cdot bigl[boldsymbol{1}(t-1)-boldsymbol{1}(t-2)bigr]+ (t-3)cdot boldsymbol{1}(t-2)=\[2pt] &=(1-t)cdotboldsymbol{1}(t)+ (t-1)cdotboldsymbol{1}(t-1)-boldsymbol{1}(t-1)+ boldsymbol{1}(t-2)+ (t-2)cdot boldsymbol{1}(t-2)-boldsymbol{1}(t-2)=\[2pt] &=(1-t)cdotboldsymbol{1}(t)+ (t-1)cdotboldsymbol{1}(t-1)-boldsymbol{1}(t-1)+ (t-2)cdot boldsymbol{1}(t-2).end{aligned}$

По формулам 1,3 из табл. 5.1 и (5.6), (5.9) $F(p)=frac{1}{p}-frac{1}{p^2}+frac{1}{p^2},e^{-p}-frac{1}{p},e^{-p}+frac{1}{p^2},e^{-2p}$ .

ж) Запишем функцию в форме f(t)= sin tcdot bigl[boldsymbol{1}(t)-boldsymbol{1}(t-pi)bigr]= sin tcdotboldsymbol{1}(t)+ sin(t-pi)cdot boldsymbol{1}(t-pi) .

По формуле 8 из табл. 5.1 и по теореме запаздывания $F(p)= frac{1}{p^2+1}+ frac{e^{pi p}}{p^2+1}$ .

з) Представим функцию в виде $f(t)= e^{-t} bigl[boldsymbol{1}(t)-boldsymbol{1}(t-1)bigr]= e^{-t}cdotboldsymbol{1}(t)-frac{e^{-(t-1)}}{e}cdot boldsymbol{1}(t-1).$ .

По формуле 6 из табл. 5.1 при a=-1 и (5.9) при tau=1 имеем

$F(p)= frac{1}{p+1}-frac{1}{e}cdot frac{e^{-p}}{p+1}= frac{1}{p+1}bigl(1-e^{-p-1}bigr).$

и) Представим функцию в виде f(t)=1cdot bigl[boldsymbol{1}(t)-boldsymbol{1}(t-1)bigr]-1cdot bigl[boldsymbol{1}(t-1)-boldsymbol{1}(t-2)bigr]= boldsymbol{1}(t)-2cdot boldsymbol{1}(t-1)+boldsymbol{1}(t-2). .

Используя формулы 2 из табл. 5.1 и (5.6), (5.9), получаем $F(p)=frac{1}{p}-frac{2}{p}e^{-p}+ frac{1}{p},e^{-2p}$ .

Во многих приложениях используются оригиналы, являющиеся периодическими функциями.

Пусть f(t) — оригинал с периодом (рис. 5.6,в), образованный повторением функции f_0(t) (рис. 5.6,б):

$f_0(t)= begin{cases}0,& tleqslant 0,\ f(t),& 0<tleqslant T,\ 0,& t>T.end{cases}$ рис. 5.6,

Для нахождения изображения F(p) периодической функции f(t) следует:
1. Найти изображение функции f_0(t)colon, F_0(p)=Lbigl[f_0(t)bigr] .
2. Найти изображение F(p) по формуле

$F(p)= frac{F_0(p)}{1-e^{-Tp}}$

(5.20)

Пример 5.23.

Найти изображения функций, представленных на рис. 5.7.
Решение

рис. 5.7.

а) По графику (рис. 5.7,в) получаем

$f_0(t)= tcdot bigl[boldsymbol{1}(t)-boldsymbol{1}(t-1)bigr]= 1cdot boldsymbol{1}(t)-(t-1)cdot boldsymbol{1}(t-1)-boldsymbol{1}(t-1).$

Поэтому $F_0(p)= frac{1}{p^2}-frac{1}{p^2},e^{-p}-frac{1}{p},e^{-p}$ .

Поскольку T=1 , по формуле (5.20) находим

$F(p)= frac{dfrac{1}{p^2}(1-e^{-p}-pe^{-p})}{1-e^{-p}}= frac{e^p(1-e^{-p}-pe^{-p})}{p^2(e^p-1)}= frac{e^p-1-p}{p^2(e^p-1)},.$

б) По графику (рис. 5.7,б) имеем $f_0(t)= boldsymbol{1}(t)-boldsymbol{1}(t-tau)$ , тогда $F_0(p)=frac{1}{p}-frac{1}{p},e^{-ptau}$ . По формуле (5.20) при T=2tau имеем

$F(p)= frac{1}{p}(1-e^{-ptau})frac{1}{1-e^{-2tau p}}= frac{1}{p(1+e^{-ptau})},.$

в) Функция, изображенная на рис. 5.7,в , имеет период T=2c . Запишем аналитическое выражение для f_0(t) и соответствующее изображение F_0(p)colon

$begin{aligned}&f_0(t)= h bigl[boldsymbol{1}(t)-boldsymbol{1}(t-c)bigr]-h bigl[boldsymbol{1}(t-c)-boldsymbol{1}(t-2c)bigr]= hcdotboldsymbol{1}(t)-2hcdot boldsymbol{1}(t-c)+hcdot boldsymbol{1}(t-2c),\ &F_0(p)= frac{h}{p}-frac{2h}{p},e^{-pc}+frac{h}{p},e^{-2pc}.end{aligned}$

По формуле (5.20) получаем $F(p)=frac{h(1+e^{-2pc}-2e^{-pc})}{p(1-e^{2pc})}$ .

г) Для функции, изображенной на рис. 5.7,г, изображением для f_0(t) является $F_0(p)= frac{1}{p^2+1}(1+e^{-pi p})$ (см. пример 5.22 п.”ж”). Тогда по формуле (5.20) при T=pi получаем $F(p)= frac{1+e^{-pi p}}{(p^2+1)(1-e^{-pi p})}$ .

Непосредственное применение формулы обращения (5.3) затруднительно, поэтому для нахождения оригинала применяются теоремы разложения и правила преобразования изображения к виду, представленному в табл. 5.1.

Применение теорем разложения

Теорема 5.1 (первая теорема разложения). Если функция F(p) аналитична в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд по степеням $frac{1}{p}$ имеет вид $textstyle{F(p)= sumlimits_{n=0}^{infty} dfrac{a_n}{p^{n+1}}}$ , то функция (5.21) является оригиналом, соответствующим изображению F(p) .

$f(t)= sumlimits_{n=0}^{infty} a_n frac{t^n}{n!},quad tgeqslant0$

(5.21)

Теорема 5.2 (вторая теорема разложения). Если изображение F(p) является однозначной функцией и имеет лишь конечное число особых точек p_1,p_2,ldots,p_n лежащих в конечной части плоскости, то

$f(t)= sumlimits_{k=1}^{n} mathop{operatorname{res}}limits_{p=p_k} bigl[e^{pt}F(p)bigr].$

(5.22)

Замечания 5.5

1. Формула (5.21) может быть записана в виде $textstyle{L^{-1}! left[sumlimits_{n=0}^{infty} dfrac{a_n}{p^{n+1}}right]= sumlimits_{n=0}^{infty}a_nL^{-1}! left[dfrac{1}{p^{n+1}}right]}$ . Задача нахождения оригинала при выполнении условий теоремы сводится к нахождению коэффициентов разложения функции в ряд Лорана в окрестности бесконечно удаленной точки.

2. Формула (5.22) принимает наиболее простой вид в случае F(p)=R(p) — рационального изображения, т.е. $F(p)= R(p)= frac{P_m(p)}{Q_n(p)}$ , где P_m(p),,Q_n(p) — многочлены степеней /пил соответственно, не имеющие общих корней. Если все полюсы p_1,p_2,ldots,p_n функции F(p) простые, то по формуле (4.24) получаем $mathop{operatorname{res}}limits_{p=p_k} frac{P_m(p)}{Q_n(p)},e^{pt}= frac{P_m(p_k)}{Q'_n(p_k)},e^{p_kt}$ , а формула (5.22) принимает вид

$f(t)= sumlimits_{k=1}^{n} frac{P_m(p_k)}{Q'_n(p_k)},e^{p_kt}.$

(5.23)

3. Если при выполнении условий п.2 коэффициенты многочлена Q_n(p) — лействительные числа, то его комплексные корни, как известно, являются по парно сопряженными. Нахождение суммы вычетов в таких точках можно заме нить нахождением действительной части вычета в одной из них. Действительио, вычет в точке $overline{p}_k$ , используя свойства сопряженных чисел, можно записать следующим образом:

$mathop{operatorname{res}}limits_{p=overline{p}_k} frac{P_m(p)}{Q_n(p)},e^{pt}= frac{P_m(overline{p}_k)}{Q'_n(overline{p}_k)},e^{overline{p}_kt}= frac{overline{P_m(p_k)}}{overline{Q'_n(p_k)}},e^{overline{p_kt}}= overline{frac{P_m(p_k)}{Q'_n(p_k)},e^{p_kt}}.$

Это означает, что вычет в точке $overline{p}_k$ есть число, сопряженное вычету в точке p_k , а сумма таких чисел равна их удвоенной действительной части:

$mathop{operatorname{res}}limits_{p=p_k} frac{P_m(p)}{Q_n(p)},e^{pt}+ mathop{operatorname{res}}limits_{p=overline{p}_k} frac{P_m(p)}{Q_n(p)},e^{pt}= 2 operatorname{Re} mathop{operatorname{res}}limits_{p=p_k} frac{P_m(p)}{Q_n(p)},e^{pt}.$

Пример 5.24

Найти оригиналы для функций:

a) $F_1(p)=frac{1}{p}exp frac{1}{p^2},quad F_2(p)=frac{1}{p}cos frac{1}{p},quad F_2(p)= frac{1}{sqrt{p}}sin frac{1}{sqrt{p}}$ ;

б) $F_1(p)=frac{p}{p^2+4p+5},quad F_2(p)=frac{p+2}{(p+1)(p-2)(p^2+4)},quad F_3(p)=frac{p^2+p+1}{(p-1)(p+1)^2}$ .

Решение. В случае “а” для решения задачи используем теорему 5.1, а в случае “б” — теорему 5.2.

а) Используем типовые разложения

$e^z=sumlimits_{n=0}^{infty} frac{z^n}{n!},qquad cos z=sumlimits_{n=0}^{infty} frac{(-1)^nz^{2n}}{(2n)!},qquad sin z=sumlimits_{n=1}^{infty} frac{(-1)^{n+1}z^{2n-1}}{(2n-1)!},.$

Для заданных изображений получаем:

$begin{aligned}F_1(p)&= frac{1}{p} sumlimits_{n=0}^{infty} frac{1}{p^{2n}n!}= sumlimits_{n=0}^{infty} frac{1}{p^{2n+1}n!},quad a_{2n}=frac{1}{n!},;\[2pt] F_2(p)&= frac{1}{p} sumlimits_{n=0}^{infty} frac{(-1)^n}{p^{2n}(2n)!}= sumlimits_{n=0}^{infty} frac{(-1)^n}{p^{2n+1}(2n)!},quad a_{2n}= frac{(-1)^n}{(2n)!},;\[2pt] F_3(p)&= frac{1}{sqrt{p}} sumlimits_{n=1}^{infty} frac{(-1)^n}{sqrt{p^{2n+1}}(2n+1)!}= sumlimits_{n=1}^{infty} frac{(-1)^n}{(2n+1)!p^{n+1}},quad a_n= frac{(-1)^n}{(2n+1)!},.end{aligned}$

Согласно первой теореме разложения

$f_1(t)= sumlimits_{n=0}^{infty} frac{1}{n!}frac{t^{2n}}{(2n)!},,qquad f_2(t)= sumlimits_{n=0}^{infty} frac{(-1)^nt^{2n}}{[(2n)!]^2},,qquad f_3(t)= sumlimits_{n=0}^{infty} frac{(-1)^nt^n}{(2n+1)!n!},.$

б) Представим F_1(p) в виде

$F_1(p)= frac{p}{p^2+4p+5}= frac{P_1(p)}{Q_2(p)}= frac{p}{bigl[p-(-2+i)bigr] bigl[p-(-2-i)bigr]},.$

где p_1=-2+i,~ p_2=-2-i — простые полюсы функции F(p) . По второй теореме разложения

$begin{aligned}f_1(t)&= sumlimits_{k=1}^{2}frac{P_1(p_k)}{Q'_2(p_k)},e^{p_kt}= sumlimits_{k=1}^{2} frac{p_k}{2p_k+4},e^{p_kt}= frac{-2+i}{-4+2i+4},e^{(-2+i)t}+ frac{-2-i}{-4-2i+4},e^{(-2-i)t}=\ &=e^{-2t}! left(frac{-2+i}{2i},e^{it}+frac{2+i}{2i},e^{-it}right)= e^{-2t}! left(frac{e^{it}+e^{-it}}{2}-2cdotfrac{e^{it}-e^{-it}}{2i}right)= e^{-2t} bigl[cos t-2sin tbigr]. end{aligned}$

Тот же результат можно получить, пользуясь пп. 2 и 3 замечаний 5.5:

$begin{aligned}f_1(t)&= 2 operatorname{Re} mathop{operatorname{res}}limits_{p=-2+i} frac{p,e^{pt}}{p^2+4p+5}= left.{2 operatorname{Re} frac{p,e^{pt}}{2p+4}}right|_{-2+i}= 2 operatorname{Re} frac{-2+i}{2i},e^{(-2+i)t}=\ &=2 operatorname{Re}! left[e^{-2t}, frac{1+2i}{2},e^{it}right]= operatorname{Re} bigl[e^{-2t}(1+2i)(cos t+isin t)bigr]= e^{-2t}(cos t-2sin t). end{aligned}$

Функция F_2(p) имеет четыре простых полюса: p_1=-1,~ p_2=2,~ p_3=2i .

Так как вычет в простом полюсе находится по формуле $mathop{operatorname{res}}limits_{p=p_k} F(p)= limlimits_{pto p_k} F(p)(p-p_k)$ , то по второй теореме разложения

$begin{aligned}f_2(t)&= sumlimits_{k=1}^{4} mathop{operatorname{res}}limits_{p_k} bigl[F(p)e^{pt}bigr]= limlimits_{pto-1} frac{(p+2)e^{pt}}{(p-2)(p^2+4)}+ limlimits_{pto2} frac{(p+2)e^{pt}}{(p+1)(p^2+4)},+\ &qquad + limlimits_{pto2i} frac{(p+2)e^{pt}}{(p-1)(p+1)(p+2i)}+ limlimits_{pto-2i} frac{(p+2)e^{pt}}{(p-1)(p+1)(p-2i)}=\[2pt] &=-frac{1}{15},e^{-t}+ frac{1}{6},e^{2t}+frac{2+2i}{8-24i},e^{2it}+ frac{2-2i}{8+24i},e^{-t}=\[2pt] &=-frac{1}{15},e^{-t}+ frac{1}{6},e^{2t}+frac{-32+64i}{640},e^{2it}+ frac{-32-64i}{640},e^{-t}=\[2pt] &=-frac{1}{15},e^{-t}+ frac{1}{6},e^{2t}-frac{64}{640}cdot frac{e^{2it}+e^{-2it}}{2}-frac{128}{640}cdot frac{e^{2it}-e^{-2it}}{2i}=\[2pt] &=-frac{1}{15},e^{-t}+ frac{1}{6},e^{2t}-frac{1}{10}cos2t-frac{1}{5}sin2t,.end{aligned}$

Функция F_3(p) имеет два полюса: простой p_1=1 и полюс второго порядка p_2=-1 .

По второй теореме разложения $f_3(t)= mathop{operatorname{res}}limits_{p_1=1} frac{(p^2+p+1)e^{pt}}{(p-1)(p+1)^2}+ mathop{operatorname{res}}limits_{p_2=-1} frac{(p^2+p+1)e^{pt}}{(p-1)(p+1)^2}$ . Находим вычеты

$begin{aligned}mathop{operatorname{res}}limits_{p_1=1} frac{(p^2+p+1)e^{pt}}{(p-1)(p+1)^2}&= limlimits_{pto1} frac{(p^2+p+1)(p-1)e^{pt}}{(p-1)(p+1)^2}= limlimits_{pto1} frac{(p^2+p+1)e^{pt}}{(p+1)^2}= frac{3}{4},e^{t},\[2pt] mathop{operatorname{res}}limits_{p_2=-1} frac{(p^2+p+1)e^{pt}}{(p-1)(p+1)^2}&= limlimits_{pto-1} frac{d}{dp}! left[frac{(p^2+p+1)e^{pt}(p+1)^2}{(p-1)(p+1)^2}right]= ldots= frac{1}{4},e^{-t}-frac{t}{2},e^{-t}, end{aligned}$

получаем окончательный ответ $f_3(t)= frac{3}{4},e^{t}+frac{1}{4},e^{-t}-frac{t}{2},e^{-t}$ .

Приведем ряд известных приемов нахождения оригинала.

1. Если изображение отличается от табличного на постоянный множитель, то его следует умножить и одновременно поделить на этот множитель, а затем воспользоваться свойством линейности.

Пример 5.25

2. Изображение, заданное в виде дроби $frac{apm b}{c}$ , разлагается на сумму дробей.

Пример 5.26

Найти оригинал для функций: а) $F(p)= frac{3p}{(p+5)^2}$ ; б) $F(p)= frac{3p-2}{(p+5)^2}$ ; в) $F(p)= frac{p^3+2p+2}{p^3(p+1)}$ .

Решение. Представим дроби в виде суммы двух слагаемых, а затем воспользуемся свойством линейности и формулами из табл. 5.1:

а) $F(p)= frac{3(p+5)-15}{(p+5)^2}= 3cdotfrac{1}{p+5}-15cdot frac{1}{(p+5)^2}quad Rightarrowquad f(t)=3e^{-5t}-15te^{-5t}$ ;

б) $F(p)= 3cdot frac{p}{(p+5)^2}-frac{2}{1!}cdot frac{1!}{(p+5)^2}quad Rightarrowquad f(t)= 3(1-5t)e^{-5t}-2te^{-5t}= e^{-5t}(3-17t)$ .

в) представим F(p) в виде $F(p)= frac{p^3+2p+2}{p^3(p+1)}= frac{p^3+2(p+ 1)}{p^3(p+1)}= frac{2}{p^3}+ frac{1}{p+1}$ . По формулам 4,6 из табл. 5.1 находим $f(t)= t^2+e^{-t}$ .

3. Если знаменатель дроби содержит квадратный трехчлен, то в нем выде ляется полный квадрат: ap^2+bp+c= a(ppmalpha)^2pmomega^2 . При этом числитель дроби представляется в виде многочлена от .

Пример 5.27

Найти оригиналы для функций: a) $F(p)=frac{3}{p^2+4p+7}$ ; б) $F(p)= frac{3p+2}{2p^2-8p+6}$ .

Решение. а) Выделим полный квадрат в знаменателе дроби и воспользуемся табл. 5.1 (по формуле 12 из табл. 5.1 при a=-2,~ b=sqrt{3} ):

$F(p)= frac{3}{(p+2)^2-4+7}= frac{3}{(p+2)^2+3}= sqrt{3}cdot frac{sqrt{3}}{(p+2)^2+(sqrt{3})^2}quad Rightarrowquad f(t)=sqrt{3},e^{-2t}sin(t sqrt{3}).$

б) Используем представление

$F(p)= frac{3p+2}{2(p^2-4p+3)}= frac{1,!5p+1}{(p-2)^2-1}= frac{1,!5(p-2)+3}{(p-2)^2-1}+ frac{1}{(p-2)^2-1}= 1,!5cdotfrac{p-2}{(p-2)^2-1}+4cdot frac{1}{(p-2)^2-1},.$

По формулам 19,20 из табл. 5.1 и по теореме смещения (формула (5.8))

$f(t)=frac{3}{2},e^{2t}operatorname{ch}t+ 4e^{2t}operatorname{sh}t= frac{3}{2},e^{2t},frac{e^t+e^{-t}}{2}+ 4e^{2t},frac{e^t-e^{-t}}{2}= frac{11}{4},e^{3t}-frac{5}{4},e^{t}.$

Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. “б” примера 5.24):

$begin{gathered}F(p)= frac{3p+2}{2(p^2-4p+3)}= frac{3p+2}{2(p-1)(p-3)}\ Downarrow\ f(t)= mathop{operatorname{res}}limits_{p=1} F(p)e^{pt}+ mathop{operatorname{res}}limits_{p=3} F(p)e^{pt}= frac{5e^t}{2cdot(-2)}+ frac{11e^{3t}}{2cdot2}= frac{11}{4},e^{3t}-frac{5}{4},e^{t}.end{gathered}$

4. Если оригинал представляет собой правильную рациональную дробь, то следует разложить ее на простейшие дроби и для каждой из полученных дробей найти оригинал.

Примеры 5.28-5.29

Пример 5.28. Найти оригиналы для функций:

а) $F(p)=frac{3p^2+3p-13}{p(p^4+4p+13)}$ ; б) $F(p)=frac{p}{(p+2)^2(p-1)}$ ; в) $F(p)=frac{p^2+4}{(p-1)(p+2)(p-3)}$ ; г) $F(p)=frac{3p}{2p^2-2p-4}$ .

Решение. а) Представим F(p) в виде $F(p)=frac{3p^2+3p-13}{p(p^4+4p+13)} = frac{A}{p}+ frac{Bp+C}{p^2+4p+13}$ , где A,,B,,C — неопределенные коэффициенты.

Отсюда следует равенство 3p^2+3p-13= Ap^2+4Ap+13A+Bp^2+Cp .

Приравнивая коэффициенты при одинаковых степенях , получаем систему уравнений для нахождения неопределенных коэффициентов:

$begin{cases}A+B=3,\ 4A+C=3,\ 13A=-13.end{cases}$ Решая ее, получаем A=-1,~B=4,~C=7 и

$F(p)=-frac{1}{p}+frac{4p+7}{p^2+4p+13}=-frac{1}{p}+ frac{4(p+2)-1}{(p+2)^2+9}=-frac{1}{p}+4cdot frac{p+2}{(p+2)^2+3^2}-frac{1}{3}cdot frac{3}{(p+2)^2+3^2},.$

По формулам 1,12,13 из табл. 5.1 $f(t)=-1+4e^{-2t}cos3t-frac{1}{3},e^{-2t}sin3t$ .

б) Представим F(p) в виде $F(p)= frac{p}{(p+2)^2(p-1)}= frac{A}{p-1}+ frac{B}{p+2}+ frac{C}{(p+2)^2}$ , где A,,B,,C — неопределенные коэффициенты.

Отсюда A(p+2)^2+ B(p-1)(p+2)+ C(p-1)=p .

Подставляя последовательно p=1,~p=-2,~ p=0 , получаем $A=frac{1}{9},~ B=frac{2}{3},~ C=-frac{1}{9}$ и поэтому

$F(p)=frac{1}{9}cdot frac{1}{p-1}-frac{1}{9}cdot frac{1}{p+2}+ frac{2}{3}cdot frac{1}{(p+2)^2},.$

По формулам 6,7 из табл. 5.1 находим $frac{1}{9},e^{t}-frac{1}{9},e^{-2t}+ frac{2}{3},t,e^{-2t}.$ .

в) Представим изображение в виде $F(p)=frac{p^2+4}{(p-1)(p+2)(p-3)}= frac{A}{p-1}+ frac{B}{p+2}+ frac{C}{p-3}$ . Отсюда

A(p+2)(p-3)+ B(p-1)(p-3)+ C(p-1)(p+2)= p^2+4.

При p=1,~p=-2,~p=3 получаем $A=-frac{5}{6},~ B=frac{8}{15},~ C=frac{13}{10}$ , поэтому

$F(p)=-frac{5}{6}cdot frac{1}{p-1}+ frac{8}{15}cdot frac{1}{p+2}+ frac{13}{10}cdot frac{1}{p-3},.$

По свойству линейности и по формуле 6 из табл. 5.1 получаем

$f(t)=-frac{5}{6},e^{t}+ frac{8}{15},e^{-2t}+ frac{13}{10},e^{3t}.$

Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. “б” примера 5.24):

$begin{gathered}F(p)= frac{p^2+4}{(p-1)(p+2)(p-3)}\ Downarrow\ begin{aligned}f(t)&= mathop{operatorname{res}}limits_{p=1} F(p)e^{pt}+ mathop{operatorname{res}}limits_{p=-2} F(p)e^{pt}+ mathop{operatorname{res}}limits_{p=3} F(p)e^{pt}=\ &= frac{5e^t}{3cdot(-2)}+ frac{8e^{-2t}}{(-3)cdot(-5)}+ frac{13e^{3t}}{2cdot5}=-frac{5}{6},e^t+ frac{8}{15},e^{-2t}+ frac{13}{10},e^{3t}.end{aligned}end{gathered}$

г) Представим F(p) в виде $F(p)= frac{3p}{2p^2-2p-4}= frac{3p}{2(p-2)(p+1)}= frac{A}{p-2}+ frac{B}{p+1}$ , где A,,B — неопределенные коэффициенты.

Из равенства $A(p+1)+B(p-2)=frac{3p}{2}$ при p=-1,~p=2 получаем $A=1,~ B=frac{1}{2}$ , поэтому $F(p)=frac{1}{p-2}+ frac{1}{2}cdot frac{1}{p+1}$ .

По формуле 6 из табл. 5.1 имеем $f(t)=e^{2t}+frac{1}{2},e^{-t}$ .

Можно также решить эту задачу иначе, используя вторую теорему разложения (см. п. “б” примера 5.24 и п. “в” данного примера):

$begin{gathered}F(p)= frac{3p}{2(p^2-p-2)}= frac{3p}{2(p+1)(p-2)}\ Downarrow\ f(t)= mathop{operatorname{res}}limits_{p=-1} F(p)e^{pt}+ mathop{operatorname{res}}limits_{p=2} F(p)e^{pt}= frac{-3e^{-t}}{2cdot(-3)}+ frac{6e^{2t}}{2cdot3}= e^{2t}+frac{1}{2},e^{-t}. end{gathered}$

Пример 5.29. Найти оригиналы для функций: a) $F(p)= frac{1}{p^2(p-1)^2}$ ; б) $F(p)= frac{p}{(p^2+1)(p^2+4)}$ .

Решение. а) Решим пример различными способами.

Первый способ. Воспользуемся разложением дроби на элементарные:

$F(p)= frac{1}{p^2(p-1)^2}= frac{2}{p}+ frac{1}{p^2}-frac{2}{p-1}+ frac{1}{(p-1)^2},.$

По формулам 2,3,6,7 из табл. 5.1 получаем f(t)=2+t-2e^t+te^t .

Второй способ. Применим вторую теорему разложения, учитывая, что p_1=0 и p_2=1 — полюсы второго порядка функции F(p)colon

$begin{aligned} f(t)= mathop{operatorname{res}}limits_{p=0}F(p)e^{pt}+ mathop{operatorname{res}}limits_{p=1}F(p)e^{pt}= limlimits_{pto0} frac{d}{dp}! left[frac{p^2e^{pt}}{p^2(p-1)^2}right]+ limlimits_{pto1} frac{d}{dp}! left[frac{(p-1)^2e^{pt}}{p^2(p-1)^2}right]= ldots= t+2+te^t-2e^t.end{aligned}$

Третий способ. Обозначим $F_1(p)= frac{1}{(p-1)^2}$ . Тогда f_1(t)=t,e^t . Рассмотрим функцию $F_2(p)= frac{1}{p}F_1(p)$ . По свойству интегрирования оригинала (формула (5.12)) получаем

$f_2(t)= intlimits_{0}^{t}tau,e^{tau},dtau= Bigl.{tau,e^{tau}}Bigr|_{0}^{t}-Bigl.{e^{tau}}Bigr|_{0}^{t}= t,e^t-e^t+1.$

Заметим, что $F(p)= frac{1}{p}F_2(p)$ . Применяя еще раз свойство интегрирования оригинала, имеем

$f(t)= intlimits_{0}^{t}(tau,e^{tau}-e^{tau}+1)dtau= ldots= t,e^t-2e^t+2+t.$

Четвертый способ. Представим изображение в виде произведения

$F(p)= frac{1}{p^2(p-1)^2}= frac{1}{p^2}cdot frac{1}{(p-1)^2}= F_1(p)cdot F_2(p)$ , где $F_1(p)=frac{1}{p^2},~~ F_2(p)=frac{1}{(p-1)^2}$ .

По формулам 3 и 7 из табл. 5.1 f_1(t)=t,~ f_2(t)=t,e^t . Далее по теореме Бореля (формула (5.15))

$f(t)= f_1(t)ast f_2(t)= intlimits_{0}^{t}tau,e^{tau}(t-tau)dtau= ldots= t,e^t-2e^t+2+t.$

б) Решим пример также несколькими способами.

Первый способ. Воспользуемся разложением дроби на элементарные:

$F(p)= frac{p}{(p^2+1)(p^2+4)}= frac{p[p^2+4-(p^2+1)]}{3(p^2+1)(p^2+4)}= frac{1}{3}cdot frac{p}{p^2+1}-frac{1}{3}cdot frac{p}{p^2+4},.$

По формуле 9 из табл. 5.1 получаем $f(t)= frac{1}{3}cos t-frac{1}{3}cos2t$ .

Второй способ. Применим вторую теорему разложения с учетом пп. 2,3 замечаний 5.5:

$f(t)= 2operatorname{Re} mathop{operatorname{res}}limits_{p=i} frac{p,e^{pt}}{(p^2+1)(p^2+4)}+ 2operatorname{Re} mathop{operatorname{res}}limits_{p=2i} frac{p,e^{pt}}{(p^2+1)(p^2+4)}= ldots= frac{1}{3}cos t-frac{1}{3}cos2t.$

Третий способ. Представим изображение в виде произведения:

$F(p)= frac{p}{(p^2+1)(p^2+4)}= frac{p}{p^2+4}cdot frac{1}{p^2+1}= F_1(p)cdot F_2(p).$

Отсюда $f_1(t)= L^{-1}! left[frac{p}{p^2+4}right]=cos2t,~ f_2(t)= L^{-1}! left[frac{1}{p^2+1}right]= sin t$ . По теореме Бореля

$f(t)=f_1(t)ast f_2(t)= intlimits_{0}^{t} cos2tausin(t-tau)dtau= ldots= frac{1}{3}cos t-frac{1}{3}cos2t.$

Четвертый способ. Используем формулу 37 из табл. 5.1. При a=1,~b=2 получаем

$f(t)=frac{cos2t-cos t}{1-4}= frac{1}{3}cos t-frac{1}{3}cos2t.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

( jω) = H (s)

(5 − ω2 )+ j4,5ω