Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.
Применение такого вида задач используется в технике и физике элементарных частиц.
Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.
При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.
Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.
Абсолютно неупругий удар. Скорость
Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.
Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.
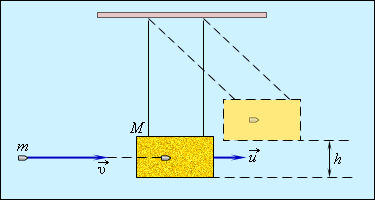
Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1.21.1, m – горизонтально летящая пуля с v→ скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.
Если скорость ящика с пулей обозначить как u→, тогда, используя формулу сохранения импульса, получаем:
mv=(M+m)u; u=mM+mv.
Когда пуля застревает в песке, то механическая энергия теряется:
∆E=mv22-(M+m)u22=MM+m·mv22.
M (M + m) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда
∆EE0=MM+m=11+mM.
Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.
Когда m << М ∆EE0→12, тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆EE0→0, только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим (m>>М), отношение принимает вид ∆EE0→0.
Расчет движения маятника производится по закону сохранения механической энергии. Получаем
(M+m)u22=(M+m)gh; u2=2gh.
В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что
v=M+mm2gh.
При известной высоте h возможно определение скорости пули v.
Рисунок 1.21.1. Баллистический маятник.
Абсолютно упругий удар
Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.
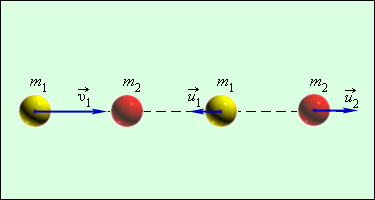
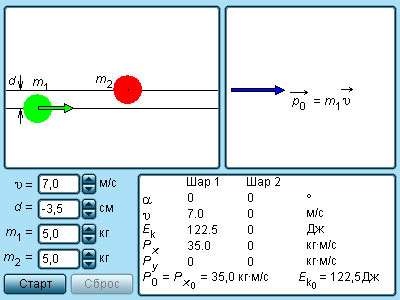
Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1.21.2.
Центральный удар – это соударение, когда скорости шаров направлены по линии центра.
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров.
Встречаются случаи, когда массы m1 и m2 не равны. Тогда, используя закон сохранения механической энергии, получаем
m1v122=m1v122+m2v222.
За v1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v2=0 скорость второго шара, u1 и u2 – скорости после столкновения.
Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:
m1v1=m1u1+m2u2.
Полученная система из двух уравнений позволяет найти неизвестные скорости u1 и u2 шаров после столкновения.
u1=m1-m2v1m1+m2; u2=2m1v1m1+m2.
Если массы равны, то есть, тогда происходит остановка первого шара (u1=0), а второй продолжает движение u2=v1. происходит обмен скоростями и импульсами.
При наличии нулевой скорости второго шара (v2≠0), задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v1’=v1–v2. После определения скорости шаров v1 и v2 производится переход к «неподвижной» системе.
С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.
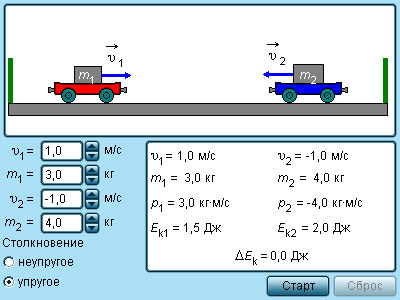
Рисунок 1.21.3. Модель упругие и неупругие соударения.
При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.
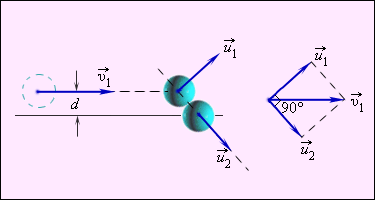
Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1.21.4.
Рисунок 1.21.4. Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.
Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v1 и v2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d, изображенное на рисунке 1.21.4.
Предельное расстояние
Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v1→ летящего шара.
При одинаковых массах шаров векторы v1→ и v2→ имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m1=m2=m, тогда определение примет вид
v1→=u1→+u2→; v12=u12+u22.
Первое равенство значит, что векторы v1→, u1→, u2→ образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u1→ и u2→, равняется 90 градусов.
Рисунок 1.21.5. Модель соударения упругих шаров
Примером применения
законов сохранения импульса и энергии
при решении реальной физической
задачи является удар абсолютно упругих
и неупругих тел.
Удар
(или соударение)
—
это столкновение двух или более тел,
при котором взаимодействие длится очень
короткое время. Исходя из данного
определения, кроме явлений, которые
можно отнести к ударам в прямом смысле
этого слова
28
(столкновения
атомов или биллиардных шаров), сюда
можно отнести и такие, как удар человека
о землю при прыжке с трамвая и т. д. При
ударе в телах возникают столь
значительные внутренние силы, что
внешними силами, действующими на
них, можно пренебречь. Это позволяет
рассматривать соударяющиеся тела
как замкнутую систему и применять к ней
законы сохранения.
Тела
во время удара претерпевают деформацию.
Сущность удара заключается в том,
что кинетическая энергия относительного
движения соударяющихся тел на короткое
время преобразуется в энергию упругой
деформации. Во время удара имеет
место перераспределение энергии между
соударяющимися телами. Наблюдения
показывают, что относительная скорость
тел после удара не достигает своего
прежнего значения. Это объясняется
тем, что нет идеально упругих тел и
идеально гладких поверхностей.
Отношение нормальных составляющих
относительной скорости тел после и до
удара называется коэффициентом
восстановления :
=
v’n/vn.
Если
для сталкивающихся тел =0,
то такие тела называются абсолютно
неупругими, если
=1—абсолютно
упругими.
На
практике для всех тел 0<<1
(например, для стальных шаров 0,56,
для шаров из слоновой кости 0,89,
для свинца 0).
Однако в некоторых случаях тела можно
с большой точностью рассматривать либо
как абсолютно упругие, либо как
абсолютно неупругие.
Прямая,
проходящая через точку соприкосновения
тел и нормальная к поверхности их
соприкосновения, называется линией
удара. Удар
называется центральным,
если
тела до удара движутся вдоль прямой,
проходящей через их центры масс. Мы
будем рассматривать только центральные
абсолютно упругие и абсолютно
неупругие удары.
Абсолютно
упругий удар — столкновение
двух тел, в результате которого в обоих
взаимодействующих телах не остается
никаких деформаций и вся кинетическая
энергия, которой обладали тела до удара,
после удара снова превращается в
кинетическую энергию
.
Для абсолютно
упругого удара выполняются закон
сохранения импульса и закон сохранения
кинетической энергии.
Обозначим
скорости шаров массами m1
и
m2
до удара через v1
и
v2,
после
удара — через v’1
и
v’2
(рис.
18). При прямом центральном ударе
векторы скоростей шаров до и после удара
лежат на прямой линии, соединяющей их
центры. Проекции векторов скорости на
эту линию равны модулям скоростей. Их
направления учтем знаками: положительное
значение припишем движению вправо,
отрицательное — движению влево.
При указанных
допущениях законы сохранения имеют вид
Произведя
соответствующие преобразования в
выражениях (15.1) и (15.2), получим
Решая уравнения
(15.3) и (15.5), находим
Разберем несколько
примеров.
29
Проанализируем
выражения (15.8) и (15.9) для двух шаров
различных масс:
а) m1
=m2.
Если
второй шар до удара висел неподвижно
(v2=0)
(рис.
19), то после удара остановится первый
шар (v’1=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(v’2
= v1);
б)
m1>m2.
Первый
шар продолжает двигаться в том же
направлении, как и до удара, но с меньшей
скоростью (v’1<v1).
Скорость
второго шара после удара больше, чем
скорость первого после удара (v’2>v’1)
(рис.20);
в)
m1<m2.
Направление
движения первого шара при ударе изменяется
— шар отскакивает обратно. Второй шар
движется в ту же сторону, в которую
двигался первый шар до удара, но с меньшей
скоростью, т.е. v’2<v1
(рис.
21);
г)
m2>>m1
(например,
столкновение шара со стеной). Из уравнений
(15.8) и (15.9) следует, что v’1=-v1,
v’22m1v1/m20.
2) При
m1=m2
выражения
(15.6) и (15.7) будут иметь вид
v’1=v2,
v’2=v1,
т. е. шары равной
массы «обмениваются» скоростями.
Абсолютно
неупругий удар — столкновение
двух тел, в результате которого тела
объединяются, двигаясь дальше как единое
целое.
Продемонстрировать
абсолютно неупругий удар можно с
помощью шаров из пластилина (глины),
движущихся навстречу друг другу (рис.
22).
Если
массы шаров m1
и
m2,
их скорости до удара v1
и
v2,
то,
используя закон сохранения импульса,
можно записать
Если
шары движутся навстречу друг другу, то
они вместе будут продолжать двигаться
в ту сторону, в которую двигался шар,
обладающий большим импульсом. В частном
случае если массы шаров равны (m1=m2),
то
v
= (v1+v2)/2.
Выясним, как
изменяется кинетическая энергия
шаров при центральном абсолютно
неупругом ударе. Так как в процессе
соударения шаров между ними дей-
30
ствуют силы,
зависящие не от самих деформаций, а от
их скоростей, то мы имеем дело с силами,
подобными силам трения, поэтому закон
сохранения механической энергии не
должен соблюдаться. Вследствие деформации
происходит «потеря» кинетической
энергии, перешедшей в тепловую или
другие формы энергии. Эту «потерю» можно
определить по разности кинетической
энергии тел до и после удара:
Если
ударяемое тело было первоначально
неподвижно (v2=0),
то
Когда
m2>>m1
(масса
неподвижного тела очень большая), то
v<<v1
и
почти
вся кинетическая энергия тела при ударе
переходит в другие формы энергии.
Поэтому, например, для получения
значительной деформации наковальня
должна быть массивнее молотка.
Наоборот, при забивании гвоздей в стену
масса молотка должна быть гораздо
большей (m1>>m2),
тогда
vv1
и
практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.
Абсолютно неупругий
удар — пример того, как происходит
«потеря» механической энергии под
действием диссипативных сил.
Контрольные
вопросы
• В чем различие
между понятиями энергии и работы?
• Как найти
работу переменной силы?
• Какую работу
совершает равнодействующая всех сил,
приложенных к телу, равномерно движущемуся
по окружности?
• Что такое
мощность? Вывести ее формулу.
• Дайте определения
и выведите формулы для известных вам
видов механической энергии. • Какова
связь между силой и потенциальной
энергией?
• Почему изменение
потенциальной энергии обусловлено
только работой консервативных сил?
• В чем заключается
закон сохранения механической энергии?
Для каких систем он выполняется?
• Необходимо
ли условие замкнутости системы для
выполнения закона сохранения механической
энергии?
• В чем физическая
сущность закона сохранения и превращения
энергии? Почему он является фундаментальным
законом природы?
• Каким свойством
времени обусловливается справедливость
закона сохранения механической энергии?
• Что такое
потенциальная яма? потенциальный барьер?
• Какие заключения
о характере движения тел можно сделать
из анализа потенциальных кривых?
• Как
охарактеризовать положения устойчивого
и неустойчивого равновесия? В чем их
различие?
• Чем отличается
абсолютно упругий удар от абсолютно
неупругого?
• Как определить
скорости тел после центрального абсолютно
упругого удара? Следствием каких законов
являются эти выражения?
31
Задачи
3.1. Определить:
1) работу поднятия груза по наклонной
плоскости; 2) среднюю и 3) максимальную
мощности подъемного устройства, если
масса груза 10 кг, длина наклонной
плоскости 2 м, угол ее наклона к горизонту
45°, коэффициент трения 0,1 и время подъема
2 с. [1) 170 Дж; 2) 85 Вт; 3) 173 Вт |
3.2. С башни высотой
35 м горизонтально брошен камень массой
0,3 кг. Пренебрегая сопротивлением
воздуха, определить: 1) скорость, с которой
брошен камень, если через 1 с после начала
движения его кинетическая энергия 60
Дж; 2) потенциальную энергию камня через
1 с после начала движения. [1) 17,4 м/с; 2)
88,6 Дж ]
3.3. Пренебрегая
трением, определить наименьшую высоту,
с которой должна скатываться тележка
с человеком по желобу, переходящему в
петлю радиусом 10 м, чтобы она сделала
полную петлю и не выпала из желоба. [25
м]
3.4.
Пуля массой m=
10 г, летевшая горизонтально со скоростью
v
= 500 м/с, попадает в баллистический
маятник длиной l=
1 м и массой М = 5 кг и застревает в нем.
Определить угол отклонения маятника.
[ 18°30′ ]
3.5.
Зависимость потенциальной энергии
частицы в центральном силовом поле от
расстояния r
до
центра
поля задается выражением П(r)
=A/r2
-B/r,
где А
и
В —
положительные постоянные.
Определить
значение r0,
соответствующее
равновесному положению частицы. Является
ли это положение положением устойчивого
равновесия? [r0
= 2А/В]
3.6.
При центральном абсолютно упругом ударе
движущееся тело массой m1
ударяется
в покоящееся тело массой m2,
в результате чего скорость первого тела
уменьшается в n=
1,5 раза. Определить: 1) отношение m1/m2;
2)
кинетическую энергию T’2,
с
которой начнет двигаться второе
тело, если первоначальная кинетическая
энергия первого тела T1
=
1000 Дж. [ 1) 5; 2) 555 Дж ]
3.7.
Тело массой m1=4
кг движется со скоростью v1=3
м/с
и ударяется о неподвижное тело такой
же массы. Считая удар центральным и
неупругим, определить количество
теплоты, выделившееся при ударе. [9 Дж ]
* У. Гамильтон
(1805—1865) — ирландский математик и
физик.
Соседние файлы в папке Трофимова Курс физики
- #
16.03.2016101.07 Кб8625.doc
- #
- #
16.03.2016139.26 Кб9127.doc
- #
16.03.2016290.82 Кб14028.doc
- #
16.03.2016364.03 Кб13729.doc
- #
16.03.2016205.31 Кб1193.doc
- #
- #
16.03.2016403.97 Кб121431.doc
- #
16.03.2016379.39 Кб15432.doc
- #
16.03.2016300.54 Кб1364.doc
- #
16.03.2016153.09 Кб895.doc
У этого термина существуют и другие значения, см. Удар (значения).
Уда́р — это кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь.
Физическая абстракция[править | править код]
| Причины отказа механики |
|---|
|
При ударе выполняются закон сохранения импульса и закон сохранения момента импульса, но обычно не выполняется закон сохранения механической энергии, заключённой в поступательном движении сталкивающихся тел. При рассмотрении упрощённой модели удара предполагается, что за время соприкосновения тел при ударе действием внешних сил можно пренебречь, тогда импульс системы тел при ударе сохраняется, в более точных моделях нужно учитывать привнесённый в систему импульс внешних сил. Часть поступательной кинетической энергии при не абсолютно упругом ударе переходит во внутреннюю энергию соударяющихся тел — на возбуждение механических колебаний и акустических волн, повышение внутренней энергии упругих связей — деформацию и на нагрев тел. Механические колебания и волны воспринимаются как звук удара и вибрации.
Результат столкновения двух тел можно полностью рассчитать, если известны их импульсы, массы и механическая энергия поступательного движения после удара. Предельные случаи — абсолютно упругий удар[⇨] и абсолютно неупругий удар[⇨], промежуточные случаи характеризуют коэффициентом сохранения энергии k, определяемым как отношение кинетической энергии после удара к кинетической энергии до удара. Технически k определяют при ударе одного тела о неподвижную стенку, сделанную из материала другого тела. Таким образом, k является внутренней характеристикой материала, из которого изготовлены тела, и в первом приближении не зависит от остальных параметров тел (формы, скорости и т. п.).
Если не известны потери энергии либо происходит одновременное столкновение нескольких тел или столкновение точечных частиц, то определить однозначно движение тел после удара невозможно. В этом случае рассматривается зависимость возможных углов рассеяния и скоростей тел после удара от начальных условий. Например, при столкновении двух элементарных частиц рассеяние может произойти лишь в некотором диапазоне углов, определяющемся предельным углом рассеяния.
В общем случае решение задачи о столкновении кроме знания начальных скоростей требует дополнительных параметров.
Абсолютно упругий удар[править | править код]
Абсолютно упругий удар — это модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошим приближением к модели абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.
Математическая модель абсолютно упругого удара работает примерно следующим образом:
- есть в наличии два абсолютно твёрдых тела, которые сталкиваются;
- в точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно и полностью переходит в энергию деформации;
- в следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации полностью обратно переходит в кинетическую энергию;
- контакт тел прекращается, и они продолжают движение.
Для математического описания абсолютно упругих ударов используется закон сохранения энергии и закон сохранения импульса.
Здесь 


Важно — импульсы складываются векторно, а энергии скалярно.
Вывод формул для конечных скоростей после столкновения[править | править код]
Зная начальные скорости и массы из законов сохранения можно вывести конечные скорости после столкновения.
Покажем это на примере, когда два тела сталкиваются вдоль одной прямой.
Законы сохранения энергии и импульса можно переписать как:
Делим одно уравнение на другое: 
Из этого уравнения выразим скорости после столкновения:
Подставим конечные скорости в закон сохранения импульса, получаем:
Выразим отсюда конечные скорости 

Абсолютно упругий удар тел равных масс
Абсолютно упругий удар двух тел разных масс
Абсолютно упругий удар тел равных масс, но с различными направлениями и модулями скоростей
Абсолютно упругий удар элементарных частиц[править | править код]
Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц при низких энергиях. Это является следствием принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы — перевода энергии частицы на верхний соседний дискретный энергетический уровень, то механическая энергия системы не меняется. Изменение механической энергии может также быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п.). Надо, однако, учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение кванта света. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новых частиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужно учитывать изменение системы.
Абсолютно упругий удар в пространстве[править | править код]
В случае столкновения двух тел в трёхмерном пространстве векторы импульсов тел до и после столкновения лежат в одной плоскости. Вектор скорости каждого тела может быть разложен на две компоненты: одна по общей нормали поверхности сталкивающихся тел в точке контакта, а другая параллельная поверхности столкновения. Поскольку сила удара действует только по линии столкновения, компоненты скорости, векторы которых проходят по касательной к точке столкновения, не изменяются. Скорости, направленные вдоль линии столкновения, могут быть вычислены с помощью тех же уравнений, что и столкновения в одном измерении. Окончательные скорости могут быть вычислены из двух новых компонентов скоростей и будут зависеть от точки столкновения.
Если предположить, что первая частица двигается, а вторая частица находится в состоянии покоя до столкновения, то углы отклонения двух частиц, θ1 и θ2, связаны с углом отклонения θ следующим выражением:
Столкновение двух тел в двумерном пространстве

Величины скоростей после столкновения будут следующими:

Двумерное столкновение двух движущихся объектов[править | править код]
В случае, когда оба тела движутся в плоскости, компоненты x и y скорости первого тела после соударения могут быть вычислена как:
![{displaystyle {begin{aligned}v'_{1x}&={frac {v_{1}cos(theta _{1}-varphi )(m_{1}-m_{2})+2m_{2}v_{2}cos(theta _{2}-varphi )}{m_{1}+m_{2}}}cos(varphi )\[0.2em]&quad +v_{1}sin(theta _{1}-varphi )cos(varphi +{frac {pi }{2}})\[0.8em]v'_{1y}&={frac {v_{1}cos(theta _{1}-varphi )(m_{1}-m_{2})+2m_{2}v_{2}cos(theta _{2}-varphi )}{m_{1}+m_{2}}}sin(varphi )\[0.2em]&quad +v_{1}sin(theta _{1}-varphi )sin(varphi +{frac {pi }{2}})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b3b7479d07075c0c5ce3f30db29f25c8a0449c)
где v1 и v2 скалярные величины двух первоначальных скоростей двух тел, m1 и m2 их массы, θ1 и θ2 углы движения, и маленькое Фи (φ)это угол соприкосновения. Чтобы получить ординату и абсциссу вектора скорости второго тела, необходимо заменить подстрочный индекс 1 и 2, на 2 и 1 соответственно.
Абсолютно неупругий удар[править | править код]

Абсолю́тно неупру́гий удар — это удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело[1]. Его скорость может быть найдена из закона сохранения импульса:
где 




Импульсы являются величинами векторными, поэтому складываются только векторно:
-
.
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соударяемых тел в результате неупругих деформаций переходит в тепловую. В случае абсолютно неупругого удара механическая энергия уменьшается на максимально возможную величину, не противоречащую закону сохранения импульса. Данное утверждение можно принять за определение абсолютно неупругого удара в терминах энергии. При помощи теоремы Кёнига легко показать, что в этом случае тела продолжают движение как единое целое: компонента кинетической энергии, отвечающая за движение центра масс всей системы соударяемых тел, должна остаться неизменной в силу закона сохранения импульса, а кинетическая энергия в системе отсчёта, связанной с центром масс, будет минимальной в том случае, когда тела в ней покоятся.
Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.
Реальный удар[править | править код]
Основной источник: [2]
При реальном соударении тел наблюдаются промежуточные варианты между случаем абсолютно упругого удара — отскока, и случаем абсолютно неупругого удара — слипания соударяющихся тел.
Степень близости соударения к случаю абсолютно упругого удара характеризуют коэффициентом восстановления 
При 

- Пример для соударения
Пусть 



,
,
.
Потеря кинетической энергии 
.
Для абсолютно неупругого удара 

Для абсолютно упругого удара 

| Материал | Коэффициент восстановления |
| Стекло | 
|
| Удар дерева о гуттаперчу | 
|
| Дерево | 
|
| Сталь, пробка | 
|
| Слоновая кость | 
|
Кроме того, при реальном ударе макроскопических тел происходит деформация соударяющихся тел и распространение по ним упругих волн, передающих взаимодействие от сталкивающихся границ по всему телу.
Пусть сталкиваются одинаковые тела. Если c — скорость звука в теле, L — характерный размер каждого тела, то время удара будет порядка времени 
Систему сталкивающихся тел можно считать замкнутой, если импульс силы внешних сил за время соударения мал по сравнению с импульсами тел.
Кроме того, само время соударения должно быть достаточно мало, иначе при рассмотрении трудно оценить потери энергии на упругую деформацию за время удара, и при этом часть энергии расходуется на внутреннее трение, а само описание сталкивающихся тел становится сложным из-за существенного вклада внутренних колебательных степеней свободы.
В приведенном анализе необходимо, чтобы линейные деформации тел при ударе были существенно меньше, чем собственные размеры тел.
См. также[править | править код]
- Рассеяние частиц
- Взаимодействие многих тел
Примечания[править | править код]
- ↑ Сивухин, 1979, с. 143.
- ↑ Зиновьев В. А. Краткий технический справочник. Том 1. — М.: Государственное издательство технико-теоретической литературы, 1949. — С. 290
Литература[править | править код]
- Сивухин Д.В. Механика. — М.: Наука, 1979. — 520 с.
Механическое взаимодействие в природе можно условно разделить на ударное и безударное.
Безударное взаимодействие – это притяжение и отталкивание.
Для ударного взаимодействия в задачах механики применяют закон сохранения импульса.
Виды ударов
В школьном курсе физики рассматривают два вида ударного взаимодействия: абсолютно упругий удар или абсолютно неупругий удар.
Если деформации тел при ударе нет, считают, что удар абсолютно упругий.
Если же деформация присутствует и после удара образуется новое тело – удар абсолютно неупругий.
Абсолютно упругий и абсолютно неупругий удары – это два крайних случая на шкале ударного взаимодействия
Рис. 1. Абсолютно упругий и абсолютно неупругий удары – крайние случаи взаимного действия тел
При ударах большинства реальных тел часть энергии всегда тратится на деформацию этих тел. Поэтому, удары большинства реальных тел лежат на шкале между двумя крайними видами ударов.
Рассмотрим движение тел вдоль одной прямой. Тела либо двигаются навстречу, либо одно тело догоняет другое.
Абсолютно неупругий удар
Суть абсолютно неупругого удара кратко можно описать так: Две капли ртути катились, ударились, слились в общую каплю ртути.
Нарисуем капли ртути до удара. Отметим на рисунке массу каждой капли. Скорости капель укажем с помощью векторов, направленных по движению каждой капли.
Вычислим импульсы тел
( m_{1} cdot vec{v_{1text{до}}} = vec{p_{1text{до}}} )
( m_{2} cdot vec{v_{2text{до}}} = vec{p_{2text{до}}} )
Рис. 2. Одно тело двигается навстречу другому вдоль одной прямой
Нарисуем ось, для того, чтобы определить знак для импульса каждой капли.
Импульс, сонаправленный с осью, будет иметь положительный знак, направленный против оси – отрицательный.
Сложим векторы импульсов, чтобы найти общий импульс системы – вектор (vec{p_{text{общ.до}}} ).
Каждый импульс запишем со своим знаком
( m_{1} cdot vec{v_{1text{до}}} — m_{2} cdot vec{v_{2text{до}}} = vec{p_{text{общ.до}}})
Сделаем второй рисунок, описывающий ситуацию после абсолютно неупругого удара.
На этом рисунке укажем массу образовавшейся капли и ее скорость. Укажем стрелкой и символом (vec{v_{text{общ.после}}} ), куда движется капля после удара .
Ось поможет выбрать знак для импульса капли.
Рис. 3. После абсолютно неупругого удара образовалось новое тело, оно движется сонаправленно с телом, имевшим наибольший до удара импульс
На рисунке скорость сонаправлена с осью, поэтому, импульс капли после удара имеет положительный знак.
( left( m_{1} + m_{2} right) cdot vec{v_{text{общ.после}}} = vec{p_{text{общ.после}}})
Примечание: Иногда в условии задачи не уточняется, в какую сторону будет двигаться тело после удара. В таком случае, направление движения выбираем сами (влево или вправо на рисунке). Если в ходе решения получим импульс тела, или его скорость со знаком минус, значит, тело движется в противоположную сторону от указанного нами направления. Такой выбор направления ошибкой считаться не будет. А знак минус подскажет, что импульс (и скорость) нужно развернуть в противоположную сторону.
По закону сохранения импульса, векторы (vec{p_{text{общ.до}}}) и (vec{p_{text{общ.после}}}) равны.
( m_{1} cdot vec{v_{1text{до}}} — m_{2} cdot vec{v_{2text{до}}} = vec{p_{text{общ.до}}})
( left( m_{1} + m_{2} right) cdot vec{v_{text{общ.после}}} = vec{p_{text{общ.после}}})
(vec{p_{text{общ.до}}} = vec{p_{text{общ.после}}})
Значит, закон сохранения импульса для абсолютно неупругого удара запишем в таком виде:
( m_{1} cdot vec{v_{1text{до}}} — m_{2} cdot vec{v_{2text{до}}} = left( m_{1} + m_{2} right) cdot vec{v_{text{общ.после}}} )
При абсолютно неупругом ударе:
— Выполняется закон сохранения импульса,
— Не выполняется закон сохранения энергии, так как часть энергии тратится на деформацию тел.
Примечание: Встречаются задачи вида: человек на льду бросил гирю в горизонтальном направлении, гиря полетела в одну сторону, а человек – в противоположную. Такие задачи решаем, применяя принципы для абсолютно неупругого удара. С той лишь разницей, что меняем местами рисунки до и после удара. Вначале тела находились вместе, после броска – разлетелись в противоположные стороны.
Абсолютно упругий удар
Кратко суть абсолютно упругого удара опишем так: Два бильярдных шара катились, без деформации ударились, и разбежались в разные стороны.
Составим рисунок для ситуации до удара. Отметим на рисунке массу каждого шара. Скорости шаров укажем с помощью векторов, направленных по движению каждого шара.
Запишем импульсы шаров до удара
( m_{1} cdot vec{v_{1text{до}}} = vec{p_{1text{до}}} )
( m_{2} cdot vec{v_{2text{до}}} = vec{p_{2text{до}}} )
Рис. 4. До удара два тела двигаются навстречу вдоль одной прямой
Нарисуем ось, чтобы определить знаки импульсов каждого шара. Сонаправленный с осью импульс имеет знак «+», направленный против оси – знак «-».
Сложим импульсы и найдем общий импульс системы – вектор (vec{p_{text{общ.до}}} ).
Каждый импульс записываем со своим знаком
( m_{1} cdot vec{v_{text{1до}}} — m_{2} cdot vec{v_{text{2до}}} = vec{p_{text{общ.до}}})
На втором рисунке опишем задачу после абсолютно упругого удара.
Укажем массы шаров, их скорости нарисуем стрелками в направлении движения каждого шара. Обозначим скорости символами (vec{v_{text{1после}}} ) и (vec{v_{text{2после}}} ).
С помощью проведенной оси выбираем знаки импульсов шаров.
Составим выражение для общего импульса после удара.
( — m_{1} cdot vec{v_{text{1после}}} + m_{2} cdot vec{v_{text{2после}}} = vec{p_{text{общ.после}}})
Рис. 5. После удара тела двигаются в противоположных направлениях
Для замкнутой системы выполняется закон сохранения импульса
(vec{p_{text{общ.до}}} = vec{p_{text{общ.после}}})
Запишем его в развернутом виде для абсолютно упругого удара:
( m_{1} cdot vec{v_{text{1до}}} — m_{2} cdot vec{v_{text{2до}}} = — m_{1} cdot vec{v_{text{1после}}} + m_{2} cdot vec{v_{text{2после}}} )
При абсолютно упругом ударе:
— Выполняется закон сохранения импульса,
— Выполняется закон сохранения энергии.
Алгоритм решения задач на тему закон сохранения импульса
Решение большинства задач на закон сохранения импульса можно проводить по такому алгоритму:
- Убеждаемся, что систем замкнутая. О видах систем написано тут.
- На рисунке описываем ситуацию до удара.
- Складываем импульсы всех тел системы до удара. Полученный вектор – это ( vec{p_{text{общ.до}}})
- Составляем второй рисунок, на котором представляем ситуацию после удара.
- Складываем импульсы всех тел системы после удара. Полученный вектор – это ( vec{p_{text{общ.после}}})
- Приравниваем импульсы ( vec{p_{text{общ.до}}}) до удара и ( vec{p_{text{общ.после}}}) после удара
Если тела двигаются под углом друг к другу (вдоль непараллельных прямых)
При решении таких задач, нужно помнить, что, векторы ( vec{p_{text{общ}}}) равны. Значит, когда нам известен один из векторов, автоматически становится известен и второй вектор.
Поэтому, когда нужно определить импульс тела в задачах, в которых тела не двигаются вдоль одной прямой, мы ищем тот импульс ( vec{p_{text{общ}}}) , который нам удобнее найти. А после этого применяем тот факт, что векторы равны ( vec{p_{text{общ.до}}} = vec{p_{text{общ.после}}}).
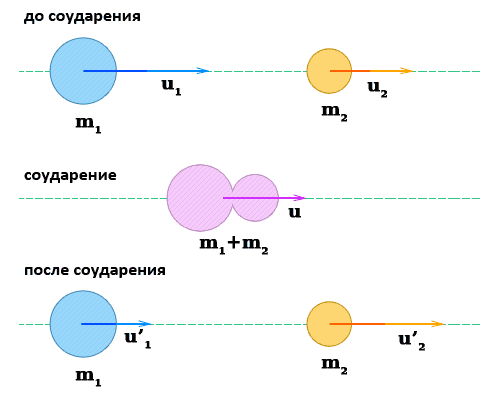
Упругое соударение
Соударение — это столкновение двух тел.
При соприкосновении тела обмениваются энергией и импульсом.
После соударения они двигаются со скоростями, которые отличаются по направлению и величине от их скоростей до столкновения.
При лобовом центральном соударении центры масс обоих тел двигаются вдоль одной линии.
Силы взаимодействия, возникающие при соударении, параллельны направлению движения.
Если применить к такой системе двух тел закон сохранения импульса, то полный импульс системы будет равен алгебраической сумме импульсов обоих тел.
Упругое соударение
При упругом соударении на протяжении кратковременного соприкосновения тела двигаются с общей скоростью,
затем они разлетаются и продолжают двигаться с разными скоростями.
Если
| m1 | масса первого тела, | кг |
|---|---|---|
| m2 | масса второго тела, | кг |
| u1 | скорость первого тела до соударения, | метр/секунда |
| u2 | масса второго тела до соударения, | метр/секунда |
| u`1 | скорость первого тела после соударения, | метр/секунда |
| u`2 | масса второго тела после соударения, | метр/секунда |
то из закона сохранения импульса следует
[ m_1 u_1 + m_2 u_2 = m_1 u`_1 + m_2 u`_2 ]
или
[ m_1 (u_1 – u`_1) = m_2 (u`_2 – u_2) ]
Из закона сохранения энергии получаем
[ frac{m_1 u_1 ^2}{2} + frac{m_2 u_2 ^2}{2} = frac{m_1 u`_1 ^2}{2} + frac{m_2 u`_2 ^2}{2} ]
или
[ m_1 (u_1 ^2 – u`_1 ^2) = m_2 (u`_2 ^2 – u_2 ^2) ]
подставив формулу разность квадратов получим
[ m_1 (u_1 – u`_1)(u_1 + u`_1) = m_2 (u`_2 – u_2)(u`_2 + u_2) ]
воспользовавшись законом сохранения импульса, находим
[ u_1 + u`_1 = u`_2 + u_2 ]
Сумма скоростей до и после соударения одинакова при любом соударении тел.
Из формулы (6) следует
[ u`_2 = u`_1 + u_1 – u_2 ]
[ u`_1 = u`_2 + u_2 – u_1 ]
Подставив эти выражения в видоизмененный закон сохранения импульса, получим
[ m_1 (u_1 – u`_1) = m_2 (u`_1 + u_1 – u_2 – u`_2) ]
[ m_1 (u_1 – u_2 – u`_2 + u_1) = m_2 (u`_2 – u_2) ]
откуда, разрешив относительно u`1 и u`2 найдем
[ u`_1 = frac{ (m_1 – m_2) u_1 + 2 m_2 u_2 }{ m_1 + m_2 } ]
[ u`_2 = frac{ (m_2 – m_1) u_2 + 2 m_1 u_1 }{ m_1 + m_2 } ]
Упругое соударение, вычислить скорости тел после упругого соударения
Упругое соударение |
стр. 477 |
|---|

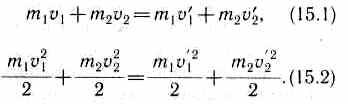





























![{displaystyle T=(1-k^{2}){frac {m_{1}m_{2}}{m_{1}+m_{2}}}{frac {(u_{1}-u_{2})^{2}}{2}}={frac {1-k}{1+k}}left[{frac {m_{1}(u_{1}-v_{1})^{2}}{2}}+{frac {m_{2}(u_{2}-v_{2})^{2}}{2}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8dcdfa863fa5c185246e1b6a0a193adf1647973)