Как работают атомы
Время на прочтение
5 мин
Количество просмотров 40K
Что удерживает электрон в атоме на орбите атомного ядра?
На первый взгляд, особенно если смотреть на мультяшную версию атома, описанную мною ранее со всеми её недостатками, электроны, двигающиеся по орбите вокруг ядра, выглядят так же, как планеты, двигающиеся по орбите вокруг Солнца. И вроде бы принцип этих процессов одинаков. Но есть подвох.
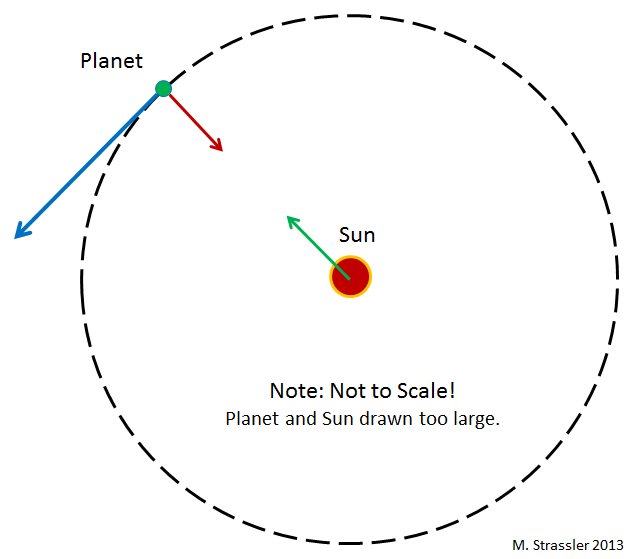
Рис 1
Что удерживает планеты на орбите вокруг Солнца? В Ньютоновской гравитации (Эйнштейновская сложнее, но тут она нам не нужна) любая пара объектов притягивается друг к другу посредством гравитационного взаимодействия, пропорционального произведению их масс. В частности, гравитация Солнца притягивает к нему планеты (с силой, обратно пропорциональной квадрату расстояния между ними. То есть, если расстояние уменьшается вдвое, сила увеличивается вчетверо). Планеты тоже притягивают Солнце, но оно настолько тяжёлое, что это почти не влияет на его движение.
Инерция, тенденция объектов к перемещению по прямым линиям в случае отсутствия действия на них других сил, работает против гравитационного притяжения, и в результате планеты двигаются вокруг Солнца. Это видно на рис.1, где изображена круговая орбита. Обычно эти орбиты эллиптические – хотя в случае планет они почти круглые, поскольку так формировалась Солнечная система. Для различных мелких камней (астероидов) и глыб льда (комет), двигающихся по орбитам вокруг Солнца, это уже не так.
Сходным образом все пары электрически заряженных объектов притягиваются или отталкиваются друг от друга, с силой, тоже обратно пропорциональной квадрату расстояния между ними. Но, в отличие от гравитации, которая всегда притягивает объекты вместе, электрические силы могут как притягивать, так и отталкивать. Объекты, обладающие одинаковыми, положительными или отрицательными зарядами, отталкиваются. А отрицательно заряженный объект притягивает положительно заряженный объект, и наоборот. Отсюда и романтическая фраза «противоположности притягиваются».
Поэтому положительно заряженное атомное ядро в центре атома притягивает легковесные электроны, двигающиеся на задворках атома, к себе, примерно как Солнце притягивает планеты. Электроны тоже притягивают ядро, но масса ядер настолько больше, что их притяжение почти не влияет на ядро. Электроны также отталкиваются друг от друга, что является одной из причин, по которым они не любят проводить время близко друг к другу. Можно было бы считать, что электроны в атоме перемещаются по орбитам вокруг ядра примерно так же, как планеты перемещаются вокруг Солнца. И на первый взгляд, именно так они и поступают, особенно в мультяшном атоме.
Но вот, в чём подвох: на самом деле, это двойной подвох, и каждый из двух подвохов оказывает эффект, противоположный другому, в результате чего они взаимно уничтожаются!
Двойной подвох: как атомы отличаются от планетных систем
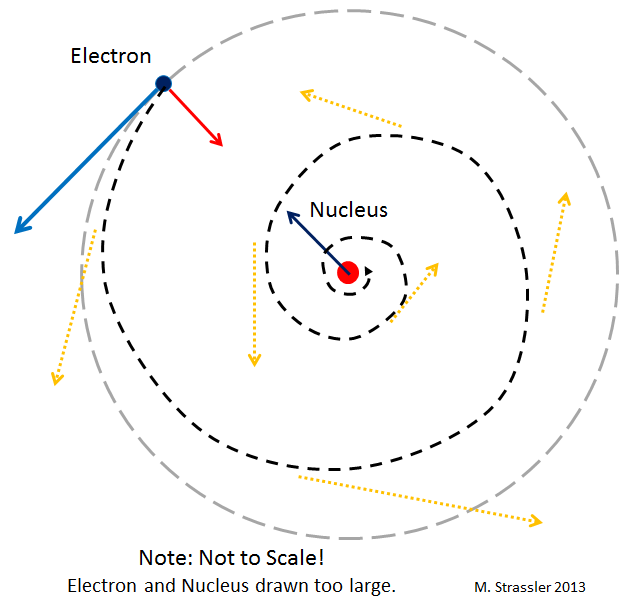
Рис 2
Первый подвох: в отличие от планет, электроны, двигающиеся по орбитам вокруг ядра, должны излучать свет (точнее, электромагнитные волны, одним из примеров которых служит свет). А это излучение должно заставлять электроны замедляться и по спирали падать на ядро. В принципе, в теории Эйнштейна существует схожий эффект – планеты могут испускать гравитационные волны. Но он чрезвычайно мал. В отличие от случая с электронами. Получается, что электроны в атоме должны очень быстро, за малую долю секунды, по спирали упасть на ядро!
И они бы так и сделали, если бы не квантовая механика. Потенциальная катастрофа изображена на рис. 2.
Второй подвох: но наш мир работает согласно принципам квантовой механики! А у неё есть свой удивительный и контринтуитивный принцип неопределённости. Этот принцип, описывающий тот факт, что электроны – это такие же волны, как и частицы, заслуживает своей собственной статьи. Но вот, что нам нужно знать о нём для сегодняшней статьи. Общее следствие этого принципа состоит в том, что невозможно знать все характеристики объекта одновременно. Существуют наборы характеристик, для которых измерение одной из них делает другие неопределёнными. Один из случаев – это местоположение и скорость таких частиц, как электроны. Если вы точно знаете, где находится электрон, вы не знаете, куда он направляется, и наоборот. Можно достичь компромисса и с некоторой точностью знать, где он, и с некоторой точностью знать, куда он направляется. В атоме так всё и получается.
Допустим, электрон по спирали падает на ядро, как на рис. 2. В процессе его падения нам всё точнее и точнее будет известно его местоположение. Тогда принцип неопределённости говорит нам, что его скорость будет становиться всё более и более неопределённой. Но если электрон остановится на ядре, его скорость не будет неопределённой! Поэтому он не может остановиться. Если он вдруг попробует упасть вниз по спирали, ему придётся всё быстрее и быстрее передвигаться случайным образом. И это увеличение скорости уведёт электрон в сторону от ядра!
Так что тенденция падения по спирали будет нейтрализована тенденцией к более быстрому движению согласно принципу неопределённости. Баланс находится, когда электрон располагается на предпочтительном расстоянии от ядра, и это расстояние определяет размер атомов!

Рис 3
Если электрон изначально находится далеко от ядра, он будет двигаться к нему по спирали, как показано на рис. 2, и излучать электромагнитные волны. Но в результате его расстояние от ядра станет достаточно малым для того, чтобы принцип неопределённости запретил дальнейшее сближение. На этом этапе, когда найден баланс между излучением и неопределённостью, электрон организует стабильную «орбиту» вокруг ядра (точнее, орбиталь – этот термин выбран, чтобы подчеркнуть, что в отличие от планет, у электрона из-за квантовой механики нет таких орбит, какие есть у планет). Радиус орбитали определяет радиус атома (рис. 3).
Ещё одна особенность – принадлежность электронов к фермионам – заставляет электроны не спускаться до одного радиуса, и выстраиваться по орбиталям разных радиусов.
Насколько атомы крупные? Приближение на основе принципа неопределённости
На самом деле мы можем примерно оценить размер атома, используя только расчёты для электромагнитных взаимодействий, массу электрона и принцип неопределённости. Для простоты проделаем расчёты для атома водорода, где ядро состоит из одного протона, вокруг которого двигается один электрон.
- Массу электрона обозначим
- Неопределённость позиции электрона обозначим Δx
- Неопределённость скорости электрона обозначим Δv
Принцип неопределённости утверждает:
где ℏ — это постоянная Планка h, делённая на 2 π. Обратите внимание, он говорит, что (Δ v) (Δ x) не может быть слишком малым, что означает, что обе определённости не могут быть слишком малыми, хотя одна из них может быть очень малой, если другая будет очень большой.
Когда атом устанавливается в предпочтительном основном состоянии, мы можем ожидать, что знак ≥ превратится в знак ~, где A ~ B означает, что «A и B не совсем равны, но и не сильно отличаются». Это очень полезный символ для оценок!
Для атома водорода в основном состоянии, в котором неопределённость положения Δx будет примерно равна радиусу атома R, а неопределённость скорости Δv будет примерно равна типичной скорости V движения электрона вокруг атома, мы получим:
Как узнать R и V? Между ними и силой, удерживающей атом вместе, существует взаимоотношение. В неквантовой физике объект массы m, находящийся на круговой орбите радиуса r, и двигающийся со скоростью v вокруг центрального объекта, притягивающего его с силой F, будет удовлетворять уравнению
К электрону в атоме напрямую это неприменимо, но приближённо это работает. Сила, действующая в атоме, это электрическая сила, с которой протон с зарядом +1 притягивает электрон с зарядом -1, и в результате уравнение принимает вид
где k – константа Кулона, e – единица заряда, c – скорость света, ℏ — это постоянная Планка h, делённая на 2 π, а α – определённая нами постоянная тонкой структуры, равная . Совместим два предыдущих уравнения для F, и оценочное соотношение получается следующим:
Теперь применим это к атому, где v → V, r → R, и m → me. Также умножим верхнее уравнение на . Это даёт:
На последнем шаге мы использовали наше соотношение неопределённости для атома, . Теперь можно вычислить радиус атома R:
И это оказывается практически точным! Такие простые оценки не дадут вам точных ответов, но очень хорошее приближение обеспечат!
Как найти силу притяжения между ядром атома водорода и электроном
Силу притяжения между ядром атома водорода и электроном, который расположен на орбите данного атома, можно найти, исходя из знания физики взаимодействия данных частиц друг с другом.

Вам понадобится
- Учебник по физике 10 класса.
Инструкция
Используя учебник по физике 10 класса, зарисуйте на листке, что собой представляет атом водорода. Как известно, данный химический элемент содержит в своем ядре всего лишь один протон, вокруг которого вращается один электрон.
Обратите внимание на то, что субатомные частицы водорода имеют разноименные заряды. Данное обстоятельство приводит к тому, что протон и электрон притягиваются друг к другу с некоторой силой.
Выпишите из учебника, как определяется кулоновская сила взаимодействия зарядов. Именно этот тип взаимодействия присущ силе притяжения электрона с ядром. Как известно, модуль кулоновской силы взаимодействия прямо пропорционален произведению зарядов взаимодействующих частиц и обратно пропорционален квадрату расстояния между данными частицами. Коэффициент пропорциональности называется электрической постоянной.
Определите, используя таблицы постоянных величин, расположенные в конце учебника, чему равна электрическая постоянная. Подставьте ее значение в формулу для силы Кулона.
Найдите в учебнике по физике таблицу характерных величин некоторых частиц. Определите по данной таблице массы и заряды электрона и протона.
Возьмите в качестве приблизительного значения расстояния между электроном и протоном величину половины ангстрема. Один ангстрем равен десяти в минус десятой степени метрам. Подставьте все необходимые величины в выражение для кулоновской силы притяжения и рассчитайте ее значение.
Вспомните, что все материальные тела также притягиваются друг к другу с силой гравитационного притяжения. Формула для данной силы аналогична выражению для силы Кулона. Отличие заключается лишь в том, что вместо произведения зарядов в выражении гравитационной силы стоит произведение масс, а в качестве коэффициента пропорциональности используется гравитационная постоянная.
Подставьте величины масс, расстояния и гравитационную постоянную в соотношение гравитационной силы притяжения и рассчитайте величину данной силы. Сложите гравитационную силу притяжения с кулоновской. Полученное значение будет равно полной силе притяжения ядра атома водорода и электрона.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
«Не
бойтесь быть независимыми мыслителями!…».
Джозеф
Томсон
В
прошлой теме говорилось о трудностях планетарной модели атома Резерфорда. Выход
из этого крайне затруднительного положения нашел Нильс Бор, благодаря своей
невероятной интуиции.
В
результате проведения опытов по рассеянию альфа-частиц, Эрнест Резерфорд
установил, что почти вся масса и весь положительный заряд атома
сконцентрированы в очень малой области – атомном ядре. Основываясь
на своих экспериментах и расчетах, Резерфорд смог вычислить размеры атома и
размеры атомного ядра. Выяснилось, что ядро в десятки или даже сотни тысяч
раз меньше самого атома. На основании всего выше перечисленного, Резерфорд
предложил планетарную модель атома, согласно которой, вокруг
положительно заряженного ядра вращаются электроны. Трудности в этой модели
возникли почти сразу же, потому что она противоречила законам электродинамики
Максвелла и законам механики Ньютона. В соответствии с ними, атом не мог
просуществовать и 1 мкс, поскольку электроны должны были бы очень скоро
упасть в ядро. Поэтому, необходимо было составить какую-то новую теорию,
подходящую для описания процессов, происходящих внутри атома.
Сегодня
такая теория называется квантовой механикой. Начало этой теории ещё в
1913 году положил Нильс Бор. Конечно, ему не удалось сразу разработать
последовательную теорию атома. Однако, он сформулировал основные положения
новой теории в виде постулатов.
Первый
постулат Бора (или постулат стационарных состояний)
гласит следующее: существуют особые, стационарные состояния атома, находясь
в которых, атом не излучает энергию, при этом, электроны в атоме движутся с
ускорением.
Второй
постулат Бора (или правило частот) говорит нам о том, что
излучение света происходит при переходе атома из стационарного состояния с
большей энергией в стационарное состояние с меньшей энергией. Энергия
излученного фотона равна разности энергий стационарных состояний. Здесь
необходимо отметить, что данный постулат распространяется не только на видимый
свет. То есть, атом может излучать энергию и в инфракрасной области спектра, и
в ультрафиолетовой.
Второй
постулат Бора описывается следующей формулой
Если
разделить всё уравнение на постоянную Планка, то получим выражение, с помощью
которого можно вычислить частоту излучения.
Таким
образом, первый постулат Бора гласит, что электрон может находиться только в
особых стационарных состояниях. То есть, существуют определенные орбиты,
каждая из которых соответствует определенному энергетическому уровню. Обратите
внимание, что в атомной физике энергия измеряется в эВ (электрон-вольтах).
1 эВ
– это энергия приобретаемая электроном при прохождении им разности потенциалов
в 1 В.
1 эВ = 1,6×10–19 Дж
В
данном примере числовые значения энергий соответствуют атому водорода.
Электрон
может обладать одной из указанных энергий и находится на соответствующей орбите.
Никаких промежуточных стадий в стабильных атомах быть не может. Если электрон
переходит с более высокого энергетического уровня на менее высокий, то он излучает
свет, и энергия излученного фотона может быть вычислена в соответствии со
вторым постулатом Бора. И, наоборот, при переходе с низкого энергетического
уровня на высокий, происходит поглощение света. Важно понимать, что энергия
излучается или поглощается дискретными порциями (то есть квантами).
Разумеется, электрон не может излучить или поглотить дробное число фотонов.
Отметим,
что состояние атома, которому соответствует наименьшая энергия, называется основным,
а все остальные состояния – возбужденными. В возбужденном состоянии
электрон может находиться очень недолго (не более, чем 10–8 с),
а в основном состоянии – неограниченно долго.
Простейшая
атомная система – это атом водорода. Именно для построения теории атома
водорода Бор и применил свои постулаты. Основной задачей являлось
нахождение частот электромагнитных волн, которые излучал атом водорода. Для
решения этой задачи, Бору пришлось сформулировать третий постулат, который
также называется правилом квантования. Анализируя данные, полученные в
результате своих исследований излучения атома водорода, Нильс Бор заметил
следующее: произведение импульса электрона и длины его орбиты всегда кратно
постоянной Планка.
В
модели Бора электрон двигался по круговой орбите, поэтому длину его окружности
можно найти по формуле
Если
перенести в
правую часть, то
где
ħ – квантовая постоянная Планка.
Очевидно,
что скорость движения электрона зависит от того, по какой орбите он вращается.
Полученное уравнение называется правилом квантования орбит, то есть из
этого уравнения можно найти стационарные электронные орбиты.
Несмотря
на свои постулаты, Нильс Бор, конечно, не отказывался полностью от классической
механики. Он также рассмотрел движение электрона как равномерное криволинейное
движение. Итак, электрон движется по круговой орбите с некоторой скоростью .
Электрон обладает элементарным отрицательным зарядом, а ядро обладает
положительным зарядом, кратным элементарному.
Из
курса физики 9 класса известно, Z
– это зарядовое число. Именно на него и умножается элементарный заряд, чтобы
найти заряд ядра данного атома. В результате электромагнитного взаимодействия,
электрон притягивается к ядру с силой, которая вычисляется в соответствии с
законом Кулона. Исходя из второго закона Ньютона, можно приравнять эту силу к
произведению массы электрона и центростремительного ускорения.
Можно
преобразовать полученное уравнение, домножив его на радиус в квадрате.
Используя
это уравнение, и правило квантования орбит, можно составить систему из двух
уравнений.
В
этой системе уравнений всего два неизвестных – это скорость электрона и радиус
орбиты. Если разделить второе уравнение на первое, то можно получить выражение,
с помощью которого вычисляется скорость электрона, вращающегося на n
орбите.
Коэффициент
пропорциональности k,
квантовая постоянная Планка и заряд электрона – всё это физические константы,
которые известны. Остается только подставить в данное выражение порядковый
номер элемента (то есть зарядовое число) и номер орбиты (который называется
главным квантовым числом). Если теперь выражение для скорости подставить в
первое уравнение, то можно вывести формулу, по которой рассчитывается радиус
орбиты.
Известно,
что зарядовое число водорода равно единице. Если подставить
единицу вместо Z и вместо n,
то убедимся, что скорость электрона в атоме водорода на первой орбите равна
а
радиус орбиты (то есть радиус атома) водорода равен
Согласно
теории Бора, энергия электрона в атоме водорода зависит только от того, на
каком энергетическом уровне он находится.
В
представленной формуле n
– это номер орбиты, а все остальные величины являются физическими константами.
Эту формулу можно вывести, если вспомнить, что кинетическая энергия равна
половине произведения массы и квадрата скорости.
Если
подставить выражение для вычисления скорости электрона на n
орбите в формулу для кинетической энергии и подставить единицу вместо Z,
то можно получить исходную формулу.
Имеется
знак минус в этой формуле, поскольку первый энергетический уровень
принимается за самый низкий.
Было
рассмотрено применение теории Бора только к атому водорода. Дело в том, что
разработать теорию для других атомов, на основе представлений Бора, не удалось.
В этом нет ничего удивительного. Ведь для создания своей теории Бор использовал
как классическую физику, так и совершенно новые постулаты, противоречащие
классической физике, в то время как требовалось разработать фундаментально
новый подход к механике и электродинамике. Такой подход был разработан в конце
двадцатых годов прошлого столетия: были разработаны такие теории, как квантовая
механика и квантовая электродинамика. Как выяснилось, первые два
постулата Бора абсолютно правильные, но третий постулат применим далеко не
всегда.
Упражнения.
Задача
1. Определите
частоту волны света, испускаемого атомом водорода при его переходе с пятого
энергетического уровня на третий энергетический уровень.
Задача
2. Найдите
силу тока, который вызывает электрон, двигаясь в атоме водорода, находящемся в
основном состоянии.
Основные
выводы:
–
Первый постулат или постулат стационарных состояний гласит: существуют
особые, стационарные состояния атома, находясь в которых, атом не излучает
энергию, при этом, электроны в атоме движутся с ускорением.
–
Второй постулат или правило частот Бор сформулировал так: излучение
света происходит при переходе атома из стационарного состояния с большей
энергией в стационарное состояние с меньшей энергией. Энергия излученного
фотона равна разности энергий стационарных состояний.
–
Энергия электрона атома водорода, находящегося на n
энергетическом уровне:
–
Радиус n-ой
орбиты электрона:
–
Скорость электрона на n-ой
орбите:
–
Модель Бора не в состоянии описать движение электронов в других атомах. Для
полного понимания, процессы, происходящие внутри атомов, нужно рассматривать с
точки зрения квантовой механики.
Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).
Планетарная модель атома Резерфорда позволила объяснить результаты опытов по рассеянию α-частиц вещества, но она не способна объяснить факт существования атома и его устойчивость.
В соответствии с планетарной моделью электроны атома должны двигаться вокруг неподвижного ядра. Двигаясь вокруг ядра с центростремительным ускорением под действием силы притяжения к ядру, электрон должен, как и всякий ускоренно движущийся электрический заряд, излучать электромагнитные волны с частотой, равной частоте обращения электрона вокруг ядра.
Энергия электрона в атоме должна при этом непрерывно уменьшаться за счёт излучения. Сам электрон должен с каждым оборотом приближаться по спирали к ядру и упасть на него под действием электрической силы притяжения. При этом атом потеряет всю электронную оболочку, а также присущие ему физические и химические свойства. Кроме того, атом должен потерять спектр излучения частоты, то есть атом должен давать излучение с непрерывным (сплошным) спектром частот.
Эти результаты, полученные с помощью классической механики и электродинамики, находятся в резком противоречии с опытом, который показывает, что
- Атомы являются весьма устойчивыми системами и в невозбуждённом состоянии могут существовать неограниченно долго, не излучая при этом электромагнитные волны
- Спектр излучения атома является линейчатым (дискретным) – образованным из отдельных линий (от латинского discretus – прерывистый, состоящий из отдельных значений)
Всё это свидетельствует о том, что законы классический физики применить к электронам в атомах нельзя, поэтому необходимы новые представления о механизме излучения и поглощения атомами электромагнитных волн. В основе современной теории атома лежитквантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов), а также связь величин, которые характеризуют частицы и системы, с физическими величинами, измеряемыми опытным путём.
В 1913 году датский физик Нильс Бор (1885 – 1962) ввёл идеи квантовой теории в ядерную модель атома Резерфорда и разработал теорию атома водорода, которая подтвердилась всеми известными тогда опытами. Бор сформулировал в виде постулатов основные положения новой теории, которые налагали лишь некоторые ограничения на допускаемые классической физикой движения. Однако последовательной теории атома Бор не дал. Впоследствии теория Бора была включена как частный случай в квантовую механику. В основе теории Бора лежат два постулата.
Первый постулат Бора: постулат стационарных состояний
Атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определённая энергия En. В стационарном состоянии атом не излучает.
Второй постулат Бора: правило частотe
Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ek в стационарное состояние с меньшей энергией En. Энергия излученного фотона равна разности энергий стационарных состояний:
hvkn = Ek — En
Частота излучения равна:
vkn = (Ek — En) / h = (Ek / h) — (En / h)
Или, длина волны излучения λ равна:
1 / λkn = (1 / hc) (Ek — En)
Где h – постоянная Планка, с – скорость света в вакууме.
Если Ek > En, то происходит излучение фотона, если Ek < En, то происходит поглощение фотона, при котором атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией. Таким образом, для каждого атома имеется ряд строго определённых дискретных значений энергии, которыми он может обладать. Физические величины, например энергия и импульс, которые могут принимать лишь дискретные (квантовые) значения, носят название квантованные физические величины (квантование физических величин). При этом энергетические уровни атома – это возможные значения энергии атома.
Правило квантования орбит позволяет определить радиусы стационарных орбит:
mvnrn = nh’
где n = 1, 2, 3…, m – масса электрона, rn – радиус n-ой орбиты, vn – скорость электрона на этой орбите.
Число n – положительное число, которое называется главное квантовое число.
Величина (mvn)rn – момент импульса электрона.
h’ – это величина, которая равна:
h’ = h/2π = 1,05445887•10-34 Дж•с
где h – постоянная Планка.
Главное квантовое число указывает номер орбиты, по которой может обращаться электрон.
Свои постулаты Н.Бор применил для построения теории простейшей атомной системы – атома водорода, состоящего из ядра – протона, и одного электрона. Эта теория также применима для водородоподобных ионов, то есть атомов с зарядом ядра Ze и потерявших все электроны, кроме одного (например, Li2+, Be3+ и т.п.). В предположении, что электрон движется по круговой орбите, постулаты Бора позволяют найти радиусы rn стационарных, возможных орбит электрона. На электрон действует кулоновская сила:
Fk = (1 / 4πε0) (ε2 / rn2)
Где е – модуль заряда электрона, равный заряду ядра, ε0 = 8,85418782 * 10-12 Ф/м – электрическая постоянная в единицах СИ.
Кулоновская сила сообщает электрону на орбите центростремительное ускорение:
aцс = (vn2) / rn
Согласно второму закону Ньютона:
Fk = maцс
Поэтому
(mvn2) / rn = e2 / (4πε0rn2)
Или
mvn2rn = e2 / (4πε0)
Используя правило квантования орбит mvnrn = nh’, можно получить выражения для возможных радиусов орбит. Исключая скорость vn из предыдущего выражения, получим:
rn = 4πε0n2h’ / me2 (так как h’ = h / 2π)
Таким образом, радиусы орбит электрона в атоме водорода прямо пропорциональны квадратам главного квантового числа n.
Наименьший радиус орбит при n = 1, то есть радиус первой орбиты в атоме водорода равен:
r1 = 4πε0h’ / me2 = 0,528 * 10-10 м = 0,528 Å
Радиус первой орбиты в атоме водорода носит название первый Боровский радиус и служит единицей длины в атомной физике.
Полная энергия Е электрона в атоме водорода, согласно механике Ньютона, равна сумме кинетической энергии Еk и потенциальной энергии П взаимодействия электрона с ядром:
E = Еk — П = (mvn2 / 2) — (e2 / 4πε0rn)
Потенциальная энергия электрона в атоме отрицательна:
П = — (e2 / 4πε0rn)
Так как нулевой уровень отсчёта берётся на бесконечности (рис. 1.3), а по мере приближения электрона к ядру его потенциальная энергия уменьшается. Взаимодействующие частицы – ядро и электрон – имеют заряды противоположных знаков.
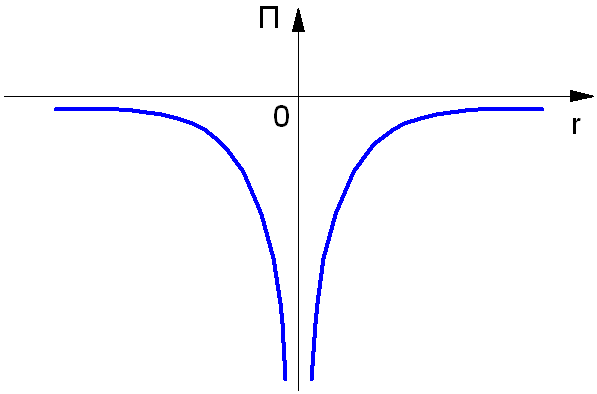
Рис. 1.3. Потенциальная энергия электрона в атоме.
Подставляя значение скорости
vn2 = — e2 / 4πε0mrn
в выражение полной энергии, получим:
E = (m / 2) (e2 / 4πε0mrn) — (e2 / 4πε0rn)
Подставляя в эту формулу выражение для радиусов орбит, получим энергетические уровни электрона в атоме водорода (значения энергий стационарных состояний атома):
En = -(1 /(4πε0)2) me4 / 2h’2n2 = — (me4 / 8h2ε02) * (1 / n2), n = 1,2,3…
Энергия Еn электрона в атоме водорода зависит от главного квантового числа n, которое определяет энергетические уровни электрона в атоме водорода.
Основное энергетическое состояние атома (нормальное состояние атома) – это энергетический уровень при n = 1.
Значение энергии, соответствующее первому (низшему) энергетическому уровню в атоме водорода равно:
E1 = -(1 /(4πε0)2) me4 / 2h’2λ = -2,485 * 10-19 Дж = -13,53 эВ
В этом состоянии атом может находиться сколько угодно долго. Для того чтобы ионизировать атом водорода, ему нужно сообщить энергию 13,53 эВ, которая называется энергия ионизации.
Энергетические уровни при n > 1 – это возбуждённые энергетические состояния (возбуждённые состояния атома). Возбуждённое состояние атома является менее устойчивым, чем основное состояние. Время жизни атома в этом состоянии имеет порядок 10-8 секунд. За это время электрон успевает совершить около ста миллионов оборотов вокруг ядра.
При переходе электрона с удалённой от ядра стационарной k-орбиты на ближайшую n-ую орбиту атом излучает фотон, энергия которогоhvnk согласно второму постулату Бора определяется:
hvkn = Ek — En = -(1 / (4πε0)2) * (me4 / 2h’2) * [(1 / n2) — (1 / k2)] = (me4 / 8h2ε02) * [(1 / n2) — (1 / k2)]
Частота излучения атома водорода:
vkn = (1 / (4πε0)2) * (me4 / h’3) * [(1 / n2) — (1 / k2)] = R[(1 / n2) — (1 / k2)]
Где
R = (me4 / (4πε0)2) * 4πh’3) = (me4 / 8h3ε02) = 3,288 * 1015 c-1— постоянная Ридберга
Постоянная Ридберга определяется через постоянную Планка, массу и заряд электрона.
Длина волны излучения определяется соотношением:
1 / λnk = vnk / c = (me4 / 8ε02h3c) * [(1 / n2) — (1 / k2)] = Rc[(1 / n2) — (1 / k2)]
Где
Rc = R / c = 1,0974 * 107 м-1 — также постоянная Ридберга
с = 3*108 м/с – скорость света в вакууме.
Теоретическое значение R совпадает с экспериментальным значением, полученным из спектроскопических измерений.
Энергия обычно измеряется в электронвольтах (эВ). Электронвольт– это значение энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов в 1 В:
1 эВ = 1,6 * 10-19 Кл * 1В = 1,6 * 10-19 Дж
Энергия связи ядра


4
Средняя оценка: 4
Всего получено оценок: 97.
4
Средняя оценка: 4
Всего получено оценок: 97.
Важнейшим понятием ядерной физики является понятие энергии связи ядра. Рассмотрим его подробнее.
Ядерные силы
По современным представлением ядро атома состоит из частиц, называемых элементарными – протонов и нейтронов (общее название – нуклоны).
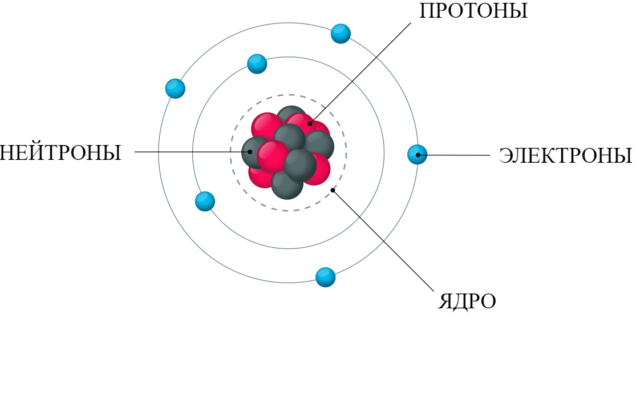
Нуклоны похожи, но протон имеет положительный заряд и стабилен. Нейтрон не имеет заряда и в свободном состоянии распадается (период полураспада ~ 10 мин).
Казалось бы, существование ядер, состоящих из многих нуклонов невозможно – протоны, обладающие одинаковым зарядом, должны разлетаться. Нестабильные нейтроны должны распадаться.
Однако, в реальности многие атомы стабильны. Это происходит в результате ядерного взаимодействия. Ядерные силы на два порядка сильнее кулоновских сил, и их с запасом хватает на преодоление отталкивания протонов.
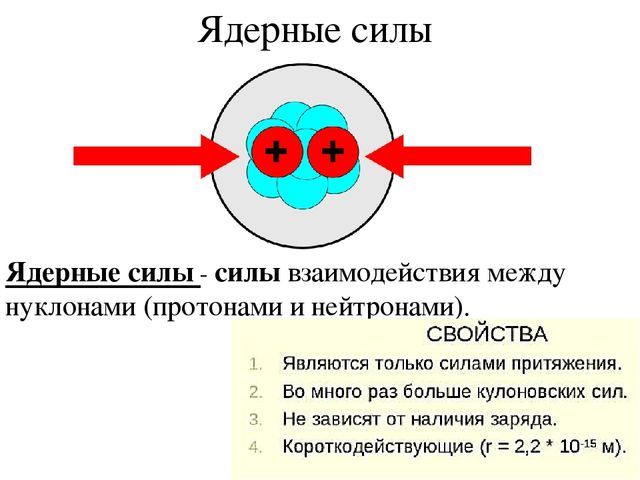
Но, если переносчики кулоновского взаимодействия – фотоны – не имеют массы покоя, и переносят взаимодействие на неограниченное расстояние, переносчики ядерного взаимодействия – глюоны или составленные из них мезоны – имеют массу, и осуществляют перенос взаимодействие на очень малые расстояния. В результате стабильными должны быть только ядра с очень небольшим числом протонов без нейтронов.
Энергия связи нуклонов
Возможность существований ядер с большим количеством протонов, а также стабильность нейтрона в составе ядра объясняется уровнем энергии связи. Ядерные силы удерживают нуклоны в ядре, и чтобы «извлечь» их оттуда, необходимо затратить энергию. Оказывается, что система из отдельных нуклонов обладает большей энергией, чем система, где нуклоны связаны. Любые процессы в Природе идут в сторону уменьшения энергии системы, поэтому нейтрон в составе ядра не распадается – это энергетически невыгодно, энергия связи удерживает его от распада. Эта же энергия удерживает протоны вместе. Лишь когда число нуклонов слишком велико, энергии связи ядра оказывается недостаточно – в этом случае протоны могут разлететься, и нейтроны также теряют стабильность.
Энергия связи – это энергия, которая выделяется при образовании ядра из отдельных частиц. Как только частицы оказываются в зоне действия ядерных сил – они устремляются друг к другу с огромным ускорением, излучая энергию связи в виде γ-квантов. Для того, чтобы расщепить ядро, необходимо вновь затратить эту энергию.
Уровень энергии связи
Для оценки энергии используется формула Эйнштейна, связывающая массу и энергию:
$$Е=mc^2$$
Теперь, если измерить массу отдельных частиц, а потом общую массу ядра – можно оценить энергию связи. Измерения показывают, что для легких элементов масса ядра оказывается меньше, чем сумма масс входящих в него частиц. А значит, подставив эту разницу в формулу энергии, можно получить формулу энергию связи ядра:
$$Е_{св} = (Zm_p+(A-Z)m_n -М_я)c^2$$
где:
- $Е_{св}$ – энергия связи ядра;
- $Z$ – число протонов в ядре (порядковый номер элемента);
- $А$ – общее число нуклонов в ядре (массовое число).
- $m_p$ – масса протона;
- $m_n$ – масса нейтрона;
- $М_я$ – масса ядра;
- с – скорость света.
Удельная энергия связи
Таким образом, наиболее устойчивыми должны оказаться ядра со средним числом нуклонов в ядре. Объясняется это тем, что энергия связи, приходящаяся на каждый нуклон, называемая удельной энергией связи, в таких ядрах максимальна. Прямые измерения подтверждают это.
Можно построить график зависимости значения удельной энергии связи от числа нуклонов в ядре:
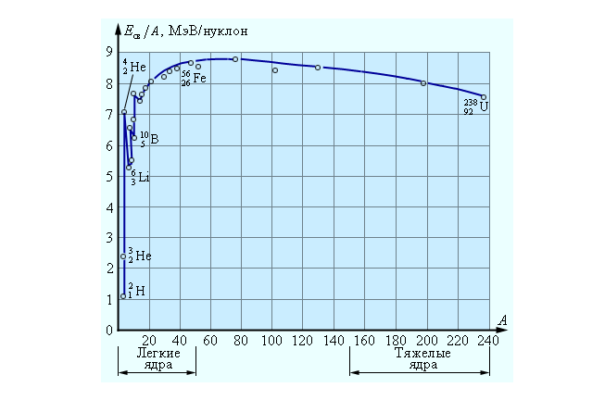
Если поглядеть на представленный график удельной энергии связи ядра, можно видеть, что реакции сливания ядер выгодны только для легких элементов вплоть до железа. Поэтому наиболее распространенными элементами в Природе (не считая простейшего водорода) являются Гелий-4 (дающий наибольший прирост удельной энергии связи при термоядерной реакции), и элементы с ядрами не тяжелее железа. Количество атомов даже стабильных, но более тяжелых элементов в Природе очень невелико.

Что мы узнали?
Частицы в ядре удерживаются ядерными силами. За счет энергии связи масса ядра получается меньше суммы масс входящих в него частиц. Наиболее стабильными являются ядра с максимальной удельной энергией связи.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 97.
А какая ваша оценка?
