Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, является мерой действия тела на другое тело.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Правило равновесия рычага
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
F1, F2 — силы, действующие на рычаг
l1, l2 — плечи этих сил
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
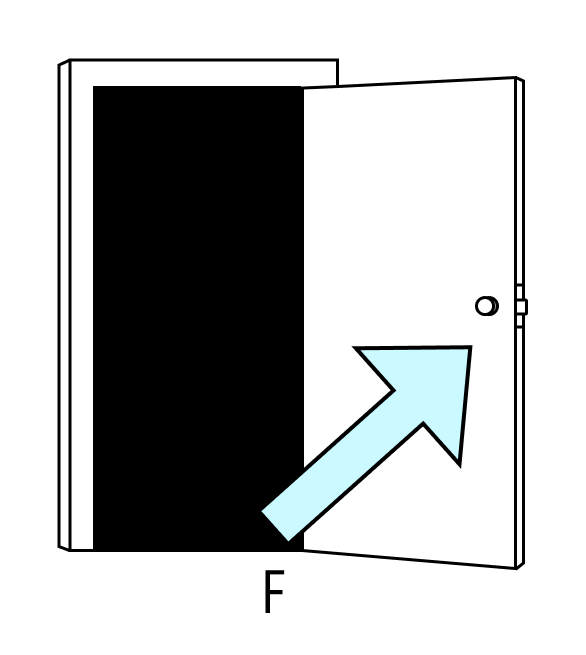
Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.
Для начала приложим силу к краю двери — туда, где самый длинный рычаг. Открылась!
А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.
Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.
Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.

Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
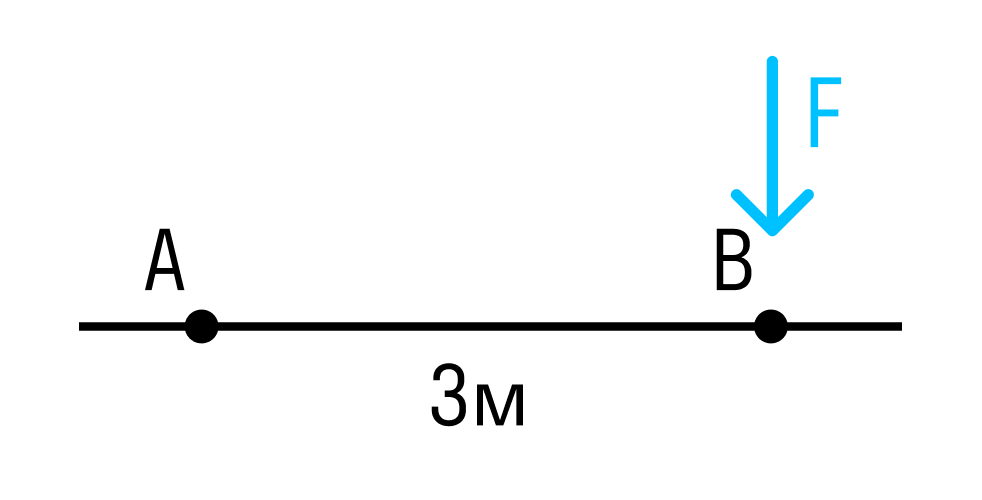
Момент силы относительно точки A:
МА=F×AB=F×3м
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
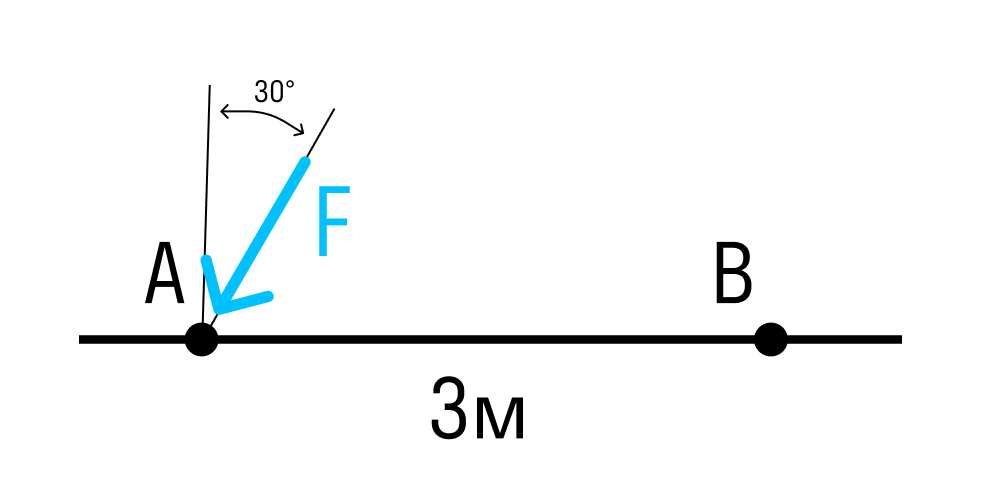
Момент силы относительно точки B:
MB=F×cos30×AB=F×cos30×3м
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
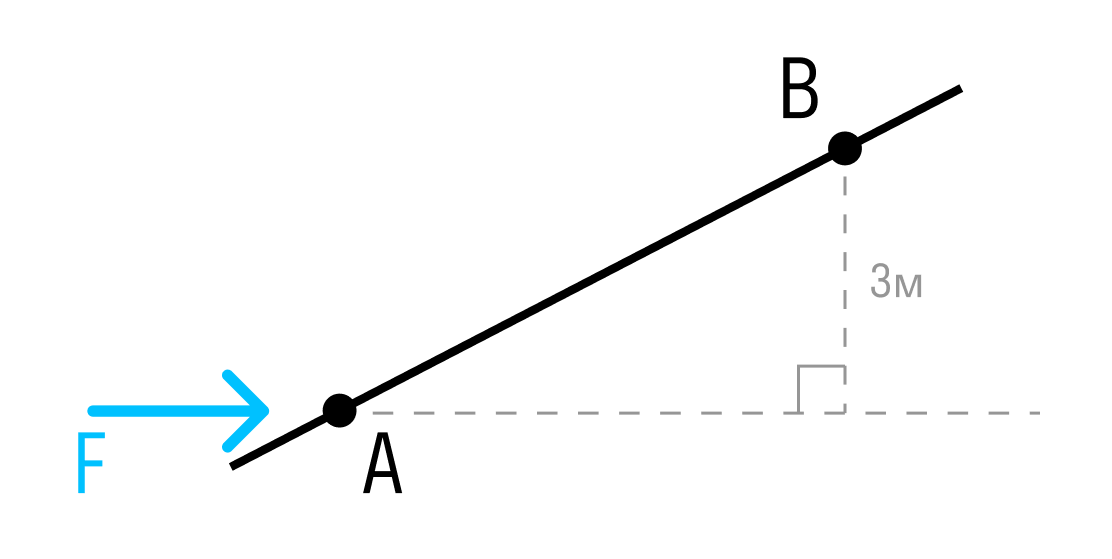
Момент силы относительно точки B:
MB=F×3м
Правило моментов
Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n
M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
M’1 + M’2 +…+ M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
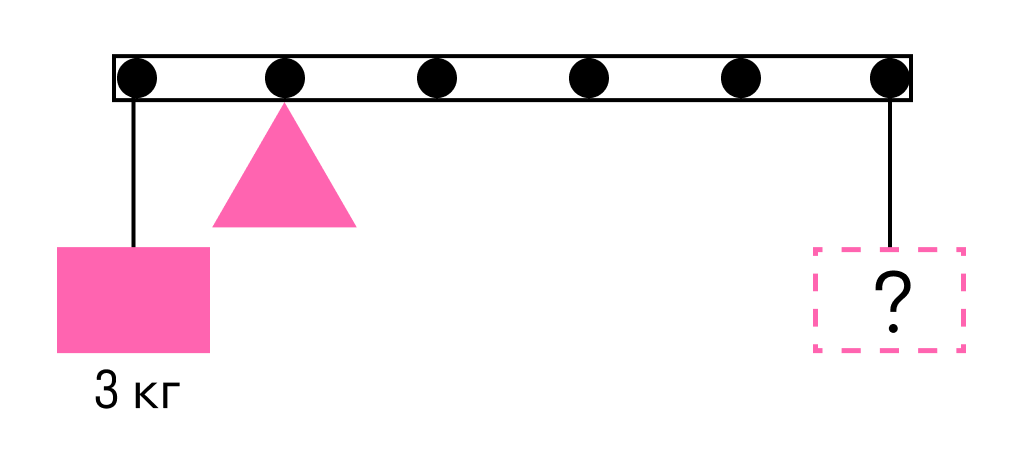
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен
он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:
— он вращает по часовой.
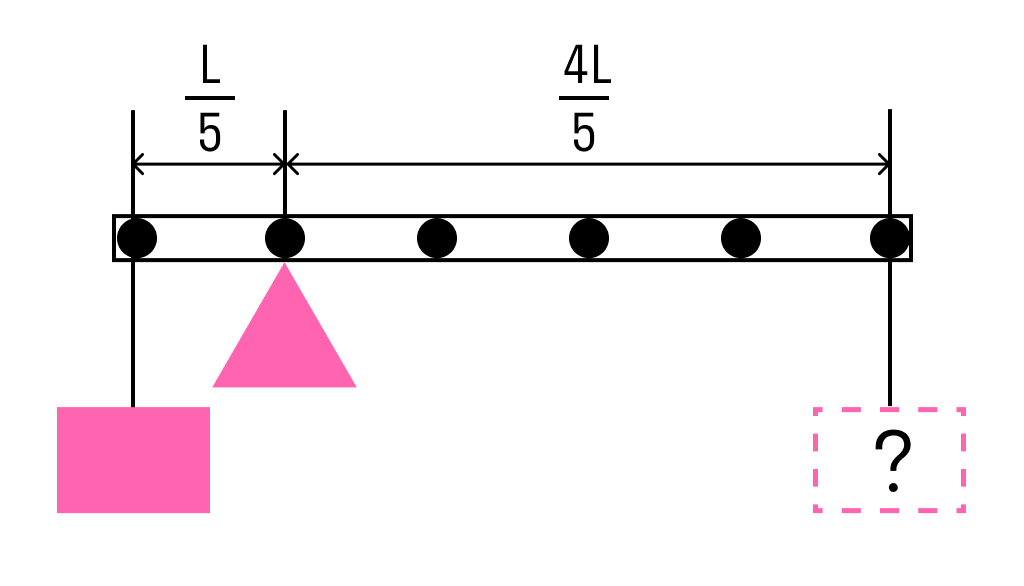
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
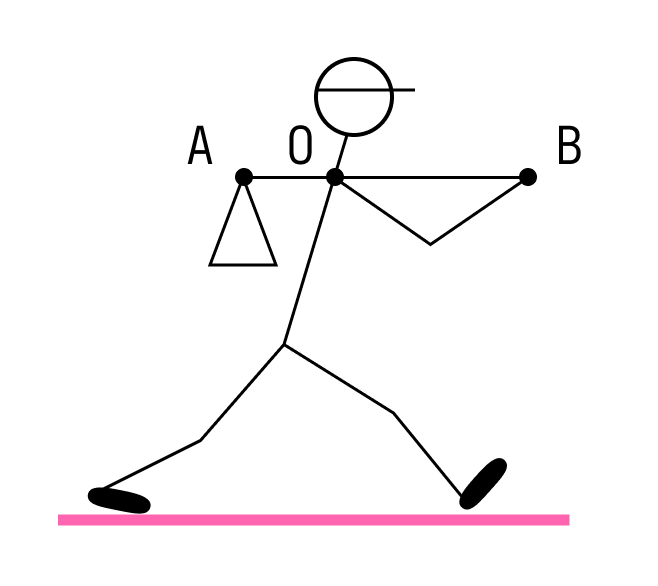
Решение:
По правилу рычага:
где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
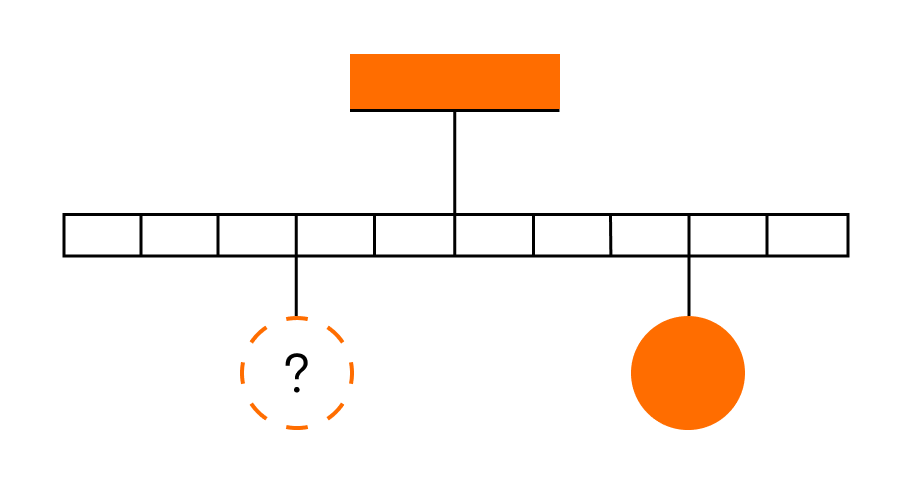
Решение:
По правилу рычага
Отсюда
Ответ: Масса груза равна 0,3 кг
Задача 4 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
Формула плеча силы в физике
Формула плеча силы
Определение и формула плеча силы
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${overline{F}}_1$ и ${overline{F}}_2$, действующие на рычаг направлены в одну сторону.
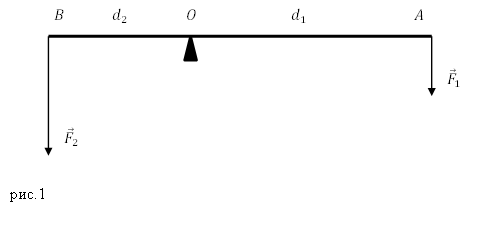
Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.
Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $left|OAright|=d_1$- плечо силы $F_1$; $left|OAright|=d_2$- плечо силы $F_2$.
Рычаг находится в состоянии равновесия, если выполняется равенство:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1right).]
Предположим, что материальная точка движется по окружности (рис.2) под действием силы $overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($varepsilon $) точки определяется тангенциальной составляющей ($F_{tau }$) силы $overline{F}$:
[mRvarepsilon =F_{tau }left(2right),]
где $m$ – масса материальной точки; $R$ – радиус траектории движения точки; $F_{tau }$ – проекция силы на направление скорости движения точки.
Если угол $alpha $ – это угол между вектором силы $overline{F}$ и радиус – вектором $overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:
[F_{tau }=F{sin alpha left(3right). }]
Расстояние $d$ между центром O и линией действия силы $overline{F}$ называют плечом силы. Из рис.2 следует, что:
[d=R{sin alpha left(4right). }]
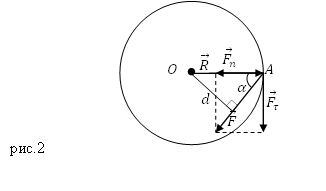
Если на точку будет действовать сила ($overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $alpha $ станет равен $frac{pi }{2}$.
Момент силы и плечо
Понятие плечо силы иногда используют, для записи величины момента силы ($overline{M}$), который равен:
[overline{M}=left[overline{r}overline{F}right]left(5right),]
где $overline{r}$ – радиус – вектор проведенный к точке продолжения силы$ overline{F}$. Модуль вектора момента силы равен:
[M=F{rsin alpha = }Fd left(6right).]
Построение плеча силы
И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.
Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).
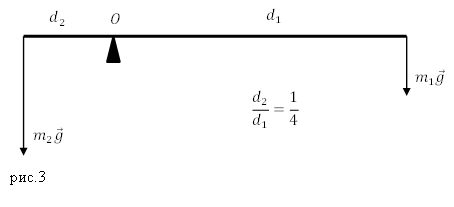
Примеры задач с решением
Пример 1
Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={rm 2 }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?
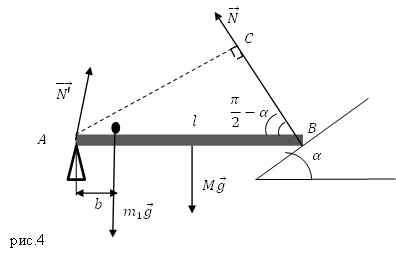
Решение. Основой решения задачи является правило равновесия рычага:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1.1right),]
где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:
[frac{m_1g}{m_2g}=frac{d_2}{d_1}to frac{m_1}{m_2}=frac{d_2}{d_1}left(1.2right).]
Из выражения (1.2) получим искомую массу $m_1$:
[m_1=frac{m_2d_2}{d_1}.]
Вычислим искомую массу:
[m_1=2cdot frac{1}{4}=0,5 (кг).]
Ответ. $m_1=0,5 кг$
Пример 2
Задание. Однородный стержень длинной $l $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $alpha $. На стержне на расстоянии $b $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?
Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $Moverline{g}$, вес груза, расположенного на нем $overline{P}=m_1overline{g}$, сила реакции наклонной плоскости: $overline{N}$; сила реакции опоры в точке A: $overline{N}’$.
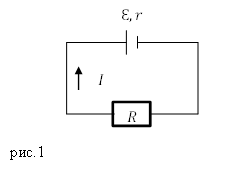
Плечи сил будем искать относительно точки A. Плечо силы $overline{N’}$ будет равно нулю, так как сила приложена к стержню в точке А:
[d_{N’}=0 left(2.1right).]
Плечо другой силы реакции опоры ($overline{N}$) равно длине перпендикуляра AC:
[d_N=l{sin (90-alpha ) }=l{cos alpha left(2.2right). }]
Плечо силы $Moverline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:
[d_{Mg}=frac{l}{2}left(2.3right).]
Плечо силы $m_1overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:
[d_{m_1g}=b.]
Ответ. $d_{N’}=0;; d_N=l{sin (90-alpha ) }=l{cos alpha left(мright), }d_{Mg}=frac{l}{2}, d_{m_1g}=b$
Читать дальше: формула полезной мощности.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Плечо силы — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения) при создании силой момента.
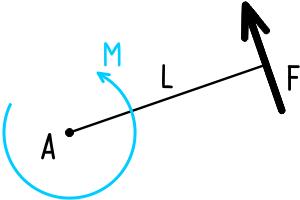

Определяется длинной нормали (перпендикуляра) к линии усилия проведенной из рассматриваемой точки.
Обозначается: L, l или h. Измеряется в метрах [м].
Плечо силы – один из двух множителей определяющих момент силы.
Наш короткий видеоурок про момент и плечо силы с примерами:
Другие видео
О плече силы можно говорить только тогда, когда есть прямая связь между силой и точкой относительно которой возникает момент.
Порядок нахождения плеча силы
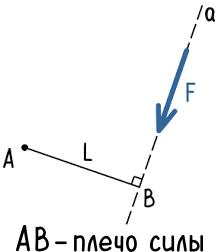
Рассмотрим порядок нахождения плеча силы F относительно точки A.

Для этого покажем прямую a, по направлению действия силы F
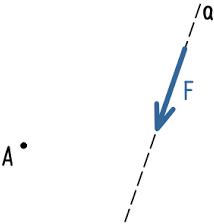
Из точки A опустим перпендикуляр к прямой a.
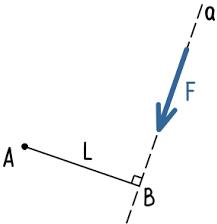
Длина этого перпендикуляра является плечом силы.
Примеры определения плеча силы
- Сила расположена перпендикулярно оси стержня и известно расстояние между точками A и B.

Плечо силы относительно точки A равно длине отрезка AB. - Сила расположена под определенным углом к оси стержня

Плечо силы относительно точки B составляет AB×cos30° - Известно расстояние от точки до линии действия силы
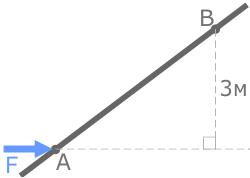
Плечо силы относительно точки B равно 3м.
Примеры решения задач >
Момент силы >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Момент силы. Условия равновесия рычага
- Устройство и виды рычагов
- Момент силы
- Правило моментов для двух сил
- Правило моментов для нескольких сил
- Применение рычагов в быту и технике
- Задачи
- Лабораторная работа №9. Проверка условия равновесия рычага
п.1. Устройство и виды рычагов
 |
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг состоит из перекладины и опоры. Назначение рычага – получить выигрыш в силе или расстоянии. |
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
п.2. Момент силы
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.

На рисунке (l_1) – плечо силы (F_1, l_2) – плечо силы (F_2).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила (F_1) вращает рычаг против часовой стрелки, а сила (F_2) – по часовой стрелке.
Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы – Н·м.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
$$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.
Например:
 |
Силы (F_1, F_2, F_3) вращают рычаг против часовой стрелки, а сила (F_4) – по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
 Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. |
 Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
 Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. |
 Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
 Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом. |
 Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
Рычаги третьего рода
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы. 
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
Дано:
(frac{l_1}{l_2}=frac 15)
(m_1=2,5 text{кг})
__________________
(m_2-?)

По правилу моментов begin{gather*} F_1l_1=F_2l_2 end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g, F_2=m_2g $$ Получаем: begin{gather*} m_1gl_1=m_2gl_2\[7pt] m_2=frac{m_1l_1}{l_2} end{gather*} Подставляем: $$ m_2=2,5cdot frac 15=0,5 (text{кг}) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
Дано:
(F_1=15 text{Н})
(F_2=60 text{Н})
(l_1+l_2=1 text{м})
__________________
(l_1, l_2-?)

По правилу моментов begin{gather*} F_1l_1=F_2l_2. end{gather*} Получаем систему уравнений begin{gather*} left{ begin{array}{l l} 15l_1=60l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 4l_2+l_2=1 end{array} right. Rightarrow \[7pt] Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 5l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=0,8 \ l_2=0,2 end{array} right. end{gather*} Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите (gapprox 10 text{м/с}^2). Ответ запишите в килоньютонах.
Дано:
(m=500 text{кг})
(gapprox 10 text{м/с}^2)
(OB=4OA)
__________________
(F_A, F_B-?)

Сила тяжести (F_{text{т}}=mg), направленная вниз, уравновешивается силами реакции опор (F_A) и (F_B), направленными вверх. begin{gather*} F_A+F_B=mg end{gather*} По правилу моментов при равновесии begin{gather*} F_Acdot OA=F_Bcdot OB=F_Bcdot 4OARightarrow F_A=4F_B \[7pt] F_A+F_B=5F_B=mgRightarrow F_B=frac{mg}{5} end{gather*} Получаем: begin{gather*} F_B=frac{500cdot 10}{5}=1000 text{Н}=1 text{кН}, F_A=4cdot 100=4000 text{Н}=4 text{кН} end{gather*} Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Теоретические сведения
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
Момент силы – это произведение силы, вращающей тело, на её плечо: (M=Fl).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
begin{gather*} M_1=M_2\[7pt] F_1l_1=F_2l_2 end{gather*} |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ Delta l=frac D2=2 text{мм} $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1 text{Н}. $$
Абсолютная погрешность определения веса $$ Delta_F=frac d2=0,05 text{Н}. $$
Относительные погрешности измерений: $$ delta_l=frac{Delta_l}{l}, delta_F=frac{Delta_F}{F}, delta_M=delta_l+delta_F $$
Абсолютная погрешность определения момента силы $$ Delta_M=Mcdot delta_M $$
Погрешности определения отношений сил и плечей: begin{gather*} r_F=frac{F_1}{F_2}, delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}, Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}\[7pt] r_l=frac{l_2}{l_1}, delta_{rF}=delta_{rl}frac{Delta_l}{l_1}+frac{Delta_l}{l_2}, Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl} end{gather*}
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес (F_1).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил (M_1) и (M_2), их относительные и абсолютные погрешности.
7. Вычислите отношение сил (frac{F_1}{F_2}) и плеч (frac{l_2}{l_1}) для этого случая, погрешности их определения.
8. Сделайте выводы.
Результаты измерений и вычислений
| (F_1, text{Н}) | (l_1, text{см}) | (F_2, text{Н}) | (l_2, text{см}) | (F_1/F_2) | (l_2/l_1) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ Delta_l=2 text{мм}=0,2 text{см}, Delta_F=0,05 text{Н} $$ Найдем моменты сил и погрешности вычислений: begin{gather*} M_1=F_1cdot l_1=2,9cdot 5=14,5 (text{Н}cdot text{м})\[7pt] delta_{M1}=frac{Delta_l}{l_1}+frac{Delta_F}{F_1}=frac{0,2}{5}+frac{0,05}{2,9}approx 0,04+0,017=0,057=5,7text{%} \[7pt] Delta_{M1}=M_1cdot delta_{M1}=14,5cdot 0,057approx 0,8 (text{Н}cdot text{м})\[7pt] M_1=(14,5pm 0,8) text{Н}cdot text{м}\[7pt] \[7pt] M_2=F_2cdot l_2=1,0cdot 15=15,0 (text{Н}cdot text{м})\[7pt] delta_{M2}=frac{Delta_l}{l_2}+frac{Delta_F}{F_2}=frac{0,2}{15}+frac{0,05}{1,0}approx 0,013+0,05=0,063=6,3 text{%} \[7pt] Delta_{M2}=M_2cdot delta_{M2}=15,0cdot 0,063approx 0,9 (text{Н}cdot text{м})\[7pt] M_2=(15,0pm 0,9) text{Н}cdot text{м} end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для (frac{F_1}{F_2}) begin{gather*} delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}=frac{0,05}{2,9}+frac{0,05}{1,0}approx 0,017+0,05=0,067=6,7text{%}\[7pt] Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}=2,9cdot 0,067approx 0,2\[7pt] frac{F_1}{F_2}=2,9pm 0,2 end{gather*}
Погрешность вычислений для (frac{l_2}{l_1}) begin{gather*} delta_{rl}=frac{Delta_l}{l_1}+frac{Delta_l}{l_2}=frac{0,2}{5}+frac{0,2}{15}approx 0,04+0,013=0,053=5,3text{%}\[7pt] Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl}=3,0cdot 0,053approx 0,2\[7pt] frac{l_2}{l_1}=3,0pm 0,2 end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ frac{F_2}{F_2}=frac{l_2}{l_1} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5pm 0,8) text{Н}cdot text{м}, M_2=(15,0pm 0,9) text{Н}cdot text{м} $$ Таким образом, с учетом вычисленных погрешностей, (M_1=M_2) – правило моментов выполняется.
Отношения сил и плечей равны begin{gather*} frac{F_1}{F_2}=2,9pm 0,2, frac{l_2}{l_1}=3,0pm 0,2 end{gather*}
Таким образом, с учетом вычисленных погрешностей (frac{F_1}{F_2}=frac{l_2}{l_1}) – правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
Словосочетания «момент силы» и «вращательный момент» — это синонимы. Можно употреблять любой из них.
Сила может заставлять тело двигаться:
- поступательно,
- или вращательно.
В этой статье будем рассматривать вращательное движение.
Рекомендую также ознакомиться со статьей о видах механического движения (откроется в новой вкладке).
Что такое линия действия силы
Линия действия – это прямая линия, на которой лежит вектор.
Провести эту линию легко. Приложить линейку к вектору и пунктиром провести прямую, продолжив ее в обе стороны от вектора.

Рис. 1. Линия (пунктир), на которой лежит вектор, называется линией действия вектора
Что такое плечо силы и как его нарисовать
Предположим, нужно с помощью ключа закрутить гайку (см. рис. 2).

Рис. 2. Красная точка, вокруг которой вращается ключ — это центр гайки
Винт, на который накручена гайка – это ось вращения. Ключ может вращаться вокруг красной точки. Для упрощения назовем ее кратко: «точка вращения».
Примечание:
Ось вращения проходит перпендикулярно плоскости рисунка через красную точку. Используем вместо оси вращения термин «точка вращения» для простоты.
Рассмотрим следующий рисунок (см. рис. 3)

Рис. 3. Плечо силы – это перпендикуляр ( l ). Он соединяет линию действия силы с точкой вращения
На рисунке 3 черная стрелка – это вектор силы, которая вращает ключ. Пунктир – линия действия силы. Из красной точки к линии действия силы проведен перпендикуляр. Этот перпендикуляр, обозначенный ( l ), называется плечом силы.
Перпендикуляр к линии действия легко провести с помощью прямоугольного треугольника (см. рис. 4):

Рис. 4. Один катет приложим к линии действия силы, вдоль второго проведем перпендикуляр к точке вращения
Плечо силы проводят так:
- взять прямоугольный треугольник;
- приложить один из катетов к линии действия;
- провести перпендикуляр к точке вращения, используя второй катет;
Момент силы, формула
Момент силы (вращательный момент) можно вычислить, когда известны сила и ее плечо.
Перемножим силу на плечо силы, получим момент силы.
[ large boxed { M = F cdot l } ]
( M left( H cdot text{м} right) ) – момент силы (вращательный момент);
( F left( H right) ) – сила, которая вращает тело;
( l left( text{м} right) ) – плечо этой силы;
Примечание:
Отрезок, не перпендикулярный силе, плечом силы не является. Сила и ее плечо всегда перпендикулярны!
Еще одна формула для момента силы
Вращательный момент можно рассчитать еще одним способом.
Для этого вместо плеча силы нужно использовать:
- величину ( d ) и
- угол ( gamma ) между силой и этим расстоянием.
Величина ( d ) – это расстояние между двумя точками:
- точкой, к которой приложена сила
- и точкой, вокруг которой происходит вращение.

Рис. 5. Момент силы можно рассчитать, зная: — силу; — расстояние между точками приложения силы и вращения; — угол между силой и этим расстоянием
На рисунке 5: черная стрелка – это вектор вращающей силы ( vec{ F } ); красная линия – это расстояние ( d ) между точкой приложения силы и точкой вращения.
[ large boxed { M = F cdot d cdot sin(gamma) } ]
Этой формулой во многих случаях пользоваться удобнее, чем формулой, содержащей ( l ) плечо силы.
Когда момент силы обращается в ноль
Рассмотрим внимательнее формулу для момента силы.
[ M = F cdot d cdot sin(gamma) ]
В правой части формулы находятся три множителя: ( F ) , (d) и ( sin(gamma) )
Если любой из трех множителей будет равен нулю, то правая часть уравнения обратится в ноль.
Левая часть уравнения, при этом, также, обратится в ноль. Потому, что между левой и правой частями записан знак равенства.
Кратко: Вращательный момент будет нулевым в любом из таких случаев:
- ( F = 0) – когда вращающая сила отсутствует;
- (d = 0 ) – когда сила приложена к точке вращения;
- ( sin(gamma) = 0 ) – когда сила ( F ) и величина (d ) лежат на одной прямой. В таком случает, угол между величинами ( F ) и (d ) равен нулю;
Действительно: ( sin(0) = 0 ), такое будет, когда ( F || d )
Эти три случая изображены на рисунке 6.

Рис. 6. Сверху вниз представлены три случая, в которых вращательный момент обращается в ноль
На рисунке 6: черная стрелка – это вектор силы, красная линия – это расстояние между точкой приложения силы и точкой вращения.
Сверху вниз представлены три случая для нулевого вращательного момента.
- В верхней части рисунка сила отсутствует;
- Средняя часть рисунка соответствует случаю, когда сила (черная стрелка) приложена к точке, вокруг которой тело может вращаться;
- Внизу — сила ( F ) параллельна величине (d ) — расстоянию между точкой приложения силы и точкой вращения.
