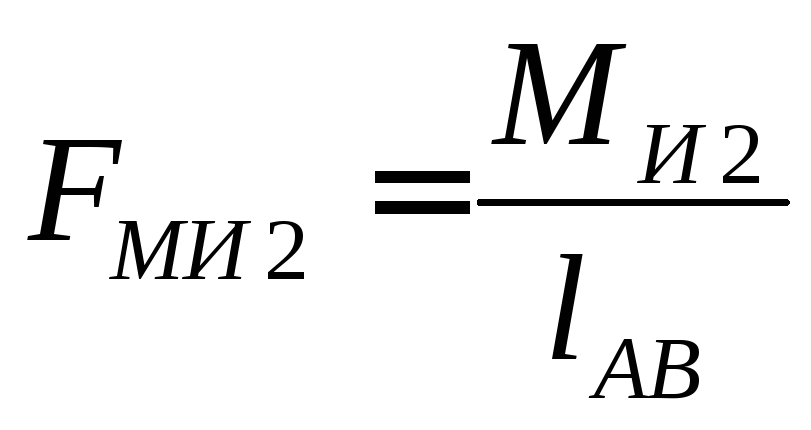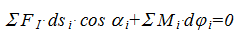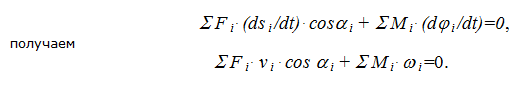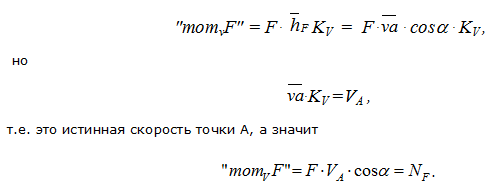В тех случаях,
когда нет необходимости определять
давления в кинематических парах, а
требуется определить уравновешивающую
силу Fу
или уравновешивающий момент Mу,
пользуются теоремой Жуковского о жестком
рычаге, основанной на принципе возможных
перемещений.
Согласно этому
принципу, сумма элементарных работ сил
активных и сил инерции, приложенных к
звеньям механизма на их возможных
перемещениях, равна нулю. Звенья
механизмов имеют не просто возможные,
а действительные перемещения точек,
движение которых определяется заданным
законом движения ведущего звена. Поэтому
элементарную работу сил, приложенных
к точкам звеньев механизма, будем
рассматривать на их действительных
перемещениях.
Обозначим F1,
F2,…Fn
силы активные и инерции, приложенные к
звеньям механизма. dS1,
dS2,…dSn
– проекции элементарных действительных
перемещений этих точек на направление
соответствующих сил. На основании
принципа возможных перемещений
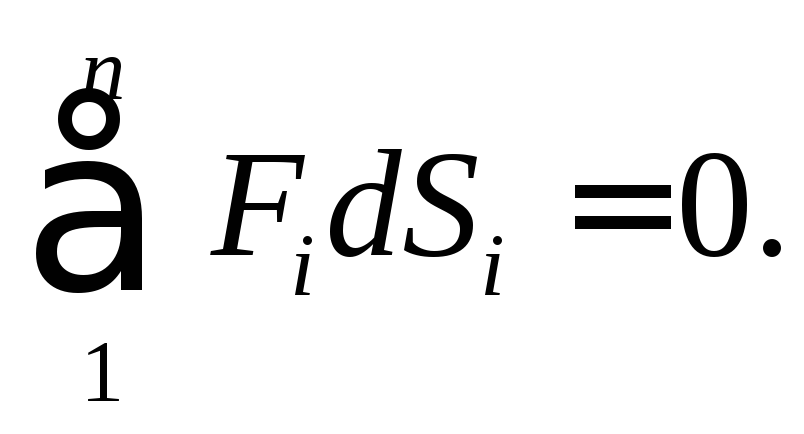
Найдем выражение
элементарной работы силы на ее элементарном
перемещении.
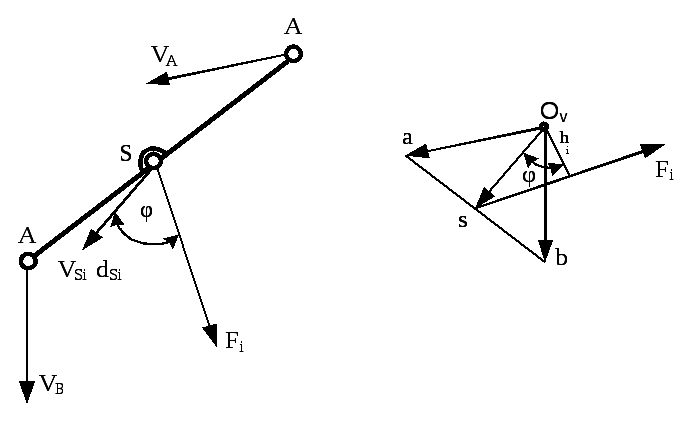
Пусть имеется
звено механизма АВ,
скорости точек которого известны (рис.
38). В точке S
звена приложена сила Fi
под углом φ
к скорости
Vs
точки S.
Построим для этого звена в масштабе kV
план скоростей. Повернем силу Fi
на угол 90о
(в любую сторону) и перенесем ее на план
скоростей в точку S.
Плечо этой силы относительно полюса OV
обозначим hi.
Рис. 38. Звено АВ
и план скоростей звена АВ.
Работа силы Fi
на ее
элементарном перемещении
.
Поскольку,
то.
Из плана скоростей,
поэтому.
Здесь– момент силы
относительно полюса плана скоростей.
Следовательно,.
Подставим это значение работы силы в
выражение (2.15) и сократив на общий
множительполучим
.
(19)
Эта формула
математически выражает теорему Н.Е.
Жуковского, которую можно сформулировать
следующим образом: если
все силы, действующие на движущиеся
звенья механизма, в том числе и
уравновешивающую, приложить в
соответствующих точках повернутого на
90о
плана скоростей, то сумма моментов всех
сил относительно полюса плана скоростей
будет равна нулю.
Обозначим силы,
приложенные к звеньям механизма через
F1,
F2,…Fn,
уравновешивающую силу через Fу.
Плечи этих сил, повернутых на угол 90о
и перенесенных в одноименные точки
плана скоростей, через h1,
h2,…hn,
hу.
Тогда по теореме Н.Е. Жуковского
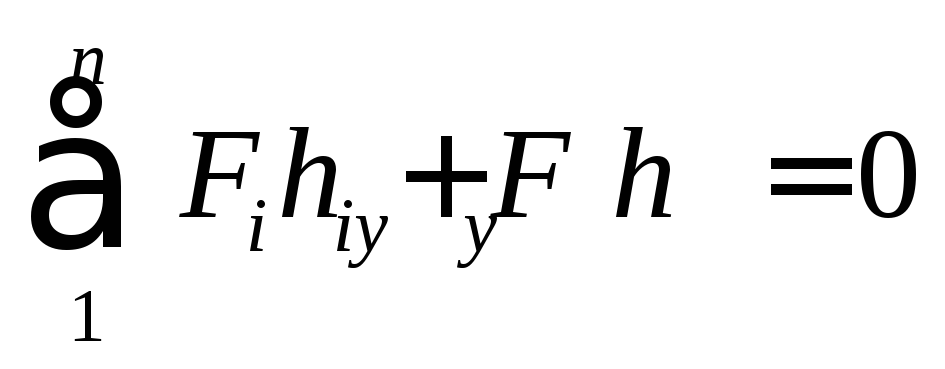
откуда
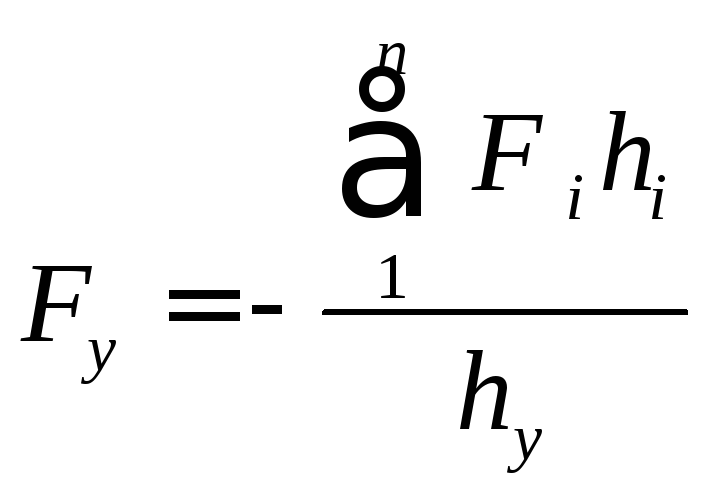
При определении
уравновешивающей
силы при помощи теоремы
Н.Е. Жуковского о
жестком рычаге моменты сил, действующие
на звенья, следует разложить на пары
сил, приложенные в тех точках звеньев,
скорости которых известны.
Пример определения уравновешивающей силы при помощи рычага Жуковского
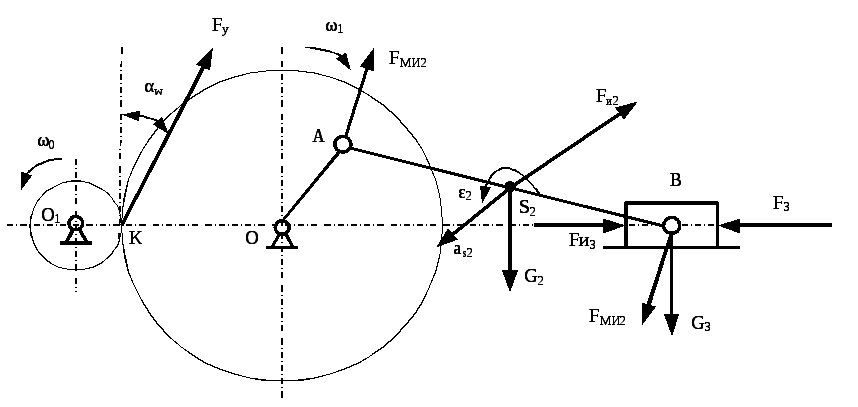
Для кривошипно –
ползунного механизма, изображенного
на рис. 39 определить Ру,
приложенную в точке К
зубчатого колеса 1.
Заданы: угловая
скорость кривошипа 1,
длины кривошипа ОА
и шатуна АВ,
модуль m
и число зубьев Z1
зубчатого колеса 1,
массы шатуна АВ
и ползуна В,
момент инерции шатуна JS2
и сила
полезного сопротивления F3,
приложенная к ползуну. Массой кривошипа
пренебречь. Конструктивно зубчатое
колесо 1
и кривошип ОА
выполнено в виде одного звена.
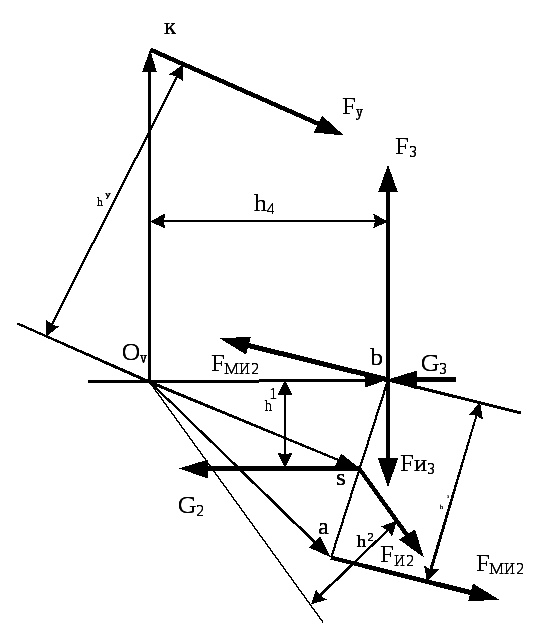
Рис. 39. Кинематическая
схема механизма с приложенными
к звеньям силами
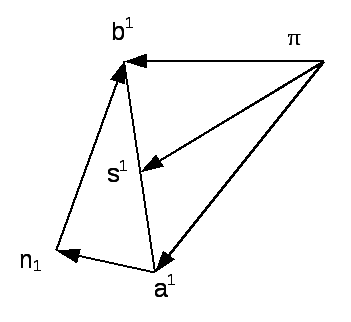
1. Строим планы
скоростей (рис.41) и ускорений (рис.40) в
произвольном масштабе, как рассмотрено
в параграфе 2.5. При этом скорость точки
К
приложения уравновешивающей силы
Vк
= ω1·lOK,
где lOK
= .
Рис.40. План ускорений
механизма
2. Определяем силы
инерции звеньев Fiи
и момент инерции шатуна MИ2.
FИi
=
– mi·a;
MИ2
= – JS2·ε2.
3. Прикладываем
все сила в соответствующих точках
звеньев механизма. Пару сил FMИ2
от MИ2
получим
делением MИ2
на действительную
величину длины шатуна 2
и полученные силы
FMИ2
прикладываем в точках А
и В
с соблюдением направления момента MИ2.
При определении направления Fу
следует учесть, что угол зацепления αw
равен 200.
4. Переносим все
силы с плана механизма, включая Fу,
в соответствующие точки плана скоростей,
предварительно повернув их на 900
по направлению движения часовой стрелки
(рис. 2.28).
5. Составляем
уравнение моментов относительно полюса
плана скоростей
.
(2.17)
6. Определяем
уравновешивающую силу
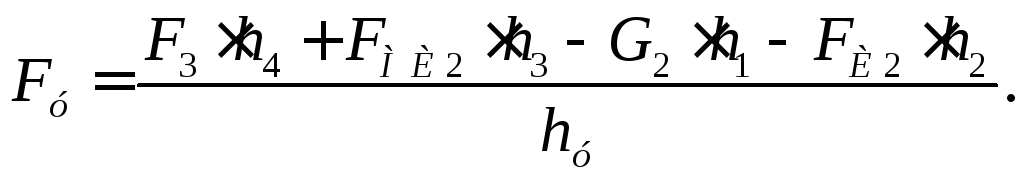
Если при решении
уравнения (2.18) Fу
получится со знаком плюс, то ее направление
на плане механизма выбрано верно. Если
со знаком минус, то выбранное направление
следует изменить на обратное.
Рис.41. Жесткий
рычаг Жуковского
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определять уравновешивающую силу или момент методом Н.Е. Жуковского можно в случаях, когда требуется найти только неизвестную внешнюю силу без определения реакций в кинематических парах, не прибегая к последовательному силовому расчету всего механизма.
Метод основан на принципе возможных перемещений – если система находится в равновесии, то сумма работ внешних сил и моментов на малых возможных перемещениях равна нулю (∑Ai = 0). Так как с помощью сил инерции (по принципу Даламбера) механизм приведен в состояние равновесия, то в данном случае принцип возможных перемещений применим.
Перейдем к конкретному мгновенному положению механизма, разделив все члены на бесконечно малый промежуток времени (dt), за который происходят указанные малые перемещения:
Таким образом, уравнение работ трансформируется в уравнение мгновенных мощностей и принцип возможных перемещений в применении к механизму можно сформулировать следующим образом – если механизм находится в равновесии, то сумма мгновенных мощностей всех внешних сил и моментов, приложенных к звеньям механизма, равна нулю.
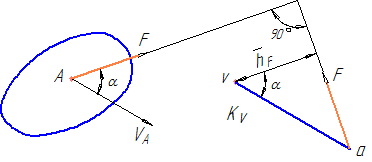
Жуковским Н.Е. был предложен метод составления этого уравнения с использованием плана скоростей (рисунок 19).
Рисунок 19
На рисунке 19 изображено некоторое звено, в точке А которого приложена сила F. Скорость VA этой точки изображается на плане скоростей вектором va в масштабе KV.
Перенесем силу F в точку «а» плана скоростей, повернув на 90° (в любую сторону). Возьмем формально момент этой повернутой силы относительно полюса плана скоростей:
В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.
Таким образом для составления уравнения Жуковского прикладывают все силы, действующие на звенья механизма (включая силы инерции), в соответствующие точки плана скоростей, предварительно повернув их на 90°. Взяв формально сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получают уравнение развиваемых ими мощностей.
К полученному уравнению добавляют мощности, развиваемые моментами (включая моменты сил инерции).
В уравнение Жуковского мощности должны входить с соответствующими знаками (см. рисунок 16 ). В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.
Примечание: для составления уравнения Жуковского можно на повернутый (на 90°) план скоростей прикладывать силы в своем истинном направлении.
Учет трения в механизмах >
Курсовой проект по ТММ >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
From Wikipedia, the free encyclopedia
In mechanics, an equilibrant force is a force which brings a body into mechanical equilibrium.[1] According to Newton’s second law, a body has zero acceleration when the vector sum of all the forces acting upon it is zero:
Therefore, an equilibrant force is equal in magnitude and opposite in direction to the resultant of all the other forces acting on a body. The term has been attested since the late 19th century.[2]
Example[edit]
Equilibrant force example
Suppose that two known forces are pushing an object and an unknown equilibrant force is acting to maintain that object in a fixed position. One force points to the west and has a magnitude of 10 N, and the other points to the south and has a magnitude of 8.0 N. By the Pythagorean theorem, the resultant of these two forces has a magnitude of approximately 12.8 N, which is also the magnitude of the equilibrant force. The angle of the equilibrant force can be found by trigonometry to be approximately 51 degrees north of east.
References[edit]
- ^ “Physics” (PDF). Retrieved 28 May 2014.
- ^ Smith Carhart, Henry; Nelson Chute, Horatio (1892). The Elements of Physics. Boston: Allyn and Bacon. pp. 36.
External links[edit]
- Equilibrium
Равновесие тела
Тело находится в состоянии покоя (или движется равномерно и прямолинейно), если векторная сумма всех сил, действующих на него, равна нулю. Говорят, что силы уравновешивают друг друга. Когда мы имеем дело с телом определенной геометрической формы, при вычислении равнодействующей силы можно все силы прикладывать к центру масс тела.
Чтобы тело, которое не вращается, находилось в равновесии, необходимо, чтобы равнодействующая всех сил, действующий на него, была равна нулю.
F→=F1→+F2→+..+Fn→=0.
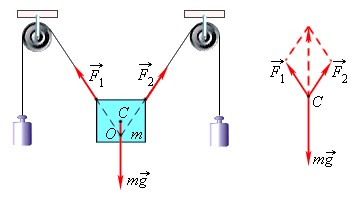
На рисунке выше изображено равновесие твердого тела. Брусок находится в состоянии равновесия под действием трех действующих не него сил. Линии действия сил F1→ и F2→ пересекаются в точке O. Точка приложения силы тяжести – центр масс тела C. Данные точки лежат на одной прямой, и при вычислении равнодействующей силы F1→, F2→ и mg→ приводятся к точке C.
Равновесие вращающегося тела. Правило моментов
Условия равенства нулю равнодействующей всех сил недостаточно, если тело может вращаться вокруг некоторой оси.
Плечом силы d называется длина перпендикуляра, проведенного от линии действия силы к точке ее приложения. Момент силы M – произведение плеча силы на ее модуль.
M=d·F.
Момент силы стремится повернуть тело вокруг оси. Те моменты, которые поворачивают тело против часовой стрелки, считаются положительными. Единица измерения момента силы в международной системе CИ – 1 Ньютонметр.
Если алгебраическая сумма всех моментов, приложенных к телу относительно неподвижной оси вращения, равна нулю, то тело находится в состоянии равновесия.
M1+M2+..+Mn=0
В общем случае для равновесия тел необходимо выполнение двух условий: равенство нулю равнодействующей силы и соблюдение правила моментов.
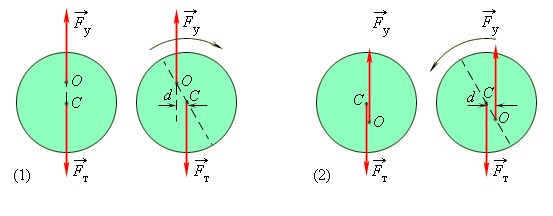
Безразличное, устойчивое и неустойчивое равновесие
В механике есть разные виды равновесия. Так, различают устойчивое и неустойчивое, а также безразличное равновесие.
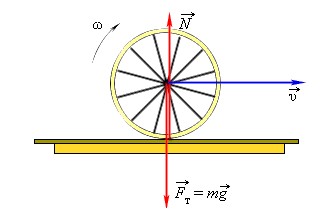
Типичный пример безразличного равновесия – катящееся колесо (или шар), которое, если остановить его в любой точке, окажется в состоянии равновесия.
Устойчивое равновесие – такое равновесие тела, когда при его малых отклонениях возникают силы или моменты сил, которые стремятся вернуть тело в равновесное состояние.
Неустойчивое равновесие – состояние равновесия, при малом отклонении от которого силы и моменты сил стремятся вывести тело из равновесия еще больше.
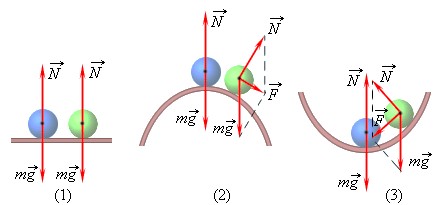
На рисунке выше положение шара (1) – безразличное равновесие, (2) – неустойчивое равновесие, (3) – устойчивое равновесие.
Тело с неподвижной осью вращения может находится в любом из описанных положений равновесия. Если ось вращения проходит через центр масс, возникает безразличное равновесие. При устойчивом и неустойчивом равновесии центр масс располагается на вертикальной прямой, которая проходит через ось вращения. Когда центр масс находится ниже оси вращения, равновесие является устойчивым. Иначе – наоборот.
Особый случай равновесия – равновесие тела на опоре. При этом упругая сила распределяется по всему основанию тела, а не проходит через одну точку. Тело покоится в равновесии, когда вертикальная линия, проведенная через центр масс, пересекает площадь опоры. Иначе, если линия из центра масс не попадает в контур, образованный линиями, соединяющими точки опоры, тело опрокидывается.
Пример равновесия тела на опоре – знаменитая Пизанская башня. По легенде с нее сбрасывал шары Галилео Галилей, когда проводил свои опыты по изучению свободного падения тел.
Линия, проведенная из центра масс башни пересекает основание приблизительно в 2,3 м от его центра.
Скажите пожалуйста, что такое уравновешивающая сила? Физика
Мыслитель
(5525),
закрыт
15 лет назад
Дополнен 15 лет назад
Найти уравновешивающую силу,если на тело действуют две силы F1и F2.(там векторные:F2 направленна вверх,F1 гаризонтально в сторону F2)НЕ ПОМНЮ ЭТУ ТЕМУ….
1 1
Мыслитель
(5108)
15 лет назад
Уравновешивающая – это сила равная по модулю и противоположная по направлению равнодействующей сил. Сначала нужно найти равнодействующую сил. Она равна геометрической сумме сил F 1 и F 2. Для того, чтобы её найти необходимо сложить два вектора F1 и F2.Если вектор F1 направлен вертикально вверх, а вектор F 2 горизонтально, то их сумма будет направлена по диагонали. А численно она будет равна корню квадратному из суммы квадратов F1 и F2.
Mila
Мудрец
(12922)
15 лет назад
Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль тон же прямой, называется уравновешивающей силой
Пользователь удален
Ученик
(134)
15 лет назад
есть вектор F1=(f1,0) or F1=(-f1,0), не указано куды, и F2=(0,f2), так вот равнодействующая сила R=F1+F2, то есть геометрической сумме этих двух, величина ее равна |R|=sqrt(f1^2+f2^2), а направление – alfa=arctg(|f2|/|f1|) – угол между этой силой и осью Ох.