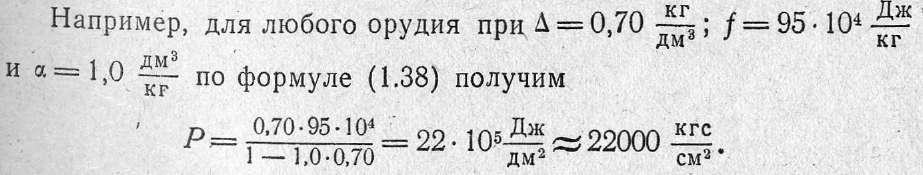Как найти силу давления пороховых газов

Рис.
1.7.
Закон образования газов Рис.
1.8.
Коэффициент
про­

грессивности

При
горении пороха в постоянном объеме,
например в мано­метрической бомбе,
вследствие непрерывного поступления
порохо­вых газов давление р будет
непрерывно возрастать до величины
наибольшего давления Р в момент окончания
горения.

Величина
давления в любой момент времени
определяется
с помощью
уравнения состояния газа с учетом
коволюма (1.12):

откуда

где
да— удельный объем газов.

При
отсутствии теплообмена в постоянном
объеме пороховые горен ^иметь
постоянную температуру Т — Т во все
время

К
росматриваемому моменту времени сгорит
и превратится в пороховые газыпороха,
а останетсяш(1—
ф) пороха. Образовавшиеся пороховые
газы будут занимать объем, равный объему

каморы
Wo,
за вычетом объема, занимаемого несгоревшим
порой

хом:где
8— плотность пороха.

Соответствующий
удельный объем пороховых газов
w
будет равен отношению объема, занимаемого
пороховыми газами, к их массе:

Подставляя
это выражение в формулу (1.32) и учитывая,
что
,
найдем

или |

Знаменатель
выражения (1.33) представляет собой
свободный объем каморы W^,
т. е. объем каморы за вычетом объема,
зани­маемого несгоревшим порохом и
самими молекулами пороховых газов:

Введем
приведенную длину свободного объема
каморы

которая
будет использоваться дальше.

Вводя
плотность заряжания А, можем записать

Ввиду
того что величины а и 1/8 мало отличаются
друг от друга, влияние последнего
слагаемого
в
знаменателе незначительно,
а зависимость
давления пороховых газов от относительной
массь сгоревшего пороха близка к
линейной.

Наибольшее
давление пороховых газов
р—Р
достигается при ф=1
и называется
полным пиростатическим давлением.
Формулу для
Р получим из выражения (1.33) или выражения
(1.36):

или

формула
впервые
была получена Л. Н. Шишковым для дымного

пороха
в
1857
г.

Уравнение
(1.38) представляет собой уравнение
гиперболы относительно
Д. С увеличением плотности заряжания А
наиболь­шее
давление
пороховых газов в постоянном объеме Р
будет расти

и
при приближении А к величине, равной,
будет стремиться кбесконечности,
так как знаменатель в выражении (1.38)
будет стремиться
к нулю.

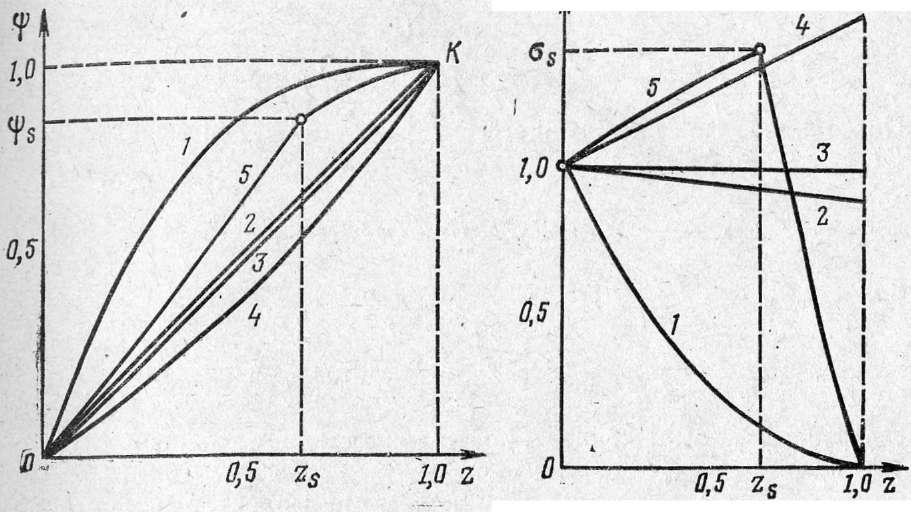
Зависимость
давления пороховых газов в постоянном
объеме от времени имеет вид

где
—давление в момент начала горения
порохового заряда, равное атмосферному
давлению или давлению пороховых газов
воспламенителя; % — пиростатический
параметр условий заряжания:

Из
выражения (1.39) следует, что параметр т
численно равен времени горения порохового
заряда, при котором давление поро­ховых
газов в постоянном объеме увеличится
в е = 2,72 раза.

Полученные
в пиростатике выражения для давления
пороховых газов применяются при
вычислении величины давления или
вели­чины сгоревшей , части порохового
заряда в орудии в предвари­тельном
периоде.

Как
видим, при сгорании всего заряда в каморе
орудия до начала движения снаряда (при
мгновенном сгорании заряда) давление
пороховых газов может достигнуть
нескольких десятков тысяч атмосфер,
что значительно превышает допустимое
по условиям прочности ствола давление.

§ 2.1. Расширение пороховых газов

При
движении снаряда по каналу ствола орудия
происходят расширение пороховых газов
и переход тепловой энергии газов
в механическую
работу, основная и полезная часть которой
равна кинетической энергии снаряда;
при этом температура пороховых газов
будет понижаться.

В
кинетическую энергию снаряда переходит
25—40% всей тепловой энергии, выделяющейся
при сгорании порохового заряда.
Приблизительно половина всей тепловой
энергии пороховых газов при выстреле
выбрасывается в атмосферу в виде тепловой
энергии струи газов и рассеивается.
Некоторая часть тепловой энергии (1—10%)
переходит в

кинетическую
энергию пороховых газов
и также
в значительной степени теряется при
истечении пороховых газов из канала
ствола. При этом в атмосфере возникают
разнообразные явления, связанные с
преобразованием энергии: перемешивание
и нагрев воздуха, возникновение ударных
волн (дульной волны), свечение струи
газов (дульное пламя), электризация
облака пороховых газов, химические
реакциии т. п. Большинство перечисленных
явлений играет отрицательную роль.

Кинетическая
и тепловая энергия пороховых газов в
орудиях с дульным тормозом частично
(до 1 % всей тепловой энергии) полезно
расходуется на работу дульного тормоза
для уменьшения силы отдачи. На откат
ствола, т. е. в кинетическую энергии
откатных частей орудия, переходит 0,5—1%
всей тепловой энергии. Тепловая энергия
пороховых газов и кинетическая энергий
откатных частей орудия в незначительных
количествах используются для совершения
полезных работ, например для заряжаних
орудия в автоматах, наката ствола,
продувки канала ствола ( эжектирование
) и т. д. Некоторая часть тепловой энергии
пороховых газов (до 5%) посредством
теплопередачи переходит стенки ствола,
а затем в охлаждающую ствол жидкость
или в атмосферу.

Считая,
что расширение пороховых газов орудия
происходя без теплообмена, т. е.
адиабатически, на основании первого
закон

термодинамики
можно получить основное уравнение
пиродинамики, описывающее процесс
расширения пороховых газов в ору­дии.
Для адиабатического процесса сумма
работ

,
совершен­ных пороховыми газами
массойпри
расширении, равна изме­нению
их внутренней тепловой энергии:

_гд_е—
тепловая энергия 1 кг пороховых газов
в момент их образования;

— тепловая
энергия 1 кг пороховых газов в
рассматривае­мый момент времени.

Из
термодинамики известно, что

где
C_w
— удельная теплоемкость пороховых
газов при постоян­ном объеме;

— температура
пороховых газов в градусах абсолютной
шкалы.

Для
момента образования пороховых газов
будем иметь
Тогда уравнение (2.1) получит вид

Воспользуемся
еще одним соотношением термодинамики:

где
R
— удельная газовая постоянная;

С_р
— удельная теплоемкость пороховых
газов при постоянном

давлении.

Введем
параметр расширения пороховых газов
0, определяе­мый равенством

в
котором
k
представляет
собой показатель адиабаты: Можем
записать

после
чего выражение (2.4) дляпримет вид

Это
и есть основное уравнение пиродинамики.

Под
величиной р здесь понимается некоторое
постоянное во всех точках заснарядного
пространства среднее давление пороховых
газов, называемое
баллистическим давлением.

Основное
уравнение пиродинамики выражает собой
закон сохранения энергии при выстреле.
Оно записывается для произвольного
момента времени, когда сгорит ф-я часть
порохового заряда, а снаряд пройдет
путь I и будет иметь скорость
v.
В правой части уравнения
(2.10)
стоит разность внутренней (тепловой)
энергий образовавшихся
пороховых газов до их расширения и после
расширения (выражена в единицах работы).
В левой части стоил механическая работа,
которую совершат пороховые газы к
рассматриваемому моменту времени.

Сила
пороха
f
определяет работоспособность
1
кг пороха,
а|произведение
fшф
—работоспособность сгоревшей части
заряда при
изобарном процессе расширения пороховых
газов. При этом

часть
тепла,
выделяемого сгоревшим
порохом,
будет тратиться на под
держание
постоянного давления. При адиабатическом
процессе расширения
пороховых газов, который происходит в
орудии, все тепло идет на совершение
работы. Поэтому для получения вели­чины
тепловой
энергии произведениеделится
на параметр рас­ширениякоторый,
следовательно, численно равен отношению
работы
расширения газов изобарного и
адиа­батического
процессов. Величинадля
поро­ховых
газов
в среднем равна 0,2, т. е. работа пороховых
газов при изобарном процессе со­ставляет
20%
работы при адиабатическом процессе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  07.02.20165.93 Mб35Организация и психология управления персоналом.PDF

• #
• #
• #
• #
• #
• #
• #
• #
• #

Условие задачи:

Из орудия вылетает снаряд массой 10 кг со скоростью 500 м/с. Найти силу давления пороховых газов, считая её постоянной во все время движения снаряда внутри ствола орудия, равное 0,01 с.

Задача №2.1.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=10) кг, (upsilon=500) м/с, (Delta t=0,01) с, (F-?)

Решение задачи:

Сила давления пороховых газов найдем согласно второму закону Ньютона, записанного в общем виде:

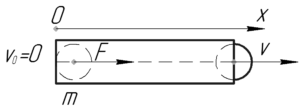
[F = frac{{Delta p}}{{Delta t}};;;;(1)]

В этой формуле ({Delta p}) – это модуль изменения импульса снаряда. Так как в момент выстрела из пушки скорость снаряда была равна нулю (значит и импульс нуль), то очевидно, что модуль изменения импульса равен конечному импульсу снаряда при вылете из ствола.

[Delta p = mupsilon ;;;;(2)]

Подставив выражение (2) в (1), получим ответ к задаче в общем виде.

[F = frac{{mupsilon }}{{Delta t}}]

Посчитаем ответ, подставив численные данные задачи в полученную формулу.

[F = frac{{10 cdot 500}}{{0,01}} = 5 cdot {10^5}; Н = 500; кН]

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.23 Тело массой 50 г, падающее со скоростью 2 м/с, упруго соударяется с горизонтальной
2.1.25 Скорость автомобиля изменяется по закону v=10+0,5t. Найдите результирующую
2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми

Сила – давление – пороховой газ

Cтраница 1

Сила давления пороховых газов является внутренней по отношению к этой системе, давление газа в ружейном стволе во все стороны одинаково и, как было показано, сумма проекций внутренних сил на любую ось равна нулю.
 [1]

Так как сила давления пороховых газов в канале орудия является внутренней силой, то действующими на систему ( орудие и снаряд) внешними силами являются только силы тяжести орудия и снаряда и нормальная реакция платформы. Эти внешние силы вертикальны, и потому сумма 2 – 1 их проекций на горизонтальную ось х равна нулю.
 [2]

Так, например, скорость вылета снаряда из орудия, принимаемая за начальную скорость его полета, учитывает результат действия на снаряд сил давления пороховых газов при движении снаряда по каналу ствола орудия до момента его вылета из орудия.
 [3]

Действие снаряда аналогично действию снаряда с выбрасыванием снаряжения через донную часть. Отличие заключается лишь в том, что здесь внутреннее снаряжение выталкивается из корпуса силой давления пороховых газов.
 [5]

В § § 97 и 98 мы видели, что можно создать запас потенциальной энергии, заставляя какую-либо силу совершать работу, поднимая груз или сжимая пружину. Например, сила давления пороховых газов в стволе ружья, выталкивая пулю, совершает работу, за счет которой и создается запас кинетической энергии пули. Обратно, если вследствие движения пули совершается работа, например, пуля поднимается вверх или, попадая в препятствие, производит разрушения, то кинетическая энергия пули уменьшается.
 [6]

При подъеме камня руками механическая работа совершается мускульной силой рук. Поезд движется под действием силы тяги электровоза, при этом совершается механическая работа. При выстреле из ружья сила давления пороховых газов совершает работу – перемещает пулю вдоль ствола, скорость пули при этом увеличивается.
 [7]

Довольно часто при решении подобных задач ошибочно прикладывают к материальной точке некую движущую силу, направленную по касательной к траектории в данной точке в сторону движения. Начальня скорость УО является результатом толчка, имевшего место в течение весьма малого промежутка времени. Это указание следует учитывать при решении задач о полете пули, снаряда и т.п. Таким образом, сила давления пороховых газов на пулю или снаряд проявляется в сообщении им начальной скорости.
 [8]

В § § 97 и 98 мы видели, что можно создать запас потенциальной энергии, заставляя какую-либо силу совершать работу, поднимая груз или сжимая пружину. Точно так же можно создать и запас кинетической энергии в результате работы какой-либо силы. Например, сила давления пороховых газов в стволе ружья, выталкивая пулю, совершает работу, за счет которой и создается запас кинетической энергии пули. Обратно, если вследствие движения пули совершается работа ( например, пуля поднимается вверх или, попадая в препятствие, производит разрушения), то кинетическая энергия пули уменьшается.
 [9]

В § § 97 и 98 мы видели, что можно создать запас потенциальной энергии, заставляя какую-либо силу совершать работу, поднимая груз или сжимая пружину. Точно так же можно создать и запас кинетической энергии в результате работы какой-либо силы. Действительно, если тело под действием внешней силы получает ускорение и перемещается, то эта сила совершает работу, а тело. Например, сила давления пороховых газов в стволе ружья, выталкивая пулю, совершает работу, за счет которой и создается запас кинетической энергии пули. Обратно, если вследствие движения пули совершается работа, например, пуля поднимается вверх или, попадая в препятствие, производит разрушения, то кинетическая энергия пули уменьшается.
 [10]

В § § 97 и 98 мы видели, что можнэ создать запас потенциальной энергии, заставляя какую-либо силу совершать работу, поднимая груз или сжимая пружину. Точно так же можно создать и запас кинетической энергии в результате работы какой-либо силы. Действительно, если тело под действием. Например, сила давления пороховых газов в стволе ружья, выталкивая пулю, совершает работу, за счет которой и создается запас кинетической энергии пули. Обратно, если вследствие движения пули совершается работа, например, пуля поднимается вверх или, попадая в препятствие, производит разрушения, то кинетическая энергия пули уменьшается.
 [11]

Страницы:  

   1

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.