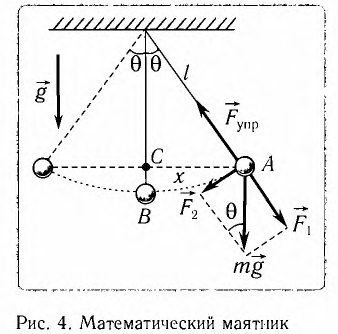
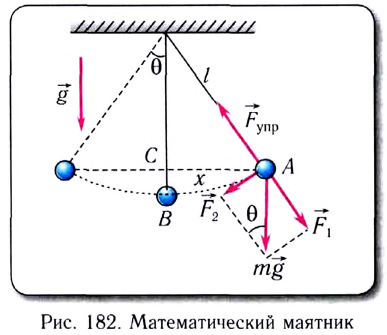
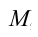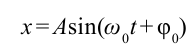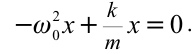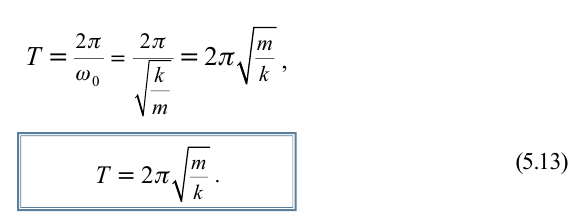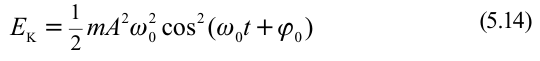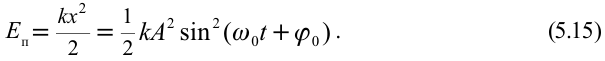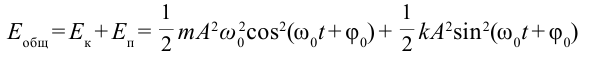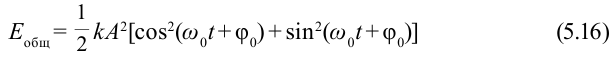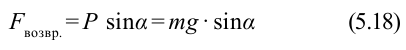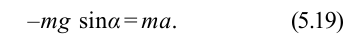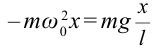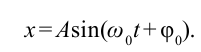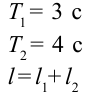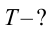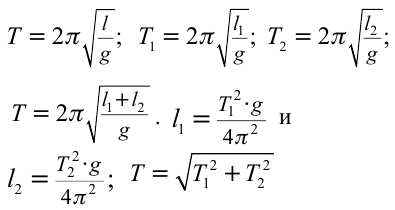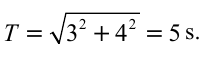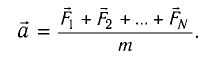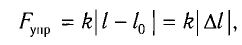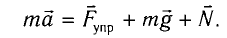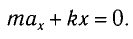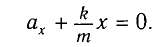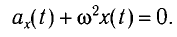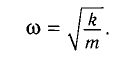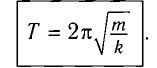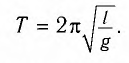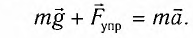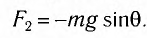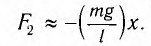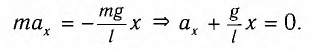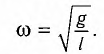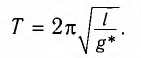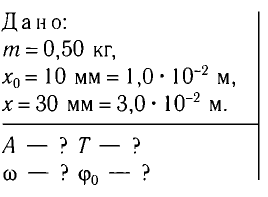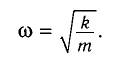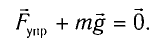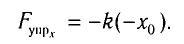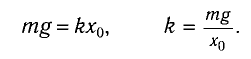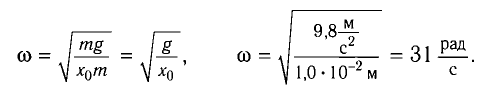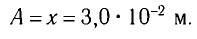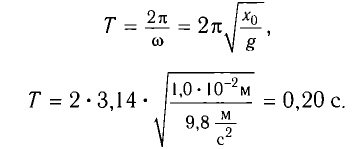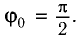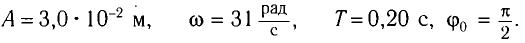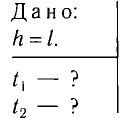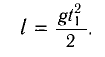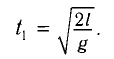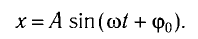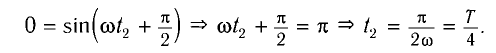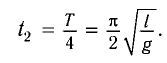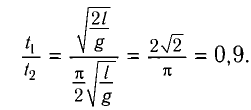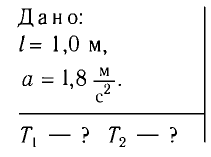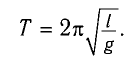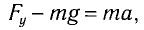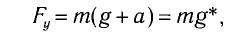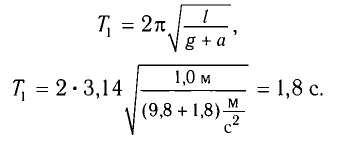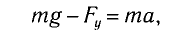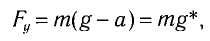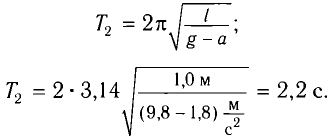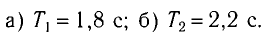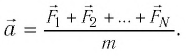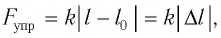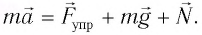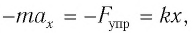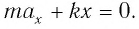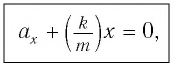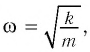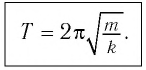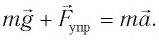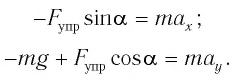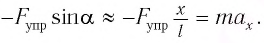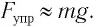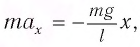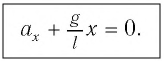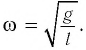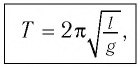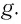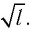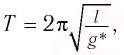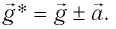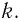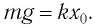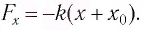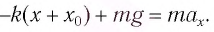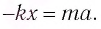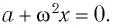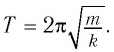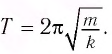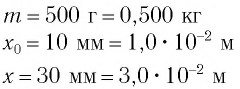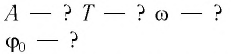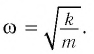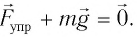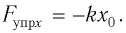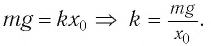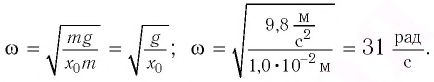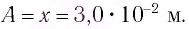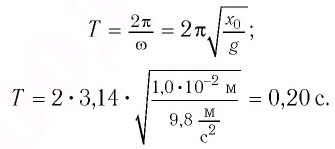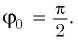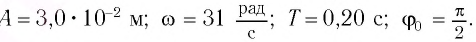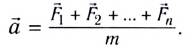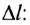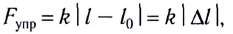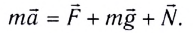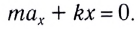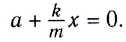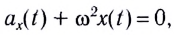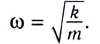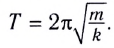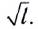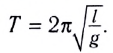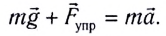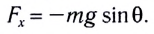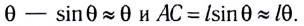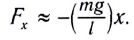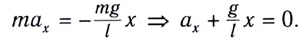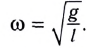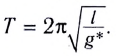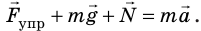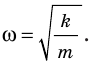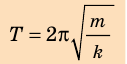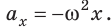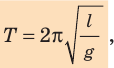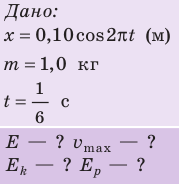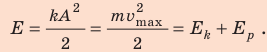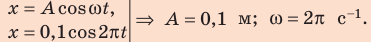Математическим маятником называют материальную точку (тело небольших размеров), подвешенную на тонкой невесомой нерастяжимой нити или на невесомом стержне.
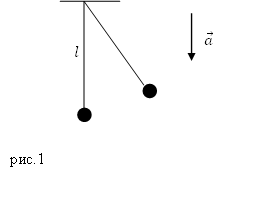
Рис. (1). Силы, действующие на материальную точку в положении равновесия и при отклонении от положения равновесия
В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое.
При отклонении материальной точки от положения равновесия на малый угол
α
на тело будет действовать возвращающая сила (F), которая является тангенциальной составляющей силы тяжести:
Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки уменьшаются. В момент прохождения положения равновесия угол отклонения
α
(=0), тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна.
Далее материальная точка проходит по инерции положение равновесия и, двигаясь далее, сбавляет скорость. В крайнем положении материальная точка останавливается и затем начинает двигаться в обратном направлении.
Период малых собственных колебаний математического маятника длины (l), неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения (g), равен
Обрати внимание!
Период колебаний математического маятника не зависит от амплитуды колебаний и массы груза.
Наиболее известным практическим использованием маятника является применение его в часах для измерения времени. Впервые это сделал голландский физик X. Гюйгенс.
Рис. (2). Колебания маятника часов
Поскольку период колебаний маятника зависит от ускорения свободного падения (g), то часы, которые идут верно в Москве, будут идти вперёд в Санкт-Петербурге. Чтобы эти часы шли верно в Санкт-Петербурге, приведённую длину их маятника нужно увеличить.
В геологии маятник применяют для опытного определения числового значения ускорения свободного падения (g) в разных точках земной поверхности. Для этого по достаточно большому числу колебаний маятника в том месте, где измеряют (g), находят период его колебаний, а затем вычисляют ускорение свободного падения, выразив его из формулы периода маятника.
Заметное отклонение величины (g) от нормы для какой-либо местности называют гравитационной аномалией.
Определение аномалий помогает находить залежи полезных ископаемых.
Опыт показывает, что качающийся маятник сохраняет плоскость, в которой происходят его колебания. Это означает, что если привести в движение маятник, установленный на диске центробежной машины, а диск заставить вращаться, то плоскость качания маятника относительно комнаты изменяться не будет. Это позволяет с помощью опыта обнаружить вращение Земли вокруг своей оси.
В (1850) г. Ж. Фуко подвесил маятник под куполом высокого здания так, что острие маятника при качании оставляло след на песке, насыпанном на полу. Оказалось, что при каждом качании острие оставляет на песке новый след. Таким образом, опыт Фуко показал, что Земля вращается вокруг своей оси. В условиях вращения Земли при достаточно большой нити подвеса плоскость, в которой маятник совершает колебания, медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли.
При исследовании гармонических колебаний твердого тела, которое не моделируют в виде материальной точки, рассматривают физический маятник.
Источники:
Рис. 1. Силы, действующие на материальную точку в положении равновесия и при отклонении от положения равновесия. . © ЯКласс.
Рис. 2. Колебания маятника часов. ЮК, Public domain, via Wikimedia Commons. 2021-08-29.
Маятниками называют
механические системы и устройства,
могущие совершать колебания вблизи
положения устойчивого равновесия.
Такими системами являются, например,
пружинный маятник, математический
маятник, физический маятник, крутильный
маятник. Эти маятники показаны на рис.
5.2. При малых смещениях от положения
равновесия маятники могут совершать
колебания, которые можно рассматривать
как гармонические, а сами маятники как
гармонические осцилляторы. Рассмотрим
колебания таких осцилляторов.
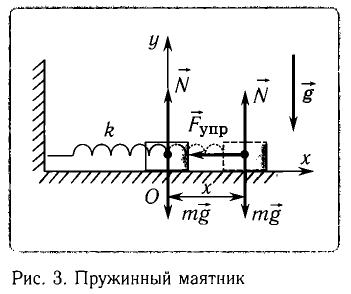
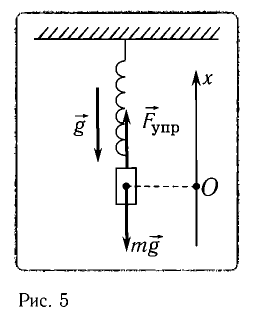
1. Пружинный маятник
Пружинный маятник
представляет собой груз, подвешенный
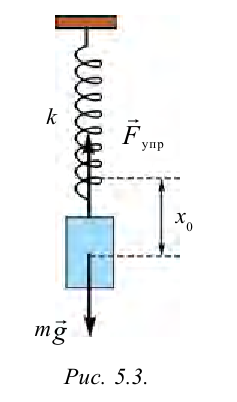
на пружине. На груз массой m
(рис. 5.3) действуют две силы:
|
Рис. |
направленная
вниз сила тяжести mg
и направленная вверх упругая сила
пружины
где
–
жесткость пружины. При некотором
растяжении пружины
эти силы уравновешивают друг друга:
Направим ось X
вертикально вниз и выберем начало
отсчета в положении равновесия грузика.
При смещении x
груза из положения равновесия полное
удлинение пружины станет равным
а упругая сила
Результирующая сила, действующая на
груз c
учетом того, что
,
будет равна

Уравнение движения
груза будет иметь вид
или
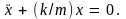
Сравнивая это с
уравнением (5.1), находим частоту колебаний
пружинного маятника
и его период
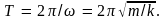
Как
видим, эти параметры колебания определяются
только величинами, характеризующие сам
маятник.
2. Математический маятник
Математический
маятник представляет собой небольшое
(точечное) тело, подвешенное в поле
тяжести Земли на невесомой
нерастяжимой
нити (или невесомом стержне), длина
которой l
много больше размеров тела. Такое тело
можно рассматривать как материальную
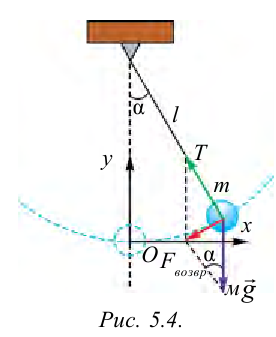
точку. Отклоним маятник от положения
равновесия на некоторый угол φ
(рис. 5.4) и определим действующую при
этом на маятник силу. Общая сила,
действующая на маятник, равна силе
тяжести mg,
где m
– масса маятника. Разложим эту силу на
составляющую вдоль нити и на составляющую,
перпендикулярную ей. Первая составляющая
уравновешивается силой натяжения нити
Т, а
вторая вызывает движение маятника к
положению равновесия
|
Рис. |
(при
φ = 0), т.е. является
возвращающей силой. Эта составляющая,
как видно из рисунка, равна
(знак минус учитывает тот факт, что эта
сила стремится уменьшить величину угла
φ). В случае
малых колебаний угол φ
все время остается малым, и поэтому дугу
окружности, по которой движется тело,
можно считать прямой. Обозначим отклонение
тела от положения равновесия через x;
тогда при малых углах φ
можно приближенно считать
где l
– длина маятника. Для возвращающей силы
при малых φ
будем иметь
Уравнение движения маятника
или
Откуда получаем частоту колебания
математического маятника
и
его период
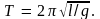
Как
видим, период колебаний математического
маятника определяется только длиной
маятника и ускорением силы тяжести в
месте его расположения.
3. Физический маятник
Этот маятник
показан на рис. 5.5. Он представляет собой
твердое тело, могущее вращаться вокруг
горизонтальной оси под влиянием силы
тяжести. При отклонении маятника на
угол φ от
вертикального положения на него
относительно оси вращения будет
действовать момент сил тяжести
где m
– масса тела, а
– расстояние от центра масс С
тела до оси враще-
|
Рис. |
ния
(она проходит через точку О)
перпендикулярно плоскости рисунка),
– расстояние от линии действия силы
тяжести mg
до оси вращения (плечо силы mg);
знак минус выражает тот факт, что момент
М стремится
уменьшить угол φ.
При малых колебаниях угол φ
мал, так что
Запишем основное уравнение динамики
вращательного движения тела
или
где I
– момент инерции тела относительно оси
вращения. Это уравнение описывает
гармонические колебания угла
отклонения
маятника от вертикального положения,
поэтому частота колебаний маятника
,
а его период

Сравнив эти
выражения с формулами для частоты и
периода колебаний математического
маятника, мы видим, что свойства движения
физического маятника совпадают со
свойствами движения математического
маятника с длиной
Ее называют приведенной длиной физического
маятника. Математический маятник
является частным случаем физического
маятника. Если считать, что вся масса
физического маятника сосредоточена в
центре масс, то его момент инерции
Тогда
а
период
Тем
самым мы пришли к формуле периода
колебаний математического маятника.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Математический маятник, теория и онлайн калькуляторы
Математический маятник
Физический маятник
Определение
Физическим маятником считают твердое тело, которое может качаться вокруг неподвижной оси, расположенной горизонтально.
Точка пересечения этой оси с вертикальной плоскостью, которая проходит через центр масс маятника называют точкой подвеса маятника. Положение тела в каждый момент времени физического маятника характеризуют углом отклонения его от положения равновесия ($varphi $). Угол $varphi $ выполняет роль обобщенной координаты. Кинетическая энергия ($E_k$) качающегося физического маятника может быть определена как:
[E_k=frac{J{dot{varphi }}^2}{2}left(1right),]
где $J$ – момент инерции маятника по отношению к точке подвеса; $omega =frac{dvarphi }{dt}=dot{varphi }$ – угловая скорость.
Потенциальная энергия ($E_p$) в случае малых колебаний маятника вычисляется как:
[E_p=frac{mga}{2}{varphi }^2left(2right),]
где $a$ – расстояние между центром масс маятника и точкой подвеса; $m$ – масса мятника; $g$ – ускорение свободного падения.
Малые колебания физического маятника можно считать гармоническими с циклической частотой (${omega }_0$) равной:
[{omega }_0=sqrt{frac{mga}{J}}left(3right).]
Полная энергия колебаний маятника равна:
[E=frac{mA^2{omega }^2_0}{2}left(4right),]
где $A$ – амплитуда колебаний.
Математический маятник – частный случай физического маятника
Определение
Математическим маятником называют физический маятник, вся масса которого сосредоточена в одной точке, центре масс маятника.
Чаще всего математический маятник рассматривают как шарик, который подвешен на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая колебания под действием силы тяжести. Хорошим приближением к математическому маятнику считают тяжелый маленький шарик, совершающий колебания на тонкой длинной нити.
Для математического маятника расстояние между центром масс маятника и точкой подвеса ($a$) равно длине нити ($l$), момент инерции шарика равен $J=ml^2$тогда формулу для циклической частоты колебаний математического маятника запишем как:
[{omega }_0=sqrt{frac{g}{l}}left(5right).]
Период колебаний математического маятника ($T$) при этом:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(6right).]
Уравнение движения математического маятника и его решение
Математический маятник является примером гармонического осциллятора, совершающим гармонические колебания описываемые уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(7right).]
Решением уравнения (7) является выражение:
[varphi ={varphi }_0{cos left({omega }_0t+alpha right)left(8right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической или квантовой механики.
Примеры задач с математическим маятником
Пример 1
Задание. Каков период (T) колебаний математического маятника, который подвешен к потолку кабины лифта, движущегося вертикально вниз 1) равномерно; 2) с ускорением $a$? Длина нити маятника равна $l$.
Решение. Сделаем рисунок.
Период колебаний при равномерном движении математического маятника равен:
[T=2pi sqrt{frac{l}{g}}left(1.1right).]
При движении с ускорением вниз период равен:
[T=2pi sqrt{frac{l}{g-a}}left(1.2right).]
Ответ. 1) $T=2pi sqrt{frac{l}{g}}.$ 2) $T=2pi sqrt{frac{l}{g-a}}$
Пример 2
Задание.Какова возвращающая сила ($F$), действующая на шарик, массой $m$, математического мятника при $t’$ и его полная энергия (E), если колебания совершаются по закону $x=0,2{cos ({omega }_0t) }$, где ${omega }_0=frac{2pi }{3}$($frac{рад}{с}$)?
Решение. 1) Для нахождения силы, действующей на материальную точку в которой сосредоточена масса математического маятника, воспользуемся вторым законом Ньютона:
[ma=F left(2.1right).]
Ускорение шарика найдем как:
[a=frac{d^2x}{dt^2}=frac{d}{dt}left(frac{d}{dt}left(A{cos left({omega }_0tright) }right)right)=-A{omega }^2_0{cos left({omega }_0tright) }=-frac{0,8cdot {pi }^2}{9}{cos left({omega }_0tright) }.]
Получаем, то сила равна:
[F=ma=-mfrac{4{pi }^2}{45}{cos left({omega }_0t’right) }.]
2) Полная энергия маятника:
[E=frac{mA^2{omega }^2_0}{2}=mfrac{0,4}{2}cdot frac{4{pi }^2}{3}=frac{4}{15}{pi }^2m.]
Ответ. $F$=$-mfrac{4{pi }^2}{45}{cos left({omega }_0t’right) left(Нright) }.E=frac{4}{15}{pi }^2m Дж$
Читать дальше: механика.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 февраля 2023 года; проверки требует 1 правка.
Математический маятник. Чёрный пунктир — положение равновесия, 
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен
и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.
Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.
Характер движения маятника[править | править код]
Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).
При колебаниях в одной плоскости маятник движется по дуге окружности радиуса 
Уравнение колебаний маятника[править | править код]
Маятник (схема с обозначениями)
Если в записи второго закона Ньютона 

,
так как 

,
где неизвестная функция 




.
Для решения ДУ второго порядка, то есть для определения закона движения маятника, необходимо задать два начальных условия — угол 


Решения уравнения движения[править | править код]
Возможные типы решений[править | править код]
В общем случае решение ДУ с начальными условиями для маятника может быть получено численно. Варианты движения (в случае, если маятник — это материальная точка на лёгком стержне), качественно, представлены на анимации. В каждом окне вверху показана зависимость угловой скорости 

-
Маятник висит
-
Малые колебания (размах 45°)
-
Колебания с размахом 90°
-
Колебания с размахом 135°
-
Колебания с размахом 170°
-
Фиксация в верхнем положении
-
Движение близкое к сепаратрисе
-
Вращение маятника
Гармонические колебания[править | править код]
Уравнение малых колебаний маятника около нижнего положения равновесия, когда уместна замена 
,
где 


.
Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону[2]:
,
где 

Если пользоваться переменной 







Случай нелинейных колебаний[править | править код]
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 


Параметр 
.
Период колебаний нелинейного маятника составляет
,
где K — эллиптический интеграл первого рода.
Для вычислений практически удобно разлагать эллиптический интеграл в ряд:
где 

При углах до 1 радиана (≈ 60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:
.
Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года[3]:
,
где 

Движение по сепаратрисе[править | править код]
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.
Факты[править | править код]
Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.
- Если амплитуда колебания маятника близка к
, то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения[4].
- Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
- В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).
См. также[править | править код]
- Физический маятник
- Маятник Фуко
- Маятник Дубошинского
Примечания[править | править код]
- ↑ 1 2 Главный редактор А. М. Прохоров. Маятник // Физический энциклопедический словарь. — М.: Советская энциклопедия. — 1983. — Статья в Физическом энциклопедическом словаре
- ↑ Скорость и ускорение маятника при гармонических колебаниях также изменяются во времени по синусоидальному закону.
- ↑ Adlaj S. An Eloquent Formula for the Perimeter of an Ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 59, no. 8. — P. 1096—1097. — ISSN 1088-9477.
- ↑ В. В. Вечеславов. Хаотический слой маятника при низких и средних частотах возмущений // Журнал технической физики. — 2004. — Т. 74, № 5. — С. 1—5. Архивировано 14 февраля 2017 года.
Ссылки[править | править код]
- Коллекция Java-апплетов, моделирующая поведение математических маятников, в частности маятника Капицы.
- Java-апплет, моделирующий колебание математического маятника при наличии вязкого трения с черчением фазовой траектории.
- Учебный фильм «Математический и физический маятник», производство СССР
Содержание:
Пружинные и математические маятники:
Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.
Система, состоящая из груза массой
Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:
Если учесть, что ускорение тела, совершающего гармонические колебания 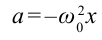
Из этого уравнения мы имеем:
Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника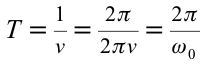
Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, 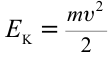
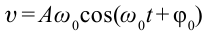
Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:
В большинстве случаев важно знать полную энергию системы:
Если учесть, что 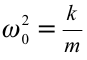
Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки 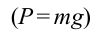

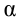
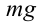

Из рис. 5.4. видим, что:
Согласно второму закону Ньютона, сила 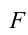
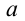
Из-за того, что угол наклона очень маленький 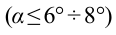
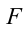
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой 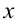
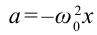
Следовательно
Исходя из смысла периода колебания и учитывая, что 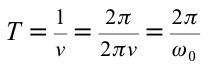
Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:
- при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
- период колебания математического маятника также не зависит от массы подвешенного на него груза;
- период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.
Отсюда колебание математического маятника записывается следующим выражением:
Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 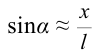
Пример:
Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.
Дано:
Найти:
Формула:
Решение:
Ответ: 5 cек.
Пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
Закон Гука: модуль силы упругости 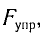
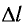
где k — жесткость тела, 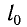
Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).
Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 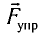
Запишем второй закон Ньютона для движения груза:
В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем
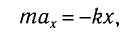
Следовательно,
Это уравнение аналогично уравнению гармонических колебаний
Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:
Тогда период колебаний пружинного маятника можно найти по формуле
Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов 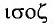
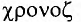
Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).
Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.
Галилео Галилей экспериментально определил, что период малых колебаний (9 < 10°) математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения 
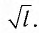
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
При углах отклонения математического маятника 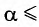
Отклонение маятника от положения равновесия будем характеризовать углом 
Согласно второму закону Ньютона для движения шарика можем записать:
Смещение маятника вдоль дуги х = l

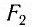
Заметим, что при малых углах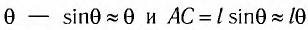
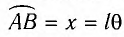
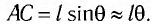


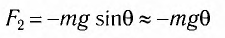
является очень хорошим приближением.
Подставляя в выражение (1) значение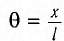
Таким образом, уравнение движения маятника запишется в виде
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 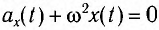
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 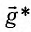
Пример:
Определите амплитуду А, циклическую частоту 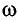
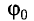
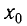
Решение
Циклическая частота колебаний «вертикального» пружинного маятника также определяется по формуле
Найдем жесткость k пружины. Из условия равновесия тела следует
По закону Гука
В проекции на ось Ох условие равновесия запишется в виде:
Отсюда для циклической частоты 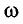
Так как по условию задачи тело сместили на расстояние х = 30 мм от положения равновесия, то амплитуда его колебаний
Период колебаний находим из соотношения
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний
Ответ:
Пример:
Металлический шарик, подвешенный на длинной легкой нерастяжимой нити, поднимают по вертикали до точки подвеса и отпускают. Затем нить маятника отклоняют на небольшой угол от вертикали и также отпускают. В каком из этих случаев шарик быстрее возвратится в начальное положение?
Решение
В первом случае шарик свободно падает без начальной скорости с высоты h = l, следовательно,
Отсюда находим промежуток времени 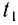
Во втором случае промежуток времени 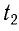
Поскольку в начальный момент времени t = 0 маятник имеет максимальное
отклонение от положения равновесия, то начальная фаза колебаний 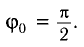
Используя формулу для периода колебаний математического маятника
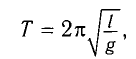
Разделив почленно уравнения для промежутков времени 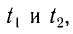
Ответ: шарик быстрее возвратится в начальное положение в случае, когда он движется вертикально вниз.
Пример:
Найдите периоды колебаний математического маятника длиной l= 1,0 м при перемещении его точки подвеса с ускорением, модуль которого а = 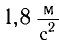
Решение
Период колебаний математического маятника в поле силы тяжести Земли
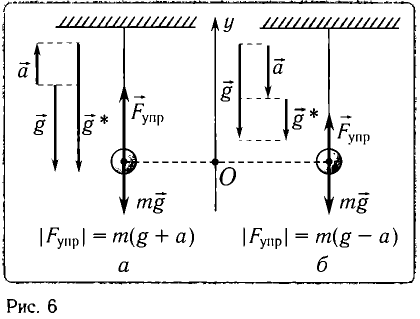
а) При движении маятника с ускорением 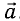
где Fy — проекция силы упругости нити.
Откуда находим
где g* = g + а — «эффективное ускорение».
Период колебаний определяется по формуле
б) При движении точки подвеса маятника с ускорением 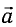
где Fy — проекция силы упругости нити. Откуда находим
где g*=g-a — «эффективное ускорение». Период колебаний
Ответ:
Что такое пружинный и математический маятники
Второй закон Ньютона (основной закон динамики): ускорение тела прямо пропорционально результирующей силе и обратно пропорционально массе тела:
Закон Гука: при упругих деформациях сжатия и растяжения модуль силы упругости прямо пропорционален модулю изменения длины тела:
где 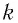
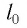
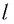
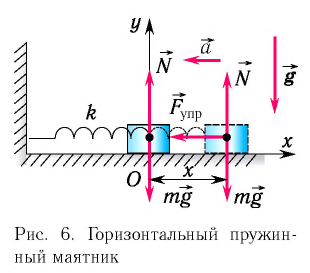
Колебательная система, состоящая из тела с прикрепленной к нему пружиной, называется пружинным маятником. Пружина может располагаться как вертикально (вертикальный пружинный маятник), так и горизонтально (горизонтальный пружинный маятник).
Рассмотрим колебания горизонтального пружинного маятника. Пусть груз массой 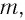
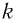
Выведем груз из положения равновесия, сместив его на расстояние 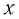
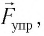
Согласно второму закону Ньютона для движения груза
В проекции на ось 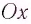
или
Перепишем полученное соотношение в виде:
которое является уравнением гармонических колебаний пружинного маятника.
Сравнивая (1) с уравнением гармонических колебаний 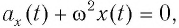
которая определяется массой 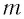
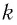
Для нахождения периода колебаний пружинного маятника воспользуемся формулой 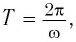
Как следует из формул (2) и (3), период и частота колебаний пружинного маятника не зависят от амплитуды его колебаний (в пределах выполнимости закона Гука).
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греч. 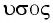
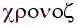
Изохронность колебаний маятника была открыта Гали-лео Галилеем в 1583 г. при изучении движения груза, подвешенного на нити. Моделью данной колебательной системы является математический маятник.
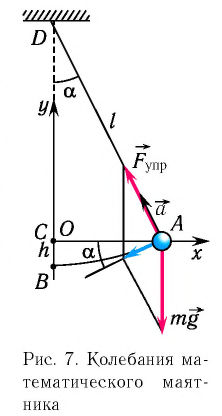
Колебательная система, состоящая из находящегося в поле силы тяжести тела, подвешенного на легкой нерастяжимой нити, размеры которого малы по сравнению с длиной нити, а его масса значительно больше массы нити, называется математическим маятником. При таких условиях тело можно считать материальной точкой, а нить — легкой нерастяжимой (рис. 7).
Рассмотрим колебания математического маятника.
Отклонение маятника от положения равновесия будем характеризовать углом 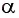
После отклонения маятника на него действуют две силы: направленная вертикально вниз сила тяжести 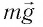
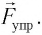
Согласно второму закону Ньютона для движения маятника можем записать:
В проекциях на выбранные оси координат 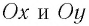
Для углов отклонения 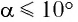
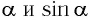
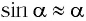
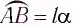
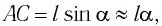
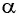
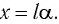
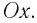
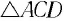
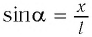
Таким образом, силой, возвращающей маятник к устойчивому положению равновесия, является сила упругости его нити.
При малых углах отклонения маятника проекция вектора ускорения 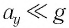
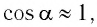
Следовательно, уравнение движения маятника вдоль оси 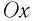
где 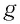
Отсюда получаем уравнение гармонических колебаний математического маятника:
При сравнении уравнения (8) с уравнением гармонических колебаний 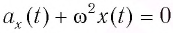
Тогда период малых колебаний математического маятника в поле тяжести Земли определяется по формуле Гюйгенса:
которую впервые получил ученик И. Ньютона Христиан Гюйгенс.
При углах отклонения математического маятника 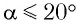
Как видно из формул (9) и (10), циклическая частота и период математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной 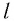
Галилео Галилей первый экспериментально определил, что период малых колебаний 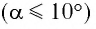
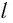
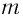
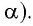
Если маятник приобретает дополнительное ускорение 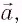
где 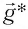
- Заказать решение задач по физике
Пример:
Выведите формулу для периода колебаний вертикального пружинного маятника, если масса груза 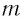
Решение
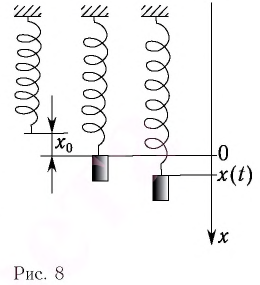
Рассмотрим вертикальное движение груза, происходящее под действием силы упругости пружины и силы тяжести груза после толчка. Начало координат поместим в точку, соответствующую равновесному положению тела (рис. 8). В этом положении пружина растянута на величину 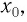
При смещении груза на величину 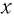
Тогда по второму закону Ньютона
С учетом соотношения (1) это уравнение перепишем в виде:
Если ввести обозначение 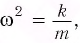
Оно описывает гармонические колебания вертикального пружинного маятника с частотой такой же, как у горизонтального пружинного маятника. Следовательно, период колебаний вертикального пружинного маятника такой же, как и горизонтального:
Ответ:
Таким образом, действующая в колебательной системе постоянная сила только смещает положения равновесия, но не изменяет частоту колебаний.
Пример:
Определите амплитуду 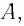
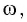
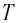
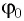
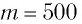
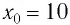
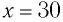
Дано:
Решение
Циклическая частота колебаний вертикального пружинного маятника так же, как и горизонтального, определяется по формуле (см. пример 1):
Для нахождения жесткости к пружины запишем условие равновесия тела:
По закону Гука
В проекции на ось 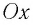
Отсюда для циклической частоты 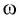
Амплитуда колебаний маятника определяется начальным смешением:
Период колебаний находим из соотношения:
Поскольку в начальный момент времени тело было смещено на максимальную величину, то начальная фаза колебаний
Ответ:
Подробное объяснение пружинного и математического маятника
Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:
Закон Гука: модуль силы упругости 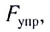
где k — жесткость тела, 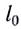
Простейшая колебательная система может быть получена с использованием груза и пружины.
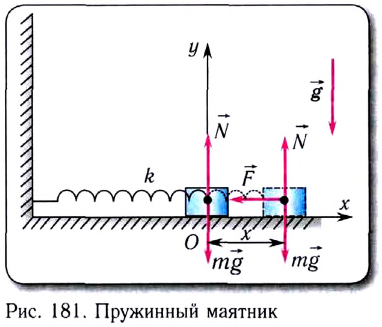
Прикрепим груз массой m, лежащий на гладкой горизонтальной поверхности, к невесомой упругой пружине жесткостью k, второй конец которой зафиксирован (рис. 181). Такая система называется пружинным маятником.
Запишем второй закон Ньютона для этой системы
В проекции на ось Ох с учетом закона Гука получаем
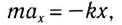
Запишем это уравнение в форме, аналогичной уравнению движения гармонического осциллятора:
Сравнивая полученное выражение с уравнением гармонических колебаний
находим циклическую частоту колебаний пружинного маятника
Тогда период колебаний пружинного маятника можно найти по формуле
Свойство независимости периода колебаний маятника от амплитуды, открытое Галилеем, называется изохронностью (от греческих слов 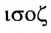
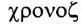
Как видим, пружинный маятник обладает свойством изохронности, поскольку период его колебаний не зависит от амплитуды.
Одной из наиболее распространенных колебательных систем является математический маятник.
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 182).
Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
При углах отклонения математического маятника 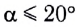
Отклонение маятника от положения равновесия будем характеризовать углом 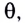
Из второго закона Ньютона следует (см. рис. 182):
Смещение маятника вдоль дуги 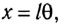
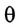
Возвращающей силой в данном случае является проекция на касательную к дуге силы тяжести 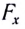
Заметим, что при малых углах 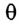
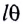
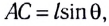
Для небольших углов (до 10°) значения 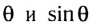
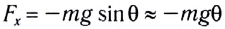
Используя полученное соотношение между координатой х и углом 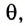
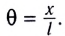
Таким образом, уравнение движения маятника запишется в виде
Поскольку полученное уравнение совпадает с уравнением гармонических колебаний 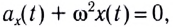
Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения.
В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 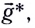
Математический и пружинный маятники и энергия колебаний
Колебательные движения очень разнообразны. При этом существует «классика» колебательных движений — они описаны сотни лет назад, их изучением занимались Галилео Галилей (1564– 1642) и Христиан Гюйгенс (1629–1695). Это колебания пружинного и математического маятников.
Колебания пружинного маятника
Пружинный маятник — это колебательная система, представляющая собой закрепленное на пружине тело.
Рассмотрим колебания горизонтального пружинного маятника — тележки массой m, закрепленной на пружине жесткостью k. Будем считать, что силы трения, действующие в системе, пренебрежимо малы, а значит, колебания маятника незатухающие (их амплитуда с течением времени не изменяется, а полная механическая энергия системы сохраняется). При этом потенциальная энергия деформированной пружины будет превращаться в кинетическую энергию движения тележки, и наоборот.
Колебания пружинного маятника:
Обратите внимание! В течение всего времени колебания сила упругости направлена в сторону, противоположную смещению тележки, — сила упругости все время «толкает» тележку к положению равновесия.
Итак, причины свободных колебаний пружинного маятника: 1) действующая на тело сила всегда направлена к положению равновесия; 2) колеблющееся тело инертно, поэтому оно не останавливается в положении равновесия (когда равнодействующая сил становится равной нулю), а продолжает движение в том же направлении.
Как вычислить период колебаний пружинного маятника
Рассмотрим колебания тележки, закрепленной на горизонтальной пружине, с точки зрения второго закона Ньютона (рис. 20.1). Запишем уравнение второго закона Ньютона в векторном виде:
Сила тяжести и сила нормальной реакции опоры уравновешивают друг друга, поэтому 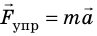
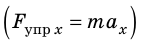
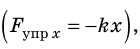
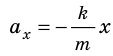
Последнее уравнение можно записать в виде 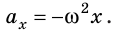
Приняв во внимание, что 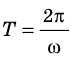
Обратите внимание! Период колебаний пружинного маятника не зависит ни от амплитуды колебаний, ни от места расположения маятника (на поверхности Земли или Луны, в космическом корабле и т. д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость k пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
Что называют математическим маятником
Любое твердое тело, которое совершает или может совершать колебания относительно оси, проходящей через точку подвеса, называют физическим маятником. Примером может быть игрушка, подвешенная на нити в салоне автомобиля. Если игрушку вывести из положения равновесия, она начнет колебаться. Однако изучать такие колебания сложно: их характер определяется размерами и формой игрушки, свойствами нити и другими факторами.
Чтобы размеры тела не влияли на характер его колебаний, следует взять нить, длина которой намного больше размеров тела, а масса незначительна по сравнению с его массой. В таком случае тело можно считать материальной точкой. А чтобы во время колебаний тело все время находилось на одинаковом расстоянии от точки подвеса, нить должна быть нерастяжимой. Таким образом будет получена физическая модель — математический маятник.
Математический маятник — это физическая модель колебательной системы, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити, и гравитационного поля.
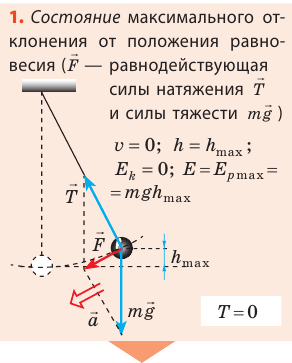
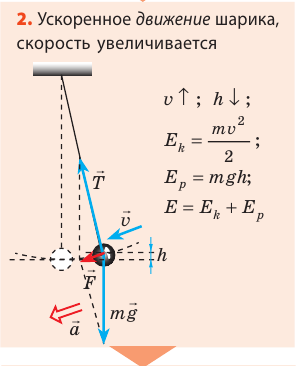
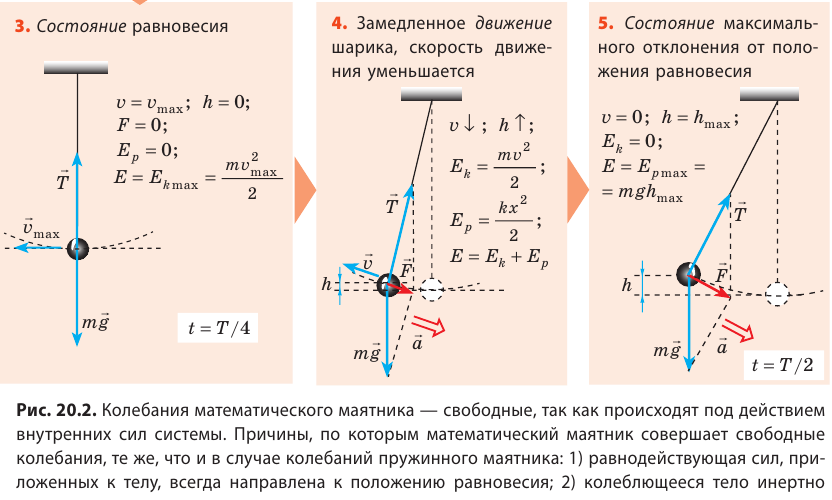
Колебания математического маятника
Возьмем небольшой, но достаточно тяжелый шарик и подвесим его на длинной нерастяжимой нити — такой маятник можно считать математическим. Если отклонить шарик от положения равновесия и отпустить, то в результате действия гравитационного поля Земли (силы тяжести) и силы натяжения нити шарик начнет колебаться около положения равновесия. Поскольку сопротивление воздуха пренебрежимо мало, а силы, действующие в системе, являются консервативными, полная механическая энергия шарика будет сохраняться: потенциальная энергия шарика будет превращаться в его кинетическую энергию, и наоборот.
Рассмотрите колебательное движение шарика (рис. 20.2). Объясните причины его движения. Какие происходят превращения энергии?
Как вычислить период колебаний математического маятника
Математический маятник, отклоненный от положения равновесия на небольшой угол (3–5°), будет совершать гармонические колебания, то есть ускорение его движения все время будет прямо пропорционально смещению и направлено в сторону, противоположную смещению:
Для математического маятника: 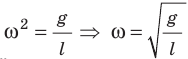
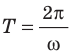
где l — длина маятника; g — ускорение свободного падения.
Данную формулу впервые получил в XVII в. голландский ученый Христиан Гюйгенс, поэтому ее называют формулой Гюйгенса.
Период колебаний математического маятника не зависит от массы маятника, а определяется только длиной нити и ускорением свободного падения в том месте, где расположен маятник. Поэтому, измерив длину нити и период колебаний маятника, можно определить ускорение свободного падения в данной местности.
Пример:
Уравнение колебаний груза массой 1 кг на пружине имеет вид: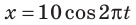
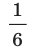
Решение:
Трение отсутствует, поэтому полная механическая энергия сохраняется:
Сравним уравнение колебаний в общем виде с уравнением, приведенным в задаче:
Поскольку
Определив удлинение пружины через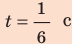
Выводы:
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники

























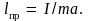























![{displaystyle T=T_{0}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {theta _{0}}{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {theta _{0}}{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {theta _{0}}{2}}right)+dots right}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5346cf06ad62d5c061cf5527d53a86e61cf89478)