Как найти силу действующую на стенку сосуда

Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?

Взгляните на рисунок 1.

Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться. 

Вывод формулы

Выведем формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда (рисунок 2).

Давление жидкости $p$ рассчитывается по формуле: $p = frac{F}{S}$, где $F$ — это сила, действующая на дно сосуда, а $S$ — это площадь дна сосуда.

1. Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде;
2. Как узнать вес жидкости? Необходимо знать массу $m$ жидкости;
3. Массу $m$ мы можем вычислить по известной нам формуле: 
   $m = rho V$;

1. Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда — $S$. Тогда объем можно вычислить по формуле:
   $V = Sh$;

1. Итак, подставляем наши данные в формулу для вычисления массы и получаем:
   $m = rho Sh$;

1. Таким образом, возвращаемся к весу жидкости и получаем, что: 
   $P = mg$, где $g$ — ускорение свободного падения, или $P = g rho Sh$.

С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Поэтому если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:
$p = frac{P}{S}$,
или $p =frac{g rho Sh}{S}$,

То есть:

$p = rho gh$.

Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($frac{кг}{м^3}$), $g = 9.8 frac{H}{кг}$, высоту столба жидкости  — в метрах ($м$). Тогда давление $p$ будет выражено в паскалях ($Па$).

Выводы

Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать? 

От каких величин зависит давление жидкости на дно сосуда?

Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба.

Обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине.

По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?

По формуле $p = rho gh$ можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.

Вопросы и пример задачи

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть ответ

Дано:
$rho = 800 frac{кг}{м^3}$
$h = 8 space м$

$p — ?$

Посмотреть решение и ответ

Скрыть

Упражнения

Дано:
$h = 0.6 space м$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p_1 — ?$
$p_2 — ?$
$p_3 — ?$

Показать решение и ответ

Скрыть

Дано:
$h = 10 space 900 space м$
$rho = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p — ?$

Показать решение и ответ

Скрыть

Дано:
$m = 5 space кг$
$h = 1 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$S — ?$

Показать решение и ответ

Скрыть

Задания

Показать ответ

Скрыть

Дано:
$h = 0.086 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p — ?$

Показать решение и овет

Скрыть

Подробности

Обновлено 20.01.2019 00:29

Просмотров: 583

1. Вывод формулы для расчета давления жидкости на дно сосуда

2. От каких величин и как зависит давление жидкости на дно сосуда?

Давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.

Следующая страница – смотреть

Назад в “Оглавление” – смотреть

Лекция
4. Давление жидкости на окружающие её
стенки

Сила
давления жидкости на плоскую стенку

Центр
давления

Сила
давления жидкости на криволинейную
стенку

Круглая
труба под действием гидростатического
давления

Гидростатический
парадокс

Основы
теории плавания тел

Важнейшей
задачей гидростатики является определение
сил, с которыми жидкость действует на
окружающие её твёрдые стенки. Очень
часто необходимо знать величину,
направление и точку приложения сил,
вызванных давлением, чтобы правильно
провести прочностные расчёты элементов
конструкции гидропривода (гидравлических
машин, аппаратов и арматуры). Подобные
задачи необходимо решать и в ходе
проектирования гидротехнических
сооружений (плотин, дамб, причалов и
т.д.). Проанализируем решение наиболее
часто возникающих (типовых) задач.

Сила давления жидкости на плоскую стенку

Р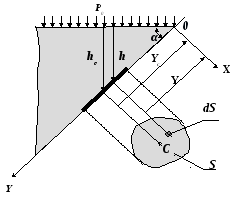ассмотрим
произвольную площадку
ds,
расположенную
на плоской наклонной стенке сосуда с
жидкостью на расстоянии Y
от оси X,
и определим силы, действующие на эту
площадку. Сила от давления, действующего
на элементарную площадку dS,
будет
описываться формулой:

Если
проинтегрировать это выражение по
площади, можно определить полную силу,
действующую на всю площадь целиком

Из
рисунка ясно, что в последнем выражении
.Подставив
значение h
в предыдущее выражение, будем иметь:

Из
теоретической механики известно, что
интеграл
есть ни что иное,
как
статический
момент площади S
относительно оси 0X.
Он равен произведению этой площади на
координату её центра тяжести, т.е. можно
записать

где
Y_с
– расстояние от оси X
до центра тяжести площади S.

Подставив
формулу момента в выражение силы,
получим:

Анализ
второго слагаемого показывает, что
произведение
это глубина положения центра тяжести
площадки, а– избыточное давление жидкости в центре
тяжести площадки. С учётом этого можно
записать

Сумма
в скобках в последнем выражении является
абсолютным давлением в центре тяжести
рассматриваемой произвольной площадки.
Таким образом, можно сделать вывод:
полная
сила давления жидкости на плоскую стенку
равна произведению её площади на величину
гидростатического давления в центре
тяжести этой стенки.

Однако необходимо
учесть, что эта сила не сконцентрирована
в точке, а распределена по площади. И
распределение это неравномерно. По этой
причине для расчётов, кроме величины
силы действующей на наклонную площадку,
необходимо знать точку приложения
равнодействующей.

Центр давления

Распределённую
нагрузку, действующую на наклонную
стенку, заменим сконцентрированной.
Для этого найдём на наклонной стенке
положение точки D,
в которой приложена равнодействующая
силы давления. Точку, в которой приложена
эта сила, называют центром
давления.
Как уже неоднократно рассматривалось,
давление, действующее в любой точке, в
соответствии с основным уравнением
гидростатики складывается из двух
частей: внешнего давления P₀,
передающегося всем точкам жидкости
одинаково, и давления столба жидкости
P,
определяемого глубиной погружения этой
точки.

Давление P0 передаётся всем точкам площадки одинаково. Следовательно, равнодействующая Fвн этого давления будет приложена в центре тяжести площадки S. При этом надо учитывать, что в большинстве случаев это давление действует и со стороны жидкости и с наружной стороны стенки.	Давление P увеличивается с увеличением глубины. При этом величина равнодействующей этой силы Fизб известна и равна , а точку её приложения необходимо определить.

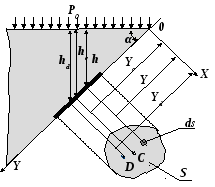Для
нахождения центра избыточного давления
жидкости применим уравнение механики,
согласно которому момент равнодействующей
силы относительно оси0X
равен сумме моментов составляющих сил,
т.е.

где
Y_D
– координата
точки приложения силы F_изб,

Y
– текущая глубина.

Заменив
в этом выражении F_изб
и Y_D
интегралом, в соответствии с упомянутым
уравнением механики, будем иметь:

Отсюда
выразим Y_D
при этом

Интеграл
в числителе дроби является статическим
моментом инерции площади S
относительно оси 0X
и обычно обозначается J_x

.

Из теоретической
механики известно, что статический
момент площади относительно оси вращения
равен сумме собственного момента инерции
(момента инерции этой площади относительно
оси проходящей через её центр тяжести
и параллельной первой оси) и произведению
этой площади на квадрат расстояния от
оси вращения до центра её тяжести

.

С
учётом последнего определения Y_D
окончательно можно выразить в виде:

.

Таким
образом, разница в положениях ∆Y
(глубинах) центра тяжести площадки (т.
C)
и центра давления (т. D)
составляет

.

В итоге
можно сделать следующие выводы. Если
внешнее давление действует на стенку
с обеих сторон, то найденная точка D
будет являться центром давления. Если
внешнее давление со стороны жидкости
выше давления с противоположной стороны
(например, атмосферного), то центр
давления находится по правилам механики
как точка приложения равнодействующей
двух сил: силы, создаваемой внешним
давлением, и силы, создаваемой весом
жидкости. При этом, чем больше внешнее
давление, тем ближе располагается центр
давления к центру тяжести.

В
гидроприводе технологического
оборудования внешние давления в десятки
и сотни раз превышают давления, вызванные
высотой столба жидкости. Поэтому в
расчётах гидравлических машин и аппаратов
положение центров давления принимаются
совпадающими с центрами тяжести.

Графическим
изображением изменения гидростатического
давления вдоль плоской стенки служат
эпюры давления
(рис. ). Площадь эпюры выражает силу
давления, а центр тяжести эпюры — это
точка, через которую проходит
равнодействующая сила давления.

При построении
эпюр учитывают, что давление направлено
нормально к стенке, а уравнение Р
= Ро + yh,
характеризующее распределение
гидростатического давления по глубине,
является уравнением прямой.

Чтобы построить
эпюры давления на вертикальную стенку,
откладывают в выбранном масштабе
давление по горизонтально­му
направлению, совпадающему с направлением
сил давления (на поверхности жидкости
и у дна), соединив концы этих отрез­ков
прямой линией.

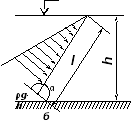
Рис. Примеры
построения эпюр давления на стенку:

Эпюра абсолютного
гидростатического давления представляет
собой трапецию, а эпюра избыточного —
треугольник (рис. а).

Если плоская
стенка, на которую действует жидкость,
накло­нена к горизонту под углом 
(рис. б),
то основное уравне­ние гидростатики
принимает следующий вид:

Таким образом,
эпюры абсолютного и избыточного
гидроста­тического давления на
наклонную стенку представляют собой
соответственно наклонную трапецию и
наклонный треугольник.

Если плоская
стенка, на которую с двух сторон оказывает
воздействие жидкость, вертикальна, то
на нее будут действовать параллельные
и противоположно направленные силы
гидроста­тического давления. Эпюра
гидростатического давления на
вер­тикальную стенку представляет
собой вертикальную трапецию.

Эпюра гидростатического
давления на горизонтальное дно ре­зервуара
представляет собой прямоугольник, так
как при посто­янной глубине избыточное
давление на дно постоянно.

Соседние файлы в папке лекции ОГИТ

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пловец, нырнувший глубоко, ощущает боль в ушах. На барабанные перепонки воздействует сила давления воды.

Корабль в воде не тонет благодаря выталкивающей силе. Вода способна легко изменять свою форму, она воздействует на поверхности тел при соприкосновении с ними.

Чему равна сила давления воды и что это такое, расскажем в статье.

Что это такое?

В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.

Оно определяется отношением силы к площади, то есть его физический смысл – это сила, действующая на единицу площади (см2).

Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.

Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.

Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.

Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.

Факторы, влияющие на показатель

При отсутствии внешнего воздействия, играют роль два фактора:

• высота столба;
• плотность.

Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.

Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.

Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:

• внешней силы;
• веса воды.

При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?

Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.

Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.

Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.

Единицы измерения

Давление воды измеряют в:

• паскалях – Па;
• метрах водяного столба – м. в. ст.
• атмосферах – атм.

Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).

Формулы расчета

Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).

Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.

Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.

Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.

Расчет давления воды на дно и стенки сосуда в видео:

Применение на практике

Примеры использования знаний свойств воды:

1. Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
2. Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
3. Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
4. Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.

Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:

• выжимка масла из семян растений;
• спуск на воду со стапелей построенного судна;
• ковка и штамповка деталей;
• домкраты для подъема грузов.

Заключение

Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.

Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.

Что это такое?

В сосуде с водой ко дну прижимается сила, равная весу столба жидкости. Это гравитационное давление называется гидростатическим давлением.

он определяется отношением прочности к площади, т.е его физический смысл — сила, действующая на единицу площади (см2).

Законы гидростатики были описаны Блезом Паскалем. В 1648 году он удивил горожан опытом, продемонстрировавшим свойства воды.

Вставив длинную узкую трубку в бочку с водой, он налил в нее несколько чашек воды, и бочка лопнула.

Согласно закону Паскаля сила, приложенная к H2O, равномерно распределена по всему объему. Это потому, что вода почти не сжимается. Это свойство используется в гидравлических прессах.

Плотность воды все равно увеличивается при высоком давлении. Это учитывается при расчете конструкций морской техники.

Выталкивающая сила

Как известно, на тело, погруженное в жидкость, действует подъемная сила. Эта сила является результатом сил давления жидкости на тело. Мы находим, например, плавучесть, действующую на реберный куб a, полностью погруженный в жидкость с плотностью. Сила давления со стороны жидкости на верхнюю грань куба равна

где h — расстояние от этой грани до поверхности жидкости (для простоты мы предполагаем, что плоскость верхней грани куба параллельна поверхности жидкости). Сила действует на нижний край куба

Силы давления на боковые грани куба уравновешивают друг друга. Результирующие силы давления, т.е плавучесть, равны

и направлен вертикально вверх. Мы получили закон Архимеда: сила плавучести равна силе тяжести, действующей на жидкость, вытесняемую телом.

В общем, закон Архимеда можно продемонстрировать с помощью принципа затвердевания. Мысленно заменяем погруженное тело жидкостью. Очевидно, эта жидкость будет находиться в равновесии. Следовательно, сила тяжести, действующая на него, уравновешивается силами давления окружающей жидкости. Если теперь мы представим, что выбранная часть затвердела, баланс оставшейся части не будет нарушен, и, следовательно, силы давления на затвердевшую жидкость не изменятся. Равнодействующая этих сил по-прежнему будет равна силе тяжести.

Во время демонстрации мы предполагали, что тело полностью погружено в жидкость. Однако аналогичные рассуждения легко провести в том случае, если в жидкости находится только одна часть тела (сделай сам). И мы все равно получаем, что сила плавучести равна силе тяжести, действующей на жидкость, вытесняемую телом:

где — плотность жидкости, V — объем погруженной в жидкость части тела, g — ускорение свободного падения.

Задача 5. В нижней части резервуара находится П-образная конструкция из трех идентичных балок, соединенных между собой (рис. 6). Как сила давления этой конструкции на дно зависит от уровня воды в баке? Рассмотрим два случая: 1) утечка воды под опоры; 2) опоры плотно прилегают к днищу. Балки имеют квадратное сечение со стороны a, длина балки l = 2a. Плотность материала балок равна плотности воды ρ0.

а

б

v

Рис. 6

Сила давления Fd на дно определяется разницей между силой тяжести конструкции и силой плавучести F. В первом случае, когда вода выходит под опоры (например, если дно резервуара покрыто гальки — рисунок 6, а), закон Архимеда справедлив. Зависимость выталкивающей силы от высоты уровня воды h определяется формулами:

Соответствующий график для силы Fd показан на рисунке 6, в — обозначен цифрой 1.

Во втором случае давление воды на опоры снизу отсутствует (рис. 6, б), и использование закона Архимеда уже невозможно. Для определения силы F необходимо найти равнодействующую сил давления:

F = 0 для h ≤ a,

Последнее выражение исчезает, и в общем случае h становится отрицательным. Это значит, что под давлением конструкция не выталкивается из воды, а, наоборот, прижимается ко дну. Зависимость силы давления внизу от высоты уровня воды показана на втором графике рис. 6, в.

Задача 6. Пробковый куб с ребром a = 0,1 м был погружен в воду на глубину h = 0,2 м с помощью тонкостенной трубы диаметром d = 0,05 м (рис. 7). Определите, какой груз нужно положить в трубку, чтобы кубик оторвался от нее. Плотность крышки ρ0 = 200 кг / м3, плотность воды ρ = 103 кг / м3.

Рис. 7

Вес груза равен разнице между выталкивающей силой F, действующей на куб, и силой тяжести куба. Если бы куб со всех сторон был окружен водой, по закону Архимеда на него действовала бы подъемная сила. В нашем случае сила плавучести будет больше, так как давление воды не действует на «заключенную» в трубку часть поверхности верхней грани куба:

где — площадь поперечного сечения трубы. Следовательно, тяжесть груза

Масса груза t = 1,2 кг.

Силу плавучести, действующую на куб, можно найти и другим способом. Думайте о кубе с трубкой как о едином теле, которое перемещает объем воды

Следовательно, согласно закону Архимеда на куб с трубкой действует подъемная сила

которая равна силе плавучести, действующей на куб, поскольку равнодействующая сил давления воды на трубу равна нулю.

Определение закона Паскаля

Итак, мы подошли к формулировке закона Паскаля, который звучит так:

Давление, приложенное к жидкости или газу, передается в любой точке одинаково во всех направлениях.

Примечание: закон действует только с жидкостями и газами. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел. Если молекулы жидкости и газа движутся почти свободно, то молекулы твердых тел не могут. Они могут только плавать, немного отклоняясь от исходного положения. Благодаря свободной циркуляции молекул газа и жидкости они оказывают давление во всех направлениях.

Давайте рассмотрим эксперимент Паскаля с мячом, чтобы было понятнее.

Прикрепляем к трубке с помощью поршня полый шар с множеством мелких отверстий. Налейте воду в шар и надавите на поршень. Давление в трубе увеличится, вода будет выходить через отверстия, и давление всех форсунок будет одинаковым. Тот же результат будет получен, если в шаре будет газ, а не вода.

Важный момент На Земле есть атмосфера. Эта атмосфера создает давление, которое усиливает все остальные. То есть, если мы прижимаем руку к столу, давление, которое испытывает стол, равно давлению нашей руки плюс атмосферное давление.

Факторы, влияющие на показатель

При отсутствии внешних воздействий играют роль два фактора:

• высота полюса;
• плотность.

Чем выше уровень воды, налитой в сосуд, тем больше давление на дно. Если в одной емкости находится ртуть, а в другой — вода, и при этом уровни жидкости одинаковы, то в первом случае давление на дне больше, так как ртуть имеет более высокую плотность.

Атмосферный воздух также давит сверху на содержимое корабля. Следовательно, в сообщающихся сосудах уровень одинаковый, потому что в каждом из них над поверхностью одинакова атмосфера.

Если поставить поршень на поверхность и надавить на него, давление будет складываться из:

• внешняя сила;
• вес воды.

В этом случае форма корабля не определяет величину силы, создаваемой колонной. Это будет то же самое для колонны той же высоты, хотя стенки емкости могут расширяться вверх или сжиматься.

U-образное колено

Колено П-образной формы состоит из двух сообщающихся сосудов, диаметры сосудов одинаковые.

Жидкости, налитые в локоть, нельзя перемешивать (рис. 3). Например, в одну трубку можно налить воду, а в другую — масло.

Рис. 3. Два сообщающихся сосуда одинакового диаметра образуют U-образный локоть

Запишем формулы для расчета давления в левой (P_ {1} ) и правой (P_ {2} ) частях колена.

large boxed { begin {cases} P_ {1} = rho_ {1} cdot g cdot h_ {1} P_ {2} = rho_ {2} cdot g cdot h_ { 2} end {case}}

Чем больше разница плотностей двух жидкостей, тем больше разница в высоте их столбов.

При устранении неисправностей не учитывается общая нижняя часть колена. На рисунке 3 он отделен сверху горизонтальной линией.

Давление стержней, оставшихся наверху, будет таким же.

(P_ {1} ) — давление жидкости в левой части колена;

(P_ {2} ) — давление жидкости в правой части колена.

large begin {cases} P_ {1} = P_ {2} rho_ {1} cdot g cdot h_ {1} = rho_ {2} cdot g cdot h_ {2} конец {случаи}

Разделим обе части последнего уравнения на ускорение свободного падения. Тогда получаем соотношение между высотой столбов жидкости и их плотностью:

large boxed { rho_ {1} cdot h_ {1} = rho_ {2} cdot h_ {2} }

Высоту столбов можно измерить линейкой. Зная плотность одной из жидкостей, можно найти плотность второй жидкости.

Примечание. Давление жидкостей часто измеряется в миллиметрах ртутного столба или метрах водяного столба. Перейдите по ссылке, чтобы узнать, как связаны эти единицы и как преобразовать давление в СИ.

На дно и стенку сосуда – в чем разница?

Вода, наполняющая контейнер, оказывает давление в направлении, всегда перпендикулярном поверхности твердого тела, на всей площади контакта с дном и стенками.

Усилие на днище распределяется равномерно, то есть одинаково в любой точке. Заполнив сито водой, можно увидеть, что струи, протекающие через отверстия, имеют одинаковое давление.

После заполнения сосуда с отверстиями одинакового диаметра в стенках на разной высоте, можно наблюдать разное давление текущей струи. Чем выше отверстие, тем слабее струя. То есть чем ближе ко дну, тем больше давление на стенки емкости.

Сообщающиеся сосуды

Сообщающиеся сосуды представляют собой емкости, расположенные на плоской горизонтальной поверхности, внизу они соединены трубами.

Если жидкость налить в один из сосудов, она будет распределена по всем сосудам, так что ее уровень будет одинаковым во всех сосудах (рис. 2).

Рис. 2. В сообщающихся сосудах уровень жидкости будет одинаковым

Неважно, какой формы корабль. Давление жидкости во всех сосудах будет одинаковым. Следовательно, высота столба жидкости h во всех сосудах будет одинаковой.

Единицы измерения

Давление воды измеряется в:

• паскаль — Па;
• метров водяного столба — м. Искусство.
• атмосферы — атм.

практически достаточно знать, что 1 атмосфера равна 10 м водяного столба или 100 000 Па (100 кПа).

Формулы расчета

Давление на днище корабля рассчитывается путем деления силы на площадь, то есть оно равно произведению плотности воды, высоты колонны и ускорения свободного падения g (величина постоянна , равное 9,8 м / с2).

Пример расчета: резервуар заполнен водой плотностью 1000 кг / м3 на высоту 1,2 м. Необходимо найти давление на дне резервуара. Решение: P = 1000 * 1,2 * 9,8 = 11760 Па или 11,76 кПа.

Чтобы рассчитать давление на стенки сосуда, используйте ту же формулу давления, что и выше. При расчете глубина берется от точки, в которой вы хотите рассчитать напор на поверхности воды.

Пример расчета: на глубине 5 м на стенку емкости с водой будет оказываться давление P = 1000 * 5 * 9, 8 = 49000 кПа, что составляет 0,5 атмосферы.

Расчет давления воды на днище и стенки корабля на видео:

Жидкость в движущемся сосуде

Теперь изучим равновесие жидкости в сосуде, движущемся с ускорением. Согласно второму закону Ньютона, в этом случае векторная сумма всех сил, действующих на любой выбранный элемент жидкости, должна быть, где m — масса выбранной жидкости,
— ускорение корабля. Но на выбранный элемент жидкости действует сила тяжести и силы давления со стороны окружающей жидкости. Их результат должен быть равен .

Задача 7. Сосуд с жидкостью плотности падает с ускорением а. Определите давление жидкости на глубине h и силу давления на дне сосуда. Высота уровня воды в емкости H, площадь дна емкости s.

Выберем столб жидкости высотой h с площадью основания s. На него действует сила тяжести и восходящее давление. Возникающая этика сил создает ускорение колонны:

где — масса колонны. Отсюда для давления p на глубине h находим

Сила давления на днище корабля

чем больше будет ускорение корабля, тем меньше будет a. Когда (свободное падение) сила давления жидкости становится равной нулю, устанавливается состояние невесомости. A жидкость будет свободно падать с ускорением g, а сосуд — с большим ускорением, и вода выйдет из сосуда.

Задача 8. На дне сосуда с жидкостью лежит тело. Может ли тело плавать, если корабль начинает с ускорением двигаться вверх? Определите силу давления тела на дно сосуда, если ускорение сосуда равно a, плотность жидкости ρ0, плотность тела и его объем V.

На тело, лежащее на днище корабля, действуют сила тяжести mg, сила реакции днища N и сила плавучести F (рис. 8). Если корабль неподвижен, сумма этих сил равна нулю. Когда корабль движется с ускорением a вверх согласно второму закону Ньютона, мы имеем

Рис восемь

Определим силу плавучести F. Аналогично решению предыдущей задачи легко получить, что при ускоренном движении корабля вверх давление на глубине h определяется формулой

те давление в несколько раз больше, чем в стационарном сосуде. В результате сила плавучести также будет больше:

где — масса воды, вытесняемой телом.

Подставляя это выражение в формулу второго закона Ньютона, для фоновой силы реакции получаем

легко видеть, что у корабля, движущегося с восходящим ускорением, сила реакции днища всегда больше, чем у неподвижного. Таким образом, корпус не только не плавает, но, наоборот, сильнее прижимается ко дну.

Задача 9. Сосуд с жидкостью движется горизонтально с ускорением а. Определите форму поверхности жидкости в сосуде.

Выберем горизонтальный столб жидкости длиной l и площадью поперечного сечения S (рис. 9). Согласно второму закону Ньютона

где — масса колонны, p1 и p2 — давления на нее слева и справа.

Рис. 9

Давление на глубине h определяется по обычной формуле (без ускорения по вертикали). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем

или

Но — это разница в высоте точек на поверхности жидкости. Получаем, что поверхность жидкости представляет собой наклонную плоскость по отношению к горизонту на угол α, причем .

Обратите внимание, что давление жидкости на данной высоте здесь не то же самое. Линии равного давления параллельны поверхности жидкости. Если ввести расстояние h ‘от точки до поверхности жидкости, то давление в этой точке

Поэтому можно сказать, что ускоренное движение корабля эквивалентно замене ускорения свободного падения
от суммы. Это утверждение в равной степени применимо к двум предыдущим задачам.

Упражнения

1. Три вазы в форме цилиндра, усеченного конуса и перевернутого усеченного конуса с одинаковыми площадями основания и быстрым объемом наполнены водой до верха. Как соотносятся друг с другом силы давления воды на дне сосудов?

2. Трубка ртутного барометра подвешена на проволоке. Определите натяжение проволоки, если высота уровня ртути и трубки H = 0,76 м, внешний диаметр трубки D = 0,02 м, внутренний диаметр d = 0,017 м. Нижний конец трубки погружен в ртуть на глубину h = 0,1 м, масса трубки m = 0,3 кг, плотность ртути = 1,36 × 104 кг / м 4. Предположим, что концы трубки плоские.

3. Длинная вертикальная трубка погружается в сосуд с ртутью на одном конце. М = 0,71 кг воды наливается в трубу, которая не выходит из трубы. Определите изменение уровня ртути в сосуде. Диаметр сосуда D = 0,06 м, плотность ртути ρ = 1,36 · 104 кг / м4. Толщиной трубки пренебрегаем.

4. В корабле с водой плывет кусок льда. Изменится ли уровень воды в корабле, если тает лед? Что произойдет, если а) кусок свинца заморожен во льду; б) кусок пробки?

5. Воду наливают в цилиндрические сообщающиеся сосуды диаметром D = 0,06 м и d = 0,02 м. Как изменится уровень воды в сосудах, если в один из сосудов, который будет плавать в воде, поместить тело массой m = 0,02 кг? Плотность воды ρ = 103 кг / м3.

6. Корабль с водой без трения течет по наклонной плоскости с углом наклона α. Определите, как будет располагаться водная поверхность и корабль.

Ответы

1 Сила давления на дно максимальна для емкости в форме усеченного конуса, минимальная — для перевернутого конуса.

4 Если лед прозрачный или в нем заморожен кусок пробки, уровень воды не изменится. Если кусок свинца заморозить во льду, уровень воды упадет.

6 Поверхность параллельна наклонной плоскости.

Как уменьшить или увеличить давление

Тяжелый гусеничный трактор создает давление на грунт 40-50 кПа. Парень весом 45 кг производит давление всего в 3 раза меньше, чем такой трактор. Это связано с большой колеей трактора.

В зависимости от того, какого давления они хотят достичь, площадь опор уменьшается или увеличивается. Например, чтобы снизить давление здания на землю, в процессе строительства увеличивают площадь нижней части фундамента.

Грузовые шины делают их намного шире легковых. Чтобы убедиться в этом, посмотрите на колеса какой-нибудь большой повозки. Более широкие шины можно увидеть на транспортных средствах для пустыни. Такой же спасательный прием используется в шасси самолетов.

Обратная зависимость также используется, например, при создании лезвий для сверлильных и режущих инструментов. У острого лезвия небольшая площадь, поэтому даже при небольшом давлении создается большое давление.

Задачка раз

Книга на столе. Вес книги 0,6 кг. Площадь его контакта со столом 0,08 м2. Определите давление книги на стол.

Решение

Сила, равная весу книги, будет давить на стол. Поскольку он находится в состоянии покоя, его вес будет равен силе тяжести. Следовательно:

p = мг / S = 0,6 × 10 / 0,08 = 75 Па

Ответ: Давление книги на стол будет 75 Па.

Задачка два

Гусеничный трактор ДТ-75М массой 6610 кг имеет площадь опоры обеих гусениц 1,4 м2. Определите давление на грунт этого трактора.

Решение:

p = мг / S = 6610 × 10 / 1,4 = 47 214 Па = 47,2 кПа

Ответ: Давление трактора на землю составляет 47,2 кПа.

Задачка три

Человек 80 кг с мешком 100 Н остается неподвижным на полу. Сила давления подошвы его ботинок на пол равномерно распределяется на площади 600 см2. Какое давление человек оказывает на пол?

Решение

Вес человека: m = 80 кг.

Вес одного места багажа: Pc = 100 Н.

Площадь контакта подошвы ботинка с полом: S = 600 см2.

600 см2 = 600/10 000 м2 = 0,06 м2

Давление — это отношение силы к площади, на которую она действует. В этом случае на область действует сила, равная сумме силы тяжести человека и веса мешка:

F = мг + Pñ

Следовательно, давление, оказываемое человеком с сумкой на пол, равно:

p = (мг + Pñ) / S = (80 × 10 + 100) / 0,06 = 15,000 Па = 15 кПа

Ответ: Давление человека с сумкой на пол 15 кПа.