Примеры решения задач
Задача 1.
Два точечных заряда
=




10 см друг от друга. Найти силу, действующую
на точечный заряд
Кл, помещённый на продолжении прямой


2 см от заряда
Дано:





см = 0,1 м
= 10-9
Кл

2 см = 2

=1;
k
= 9 .

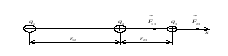
Рис.7.5
Решение
Сила, действующая
на заряд

будет складываться из сил, действующих
на него со стороны полей первого и
второго зарядов
(см. рис.7.5).
Следовательно,
Учёт
знаков зарядов и их расположения
указывают, что силы F12
и F23
коллинеарные и направлены в разные
стороны. Считать ось x
направленной вправо, можно векторное
уравнение заменить скалярным, тогда

Силы
и

заряды – точечные по условию.
На основании закона
Кулона
где

зарядами, равное
Подставив
эти выражения в формулу (1), получим


Ответ:
= 3,3

Задача 2.
Тонкий стержень длиной L
= 10 см равномерно заряжен. Линейная
плотность заряда
= 1 мкКл/м. На
продолжении оси стержня на расстоянии
а
= 20 см от ближайшего его конца находится
точечный заряд q
= 10-7
Кл. Определить силу взаимодействия
заряженного стержня и точечного заряда
(рис.7.6).
Дано:
L
= 10 см = 0,1 м
= 1 мкКл/м = 10-6
Кл/м
а
= 20 см = 0,2 м
q
= 10-7
Кл

Рис.7.6
Решение
Заряженный стержень
является неточечным зарядом. Непосредственно
применить закон Кулона к такому заряду
нельзя. Можно выделить на стержне элемент
длиной dl,
имеющий заряд dq
=
dl,
где
– линейная
плотность заряда стержня. Тогда
где dF
– сила взаимодействия элементарного
заряда с зарядом q.
Все элементы заряда стержня действуют
на заряд q
в одном и том же направлении, вдоль оси
стержня.
Тогда векторная
сумма всех сил

равна алгебраической. Она может быть
найдена как интеграл:
Подставив численные
значения величин, получим

Ответ:
F
= 1,5

Задача 3.
Найти силу, действующую на точечный
заряд

2.
10-9
Кл, расположенный в центре полукольца
радиусом

5 см, со стороны этого полукольца, по
которому равномерно распределён зарядq
= 3

Дано:

10-9
Кл
q
= 3 .
10-7
Кл

10-2
м

?
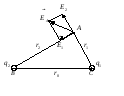
Рис.7.7
Решение
Определить силу
здесь можно как результирующую
элементарных сил

действующих на заряд
полукольца (см.рис.7.7).
Произвольно взятый
элемент создаёт силу

направленную под углом
к оси y.
Элемент имеет заряд

– линейная плотность заряда, равная
=

где q
– равномерно распределённый по полукольцу
заряд, а

длина полукольца;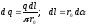
чертежа).
Тогда
Направление сил

элемента к другому, поэтому нужно найти
проекции силы
и на ось y:
по полукольцу
по полукольцу
Интеграл берётся
по полукольцу, следовательно, угол
изменяется от 0 до :
Следовательно,

Ответ:
F
= 1,4 Н.
Задача 4.
Расстояние между двумя точечными
зарядами


электростатического поля в точке,
находящейся на расстоянии 0,03 м от
положительного заряда и 0,04 м от
отрицательного заряда (рис.7.8).
Дано:
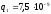




Рис.7.8
Соседние файлы в папке Часть 2
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закон Кулона
Между электрическими зарядами действует сила. Как она зависит от величины зарядов и других факторов?
Этот вопрос исследовал в 1780-е годы французский физик Шарль Кулон (1736-1806). Он воспользовался крутильными весами, очень похожими на те, которые применял Кавендиш для определения гравитационной постоянной.
Если к шарику на конце стержня, подвешенного на нити, подности заряд, стержень слегка отклоняется, нить закручивается, и угол поворота нити будет пропорционален действующей между зарядами силе (крутильные весы). С помощью этого прибора Кулон определил зависимость силы от величины зарядов и расстояния между ними.
В те времена еще не было приборов для точного определения величины заряда, но Кулон сумел приготовить небольшие шарики с известным соотношением зарядов. Если заряженный проводящий шарик, рассуждал он, привести в соприкосновение с точно таким же незаряженным шариком, то имевшийся на первом заряд в силу симметрии распределится поровну между двумя шариками.
Это дало ему возможность получать заряды, составлявшие 1/2, 1/4 и т.д. от первоначального.
Несмотря на некоторые трудности, связанные с индуцированием зарядов, Кулону удалось доказать, что сила, с которой одно заряженное тело действует на другое малое заряженное тело, прямо пропорциональна электрическому заряду каждого из них.
Другими словами, если заряд любого из этих тел удвоить, то удвоится и сила; если же удвоить одновременно заряды обоих тел, то сила станет вчетверо больше. Это справедливо при условии, что расстояние между телами остается постоянным.
Изменяя расстояние между телами, Кулон обнаружил, что действующая между ними сила обратно пропорциональна квадрату расстояния: если расстояние, скажем, удваивается, сила становится вчетверо меньше.
Итак, заключил Кулон, сила, с которой одно малое заряженное тело (в идеальном случае -точечный заряд, т.е. тело, подобно материальной точке не имеющее пространственных размеров) действует на другое заряженное тело, пропорциональна произведению их зарядов Q1 и Q2 и обратно пропорциональна квадрату расстояния между ними:
Здесь k -коэффициент пропорциональности.
Это соотношение известно как закон Кулона; его справедливость подтверждена тщательными экспериментами, гораздо более точными, чем первоначальные трудно воспроизводимые опыты Кулона. Показатель степени 2 установлен в настоящее время с точностью 10 -16 , т.е. он равен 2 ± 2?10 -16 .
Коль скоро мы теперь имеем дело с новой величиной — электрическим зарядом, мы можем подобрать такую единицу измерения, чтобы постоянная к в формуле равнялась единице. И действительно, такая система единиц еще недавно широко использовалась в физике.
Речь идет о системе СГС (сантиметр-грамм-секунда), в которой используется электростатическая единица заряда СГСЭ. По определению два малых тела, каждое с зарядом 1 СГСЭ, расположенные на расстоянии 1 см друг от друга, взаимодействуют с силой 1 дина.
Теперь, однако, заряд чаще всего выражают в системе СИ, где его единицей является кулон (Кл).
Точное определение кулона через электрический ток и магнитное поле мы приведем позднее.
В системе СИ постоянная k имеет величину k = 8,988?10 9 Нм 2 /Кл 2 .
Заряды, возникающие при электризации трением обычных предметов (расчески, пластмассовой линейки и т.п.), по порядку величины составляют микрокулон и меньше (1 мкКл = 10 -6 Кл).
Заряд электрона (отрицательный) приблизительно равен 1,602?10 -19 Кл. Это наименьший известный заряд; он имеет фундаментальное значение и обозначается символом е, его часто называют элементарным зарядом.
е = (1,6021892 ± 0,0000046)?10 -19 Кл, или е ? 1,602?10 -19 Кл.
Поскольку тело не может приобрести или потерять долю электрона, суммарный заряд тела должен быть целым кратным элементарного заряда. Говорят, что заряд квантуется (т.е. может принимать лишь дискретные значения). Однако, поскольку заряд электрона е очень мал, мы обычно не замечаем дискретности макроскопических зарядов (заряду 1 мкКл соответствуют примерно 10 13 электронов) и считаем заряд непрерывным.
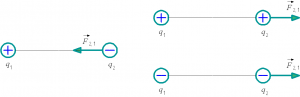
Формула Кулона характеризует силу, с которой один заряд действует на другой. Эта сила направлена вдоль линии, соединяющей заряды. Если знаки зарядов одинаковы, то силы, действующие на заряды, направлены в противоположные стороны. Если же знаки зарядов различны, то действующие на заряды силы направлены навстречу друг другу.
Заметим, что в соответствии с третьим законом Ньютона сила, с которой один заряд действует на другой, равна по величине и противоположна по направлению силе, с которой второй заряд действует на первый.
Закон Кулона можно записать в векторной форме подобно закону всемирного тяготения Ньютона:
где F12 — вектор силы, действующей на заряд Q1 со стороны заряда Q2, 

Следует иметь в виду, что формула применима лишь к телам, расстояние между которыми значительно больше их собственных размеров. В идеальном случае это точечные заряды. Для тел конечного размера не всегда ясно, как отсчитывать расстояние r между ними, тем более что распределение заряда может быть и неоднородным. Если оба тела — сферы с равномерным распределением заряда, то r означает расстояние между центрами сфер. Важно также понимать, что формула определяет силу, действующую на данный заряд со стороны единственного заряда. Если система включает несколько (или много) заряженных тел, то результирующая сила, действующая на данный заряд, будет равнодействующей (векторной суммой) сил, действующих со стороны остальных зарядов. Постоянная к в формуле Закона Кулона обычно выражается через другую константу, ?0, так называемую электрическую постоянную, которая связана с k соотношением k = 1/(4??0). С учетом этого закон Кулона можно переписать в следующем виде:
где с наивысшей на сегодня точностью
Запись большинства других уравнений электромагнитной теории упрощается при использовании ?0, поскольку 4? в окончательном результате часто сокращается. Поэтому мы будем обычно использовать Закон Кулона, считая, что:
Закон Кулона описывает силу, действующую между двумя покоящимися зарядами. Когда заряды движутся, между ними возникают дополнительные силы, и их мы обсудим в последующих главах. Здесь же рассматриваются только покоящиеся заряды; этот раздел учения об электричестве называется электростатикой.
Продолжение следует. Коротко о следующей публикации:
Электрическое поле — один из двух компонентов электромагнитного поля, представляющий собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, либо возникающий при изменении магнитного поля.
Закон Кулона.
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов. Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
.
где |q1| и |q2| — модули зарядов; r — расстояние между ними; k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.
Заряд в 1 Кл очень велик. Сила взаимодействия двух точечных зарядов по 1 Кл каждый, расположенных на расстоянии 1 км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой 1 т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в 1 А — вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент k в законе Кулона при его записи в СИ выражается в Н · м 2 /Кл 2 . Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
Часто его записывают в виде , где ɛ0 =8,85 · 10 — 12 Kл 2 /H·м 2 — электрическая постоянная. В среде с диэлектрической проницаемостью ɛ закон Кулона имеет вид:
.
Закон Кулона простым языком
Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.
Рисунок 1. Закон Кулона
История открытия
Эксперименты с заряженными частицами проводили много физиков:
- Г. В. Рихман;
- профессор физики Ф. Эпинус;
- Д. Бернулли;
- Пристли;
- Джон Робисон и многие другие.
Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.
Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).
Рис. 2. Крутильные весы
У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10 -9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1 º . Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.
Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.
Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r 2
Рис. 3. Взаимодействие точечных зарядов
Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Границы применения
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 – 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10 18 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r 2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент k
Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.
Коэффициент k в СИ выражается следующим образом: k = 1/4πε0, где ε0 – электрическая постоянная: ε0 = 8,85 ∙10 -12 Кл 2 /Н∙м 2 . Выполнив несложные вычисления, мы находим: k = 9×10 9 H*м 2 / Кл 2 . В метрической системе СГС k =1.
На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.
Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.
Закон Кулона в диэлектриках
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Применение на практике
Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).
Рис. 4. Большой адронный коллайдер
Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
Напряженность поля .
Напряженностью поля называют отношение силы, действующей на пробный электрический заряд
к величине этого заряда.
(E=dfrac {F}{q} )
Задача 1.
Найти напряженность электрического поля, если сила, действующая на заряд (q=0,001 Кл )
равна (F=0,01 Н )
Показать ответ
Показать решение
Видеорешение
Задача 2.
Найти силу, действующую на точечный заряд (q=100 мкКл) , помещенный в однородное электрическое
поле напряженностью (E=1000 В/м )
Показать ответ
Показать решение
Видеорешение
Задача 4.
Найти величину электрического заряда (q) , если в поле напряженностью (E=1000 В/м )
на него действует сила (F=0,005 Н )
Дать ответ в микрокулонах
Показать ответ
Показать решение
Видеорешение
Задача 5.
Найти напряженность однородного электрического поля, если
протон массой (m=1,67 cdot 10^{-27} кг ) и зарядом (q=1,6 cdot 10^{-19} Кл ) движется в нем
с ускорением (a=160000 м/с^2 )
Показать ответ
Показать решение
Видеорешение
Задача 6.
С каким ускорением будет двигаться шарик, находящийся в космосе вдали от небесных тел в однородном электрическом поле
напряженностью ( E=1000 В/м ? )
Заряд шарика (q=70 мкКл)
Масса шарика (m=5 г )
Показать ответ
Показать решение
Видеорешение
Задача 7.
Найти ускорение пылинки массой (m=0,001 г ) и зарядом (q=625 нКл ), находящейся в однородном электрическом поле
напряженностью ( E=500 В/м ? )
Силой тяжести пренебречь.
Показать ответ
Показать решение
Видеорешение
Задача 8.
С каким ускорением движется электрон в однородном электрическом поле напряженностью ( E=90 В/м ),
если заряд электрона (e=1,6 cdot 10^{-19} Кл ), а его масса (m=9 cdot 10^{-31} кг ?)
Показать ответ
Показать решение
Видеорешение
Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.
Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.
Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональная произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:
F = k · (|q1| · |q2|) / r2
где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.
Коэффициент k в СИ принято записывать в форме:
k = 1 / (4πε0ε)
где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.
Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.
Сила взаимодействия неподвижных точечных зарядов в вакууме:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]
Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.
Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).
Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.
Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:
F1,2 = -F2,1
Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.
Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.
Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.
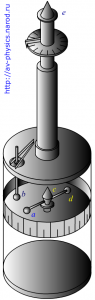
В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.
Рис. 1.10. Опыт Кулона (крутильные весы).
При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.
|
|
Макеты страниц
Вопрос о силе, действующей на точечный заряд, помещенный в заданное электрическое поле, решается элементарно: эта сила равна произведению заряда на напряженность поля, 
Диполь в однородном поле. Если диполь поместить в однородное электрическое поле, то полная действующая на него сила будет равна нулю. Так получается потому, что действующие на входящие в диполь заряды силы равны по модулю и противоположны по направлению. Однако силы приложены в разных точках: это так называемая пара сил.

Рис. 36. Силы, действующие на диполь в однородном электрическом поле

Рис. 37. К расчету момента сил, действующих на диполь
Поэтому в общем случае на диполь действует момент сил, стремящийся ориентировать диполь так, чтобы его дипольный момент 
Обозначим через 


где использовано обычное обозначение для векторного произведения. Поскольку 


Произведение 



Модуль момента сил М зависит от угла а между направлениями 

При двух ориентациях диполя — по полю 



Энергия диполя во внешнем поле. Характер равновесия диполя в каждом из этих положений можно также установить, рассматривая зависимость потенциальной энергии диполя во внешнем поле от его ориентации. Энергия диполя как совокупности зарядов 

где 


Поэтому

Формулу (7) для энергии диполя с моментом 

Из формулы (7) видно, что значению 

Диполь в неоднородном поле. В неоднородном внешнем поле на диполь кроме ориентирующего момента сил действует еще и отличная от нуля сила, втягивающая диполь в область с большей напряженностью поля. Эта сила возникает как равнодействующая сил, действующих на входящие в диполь заряды, благодаря тому, что в местах расположения этих зарядов напряженность поля имеет разные значения. Ясно, что эта сила тем больше, чем больше неоднородность поля, т. е. чем больше градиент напряженности.
Попадая в неоднородное электрическое поле, диполь ориентируется в нем должным образом и втягивается в область с большей напряженностью, так как на попадающий туда конец сориентированного диполя действует бблыиая сила, чем на противоположный. Именно таким поведением поляризованных молекул воздуха объясняется возникновение электрического ветра вблизи острия (см. § 5). Такое поведение индуцированных на мелких частицах диполей можно использовать для экспериментальной «визуализации» электростатических полей. Для этого используют ванну с подходящим жидким диэлектриком, к которому подмешен порошок из мелких твердых частичек. Частицы порошка образуют в электрическом поле множество цепочек, простирающихся от одного заряженного электрода до другого, и воспроизводят форму и расположение силовых линий.
На рис. 38 приведена полученная таким способом картина линий напряженности электрического поля двух одинаковых шариков, заряженных разноименно.

Рис. 38. Линии напряженности электрического поля между двумя разноименно заряженными шариками
Картина на рис. 39 дает представление об электрическом поле двух параллельных пластин с одинаковыми зарядами противоположного знака. Поле между пластинами можно считать однородным в случае, когда расстояние между пластинами малб по сравнению с их размерами, так как в средней части линии напряженности имеют вид параллельных прямых,
расположенных с одинаковой густотой. Вблизи краев пластин силовые линии искривляются, т. е. поле становится неоднородным.

Рис. 39. Картина линий напряженности электрического поля двух разноименно заряженных пластин
И, наконец, именно таким поведением диполей объясняется один из самых известных электростатических опытов — притяжение мелких клочков бумаги наэлектризованной расческой.
Диполь в поле точечного заряда. Количественные закономерности поведения диполя в неоднородном электрическом поле рассмотрим на примере взаимодействия диполя с точечным зарядом. Чтобы не рассматривать силы, действующие на каждый из зарядов диполя, и находить их равнодействующую, найдем силу, действующую на точечный заряд со стороны диполя.
По третьему закону Ньютона она равна по модулю и противоположна по направлению интересующей нас силе, действующей на диполь в неоднородном поле точечного заряда. При этом для напряженности поля диполя мы воспользуемся формулами (15) и (16) § 5.
Приведем результат для двух частных случаев, когда диполь ориентирован вдоль прямой, соединяющей его с точечным зарядом, и перпендикулярно ей. В первом случае угол 


Направлена эта сила вдоль линии, соединяющей диполь с точечным зарядом. Диполь притягивается к заряду 

Во втором случае, когда диполь ориентирован поперек, угол 
выражаемая формулой (16) §5. Для силы, действующей на точечный заряд 

По модулю она вдвое меньше, чем в первом случае, а направлена перпендикулярно прямой, соединяющей диполь с точечным зарядом 
В обоих случаях сила взаимодействия точечного заряда и диполя обратно пропорциональна третьей степени расстояния между ними, т. е. убывает с расстоянием быстрее, чем сила взаимодействия точечных зарядов. Можно убедиться, что она пропорциональна градиенту напряженности поля точечного заряда, убывающей как 

Рис. 40. При таком расположении диполя и точечного заряда силы их взаимодействия 
Силы, действующие на проводник. В тех случаях, когда нас интересует сила, действующая на проводник, помещенный в электрическое поле, приходится учитывать изменение этого поля, связанное с возможным перераспределением зарядов на самом проводнике. Рассмотрим сначала силу, действующую не на весь проводник, а на малый участок его поверхности 

Однако если умножить заряд 

Согласно принципу суперпозиции эту напряженность можно рассматривать как векторную сумму напряженностей полей, создаваемых выделенным элементом поверхности проводника 


плоскости:

Это поле существует по обе стороны от плоскости.
Внутри проводника вплоть до самой его поверхности результирующая напряженность поля равна нулю. Значит, внутри проводника вблизи элемента его поверхности 




Сила, действующая на элемент поверхности 



Эта сила направлена наружу по нормали к поверхности проводника независимо от знака заряда этого участка.
Электростатическое давление. Отношение силы (13) к площади поверхности, на которую она действует, представляет собой электростатическое давление 

Электрические силы как бы «распирают» проводник. Чтобы определить силу, действующую на все заряженное тело, нужно найти распределение заряда а на его поверхности и просуммировать векторно силы электростатического давления, действующие на отдельные элементы поверхности тела.
• Докажите, что момент любой пары сил, т. е. двух равных по модулю и противоположно направленных сил, не зависит от выбора точки, относительно которой рассматриваются моменты сил.
• Объясните появления знака минус в правой части формулы (6), учитывая, что вектор Е всегда направлен в сторону убывания потенциала.
• Почему при нахождении силы, действующей на диполь во внешнем электрическом поле, приходится учитывать неоднородность этого поля, в то время как при расчете действующего на диполь ориентирующего момента неоднородностью электрического поля можно пренебречь?
• Докажите, что на диполь, который может свободно ориентироваться в электрическом поле, во всех случаях действует именно втягивающая сила.
• Почему электрически нейтральные кусочки бумаги притягиваются наэлектризованной расческой? Проделайте такой опыт и постарайтесь объяснить все, что вам при этом удастся наблюдать.
• Объясните направление сил взаимодействия точечного заряда и диполя, показанных на рис. 40, рассматривая взаимодействие точечного заряда 
• Будет ли действовать сила на незаряженный проводящий шар, помещенный в поле точечного заряда? Если да, то как направлена эта сила?
• Какая сила действует на плоскую поверхность проводника, на расстоянии 


Оглавление
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение