Страница 1 из 7
Если в условии задачи не указано, в какой среде находятся заряды, то будем считать, что они находятся в воздухе, относительная диэлектрическая проницаемость которого E = 1. Для некоторых других диэлектриков значение относительной диэлектрической проницаемости приведено в таблице 14 приложения. Если в задаче приведена графическая зависимость нескольких величин от какой-либо одной и при этом все кривые изображены на одном графике, то по оси у задаются условные единицы. В задачах 9.32, 9.122, 9.123 дан авторский вариант решения.
9.1. Найти силу F притяжения между ядром атома водорода и электроном. Радиус атома водорода r = 0,5 • 10-10м; заряд ядра равен по модулю и противоположен по знаку заряду электрона.
9.2. Два точечных заряда, находясь в воздухе (е = 1 ) на расстоянии r1 = 20 см друг от друга, взаимодействуют с некоторой силои. На каком расстоянии r2 нужно поместить эти заряды в масле, чтобы получить ту же силу взаимодействия?
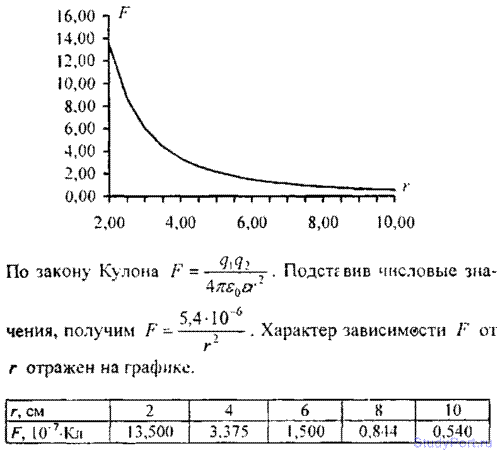
9.3. Построить трафик зависимости силы F взаимодействия между двумя точечными зарядами от расстояния r между ними в интервале 2< r < 10 см через каждые 2см. Заряды q1 = 20 нКл и q2 = 10 нКл.
9.4. Во сколько раз сила гравитационного притяжения между двумя протонами меньше силы их электростатического отталкивания? Заряд протона равен по модулю и противоположен по знаку заряду электрона.
9.5. Найти силу F электростатического отталкивания между ядром атома натрия и бомбардирующим его протоном, считая, что протон подошел к ядру атома натрия на расстояние
r = 6*10-14 м. Заряд ядра натрия в 11 раз больше заряда протона. Влиянием электронной оболочки атома натрия пренебречь.
9.6. Два металлических одинаково заряженных шарика массой т – 0,2 кг каждый находятся на некотором расстоянии друг от друга. Найти заряд q шариков, если известно, что на этом расстоянии энергия Wэл их электростатического взаимодействия в миллион раз больше энергии 1Vгр их гравитационного взаимодействия.
9.7. Во сколько раз энергия Wэл электростатического взаимодействия двух частиц с зарядом q и массой т каждая больше энергии Wгр их гравитационного взаимодействия? Задачу решить для: а) электронов; б) протонов.
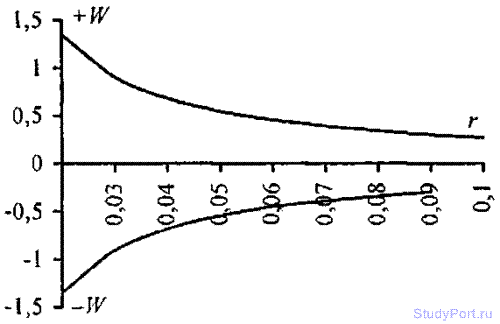
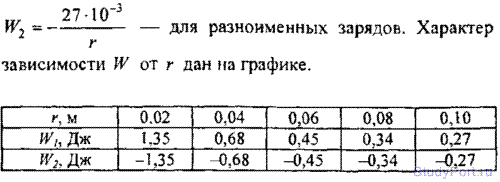
9.8. Построить график зависимости энергии Wэл электростатического взаимодействия двух точечных зарядов от расстояния между ними в интервале 2 < r < 10 см через каждые 2 см. Заряды q1 = 1 нКл и q2 = 3 нКл. График построить для: а) одноименных зарядов; б) разноименных зарядов.
9.9. Найти напряженность ? электрического поля в точке, лежащей посередине между точечными зарядами q1 = 8 нКл и
q2 = -6 нКл. Расстояние между зарядами r=10 см; e = 1.
9.10. В центр квадрата, в каждой вершине которого находится заряд q = 2,33 нКл, помещен отрицательный заряд q0. Найти этот заряд, если на каждый заряд q действует результирующая сила F = 0 .
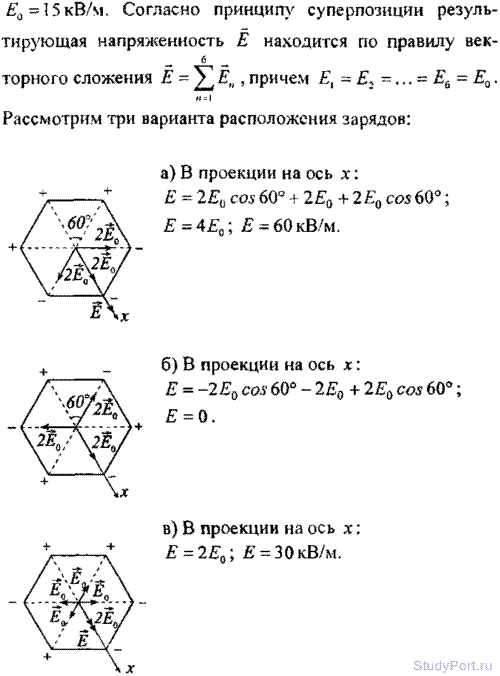
9.11. В вершинах правильного шестиугольника расположены три положительных и три отрицательных заряда. Найти напряженность Е электрического поля в центре шестиугольника при различных комбинациях в расположении этих зарядов. Каждый заряд q = 1,5 нКл; сторона шестиугольника а = 3 см.
9.12. Решить предыдущую задачу при условии, что все шесть зарядов, расположенных в вершинах шестиугольника, положительны.
9.13. Два точечных заряда q1 =7,5нКл и q2 =-14,7 нКл расположены на расстоянии r = 5см. Найти напряженность Е электрического поля в точке, находящейся на расстояниях а = 3 см от положительного заряда и b = 4 см от отрицательного заряда.
9.14. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. После сообщения шарикам заряда q0 = 0,4 мкКл они оттолкнулись друг от друга и разошлись на угол 2а = 60°. Найти массу т каждого шарика, если расстояние от центра шарика до точки подвеса l = 20 см.
9.15. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд q нужно сообщить шарикам, чтобы сила натяжения нитей стала равной Т = 98 мН? Расстояние от центра шарика до точки подвеса l = 10см; масса каждого шарика m = 5 г.
9.16. Найти плотность материала р шариков задачи 9.14, если известно, что при погружении этих шариков в керосин угол расхождения нитей стал равным 2аk: = 54°.
9.17. Два заряженных шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины и опущены в жидкий диэлектрик, плотность которого равна р и диэлектрическая проницаемость равна e, Какова должна быть плотность р0 материала шариков, чтобы углы расхождения нитей в воздухе и в диэлектрике были одинаковыми?
9.18. На рисунке АА — заряженная бесконечная плоскость с поверхностной плотностью заряда ? = 40мкКл/м2 и В — одноименно заряженный шарик с массой т = 1 г и зарядом q = 1 нКл. Какой угол а с плоскостью АА образует нить, на которой висит шарик?
9.19. На рисунке AA — заряженная бесконечная плоскость и В — одноименно заряженный шарик с массой т= 0,4 мг и зарядом q = 667 пКл. Сила натяжения нити, на которой висит шарик, T = 0,49мН. Найти поверхностную плотность заряда σ на плоскости АА.
9.20. Найти силу F, действующую на заряд q = 2 СГСq, если заряд помещен: а) на расстоянии r = 2 см от заряженной нити с линейной плотностью заряда τ = 0,2 мкКл/м; б) в поле заряженной плоскости с поверхностной плотностью заряда σ = 20 мкКл/м2; в) на расстоянии r = 2 см от поверхности заряженного шара с радиусом R = 2 см и поверхностной плотностью заряда σ = 20 мкКл/м2. Диэлектрическая проницаемость среды e = 6.
- О законе сухого трения см. Закон Амонтона — Кулона.
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Зако́н Куло́на — физический закон, описывающий взаимодействие между двумя неподвижными точечными электрическими зарядами в вакууме. Сила, с которой заряд 

,
где 




Также под законом Кулона понимается формула для вычисления электрического поля точечного заряда, вместе с её обобщением на произвольное распределение зарядов в пространстве:
.
Здесь 




Закон Кулона в классической электродинамике[править | править код]
Установление и формулировки закона[править | править код]
Закон открыт Шарлем Кулоном в 1785 году. Проведя большое количество опытов с металлическими шариками, Кулон дал такую формулировку закона:
Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.
Современная формулировка[1]:
Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
В векторном виде в формулировке Ш. Кулона закон записывается как
,
где 




Условия применимости[править | править код]
Для того, чтобы закон был верен, необходимы:
- точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров. Здесь две оговорки: а) существует обобщение закона Кулона на случай тел конечных размеров; б) можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
- их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
- расположение зарядов в вакууме.
В отдельных ситуациях, с корректировками, закон может быть применен также для взаимодействий зарядов в среде и для движущихся зарядов[2]. Но в общем случае при наличии неоднородных диэлектриков он неприменим, поскольку помимо заряда 

Выражения в разных системах единиц[править | править код]
В СГСЭ единица измерения заряда выбрана таким образом, что коэффициент 
В Международной системе единиц (СИ) одной из основных единиц является единица силы электрического тока — ампер, а единица заряда — кулон — производная от него. Величина ампера определена таким образом, что k = c2·10−7 Гн/м = 8,9875517873681764⋅109 Н·м2/Кл2 (или Ф−1·м). В СИ коэффициент k записывается в виде:
,
где 
В случае среды, заполненной бесконечным однородным изотропным диэлектрическим веществом, в знаменатель формулы закона Кулона добавляется диэлектрическая проницаемость среды ε. Тогда
(в СГСЭ)
(в СИ).
Закон Кулона и уравнения Максвелла[править | править код]
Закон Кулона и принцип суперпозиции для электрических полей в вакууме полностью равносильны уравнениям Максвелла для электростатики 




Исторически закон Кулона был одним из эмпирических законов, служивших предпосылками для формулирования уравнения Максвелла. Однако при современном изложении учения об электромагнетизме этот закон (равно как и, скажем, закон Ампера) нередко позиционируется как следствие уравнений Максвелла, которым придаётся статус фундаментальных аксиом.
Вывод закона Кулона из уравнений Максвелла[править | править код]
Уравнение Максвелла 
,
где 










Обобщение на случай распределения заряда[править | править код]
Если на заряд 






,
где радиус-вектором 





Если же не только заряд 

.
Закон Кулона и расчёт электрического поля[править | править код]
Взаимодействие двух зарядов может быть истрактовано как взаимодействие одного из зарядов с электрическим полем, создаваемым другим зарядом. Это становится виднее, если соответствующим образом перегруппировать сомножители в выражении для силы:
.
Тем самым закон Кулона фактически становится основой для вычисления поля. Так же, как и при рассмотрении силы, возможно обобщение последнего равенства на случай распределения зарядов.
Для нахождения поля 



,
где заряд 





Если всё пространство заполнено однородным диэлектриком с проницаемостью 





Аналогии в других областях классической физики[править | править код]
Закон Кулона совершенно аналогичен по форме закону всемирного тяготения. При этом функцию гравитационных масс выполняют электрические заряды[4] разных знаков.
Магнитостатическими аналогами закона Кулона являются закон Ампера (в части нахождения сил взаимодействия) и закон Био — Савара — Лапласа (в части расчёта по́ля).
Об открытии и исторической значимости закона[править | править код]
Впервые исследовать экспериментально закон взаимодействия электрически заряженных тел предложил[5] Г. В. Рихман в 1752—1753 гг. Он намеревался использовать для этого сконструированный им электрометр-«указатель». Осуществлению этого плана помешала его трагическая гибель.
В 1759 г. профессор физики Санкт-Петербургской академии наук Ф. Эпинус, занявший кафедру Рихмана после его гибели, впервые предположил[6], что заряды должны взаимодействовать обратно пропорционально квадрату расстояния. В 1760 г. появилось краткое сообщение[7] о том, что Д. Бернулли в Базеле установил квадратичный закон с помощью сконструированного им электрометра. В 1767 г. Пристли в своей «Истории электричества»[8] отметил, что опыт Франклина, обнаружившего отсутствие электрического поля внутри заряженного металлического шара, может означать, что «сила электрического притяжения подчиняется тем же законам, что и сила тяжести, а следовательно, зависит от квадрата расстояния между зарядами»[9]. Шотландский физик Джон Робисон утверждал (1822), что в 1769 г. обнаружил, что шары с одинаковым электрическим зарядом отталкиваются с силой, обратно пропорциональной квадрату расстояния между ними, и таким образом предвосхитил открытие закона Кулона (1785)[10].
Примерно за 11 лет до Кулона, в 1771 г., закон взаимодействия зарядов был экспериментально открыт Г. Кавендишем, однако результат не был опубликован и долгое время (свыше 100 лет) оставался неизвестным. Рукописи Кавендиша были вручены Дж. Максвеллу лишь в 1874 г одним из потомков Кавендиша на торжественном открытии Кавендишской лаборатории и опубликованы в 1879 г.[11].
Сам Кулон занимался исследованием кручения нитей и изобрел крутильные весы. Он открыл свой закон, измеряя с помощью них силы взаимодействия заряженных шариков.
Закон Кулона является первым открытым количественным и сформулированным на математическом языке фундаментальным законом для электромагнитных явлений. С открытия закона Кулона началась современная наука об электромагнетизме[12].
Закон Кулона в квантовой механике[править | править код]
В квантовой механике закон Кулона формулируется не при помощи понятия силы, как в классической механике, а при помощи понятия потенциальной энергии кулоновского взаимодействия. В случае, когда рассматриваемая в квантовой механике система содержит электрически заряженные частицы, к оператору Гамильтона системы добавляются слагаемые, выражающие потенциальную энергию кулоновского взаимодействия, так, как она вычисляется в классической механике[13]. Это утверждение не следует из остальных аксиом квантовой механики, а получено путём обобщения опытных данных.
Так, оператор Гамильтона атома с зарядом ядра Z имеет вид:
Здесь m — масса электрона, е — его заряд, 


Закон Кулона с точки зрения квантовой электродинамики[править | править код]
Согласно квантовой электродинамике, электромагнитное взаимодействие заряженных частиц осуществляется путём обмена виртуальными фотонами между частицами. Принцип неопределённости для времени и энергии допускает существование виртуальных фотонов на время между моментами их испускания и поглощения. Чем меньше расстояние между заряженными частицами, тем меньшее время нужно виртуальным фотонам для преодоления этого расстояния и следовательно, тем большая энергия виртуальных фотонов допускается принципом неопределенности. При малых расстояниях между зарядами принцип неопределённости допускает обмен как длинноволновыми, так и коротковолновыми фотонами, а при больших расстояниях в обмене участвуют только длинноволновые фотоны. Таким образом, с помощью квантовой электродинамики можно вывести закон Кулона[15][16].
Степень точности закона Кулона[править | править код]
Закон Кулона — экспериментально установленный факт. Его справедливость неоднократно подтверждалась всё более точными экспериментами. Одним из направлений таких экспериментов является проверка того, отличается ли показатель степени r в законе от 2. Для поиска этого отличия используется тот факт, что если степень точно равна двум, то поле внутри полости в проводнике отсутствует[пояснить], какова бы ни была форма полости или проводника[17].
Такие опыты впервые провел Кавендиш и повторил Максвелл в усовершенствованном виде, получив для максимального отличия показателя в степени от двух величину 
Эксперименты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, показали, что показатель степени в законе Кулона равен 2 с точностью до 
Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были использованы измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10−8 см, показатель степени в законе Кулона отличается от 2 не более чем на 10−9[20][21].
Коэффициент 
Поправки к закону в квантовой электродинамике[править | править код]
На небольших расстояниях (порядка комптоновской длины волны электрона):
м[22],
где 



Например, выражение для потенциала точечного заряда 
[23]:
где 


На расстояниях порядка 

В сильных внешних электромагнитных полях, составляющих заметную долю от поля пробоя вакуума (порядка 

Закон Кулона и поляризация вакуума[править | править код]
Явление поляризации вакуума в квантовой электродинамике заключается в образовании виртуальных электронно-позитронных пар. Облако электронно-позитронных пар экранирует электрический заряд электрона. Экранировка растет с ростом расстояния от электрона, в результате эффективный электрический заряд электрона 





где
— постоянная тонкой структуры;
см — классический радиус электрона[26][27].
Эффект Юлинга[править | править код]
Явление отклонения электростатического потенциала точечных зарядов в вакууме от значения закона Кулона известно как эффект Юлинга, который впервые вычислил отклонения от закона Кулона для атома водорода. Эффект Юлинга даёт поправку к лэмбовскому сдвигу 27 МГц[28][29].
Закон Кулона и сверхтяжёлые ядра[править | править код]
В сильном электромагнитном поле вблизи сверхтяжёлых ядер с зарядом 
См. также[править | править код]
- Электростатика
- Электрическое поле
- Дальнодействие
- Закон Био — Савара — Лапласа
- Закон притяжения
- Шарль Огюстен де Кулон
- Кулон (единица измерения)
- Принцип суперпозиции
- Уравнения Максвелла
Примечания[править | править код]
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — С. 17. — 656 с. — ISBN 5-9221-0227-3.
- ↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 8-е, стереотипное. — М.: Физматлит, 2001. — С. 132. — («Теоретическая физика», том II). — ISBN 5-9221-0056-4.
- ↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 4 «Электростатика», п. 1 «Статика», с. 70-71;
- ↑ Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм. — М.: Наука, 1964. — Тираж 100 000 экз. — С. 33.
- ↑ Novi Comm. Acad. Sc. Imp. Petropolitanae, v. IV, 1758, p. 301.
- ↑ Эпинус Ф. Т. У. Теория электричества и магнетизма. — Л.: АН СССР, 1951. — 564 с. — (Классики науки). — 3000 экз. Архивировано 17 ноября 2012 года.
- ↑ Abel Socin (1760) Acta Helvetica, vol. 4, pages 224-225.
- ↑ J. Priestley. The History and present state of Electricity with original experiments. London, 1767, p. 732.
- ↑ Уиттекер Э. История теории эфира и электричества. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 76. — 512 с. — ISBN 5-93972-070-6.
- ↑ John Robison, A System of Mechanical Philosophy (London, England: John Murray, 1822), vol. 4. На стр. 68 Робисон заявляет, что в 1769 он обнародовал свои измерения силы, действующей между сферами с одинаковым зарядом, и описывает также историю исследований в этой области, отмечая имена Эпинуса, Кавендиша и Кулона. На стр. 73 Архивная копия от 1 декабря 2016 на Wayback Machine автор пишет, что сила изменяется как x−2,06.
- ↑ ‘Филонович С. Р. Кавендиш, Кулон и электростатика. — М.: Знание, 1988. — С. 48.
- ↑ Спиридонов О. П. Универсальные физические постоянные.— М.: Просвещение.— 1984.— с. 52-53;
- ↑ Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — М., 2002. — С. 74. — («Теоретическая физика», том III).
- ↑ Бете Х. Квантовая механика. — Пер. с англ., под ред. В. Л. Бонч-Бруевича. — М.: Мир, 1965. — С. 11.
- ↑ Пайерлс Р. Е. Законы природы. пер. с англ. под ред. проф. Халатникова И. М. , Государственное издательство физико-математической литературы, М., 1959, тир. 20000 экз., 339 с., Гл. 9 «Электроны при высоких скоростях», п. «Силы при больших скоростях. Другие трудности», c. 263
- ↑ Окунь Л. Б.
… z Элементарное введение в физику элементарных частиц Архивная копия от 25 ноября 2010 на Wayback Machine, М., Наука, 1985, Библиотечка «Квант», вып. 45, п. «Виртуальные частицы», с. 57.
- ↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 10 «Поле внутри полости проводника», с. 106—108;
- ↑ Калашников С. Г.,
Электричество, М., ГИТТЛ, 1956, гл. III «Разность потенциалов», п. 34 «Точная проверка закона Кулона», с. 68—69; «Добавления», 1. «Теория опытов Кавендиша и Максвелла», с. 642—645; - ↑ E. R. Williams, J. E. Faller, H. A. Hill «New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest Mass», Phys. Rev. Lett. 26, 721—724 (1971);
- ↑ W. E. Lamb, R. C. Retherford. Fine Structure of the Hydrogen Atom by a Microwave Method (англ.) // Physical Review. — 1947. — Vol. 72, no. 3. — P. 241—243.
- ↑ 1 2 Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 8 «Точен ли закон Кулона?», с. 103;
- ↑ CODATA Архивная копия от 11 февраля 2012 на Wayback Machine (the Committee on Data for Science and Technology)
- ↑ Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая электродинамика. — Издание 3-е, исправленное. — М.: Наука, 1989. — С. 565—567. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-02-014422-3.
- ↑ Neda Sadooghi. Modified Coulomb potential of QED in a strong magnetic field (англ.). Архивировано 18 января 2015 года.
- ↑ Окунь Л. Б. Физика элементарных частиц. Изд. 3-е, М.: «Едиториал УРСС», 2005, ISBN 5-354-01085-3, ББК 22.382 22.315 22.3о, гл. 2 «Гравитация. Электродинамика», «Поляризация вакуума», с. 26-27;
- ↑ «Физика микромира», гл. ред. Д. В. Ширков, М., «Советская энциклопедия», 1980, 528 с., илл., 530.1(03), Ф50, ст. «Эффективный заряд», авт. ст. Д. В. Ширков, стр. 496;
- ↑ Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-e изд., перераб. и испр., М.: ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, 1056 стр.: илл., ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Я22, «Приложения», «Фундаментальные физические постоянные», с. 1008;
- ↑ Uehling E. A ., Phys. Rev., 48, 55, (1935)
- ↑ Швебер С., Бете Г., Гофман Ф. Мезоны и поля. Том 1 Поля гл. 5 Свойства уравнения Дирака п. 2. Состояния с отрицательной энергией c. 56, гл. 21 Перенормировка, п. 5 Поляризация вакуума с 336
- ↑ Мигдал А. Б. Поляризация вакуума в сильных полях и пионная конденсация// Успехи физических наук Т. 123— в. 3.— 1977 г., ноябрь.— с. 369—403;
Литература[править | править код]
- Филонович С. Р. Судьба классического закона. — М.: Наука, 1990. — 240 с., ISBN 5-02-014087-2 (Библиотечка «Квант», вып. 79), тир. 70500 экз.
Ссылки[править | править код]
- Закон Кулона (видеурок, программа 10 класса)
Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.
Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.
Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональная произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:
F = k · (|q1| · |q2|) / r2
где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.
Коэффициент k в СИ принято записывать в форме:
k = 1 / (4πε0ε)
где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.
Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.
Сила взаимодействия неподвижных точечных зарядов в вакууме:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]
Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.
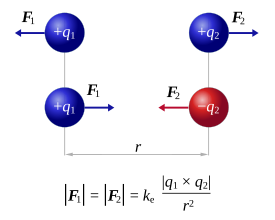
Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).
Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.
Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:
F1,2 = -F2,1
Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.
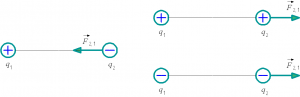
Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.
Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.
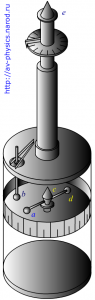
В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.
Рис. 1.10. Опыт Кулона (крутильные весы).
При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 17. Взаимодействие точечных зарядов. Закон Кулона |
| Напечатано:: | Гость |
| Дата: | Понедельник, 15 Май 2023, 00:34 |
Оглавление
- Взаимодействие точечных зарядов. Закон Кулона
- Закон Кулона
- Взаимодействие системы точечных зарядов
- Диэлектрическая проницаемость вещества
- Примеры решения задач
- Упражнение 13
Электрически заряженные тела (частицы) взаимодействуют друг с другом. Но как определить силу, которой одно заряженное тело притягивает или отталкивает другое?
Вы уже встречались с физическими моделями при изучении механики (материальная точка) и молекулярной физики (идеальный газ). В электростатике при изучении взаимодействия электрически заряженных тел эффективной оказывается модель «точечный заряд».
Точечный заряд — заряд такого заряженного тела, размеры которого значительно меньше расстояния от этого тела до точки наблюдения и до других тел (т. е. размерами заряженного тела в условиях данной задачи можно пренебречь).
Вспомните, закон всемирного тяготения также сформулирован для точечных тел (материальных точек).
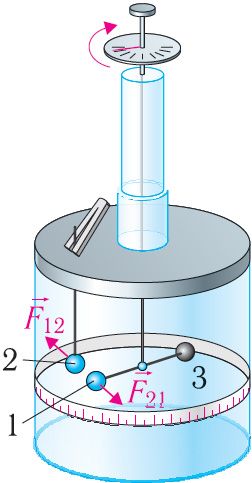
Закон Кулона. Кулон детально исследовал взаимодействие неподвижных точечных зарядов. Он на опыте изучил зависимость сил электрического взаимодействия тел от модулей зарядов этих тел и расстояния между ними.
В своих опытах Кулон использовал специальный прибор — крутильные весы (рис. 98). Крутильные весы представляют собой два стеклянных цилиндра, внутри которых на тонкой серебряной нити подвешено лёгкое непроводящее коромысло. На одном конце коромысла закреплён проводящий шар 1, а на другом — бумажный противовес 3. Шар 1 можно заряжать с помощью такого же проводящего шара 2. Он находится на изолирующем стержне, закреплённом на крышке нижнего цилиндра. При соприкосновении шара 1 с заряженным шаром 2 заряд распределяется между ними поровну, и шары отталкиваются.
Используя крутильные весы, Кулон получил зависимость модуля сил взаимодействия двух заряженных шаров от величин зарядов и от расстояния между ними. По углу закручивания нити, отсчитываемому по шкале прибора, можно определить силу взаимодействия заряженных шаров. Кулон установил, что модуль сил взаимодействия двух заряженных шаров обратно пропорционален квадрату расстояния между ними:
.
Для измерения зависимости модуля сил взаимодействия шаров от их зарядов учёный нашёл простой способ. Разряжая шар 2 прикосновением руки, а затем касаясь им уже заряженного шара 1, Кулон смог получить на нём заряды, модуль которых в 2, 4, 8 и т. д. раз меньше первоначального. Он выяснил, что при неизменном расстоянии модуль сил взаимодействия двух неподвижных небольших заряженных тел прямо пропорционален произведению модулей электрических зарядов каждого из них: .
Обобщив экспериментальные данные, Кулон сформулировал закон, получивший его имя.
Закон Кулона: модули сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорциональны произведению модулей зарядов этих тел, обратно пропорциональны квадрату расстояния между ними, а сами силы направлены вдоль прямой, соединяющей эти тела:
(17.1)
где k — коэффициент пропорциональности, зависящий от выбора единиц физических величин; |q1| и |q2| — модули точечных зарядов; r — расстояние между ними.
В СИ коэффициент пропорциональности
где — электрическая постоянная.
От теории к практике
Два маленьких положительно заряженных шарика закреплены на расстоянии r друг от друга. Как изменится модуль сил электростатического взаимодействия шариков, если: 1) уменьшить заряд каждого шарика в четыре раза; 2) увеличить расстояние между шариками в четыре раза; 3) увеличить заряд каждого шарика и расстояние между ними в два раза?
Как изменились бы силы электростатического взаимодействия шариков, если бы: 1) шарики были заряжены отрицательно; 2) один из шариков зарядить отрицательно, а другой положительно?
Интересно знать
Экспериментальные факты свидетельствуют о том, что воздействие неподвижного в данной инерциальной системе отсчёта точечного заряда на движущийся точечный заряд может быть описано законом Кулона с приемлемой точностью. Так, описание рассеяния α-частиц на ядрах атомов золота в опытах Резерфорда с помощью модели точечного заряда, на который действует кулоновская сила со стороны неподвижного ядра, согласуется с экспериментальными данными в пределах точности последних.
Два и более движущихся в данной инерциальной системе заряда не могут характеризоваться только кулоновским взаимодействием, так как каждый из них создаёт в окружающем пространстве магнитное поле, которое действует магнитной силой на остальные заряды, движущиеся в нём.
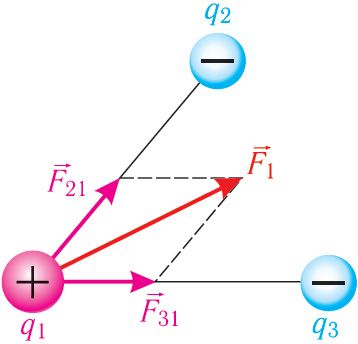
Взаимодействие системы точечных зарядов. Экспериментально установили, что силы взаимодействия двух точечных зарядов не изменяются при появлении третьего точечного заряда или любого числа точечных зарядов. В этом случае силы воздействия ,
, …,
каждого из зарядов q2, q3, …, qn на заряд q1 определяют по закону Кулона. Результирующая сила является векторной суммой сил, которыми каждый из этих зарядов в отдельности воздействует на заряд q1 (принцип суперпозиции).
Используя принцип суперпозиции и закон Кулона, можно описать электростатическое взаимодействие любой системы точечных зарядов. На рисунке 100 представлены три взаимодействующих между собой точечных электрических заряда: q1 > 0, q2 < 0, q3 < 0. Результирующей сил, действующих на заряд q1 со стороны зарядов q2 и q3, является сила , которая равна векторной сумме сил
и
:
. Силы
и
воздействия зарядов q2 и q3 на заряд q1 определяют по закону Кулона.
От теории к практике
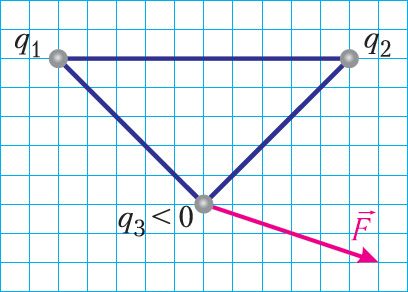
Точечные заряды q1, q2 и q3 закреплены в вершинах треугольника. Направление результирующей электростатической силы, действующей на отрицательный заряд q3 со стороны зарядов q1 и q2, представлено на рисунке 101. Каковы знаки зарядов q1 и q2? Во сколько раз отличаются модули зарядов q1 и q2?
Интересно знать
Понятие электрического заряда в некоторой степени сходно с понятием гравитационной массы. Электрический заряд определяет интенсивность электромагнитных взаимодействий, а масса — гравитационных. Закон Кулона, описывающий электростатическое взаимодействие, формально похож на закон всемирного тяготения Ньютона, определяющий силы гравитационного взаимодействия:
В обоих случаях модуль сил взаимодействия:
– обратно пропорционален квадрату расстояния между материальными точками;
– прямо пропорционален величинам, характеризующим те свойства тел (материальных точек), которые определяют взаимодействия, — массам в одном случае и электрическим зарядам — в другом.
Для измерения сил электрического отталкивания (Ш. Кулон, 1785 г.) и гравитационной постоянной (Г. Кавендиш, 1788 г.) учёные использовали похожие по устройству экспериментальные установки.
Однако между силами гравитационного и электростатического взаимодействий существует и важное различие. Ньютоновские силы тяготения — это всегда силы притяжения. кулоновские же силы взаимодействия зарядов могут быть как силами притяжения (между разноимёнными зарядами), так и силами отталкивания (между одноимёнными зарядами).
От теории к практике
Известно, что масса электрона mе = 9,1· 10–31 кг. Во сколько раз модуль сил электрического отталкивания между двумя электронами больше модуля сил их гравитационного притяжения?
Диэлектрическая проницаемость вещества. Из опытов следует, что взаимодействие электрически заряженных тел в воздухе практически не отличается от их взаимодействия в вакууме. Если заряженные тела находятся в воде, керосине, масле или какой-нибудь другой непроводящей среде, то модуль сил их взаимодействия оказывается меньше, чем в вакууме. Чтобы учесть влияние среды, ввели её специальную характеристику, называемую диэлектрической проницаемостью.
Диэлектрическая проницаемость вещества — физическая величина, показывающая, во сколько раз модуль сил электростатического взаимодействия зарядов в данной однородной среде меньше модуля сил взаимодействия этих же зарядов в вакууме:
(17.2)
где F0 и F — модули сил электростатического взаимодействия зарядов в вакууме и в однородной среде соответственно.
С учётом соотношения (17.2) закон Кулона можно записать следующим образом:
Диэлектрическая проницаемость вакуума равна 1. За 1 принимают и диэлектрическую проницаемость воздуха, поскольку её значение (при нормальном атмосферном давлении) 1,0006. Диэлектрические проницаемости других однородных сред всегда больше единицы. Например, у воды диэлектрическая проницаемость 81, у глицерина — 56, а у керосина — 2.
От теории к практике
Как и во сколько раз отличаются модули сил электростатического взаимодействия двух точечных зарядов, находящихся на одинаковом расстоянии друг от друга в воде, керосине и глицерине?
Интересно знать
Диэлектрическая проницаемость дистиллированной воды при температуре 25 °C равна 78,54, а при температуре 0 °C — 88. Обычно без указания температуры диэлектрическую проницаемость воды полагают равной 81.
1. К какому виду взаимодействий относят взаимодействие неподвижных электрических зарядов (заряженных тел)?
2. Заряды каких заряженных тел можно считать точечными?
3. Опишите эксперименты Кулона по исследованию взаимодействия электрических зарядов.
4. Сформулируйте закон Кулона. Каковы условия применимости закона Кулона?
5. Чему равен в СИ коэффициент k? Выразите наименование коэффициента пропорциональности k в законе Кулона в основных единицах СИ.
6. В чём суть принципа суперпозиции для электрического взаимодействия точечных зарядов?
7. Что называют диэлектрической проницаемостью среды?
Примеры решения задач
Пример 1. Два точечных заряда находятся в керосине на расстоянии r1 = 42 см. Определите, на каком расстоянии должны находиться эти заряды в глицерине, чтобы модуль сил их электростатического взаимодействия остался прежним. Диэлектрические проницаемости керосина ε1 = 2,0, глицерина ε2 = 56,2.
Дано:
r1 = 42 см
Fк1 = Fк2
ε1 = 2,0
ε2 = 56,2
r2 — ?
Решение: Поскольку Fк1 = Fк2, то, воспользовавшись законом Кулона, можно записать: .
Следовательно, .
Ответ: r2 = 7,9 см.
Пример 2. Точечные заряды q1 = 3,4 нКл и q2 = –5,6 нКл находятся в вакууме на расстоянии r = 36 см. Определите модуль и направление результирующей силы, действующей на заряд q3 = 3,2 нКл, помещённый в точку пространства, находящуюся на середине отрезка, соединяющего эти заряды.
Дано:
q1 = 3,4 нКл = 3,4 · 10–9 Кл
q2 = –5,6 нКл = –5,6 · 10–9 Кл
r = 36 см = 0,36 м
q3 = 3,2 нКл = 3,2 · 10–9 Кл
— ?
Решение: Изобразим на рисунке силы и
, действующие на точечный заряд q3 со стороны точечных зарядов q1 и q2 соответственно. Построив векторную сумму сил
и
, определим, что результирующая
этих сил направлена к заряду q2 (рис. 102).
Поскольку силы и
направлены одинаково, то модуль результирующей силы
.
Таким образом,
Ответ: Fp = 8,0 мкН; сила направлена к заряду q2.
Пример 3. Две бусинки, электрические заряды которых q1 = 40 нКл и q2 = 90 нКл, закреплены на непроводящем стержне на расстоянии r = 40 см друг от друга. Определите: а) где надо поместить третью бусинку, имеющую заряд q3, чтобы она оказалась в равновесии; б) каким должен быть заряд q3 третьей бусинки, чтобы результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равнялась нулю.
Дано:
q1 = 40 нКл = 4,0·10–8 Кл
q2 = 90 нКл = 9,0·10-8 Кл
r = 40 см = 0,40 м
х — ?
q3 — ?
Решение: а) Третья бусинка, имеющая заряд q3, будет находиться в равновесии, если её поместить в некоторую точку А между зарядами q1 и q2 на прямой, соединяющей эти заряды (рис. 102.1). Пусть заряд q3 < 0. Тогда со стороны зарядов q1 и q2 на заряд q3 будут действовать противоположно направленные кулоновские силы притяжения и
. Согласно второму закону Ньютона, эта бусинка будет покоиться, если модули сил F13 и F23 равны. Тогда, приняв расстояние от заряда q1 до точки А равным х, запишем:
. Так как k и q3 не равны нулю, то это выражение можно сократить:
. Извлечём из обеих частей равенства квадратный корень
. Отсюда:
Такое же значение х мы получим, если примем заряд q3 бусинки положительным (проверьте это самостоятельно).
б) Результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю, если, например, третья бусинка притягивает вторую силой, модуль которой равен модулю силы
, какой её отталкивает первая бусинка (рис. 102.2). При этом заряд третьей бусинки должен быть отрицательным, т. е. q3 < 0. Тогда
. Отсюда
.
Ответ: х = 16 см, расстояние до бусинки с зарядом q3 не зависит от значения и знака её заряда; если заряд бусинки q3 = ‒14 нКл, то результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю.
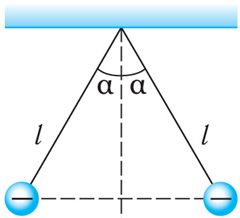
Пример 4. Два одинаковых маленьких проводящих шарика массой m = 20 мг каждый подвешены в воздухе на лёгких нерастяжимых нитях длиной l = 0,20 м, закреплённых в одной точке подвеса. Один из шариков отвели в сторону, сообщили ему заряд q < 0 и отпустили. После столкновения шарики разошлись так, что угол между нитями составил 2α = 60° (рис. 102.3). Определите заряд, который был сообщён первому шарику, а также количество избыточных электронов на каждом из шариков после их столкновения.
Дано:
m = 20 мг = 2,0·10–5 кг
l = 0,20 м
2α = 60°
q – ?
N – ?
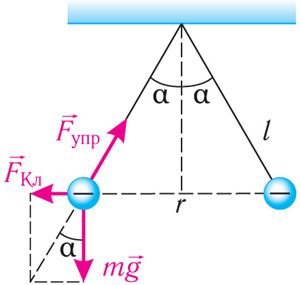
Решение: Воспользуемся законом сохранения электрического заряда. При столкновении двух одинаковых проводящих шариков сообщённый одному из них заряд разделился поровну и на каждом шарике оказался избыточный отрицательный заряд . На каждый шарик действуют сила тяжести
сила электростатического взаимодействия
и сила упругости нити
(рис. 102.4). После столкновения шарики разошлись, и установилось равновесие. Векторная сумма сил, действующих на каждый шарик, стала равной нулю:
. Модуль силы электростатического взаимодействия
. Поскольку шарики разошлись симметрично относительно вертикали, проходящей через точку подвеса нитей, то
(рис. 102.4). Следовательно,
. Так как
, то
, откуда
. Примем
.
Количество избыточных электронов на каждом шарике .
Ответ: q = ‒45 нКл, N = 1,4 · 1011.
Упражнение 13
1. Определите модуль сил взаимодействия двух одинаковых неподвижных точечных зарядов q1 = q2 = 9,0 нКл, находящихся на расстоянии r = 0,30 м в вакууме. Во сколько раз уменьшится или увеличится модуль сил взаимодействия этих зарядов при помещении их в керосин, диэлектрическая проницаемость которого ε = 2,0?
2. Определите, во сколько раз следует увеличить расстояние между двумя неподвижными точечными зарядами, чтобы модуль сил взаимодействия остался прежним при увеличении численного значения одного из зарядов в α = 4 раза.
3. Два одинаковых маленьких проводящих шарика, заряды которых отличаются в два раза, находятся на расстоянии r = 50 см. Определите расстояние, на которое необходимо развести шарики после соприкосновения, чтобы модуль сил их взаимодействия остался прежним.
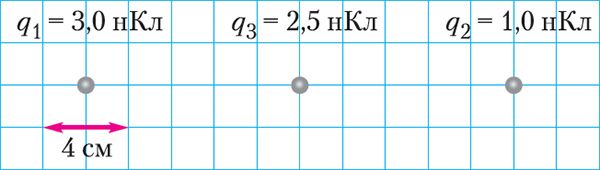
4. Точечные заряды q1 и q2 закреплены в вакууме (рис. 103). Определите модуль и направление результирующей силы, действующей на заряд q3, помещённый в точку, находящуюся на середине отрезка, соединяющего эти заряды.
5. Заряды двух одинаковых маленьких шариков массой m = 40 г каждый одинаковые. Расстояние между шариками существенно превышает их размеры. Определите модуль зарядов шариков, если кулоновская сила их отталкивания уравновешивает силу гравитационного притяжения этих шариков.
6. Небольшой шарик, заряд которого q1 = 20 нКл и масса m = 60 мг, подвешен в воздухе на шёлковой нити. После того как на вертикали, проходящей через центр шарика, на расстоянии r = 15 см ниже его поместили другой маленький шарик, заряженный отрицательно, модуль силы упругости нити увеличился в два раза. Определите заряд второго шарика.
7. Три первоначально закреплённых одинаковых точечных заряда q1 = q2 = q3 = q0 = 1,0 мкКл расположены в вершинах равностороннего треугольника. Определите, какой точечный заряд нужно поместить в центр треугольника, чтобы вся система находилась в равновесии после освобождения первоначально закреплённых зарядов.
Основной
закон взаимодействия электрических
зарядов был найден Шарлем Кулоном в
1785 г. экспериментально. Кулон установил,
что сила
взаимодействия
между двумя небольшими заряженными
металлическими шариками обратно
пропорциональна квадрату расстояниямежду ними и зависит от величины зарядов
и
:
,
где
–коэффициент
пропорциональности
.
Силы,
действующие на заряды,
являются центральными,
то есть они направлены вдоль прямой,
соединяющей заряды.
-
Для
одноименных зарядов произведение
и сила
соответствует взаимному отталкиванию
зарядов, -
для
разноимнных зарядов
,
и силасоответствует взаимному притяжению
зарядов.
Закон
Кулона
можно записать в
векторной форме:,
где
–вектор
силы, действующей на заряд
со стороны заряда
,
– радиус-вектор,
соединяющий заряд
с зарядом
;
– модуль радиус-вектора.
Сила,
действующая на заряд
со стороны
равна
,
.
Закон Кулона в
такой форме
-
справедлив
только
для взаимодействия точечных электрических
зарядов,
то есть таких заряженных тел, линейными
размерами которых можно пренебречь по
сравнению с расстоянием между ними. -
выражает
силу взаимодействия
между неподвижными электрическими
зарядами, то есть это электростатический
закон.
Формулировка
закона Кулона:
Сила
электростатического взаимодействия
между двумя точечными электрическими
зарядами прямо пропорциональна
произведению величин зарядов и обратно
пропорциональна квадрату расстояния
между ними.
Коэффициент
пропорциональности
в законе Кулоназависит
-
от свойств среды
-
выбора единиц
измерения величин, входящих в формулу.
Поэтому
можно
представить отношением,
где
–коэффициент,
зависящий только от выбора системы
единиц измерения;
– безразмерная
величина, характеризующая электрические
свойства среды, называется относительной
диэлектрической проницаемостью среды.
Она не зависит от выбора системы единиц
измерения и равна единице в вакууме.
Тогда
закон Кулона примет вид:,
для
вакуума
,
тогда
–относительная
диэлектрическая проницаемость среды
показывает, во сколько раз в данной
среде сила взаимодействия между двумя
точечными электрическими зарядами
и
,
находящимися друг от друга на расстоянии,
меньше, чем в вакууме.
В
системе СИ коэффициент
,
и
закон
Кулона имеет вид:.
Это
рационализированная
запись закона Кулона.
– электрическая
постоянная,
.
В
системе СГСЭ
,
.
В
векторной форме закон Кулона
принимает вид
где
–вектор
силы, действующей на заряд
со стороны заряда
,

радиус-вектор, соединяющий заряд
с зарядом
(рис. 1.2),
r
–модуль радиус-вектора
.
Всякое
заряженное тело состоит из множества
точечных электрических зарядов, поэтому
электростатическая
сила, с которой одно заряженное тело
действует на другое, равна векторной
сумме сил, приложенных ко всем точечным
зарядам второго тела со стороны каждого
точечного заряда первого тела.
1.3.Электрическое поле. Напряженность.
Пространство,
в котором находится электрический
заряд, обладает определенными физическими
свойствами.
-
На
всякий
другой заряд,
внесенный в это пространство, действуют
электростатические силы Кулона. -
Если в каждой
точке пространства действует сила, то
говорят, что в этом пространстве
существует силовое поле. -
Поле наряду с
веществом является формой материи. -
Если
поле стационарно, то есть не меняется
во времени, и создается неподвижными
электрическими зарядами, то такое поле
называется электростатическим.
Электростатика
изучает только электростатические поля
и взаимодействия неподвижных зарядов.
Для
характеристики электрического поля
вводят понятие напряженности.
Напряженностью
в каждой точке электрического поля
называется вектор
,
численно равный отношению силы, с которой
это поле действует на пробный положительный
заряд, помещенный в данную точку, и
величины этого заряда, и направленный
в сторону действия силы.
Пробный
заряд,
который вносится в поле, предполагается
точечным и часто называется пробным
зарядом.
– Он
не участвует в создании поля,
которое с его помощью измеряется.
–
предполагается, что этот заряд не
искажает исследуемого поля,
то есть он достаточно мал и не вызывает
перераспределения зарядов, создающих
поле.
Если
на пробный точечный заряд
поле действует силой
,
то напряженность.
Единицы напряженности:
СИ:
СГСЭ:
В
системе СИ выражение
для
поля точечного заряда:
.
В векторной форме:
Здесь
– радиус-вектор, проведенный из зарядаq
, создающего поле, в данную точку.
Т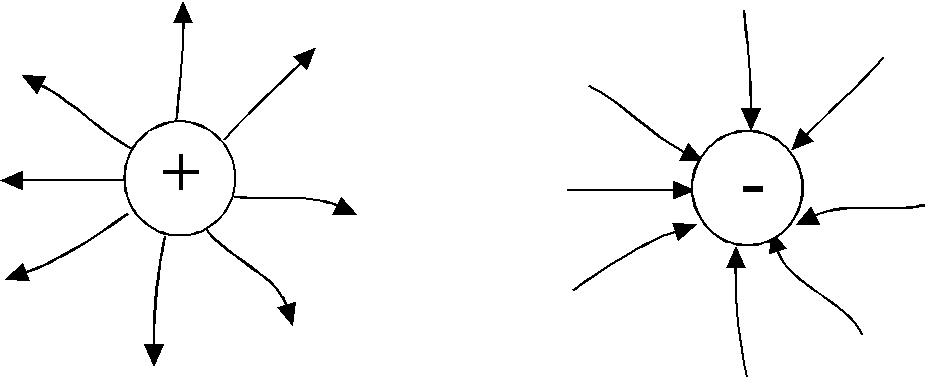
образом,векторы
напряженности электрического поля
точечного заряда q
во всех точках поля направлены радиально
(рис.1.3)
– от
заряда, если он положительный, «исток»
– и
к заряду, если он отрицательный
«сток»
Для
графической интерпретации
электрического поля вводят понятие
силовой линии или линии
напряженности.
Это
-
кривая,
касательная в каждой точке к которой
совпадает с вектором напряженности. -
Линия напряженности
начинается на положительном заряде и
заканчивается на отрицательном. -
Линии напряженности
не пересекаются, так как в каждой точке
поля вектор напряженности имеет лишь
одно направление.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

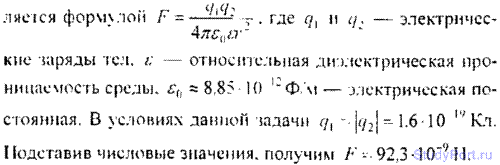
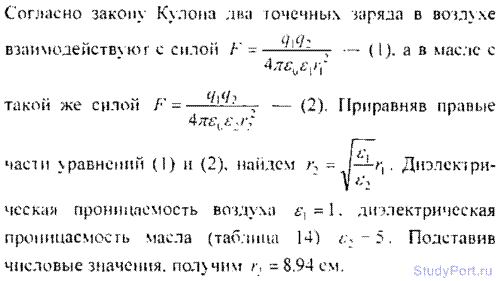











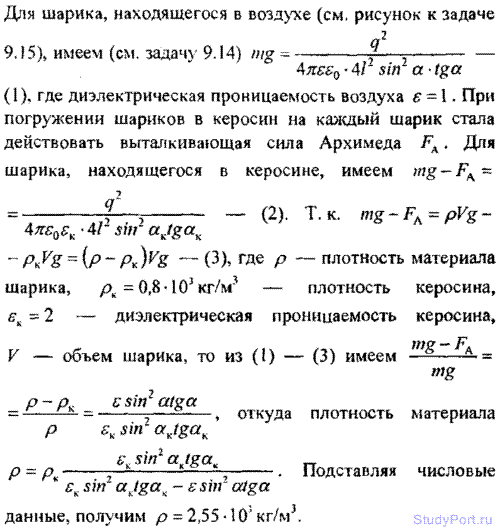














![{displaystyle {vec {F}}_{12}={frac {1}{4pi varepsilon _{0}}}cdot {frac {q_{1}q_{2}({vec {r}}_{2}-{vec {r}}_{1})}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}=q_{2}cdot left[{frac {1}{4pi varepsilon _{0}}}cdot {frac {q_{1}({vec {r}}_{2}-{vec {r}}_{1})}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}right]=q_{2}cdot E_{1}({vec {r}}_{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0e25ba88f2895320a718c679386b044aa2eaa04)