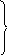Наблюдатель, вращающийся вместе с каруселью, может объяснить отклонение кресел на аттракционе действием центробежной силы инерции
Си́ла ине́рции (также инерционная сила) — многозначное понятие, применяемое в механике по отношению к трём различным физическим величинам. Одна из них — «даламберова сила инерции»[⇨] — вводится в инерциальных системах отсчёта для получения формальной возможности записи уравнений динамики в виде более простых уравнений статики. Другая — «эйлерова сила инерции»[⇨] — используется при рассмотрении движения тел в неинерциальных системах отсчёта[1]
[2]. Наконец, третья — «ньютонова сила инерции»[⇨] — сила противодействия, рассматриваемая в связи с третьим законом Ньютона[3].
Общим для всех трёх величин является их векторный характер и размерность силы. Кроме того, первые две величины объединяет возможность их использования в уравнениях движения, по форме совпадающих с уравнением второго закона Ньютона[1][4][5], а также их пропорциональность массе тел[6][4][5].
Терминология[править | править код]
Русскоязычный термин «сила инерции» произошёл от французского словосочетания фр. force d’inertie. Термин применяется для описания трёх различных векторных физических величин, имеющих размерность силы:
- величин, которые вводят при описании движения тел в неинерциальных система отсчёта — «эйлеровы силы инерции»;
- величины, используемой в принципе Д’Аламбера — «даламберова сила инерции»;
- силы-противодействия из третьего закона Ньютона — «ньютонова сила инерции».
Определения «эйлерова», «даламберова» и «ньютонова» предложены академиком А. Ю. Ишлинским[7][8]. Они используются в литературе, хотя и не получили пока повсеместного распространения. В дальнейшем мыкто? будем придерживаться данной терминологии, как позволяющей сделать изложение более сжатым и ясным.
Эйлерова сила инерции в общем случае складывается из нескольких составляющих различного происхождения, которым также присвоены специальные наименования («переносная», «кориолисова» и др.). Более детально об этом говорится в соответствующем разделе ниже.
В других языках используемые названия сил инерции более явно указывают на их особые свойства: в немецком нем. Scheinkraft[9] («мнимая», «кажущаяся», «видимая», «ложная», «фиктивная» сила), в английском англ. pseudo force[10](«псевдосила») или англ. fictitious force («фиктивная сила»). Реже в английском используются названия «сила д’Аламбера» (англ. d’Alembert force[11]) и «инерционная сила» (англ. inertial force[12]). В литературе, издаваемой на русском языке, по отношению к эйлеровой и даламберовой силам также используют аналогичные характеристики, называя эти силы «фиктивными»[13], «кажущимися»[14], «воображаемыми»[8] или «псевдосилами»[15].
Одновременно с этим в литературе иногда подчёркивают реальность сил инерции[16][17], противопоставляя значение данного термина значению термина фиктивность. При этом, однако, различные авторы вкладывают в эти слова различный смысл, и силы инерции оказываются реальными или фиктивными не из-за отличий в понимании их основных свойств, а в зависимости от избранных определений. Такое употребление терминологии некоторые авторы считают неудачным и рекомендуют просто избегать его в учебном процессе[18][19].
Хотя дискуссия по поводу терминологии ещё не закончена, имеющиеся разногласия не влияют на математическую формулировку уравнений движения с участием сил инерции и не приводят к возникновению каких-либо недоразумений при использовании уравнений на практике.
Силы в классической механике[править | править код]
В классической механике представления о силах и их свойствах основываются на законах Ньютона и неразрывно связаны с понятием «инерциальная система отсчёта». Хотя в наименованиях эйлеровых и даламберовых сил инерции содержится слово сила, эти физические величины силами в смысле, принятом в механике, не являются[20][15].
Действительно, физическая величина, называемая силой, вводится в рассмотрение вторым законом Ньютона, при этом сам закон формулируется только для инерциальных систем отсчёта[21]. Соответственно, понятие силы оказывается определённым только для таких систем отсчёта[22].
Уравнение второго закона Ньютона, связывающее ускорение 


Из уравнения непосредственно следует, что причиной ускорения тел являются только силы, и наоборот: действие на тело не скомпенсированных сил обязательно вызывает его ускорение.
Третий закон Ньютона дополняет и развивает сказанное о силах во втором законе.
Учёт содержания всех законов Ньютона приводит к заключению о том, что силы, о которых идёт речь в классической механике, обладают неотъемлемыми свойствами:
- сила есть мера механического действия на данное материальное тело других тел.[23]
- в соответствии с третьим законом Ньютона силы способны существовать лишь попарно, при этом природа сил в каждой такой паре одинакова[24][25].
- любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, силы обязательно представляют собой результат взаимодействия тел[26].
Никакие другие силы в классической механике в рассмотрение не вводятся и не используются[22][27]. Возможность существования сил, возникших самостоятельно, без взаимодействующих тел, механикой не допускается[26][28].
Ньютоновы силы инерции[править | править код]
Некоторые авторы используют термин «сила инерции» для обозначения силы-противодействия из третьего закона Ньютона. Понятие было введено Ньютоном в его «Математических началах натуральной философии»[29]: «Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения. От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому врожденная сила могла бы быть весьма вразумительно названа силою инерции. Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко — и как сопротивление, и как напор.», а собственно термин «сила инерции» был, по словам Эйлера, впервые употреблён в этом значении Кеплером([29], со ссылкой на Е. Л. Николаи).
Для обозначения этой силы-противодействия (действующей на ускоряющее тело со стороны ускоряемого тела[29]) некоторые авторы предлагают использовать термин «ньютонова сила инерции» во избежание путаницы с фиктивными силами, применяемыми при вычислениях в неинерциальных системах отсчёта и при использовании принципа д’Аламбера.
Отголоском мистических и теологических взглядов Ньютона[30] является применённая им терминология при описании силы инерции: «врождённая сила материи», «сопротивление». Такой подход к описанию ньютоновской силы инерции хотя и сохранился в современном обиходе[где?], однако является нежелательным, поскольку вызывает ассоциации с некой способностью тела сопротивляться изменениям, волевым усилием сохранить параметры движения. Максвелл заметил, что с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, так как сладким он становится не сам по себе, а лишь после добавления сахара[29].
Эйлеровы силы инерции[править | править код]
Уравнение движения материальной точки в инерциальной системе координат (ИСО), представляющее собой уравнение 2-го закона Ньютона
в неинерциальной системе отсчёта (НСО) приобретает четыре дополнительных члена с размерностью силы — так называемые «силы инерции»[31], иногда называемые «эйлеровыми»:
где:
Классификация[править | править код]
Четыре дополнительных члена в уравнении движения принято рассматривать как отдельные силы инерции, которые получили собственные названия:
называется поступательной силой инерции. Сила связана с линейным ускорением НСО[32] и противонаправлена ему;
называется вращательной силой инерции. Сила связана с угловым ускорением НСО[32];
называется центробежной силой. Сила связана с вращением НСО и потому проявляется и в случае равномерного вращения[33];
называется силой Кориолиса[34].
Первые три силы, не связанные с движением точки, объединяются термином «переносные силы инерции»[32].
Примеры использования[править | править код]
В некоторых случаях при расчётах удобно использовать неинерциальную систему отсчёта, например:
- движение подвижных деталей автомобиля удобно описывать в системе координат, связанных с автомобилем. В случае ускорения автомобиля эта система становится неинерциальной;
- движение тела по круговой траектории иногда удобно описывать в системе координат, связанной с этим телом. Такая система координат неинерциальна из-за центростремительного ускорения.
В неинерциальных системах отсчёта стандартные формулировки законов Ньютона неприменимы. Так при ускорении автомобиля, в системе координат, связанной с корпусом автомобиля, незакреплённые предметы внутри получают ускорение в отсутствие какой-либо силы, прикладываемой непосредственно к ним; а при движении тела по орбите, в связанной с телом неинерциальной системе координат тело покоится, хотя на него действует ничем не сбалансированная сила гравитации, выступавшая в качестве центростремительной в той инерциальной системе координат, в которой наблюдалось вращение по орбите.
Для восстановления возможности применения в этих случаях привычных формулировок законов Ньютона и связанных с ними уравнений движения для каждого рассматриваемого тела оказывается удобно ввести фиктивную силу — силу инерции — пропорциональную массе этого тела и величине ускорения системы координат, и противонаправленную вектору этого ускорения.
С использованием этой фиктивной силы появляется возможность краткого описания реально наблюдаемых эффектов в неинерциальной системе отсчёта (в разгоняющемся автомобиле): «почему при разгоне автомобиля пассажира прижимает к спинке сиденья?» — «на тело пассажира действует сила инерции». В инерциальной системе координат, связанной с дорогой, сила инерции для объяснения происходящего не требуется: тело пассажира в ней ускоряется (вместе с автомобилем), и это ускорение производит сила, с которой сиденье действует на пассажира.
Сила инерции на поверхности Земли[править | править код]
В инерциальной системе отсчёта (наблюдатель вне Земли) тело, находящееся на поверхности Земли, испытывает центростремительное ускорение 





Для наблюдателя, вращающегося вместе с Землёй, тело неподвижно, хотя на него действуют в точности те же силы, что и в предыдущем случае: сила гравитации 




Сумму сил гравитации 





Работа сил инерции[править | править код]
В классической физике силы инерции встречаются в двух различных ситуациях в зависимости от системы отсчёта, в которой производится наблюдение[29]. Это — сила, приложенная к связи при наблюдении в инерциальной СО, или сила, приложенная к рассматриваемому телу, при наблюдении в неинерциальной системе отсчёта. Обе эти силы могут совершать работу. Исключением является сила Кориолиса, которая работы не совершает, поскольку всегда направлена перпендикулярно вектору скорости. В то же время сила Кориолиса может изменить траекторию движения тела и, тем самым, способствовать совершению работы другими силами (такими, как сила трения). Примером этому может служить эффект Бэра.
Кроме того, в некоторых случаях бывает целесообразно разделить действующую силу Кориолиса на две составляющие, каждая из которых совершает работу. Суммарная работа, производимая этими составляющими, равна нулю, но такое представление может оказаться полезным при анализе процессов перераспределения энергии в рассматриваемой системе[38].
При теоретическом рассмотрении, когда искусственно сводят динамическую задачу движения к задаче статики, вводят третий вид сил, называемый силами Даламбера, которые работы не совершают ввиду неподвижности тел, на которые эти силы действуют.
Эквивалентность сил инерции и гравитации[править | править код]
Согласно принципу эквивалентности сил гравитации и инерции локально невозможно отличить, какая сила действует на данное тело — гравитационная сила или сила инерции. В этом смысле глобальные или даже конечные инерциальные системы отсчёта в общей теории относительности в общем случае отсутствуют.
Д’Аламберовы силы инерции[править | править код]
В принципе д’Аламбера в рассмотрение вводятся подлинно отсутствующие в природе силы инерции, которые невозможно измерить никакой физической аппаратурой.
Эти силы вводятся ради использования искусственного математического приёма, основанного на применении принципа Д’Аламбера в формулировке Лагранжа, где задача на движение с помощью введения сил инерции формально сводится к проблеме равновесия[29].
См. также[править | править код]
- Центробежная сила
- Сила Кориолиса
- Сила Кориолиса в гидроаэромеханике
Приложения[править | править код]
- ↑ 1 2 Тарг С. М. Сила инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494—495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Сила инерции / Самсонов В. А. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—15. — 320 с.
- ↑ 1 2 Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М., Наука, 1987. — Тираж 233000 экз. — с. 119—120
- ↑ 1 2 Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М., Наука, 1975. — Тираж 350000 экз. — с. 291—292
- ↑ Кошкин Н. И., Ширкевич М. Г. Справочник по элементарной физике.- М., Наука, 1988. — Тираж 300000 экз. — с. 33
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 14—18. — 320 с.
- ↑ 1 2 Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3—8. Архивировано 29 октября 2013 года.
- ↑ Walter Greiner Klassische Mechanik II. Wissenschaftlicher Verlag Harri Deutsch GmbH. Frankfurt am Main. 2008 ISBN 978-3-8171-1828-1
- ↑ ^Richard Phillips Feynman, Leighton R. B. & Sands M. L. (2006). The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley. Vol. I, section 12-5. ISBN 0-8053-9049-9. https://books.google.com/books?id=zUt7AAAACAAJ& <=intitle:Feynman+intitle:Lectures+intitle: on+intitle:Physics&lr=&as_brr=0.
- ↑ ^Cornelius Lanczos (1986). The Variational Principles of Mechanics. New York: Courier Dover Publications. p. 100. ISBN 0-486-65067-7. https://books.google.com/books?id=ZWoYYr8wk2IC&pg=PA103&dq=%22Euler+force%22&lr=&as_brr=0&sig=UV46Q9NIrYWwn5EmYpPv-LPuZd0#PPA100,M1 Архивная копия от 25 февраля 2014 на Wayback Machine.
- ↑ ^ Max Born & Günther Leibfried (1962). Einstein’s Theory of Relativity. New York: Courier Dover Publications. pp. 76-78. ISBN 0-486-60769-0. https://books.google.com/books?id=Afeff9XNwgoC&pg=PA76&dq=%22inertial+forces%22&lr=&as_brr=0&sig=0kiN27BqUqHaZ9CkPdqLIjr-Nnw#PPA77,M1 Архивная копия от 9 июня 2016 на Wayback Machine.
- ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
- ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
- ↑ 1 2 Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
- ↑ Седов Л. И. Об основных моделях механики. М.: МГУ, 1992. Стр 17.; Седов Л. И. Очерки, связанные с основами механики и физики. М.: Знание, 1983. Стр 19.
- ↑ Матвеев А. Н. Механика и теория относительности. М.: Высшая школа, 1979. Стр 393. (в 3-е изд. 2003. Стр.393)
- ↑ [1] Архивная копия от 28 февраля 2014 на Wayback Machine. Вестник высшей школы. Советская наука, 1987. С. 248.
- ↑ А. Ишлинский при переиздании своей работы удалил эти термины («Классическая механика и силы инерции», 1987, с. 279): … термин «реальная сила» и «фиктивная сила» понимались по-разному. Считаю, что лучше не спорить на эту тему и от упомянутых слов вообще отказаться.
- ↑ «„Силы инерции“ — не силы».
Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с. - ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 182. — 416 с. — ISBN 5-06-003117-9.
- ↑ 1 2 Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 19. — 46 с.
- ↑ Тарг С. М. Сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 16. — 368 с. — ISBN 5-93972-051-X.
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2005. — Т. I. Механика. — С. 84. — 560 с. — ISBN 5-9221-0225-7.
- ↑ 1 2 Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 59—60. — 546 p. — ISBN 0-07-035048-5. Архивная копия от 17 июня 2013 на Wayback Machine Архивированная копия. Дата обращения: 14 мая 2013. Архивировано 17 июня 2013 года.
- ↑ Встречается утверждение, что применительно к силе Лоренца сказанное не верно и требует дополнительного уточнения (Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132). Согласно другой точке зрения, «в электродинамике силы противодействия силам Лоренца приложены к электромагнитному полю (подстрочное примечание: Стоит отметить, что ещё недавно некоторые видные учёные считали, что сила Лоренца вообще не удовлетворяет закону действия и противодействия…) как к физическому объекту, претерпевающему соответствующее влияние» (Седов, Очерки, с. 17).
- ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 8. — 320 с.
- ↑ 1 2 3 4 5 6 Хайкин, Семён Эммануилович. Силы инерции и невесомость. — 1. — М., «Наука». Главная редакция физико-математической литературы. 1967 г..— С. 129—130, 188—189. — 312 с.
- ↑ Ньютон: Физика в контексте Теологии. snob.ru. Дата обращения: 24 января 2020. Архивировано 6 марта 2021 года.
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 362. — 560 с. — ISBN 5-9221-0225-7.
- ↑ 1 2 3 Егоров Г. В. О силах инерции Архивная копия от 29 января 2020 на Wayback Machine // Вестник БГУ. 2013. № 1.
- ↑ Ландавшиц, 1988, с. 165—166.
- ↑ Ландавшиц, 1988, с. 165.
- ↑ Китайгородский А. И. Введение в физику. М:Изд.-во «Наука», гл.ред.физико-математической литературы.1973
- ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Грушинский Н. П. Основы гравиметрии. — М.: «Наука», 1983. — С. 34. — 351 с.
- ↑ Krigel A. M. The theory of the index cycle in the general circulation of the atmosphere // Geophys. Astrophys. Fluid Dynamics.— 1980.— 16.— p. 1-18.
Литература[править | править код]
- Ишлинский А. Ю. Классическая механика и силы инерции. — Изд. 2. — М.: URSS, 2018. — 320 с. — ISBN 978-5-9710-5075-9.
- Ландау Л. Д., Лифшиц Е. М. § 39. Движение в неинерциальной системе отсчёта // Теоретическая физика. — М.: Наука, 1988. — Т. I. Механика. — С. 163—167. — 216 с. — ISBN 5-02-013850-9.
- Понятов А. Эти странные силы инерции // Наука и жизнь. — 2020. — № 10. — С. 22—31.
- Седов Л. И. Об основных моделях механики. М.: МГУ, 1992. — 151с. ISBN 5-211-01570-3 Глава 1 «О силах инерции» стр.6-17.
- Седов Л. И. Очерки, связанные с основами механики и физики. М.: Знание, 1983. — 64с. Раздел «О силах инерции» стр.5-18.
- Хайкин С. Э. Силы инерции и невесомость. Издательство «Наука». Главная редакция физико-математической литературы. М.,1967 г.
Сила инерции
Силы являются причиной любого изменения состояния движения, т.е. любого ускорения. Ускорение возникает в направлении действия силы. Кроме того, существуют так называемые силы инерции, которые возникают как следствие ускорений. Они направлены в сторону, противоположную ускорению. Силы инерции возникают только в системе отсчета, движущейся с ускорением, т. е. это кажущиеся силы.
Силы, вызывающие ускорение данного тела, и силы инерции, возникающие вследствие ускорения, всегда равны по величине и противоположно направлены.
[ vector{F}_{и} = – vector{F} ]
[ vector{F} – m vector{a} = 0 ]
[ vector{F}_{и} = – m vector{a} ]
Здесь:
F — сила, сообщающая телу ускорение (Ньютон),
Fи — сила инерции (Ньютон),
m — масса тела (кг),
a — ускорение (м/с2),
Чтобы установить, как движется тело, на которое действует сразу несколько сил, часто пользуются принципом динамического равновесия (ΣF = 0), причем в этом случае кроме действующих сил и сил трения следует также учитывать кажущиеся силы инерции (принцип ДАламбера).
Вычислить, найти силу инерции по формуле (3)
Сила инерции |
стр. 451 |
|---|
Как найти силы инерции
Инерция – это понятие, обозначающее сохранение скорости тела и продолжении движения тела без воздействия на него внешних сил. Например, если какая либо сила оттолкнула шарик, он будет продолжать двигаться то или иное время после воздействия силы – это и есть движение по инерции.

Инструкция
Определите силу инерции. Сила инерции – величина имеющая направление, или векторная, она равна массе m материальной точки, умноженной на ее ускорение, а направлена она противоположно ускорению. Если в задаче дано криволинейное движение, силу инерции разложите на касательную, или так называемую тангенциальную составляющую (обозначение: Jt ), которая будет направлена противоположно касательному ускорению (обозначение: wt), а также на центробежную составляющую (обозначение: Jn), она направлена вдоль главной нормали к траектории от центра кривизны.
Запомните формулу:
Jt = nwt, Jn = mv2/r,
где v — скорость данной точки, r — радиус окружности кривизны, представленной в задаче, траектории.
При изучении движения по отношению к такой инерциальной системе отсчета силу инерции обычно вводят для возможности (только формальной) составлять уравнения динамики в виде простых уравнений статики ( по принципу Д’ Аламбера, Кинетостатика).
Понятие «сила инерции» используется при изучении относительного движения. В таком случае присоединение к силам, действующим на материальную точку прибавляются еще и взаимодействия с иными телами переносной Jпер и Кориолиса Jкop Силы инерции, что позволяет составлять уравнения движения этой точки в неинерциальной (или подвижной) системе отсчета точно так же, как и в инерциальной (неподвижной).
Обратите внимание
Иногда понятие «Ньютонова сила инерции» используется как обозначение силы противодействия (третий закон Ньютона). Понятие ввел Ньютон в свой труд «Математические начала натуральной философии», «Врожденная сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состояние покоя или равномерного прямолинейного движения», а сам термин «сила инерции» появился впервые, по словам ученого Эйлера, у Кеплера.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
ЭЛЕМЕНТЫ
АНАЛИТИЧЕСКОЙ МЕХАНИКИ
ЛЕКЦИЯ 11Д
ПРИНЦИП ДАЛАМБЕРА
-
Сила инерции
материальной точки. -
Принцип Даламбера
для материальной точки и механической
системы. -
Приведение сил
инерции точек твёрдого тела к простейшему
виду.
-
Сила инерции
материальной точки
Если в результате
механического воздействия некоторого
тела А на материальную точку М
массой m
эта точка
получает ускорение
,
то сила
,
выражающая действие тела А на точку М,
определяется вторым законом динамики
(11.1)
По закону равенства
действия и противодействия со стороны
материальной точки М
на тело А
действует
сила
,
равная по модулю силе
и направленная по той же прямой в
противоположную сторону
или
(11.2)
|
|
|
Сила |
-
Принцип Даламбера
для материальной точки и
механической
системы
|
Для материальной
Предположим, что
Основное уравнение
так как
|
|
Принцип Даламбера
Геометрическая |
|
|
|
Для несвободной
При изучении
Рассмотрим
где
|
|
Принцип
В любой момент
Сложим все n
где |
|
Принцип Даламбера
В любой момент |
|
Проведём из
Сложим все n
здесь
|
|
Принцип
В |
-
Приведение сил
инерции точек твёрдого тела к простейшему
виду
|
К системе сил
где |
|
|
Дальнейшая |
|
|
Количество
Продифференцируем
Пользуясь этим
остаётся |
|
|
Поступательное
Ускорения всех При этом условии:
так как |
|
|
При |
|
|
Вращение В |
|
|
|
|
|
Отсюда |
|
|
Приведём силы
Для определения
Их модули определим
Так как линии
здесь Таким образом
|
|
|
Вращение |
|
|
|
|
|
Таким |
|
|
Плоское движение
имеющего |
|
|
|
(11.14)
|
|
Таким |
Соседние файлы в папке ЛЕКЦИИ ТЕОРМЕХ
- #
- #
- #
- #
- #
- #
- #
Сила инерции
Инертность — способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных тел.
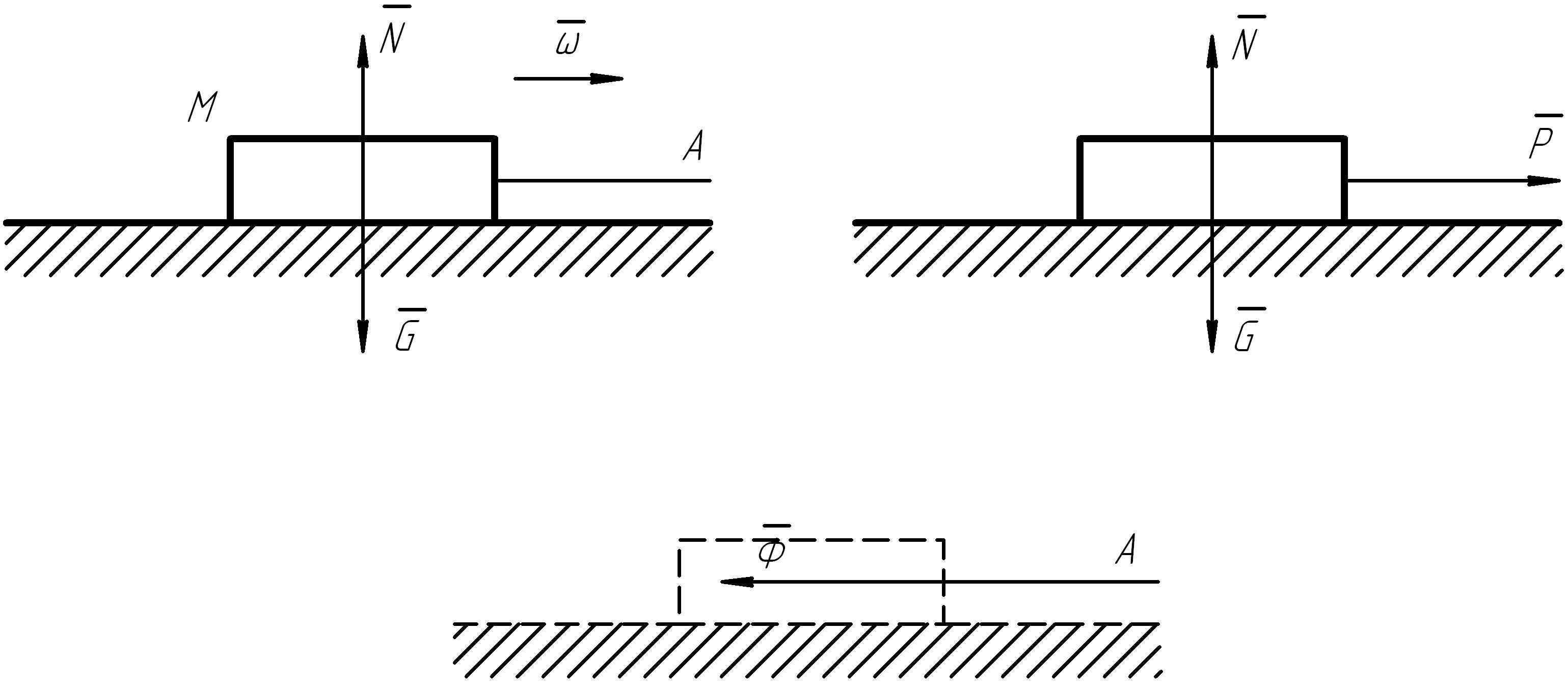
Сила инерции — сила, возникающая при разгоне или торможе -нии тела (материальной точки) и направленная в обратную сторону от ускорения. Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом.
Рассчитано, что сила инерции равна
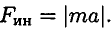
Таким образом, силы, действующие на материальные точки 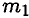
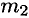
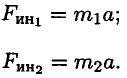
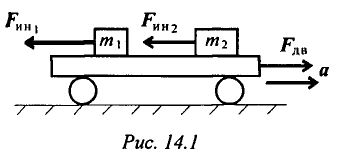
Разгоняющееся тело (платформа с массой 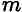
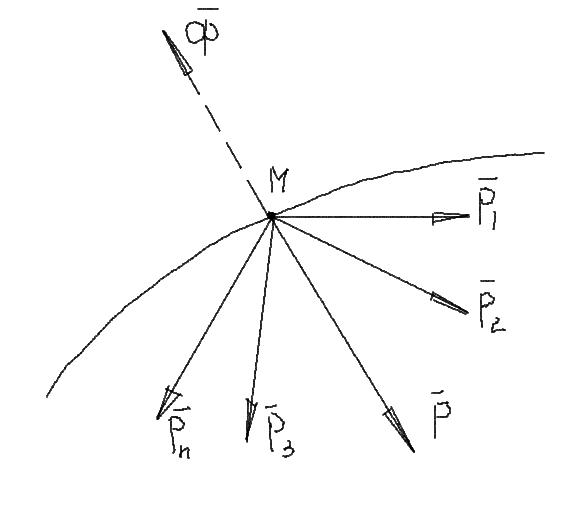
При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нормального 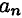
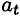
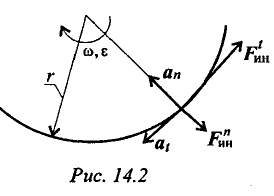
Поэтому при рассмотрении криволинейного движения могут возникнуть две составляющие силы инерции: нормальная и касательная
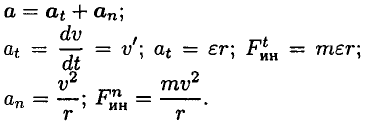
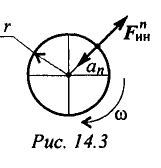
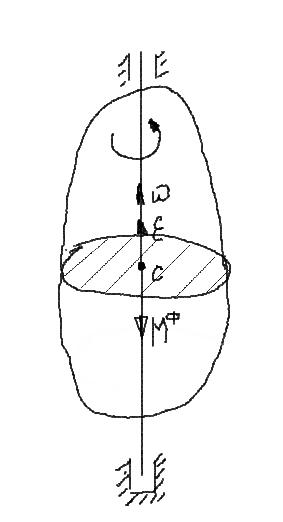
При равномерном движении по дуге всегда возникает нормальное ускорение, касательное ускорение равно нулю, поэтому действует только нормальная составляющая силы инерции, направленная по радиусу из центра дуги (рис. 14.3).
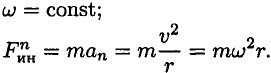
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:



![{displaystyle mmathbf {a} =mathbf {F} -m{frac {dmathbf {V} }{dt}}+m[mathbf {r} {frac {dmathbf {Omega } }{dt}}]+2m[mathbf {v} mathbf {Omega } ]+m[mathbf {Omega } [mathbf {r} mathbf {Omega } ]],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1480f8f5b9776838ae0424c9bf375578a5891703)

![{displaystyle m[mathbf {r} {frac {dmathbf {Omega } }{dt}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0c90362d7ddab73cb74d28621118eb59fcbb0a3)
![{displaystyle m[mathbf {Omega } [mathbf {r} mathbf {Omega } ]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce25d3b9ce9eba8e2e5d5c7c93d18b3defe116c7)
![{displaystyle 2m[mathbf {v} mathbf {Omega } ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4834d8a16a22210a0b2779ab3e0003b9caba7279)