Силы, действующие в кшм
Сила
Р. Действующая на поршень, может быть
разложена на составляющие: Рш,
направленную вдоль оси шатуна, и Рн
– перпендикулярно (нормально) оси
цилиндра (рис. 1). Для большей общности
в расчете используются также удельные
силы.
Удельная
нормальная сила
выражается как
рн=рtgβ,
(1)
где
β=arcsin(λsinφ)
– угол отклонения оси шатуна от оси
цилиндра. Сила Рн
оказывает влияние на трение и износ
поверхностей цилиндра и поршня.
Сопутствующим фактором при этом является
скорость движения поршня, которая
изменяет величину и направление силы.
Ранее отмечалось, что обычно силы трения
и скорость поршня при динамическом
расчете не учитывают, но они оказывают
большое влияние на характер и величину
износа. Сила Рн
считается положительной, если она
направлена влево.
Сила,
действующая вдоль оси шатуна,
имеет вид
рш= ,
,
(2)

Рисунок
1. Силы, действующие в КШМ.
За
цикл сила Рш,
изменяя величину и направление, вызывает
растяжение, сжатие и продольный изгиб
шатуна. Она положительна, если сжимает
шатун.
Силу
Рш
перенесем вдоль оси шатуна и приложим
к оси шатунной шейки. В результате
разложения получим составляющие,
действующие по оси кривошипа Рz
и перпендикулярно его оси (касательную)
Рт.
Сила,
действующая по оси кривошипа,
имеет выражение
pz=p ,
,
(3)
Сила
Pz,
изменяя величину и направление, вызывает
сжатие и растяжение щек кривошипа. Она
положительна, если сжимает щеки вала.
Удельная
тангенциальная сила
находится из соотношения
pт=p ,
,
(4)
Сила
Рт,
изменяя величину и направление, вызывает
изгиб щек, кроме того, приложенная к
шатунной шейке, она создает крутящий
момент двигателя. Сила Рт
считается положительной, если создаваемый
ею моментимеет направление, совпадающее
с направлением вращения вала.
Удельная
сила инерции вращающейся массы шатуна
определяется формулой
pc= ,
,
(5)
где
m2
– часть массы шатуна, приведенная к оси
шатунной шейки. Сила рс
действует по радиусу кривошипа, имеет
неизменное направление и значение.
Силы,
действующие на шатунную шейку.
Шатунная шейка нагружена силой рш
и центробежной силой инерции рс(рис.2).
Эти силы определяют прочность и износ
шатунных и коренных шеек, а также их
подшипников. Анализируя картину их
действия, условно принимают колено вала
неподвижным, а цилиндр вращающимся в
направлении, обратном угловой скорости
вращения коленчатого вала, но при этом
абсолютное значение скорости вращения
сохраняется. Может использоваться
графический или расчетный метод
построения диаграммы. Ниже рассмотрен
последний, поскольку он позволяет
полностью выполнить расчет с помощью
ЭВМ.

Рисунок
2. Силы, действующие на шатунную шейку
Исходя
из значений pz
и рс,
определим их схему
pzc=
pz
+ рс,
(6)
Результирующая
сила, действующая на шатунную шейку,
имеет вид
qш.ш.= ,
,
(7)
Векторная
диаграмма сил, действующих на шатунную
шейку
Векторная
диаграмма позволяет судить о величине
и направлении сил, действующих на
шатунную шейку при разных значениях
угла поворота кривошипа. Ее построение
осуществляется следующим образом. По
оси абцисс прямоугольной системы
координат откладывают значения силы
рт,
принимая за положительное направление
от ноля вправо, по оси ординат – значение
силы pzc,
принимая за положительное, – направление
к оси коренной шейки.
Откладывая
рт
и pzc,
соответствующие определенному значению
угла поворота коленчатого вала, определяют
их равнодействующую, конец которой
обозначают точкой, помеченной номером
или указанием угла поворота кривошипа,
которому она соответствует. Выполнив
такие построения для всех значений
углов расчетного цикла, проводят через
точки концов векторов кривую, которая
является векторной диаграммой сил,
действующих на шатунную шейку (рисунок
3).

Векторная
диаграмма сил, действующих на шатунную
шейку
Динамический
расчет в объеме данной курсовой работы
заканчивается анализом диаграммы
предполагаемого износа шатунной шейки,
которая, в свою очередь, строится при
помощи векторной диаграммы сил.
Соседние файлы в папке курсач docx180
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).

Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).

Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Сила, действующая на поршень или поршень Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Механика жидкости ↺ | |
| Механика жидкости | Гидравлические линейные приводы ↺ |
|
✖Площадь поршня – это значение площади поршня в поршневом насосе.ⓘ Площадь поршня [Ap] |
+10% -10% |
||
|
✖Давление — это сила, приложенная перпендикулярно поверхности объекта на единицу площади, по которой распределяется эта сила.ⓘ Давление [p] |
+10% -10% |
|
✖Сила — это любое взаимодействие, которое, если ему не противодействовать, изменит движение объекта. Другими словами, сила может заставить объект с массой изменить свою скорость.ⓘ Сила, действующая на поршень или поршень [F] |
⎘ копия |
Сила, действующая на поршень или поршень Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Площадь поршня: 0.05 Квадратный метр –> 0.05 Квадратный метр Конверсия не требуется
Давление: 800 паскаль –> 800 паскаль Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
40 Ньютон –> Конверсия не требуется
10+ Гидравлические линейные приводы Калькуляторы
Сила, действующая на поршень или поршень формула
Сила = Площадь поршня*Давление
F = Ap*p
Что такое линейный привод?
Линейный привод – это привод, который создает движение по прямой линии, в отличие от кругового движения обычного электродвигателя.
I. КИНЕМАТИКА ШПГ
Рассмотрим движение поршня внутри цилиндра. Заметим, что он совершает поступательное движение (точнее, возвратно-поступательное), поэтому кинематика поршня целиком описывается движением его любой, наперёд выбранной точки. Движение же коленвала является чисто вращательным, и его положение описывается углом поворота. При этом у шатуна имеется более сложный характер плоско-параллельного движения, что проще всего описать вращением относительно движущегося центра тяжести (ЦТ).
I.1. Движение поршня
Для начала изобразим некоторое (промежуточное) положение поршня между верхней мёртвой точкой (ВМТ) и нижней мёртвой точкой (НМТ):
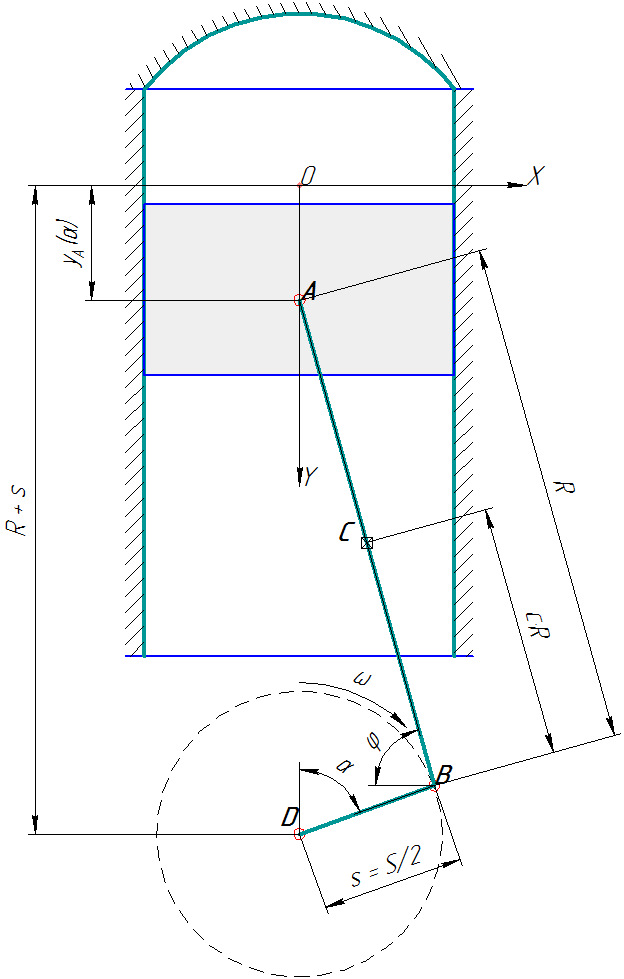
Рис. 1 — Движение поршня от ВМТ к НМТ
Введём следующие обозначения:
R — длина шатуна;
S — ход поршня (размах колевала);
s = S/2 — половина хода поршня (длина “колена”);
r = R/s = 2R/S — удвоенное отношение R/S;
α — угол поворота коленвала, отсчитываемый от вертикали (α = 0° — поршень в ВМТ, α = 180° — поршень в НМТ);
ω = α = const — угловая скорость коленвала (частота вращения);
φ — угол наклона шатуна.
Положение поршня характеризуется перемещением y, пройденным его точкой A от ВМТ (y_A = 0 — поршень в ВМТ, y_A = S — поршень в НМТ), которое меняется с изменение угла α поворота коленвала. Найдём связь между положением поршня и углом поворота коленвала.
Сначала заметим, что горизонтальные проекции шатуна и “колена” равны (см. рис. 1):
R∙cos(φ) = s∙sin(α),
откуда
cos(φ) = sin(α)∙s/R = sin(α)/r. (1)
Теперь напишем связь вертикальных проекций (см. рис. 1):
y_A(α) + R∙sin(φ) + s∙cos(α) = R + s. (2)
Осталось подставить (1) в (2) и выразить y_A через α, принимая во внимание основное тригонометрическое тождество:
y_A(α) = R − √[R² − s²∙sin²(α)] + s − s∙cos(α). (3)
Если в правой части (3) вынести s за скобки, то получится
y_A(α) = s∙{ r − √[r² − sin²(α)] + 1 − cos(α) }. (4)
Для нахождения скорости v движения поршня достаточно продифференцировать (4) по времени:
v(α) = ẏ_A(α) = s∙ω∙{ sin(α) + ½∙sin(2α)/√[r² − sin²(α)] }. (5)
В свою очередь, чтобы найти ускорение w поршня нужно продифференцировать по времени скорость (5) (рассматриваем случай постоянных оборотов двигателя, т.е. ω ≡ 0):
w(α) = v(α) = s∙ω²∙{ cos(α) + cos(2α)/√[r² − sin²(α)] + ¼∙sin²(2α)/√[r² − sin²(α)]³ }. (6)
Ещё одним важным параметром, характеризующим вибрационную нагруженность двигателя, является биение (рывок), которое обозначается a и представляет собой скорость изменения ускорения:
a(α) = ẇ(α) = s∙ω³∙{ −sin(α) − 2∙sin(2α)/√[r² − sin²(α)] + ¾∙sin(4α)/√[r² − sin²(α)]³ + ⅜∙sin³(2α)/√[r² − sin²(α)]⁵ }. (7)
Если внимательно посмотреть на выражения (4), (5), (6) и (7), то можно заметить, что:
1) перемещение y, скорость v, ускорение w и биение a поршня линейно зависят от длины s “колена”;
2) скорость v пропорциональна частоте вращения коленвала ω в первой степени;
3) ускорение w пропорционально частоте вращения коленвала ω во второй степени;
4) биение a пропорционально частоте вращения коленвала ω в третьей степени.
На следующем рисунке показаны графики удельного ускорения w/(s∙ω²) и удельного биения a/(s∙ω³) поршня (по сути это графики выражений, стоящих в фигурных скобках) для моторов с R/S = 1.763 (сплошные линии, это двигатели ВАЗ 21126/21127/21129) и R/S = 1.524 (пунктирные линии, это двигатель ВАЗ 21179):
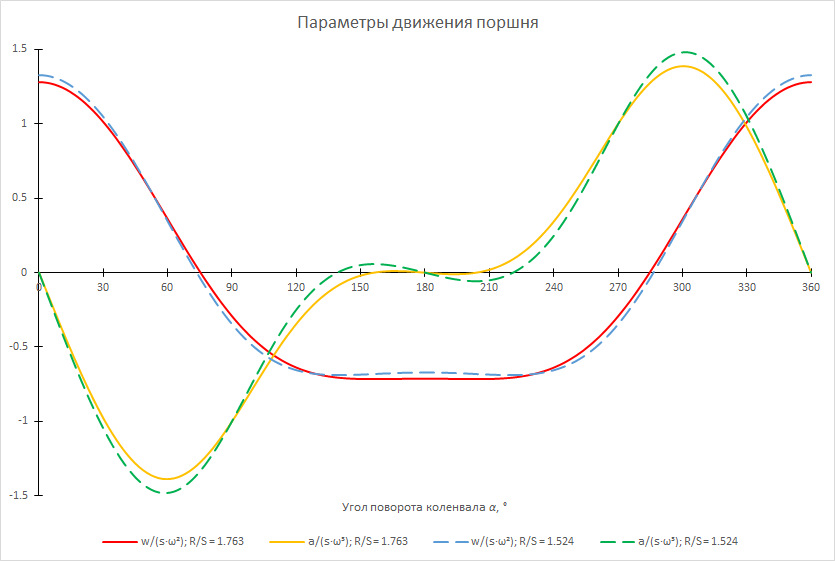
Рис. 2 — Графики удельного ускорения и удельного биения поршня для моторов с R/S = 1.763 (сплошные линии) и R/S = 1.524 (пунктирные линии)
Как видно, с падением R/S растут и ускорение, и биение поршня: разница удельных ускорений при положении поршня в ВМТ (α = 0°) составляет почти 3.5%.
Интересен тот факт, что у моторов 21126/21127/21129, обладающих более высоким R/S по сравнению с мотором 21179, при угле поворота коленвала от 150 до 210° биение практически равно нулю, а ускорение, соответственно, постоянно. При переходе от удельных величин к абсолютным ситуация с двигателем 21179 усугубляется тем, что он имеет “колено” на 11% больше, чем у двигателей 21126/21127/21129, т.е. графики, показанные на рис. 2, в абсолютных величинах будут различаться ещё больше.
I.2. Движение шатуна
I.2.1 Движение центра тяжести шатуна
В самом начале было отмечено, что кинематику шатуна удобно описывать перемещением его ЦТ C с одновременным вращением вокруг ЦТ. Положение точки C целиком определяется положением точек A и B (см. рис. 1). Положение y_A(α) точки A уже найдено выше, осталось найти положения x_B(α) и y_B(α) точки B:
x_B(α) = s∙sin(α),
y_B(α) = R + s∙[1 − cos(α)]. (8)
Координаты точки C описываются уравнениями (см. рис. 1)
x_C = c∙x_A + (1 − c)∙x_B,
y_C = c∙y_A + (1 − c)∙y_B. (9)
После подстановки (4) и (8) в (9), учитывая x_A ≡ 0, получаем
x_C(α) = (1 − c)∙s∙sin(α),
y_C(α) = c∙y_A(α) + (1 − c)∙s∙[r + 1 − cos(α)]. (10)
Компоненты скорости точки C находятся дифференцированием (10):
Vx_C(α) = ẋ_C(α) = (1 − c)∙s∙ω∙cos(α),
Vy_C(α) = ẏ_C(α) =c∙v(α) + (1 − c)∙s∙ω∙sin(α). (11)
Теперь дифференцированием (11) находим ускорение ЦТ шатуна:
Wx_C(α) = Vx_C(α) = −(1 − c)∙s∙ω²∙sin(α),
Wy_C(α) = Vy_C(α) = c∙w(α) + (1 − c)∙s∙ω²∙cos(α); (12)
|W_C| = √[Wx_C² + Wy_C²].
Если внимательно посмотреть на выражения (12), то можно заметить, что:
1) боковое ускорение ЦТ шатуна Wx_C не зависит от R/S;
2) все компоненты ускорения ЦТ шатуна линейно зависят от длины s “колена”;
3) все компоненты ускорения ЦТ шатуна пропорциональны частоте вращения коленвала ω во второй степени.
На следующем рисунке показаны графики удельного ускорения ЦТ шатуна Wx_C/(s∙ω²), Wy_C/(s∙ω²) и |W_C|/(s∙ω²) при c = 0.4 для моторов с R/S = 1.763 (сплошные линии, это двигатели ВАЗ 21126/21127/21129) и R/S = 1.524 (пунктирные линии, это двигатель ВАЗ 21179):
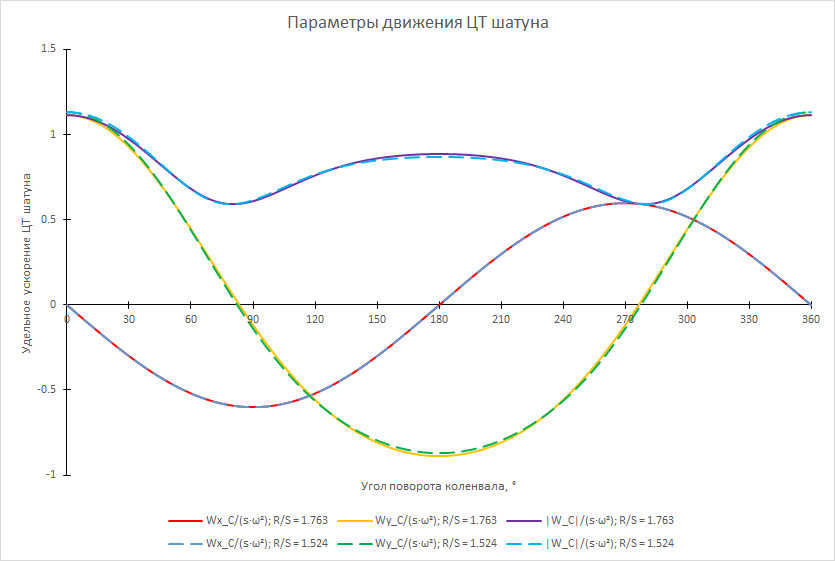
Рис. 3 — Графики удельного ускорения ЦТ шатуна для моторов с R/S = 1.763 (сплошные линии) и R/S = 1.524 (пунктирные линии)
Разница удельных вертикальных ускорений при положении поршня в ВМТ (α = 0°) составляет около 1.5%, а при положении поршня в НМТ (α = 180°) — чуть менее 2%.
Здесь необходимо отметить, что уменьшение величины c до 0.2 (т.е. смещение ЦТ шатуна ближе к коленвалу) приводит к почти полному исчезновению разницы в удельных ускорениях при различных R/S. Но всё же стоит помнить, что абсолютные величины ускорений шатуна зависят от длины “колена”.
I.2.2 Вращение шатуна вокруг центра тяжести
Для определения угловой скорости вращения шатуна необходимо найти компоненты скоростей точек A и B, перпендикулярные линии шатуна AB.
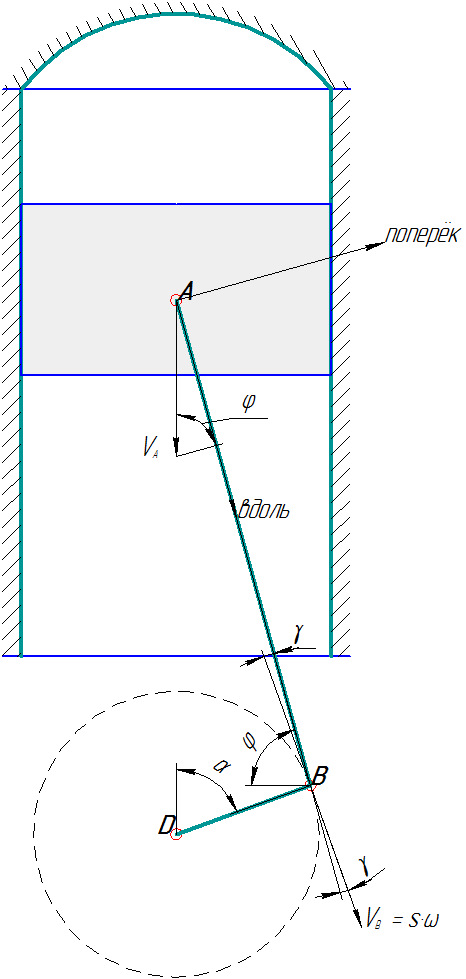
Рис. 4 — Скорости точек A и B шатуна
V_A = v(α);
|V_B| = s∙ω;
γ = φ + (90° − α) − 90° = φ − α. (13)
Угловая скорость шатуна Ω определяется через разность поперечных проекций скоростей точек A и B (см. рис. 4), отнесённую к длине шатуна:
Ω = [(−V_A)∙cos(φ) − V_B∙sin(γ)]/R,
откуда с учётом (1) и (13)
Ω(α) = −(ω/r)∙{ v(α)/(s∙ω)∙sin(α)/r + cos(α)∙√[1 − sin²(α)/r²] − sin²(α)/r }. (14)
Угловое ускорение ϵ шатуна определяется с помощью дифференцирования (14):
ϵ(α) = Ω(α)= −(ω²/r)∙{ w(α)/(s∙ω²)∙sin(α)/r + v(α)/(s∙ω)∙cos(α)/r − sin(α)∙√[1 − sin²(α)/r²] − ½∙(cos(α)/r)∙sin(2α)/√[r² − sin²(α)] − sin(2α)/r }. (15)
Если внимательно посмотреть на выражения (14) и (15), то можно заметить, что:
1) угловая скорость Ω и угловое ускорение ϵ шатуна хотя и зависят от R/S, но НЕ зависят от длины s “колена”;
2) угловая скорость шатуна Ω пропорциональна частоте вращения коленвала ω в первой степени;
3) угловое ускорение шатуна ϵ пропорциональны частоте вращения коленвала ω во второй степени.
На следующем рисунке показаны графики удельной угловой скорости Ω/ω и удельного углового ускорения шатуна ϵ/ω² для моторов с R/S = 1.763 (сплошные линии, это двигатели ВАЗ 21126/21127/21129) и R/S = 1.524 (пунктирные линии, это двигатель ВАЗ 21179):
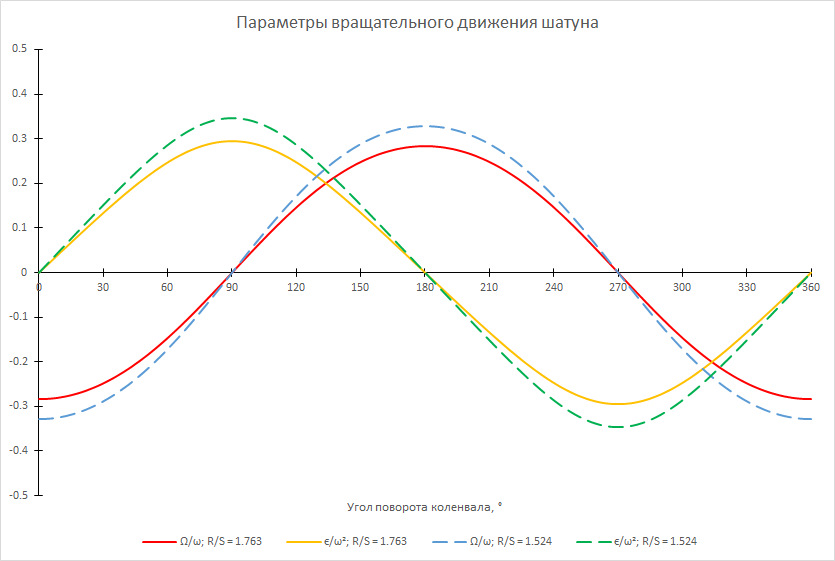
Рис. 5 — Графики удельной угловой скорости и удельного углового ускорения шатуна для моторов с R/S = 1.763 (сплошные линии) и R/S = 1.524 (пунктирные линии)
Как видно, с падением R/S растут и угловая скорость, и угловое ускорение шатуна: разница удельных угловых ускорений при α = 90° составляет почти 17.5%.
II. УСИЛИЯ В МЕХАНИЗМЕ ШПГ
II.1. Инерционные силы
Инерционные силы имеют наибольшее влияние в последовательности тактов выпуск-впуск, т.к. на данных тактах камера сгорания (КС) открыта, и воздушного подпора за счёт сжатия газа или горения смеси не создаётся.
За инерционную нагрузку на шатун и коленвал отвечает ускорение поршня. Согласно второму закону Ньютона сила инерции поршня Fп равна произведению его массы mп на ускорение w (6):
Fп = mп∙w. (16)
Поскольку ускорение зависит от частоты вращения коленвала во второй степени, сила инерции поршня растёт пропорционально квадрату оборотов двигателя. Эта сила растягивает шатун, когда поршень находится у ВМТ, и, наоборот, сжимает шатун, когда поршень находится у НМТ:
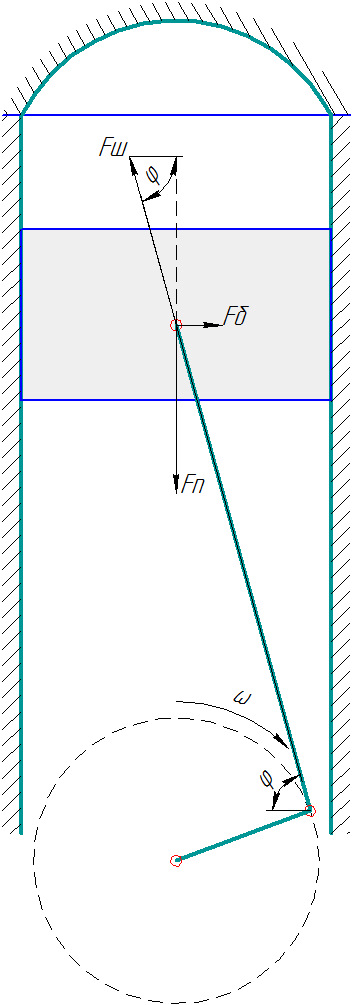
Рис. 6 — Усилия в последовательности тактов выпуск-впуск (силы трения и сопротивления воздуха пренебрегаются)
Найдём силу Fш, действующую вдоль шатуна, исходя из равенства вертикальных проекций (см. рис. 6):
Fш∙sin(φ) = Fп,
откуда с учётом (1) и (16)
Fш = Fп/sin(φ) = mп∙w∙r/√[r² − sin²(α)]. (17)
Равенство горизонтальных проекций даёт величину боковой силы Fб, действующей на стенки цилиндра, когда поршень тянется/толкается шатуном (см. рис. 6):
Fб = Fш∙cos(φ),
откуда с учётом (1) и (17)
Fб = mп∙w∙sin(α)/√[r² − sin²(α)]. (18)
Из выражений (17) и (18) видно, что силы Fш и Fб линейно зависят от массы поршня mп (точнее, суммарной массы поршня с пальцем и кольцами), поэтому снижение этой массы приводит к снижению нагрузки на шатун и стенки цилиндра.
На следующем рисунке показаны графики удельных сил Fш/(mп∙s∙ω²) и Fб/(mп∙s∙ω²) для моторов с R/S = 1.763 (сплошные линии, это двигатели ВАЗ 21126/21127/21129) и R/S = 1.524 (пунктирные линии, это двигатель ВАЗ 21179):
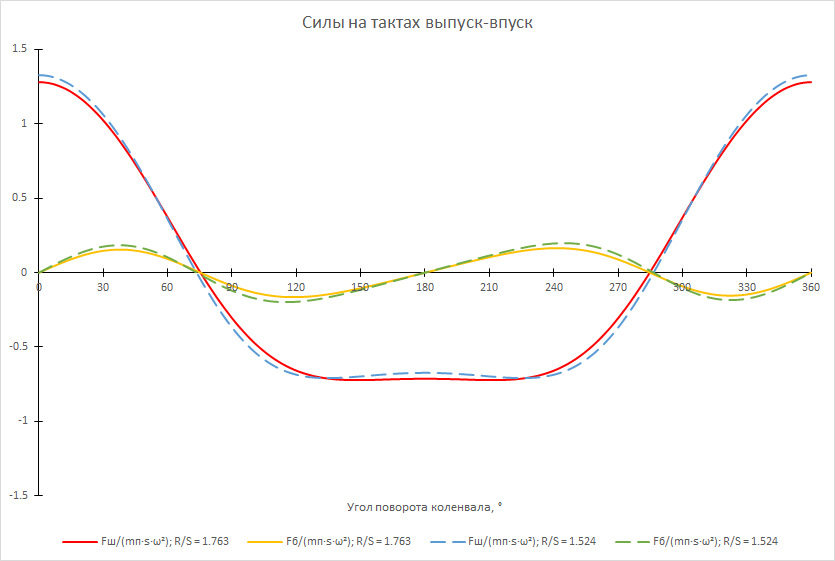
Рис. 7 — Графики удельной силы растяжения/сжатия шатуна и удельной боковой силы на стенки цилиндра для моторов с R/S = 1.763 (сплошные линии) и R/S = 1.524 (пунктирные линии)
Как и ранее, видно, что с падением R/S растут обе силы: разница удельных сил растяжения шатуна при положении поршня в ВМТ (α = 0°) составляет почти 3.5%, а максимальных удельных боковых сил — более 19%.
Также при переходе от удельных величин к абсолютным ситуация с двигателем 21179 усугубляется тем, что он имеет колено на 11% больше, чем у двигателей 21126/21127/21129, т.е. графики, показанные на рис. 4, в абсолютных величинах будут различаться ещё больше. Для сохранения ресурса мотора 21179 на уровне 21126 требуется снижение его максимальных рабочих оборотов как минимум на 5.5% (т.е. до 5100 вместо 5500 об/мин).
II.2. Крутящий момент двигателя
Здесь уже рассматриваются такты сжатия и горения.
Как отмечалось ранее, с точки зрения термодинамики процесс расширения газа на рабочем цикле является политропным:
p = p0/(V/V0)ⁿ, (19)
где
1 < n < 1.4 — показатель политропы;
p — текущее давление в цилиндре;
V — текущий объём цилиндра;
p0 — давление в цилиндре при положении поршня в ВМТ;
V0 = VΣ/ε — объём цилиндра при положении поршня в ВМТ (объём КС):
VΣ — объём цилиндра при положении поршня в НМТ;
ε — степень сжатия (СЖ).
Выразим текущий объём V цилиндра в зависимости от угла α поворота коленвала:
V(α) = V0 + y(α)∙Aц, (20)
где
Aц = ¼∙π∙D² — площадь цилиндра;
D — диаметр цилиндра.
Сила P, действующая на поверхность поршня, определяется давлением p газа и площадью поршня Aп:
P = p∙Aп,
где Aп ≈ Aц, откуда с учётом (19) и (20)
P ≈ p0∙Aц/(1 + x(α)∙Aц/V0)ⁿ. (21)
Эта сила P порождает крутящий момент T двигателя:
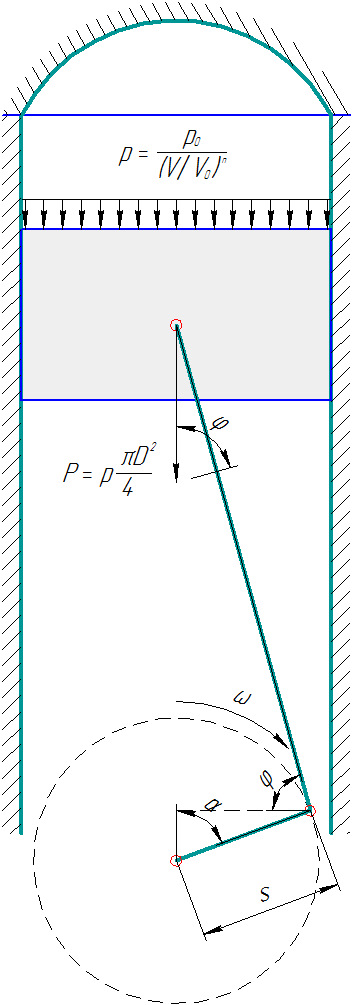
Рис. 8 — Усилия на рабочем такте двигателя
T = P∙sin(φ)∙s∙sin(φ + 90° − α) = P∙s∙sin(φ)∙{ sin(α)∙sin(φ) + cos(α)∙cos(φ) },
откуда с учётом (1) и (21)
T = p0∙Aц/(1 + x(α)∙Aц/V0)ⁿ∙s∙√[1 − sin²(α)/r²]∙{ sin(α)∙√[1 − sin²(α)/r²] + cos(α)∙sin(α)/r }. (22)
Заметим, что в данном случае, как и в предыдущем, возникает боковая сила Pб, которая является горизонтальной проекцией силы, действующей вдоль шатуна:
Pб = P∙sin(φ)∙cos(φ),
откуда с учётом (1) и (21)
Pб = p0∙Aц/(1 + x(α)∙Aц/V0)ⁿ∙sin(α)/r∙√[1 − sin²(α)/r²]. (23)
На следующем рисунке показаны графики удельного крутящего момента T/p0 и удельной боковой силы 10Pб/p0 для моторов с R/S = 1.763 (сплошные линии, это двигатели ВАЗ 21126/21127/21129), R/S = 1.524 (пунктирные линии, это двигатель ВАЗ 21179) и R/S = 1.601 (штрих-пунктирные линии, это двигатель ВАЗ 21126 с укороченным шатуном 121 мм и поршнем с увеличенной компрессионной высотой):
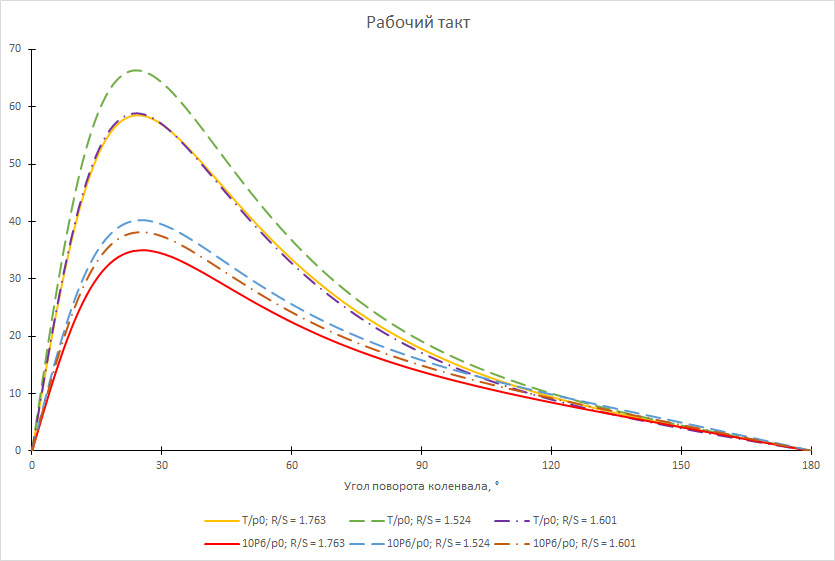
Рис. 9 — Графики удельного крутящего момента и удельной боковой силы для моторов с R/S = 1.763 (сплошные линии, 1597 см³, S = 75.6 мм, R = 133.32 мм, ε = 10.5), R/S = 1.524 (пунктирные линии, 1774 см³, S = 84.0 мм, R = 128.00 мм, ε = 10.3) и R/S = 1.601 (штрих-пунктирные линии, 1597 см³, S = 75.6 мм, R = 121.00 мм, ε = 10.5)
Здесь видно, что основной вклад в крутящий момент делает колено s: у мотора 21179 максимальный удельный крутящий момент на 13% больше, чем у мотора 21126.
При этом уменьшение R/S за счёт установки коротких шатунов без изменения коленвала приводит лишь к незначительному (около 1%) увеличению удельного крутящего момента при α от 0 до 60° и чуть большему падению удельного крутящего момента при α от 60 до 180°, причём среднее значение удельного крутящего момента даже уменьшается на 1%. Следует обратить внимание, что в такой конфигурации максимальная удельная боковая сила возрастает на 9%.
III. ВЫВОДЫ
Рассмотрим два самых распространённых случая, в которых блок цилиндров остаётся неизменным, а происходит замена шатунов или коленвала.
III.1. Увеличение объёма за счёт увеличения хода поршня
В этом случае увеличение колена s приводит к сокращению длины шатуна R (т.к. резервы по сокращению компрессионной высоты поршня обычно отсутствуют). Без изменения высоты блока цилиндров суммарная длина колена и шатуна остаётся практически неизменной:
R0 + s0 ≈ R1 + s1,
откуда
s0∙(r0 + 1) ≈ s1∙(r1 + 1).
Таким образом, увеличение колена без (существенного) изменения высоты блока приводит к падению R/S. Как было показано выше, в таком случае нагрузки на шатуны и цилиндры растут как за счёт падения R/S, так и за счёт увеличения колена s. Поэтому в данном случае для сохранения ресурса мотора требуется либо усиление шатунов и цилиндров, либо сокращение максимальных оборотов двигателя, в противном случае его ресурс резко упадёт. Плюсами данной конфигурации является очень существенное увеличение крутящего момента двигателя (как за счёт увеличения объёма, так и за счёт увеличения колена).
III.2. Снижение R/S за счёт укорочения шатуна
В этом случае колено s остаётся неизменным, а меняются шатуны и поршни. Изменение длины шатуна компенсируется изменением компрессионной высоты поршня (последняя уменьшается в случае удлинения шатуна и увеличивается в случае укорочения шатуна). В отличие от предыдущего случая, здесь нагрузки на шатуны и цилиндры растут только за счёт уменьшения R/S, что не так сильно сказывается на ресурсе двигателя. Стоит отметить что боковая сила на рабочем такте растёт. Однако укорочение шатуна потенциально может привести к снижению инерционных сил за счёт общего уменьшения массы подвижных частей ШПГ. Из плюсов можно отметить потенциально бОльшую площадь юбки поршня, что снижает пиковое давление на стенки цилиндра.
____________________________________________________
Радиус качения шины, скорость и КПП
Степень сжатия, бензин и избыточное давление
Оценка влияния R/S на работу мотора
Турбулизаторы или вихревые генераторы
Расчёт минимально возможного времени разгона
Фаза впрыска
Почему нельзя крутить мотор на заводских прошивках?
Оптимальные формы каналов ГБЦ. Часть 1
Оптимальные формы каналов ГБЦ. Часть 2
Влияние перекрытия распредвалов на ВСХ мотора
Влияние состава смеси на мощность мотора
Влияние угла опережения зажигания на мощность мотора
Расчёт ряда КПП
Содержание:
- § 1 Гидравлическая машина
- § 2 Гидравлический пресс
- § 3 Решение задач
- § 4 Важно запомнить
§ 1 Гидравлическая машина
В этом уроке мы изучим устройство и принцип действия гидравлических машин.
В жизни человеку очень часто приходится сталкиваться с такими ситуациями, где нужно поднять груз большой массы на высоту или сжать какое-либо тело. Например, автомобилисту нужно сменить проколотое колесо. Для этого нужно приподнять автомобиль. Поднять 5 кг, 10 кг взрослому человеку не так сложно. Но поднять автомобиль? Или нужно выжать масло из семян подсолнуха, спрессовать бумагу. И вот в таких случаях на помощь приходят разные механизмы, позволяющие получить большую силу, прилагая незначительные усилия.
Одним из таких механизмов является гидравлическая машина.
Гидравлическая машина (от греческого слова гидравликос – водяной) – это машина, действие которой основано на законах движения и равновесия жидкостей. Первая гидравлическая машина была создана Паскалем, который называл ее машиной для увеличения силы.
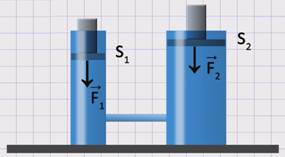
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью (водой или маслом).
Рассмотрим принцип действия гидравлической машины. Обозначим площадь поршня в малом цилиндре S1, площадь поршня в большом цилиндре – S2, F1 и F2 – силы, действующие на поршни.
Если на поршень S1 подействовать с силой F1, то давление в малом цилиндре будет определяться по формуле:
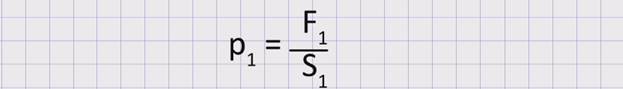
Давление в большом цилиндре:
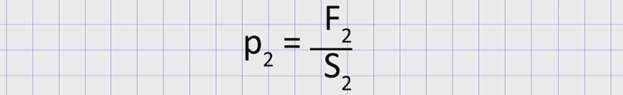
По закону Паскаля давление, производимое на жидкость или газ, передается в каждую точку по всем направлениям одинаково. Значит, давление в обоих цилиндрах будет одинаковым: p1 = p2 . Тогда можем приравнять правые части этих формул:

Читается эта формула так: сила F2, действующая на большой поршень, во столько раз больше силы F1, действующей на малый поршень, во сколько раз площадь большого поршня S2 больше площади малого поршняS1. Отношение F2 к F1показывается выигрышем в силе.
Итак, сделаем вывод. Приложив незначительное усилие F1 к малому поршню, мы можем получить во столько раз большую силу F2 на большом поршне, во сколько раз его площадь превышает площадь малого поршня.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
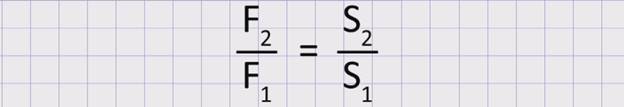
§ 2 Гидравлический пресс
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
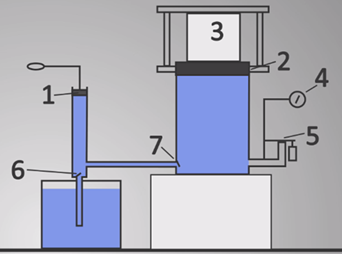
Принцип действия гидравлического пресса таков: на платформу большого поршня 2 кладется прессуемое тело 3. При помощи малого поршня 1 создается давление на жидкость, которое по закону Паскаля передается в каждую точку жидкости, заполняющей цилиндры. Так как площадь большого поршня во много раз больше площади малого, то и действующая на него сила окажется во столько же раз больше. Под действием этой силы большой поршень поднимается и сжимает тело. За значением давления, возникающего в жидкости, следят при помощи деформационного манометра 4, соединенного с предохранительным клапаном 5, который автоматически открывается при превышении допустимого значения давления. Клапаны 6 и 7 служат для перекачивания жидкости: при подъеме малого поршня 1 открывается клапан 6, и жидкость поступает в малый сосуд; при нажатии давление увеличивается, и этот клапан закрывается; открывается клапан 7, и жидкость переходит в большой сосуд.
Гидравлические прессы применяются для выжимания масла на маслобойных заводах, для прессования фанеры, картона, сена. В автомобилях используется гидравлический тормоз, в мастерских и в быту применяют гидравлический домкрат.
§ 3 Решение задач
Рассмотрим решение задачи на расчет выигрыша в силе в гидравлических машинах.

Запишем условие задачи. Нам известны масса m= 1500 кг, площадь малого поршня S1 = 10 см2 = 0, 001 м2, площадь большого поршня S2 = 0,1 м2. Найти F1.
Решение: Запишем формулу выигрыша в силе при помощи гидравлической машины:

Ответ: сила, приложенная к малому поршню,150 Н

Запишем условие задачи: F1= 200 Н, p = 400000 Па, S2 =0,04 м2. Найти показания динамометра, т.е. силу F2 = ? S1 =?

Ответ:F2 = 16 000 Н, S1 = 5 см2
§ 4 Важно запомнить
Гидравлическая машина – это машина, действие которой основано на законе Паскаля.
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
Гидравлические прессы применяются для выжимания масла, для прессования фанеры, картона, сена. В автомашинах используется гидравлический тормоз, для подъема груза предназначен гидравлический домкрат.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.
Использованные изображения:
