Загрузить PDF
Загрузить PDF
Сила — это толчок или усилие, приложенное к объекту, которое заставляет его сдвинуться с места или ускориться. Второй закон Ньютона описывает связь силы с массой и ускорением, позволяя вычислить силу. Как правило, чем больше масса объекта, тем бóльшая сила требуется для того, чтобы сдвинуть его с места.[1]
-

1
Умножьте массу на ускорение. Сила F, необходимая для того, чтобы придать объекту массой m ускорение a, определяется по следующей формуле: F = m x a. То есть сила равна массе, умноженной на ускорение.[2]
-

2
Переведите единицы измерения в систему СИ. В Международной системе единиц (СИ) основной единицей измерения массы служит килограмм, а ускорения — м/с2 (метр на секунду в квадрате). Выразив массу и ускорение в единицах СИ, мы получим значение силы в ньютонах (Н).[3]
- Например, если масса объекта составляет 3 фунта, необходимо перевести ее в килограммы. 3 фунта равны 1,36 кг, то есть масса объекта равна 1,36 кг.
-

3
Помните о том, что в физике вес и масса — это разные понятия. Если вес объекта дан в ньютонах, для нахождения массы его следует разделить на 9,8. Например, 10 Н эквивалентны 10/9,8 = 1,02 кг.[4]
Реклама
-

1
Найдите силу, необходимую для того, чтобы разогнать автомобиль массой 1000 кг до 5 м/с2.[5]
- Сначала проверим, все ли величины приведены в единицах измерения системы СИ.
- Умножив массу (1000 кг) на ускорение (5 м/с2), получим силу (5000 Н).
-

2
Вычислите силу, необходимую для того, чтобы разогнать тележку массой 8 фунтов до ускорения 7 м/с2.
- Сначала выразим все величины в единицах измерения СИ. Один фунт равен 0,453 кг, поэтому, умножив 8 фунтов на этот коэффициент, находим, что масса тележки составляет 3,62 кг.
- Умножив массу (3,62 кг) на заданное ускорение (7 м/с2), находим необходимую силу (25,34 Н).
-

3
Найдите силу, действующую на тележку весом 100 Н, которая движется с ускорением 2,5 м/с2.
- Как мы помним, вес в ньютонах следует перевести в массу в килограммах, поделив на 9,8. Разделив 100 Н на 9,8, получаем массу 10,2 кг.
- Умножив найденную массу тележки (10,2 кг) на заданное ускорение (2,5 м/с2), получаем силу (25,5 Н).
Реклама
Советы
- Всегда внимательно читайте условие задачи, чтобы определить, что дано: масса или вес.
- Проверьте единицы измерения и при необходимости выразите массу в килограммах, а ускорение — в м/с2.
- Согласно определению основной единицы измерения силы в системе СИ, Н = кг * м/с2.[6]
Реклама
Об этой статье
Эту страницу просматривали 64 479 раз.
Была ли эта статья полезной?

В этой главе…
- Прилагаем силу
- Открываем три закона Ньютона
- Используем векторы силы для законов Ньютона
В этой главе описываются знаменитые три закона Ньютона. Вероятно, вам уже приходилось встречаться с разными формулировками этих законов, например “всякому действию всегда есть равное ему противодействие”. Эта формулировка не совсем верна, поскольку “всякой силе всегда есть равная ей противоположная сила”. В этой главе будут прояснены различия между этими формулировками. Законы Ньютона в данной главе используются для фокусировки вашего внимания на силах и их влиянии на окружающий нас мир.
Содержание
- Форсируем тему
- Первый закон Ньютона
- Поддерживаем движение: инерция и масса
- Измеряем массу
- Леди и джентльмены, встречайте второй закон Ньютона!
- Выбираем единицы измерения силы
- Вычисляем результирующую силу
- Вычисляем перемещение по известному времени, массе и действующим силам
- Вычисляем результирующую силу по известному времени и скорости
- Торжественный финал: третий закон Ньютона
- Учитываем трение
- Анализируем углы и величины в третьем законе Ньютона
- Ищем состояние равновесия
Форсируем тему
В окружающем нас мире нельзя избежать встречи с силами: силы используются для открытия двери, нажатия клавиш клавиатуры, управления автомобилем, подъема по ступенькам лестницы к Статуе Свободы, вытаскивания кошелька из кармана, разговора и даже для дыхания. Силы незримо присутствует всюду: во время пешеходной прогулки, катании на коньках, пережевывании хот-дога, открывании бутылки или моргании ресниц вашей ненаглядной спутницы. Сила неразрывно связана с движением объектов, а физика помогает понять, как эта связь работает.
Сила — это на самом деле довольно забавная тема. Как и другие физические темы, она кажется сложной только до настоящего знакомства с ней. Как наши старые “друзья”, перемещение, скорость и ускорение (см. главы 3 и 4), сила является вектором, т.е. имеет величину и направление.
Сэр Исаак Ньютон первым включил силу, массу и ускорение в одно уравнение в XVII веке. (Помните исторический анекдот с падением яблока на его голову, в результате чего он якобы придумал, как математически описать силу тяготения. Подробнее об этом рассказывается в главе 6, где Ньютон также является одним из основных действующих лиц.)
Законы Ньютона и скорость света
Законы Ньютона были пересмотрены Альбертом Эйнштейном в его теории относительности. В ней было показано, что законы Ньютона не выполняются для движения со скоростью, близкой к скорости света. Основная идея теории относительности заключается в том, что скорость света является наибольшей возможной скоростью. Это значит, что любое взаимодействие может происходить только с этой или меньшей скоростью. Следовательно, при приближении к этой скорости нужно учитывать изменяющийся характер взаимодействия; Например, измерение длины ракеты, движущейся со скоростью света, будет отличаться от измерения длины неподвижной ракеты. Как будет показано в главе 21, теория относительности Эйнштейна в значительной степени изменила представленный Ньютоном взгляд на мир и его законы.
Как часто происходит со многими физическими открытиями, Ньютон сначала внимательно наблюдал за поведением объектов, мысленно моделировал его, а затем выразил в математической форме. Зная основные сведения о векторах (которые изложены в главе 4), эта математика не вызовет у вас никаких трудностей.
Ньютон описал свою модель с помощью трех утверждений, которые теперь называются законами Ньютона. Однако нужно помнить, что на самом деле это не окончательные “законы природы”, ведь физики могут создавать лишь модели природы, которые часто впоследствии пересматриваются и уточняются.
Первый закон Ньютона
Барабанную дробь, пожалуйста! Законы Ньютона описывают силы и движение, а его первый закон гласит: “Объект находится в состоянии равновесия или прямолинейном движении с постоянной скоростью, если не подвергается внешнему воздействию”. Нужен перевод? Если вы не прилагаете силу к объекту в покое или “постоянном” движении, то он останется в покое или таком же движении по прямой. Причем вечно!
Например, при игре в хоккей шайба после удара движется к воротам по прямой, скользя по льду почти без трения. В случае удачи соперник не сможет зацепить шайбу своей клюшкой, т.е. не сможет изменить “постоянное” движение шайбы по прямой (и воспрепятствовать голу).
В повседневной жизни объекты не движутся так беспрепятственно, как в случае с шайбой на льду. Большинство окружающих нас объектов испытывает силу трения. Например, при скольжении кофейной чашки по гладкому столу она постепенно замедляет свое скольжение и останавливается (иногда с проливанием кофе не стоит чересчур упражняться, ибо вы рискуете испачкаться или ошпариться горячим кофе). Это совсем не значит, что первый закон Ньютона неверен. Наоборот, именно сила трения принуждает чашку изменить свое движение и остановиться.
Выражение “если не прилагать никакого действия к постоянно движущемуся объекту, он будет двигаться вечно” выглядит так же ужасно, как идея “вечного двигателя”. Однако полностью избавиться от внешнего воздействия сил невозможно, даже если объект находится в межзвездном пространстве. Даже на объекты в самых далеких уголках космоса оказывает воздействие (пусть даже очень слабое) масса других объектов Вселенной. А это значит, что на любое движение всегда оказывается внешнее воздействие, потому вечное постоянное движение в принципе невозможно.
Первый закон Ньютона утверждает лишь то, что единственным способом изменения движения является приложение внешней силы. Иначе говоря, сила является причиной движения. Кроме того, он гласит, что движущийся объект стремится оставаться в движении, что приводит к идее инерции.
Поддерживаем движение: инерция и масса
Инерция — это естественная тенденция объекта оставаться в покое или в движении с постоянной скоростью вдоль прямой линии. Инерция вызвана массой, а масса объекта является мерой инерции. Чтобы привести объект в движение, т.е. изменить его текущее состояние движения, необходимо приложить силу для преодоления инерции.
Представьте себе причал с маленькой шлюпкой и большим танкером с нефтью. Если попробовать толкнуть их ногой, то поведение этих судов будет разным. Шлюпка заскользит по водной глади, а танкер едва “вздрогнет” (да и для этого потребуется невероятно сильный толчок!). Дело в том, что они обладают совершенно разной массой и потому разной инерцией. В ответ на одинаковую силу объект с малой массой (и малой инерцией) ускорится в большей мере, чем объект с малой массой и большей инерцией.
Инерция, т.е. тенденция массы сохранять неизменность текущего состояния движения, иногда может представлять проблему. Например, в рефрижераторе тяжелые туши мороженного мяса подвешены к потолку кузова. Если рефрижератор войдет в крутой поворот на большой скорости, то туши по инерции начнут раскачиваться, как маятники, и их трудно будет остановить. Часто неопытные водители не учитывают инерцию туш мяса, и это приводит к печальным последствиям, например к опрокидыванию машины.
Поскольку масса обладает инерцией, то она сопротивляется изменению движения. Именно поэтому нам приходится прилагать силу для ускорения своего движения. Масса связывает силу и ускорение.
Измеряем массу
В разных системах измерения физических величин для указания массы (а значит, и инерции) используются разные единицы. В системе СГС используется грамм, а в системе СИ — килограмм, который содержит 1000 грамм.
А какая единица используется в Английской системе мер на основе фута-фунта- дюйма? Наберитесь мужества: в ней используется единица “слаг”, которая эквивалентна 14,5939 килограмма.
Учтите, что масса не равна весу. Масса — это мера инерции, а вес — это сила, которую оказывает сила притяжения Земли, измеренная на ее поверхности. Например, в Английской системе мер на основе фута-фунта-дюйма слаг имеет вес около 32 фунтов.
Леди и джентльмены, встречайте второй закон Ньютона!
Первый закон Ньютона очень и очень серьезен, но не выражается в математической формулировке, которая так необходима физикам. Потому Ньютон предложил свой второй закон: “если результирующая сила ( sum!F ) действует на объект массы ( m ), то ускорение ( a ) объекта можно вычислить по формуле ( sum!F=ma )”. В “переводе” это значит: сила равна массе, умноженной на ускорение. Символ ( sum ) означает суммирование, а значит, точнее говоря, закон гласит: суммарная, или результирующая, сила равна массе, умноженной на ускорение. (С точки зрения физики процесса, а не формальной математики, ускорение является следствием действия силы, а не наоборот. Потому логичнее было бы сформулировать второй закон Ньютона так: ( a=sum!F/m ), т.е. ускорение объекта прямо пропорционально результирующей силе на него и обратно пропорционально массе.)
Согласно первому закону Ньютона, движущееся тело остается в прямолинейном движении с постоянной скоростью, если на него не действует сила. Получается, что на самом деле он является частным случаем второго закона Ньютона, когда ( sum!F=0 ). Ведь в таком случае ускорение равняется нулю, о чем говорится в первом законе Ньютона. Взгляните на хоккейную шайбу на рис. 5.1: шайба ускоряется, пока на нее действует сила.
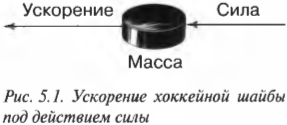
Попробуйте применить уже полученные знания физики в этом примере. Действительно, если даже на долю секунды с помощью клюшки применить силу к шайбе, то она ускорится и, несомненно, попадет в сетку! В данном примере сила применена к клюшке с определенной массой, которая ускорилась и придала это ускорение шайбе.
Чему равно это ускорение? Эта величина зависит не только от единиц измерения массы, но и от единиц измерения силы.
Выбираем единицы измерения силы
Итак, в каких единицах выражается сила? Поскольку ( sum!F=ma ), то, например, в системе СИ сила выражается следующим образом:
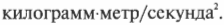
Поскольку большинство людей считают эту единицу чересчур сложной, то в системе СИ используется специальная единица — ньютон (угадайте, в честь кого?). Сокращенно “ньютон” записывается как Н. В системе СГС сила выражается следующим образом:
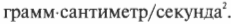
Это тоже довольно неуклюжая единица, и в системе СГС для силы предложено использовать особую единицу — дина, причем 1 ньютон равен 105 динам.
Еще проще выражается единица сила в Английской системе мер на основе фута-фунта-дюйма-секунды — фунт, который выражается следующим образом:
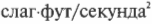
и равен 4,48 ньютонам.
Вычисляем результирующую силу
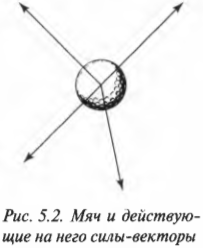
В большинстве учебников вместо полной записи ( sum!F=ma ) используется сокращенная — ( F=ma ), где под ( F ) подразумевается результирующая сила. Объект реагирует именно на результирующую силу, которая является суммой всех сил-векторов. Например, на рис. 5.2 показан мяч для игры в гольф и действующие на него силы. Как и в каком направлении будет двигаться мяч?
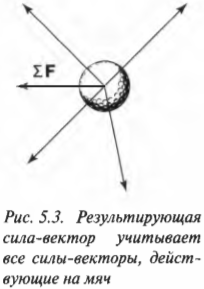
Поскольку во втором законе Ньютона говорится о результирующей силе, то задача упрощается. Все, что нужно сделать, так это сложить все силы-векторы для получения результирующей силы-вектора, как показано на рис. 5.3. Далее, для определения характера движения мяча нужно применить формулу ( sum!F=ma ).
Вычисляем перемещение по известному времени, массе и действующим силам
Допустим, что во время игры в мяч вы заинтересовались силами, действующими на мяч. Вот в одной из игровых ситуаций три игрока одновременно пытаются завладеть мячом и действуют на него тремя силами, как показано на рис. 5.4.
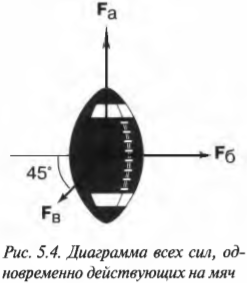
Схема на рис. 5.4 в физике называется диаграммой сил, действующих на тело. С ее помощью можно определить компоненты сил и результирующую силу.
Допустим, что с риском для жизни во имя науки вам удалось определить величины сил игроков:
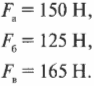
Допустим, что масса мяча точно равна 1,0 кг. Вопрос звучит так: где будет мяч через 1 секунду? Вот те этапы, которые нужно пройти, чтобы вычислить перемещение мяча по известному времени движения и ускорению (которое еще нужно определить по известной массе и действующим силам), т.е. дать окончательный ответ на этот вопрос.
- Найти результирующую силу ( sum!F) с помощью операции сложения векторов (подробное описание этой операции приводится в главе 4), складывая все силы, действующие на объект.
- Определить вектор ускорения по формуле ( sum!F=ma ).
- Вычислить пройденное расстояние за заданное время по формуле ( mathbf{s}=mathbf{v_0}(t_1-t_0)+{}^1!/!_2mathbf{a}(t_1-t_0)^2 ) (см. главу 3, где подробно описывается эта формула).
Пора подставлять числа и доставать калькулятор. Итак, для связи силы, массы и ускорения нужно, прежде всего, определить результирующую силу. Для этого нужно разложить на компоненты все векторы-силы на рис. 5.4, а потом сложить компоненты, чтобы получить компоненты вектора результирующей силы (более подробно операция разбиения вектора на компоненты приводится в главе 4).
Компоненты векторов ( mathbf{F_а} ) и ( mathbf{F_б} ) можно определить очень легко, поскольку вектор ( mathbf{F_а} ) ориентирован вдоль положительного направления оси Y, а вектор ( mathbf{F_б} ) — вдоль положительного направления оси X. Это значит, что компоненты этих векторов выражаются следующим образом:
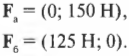
Компоненты вектора ( mathbf{F_в} ) определяются немного сложнее, поскольку нам все придется их вычислить:
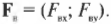
Вектор ( mathbf{F_в} ) направлен под углом 45° по отношению к отрицательному направлению оси Х, как показано на рис. 5.4, и под углом ( theta ) = 180°+45°=225° к положительному направлению оси X. Тогда компоненты вектора ( mathbf{F_в} ) определяются следующим образом:
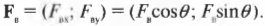
После подстановки чисел получим:
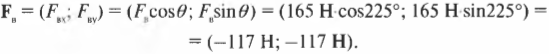
Обратите внимание на знак “минус” — оба компонента вектора ( mathbf{F_в} ) отрицательные. Полученный результат всегда можно быстро проверить на непротиворечивость. Вектор ( mathbf{F_в} ) направлен вниз и вправо, т.е. вдоль отрицательных направлений оси X и Y. Это значит, что оба компонента ( F_{вx} ) и ( F_{вy} ) должны быть отрицательными. Мне доводилось видеть людей, которые не могли правильно определить знак компонентов вектора, поскольку они не умели выполнять такую простую проверку непротиворечивости.
Всегда сравнивайте знаки компонентов векторов с фактическим направлением вдоль осей. Такая простая и быстрая проверка позволяет избежать многих потенциальных проблем.
Теперь нам известно, что:

И можно приступать к сложению векторов:
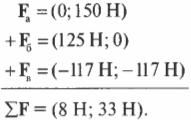
Итак, мы вычислили результирующую силу ( sum!mathbf{F} ), которая равна (8 Н; 33 Н). Мы тем самым также определили направление движения мяча. На следующем этапе нужно определить ускорение на основании второго закона Ньютона:
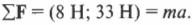
Это означает, что:
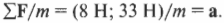
Поскольку масса мяча равна 1 кг, то, подставляя это значение в предыдущую формулу, получим:
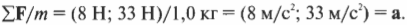
Неплохой прогресс: теперь вы знаете ускорение мяча. Теперь, чтобы узнать расстояние ( mathbf{s} ), которое преодолеет мяч за 1 секунду, нужно использовать приведенную ниже формулу (из главы 3):
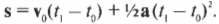
После подстановки чисел получим:
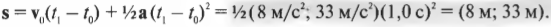
Ну что ж, совсем неплохо. После 1 секунды движения мяч продвинется на 8 метров вдоль положительного направления оси X и на 33 метра вдоль положительного направления оси Y. Достаньте секундомер, засеките промежуток времени длительностью 1 с и убедитесь, что мяч продвинулся на 8 метров вдоль горизонтальной линии и на 33 метра вдоль вертикальной линии. Вот вам еще один успешный физический эксперимент.
Вычисляем результирующую силу по известному времени и скорости
В предыдущем разделе перемещение объекта было вычислено по известному времени движения с постоянным ускорением. А как поступить, если нужно решить обратную задачу: как определить результирующую силу по известному времени и достигнутой скорости? Допустим, что нужно ускорить автомобиль от 0 до 60 миль в час за 10 секунд. Какую силу нужно приложить для этого? Сначала нужно преобразовать единицы измерения для более удобной работы со значениями скоростей, т.е. мили в час преобразовать в футы в секунды.

Обратите внимание на то, что часы и минуты в итоге сократились, а остались только мили и секунды. Теперь нужно выразить результат в футах в секунду:
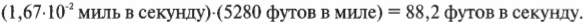
Итак, за 10 секунд автомобиль разгонится до скорости около 88 футов в секунду. Если автомобиль весит около 2000 фунтов, то какая сила потребуется для такого ускорения? Сначала найдем величину самого ускорения на основе приведенной ниже формулы (более подробно она описывается в главе 3):
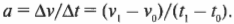
Подставляя числа, получим:
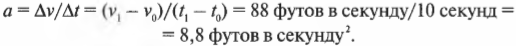
Итак, искомое ускорение равно 8,8 футов в секунду2. Согласно второму закону Ньютона:
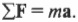
Нам известно, что вес автомобиля равен 2000 фунтам. Чему равна масса автомобиля в другой системе единиц измерения, а именно в системе на основе фута-фунта-дюйма- секунды или в слагах? В этой системе единиц измерения нужно поделить вес на ускорение свободного падения под действием гравитации, т.е. 32,17 фута в секунду2 (эта величина получена после преобразования уже известной нам величины 9,8 метра в секунду2):
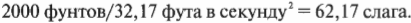
Теперь у нас есть все, что нужно для вычисления силы. Какая сила потребуется, чтобы автомобиль весом 62,17 слага двигался с ускорением 8,8 фута в секунду2. Нам нужно просто перемножить эти численные значения:
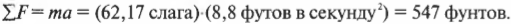
Итак, после округления до 2 значащих цифр получим, что для ускорения автомобиля до скорости 60 миль в час за 10 секунд потребуется сила 550 фунтов.
Учтите, что в данной задаче игнорируются такие особенности, как трение и наклон дороги. Более подробно эти вопросы рассматриваются в главе 6. Даже при движении по плоской поверхности без наклона трение может играть очень большую роль, и для ускорения автомобиля с учетом трения часто требуется приложить силу на 30% больше, чем 550 фунтов.
Торжественный финал: третий закон Ньютона
Этот закон движения особенно популярен среди борцов и инструкторов вождения автомобилей. Он гласит: сила действия одного объекта на другой равна по величине силе противодействия другого объекта, направленной в противоположную сторону.
Наиболее популярной формулировкой этого закона является следующая: “для любого действия всегда найдется равное ему и противоположное действие”. Однако физики предпочитают вместо неконкретного термина “действие” использовать более точный термин “сила”. Дело в том, что под действием часто подразумеваются совершенно разные явления, например характер голосования на избирательном участке или изменение температуры.
Допустим, что вы едете в автомобиле и для движения шина автомобиля должна прилагать силу к дороге (т.е. отталкиваться от нее), ибо иначе автомобиль не сможет двигаться. В таком случае дорога оказывает такую же силу на шину автомобиля, как показано на рис. 5.5.
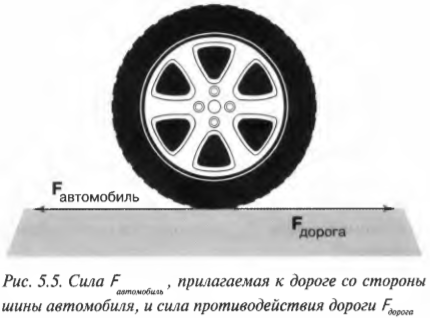
Если бы силы действия автомобиля была больше силы противодействия, то шина проскальзывала бы по дороге, как при движении по льду.
У внимательного читателя может возникнуть вопрос: а почему дорога не движется в обратную сторону? На самом деле, верьте или нет, но третий закон Ньютона действует и дорога движется в обратную сторону. Действительно, шина автомобиля прилагает силу к поверхности дороги и приводит в движение Землю. Однако, учитывая, что масса Земли в 6⋅1021 раз больше массы автомобиля, это действие практически незаметно.
Учитываем трение
Когда хоккеист бьет клюшкой по шайбе, она ускоряется с места удара и ускоряется сам хоккеист. Если бы шайба имела массу 1000 кг (а не 105-185 г), то хоккеист, несомненно, ощутил бы это ускорение в гораздо большей мере. При таком нереальном соотношении масс хоккеиста и шайбы могло случиться так, что после удара шайба едва сдвинулась бы, а хоккеист заскользил бы в обратном направлении. (Более подробно такая ситуация описывается в части III.)
Допустим, что в данном фантасмагорическом примере по окончании игры нужно оттащить такую чудовищно тяжелую шайбу в сторону с помощью каната, как показано на рис. 5.6.
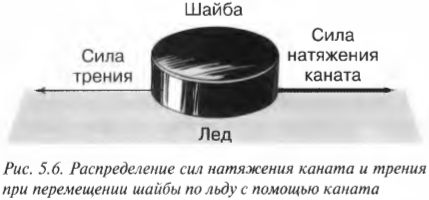
В физических задачах часто используются канаты, а также блоки, причем сила, с которой канат тянут с одного конца, равна силе сопротивления на другом конце каната.
В данном случае 1000-килограммовая шайба будет испытывать силу трения, пусть небольшую, но ощутимую. Итак, результирующая сила равна:

Поскольку сила натяжения каната ( F_{канат} ) больше силы трения ( F_{трение} ), то шайба начнет движение, причем ускоренное. Величину ускорения можно определить по известной формуле из второго закона Ньютона:
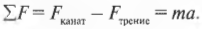
Одна часть силы натяжения каната ( F_{канат} ) расходуется на ускорение шайбы, а другая — на преодоление силы трения ( F_{трение} ):
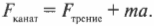
Однако сила натяжения каната с одной стороны равна силе натяжения каната с другой, согласно третьему закону Ньютона.
Рассмотрим теперь немного другую ситуацию, показанную на рис. 5.7. Допустим, что канат перекинут через блок и таким образом вам нужно поднять груз массы ( M ). Чтобы поднять груз, нужно преодолеть силу тяжести, которая действует на груз весом ( Mg ). Здесь ( g ) — это ускорение свободного падения под действием гравитации, равное 9,8 см/с2 (более подробно сила гравитации описывается в главе 6). На рис. 5.7 показана общая схема приложения силы к канату, необходимая для удержания груза.
Канат и блок используются не только для удержания груза, но и для изменения направления приложения силы. Сила прилагается вниз, а груз под ее действием движется вверх, поскольку канат перекинут через блок, где и происходит изменение направления действия силы. В данном случае, если сила натяжения каната ( F ) на свободном конце больше веса груза ( Mg ), то груз будет двигаться вверх с ускорением ( a ), согласно формуле:
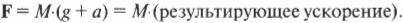
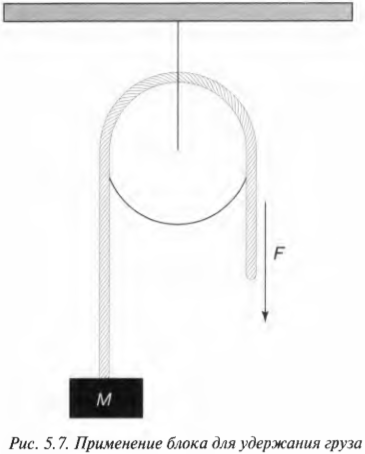
Подсчитаем теперь силу, действующую на потолок, к которому прикреплен блок. Если блок находится в покое, то действующая на него результирующая сила ( sum!F=0 ). Это значит, что все силы, которые действуют на блок, в сумме дают 0.
На блок действуют две силы, направленные вниз: сила натяжения каната ( F ) на свободном конце и сила со стороны груза с весом ( Mg ), движущегося с ускорением ( a ). Согласно третьему закону Ньютона, они равны, и сумма двух сил, направленных вниз, равна ( 2F ). Поскольку действующая на блок результирующая сила ( sum!F=0 ), то действующая на блок и направленная вверх сила со стороны потолка тоже равна ( 2F ).
Ни одна сила не может прилагаться к объекту без возникновения равной по величине и противоположной по направлению силы (даже если какая-то ее часть порождается ускоренным движением объекта). В предыдущем примере канат и блок позволяют изменять направление действия силы. Однако такое изменение направления силы от ( -F ) до ( +F ) возможно за счет приложение силы ( 2F ) к блоку со стороны потолка.
Анализируем углы и величины в третьем законе Ньютона
Чтобы учесть углы приложения силы, нужно вспомнить правила сложения векторов. Взгляните на рис. 5.8, где с помощью каната и блока сила ( F ) прилагается для удержания в состоянии покоя груза с массой ( M ). Вопрос: с какой величиной и в каком направлении действует сила ( F_{опора} ) на опору блока?
Поскольку блок не движется, то действующая на него результирующая сила ( sum!F=0 ). Теперь нужно найти все силы, которые действуют на блок. Во-первых, нужно учесть силу тяжести ( mathbf{F_{груз}}=Mmathbf{g} ), которая действует на груз. После разложения вектора этой силы на компоненты (подробнее об этом рассказывается в главе 4) получим (Y-компонента силы имеет отрицательный знак, поскольку она направлена вниз, т.е. вдоль отрицательного направления оси Y):
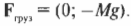
Теперь вычислим силу натяжения каната с другого конца ( F_{канат} ). Поскольку груз не движется, то сила натяжения каната на одном конце равна силе натяжения каната на другом конце. После разложения вектора силы натяжения каната на компоненты получим (Х-компонента силы имеет положительный знак, поскольку она направлена вправо, т.е. вдоль положительного направления оси X):
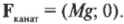
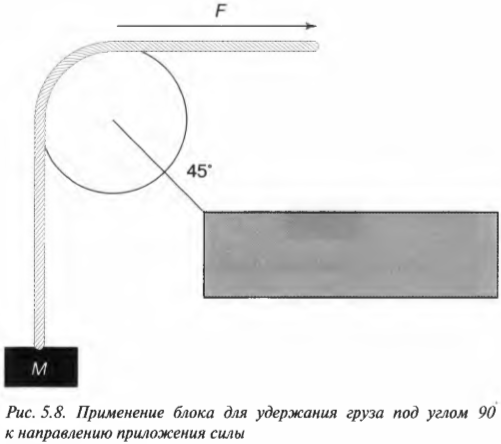
Теперь, чтобы найти результирующую силу, действующую на блок со стороны каната, нужно сложить компоненты сил ( F_{груз} ) и ( F_{канат} ):
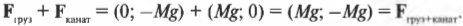
Нам известно, что:

где ( F_{опора} ) — это сила, которая действует на опору блока.
Это значит, что:
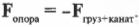
Следовательно:
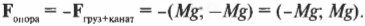
Глядя на рис. 5.8, можно легко проверить направление этого вектора. Действительно, блок должен противостоять силе тяжести груза (т.е. возникает сила противодействия, направленная вверх) и натяжению каната (т.е. возникает сила противодействия, направленная вправо).
Попробуем теперь определить величину и направление вектора силы ( F_{опора} ) (подробнее об этом рассказывается в главе 4). Величина этого вектора определяется по теореме Пифагора:
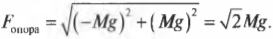
Обратите внимание на то, что здесь (как и в предыдущем примере) величина силы на опору блока больше величины каждой из сил по отдельности. Такова плата за изменение направления силы.
А в каком направлении действует сила ( F_{опора} )? Из рис. 5.8 ясно, что сила ( F_{опора} ) должна быть направлена влево и вверх, а теперь попробуем проверить это предположение с помощью тригонометрии. Если ( theta ) — это угол, под которым сила ( F_{опора} ) направлена по отношению к положительному направлению оси X, то Х-компонента силы ( F_{опора} ) имеет вид:
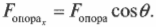
Следовательно:
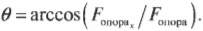
Нам уже известно, что:
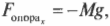
а также:
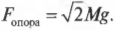
В итоге получим:
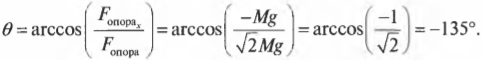
Нетрудно проверить, глядя на рис. 5.8, что найденное значение для направления силы на опору (-135) соответствует нашим предварительным оценкам и ожиданиям.
Если вы не уверены в правильности определения знаков сил, то всегда пробуйте проверить полученные значения с помощью визуального анализа нарисованной схемы распределения сил. Один рисунок порой стоит больше тысячи слов, особенно в физике!
Ищем состояние равновесия
В физике считается, что объект находится в состоянии равновесия, если его ускорение равно нулю, т.е. действующая на него результирующая сила равна 0. При этом объект необязательно должен находиться в покое — он может двигаться даже со скоростью 1000 километров в час, но без ускорения. Конечно, на объект в состоянии равновесия могут действовать самые разные силы, но их векторная сумма должна быть равна нулю.
На рис. 5.9 показана схема распределения сил, действующих на рекламную вывеску перед магазином, которую вы собираетесь подвесить на проволоке, выдерживающей силу 15 Н.
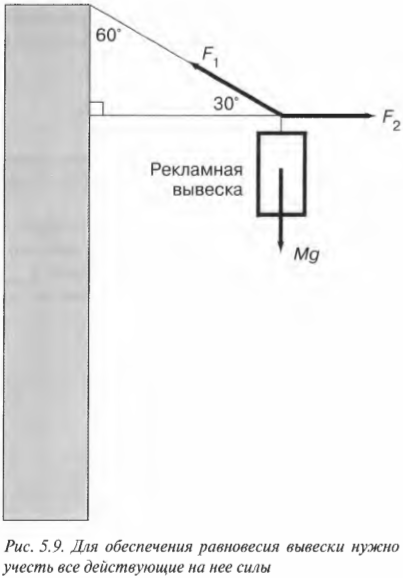
Допустим, что вес вывески равен 8 Н. Хватит ли прочности проволоки для ее подвешивания? Иначе говоря, чему равна сила натяжения проволоки ( F_1 ) на этой схеме? Вывеска должна быть в состоянии равновесия, значит, результирующая сила на нее ( sum!F=0 ). Следовательно, весь вес вывески ( Mg ) должен быть уравновешен силой натяжения проволоки ( F_1 ).
В данном примере единственная направленная вверх сила — это Y-компонента силы ( F_1 ), как показано на рис. 5.9. Сила сопротивления ( F_2 ) горизонтальной балки направлена только по горизонтали, а потому не оказывает никакого влияния на вертикальную компоненту результирующей силы. С помощью навыков тригонометрии (более подробно базовые сведения по тригонометрии приводились в главе 4) можно определить Y-компоненту силы ( F_1 ):
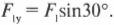
Величина этой компоненты силы равна весу вывески:
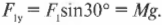
Отсюда получаем натяжение проволоки:
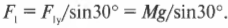
Поскольку вес ( Mg ) вывески равен 8 Н, то получим
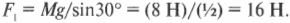
Ну и дела! Похоже, что проволока должна выдерживать силу 16 Н, а мы уже купили проволоку, выдерживающую всего 15 Н. Мораль сей задачи такова: нужно купить проволоку попрочнее!
Допустим, что мы купили более прочную проволоку и теперь интересуемся, достаточно ли прочна горизонтальная балка, чтобы выдержать силу сопротивления ( F_2 ), как показано на рис. 5.9. Какую прочность должна иметь балка, чтобы выдержать вес вывески? Иначе говоря, какую силу должна выдержать балка? На рис. 5.9 показаны только две горизонтальные силы: сила сопротивления балки ( F_2=F_{балка} ) и Х-компонента силы ( F_1 ). Нам уже известно, что ( F_1 ) = 16 Н. Теперь нам осталось только вычислить ( F_2 ). Для начала нужно определить Х-компоненту силы ( F_1 ) Глядя на рис. 5.9 и используя тригонометрию, получим:
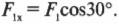
Именно эта компонента силы натяжения проволоки равна силе сопротивления балки:
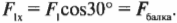
Это значит, что:
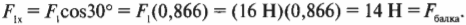
Итак, балка должна выдерживать силу около 14 Н.
Для подвешивания вывески весом около 8 Н потребуется проволока, выдерживающая силу около 16 Н, и балка, выдерживающая силу около 14 Н. Посмотрите снова на рис. 5.9: Y-компонента силы натяжения проволоки должна выдерживать вес груза. Такая прочность проволоки и балки нужна для того, чтобы изменить направление силы тяжести груза.
Глава 5. Толкаем, чтобы привести в действие: сила
2.9 (58.71%) 31 votes
Download Article
Download Article
Force is the “push” or “pull” exerted on an object to make it move or accelerate. Newton’s second law of motion describes how force is related to mass and acceleration, and this relationship is used to calculate force. In general, the greater the mass of the object, the greater the force needed to move that object.[1]
-

1
Multiply mass times acceleration. The force (F) required to move an object of mass (m) with an acceleration (a) is given by the formula F = m x a. So, force = mass multiplied by acceleration.[2]
-

2
Convert figures to their SI values. The International System of Units (SI) unit of mass is the kilogram, and the SI unit of acceleration is m/s2 (meters per second squared). So when mass and acceleration are expressed in their SI units, we get the force in its SI units which is N (Newtons).[3]
- As an example, if the mass of the object is given to be 3 pounds, you’ll need to convert those pounds to kilograms. 3 pounds make 1.36 kg, so the mass of the object is 1.36 kg.
Advertisement
-

3
Keep in mind that weight and mass mean different things in Physics. If the weight of an object is given in N (Newtons), then divide it by 9.8 to get the equivalent mass. For example, 10 N weight is equivalent to 10/9.8 = 1.02 kg.[4]
Advertisement
-

1
Find the force that is required to accelerate a 1,000 kg car at 5 m/s2.
- Check to make sure all your values are in the correct SI unit.
- Multiply your acceleration value (1000 kg) by 5 m/s2 to calculate your value.
-

2
Calculate the force required for an 8 pound wagon to accelerate at 7 m/s2.
- First, convert all your units to SI. One pound is equal to .453 kg,[5]
so you’ll need to multiply that value by your 8 pounds to determine the mass. - Multiply your new value for the mass (3.62 kg) by your acceleration value (7 m/s2).
- First, convert all your units to SI. One pound is equal to .453 kg,[5]
-

3
Find the magnitude of force acting upon a cart weighing 100 N and accelerating at the rate of 2.5 m/s2.
- Remember, 9.80 N is equal to 1.00 kg.[6]
So, convert Newtons to kg by dividing by 9.8 kg. Your new kg value should be 10.2 kg for the mass. - Multiply your new mass value (10.2 kg) times the acceleration (2.5 m/s2).
- Remember, 9.80 N is equal to 1.00 kg.[6]
Advertisement
Add New Question
-
Question
How do I change Newtons into mass?

Tiagoroth
Community Answer
The formula for force is force = mass * acceleration. To find mass, simply divide the force by the acceleration.
-
Question
Is force the same as weight?

Weight is a force. When a force is due to gravity, it can be called “weight”. “Weight” is only a human distinction for a specific case.
-
Question
What is the acceleration of a 130 kg object push by a man with 650 newtons of force?

You will need to know the formula of acceleration, once you know that. You can easily get the acceleration. So by using this formula, you can figure out what acceleration. It is simply just Algebra in this case.
Formula:
f/m=a
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
The definition of a Newton, the standard unit of force, is N = kg * m/s^2.[7]
-
Always read a question carefully to determine whether weight or mass is given.
-
Check to be sure all numbers have been converted to kilograms and m/s^2.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate force, use the formula force equals mass times acceleration, or F = m × a. Make sure that the mass measurement you’re using is in kilograms and the acceleration is in meters over seconds squared. When you’ve solved the equation, the force will be measured in Newtons. Now, simply plug the values you know into the equation and solve. If you need to find acceleration, find the difference between the start and final velocity and divide them by the time difference. If you want to learn how to convert weights to mass for your equation, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,400,146 times.
Did this article help you?
По какой формуле рассчитать силу для поднятия объекта?
Ученик
(99),
закрыт
6 лет назад
Maria ØØØ
Гуру
(3721)
6 лет назад
По формуле F = mg. Вам главное поднять этот груз, чтобы поднять его требуется сила mg Н, а то, что высота есть какая-то чаще всего не имеет значения, вот в нашем случае как раз не имеет. Почему? Да потому, что на высоте один метр ускорение свободного падения, ну, приблизительно равно 9.8, то есть можно сказать, что при поднятии тела ускорение свободного падения не изменяется, так что, чтобы поднять на высоту 1 метр нужно использовать F = mg.
Содержание:
Сила:
При изучения природных явлений используют разные физические величины. Для того чтобы описать качественно и количественно взаимодействие тел, вводят физическую величину, которую называют силой.
Определение силы
Сила – это физическая величина, которая служит мерой взаимодействия тел и является причиной изменения скоростей тел или их частей.
Наблюдение. Если мы рассматриваем, например, взаимодействие руки с волейбольным мячом, то мы говорим: «Мяч действует с силой на руку или рука действует с силой на мяч».
Опыт. Подвесим на пружину яблоко (рис. 66).

Пружина удлинится. Если на неё подвесить два яблока, то она удлинится больше. Итак, два яблока действуют на пружину с большей силой, чем одно.
Результат действия одного тела на другое зависит от значения приложенной силы.
Чем плотнее закрыта дверь, тем с большей силой мы должны её толкать или тянуть на себя, чтобы отворить.
Для того чтобы легче открывать дверь, её ручку прикрепляют как можно дальше от петель. Попробуйте открыть дверь, толкая её в точке, размещённой вблизи петель. Вы убедитесь, что это сделать намного труднее, чем с помощью ручки. Результат действия одного тела на другое зависит от точки приложения силы.
Для достижения определённого результата действия, например, растяжения или сжатия пружины, закрытия или открытия двери, нужно прикладывать силы в разных направлениях.
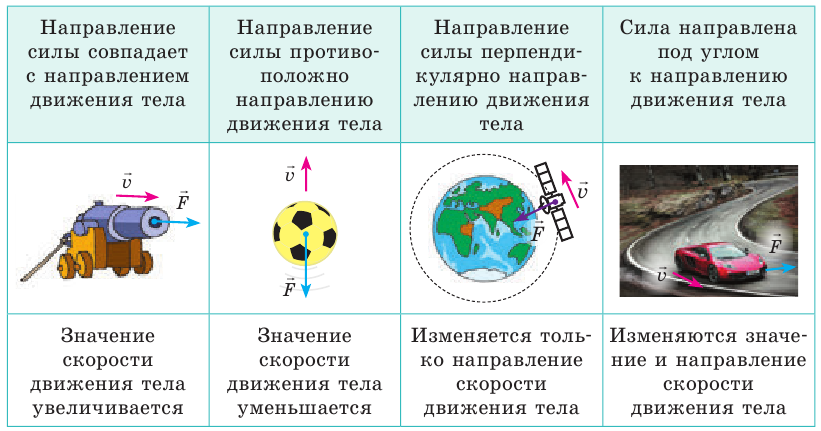
Действие одного тела на другое зависит от направления действия силы.
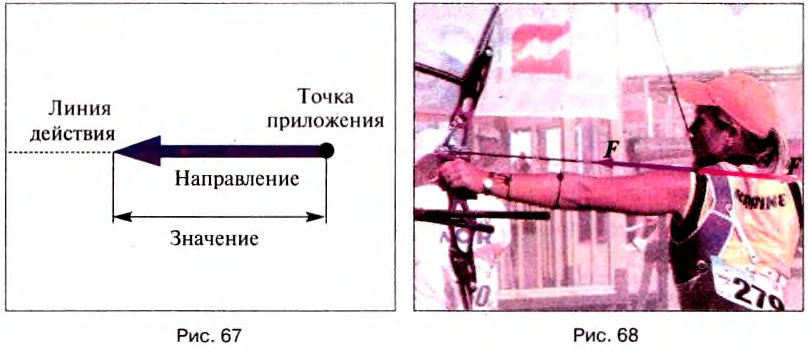
Графически силу изображают в виде отрезка прямой со стрелкой на конце (рис. 67).
Начало отрезка совмещают с точкой приложения силы. Длина отрезка в определённом масштабе равна значению силы. Стрелка показывает направление силы. Величины, характеризующиеся кроме числового значения еще и направлением в пространстве, называют векторными, или векторами (от латинского слова вектор — ведущий, несущий).
Почему тела изменяют свое состояние в пространстве
Любые изменения в природе происходят в результате взаимодействия между телами. Чтобы изменить положение вагона на рельсах, железнодорожники направляют к нему локомотив, который смещает вагон с места и приводит его в состояние движения (рис. 32). 
Парусник может длительное время стоять возле берега до тех пор, пока не подует попутный ветер и подействует на его паруса (рис. 33). Колеса игрушечного автомобиля могут вращаться с любой скоростью, но игрушка не изменит своего положения, если под игрушку не положить дощечку или линейку (рис.34). Форму или размер пружины можно изменить, лишь подвесив к ней груз или потянув рукой за один из его концов.
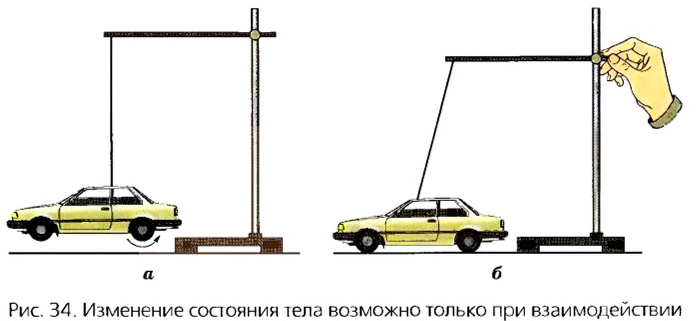
Все тела в природе так или иначе связаны между собой и действуют друг на друга или непосредственно, или через физические поля. Такое действие всегда является взаимным. Если тепловоз действует на вагон и изменяет его скорость, то скорость тепловоза при этом также изменяется благодаря обратному действию вагона. Солнце действует на все тела на Земле и на саму Землю, удерживая ее на орбите. Но и Земля притягивает Солнце и, в свою очередь, изменяет его траекторию. Таким образом, во всех случаях можно говорить только о взаимном действии тел – взаимодействии.
При взаимодействии могут изменяться скорости тел или их частей.
Однако, взаимодействуя с различными телами, данное тело будет изменять свою скорость по-разному. Так, парусник может приобрести скорость вследствие действия на него ветра. Но такой же результат можно получить, включив двигатель, который находится на паруснике. Парусник может сдвинуть с места и катер, действуя на него через трос. Чтобы каждый раз не называть все взаимодействующие тела, все эти действия объединяют одним понятием силы.
Что такое сила
Сила как физическое понятие может быть большей или меньшей, как и вызванные ею изменения в состоянии тела или его частей.
Сила – это физическое понятие, которое обобщает все взаимодействия, вследствие чего тело или его части изменяют свое состояние.
Действие тепловоза на вагон будет значительно интенсивнее, чем действие нескольких грузчиков. Под действием тепловоза вагон быстрее сдвинется с места и начнет двигаться с большей скоростью, чем тогда, когда вагон будут толкать грузчики, которые еле сдвинут его на небольшое расстояние или совсем его не сдвинут.
Сила как физическая величина количественно характеризует действие одного тела на другое.
Для того чтобы можно было производить математические расчеты, силу обозначают определенной буквой. Как правило, это латинская буква F.
Как и все другие физические величины, сила имеет единицы измерения. Современная наука пользуется единицей, которая называется ньютоном (Н). Единица получила такое название в честь английского ученого Исаака Ньютона, который внес значительную лепту в развитие физической и математической наук.
 Исаак Ньютон (1643-1727) – выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.
Исаак Ньютон (1643-1727) – выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.
Силы могут иметь различные значения. Так, на стакан с водой действует сила со стороны Земли, которая равна примерно 2 Н. А трактор, когда тянет плуг, действует на него с силой в несколько тысяч ньютонов.
Чем измеряют силу
Для измерения силы используют специальные приборы, называющиеся динамометрами (dina – сила; metro – меряю). Как правило, каждый такой прибор имеет измерительный элемент в виде пружины определенной формы (рис. 35).

Сила характеризуется направлением.
Указать числовое значение силы не всегда достаточно для определения результата ее действия. Важно знать точку ее приложения и направление действия.
Если высокий брусок, стоящий на столе, толкать в нижней части, то он будет скользить по поверхности стола. Если же к бруску приложить силу в верхней его части, то он просто перевернется (рис. 36).

Понятно, что направление падения бруска зависит от того, в каком направлении будем его толкать. Следовательно, сила имеет направление. От направления силы зависит изменение скорости тела, на которое эта сила действует.
Учитывая, что сила имеет направление и числовое значение, ее изображают в виде стрелки определенной длины и направления (вектора). Такая стрелка начинается в точке на теле, которая называется точкой приложения силы. На рисунке 37 изображена сила, значение которой равно 10 Н, направлена она слева направо и приложена в точке А.
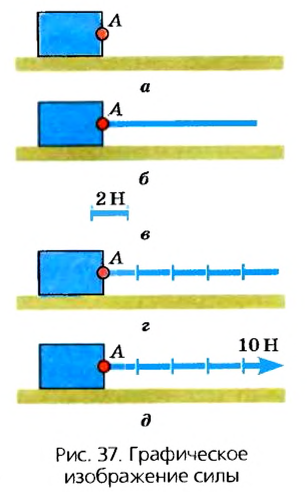
Пользуясь графическим методом, можно производить различные математические операции с силами. Так, если к одной точке на теле приложены силы 2 Н и 3 Н, которые действуют в одном направлении, то их можно заменить одной силой, которая будет приложена в той же точке и действовать в том же направлении, а ее значение будет равно сумме значений каждой из сил (рис. 38). Вектор этой силы будет иметь длину, равную сумме длин двух векторов.
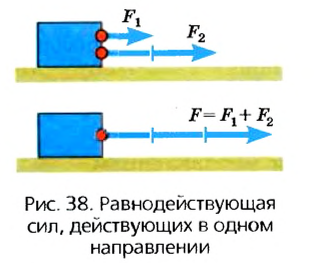
Возможен и другой случай, когда силы, приложенные в одной точке тела, действуют в противоположных направлениях. Тогда их можно заменить одной силой, направленной в направлении большей силы, а ее значение будет равняться разности значений каждой силы (рис. 39). Длина вектора этой силы будет равна разности длин векторов приложенных сил.
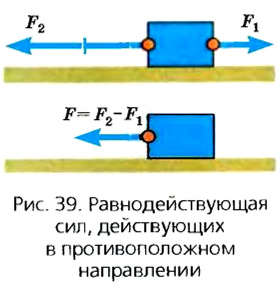
Сила, которой можно заменить действие нескольких сил, приложенных в определенной точке тела, называется равнодействующей.
Равнодействующая – это сила, действие которой равнозначно действию нескольких сил, приложенных к телу в определенной его точке.
Силу обозначают большой латинской буквой 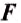 .
.
На рис. 68 спортсменка приготовилась стрелять из лука. В этом случае её рука действует на тетиву с силой направленной вправо, а тетива действует на руку с такой же по значению силой, направленной влево. Итак, значения сил одинаковы, но их направления противоположны.
- Заказать решение задач по физике
Сложение сил
Главная задача динамики – по действующей силе определить движение тела или по характеру движения тела установить, какая сила на него действует. Понятие о силе является основным в механике. И. Ньютон утверждал то, что мы называем силой, есть действие одного тела на другое, или их взаимодействие.
Действие одних тел на другие сообщает ускорение их движению. Полученное телом ускорение является внешним проявлением того, что оно взаимодействовало с другим телом. Когда мы говорим «сила», то подразумеваем, что на данное тело действуют другие тела.
Сила, являющаяся причиной изменения состояния движения тел или их деформации, характеризует взаимодействие тел, которое происходит при их непосредственном контакте (например столкновении) или через поля (рис. 2.2).
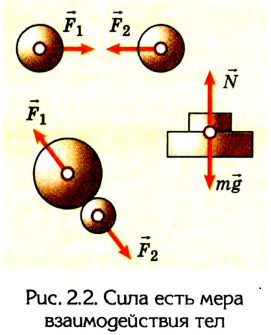
Сила – векторная величина, характеризующая действие, которое является причиной изменения состояния движения или покоя.
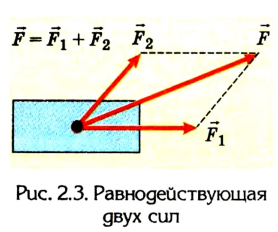
Действие на тело нескольких сил может быть заменено их равнодействующей (рис. 2.3), которую определяют геометрическим сложением этих сил как векторов:
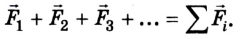
Не скорость тела, а ее изменение есть следствием действия силы (действия других тел).
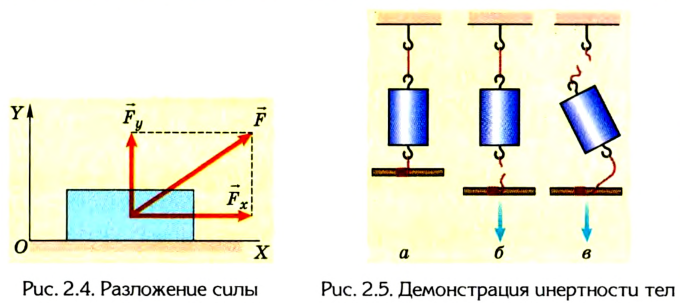
Помимо значения и направления сила характеризуется еще и точкой приложения, которую можно перемещать вдоль линии действия силы, если тело абсолютно твердое (не деформируется). Поскольку действия сил независимы, то сила может быть разложена на составляющие 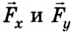 (рис. 2.4) как проекции на оси координат.
(рис. 2.4) как проекции на оси координат.
Для того чтобы выявить инертность тел и увидеть, как на нее влияет время их взаимодействия, проведем такой опыт. На тонкой нитке подвесим груз (рис. 2.5, а). Снизу к грузу прикрепим точно такую же нитку. Если резко дернуть за нижнюю нитку, то она оборвется, а груз останется висеть на верхней нитке (рис. 2.5, б). Если нижнюю нитку натягивать медленно, то оборвется верхняя нитка (рис. 2.5, в).
Когда мы резко дергаем за нижнюю нитку, взаимодействие руки и нитки кратковременно, груз не успевает изменить свою скорость – верхняя нитка не обрывается, т. к. груз имеет значительную инертность.
Если же за нижнюю нитку тянуть медленно (рука действует на груз продолжительное время), то груз набирает такую скорость, что его перемещение достаточно для разрыва и без того натянутой верхней нитки.
Как вы уже знаете, инертность тел определяется их массой, т. е. масса тела характеризует его инертность.
Во время тщательных исследований взаимодействия двух тел, например столкновения двух абсолютно упругих шаров, установлено, что отношение модулей ускорений взаимодействующих тел равно обратному отношению их масс: 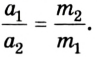
Следствием этого соотношения является один из методов измерения массы тел. Сначала выбирают тело, массу которого условно берут за единицу, – эталон массы. Между эталоном массы и телом, массу которого нужно измерить, можно поместить сжатую при помощи нитки пружину. Потом нитку поджечь и определить ускорение эталона 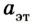 и исследуемого тела
и исследуемого тела 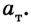 Из соотношения
Из соотношения 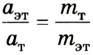 находим массу исследуемого тела:
находим массу исследуемого тела: 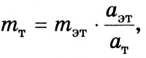
где 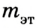 и
и 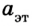 – масса и ускорение эталона (1 единица массы). Отсюда
– масса и ускорение эталона (1 единица массы). Отсюда 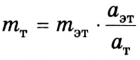 единиц массы.
единиц массы.
По международному соглашению за единицу массы принята масса эталона килограмма (рис. 2.6).

Килограмм (кг) – основная единица массы в Международной системе единиц (СИ). Килограмм равен массе международного прототипа килограмма – гире из платино-иридиевого сплава (90 % Pt, 10 % lr) в виде цилиндра диаметром и высотой 39 мм, хранящейся в Международном бюро мер и весов (г. Севр, предместье Парижа).
С достаточной точностью можно сказать, что массу 1 кг имеет 1  чистой воды
чистой воды 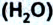 при 15 °C.
при 15 °C.
Для измерения массы тела часто используют способ сравнения масс тел с помощью весов. При этом учитывают способность тел взаимодействовать с Землей. Как подтверждают опыты, тела, имеющие одинаковую массу, одинаково притягиваются к Земле в данном месте.
Равнодействующая сила
При изучении физики в 7-м классе вы познакомились с понятием «сила», которое используется для описания взаимодействия тел.
Чтобы вспомнить основные характеристики силы, проведем опыт, например, с куском поролона, покоящимся на неподвижном столе, так как притяжение Земли уравновешено воздействием стола.
Используя пинцет, можно действовать на поролон в различных точках и видеть его поступательное, вращательное или более сложное движение в зависимости от направления, места и величины воздействия.
При этом легко наблюдать не только изменение скорости поролона, но и его деформацию (изменение формы и размеров) (рис. 34) в местах контакта поролона с пинцетом.

Рис. 34
Изменение скорости и деформация тел проявляются в любых опытах при самых разнообразных взаимодействиях, и поэтому принято следующее определение силы:
- сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
Опыт показывает, что результат воздействия силы определяется не только ее направлением и модулем, но и точкой приложения.
Единицей измерения силы в СИ является 1 ньютон (сокращенно 1 Н).
Вспомним исторически сложившиеся названия сил и их обозначения.
Силой тяжести 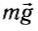 называется сила, с которой тело притягивается к Земле. Силой давления
называется сила, с которой тело притягивается к Земле. Силой давления 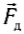 называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости
называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости 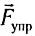 называется сила, возникающая при деформации тела. Силой реакции
называется сила, возникающая при деформации тела. Силой реакции 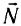 называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления
называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления 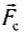 и силой трения
и силой трения 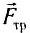 называются силы, препятствующие механическому движению тела.
называются силы, препятствующие механическому движению тела.
Силы могут действовать на поверхность тела (например, сила давления воздуха) (рис. 35) или быть приложены в некоторой условной точке (например, сила упругости нити в точке ее крепления к телу) (рис. 36).
Для упрощения математического описания механического движения тело рассматривается как материальная точка, если не указаны его размеры и форма. На рисунке тело чаще всего изображают прямоугольником.
Можно изображать силы, действующие на тело, приложенными в центре прямоугольника. Но обычно в центре прямоугольника изображают приложенной силу тяжести, а силу трения и силу реакции опоры рисуют приложенными в точке на нижней грани тела под его центром (рис. 37). Если на тело действуют другие тела, то необходимо учесть одновременно действие нескольких сил.
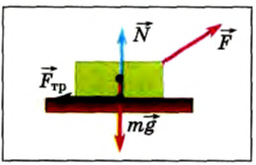
Рис. 37
При изучении физики в 7-м классе вы познакомились со сложением сил и научились складывать силы, действующие на тело вдоль одной прямой.
В этом случае действие, например, двух сил можно заменить одной силой. Модуль равнодействующей силы равен сумме или разности модулей двух слагаемых сил в зависимости от того, совпадают их направления (рис. 38, а, б) или противоположны (рис. 39. а, б). Направление равнодействующей двух сил совпадает с направлением большей силы.
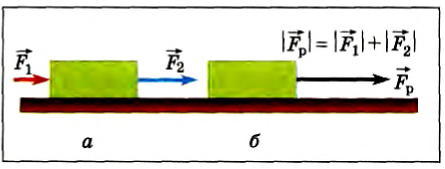
Рис. 38
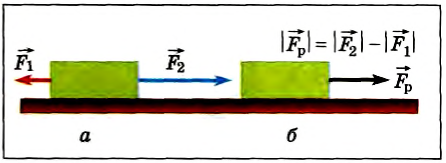
Рис. 39
А как складываются силы, если они направлены под некоторым углом друг к другу? Покажем на опыте, что они складываются также векторно. Подвесим груз массой 0,2 кг на динамометре, закрепленном на неподвижном штативе. Если груз покоится, то сила упругости пружины динамометра уравновешивает силу тяжести груза (рис. 40), а показания прибора равны: Fупр = mg = 2H ( )
)
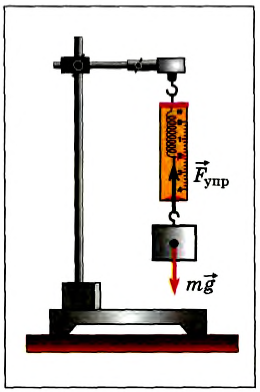
Рис. 40
Теперь подвесим этот же груз с помощью двух одинаковых динамометров (рис. 41, а), закрепленных на одной высоте. Меняя положения динамометров, а следовательно, угол между силами 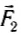 и
и 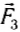 , действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.
, действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.
Следовательно, совместное действие сил 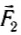 и
и 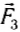 уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.
уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.
Когда угол между силами 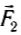 и
и 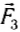 равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму
равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму 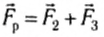 по правилу сложения векторов, то она по модулю равна Fp= 2 Н.
по правилу сложения векторов, то она по модулю равна Fp= 2 Н.
Следовательно, силы нужно складывать по правилам сложения векторов.
Модуль векторной суммы сил 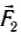 и
и 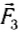 равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).
равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).
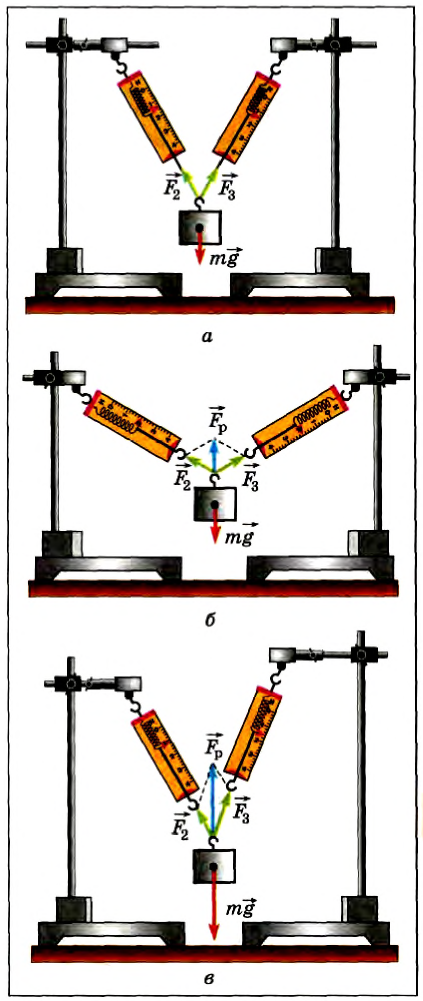
Рис. 41
Какие бы более сложные опыты не проводились (и при действии на тело нескольких сил), всегда результаты измерений показывают, что действие нескольких сил можно заменить их векторной суммой, т. е. силы складываются, как векторы, — геометрически.
Векторная сумма сил, действующих на тело, называется равнодействующей и определяется по формуле:
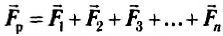
Если размерами тела нельзя пренебречь и силы приложены в разных его точках, то векторы сил можно перенести в одну точку, сохраняя модуль и направление, и векторно сложить (рис. 42).
Необходимо понимать, что равнодействующая сила заменяет действие нескольких сил только по отношению к движению тела в целом, но не заменяет действие каждой слагаемой силы в других отношениях.
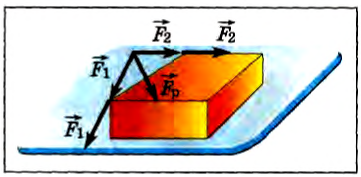
Рис. 42
Например, растянутая двумя руками пружина покоится (рис. 43), а значит, равнодействующая сил 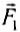 и
и 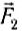 равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.
равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.
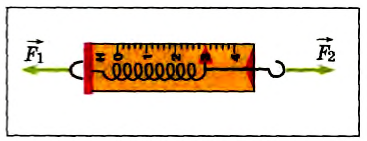
Рис. 43
Если тело движется с постоянной скоростью, то согласно первому закону Ньютона все воздействия на тело скомпенсированы, т. е. равнодействующая всех сил также должна быть равна нулю.
Главные выводы:
- Сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
- Сила характеризуется модулем, направлением, а также точкой приложения.
- Заменить действие нескольких сил можно равнодействующей силой, которая определяется как векторная сумма этих сил.
- При движении тела с постоянной скоростью (или в состоянии покоя) равнодействующая всех сил, действующих на него, равна нулю.
Что означает понятие “Сила” в физике
Вам хорошо известно слово «сила». Обычно смысл слова «сила» и образованных от него слов «силач», «сильный» и т. д. связан с возможностями человека, животного, механизма, с интенсивностью проявления природных явлений. Мы говорим «самый сильный человек», «сила воли», «сильные чувства», «сильный мороз», «сильный двигатель». А какое содержание вкладывают в слово «сила» физики?
Мы уже говорили о том, что причина изменения скорости движения тела — его взаимодействие с другими телами.
Чтобы теннисный мяч вернулся на сторону соперника, вы бьете по мячу ракеткой, но и мяч «бьет» по ракетке. Чтобы остановить велосипед, вы нажимаете на ручки тормоза и в то же время ощущаете, как они давят на ваши ладони. Обратите внимание: в любом случае результат зависит от того, насколько «сильным» будет взаимодействие: сильнее ударите по мячу — мяч наберет большую скорость (рис. 18.1); сильнее нажмете на тормоз — быстрее остановится велосипед. Мерой действия одного тела на другое служит физическая величина сила.
Сила — это физическая величина, которая является мерой действия одного тела на другое (мерой взаимодействия тел).
Силу обычно обозначают символом F. Единица силы в СИ — ньютон (названа в честь Исаака Ньютона): [F]=Н. 1 Н — это сила, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 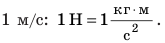 Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).
Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).


Графическое изображение сил
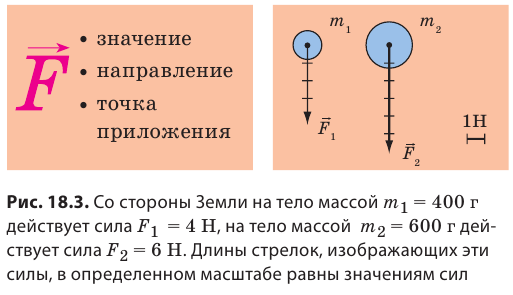
Сила, действуя на тело, может изменить скорость его движения как по значению, так и по направлению, поэтому сила определяется и значением, и направлением. Уже говорилось о том, что физические величины, имеющие значение и направление, называют векторными. Итак, сила — векторная величина. На рисунках вектор силы начинают в точке, к которой приложена сила (эту точку так и называют — точка приложения силы), и направляют в сторону действия силы. Длину стрелки иногда выбирают так, чтобы она в определенном масштабе соответствовала значению силы (рис. 18.3). Изменение скорости движения тела (по значению, по направлению) зависит от направления силы (см. таблицу на с. 123).
Сложение сил, действующие вдоль одной прямой
Обычно на тело действует не одна сила, а две, три или больше. Проведем опыт. Поставим на стол тележку и привяжем к ней две нити. Потянем за одну нить с силой 5 Н, а за другую — в том же направлении — с силой 3 Н (рис. 18.4). Тележка придет в движение, увеличивая свою скорость так, как если бы на нее действовала одна сила 8 Н. Силу 8 Н, которой в данном случае можно заменить две силы 5 и 3 Н, называют равнодействующей двух сил и обозначают символом R (или F). Силу, которая производит на тело такое же действие, как несколько одновременно действующих сил, называют равнодействующей этих сил. Если тележку одновременно тянуть за две нити в противоположные стороны (рис. 18.5), то силы не будут «помогать» друг другу разгонять тележку, а наоборот — будут «мешать». В этом случае тележка будет двигаться так, будто на нее действует одна сила 2 Н в направлении, в котором действует сила 5 Н, то есть равнодействующей сил 5 и 3 Н будет сила 2 Н.
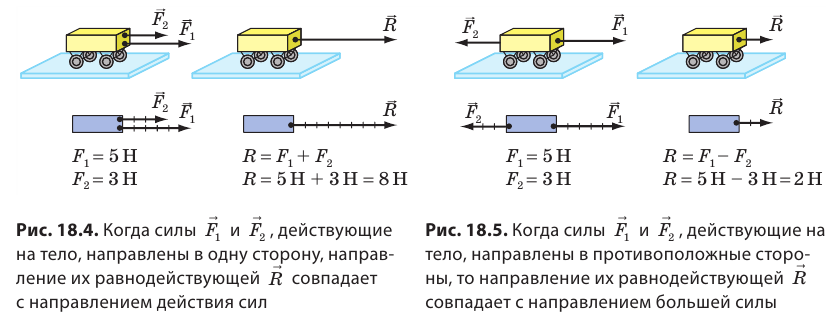
Как вы считаете, какой будет равнодействующая, если нити, привязанные к тележке с противоположных сторон, потянуть с силами, одинаковыми по значению, например 5 Н? Изменится ли в этом случае скорость движения тележки? 4 Выясняем, когда силы компенсируют друг друга Надеемся, вы правильно ответили на вопрос в п. 3 и самостоятельно пришли к выводу: если две силы равны по значению, противоположны по направлению и приложены к одному телу, то равнодействующая этих сил равна нулю. Силы уравновешивают (компенсируют) друг друга, поэтому причины для изменения скорости движения тела нет. Так, по горизонтальному прямолинейному отрезку шоссе автомобиль движется равномерно (рис. 18.6, а), если сила тяги его двигателя компенсирует силу сопротивления движению (сила сопротивления движению достаточно быстро остановит автомобиль, если двигатель не будет работать). Портфель в руке находится в состоянии покоя, если сила притяжения Земли, действующая на портфель, компенсируется силой, которую прикладывает к портфелю человек (рис. 18.6, б).
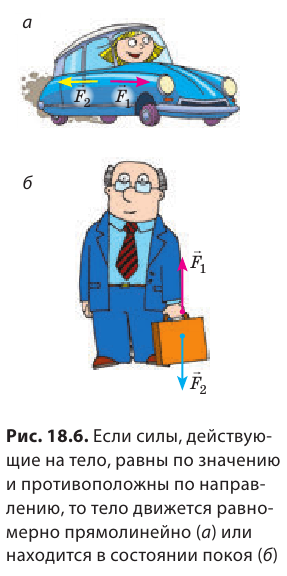
Итоги:
Сила F — физическая величина, являющаяся мерой действия одного тела на другое (мерой взаимодействия тел). Сила — причина изменения скорости движения тела. Единица силы в СИ — ньютон (Н). 1 Н равен силе, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 1 м/с.
Сила — векторная величина. Чтобы охарактеризовать силу, необходимо указать значение, направление и точку приложения силы. Если на тело действуют несколько сил, то их общее действие всегда можно заменить действием одной силы — равнодействующей. Равнодействующей сил, которые действуют на тело в одном направлении, является сила, значение которой равно сумме значений сил, а направление совпадает с направлением этих сил. Если две силы, действующие на тело, направлены в противоположные стороны, то направление равнодействующей совпадает с направлением большей силы, а для нахождения значения равнодействующей нужно из значения большей силы вычесть значение меньшей. Две силы компенсируют (уравновешивают) друг друга, если они равны по значению, противоположны по направлению и приложены к одному телу.
- Силы в механике
- Сила тяжести в физике
- Сила упругости в физике и закон Гука
- Деформация в физике
- Звук в физике и его характеристики
- Звуковые и ультразвуковые колебания
- Инерция в физике
- Масса тела в физике
