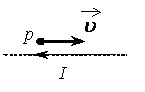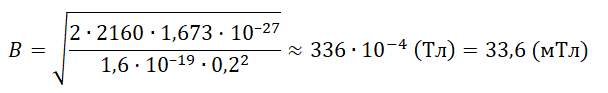Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
[ е = – 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
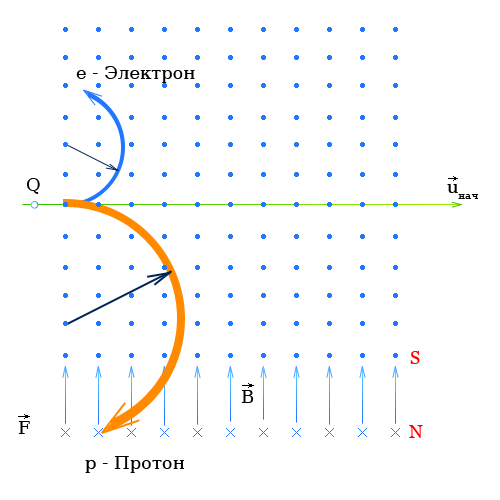
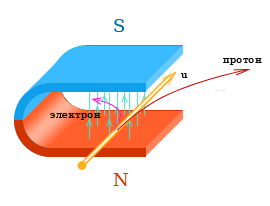
Сила Лоренца действующая на электрон и протон
Величина и направление силы Лоренца определяются соотношением
[ vector{F_{L}}= e vector{v} × vector{B} ]
где $vector{v}$, $vector{B}$ и $vector{F}$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
[ F_{L} = e v B ]
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины.
Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
Если
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10-31 кг — масса электрона, | кг |
| e | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
[ evB = frac{m_{e} v^{2}}{r} ]
и, следовательно,
[ r = frac{m_{e} v}{eB} ]
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
[ p = + 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Сила Лоренца действующая на протон
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
Если
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10-27 кг — масса протона, | кг |
| p | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
[ r = frac{m_{p} v}{p B} ]
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Сила Лоренца |
стр. 667 |
|---|
Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
FЛ=FN
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля →B можно считать неизменным в пределах этого отрезка проводника.
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I=qnvS
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F=|I|ΔlBsinα
Подставляя сюда выражение, полученное для силы тока, получим:
F=|qnvS|ΔlBsinα=|q|nvSΔlBsinα
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
N=nSΔlB
Тогда:
F=|q|vNBsinα
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
FЛ=FN=|q|vNBsinαN=|q|vBsinα
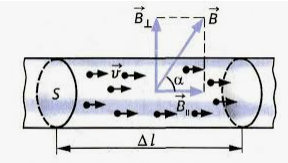
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.
FЛ=|q|vBsinα=0,005·200·0,3·√22≈0,2 (Н)
Направление силы Лоренца
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:
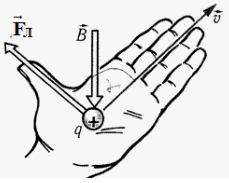
Если левую руку расположить так, чтобы составляющая магнитной индукции →B, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
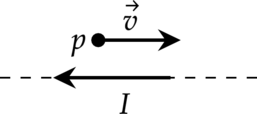
Пример №2. Протон p имеет скорость →v, направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.
Работа силы Лоренца
Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90о. Работа любой силы определяется формулой:
A=Fscosα
Но так как косинус 90о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.
Полная сила, действующая на заряд
При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила →Fэл, действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:
→Fэл=q→E
Следовательно, полная сила, действующая на заряд, равна:
→F=→Fэл+→Fл=q→E+|q|→v→Bsinα
Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна →E. Какова индукция →B магнитного поля?
Прямолинейное движение протона возможно в двух случаях:
- Вектор →E направлен вдоль траектории движения протона. Тогда вектор →B также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
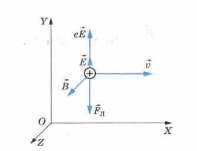
- Векторы →E, →B и →v взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).
Заряд протона равен модулю заряда электрона — e. Сложим силы, действующие на протон по оси ОУ:
e→E+→FЛ=0
В скалярной форме:
eE−evB=0
Следовательно:
B=Ev
Задание EF17621
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Лоренца.
3.Выразить модуль вектора магнитной индукции.
4.Определить недостающие величины.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Напряжение на обкладках конденсатора: U = 2160 В.
• Радиус окружности, по которой движется протон в однородном магнитном поле: R = 20 см.
• Масса протона: m = 1,673·10–27 кг.
• Заряд протона: q = 1,6·10–19 Кл.
20 см = 0,2 м
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:
FЛ=qvB
Сила Лоренца сообщает протону центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
qvB=mv2R
Отсюда модуль вектора магнитной индукции равен:
B=mv2qvR=mvqR
Энергия заряда, движущегося в электрическом поле, определяется формулой:
W=qU
Но энергию заряда также можно выразить как кинетическую энергию движения:
W=Eк=mv22
Приравняем правые части выражений и получим:
qU=mv22
Отсюда ускорение протона равно:
v=√2qUm
Конечная формула для определения модуля вектора магнитной индукции:
B=mvqR=mqR√2qUm=√2UmqR2
Ответ: 33,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17600
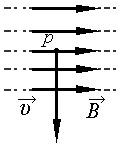
а) влево
б) вправо
в) к нам
г) от нас
Алгоритм решения
- Определить, каким способом можно найти направлений силы Лоренца, действующей на протон.
- Применить правила и найти направление силы Лоренца.
Решение
Силу Лоренца, действующую на заряженную частицу, можно найти с помощью правила левой руки. Для этого мысленно расположим четыре пальца левой руки в сторону, совпадающей с направлением движения положительной частицы (протона). Относительно рисунка пальца будут направлены вниз. Теперь развернем ладонь так, чтобы в нее входили линии магнитной индукции. Теперь отклоним на 90 градусов большой палец. Он будет направлен от плоскости рисунка к нам. Это и есть направление силы Лоренца, действующей на протон.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17749
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, частота обращения и энергия α-частицы по сравнению с протоном должны:
- увеличиться
- уменьшиться
- не измениться
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Записать формулу для определения силы Лоренца.
2.Установить, от чего зависят перечисленные в таблице физические величины.
3.Определить характер их изменения при изменении заряда.
Решение
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
Если вместо протона взять альфа-частицу, то заряд увеличится вдвое, так как альфа-частица содержит 2 протона. Сила Лоренца прямо пропорционально зависит от величины заряда. Следовательно, она тоже увеличится вдвое. Скорость движения заряда по условию задачи остается постоянной, как и модуль вектора магнитной индукции.
Сила Лоренца будет сообщать альфа-частице центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
|q|vBsinα=mv2R
Отсюда:
|q|Bsinα=mvR
R=mv|q|Bsinα
Заряд альфа-частицы больше заряда протона вдвое. Она также содержит 2 нейтрона, поэтому ее масса примерно в 4 раза больше массы протона. Следовательно, радиус движения альфа-частицы увеличится примерно вдвое.
Частота обращения альфа-частицы связана с ее линейной скоростью формулой:
v=2πRν
Так как скорость остается постоянной, то при увеличении радиуса частота обращения должна уменьшиться.
Энергия альфа-частицы будет больше, чем у протона, вращающегося с той же скоростью. Это связано с тем, что ее кинетическая энергия будет примерно в 4 раза больше (так как во столько раз больше ее масса).
Ответ: 121
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.8k
Сила лоренца протон по окружности
Протон в однородном магнитном поле между полюсами магнита под действием силы Лоренца движется по окружности радиусом R. В этом же поле движется -частица. Как изменятся по сравнению с протоном модуль силы Лоренца и период обращения -частицы, если она будет двигаться по окружности такого же радиуса, что и протон?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Модуль силы Лоренца | Период обращения -частицы |
На заряженную частицу в магнитном поле действует сила Лоренца, которая сообщает ей центростремительное ускорение:
Поскольку массы и заряды протона и -частицы связаны соотношениями
заключаем, что при таком же радиусе окружности, скорость -частицы должна быть в 2 раза меньше скорости протона. Следовательно,модуль силы Лоренца не изменится.
Период обращения при этом увеличится в два раза.
Сила лоренца протон по окружности
Задание 17. Протон движется по окружности в однородном магнитном поле между полюсами магнита под действием силы Лоренца. Как изменятся по сравнению с протоном модуль силы Лоренца и период обращения α-частицы, если она будет двигаться в этом же поле по окружности с той же скоростью?
Для каждой величины определите соответствующий характер изменения:
На α-частицу со стороны магнитного поля действует сила Лоренца 


В соответствии со вторым законом Ньютона, силу Лоренца также можно записать как 


Теперь вычислим изменение радиуса окружности для альфа-частицы, движущейся с той же скоростью. Альфа-частица имеет в своем составе два протона и два нейтрона, то есть ее масса в 4 раза больше массы протона, а заряд в 2 раза больше заряда протона. В итоге получаем:

то есть радиус окружности увеличится в 2 раза. Так как период обращения T – это время одного полного оборота, а радиус увеличился в 2 раза при сохранении той же скорости, то период 
Модуль силы Лоренца возрастает, так как заряд α-частицы выше заряда протона.
Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Величина и направление силы Лоренца определяются соотношением
где $vector$, $vector$ и $vector$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10 -31 кг — масса электрона, | кг |
| e | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
При больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя электронов me, а необходимо учитывать релятивистское увеличение массы.
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10 -27 кг — масса протона, | кг |
| p | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Аналогично при больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя протонов mp, а необходимо учитывать релятивистское увеличение массы.
[spoiler title=”источники:”]
http://self-edu.ru/ege2019_phis_30.php?id=7_17
http://www.fxyz.ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5/%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%BE/%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D0%BE%D0%BB%D0%B5/%D1%81%D0%B8%D0%BB%D1%8B_%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D1%83%D1%8E%D1%89%D0%B8%D0%B5_%D0%B2_%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%BC_%D0%BF%D0%BE%D0%BB%D0%B5/%D1%81%D0%B8%D0%BB%D0%B0_%D0%BB%D0%BE%D1%80%D0%B5%D0%BD%D1%86%D0%B0/
[/spoiler]
У нас давно не было, что называется, “практического” параграфа, в котором бы рассматривалась какая-нибудь задача на применение ранее изученного материала. Сейчас мы это исправим.
Пусть есть протон, движущийся в однородном магнитном поле со скоростью, равной 1/10 скорости света. Величина магнитной индукции равна 2 теслам.
Сперва нужно найти как величину, так и направление силы Лоренца, которая будет действовать на эту заряженную частицу.
Как мы помним, для магнитного поля прежде всего важны заряд частицы и ее скорость. Что занимательно, потому что пока не очень понятно, чем таким особенным отличаются движущиеся частицы от неподвижных. Первых магнитное поле распознает, а вот вторых – нет. Ну ладно, не об этом сейчас речь. В данный момент для нас имеет значение тот факт, что величину силы Лоренца мы вычислить способны:
F_л=qvBsinalpha
Учитывая, что заряд нашей элементарной частицы равен по величине заряду электрона, скорость света равна c=3⋅10^8,м/с (не забывайте, что скорость протона в 10 раз меньше), а угол между вектором скорости и вектором магнитной индукции составляет 90 градусов, найдем значения силы, действующей на протон со стороны магнитного поля:
F_л=1.6⋅10^{-19},Кл×3⋅10^7,м/с×2,Тл×sin90degree
F_л=9.6⋅10^{-12},Н
Теперь нужно определить ее направление. Для этого воспользуемся правилом левой руки.
Вектор магнитной индукции направлен на нас, а вектор скорости протона направлен вправо. Отогнутый на 90 градусов большой палец левой руки в плоскости рисунка указывает на юг.
Как видите, сила Лоренца направлена перпендикулярно к вектору скорости, поэтому она не будет менять его величину. Но она будет менять его направление. В данном случае сила Лоренца будет центростремительной силой, заставляющей протон двигаться по окружности.
Предположим, что нам нужно определить радиус этой окружности. Это нетрудно сделать, если применить пару фактов из области механики.
Вспомним второй закон Ньютона:
F=ma
В данном случае мы можем не учитывать направления векторных величин, а работать только с их модулями.
Единственная сила, которая будет действовать на протон, – это сила Лоренца. Она будет сообщать ему центростремительное ускорение, которое может быть найдено через квадрат скорости частицы и радиус окружности, по которой она вращается:
F_л=m×dfrac{v^2}{R}
R=dfrac{mv^2}{F_л}
Нам осталось посмотреть значение массы протона в справочных таблицах (mapprox{1.7⋅10^{-27},кг}) и подставить числа в полученное выражение, чтобы найти ответ:
R=dfrac{1.7⋅10^{-27},кг×(3⋅10^7,м/с)^2}{9.6⋅10^{-12},Н}
Rapprox1.6⋅10^{-1},м=16,см
13. Электрическое и магнитное поле
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила Лоренца
Протон (p), влетевший в зазор между полюсами электромагнита, имеет скорость (v), которая перпендикулярна вектору индукции (B) магнитного поля, направленному вертикально (см. рис.). Как направлена действующая на протон сила Лоренца (F)?
1) горизонтально влево
2) от наблюдателя
3) вертикально вверх
4) к наблюдателю
По правилу левой руки: «Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением движения заряда, то отогнутый большой палец укажет направление силы Лоренца, действующей на положительный заряд».Поскольку протон несет положительный заряд, мысленно проделав указанные действия, получаем, что сила Лоренца направлена к наблюдателю.
Ответ: 4
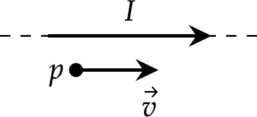
Протон (p) имеет горизонтальную скорость (v), направленную вдоль прямого длинного проводника с током (I) (см. рисунок). Куда направлена действующая на протон сила Лоренца (F)?
1) вертикально вверх в плоскости рисунка
2) вертикально вниз в плоскости рисунка
3) горизонтально влево в плоскости рисунка
4) перпендикулярно плоскости рисунка к нам
Направление вектора магнитной индукции определим по правилу правой руки. В соответствии с этим правилом, получаем направление вектора (vec{B}) от нас перпендикулярно плоскости чертежа.
По правилу левой руки: «Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением движения заряда, то отогнутый большой палец укажет направление силы Лоренца, действующей на положительный заряд».Поскольку протон несет положительный заряд, мысленно проделав указанные действия, получаем, что сила Лоренца направлена вверх в плоскости рисунка.
Ответ: 1
В некоторый момент времени скорость (v) электрона (e) движущегося в магнитном поле, направлена вдоль оси x (см. рисунок). Как направлен вектор магнитной индукции B, если в этот момент сила Лоренца, действующая на электрон, направлена вдоль оси y?
1) из плоскости чертежа от нас
2) в отрицательном направлении оси х
3) в положительном направлении оси х
4) из плоскости чертежа к нам
По правилу левой руки: «Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением движения заряда, то отогнутый большой палец укажет направление силы Лоренца, действующей на положительный заряд».Поскольку электрон несет отрицательный заряд (то пальцы направляем против скорости), мысленно проделав указанные действия, получаем, что вектор магнитной индукции направлен от нас в плоскости чертежа.
Ответ: 1
Протон (р) имеет скорость (v), направленную горизонтально вдоль прямого длинного проводника с током (I) (см. рис.). Определите направление действующей на протон силы Лоренца?
1) перпендикулярно плоскости рисунка от нас
2) вертикально вверх в плоскости рисунка
3) горизонтально влево в плоскости рисунка
4) вертикально вниз в плоскости рисунка
Направление вектора магнитной индукции определим по правилу правой руки. “Если обхватить проводник правой рукой так, чтобы оттопыренный большой палец указывал направление тока, то остальные пальцы покажут направление огибающих проводник линий магнитной индукции поля, создаваемого этим током, а значит и направление вектора магнитной индукции, направленного везде по касательной к этим линиям.” В соответствии с этим правилом, получаем направление вектора (vec{B}) от нас перпендикулярно плоскости чертежа.
По правилу левой руки: «Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением движения заряда, то отогнутый большой палец укажет направление силы Лоренца, действующей на положительный заряд».Поскольку протон несет положительный заряд, мысленно проделав указанные действия, получаем, что сила Лоренца направлена вверх в плоскости рисунка.
Ответ: 2
Электрон (e), влетевший в зазор между полюсами электромагнита, имеет горизонтальную скорость (v) которая перпендикулярна вектору индукции B магнитного поля, направленному горизонтально (см. рисунок). Как направлена действующая на электрон сила Лоренца F?
1) вертикально вниз
2) вертикально вверх
3) горизонтально влево
4) горизонтально вправо
По правилу левой руки: «Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением движения заряда, то отогнутый большой палец укажет направление силы Лоренца, действующей на положительный заряд». Поскольку электрон несет отрицательный заряд (то пальцы направляем против скорости), мысленно проделав указанные действия, получаем, что вектор магнитной индукции направлен вертикально вверх.
Ответ: 2
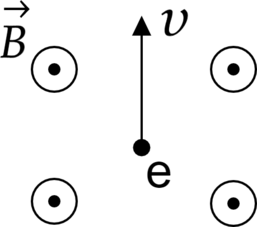
Электрон (e) движется в магнитном поле с индукцией (B) со скоростью (v). Как направлена относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вызванная этим полем сила Лоренца, действующая на электрон? Ответ запишите словом (словами) без разделения пробелом.
На электрон будет действовать сила Лоренца, которая определяется по правилу левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили во внутреннюю сторону ладони, перпендикулярно к ней, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца. Так как электрон это отрицательно заряженная частица, то сила Лоренца будет действовать влево.
Ответ: ВЛЕВО
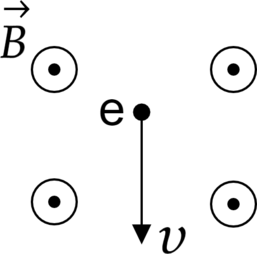
Электрон (e) движется в магнитном поле с индукцией (B) со скоростью (v). Как направлена относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вызванная этим полем сила Лоренца, действующая на электрон? Ответ запишите словом (словами) без разделения пробелом.
На электрон будет действовать сила Лоренца, которая определяется по правилу левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили во внутреннюю сторону ладони, перпендикулярно к ней, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца. Так как электрон это отрицательно заряженная частица, то сила Лоренца будет действовать вправо.
Ответ: ВПРАВО

УСТАЛ? Просто отдохни