Решение задач – обязательная практика в жизни всех студентов-технарей. В сегодняшней статье разберемся, как решать задачи на силу Лоренца.
Если вам скучно читать про решение задач, переходите в наш телеграм-канал. Там найдется интересная информация и новости для всех специальностей. А еще, у нас есть второй канал, где мы рассказываем об акциях нашего сервиса и дарим приятные скидки. Проверьте — и не упустите выгоду!
Задачи по теме «сила Лоренца»
Даже если вы не новичок, прежде чем решать задачи, прочтите общую памятку и на всякий случай держите под рукой полезные формулы.
Задача на силу Лоренца №1
Условие
Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона.
Решение
Скорость электрона можно найти из формулы кинетической энергии:
Eк=m·v22v=2Eкm
Сила Лоренца является центростремительной силой, значит, по второму закону Ньютона, можно записать:
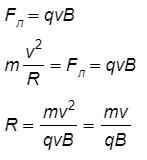
Магнитная индукция равна напряженности, умноженной на магнитную постоянную. Подставив ранее найденное выражение для скорости в формулу для радиуса и силы Лоренца, запишем:
R=m2Eктqμ0H=2Eктqμ0HFл=q2Eктμ0H
Теперь осталось только подставить значения и вычислить:
v=2·4,8·10-169,1·10-31=3,25·107 мсFл=4·3,14·10-7·465·1,6·10-19·3,25·107=3·10-15НR=2·4,8·10-16·9,1·10-314·3,14·10-7·465·1,6·10-19=0,32 м
Ответ: v=3,25·107 мс; Fл=3·10-15Н; R=0,32 м.
Задача на силу Лоренца №2
Условие
Альфа-частица влетает в магнитное поле с индукцией 1 Тл перпендинулярно силовым линиям. Найти момент импульса частицы относительно центра окружности, по которой она будет двигаться.
Решение
Когда частица влетает в поле перпендикулярно силовым линиям, на нее начинает действовать сила Лоренца, которая выполняет роль центростремительной силы. Радиус окружности, по которой будет двигаться частица:
R=mvQBm=6,65·10-27 кг – масса альфа частицыQ=2e=3,2·10-19Кл – заряд альфа частицы
Момент импульса частицы относительно центра окружности найдем по формуле:
L=mvR=m2v2QB=6,65·10-272·0,35·10723,2·10-19·1=5,42·10-21кг·м2с
Ответ: 5,42·10-21 кг·м2с.
Задача на силу Лоренца №3
Условие
В однородном магнитном поле с индукцией В = 0,5 Тл вращается с частотой n = 10 с-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определите разность потенциалов U на концах стержня.
Решение
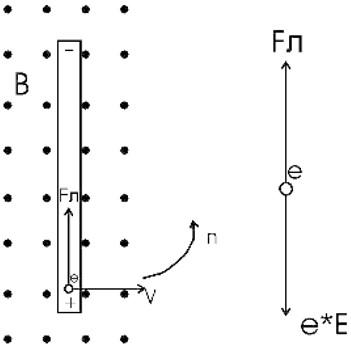
Рассмотрим физическую суть процессов, проходящих в стержне. Когда стержень движется в магнитном поле, в нем возникает ЭДС индукции, которая обусловлена действием силы Лоренца на заряды стержня.
Под действием этой силы в стержне происходит разделение зарядов: свободные электроны перемещаются вверх и между концами стержня возникает разность потенциалов.
Заряды на концах стержня создают поле E, препятствующее дальнейшему разделению зарядов. В какой-то момент сила Лоренца уравновесится с силой возникающего поля:
Fл=e·ЕЕ=Fле=evBe=vB
Скорость нижнего конца стержня, а значит, и скорость электронов в нем, можно найти, зная частоту вращения и длину стержня:
v=2π·n·l
C учетом этого, перепишется выражения для напряженности электрического поля:
Е=2πnlB
Индуцируемая разность потенциалов, по определению, равна:
U=Е·lU=2πnl2B=2·3,14·10-1·0,22·0,5=1,3В
Ответ: 1,3 В.
Задача на силу Лоренца №4
Условие
Какая сила действует на заряд 0,005 Кл, движущийся в магнитном поле с индукцие 0,5 Тл со скоростью 150 м/с под углом 45 градусов к вектору магнитной индукции?
Решение
Это простейшая задача на определение силы Лоренца. Вспомним формулу и запишем, что на заряд действует сила Лоренца, равная:
F=q·v·B·sinα
Подставим значения и вычислим:
F=0,005·150·0,5·22=0,26 Н
Ответ: 0,26 Н.
Задача на силу Лоренца №5
Условие
На тело с зарядом 0,8 мКл, движущееся в магнитном поле, со стороны поля действует сила, равная 32Н. Какова скорость тела, если вектор магнитного поля перпендикулярен ей?
Решение
Это классическая задача на применение формулы силы Лоренца. Так как векторы скорости и магнитной индукции перпендикулярны, можно записать:
F=qvBsinα=qvBv=FqB=320,8·10-3·2=20·103 мс
Ответ: 20000 м/с.
Проходите магнитостатику? Вам также может быть интересно:
- Задачи на закон Био-Савара-Лапласа.
- Задачи на теорему о циркуляции магнитного поля.
Вопросы на тему «Сила Лоренца»
Вопрос 1. Что такое сила Лоренца?
Ответ. Сила Лоренца — это сила, с которой магнитное поле действует на заряженную частицу, движущуюся в нем.
Сила Лоренца действует только на движущиеся заряды.
Вопрос 2. Как определить направление силы Лоренца?
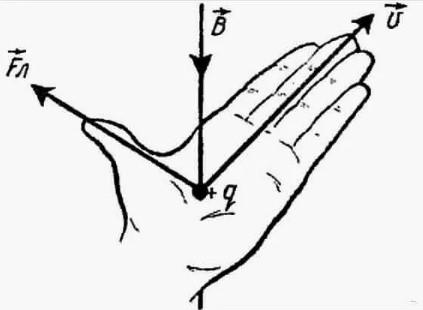
Ответ. Направление силы Лоренца определяется по правилу левой руки:
Если левую руку расположить так, чтобы составляющая вектора В, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движении положительного заряда (= против движения отрицательного заряда), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
Вопрос 3. Зависит ли сила Лоренца от знака заряда?
Ответ. Да, зависит. Для противоположных зарядов сила Лоренца будет направлена в противоположные стороны.
Вопрос 4. Совершает ли сила Лоренца работу?
Ответ. Нет. Сила Лоренца не совершает работу, т.к., являясь перпендикулярной вектору скорости частицей, может изменить лишь направление скорости, но не ее значение. Работа силы Лоренца всегда равна нулю!
Вопрос 5. По какой траектории движется частица, попадающая в магнитное поле, перпендикулярное вектору скорости?
Ответ. Частица, влетающая в магнитное поле перпендикулярно линиям магнитной индукции, будет двигаться в этом поле по окружности определенного радиуса под действием силы Лоренца.
Нужна помощь в решении задач и других заданий по учебе? Профессиональный сервис для студентов посодействует, обращайтесь в любое время!
Содержание:
Сила Лоренца:
Центростремительное (нормальное) ускорение появляется при криволинейном движении тела и характеризует скорость изменения направления скорости с течением времени. Оно вычисляется по формуле 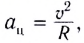
Согласно закону Ампера на проводник с током в магнитном поле действует сила, которую можно рассматривать как результат действия магнитного поля на все движущиеся в проводнике заряды. Отсюда можно сделать вывод, что магнитное поле оказывает силовое действие на каждый движущийся заряд.
По закону Ампера на проводник длиной 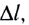
Поскольку электрический ток — направленное движение заряженных частиц, то силу тока можно представить в виде
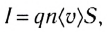
где q — величина заряда одной частицы, n — концентрация заряженных частиц (число частиц в единице объема проводника), 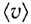 — средняя скорость упорядоченного движения заряженных частиц, S — площадь поперечного сечения проводника.
— средняя скорость упорядоченного движения заряженных частиц, S — площадь поперечного сечения проводника.
Тогда
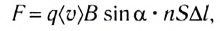
где 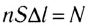 — число заряженных частиц, упорядоченно движущихся во всем объеме проводника длиной
— число заряженных частиц, упорядоченно движущихся во всем объеме проводника длиной 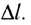
Разделив модуль силы F на число частиц N, получим модуль силы, действующей на один движущийся заряд со стороны магнитного поля:
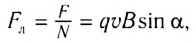
где v — модуль скорости движущегося заряда.
Выражение для силы, с которой магнитное поле действует на движущийся заряд, в 1895 г. впервые получил голландский физик Хендрик Антон Лоренц. В его честь эта сила называется силой Лоренца:

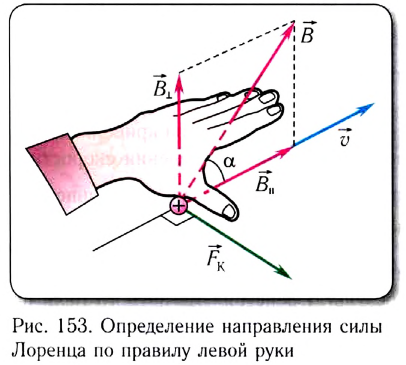
Как определить направление силы Лоренца
Направление силы Лоренца определяется по правилу левой руки (рис. 153):
если левую руку расположить так, чтобы перпендикулярная к скорости 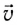 составляющая вектора индукции
составляющая вектора индукции 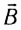 магнитного поля входила в ладонь, а четыре вытянутых пальца указывали направление движения положительно заряженной частицы, то отогнутый на 90° большой палец укажет направление силы Лоренца
магнитного поля входила в ладонь, а четыре вытянутых пальца указывали направление движения положительно заряженной частицы, то отогнутый на 90° большой палец укажет направление силы Лоренца 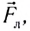 действующей на частицу со стороны магнитного поля. Для отрицательно заряженной частицы (например, для электрона) направление силы будет противоположным.
действующей на частицу со стороны магнитного поля. Для отрицательно заряженной частицы (например, для электрона) направление силы будет противоположным.
Поскольку сила Лоренца перпендикулярна вектору скорости, то она не может изменить модуль скорости, а изменяет только ее направление и, следовательно, работы не совершает.
Таким образом, если поле однородно, то при движении частицы перпендикулярно к магнитной индукции поля ее траекторией будет окружность (рис. 154, а), плоскость которой перпендикулярна к магнитному полю.
Ускорение частицы 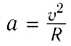 (R — радиус окружности) направлено к центру окружности. Используя второй закон Ньютона, можем найти период обращения частицы по окружности
(R — радиус окружности) направлено к центру окружности. Используя второй закон Ньютона, можем найти период обращения частицы по окружности
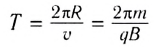
и радиус окружности
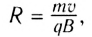
описываемой частицей в магнитном поле.
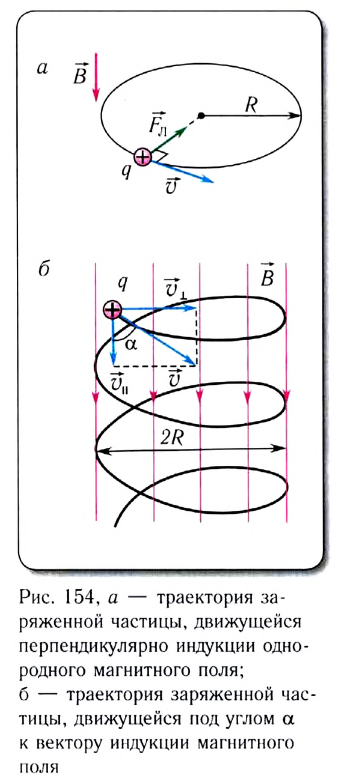
Если скорость направлена под углом к индукции магнитного поля, движение заряда можно представить в виде двух независимых движений (рис. 154, б):
В результате сложения обоих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю (см. рис. 154, б). Период этого движения определяется по формуле
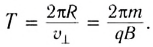
Действие силы Лоренца широко применяется в различных электротехнических устройствах:
- электронно-лучевых трубках телевизоров и дисплеев;
- ускорителях заряженных частиц (циклотронах);
- масс-спектрометрах — приборах, определяющих отношение зарядов частиц к их массе по радиусу окружности, описываемой ими в магнитном поле;
- магнитогидродинамических генераторах ЭДС (МГД-генератор — устройство для генерации электрических токов, использующее проводящие жидкости, движущиеся в магнитном поле).
Что такое сила Лоренца
Силой Лоренца FЛ называют силу, действующую на электрически заряженную частицу, двигающуюся в электромагнитном поле, определяя действия на нес электрической» и магнитного полей одновременно. Это выражается формулой:
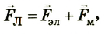
где 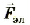 – электрическая составляющая силы Лоренца, описывающая взаимодействие движущейся частицы и равная
– электрическая составляющая силы Лоренца, описывающая взаимодействие движущейся частицы и равная 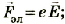
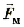 – магнитная составляющая силы Лоренца, определяющая взаимодействие заряженной частицы с магнитным полем.
– магнитная составляющая силы Лоренца, определяющая взаимодействие заряженной частицы с магнитным полем.
Сила Лоренца действует на движущуюся электрически заряженную частицу в электромагнитном поле.
Для упрощения рассмотрим случай, когда 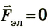 , а сила Лоренца равна магнитной составляющей.
, а сила Лоренца равна магнитной составляющей.
Выясним, как можно рассчитать силу, действующую на движущуюся заряженную частицу в магнитном поле. Как известно, электрический ток в проводнике – это упорядоченное движение заряженных частиц. Согласно электронной теории сила тока рассчитывается по формуле:
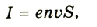
где I – сила тока; е – заряд частицы; 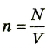 — концентрация частиц в проводнике; V – объем;
— концентрация частиц в проводнике; V – объем; 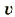 – скорость движения частиц; S площадь поперечного сечения проводники.
– скорость движения частиц; S площадь поперечного сечения проводники.
- Заказать решение задач по физике
Действие магнитного поля на проводник с током является действием магнитного поля на все движущиеся заряженные частицы. Поэтому формулу силы Ампера можно записать с учетом выражения силы тока в электронной теории:
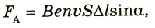
или
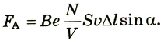
Если учесть, то 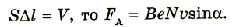
Если сила Ампера является равнодействующей всех сил, действующих на N частиц, то на одну частицу будет действовать сила в N раз меньше:
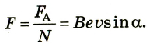
Это и есть формула для расчета магнитной составляющей силы Лоренца:
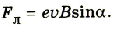
Магнитная составляющая силы Лоренца

Анализ этой формулы позволяет сделать выводы, что:
- магнитная составляющая силы Лоренца действует только на движущуюся частицу (
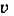 ≠ 0);
≠ 0); - магнитная составляющая не действует на движущуюся частицу, которая движется вдоль линии магнитной индукции (а = 0).
Направление магнитной составляющей силы Лоренца, как и силы Ампера, определяется по правилу левой руки. При этом необходимо учитывать, что это справедливо для положительно заряженных частиц. Если определять направление силы Лоренца, действующей на электрон или другую отрицательно заряженную частицу, то, применяя правило левой руки, нужно мысленно изменять направление движения на противоположное.
Сила Лоренца направлена всегда под некоторым углом к скорости частицы, поэтому она придает ей центростремительное ускорение (рис. 2.15).
Для случая, если
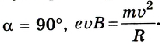
Откуда
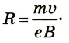
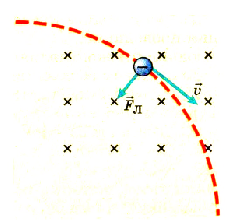
Рис. 2.15. Сила Лоренца придает частице центростремительное ускорение
Таким образом, заряженная частица, попадая в магнитной поле, начинает двигаться по дуге окружности. При иных значениях α ≠ О траектория движения частицы в магнитном поле приобретает форму спирали.
Наблюдать действие силы Лоренца можно с помощью электронно-лучевой трубки, которая есть во многих осциллографах (рис. 2.16), Если включить питание осциллографа, то на его экране можно увидеть светлое пятно, появившееся в месте падения электронов на экран. Если теперь сбоку поднести к трубке постоянный магнит, то пятно сместится, что подтверждает действие магнитного поля на движущиеся электроны.
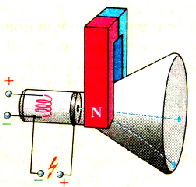
Рис. 2.16. Магнитное поле смещает электронный пучок в трубке осциллографа
Действие силы Лоренца применяется во многих приборах и технических установках. Так, смещение электронного луча, который «рисует» изображение на экране вакуумного кинескопа телевизора или дисплея компьютера, совершается магнитным полем специальных катушек, в которых проходит электрический ток, изменяющийся во времени по определенному закону,
В научных исследованиях применяют так называемые циклические ускорители заряженных частиц, в них магнитное поле мощных электромагнитов удерживает заряженные частицы на круговых орбитах.
Весьма перспективными для развития электроэнергетики являются магнито-гидродипамические генераторы (МГД-генераторы) (рис. 2.17). Поток высокотемпературного газа (плазмы), который образуется при сгорании органического топлива и имеет высокую концентрацию ионов обоих знаков, пропускается через магнитное ноле.
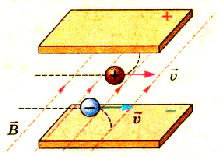
Puc. 2.17. Схема, объясняющая действие МГД-генератора
Вследствие действия силы Лоренца ионы отклоняются от прежнего направления движения и оседают на специальных электродах, сообщая им определенный заряд. Полученную при этом разность потенциалов можно использовать для получения электрического тока. Такие установки в будущем могут существенно повысить КПД тепловых «электростанций за счет выработки дополнительной электроэнергии при прохождении газов, которые после выхода из топки имеют довольно высокую температуру и высокую ионизацию, через MГД-генераторы.
Пример решения задачи
Электрон влетает в однородное магнитное поле с индукцией 10-4 Тл перпендикулярно к линиям магнитной индукции. Его скорость 1.6 . 106 м/с. Найти радиус окружности, по которой движется электрон.
Отсюда
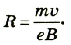
Подставим значения физических величин:
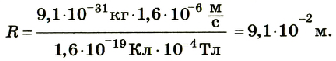
Ответ: электрон будет двигаться по круговой орбите, радиус которой 9,1 ∙ 10-2 м.
- Правило Буравчика в физике
- Шунт и добавочное сопротивление
- Электродвижущая сила
- Электрические измерительные приборы
- Закон Ома для полной цепи
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
- Сила и закон Ампера
- Закон взаимодействия прямолинейных параллельных проводников с током
Сила Лоренца .
Сила Лоренца действует на заряженную частицу, движущуюся в магнитном поле.
( F_л=Bqv cdot sin alpha )
(B) -магнитная индукция, единица измерения Тесла [Тл]
(q) – заряд частицы, единица измерения Кулон [Кл] )
(v) – скорость частицы
( alpha )- угол между вектором магнитной индукции ( vec{B} ) и вектором скорости частицы ( vec{v} )
Направление силы Лоренца, действующей на положительно заряженную частицу .
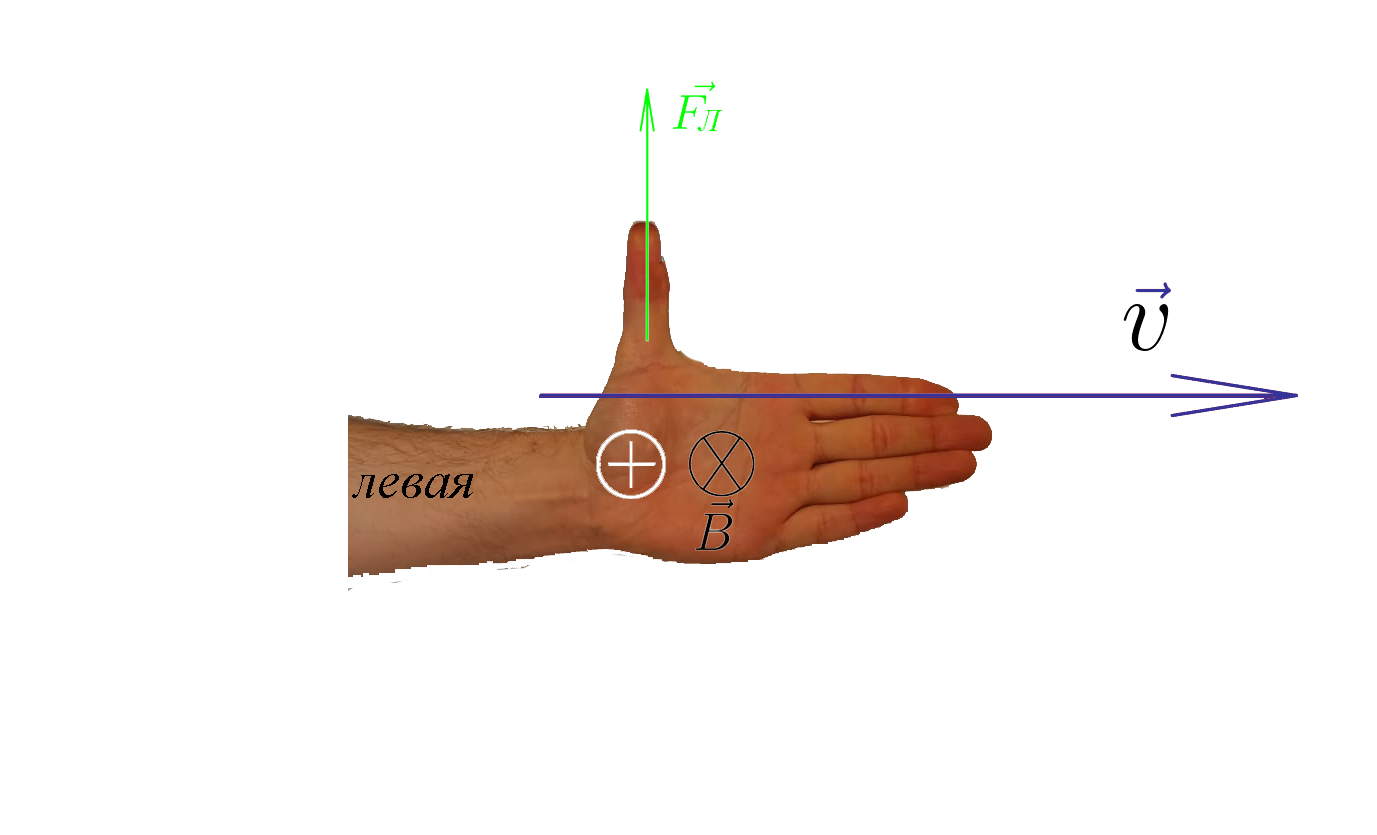
Если вектор магнитной индукциии входит в ладонь левой руки, а четыре пальца сонаправлены с
направлением вектора скорости положительно заряженной частицы, то отогнутый на ( 90^0 )
большой палец показывает направление силы Лоренца действующей на эту частицу.
Задача 1. (Сила Лоренца)
Пылинка, имеющая заряд (q=10^{-6} Кл) движется в магнитном поле с индукцией
(B=20 Тл) . Скорость пылинки перпендикулярна линиям магнитной индукции и равна
(100 м/с )
Вычислить значение силы Лоренца, действующей на пылинку со стороны магнитного поля.
Дать ответ в миллиньютонах.
Показать ответ
Показать решение
Видеорешение
Задача 2.
Шарик с зарядом (q=100 мкКл) влетает в магнитное поле с
индукцией (B=100 Тл) со скоростью (v=30 м/с .)
Угол между вектором магнитной индукции ( vec{B} ) и вектором скорости частицы
( vec{v} ) составляет ( alpha=30^0 . )
Найти значение силы Лоренца, действующей на шарик со стороны поля.
Показать ответ
Показать решение
Видеорешение
Задача 3. (Сила Лоренца)
Электрон движется в магнитном поле с индукцией
(B=1 Тл) перпендикулярно линиям магнитного поля со скоростью (v=10^8 м/с . )
Вычислить значение силы Лоренца, действующей на электрон со стороны магнитного поля.
Заряд электрона ( q=1,6 cdot 10^{-19} Кл . )
Дать ответ в пиконьютонах.
1 пН ( = 10^{-12} Н . )
Показать ответ
Показать решение
Видеорешение
Задача 4. (Сила Лоренца)
С какой скоростью двигался протон в магнитном поле с индукцией (B=10^{-2} Тл) перпендикулярно линиям поля,
если на него действовала сила Лоренца (F_л=3,2 cdot 10^{-17 } Н ? )
Заряд протона ( q=1,6 cdot 10^{-19} Кл . )
Дать ответ в километрах в секунду.
Показать ответ
Показать решение
Видеорешение
Задача 5. (Сила Лоренца)
Альфа-частица движется в магнитном поле с индукцией (B=10^{-3} Тл) перпендикулярно линиям поля, при этом на нее действует сила Лоренца (F_л=6,4 cdot 10^{-15 } Н . )
Вычислить скорость альфа-частицы, если ее заряд (q=3,2 cdot 10^{-19} Кл . )
Дать ответ в километрах в секунду.
Показать ответ
Показать решение
Видеорешение
Задача 8. (Сила Лоренца)
Протон влетает в магнитное поле со скоростью (v= 10^{5} м/с ) перпендикулярно линиям индукции,
после чего он движется по окружности.Найти радиус этой окружности, если индукция поля
(B=0,01 Тл . )
Заряд протона (q=1,6 cdot 10^{-19} Кл )
Масса протона (m=1,6 cdot 10^{-27} кг )
Показать ответ
Показать решение
Видеорешение
Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
FЛ=FN
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля →B можно считать неизменным в пределах этого отрезка проводника.
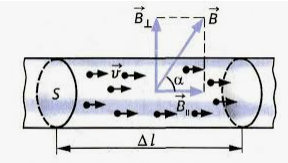
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I=qnvS
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F=|I|ΔlBsinα
Подставляя сюда выражение, полученное для силы тока, получим:
F=|qnvS|ΔlBsinα=|q|nvSΔlBsinα
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
N=nSΔlB
Тогда:
F=|q|vNBsinα
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
FЛ=FN=|q|vNBsinαN=|q|vBsinα
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.
FЛ=|q|vBsinα=0,005·200·0,3·√22≈0,2 (Н)
Направление силы Лоренца
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:
Если левую руку расположить так, чтобы составляющая магнитной индукции →B, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
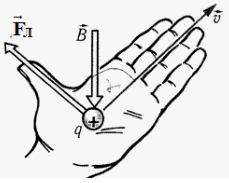
Пример №2. Протон p имеет скорость →v, направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?
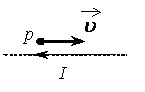
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.
Работа силы Лоренца
Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90о. Работа любой силы определяется формулой:
A=Fscosα
Но так как косинус 90о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.
Полная сила, действующая на заряд
При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила →Fэл, действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:
→Fэл=q→E
Следовательно, полная сила, действующая на заряд, равна:
→F=→Fэл+→Fл=q→E+|q|→v→Bsinα
Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна →E. Какова индукция →B магнитного поля?
Прямолинейное движение протона возможно в двух случаях:
- Вектор →E направлен вдоль траектории движения протона. Тогда вектор →B также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
- Векторы →E, →B и →v взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).
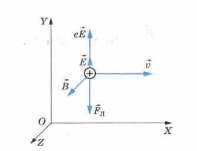
Заряд протона равен модулю заряда электрона — e. Сложим силы, действующие на протон по оси ОУ:
e→E+→FЛ=0
В скалярной форме:
eE−evB=0
Следовательно:
B=Ev
Задание EF17621
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Лоренца.
3.Выразить модуль вектора магнитной индукции.
4.Определить недостающие величины.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Напряжение на обкладках конденсатора: U = 2160 В.
• Радиус окружности, по которой движется протон в однородном магнитном поле: R = 20 см.
• Масса протона: m = 1,673·10–27 кг.
• Заряд протона: q = 1,6·10–19 Кл.
20 см = 0,2 м
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:
FЛ=qvB
Сила Лоренца сообщает протону центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
qvB=mv2R
Отсюда модуль вектора магнитной индукции равен:
B=mv2qvR=mvqR
Энергия заряда, движущегося в электрическом поле, определяется формулой:
W=qU
Но энергию заряда также можно выразить как кинетическую энергию движения:
W=Eк=mv22
Приравняем правые части выражений и получим:
qU=mv22
Отсюда ускорение протона равно:
v=√2qUm
Конечная формула для определения модуля вектора магнитной индукции:
B=mvqR=mqR√2qUm=√2UmqR2
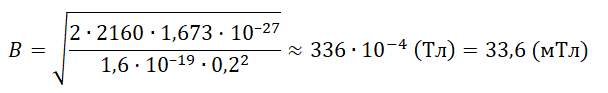
Ответ: 33,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17600
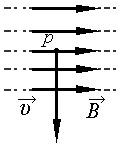 Протон движется в однородном магнитном поле со скоростью υ, направленной перпендикулярно вектору магнитной индукции B (см. рисунок). Как направлена сила Лоренца, действующая на протон?
Протон движется в однородном магнитном поле со скоростью υ, направленной перпендикулярно вектору магнитной индукции B (см. рисунок). Как направлена сила Лоренца, действующая на протон?
а) влево
б) вправо
в) к нам
г) от нас
Алгоритм решения
- Определить, каким способом можно найти направлений силы Лоренца, действующей на протон.
- Применить правила и найти направление силы Лоренца.
Решение
Силу Лоренца, действующую на заряженную частицу, можно найти с помощью правила левой руки. Для этого мысленно расположим четыре пальца левой руки в сторону, совпадающей с направлением движения положительной частицы (протона). Относительно рисунка пальца будут направлены вниз. Теперь развернем ладонь так, чтобы в нее входили линии магнитной индукции. Теперь отклоним на 90 градусов большой палец. Он будет направлен от плоскости рисунка к нам. Это и есть направление силы Лоренца, действующей на протон.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17749
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, частота обращения и энергия α-частицы по сравнению с протоном должны:
- увеличиться
- уменьшиться
- не измениться
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
1.Записать формулу для определения силы Лоренца.
2.Установить, от чего зависят перечисленные в таблице физические величины.
3.Определить характер их изменения при изменении заряда.
Решение
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
Если вместо протона взять альфа-частицу, то заряд увеличится вдвое, так как альфа-частица содержит 2 протона. Сила Лоренца прямо пропорционально зависит от величины заряда. Следовательно, она тоже увеличится вдвое. Скорость движения заряда по условию задачи остается постоянной, как и модуль вектора магнитной индукции.
Сила Лоренца будет сообщать альфа-частице центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
|q|vBsinα=mv2R
Отсюда:
|q|Bsinα=mvR
R=mv|q|Bsinα
Заряд альфа-частицы больше заряда протона вдвое. Она также содержит 2 нейтрона, поэтому ее масса примерно в 4 раза больше массы протона. Следовательно, радиус движения альфа-частицы увеличится примерно вдвое.
Частота обращения альфа-частицы связана с ее линейной скоростью формулой:
v=2πRν
Так как скорость остается постоянной, то при увеличении радиуса частота обращения должна уменьшиться.
Энергия альфа-частицы будет больше, чем у протона, вращающегося с той же скоростью. Это связано с тем, что ее кинетическая энергия будет примерно в 4 раза больше (так как во столько раз больше ее масса).
Ответ: 121
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.9k
Для школьников (в помощь желающим лучше понять физику).
Сила Ампера
Сила Ампера – это сила, с которой магнитное поле действует на проводник с током.
Опытным путём найдено, что на прямой провод с током со стороны магнитного поля действует сила:
Из формулы видно, что сила Ампера пропорциональна индукции магнитного поля, току в проводнике, длине проводника и зависит от расположения проводника в магнитном поле:
Или действие магнитного поля на проводник определяется лишь перпендикулярной составляющей индукции магнитного поля.
Когда проводник расположен вдоль поля, сила Ампера равна нулю.
Для нахождения направления силы Ампера удобно пользоваться правилом л е в о й р у к и: левую руку располагаем так, чтобы силовые линии магнитного поля входили в ладонь, четыре вытянутых пальца направляем по току, тогда отставленный большой палец покажет направление силы Ампера.
На рисунке ниже показан проводник с током, помещённый в однородное магнитное поле, направленное к нам. Тогда, согласно правилу левой руки, сила Ампера, действующая на проводник с током, направлена вправо.
Сила Лоренца
Сила Лоренца – это сила, с которой магнитное поле действует на движущийся заряд.
Выражение для силы Лоренца (как и для силы Ампера) получено опытным путём:
Опять представим ток в прямом проводе. Воспользуемся тем же рисунком, на котором показана сила Ампера.
Ток в проводнике есть направленное движение свободных электронов.
На рисунке ток по проводнику течёт вверх, а свободные электроны, под действием сил электрического поля внутри проводника, двигаются вниз.
На каждый электрон действует сила Лоренца.
Направление силы Лоренца тоже находится по правилу л е в о й р у к и: левую руку располагаем так, чтобы силовые линии магнитного поля входили в ладонь, четыре вытянутых пальца направляем против скорости движения электрона или по направления тока в проводе (так как за направление тока условились принимать направленное движение положительных зарядов), тогда большой отогнутый палец покажет направление силы Лоренца, действующей на каждый свободный электрон в проводе. Её направление совпадает с направлением сила Ампера.
Сложение сил Лоренца, действующих на каждый электрон в отдельности, даёт силу Ампера (видим, как выражения для этих сил похожи друг на друга).
Чтобы представить свободные электроны и их движение в металлическом проводнике, надо вспомнить строение металла.
А именно, металлический проводник имеет кристаллическое строение. В узлах кристаллической решётки металла находятся ионы (атомы, от которых оторвались валентные электроны).
Если по металлу проходит ток, то свободные электроны двигаются между ионами упорядоченно, взаимодействуя с ними.
Магнитное поле, в котором находится проводник с током или движущийся заряд, создаётся или постоянным магнитом, или электромагнитом, или током.
Т а к и м о б р а з о м, силы взаимодействия между током в проводе и магнитным полем сводятся к силам Лоренца.
Возникающие силы Лоренца действуют на весь проводник, так как движущиеся в проводнике электроны взаимодействуют с атомами проводника (возникает своего рода “трение” между ними).
Наличие этого взаимодействия (“трения”) между упорядоченно движущимися электронами и атомами твёрдого металла, демонстрируется следующим опытом.
Между полюсами подковообразного магнита 2 может вращаться медный диск 1, кромка которого погружена в жёлоб с ртутью 3, служащий для подведения тока от батареи к кромке диска. Второй полюс батареи соединён с осью диска.
При замыкании ключа, благодаря “трению”, диск начинает вращаться. При изменении направления тока или направления магнитного поля направление вращения диска изменится на обратное. Как это происходит?
При прохождении тока электроны двигаются вдоль радиуса диска между центром диска и точкой соприкосновения диска с ртутью.
Сила Лоренца стремится отклонить электроны в перпендикулярном направлении. Вследствие “трения” между электронами и атомами металла весь диск приходит во вращение.
Направление вращения можно установить, пользуясь правилом левой руки.
Задачи
Задача 1.
По проводнику течёт ток, сила которого равна 10 А. Площадь поперечного сечения проводника 5 квадратных сантиметров, а число свободных электронов в одном кубическом сантиметре проводника составляет 10 в двадцать третьей степени. Определить направленную скорость электронов, считая её одинаковой для всех электронов.
Решение
За 1 с через поперечное сечение А проводника пройдут все те электроны, которые содержатся в показанном на рисунке объёме, равном произведению площади поперечного сечения проводника на длину части проводника, равную произведению скорости на 1 с.
Следовательно, сила тока равна произведению указанного объёма на концентрацию электронов и на заряд одного электрона
Ответ: найдена скорость направленного движения электронов в проводнике.
Можно было бы продолжить решение этой задачи, представив, что рассмотренный в задаче проводник с током силой
находится в магнитном поле.
Зная магнитную индукцию этого поля, могли бы найти силу Ампера, действующую на участок проводника с током, изображённом на рисунке выше.
Затем, разделив силу Ампера на число электронов участка провода
смогли бы найти силу, действующую на один движущийся электрон, то есть смогли бы найти силу Лоренца.
Задача 2.
Электрический ток в металлических проводниках представляет собой движение свободных электронов, сталкивающихся с ионами, из которых построена кристаллическая решётка металла, и отдающих при этом ионам ту энергию, которую они приобрели до соударения. Почему же металлический проводник, по которому идёт ток, не испытывает никаких механических сил в направлении движения электронов?
Ответ.
Электрическое поле в металле, вызывающее движение электронов, действует с одинаковой силой и на электроны и на ионы решётки, но силы эти направлены в противоположные стороны. Сила, действующая на электроны, вызывает их ускоренное движение. Под действием поля электроны приобретают энергию, которую они при столкновении отдают ионам. При этом средняя сила, с которой электроны действуют на проводник, сталкиваясь с ионами решётки, равна той силе, с которой электрическое поле действует непосредственно на ионы решётки, но противоположна ей по направлению. Поэтому металлический проводник, по которому идёт ток, не испытывает никаких механических сил в направлении движения электронов.
Таким образом, рассмотрев теорию и задачи к ней, мы убедились, что взаимодействие тока в проводнике с магнитным полем сводится к силам Лоренца.
Действие силы Лоренца на свободно движущуюся заряженную частицу, влетающую в магнитное поле, подробно рассмотрено с решением ряда задач в Занятии 67 и в статье “Поведение электрона в электрическом и магнитном полях”
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Действие магнитного поля на контур с током.
Следующая запись: Зарядка конденсатора. Зарядный и разрядный ток проводимости.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
