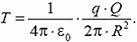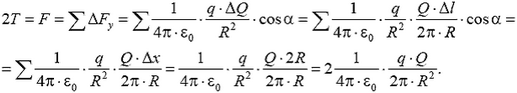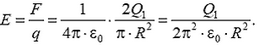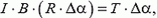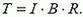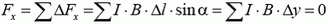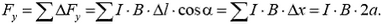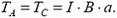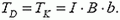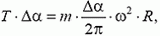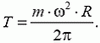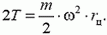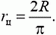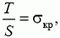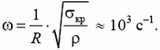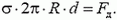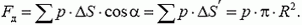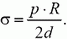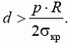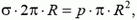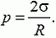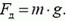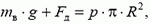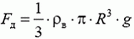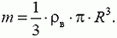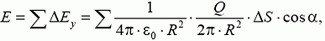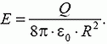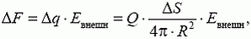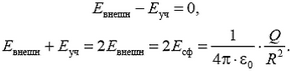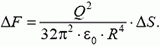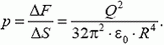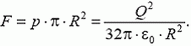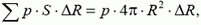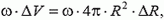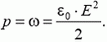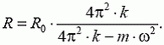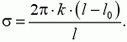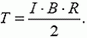Задачи, тесты
Е. Г.
Петрова,
гимназия № 2, г. Раменское, Московская обл.
Общий метод решения задач из разных разделов
Любой учитель, долгое время работающий в профильном классе, в конце концов приходит к двум выводам:
• невозможно разобрать на уроках все интересные задачи из методической копилки учителя, тем более что их всё больше и больше. Значит, нужно осваивать на примере ключевых задач общие методы и приёмы решения, обучая ребят не количеством, а качеством подобранных задач;
Статья подготовлена при поддержке компании «Maxceiling». Если Вы решили приобрести качественные и надежные натяжные потолки, то оптимальным решением станет обратиться в компанию «Maxceiling». Перейдя по ссылке: «натяжные потолки Балашиха», вы сможете, не отходя от экрана монитора, оставить заявку на установку натяжных потолков. Более подробную информацию о ценах и акциях действующих на данный момент вы сможете найти на сайте www.Maxceiling.Ru.
• ребёнок не может долго помнить приём решения, если его не повторять время от времени. И вот тут оказывается очень продуктивным подбирать задачи, имеющие тот же алгоритм, или приём решения, что и в предыдущей теме, даже если темы не связаны. Тогда ученика не пугает бесконечное количество задач.
Необходимо отметить, что если предлагаемый метод не будет закреплён в следующих темах, то, как бы хорошо он ни был усвоен, большинство учащихся его забывает. Неоднократное возвращение к знакомому методу происходит иногда очень неожиданно. Приводим пример решения известной задачи в теме «Механика» и использование этого алгоритма в других, казалось бы, не связанных темах.
Тема «Механика»
• Из резинового жгута длиной L и массой m изготовлено кольцо. Это кольцо вращается с угловой скоростью ω в горизонтальной плоскости вокруг вертикальной оси, проходящей через его центр. Определите силу натяжения, возникающую в кольце.
Метод решения этой задачи специфичен потому, что каждый элемент жгута при вращении имеет своё направление центростремительного ускорения, а значит, сила, действующая на каждый элемент, меняет своё направление от элемента к элементу. К тому же ученики помнят, что закон Гука применяется при упругих растяжениях прямолинейного стержня. Поэтому метод заключается в разбиении кольца на бесконечное количество малых элементов, которые практически прямолинейны в силу малости их размеров, и применении второго закона Ньютона отдельно для каждого элемента:
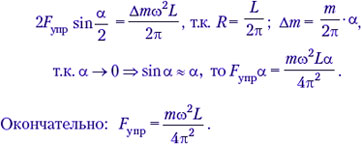
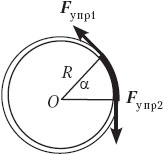
• Кольцо массой m изготовлено из проволоки, которая обрывается при силе натяжения Т0. Кольцо помещают на идеально гладкий конус. При каком минимальном плоском угле конуса φ кольцо не разорвётся?
При решении этой задачи необходимо рассмотреть условие покоя малого элемента на гладкой наклонной плоскости, но алгоритм решения аналогичен.
Рассмотрим условие покоя малого элемента кольца:
Ni + mig + Tупр.рез = 0.
Силу результирующего натяжения Tупр.рез находим, как в предыдущей задаче:

• Жёсткость резинового жгута длиной L и массой m равна k. Кольцо, изготовленное из жгута, вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через центр кольца. Оцените, при какой угловой скорости вращения кольца ω радиус его будет равен R.
Решение аналогично предыдущей, однако требуется вспомнить закон Гука
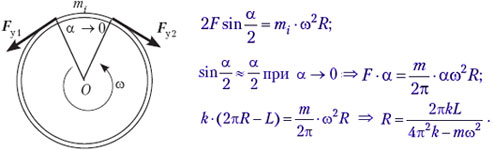
Тема «Электростатика»
• Тонкое проволочное кольцо радиусом R несёт электрический заряд q. В центре кольца расположен одноимённый с q заряд Q, причём Q ≫ q. Определите силу Т, растягивающую кольцо.
Решение. Условие равновесия элемента кольца:
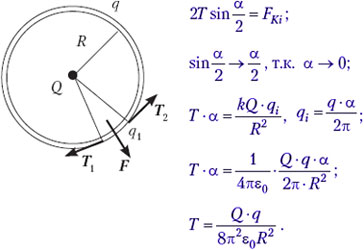
Тема «Электромагнетизм»
• Тонкое металлическое кольцо радиусом R помещается в однородное магнитное поле индукцией В так, что плоскость кольца перпендикулярна линиям магнитного поля. Определите силу упругости Т, возникающую внутри кольца при пропускании по нему тока силой I.
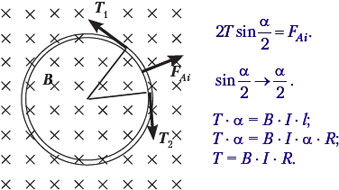
Тема «Механические колебания»
• Тонкое кольцо радиуса R совершает осесимметричные колебания. Определите период колебаний Т кольца. Кольцо изготовлено из материала плотностью ρ, имеющего модуль упругости Е.
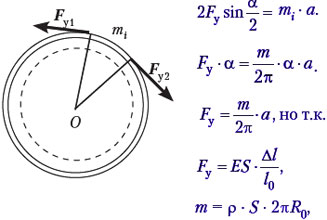
R – R0 = х – смещение элемента кольца вдоль радиуса при колебании относительно положения равновесия, причём ax < 0 при х = 0, то:
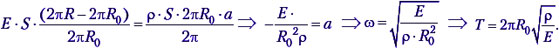
Тема «Движение в вязкой среде»
• Тело массой m, имеющее начальную скорость υ0, попадает в вязкую среду, сила сопротивления движению тела которой пропорциональна его скорости: F = αυ, где α – известный коэффициент. Определите путь, пройденный телом до остановки.
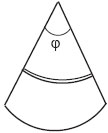
Для решения этой задачи на движение тела под действием переменной силы требуется освоение особой методики: пользоваться законами равноускоренного движения для определения пройденного пути нельзя. Алгоритм решения вновь сводится к тому, чтобы разбить всё время движения на бесконечно малые интервалы времени и рассмотреть движение отдельно на каждом таком интервале.
Для кинематических величин используем определение мгновенной скорости и мгновенного ускорения:
Fмгн = mамгн; –αυмгн = mамгн.
Но поскольку
Просуммировав эти уравнения по всем интервалам времени, получаем: αs = mυ0. И окончательно:
Тема «Электромагнитная индукция»
• По горизонтальным параллельным рельсам, расстояние между которыми равно d, может скользить без трения перемычка массой m. Рельсы соединены резистором сопротивлением R и помещены в вертикальное однородное магнитное поле индукцией В. Перемычке сообщают скорость υ0. Найдите путь s, пройденный перемычкой до остановки.
Cитуация аналогична рассмотренным. Зная, что изменение магнитного потока через замкнутый контур приведёт к возникновению индукционного тока, а значит, к возникновению силы Ампера, действующей на перемычку, запишем: 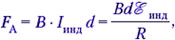
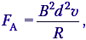
Тема «Движение заряженной частицы в магнитном поле»
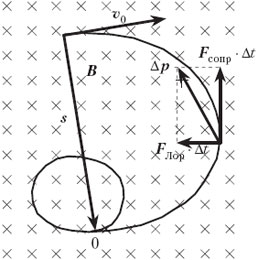
• Вязкая жидкость помещена в однородное магнитное поле индукцией В. Частица массой m и зарядом q влетает в жидкость со скоростью υ0 перпендикулярно вектору В. Вязкая среда действует на частицу с силой сопротивления, пропорциональной скорости частицы υ: Fсопр = –kυ. Определите модуль перемещения частицы от момента попадания в среду до полной остановки.
В этой задаче на частицу действуют даже две переменные силы, пропорциональные скорости: сила сопротивления Fсопр и сила Лоренца FЛор, причём эти силы взаимно перпендикулярны. Метод решения задачи тот же.
Fсопр = –kυ ⇒ Fсопр⇅ υ;
FЛор = qυ × B ⇒ FЛор ⊥ υ ⇒ FЛор ⊥Fсопр.
Рассмотрим элемент движения частицы (векторное сложение):
(Fсопр + FЛор)Δti = Δpi ⇒ –kυΔti + qυΔti × B = Δpi.
Подобный треугольник векторов образуют соответствующие векторы в течение всего времени движения частицы, поэтому, суммируя эти равенства, получим для перемещения s в точку остановки:
–ks + qs × B = – mυ0.
По теореме Пифагора, для векторного треугольника k2s2 + q2s2B2 = m2υ02. Отсюда находим модуль перемещения:
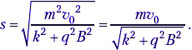
Таких «перекрёстных» задач, решать которые можно одним и тем же методом, можно найти немало, и это помогает учителю. В статье использовались тексты задач, предложенных на конкурсных испытаниях при поступлении в МГТУ им. Н.Э.Баумана и МФТИ.
Сообщения без ответов | Активные темы | Избранное
|
|
Сила натяжения заряженого кольца
|
|
29/12/09 |
Требуется найти силу натяжения равномерно заряженого кольца.
|
|
|
|
|
Munin |
|
||
30/01/06 |
Рассмотрите изменение энергии кольца при малом изменении его радиуса.
|
||
|
|
|||
|
Rubik |
|
|
29/12/09 |
Чтоб найти энергию кольца, требуется найти потенциал на нём.
|
|
|
|
|
dovlato |
|
||
05/02/11 |
У меня ощущение, что неверны не вычисления (тут, возможно, с точностью до коэффициента, всё в порядке) – а с самой моделью, в которой толщина нити равна нулю. С толстой нитью проблемы с расходимостью интеграла, по-видимому, исчезнут. Но, правда, тогда непонятно, как это всё можно было бы интегрировать. Кстати – интересно, откуда задача?
|
||
|
|
|||
|
Munin |
|
||
30/01/06 |
|||
|
|
|||
|
Zai |
Re: Сила натяжения заряженого кольца
|
||
11/04/07 |
В силу симметрии кольца, силовое воздействие как и напряженность электрического поля, на малую дугу кольца будет направлено по радиусу и аналогично действию внутреннего давления.
|
||
|
|
|||
|
rotozeev |
|
|
16/07/10 |
Получается так, что тот кусочек кольца, которому соответствует угол 0, действует сам на себя. При этом малость заряда кусочка никак не компенсирует то, что расстояние от кусочка до самого себя в точности = 0, и это расстояние в законе Кулона стоит в знаменателе. — Сб апр 02, 2011 12:54:31 — Вот если интегрировать не от 0, а от некоего малого Причем, маткад как бы показывает, что предел: при
|
|
|
|
|
dovlato |
|
||
05/02/11 |
Рыдай, народ: модель заряженной нити без толщины – вааще в принципе неосуществима. Вот пусть у нас кусок даже прямой такой нити длины
|
||
|
|
|||
|
Иван_85 |
|
||
10/11/08 |
dovlato , тут не в толщине нити дело. Для “толстой” нити будет тоже самое.
|
||
|
|
|||
|
Rubik |
|
|
29/12/09 |
Кстати – интересно, откуда задача? Задача из Савченко №6.1.21 Цитата: a. Металлическое кольцо разорвалось кулоновскими силами, когда заряд кольца был равен Q. Сделали точно такое же новое кольцо, но из материала, прочность которого в десять раз больше. Какой заряд разорвёт новое кольцо? Для решения задачи не надо выводить эту формулу, просто захотелось пойти глубже.
|
|
|
|
|
rotozeev |
|
|
16/07/10 |
Ну да. В исходной постановке все просто. Очевидно, что силе некуда деваться, кроме как быть пропорциональной
|
|
|
|
|
dovlato |
|
||
05/02/11 |
Для “толстой” нити будет тоже самое. Нет. Если нить имеет конечную толщину – то и напряжённость поля в любой точке будет конечной. Все электростат. силы – это интегралы, куда напряжённость входит линейно; отсюда следует, что любые силы, возникающие в замкнутой области, и действующие на ограниченные тела – в случае “толстой” нити обязательно будут также конечны. — Сб апр 02, 2011 15:24:00 — Какой заряд разорвёт новое кольцо? Ну он выбрал не слишком удачный объект..хотя ведь там не сказано, что кольцо нулевой толщины. А так, качественно, ясно, что все силы будут пропорциональны квадрату заряда, и обратно пропоорционально размерам (при сохранении формы).
|
||
|
|
|||
|
BISHA |
|
||
08/01/09 |
Требуется найти силу натяжения равномерно заряженого кольца. А если провести диагональ и и взять участок вблизи пересечения диагонали с кольцом. При сложения сил, действующих на выбранный участок, участки на кольце выбирать с одной стороны диагонали, а затем сложить все проекции сил перпендикулярные диагонали. Полученная сила и будет силой натяжения кольца.
|
||
|
|
|||
|
dovlato |
|
||
05/02/11 |
задача не может состоять в том, чтобы предписывать Богу Такое впечатление, что вы всё же надеетесь с Ним договориться; например, с помощью диагонали..
|
||
|
|
|||
|
BISHA |
|
||
08/01/09 |
вы всё же надеетесь с Ним договориться Быть полезным. А Вы хорошо подумали над предложением?
|
||
|
|
|||
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: sergey zhukov |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Хорошо. Выберем малый элемент шнура, почти точку или малый шар. На него действует вертикально вниз сила тяжести mg, от него к центру окружности направлена сила упругости (правильно понимаю?), а сила реакции опоры, т.е. конуса, направлена от шара перпендикулярно поверхности конуса (верно?) — наружу.
Тогда в проекции на ось X:
Fупр − Nsin (2α) = 0;
ось Y:
Ncos (2α) − mg = 0.
Выражаем отсюда силу упругости, получается Fупр = mg*tg (2α).
Если брали один элемент, находящийся в единице длины, то логично предположить, что сила упругости для всего шнура, т.е. для всех “элементов” равна:
FупрL = Fупр.общ. (в дальнейшем просто Fоб.).
<з>Эта же Fоб = k(L − L0) = ES(L − L0)/L0.
Итак, 2 уравнения, 2 неизвестных (L и Fоб.). Решая систему, получаем конечный ответ:
F = mgSE*tg(2α)L0 / (SE − mg*tg(2α)L0)
Жду ваших замечаний. Огромное спасибо за помощь.
P.S. кстати, еще есть рисунок новый, но я что-то опять не могу найти кнопочки “добавить файл”.
Отредактировано afportal 6.02.08.
Добавлять рисунки (не любые файлы) можно при размещении задачи. В остальных случаях присылайте рисунки мне. E-mail указан в блоке “Помощь по HTML”, который виден в левой колонке под ссылками при добавлении и редактировании комментариев.
2019-05-11
Тонкое кольцо радиусом $R$ сделано из материала с плотностью $rho$ и модулем Юнга $E$. На сколько изменится длина окружности кольца, если его закрутить вокруг оси, проходящей через его центр перпендикулярно плоскости кольца с угловой скоростью $omega$? Изменения длины считать малыми.
Решение:
Пусть $S$ – площадь поперечного сечения кольца, $T$ -сила натяжения в кольце. Рассмотрим малый участок кольца длиной $R Delta theta$ (рис.). Его масса равна $rho SR Delta theta$. Этот участок находится под действием двух сил натяжения $T$, которые в сумме обеспечивают центростремительное ускорение $omega^{2}R$, чтобы он вместе с кольцом двигался по окружности с заданной угловой скоростью $omega$. Векторная сумма сил натяжения равна $2T sin frac{ Delta theta}{2}$. Следовательно,
$rho SR^{2} omega^{2} Delta theta = 2T sin frac{ Delta theta}{2} approx T Delta theta$,
откуда получаем силу натяжения, приходящуюся на единицу площади поперечного сечения кольца:
$frac{T}{S} = rho R^{2} omega^{2}$.
Относительное удлинение стержня под действием силы растяжения пропорционально силе натяжения, деленной на площадь сечения и на модуль Юнга:
$epsilon = frac{T/S}{E}$.
Таким образом, окончательно получаем, что длина окружности кольца увеличится на
$Delta l = epsilon cdot 2 pi R = frac{2 pi rho R^{3} omega^{2}}{E}$.
Жорина Л., Черноуцан А.И. Решение задач с распределенной силой // Квант. — 2004. — № 6. — С. 36-38.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
При решении задач из различных разделов физики приходится встречаться с ситуациями, когда силы непрерывно распределены вдоль какой-нибудь линии или поверхности. Обычно требуется найти или равнодействующую этих сил, или возникающие в объекте их приложения (линейном или плоском) натяжения и деформации.
При решении таких задач удобно использовать один из двух подходов. В первом подходе — назовем его дифференциальным — анализируют силы, действующие на маленький элемент линии или поверхности, при этом размер этого элемента в окончательный ответ не входит. Во втором — инmегральном — подходе производят суммирование по всем элементам, опираясь при этом на симметрию системы и стараясь избежать прямого интегрирования. Впрочем, как мы увидим, эти подходы тесно друг с другом связаны.
Начнем с рассмотрения линейных объектов.
Задача 1. Точечный заряд q находится в центре кольца радиусом R, по которому равномерно распределен одноименный заряд Q. Найдите силу натяжения кольца. Взаимодействие зарядов кольца друг с другом не учитывать.
Разберем два способа решения этой задачи.
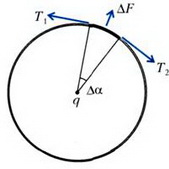
Способ 1. Запишем условие равновесия элемента кольца, видного из центра под маленьким углом Δα (рис. 1).
Рис. 1.
Заряд этого элемента равен 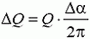
от заряда qи две одинаковые по модулю силы натяжения
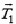
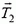
. Равнодействующая сил натяжения (с учетом малости Δα) составляет
, и условие равновесия этого элемента принимает вид
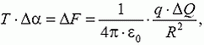
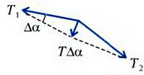
Способ 2. Рассмотрим силы, приложенные к полукольцу (рис. 2).
Рис. 2.
На него действуют две параллельные силы натяжения. Их сумма, равная 2T, уравновешивается равнодействующей всех электростатических сил, приложенных к различным элементам полукольца. Из симметрии системы очевидно, что равнодействующая электростатических сил направлена по оси у. Получаем
Смысл приведенного расчета состоит в следующем: вместо того чтобы брать проекцию силы, приложенной к элементу кольца, на ось у, мы заменили этот элемент его проекцией на ось х: . Мы как бы «выпрямили» полуокружность, после чего все силы стали параллельны друг другу. Отметим, что, в соответствии с третьим законом Ньютона, мы одновременно вычислили силу, действующую на точечный заряд qсо стороны полукольца, т.е. нашли напряженность поля, создаваемую полукольцом с зарядом
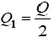
На первый взгляд, второй способ решения выглядит более громоздким и искусственным. Однако в некоторых случаях, особенно при вычислении равнодействующей силы, он имеет определенные преимущества.
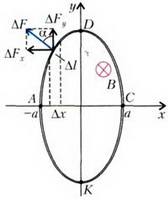
Задача 2. Плоский контур расположен в однородном магнитном поле с индукцией В перпендикулярно линиям индукции. По контуру течет ток силой I. Найдите натяжение провода контура в двух случаях: а) контур имеет форму окружности радиусом R; б) контур имеет форму эллипса с полуосями a и b. Во втором случае следует найти натяжение в точках пересечения эллипса с осями. Силой магнитного взаимодействия частей контура пренебречь.
Первый случай очень похож на задачу 1, и его можно решать любым из двух способов. При решении первым способом получаем уравнение, связывающее силу натяжения провода с магнитной силой (силой Ампера), действующей на контур со стороны магнитного поля:
откуда
Однако ясно, что такое решение не применимо к контуру в форме эллипса. Что же касается второго подхода, то он применим как в первом, так и во втором случаях.
Чтобы найти натяжение провода в точках А и С эллипса (рис. 3), надо вычислить магнитную силу , действующую на примыкающую к этим точкам половину эллипса.
Рис. 3.
Проекции этой силы на оси x и yравны, соответственно,
и
Поскольку магнитная сила равна двум силам натяжения, получаем
Аналогично найдем натяжение провода в точках D и К:
Можно заметить, что такой же расчет применим к участку контура любой формы. Сформулируем утверждение: сила, действующая со стороны однородного магнитного поля на участок контура с током любой формы, соединяющий какие-то две точки, равна силе, действующей на соединяющий эти точки прямой провод с таким же током. Физический смысл этого утверждения состоит в том, что полная сила, действующая на замкнутый контур с током со стороны однородного магнитного поля, должна быть равна нулю (иначе бы нарушался закон сохранения энергии).
Задача 3. Тонкое кольцо массой m и радиусом R вращается вокруг своей оси с угловой скоростью ω. Найдите натяжение кольца.
Запишем второй закон Ньютона для малого элемента кольца. Равнодействующая двух сил натяжения сообщает этому элементу центростремительное ускорение:
откуда
Это решение аналогично первому, т.е. дифференциальному, подходу в статических задачах. А применим ли в этом случае интегральный подход? Если мы запишем второй закон Ньютона для половины кольца, то в формулу для центростремительного ускорения центра масс полукольца войдет расстояние rц от центра масс до оси:
Если бы мы знали rц, то нашли бы натяжение Τ вторым способом. Однако можно использовать это уравнение именно для вычисления rц: подставив сюда T, вычисленное первым способом, получим
Задача 4. Тонкое алюминиевое кольцо радиусом R = 10 см вращается вокруг своей оси. При какой угловой скорости кольцо разорвется, если разрыв происходит при механическом напряжении σκρ = 2•107 Н/м2. Плотность алюминия ρ = 2700 кг/м3.
Условие разрыва кольца запишем в виде
где Τ — натяжение кольца, S — площадь сечения. Подставим Τ из решения предыдущей задачи и учтем, что 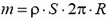
Получим
Интересно, что ответ не зависит от толщины кольца.
Перейдем теперь к рассмотрению не линейных, а плоских объектов. Обычно в этих задачах удобнее применять второй (интегральный) подход. Однако попробуйте самостоятельно решить их и с помощью дифференциального метода.
Задача 5. Внутри тонкой сферы радиусом R создано избыточное давление р. Какой должна быть толщина сферы, чтобы она при этом не разорвалась, если разрыв происходит при напряжении σκρ?
Из условия равновесия полусферы следует, что сила упругости в диаметральном сечении равна равнодействующей сил давления:
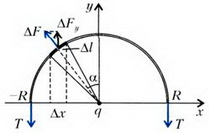
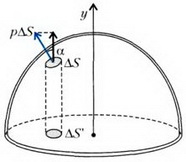
Для вычисления равнодействующей сил давления отметим, что она направлена вдоль оси симметрии полусферы (рис. 4):
Рис. 4.
Как и в задачах 1 и 2, мы, вместо того чтобы проецировать силу на ось симметрии, взяли проекцию площади площадки ΔS на плоскость, на которую опирается полусфера (т.е. как бы «выпрямили» полусферу). Подставив в предыдущую формулу, получим
Из условия σ < σκρ найдем
Обратите внимание на близкую аналогию этой задачи с задачей вычисления избыточного давления под искривленной поверхностью жидкости, возникающего вследствие поверхностного натяжения (так называемое лапласово давление). В этом случае условие равновесия поверхностной пленки имеет вид
где σ в данном случае — коэффициент поверхностного натяжения жидкости. Отсюда получаем
Аналогично случаю линейных объектов (см. задачу 2), расчет равнодействующей сил давления можно обобщить на поверхность любой формы. Обобщение выглядит так: если давление постоянно, то равнодействующая сил давления, действующих на произвольную поверхность, опирающуюся на плоский участок, равна силе давления, приложенной к этому участку. Физический смысл этого утверждения состоит в том, что полная сила давления на замкнутую поверхность равна нулю (если давление постоянно).
Умение увидеть физический смысл рассчитываемой величины позволяет иногда заметно упростить задачу, которая изначально выглядит сложной.
Задача 6. Тонкий полусферический колокол радиусом R стоит на горизонтальной поверхности. Через маленькое отверстие в верхней точке колокол заполняют водой. Чему равна масса колокола, если в тот момент, когда вода полностью заполнила колокол, она начала из под него вытекать?
Условие отрыва колокола от горизонтальной поверхности сводится к тому, что равнодействующая сил давления, действующих на него со стороны воды, равна его силе тяжести:
Прямое вычисление равнодействующей сил давления сложнее, чем в предыдущей задаче. Поскольку давления в разных точках колокола разные, избежать интегрирования в прямом расчете не удается. Однако если заметить, что искомая сила давления приложена не только к колоколу, но и к воде, то ее можно найти из условия равновесия объема воды:
где 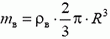
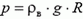
или
Задача 7. Вычислите напряженность электрического поля в центре полусферы радиусом R, по поверхности которой равномерно распределен заряд Q.
Как отмечалось в задаче 1, такая задача идентична задаче о силе, действующей на заряженную полусферу со стороны точечного заряда, помещенного в ее центр. Однако в данном случае мы проведем расчет непосредственно для напряженности.
Поскольку напряженность направлена вдоль оси симметрии полусферы, то возьмем проекцию на это направление от напряженности, создаваемой маленьким участком полусферы площадью ΔS:
где 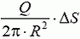
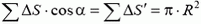
Задача 8. Проводящая сфера радиусом R заряжена зарядом Q. С какой силой отталкиваются друг от друга две половинки сферы?
Вычислим силу, действующую на маленький участок поверхности площадью ΔS . Эта сила равна
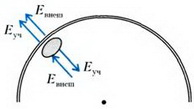
где Евнеш — напряженность поля, создаваемого внешними (по отношению к данному участку) зарядами сферы. Чтобы найти Евнеш, заметим, что полная напряженность среды вблизи поверхности равна (рис. 5)
где 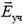
Рис. 5.
По разные стороны выделенного участка векторы 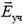
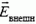
Тогда получаем
Следовательно, внутри заряженной сферы как бы существует давление
Как было показано в задаче 5, сила, действующая на полусферу, равна
Заметим, что формула для давления может быть получена и из энергетических соображений. Мысленно уменьшая радиус сферы на ΔR, мы совершим работу против силы давления, равную
которая равна изменению электростатической энергии
где ω — объемная плотность энергии. Видно, что электростатическое давление на металлическую поверхность отрицательно (направлено в сторону поля) и равно объемной плотности энергии поля:
Упражнения
1. Резиновое кольцо массой m и радиусом R0 раскрутили вокруг его оси до угловой скорости ω. Найдите новый радиус кольца, если жесткость резины k.
2. Петлю из резинового шнура длиной l0 положили на пленку жидкости. Пленку прокололи внутри петли, в результате чего она растянулась в окружность длиной l. Считая известной жесткость резины k, определите коэффициент поверхностного натяжения жидкости.
3. По длинному соленоиду радиусом R течет ток силой I. При этом индукция магнитного поля соленоида равна В. Найдите силу натяжения провода соленоида. Указание: учтите отличие внешнего поля от поля самого соленоида (см. задачу 8).
4. Тонкостенный цилиндр длиной l и радиусом R заполнили газом под давлением р. Найдите силу взаимодействия двух половинок цилиндра, если его мысленно разрезать плоскостью: а) перпендикулярной оси цилиндра, б) проходящей через ось цилиндра.
Ответы
1.
2.
3.
4. а) 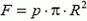
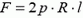
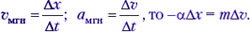
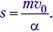
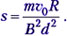
 , радиус
, радиус  , тогда линейная плотность заряда на нём
, тогда линейная плотность заряда на нём  . Пусть напряжённость поля, создаваемого кольцом на неком малом участке самого кольца равна
. Пусть напряжённость поля, создаваемого кольцом на неком малом участке самого кольца равна  . Выделим малый участок кольца, видимый из центра под углом
. Выделим малый участок кольца, видимый из центра под углом  . Заряд участка
. Заряд участка  . Электростатическая сила, действующая на участок
. Электростатическая сила, действующая на участок  . Сила натяжения кольца
. Сила натяжения кольца  . Тогда
. Тогда  ,
,  . Требуется найти напряженность E.
. Требуется найти напряженность E. начнём от точки, напряжённость в которой нас интересует. Найдём напряжённость, создаваемую в одной из точек кольца участком, видимым из центра под углом
начнём от точки, напряжённость в которой нас интересует. Найдём напряжённость, создаваемую в одной из точек кольца участком, видимым из центра под углом  . Проекция напряженности на радиус:
. Проекция напряженности на радиус:  .
. .
. ;
;  . Интеграл идентичен предыдущему, не сходится.
. Интеграл идентичен предыдущему, не сходится. , то для силы получаем выражение:
, то для силы получаем выражение:

 стремится к 4.
стремится к 4. . Подсчитаем, с какой силой левая и правая половины отталкиваются друг от друга.
. Подсчитаем, с какой силой левая и правая половины отталкиваются друг от друга.
 , и для поставленных вопросов коэффициент пропорциональности роли не играет.
, и для поставленных вопросов коэффициент пропорциональности роли не играет.