Как найти силу нормального давления формула

Leonid

Высший разум

(388685)


12 лет назад

Опечатка. Должно быть N=mg.
А определение дано верно. Если сила давления направлена под углом к поверхности, то её можно разложить на две составляющие: одна по касательной (параллельно поверхности, если она плоская) , другая – перпендикулярно касательной, то есть по нормали. Вот её и называют силой нормального давления.

Миша Еременчук

Гуру

(2952)


12 лет назад

Ivan Lakotko

Знаток

(292)


1 год назад

Опечатка. Должно быть N=mg.
А определение дано верно. Если сила давления направлена под углом к поверхности, то её можно разложить на две составляющие: одна по касательной (параллельно поверхности, если она плоская) , другая – перпендикулярно касательной, то есть по нормали. Вот её и называют силой нормального давления.

Лабораторная работа №1

Исследование зависимости силы трения скольжения от веса тела

   Цель работы: 1. выяснить, зависит ли сила трения скольжения от силы нормального давления, если зависит, то как.

                           2. Определить коэффициент трения дерева по дереву.

   Приборы и материалы: динамометр, деревянный брусок, деревянная линейка или деревянная плоскость, набор грузов по 100 г.

 Выполнение работы.

1. Определили цену деления шкалы динамометра.

Цена деления динамометра: 

(2H-1H)/10 дел = 0,1Н/дел

2. Определили массу бруска. Сначала подвесив брусок к динамометру нашли вес бруска   Pбруска=0,7Н

Зная, что  P=mg  и   g=10м/с²   получим m_бруска=P/g 

m_бруска=0,7Н/10м/с²=0,07кг

Определяем общий вес тела (силу нормального давления по формуле:

Р=N=(m1+m2)∙g

1.Р=N=(0,07кг+0,1кг)∙10м/с2=1,7Н

2.Р=N=(0,07кг+0,2кг)∙10м/с2=2,7Н

3.Р=N=(0,07кг+0,3кг)∙10м/с2=3,7Н

4.Р=N=(0,07кг+0,4кг)∙10м/с2=4,7Н

5.Р=N=(0,07кг+0,5кг)∙10м/с2=5,7Н

Провели измерения силы трения.

5. Подготовили таблицу для записи результатов измерений и вычислений:

6. Из опыта видим, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения)

7. В каждом опыте рассчитали коэффициент трения по формуле: . 

μ=0,4Н/1,7Н=0,235

μ=0,6Н/2,7Н=0,222

μ=0,8Н/3,7Н=0,216

μ=1,0Н/4,7Н=0,213

μ=1,2Н/5,7Н=0,211

Результаты расчётов занесли в таблицу.

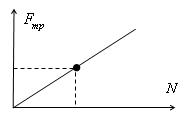
8. По результатам измерений построили график зависимости силы трения от силы нормального давления: 

Определили по графику средние значения силы трения и силы нормального давления:

N=3Н

Fтр=0,68Н

Вычислили среднее значение коэффициент трения:

μ_ср=0,68Н/3Н=0,227

Вывод: мы определили, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения). Коэффициент трения дерева по дереву получился равен 0,227

Ответы на контрольные вопросы.

1. Что называется силой трения?

Сила трения – это сила, которая возникает в том месте, где тела соприкасаются друг с другом, и препятствует перемещению тел.

2. Какова природа сил трения?

Сила трения – это сила электромагнитной природы.

3. Назовите основные причины, от которых зависит сила трения?

Возникновение силы трения объясняется двумя причинами:

   1) Шероховатостью поверхностей
   2) Проявлением сил молекулярного взаимодействия.

4. Перечислите виды трения.

Силы трения подразделяются на силы трения покоя, скольжения, качения.

5. Можно ли считать явление трения вредным? Почему?

Физика, 10 класс

Урок 15. Основы гидромеханики

Перечень вопросов, рассматриваемых на уроке:

1.Сила давления

2.Давление

3.Закон Паскаля

4.Гидростатическое давление

5.Атмосферное давление

6.Закон Архимеда

Глоссарий по теме

Гидростатика – раздел механики, в котором изучается равновесие покоящихся жидкостей и их давление на погруженные в них тела.

Давление – это величина равная отношению силы давления к площади поверхности, на которую эта сила действует.

Нормальное атмосферное давление – это величина давления, равная 760 мм рт. ст. или 101325 Па.

Сила Архимеда –выталкивающая сила, действующая на тело, погруженное в жидкость или газ

Основная и дополнительная литература по теме урока:

Грачев А.В., Погожев В.А., Салецкий А.М., Боков П.Ю. Физика.10 класс. М.: Вентана-Граф, 2017. – С. 222 – 229.

Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006, С.36-50.

Основное содержание урока

Силой давления называется сила, действующая перпендикулярно некоторой поверхности.

Результатом действия силы давления является давление.

Отношение модуля силы давления F к площади поверхности S, на которую эта сила действует, называется давлением

Закон Паскаля.

Силы давления в данной точке покоящейся жидкости (газа) действуют во всех направлениях одинаково. При ведём простое доказательство закона.

Выделим в какой-нибудь точке покоящейся жидкости её малый объём в форме прямоугольного параллелепипеда или куба.

Если кубик покоится, значит сумма сил, действующих на его 6 граней равна нулю. Это означает, что силы, действующие попарно на противоположные грани куба, равны по модулю, а, следовательно, и давления будут равны по всем направлениям.

Ввиду произвольности ориентации выбранного нами малого объёма жидкости, очевидно, что давление по всем направлениям должно быть одинаково.

Гидростатическое давление. Атмосферное давление.

Это давление, оказываемое «столбом» жидкости на уровне плоскости своего нижнего основания.

Выделим в покоящейся жидкости «столб» – цилиндр высотой h и площадью основания S, верхнее основание которого совпадает со свободной поверхностью жидкости.

По первому закону Ньютона сумма проекций трех сил, действующих на столб жидкости: силы атмосферного давления, силы тяжести и силы давления жидкости- равна нулю

F_p– mg – F_атм = 0;

Но так как mg=ρ·V·g=ρ·S·h·g; F_p = p·S; F_атм = p_атм ·S,

Получим p = p_атм+ ρ·g·h;

где p_атм – атмосферное давление; ρ – плотность жидкости; g – ускорение свободного падения; h – глубина.

Величина ρ·g·h называется гидростатическим давлением.

Атмосферное давление – это давление в какой-нибудь точке атмосферы.

Нормальное или среднее значение атмосферного давления равно 760 мм ртутного столба, что соответствует 101325 Па. Т.е. 1 мм рт. ст. = 133,322 Па.

Зависимость атмосферного давления от высоты имеет сложный вид из-за сжимаемости воздуха (в отличие от жидкостей).

Закон Архимеда. Сила Архимеда.

Выделим в жидкости объем прямоугольного параллелепипеда, ориентированного для удобства анализа так, чтобы нижняя и верхняя грани были параллельны поверхности жидкости

На тело в жидкости действуют сила тяжести и силы давления со стороны жидкости. Давление на боковые стенки равны. Сила давления снизу больше, чем сила давления сверху. Разность этих двух сил и есть выталкивающая сила – сила Архимеда.

F_A=p₂ S – p₁ S =S( p₂ – p₁) = ρ g S(h₂ – h₁) = ρ gV

На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости.

где – плотность жидкости; g – ускорение свободного падения; V_m – объём погруженной в жидкость части тела

Разбор тренировочных заданий

1. Найдите силу нормального атмосферного давления на грань куба с ребром 1 м. Округлите до целых кПа.

Варианты ответов:

1) 100;

2) 125;

3) 101;

4) 110

Решение. По определению сила давления равна F = p x S;

Нормальное атмосферное давление p = 101325 Па; площадь грани куба (1м)² = 1м²;

Получим значение силы давления F = (101325 Н/м² ) х (1 м²) = 101325 Н =101,325 кН.

Ответ: 3) 101

2. В первой строке таблицы приведены значения атмосферного давления на разных высотах. Занесите во вторую строку соответствующие значения высот из перечня: h₁, h₂, h_3, h₄, если известно, что h₃ > h₄ > h₁ > h₂

Решение. Как известно, давление атмосферы падает с высотой. Выпишем в порядке убывания давления: 750,738,550,525. Из приведённого неравенства имеем, что наименьшая высота h₂, затем h₁, h₄ и h₃. Наименьшей высоте соответствует наибольшее давление и т.д. Высота растёт, давление падает. Или наоборот. В таблицу теперь под каждым давлением впишем соответствующее значение высоты.

Ответ:

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Силы давления

Д

авление
– напряжение, возникающее в жидкости
под действием сжимающих сил.

В общем случае
поверхностная сила

,
действующая на площадке

под некоторым
углом к ней, может быть разложена на
нормальную

и тангенциальную

составляющие. Первая, направленная
внутрь объема, называется силой давления,
вторая – силой трения. Нормальная
составляющая вызывает в жидкости
нормальные напряжения или гидромеханическое
давление,
которое в покоящейся жидкости называется
гидростатическим.
Если сила

равномерно распределена по площадке

,
то

,

или переходя, к
пределу

.

В любом случае
причиной возникновения давления является
внешняя сила, приложенная к жидкости.
Часто в гидроприводе такой силой является
нагрузка F,
приложенная к исполнительному органу.
Эта нагрузка воздействует на жидкость
через какую-то жёсткую поверхность и,
следовательно, распределена равномерно,
например площадь поршня гидроцилиндра
S.
В таком случае давление P
определяется по формуле

.

Если давление
отсчитывается от нуля, оно называется
абсолютным
и обозначается


,
если от атмосферного, – избыточным
и обозначается

.
Атмосферное
давление обозначается

.

Кроме того, различают
давление гидродинамическое
и гидростатическое.
Гидродинамическое давление возникает
в движущейся жидкости. Гидростатическое
давление – давление в покоящейся
жидкости.

Свойства гидростатического давления

Первое свойство
формулируется следующим образом: на
внешней поверхности жидкости
гидростатическое давление всегда
направлено по нормали внутрь
рассматриваемого объёма.

В приведённой
формулировке «внешняя поверхность»
это любая поверхность, которую можно
выделить внутри жидкости (даже мысленно),
или поверхность раздела сред.

Д

оказывается
первое свойство путём рассуждений
методом «от противного».

Рассмотрим
покоящуюся жидкость. Известно, что
жидкость плохо сопротивляется касательным
усилиям. Если бы сила, от давления R
действовала бы не по нормали к площадке,
то её можно было бы представить в виде
двух составляющих – нормальной F_n
и касательной
F_τ.
Тогда касательная составляющая смещала
бы слои жидкости друг относительно
друга. Это означало бы, что жидкость не
находилась бы в покое. Это противоречит
начальному утверждению.

Из первого свойства
следует, что напряжение сжатия –
единственный вид напряжений в покоящейся
жидкости

Второе свойство
состоит
в том, что в
любой точке внутри жидкости давление
по всем направлениям одинаково. Иначе
это свойство давления звучит так: на
любую площадку внутри объёма жидкости,
независимо от её угла наклона, действует
одинаковое давление.

Докажем второе
свойство. Для этого рассмотрим произвольный
объём в неподвижной жидкости в виде
прямоугольного тетраэдра с размерами

.
Будем рассматривать
этот объём в некоторой произвольной
системе координат X,Y,Z.

На рисунке приведены
следующие буквенные обозначения:

–
гидростатическое давление, действующее
на грань, перпендикулярную соответствующей
оси,

–
гидростатическое давление, действующее
на наклонную грань dS,

F–
инерционные силы
(или силы веса).

Тетраэдр dx,
dy,
dz
по определению находится в покое,
следовательно, сумма сил, действующих
на него равна 0,
т.е.

Подробно рассмотрим
эти силы. Прежде всего, на выделенный
тетраэдр действуют силы давления. В
проекциях на оси системы координат по
направлению каждой из осей действует
сила от давления на грань, перпендикулярную
этой оси. Этой силе противодействует
проекция на соответствующую ось силы
давления на наклонную (большую) грань
тетраэдра. Получаются три пары сил,
соответственно осям:

Вместе с силами
давления, в общем случае, на тетраэдр
действуют инерционные силы (или в
простейшем случае сила веса), которые
равны произведению массы на проекцию
ускорения на соответствующую ось. Массу
определим как произведение плотности
жидкости и объёма тетраэдра. Объём для
прямоугольного тетраэдра равен

.
В этом случае инерционные силы примут
вид:

.

Сложив обе полученные
системы уравнений, и, приравняв их 0
по причине равновесия тетраэдра, получим
общую систему уравнений сил, действующих
в покоящейся жидкости:

Если учесть, что
площадь каждой грани тетраэдра,
параллельной плоскостям координат,
равна площади проекции наклонной грани
на соответствующую координатную
плоскость, получим следующее равенство:

.

Разделив уравнения
сил на соответствующие одинаковые
площади, получим:

.

Устремив размеры
тетраэдра к 0,
т.е.

и

последняя система уравнений примет
вид:

.

Приравняв все три
уравнения, получим следующее равенство:

.

В результате можно
сделать следующий вывод:
давление
не зависит от направления, или другими
словами: давление
– величина скалярная.

Однако возникает
вопрос, каким образом получается, что
давление и площадь величины скалярные,
а их произведение сила – величина
векторная.

.

Ответ на этот
вопрос заключается в следующем.
Направление вектора
силы
задаёт площадка, на которую действует
давление. Это направление всегда
перпендикулярно
площадке действия
и направлено внутрь рассматриваемого
объёма.