Как найти силу по уравнению координаты

Как составить силовые уравнения

В задачах динамики учитывают силы, действующие на тело. Векторы сил могут действовать в различных направлениях. Большинство школьных задач можно решить, располагая векторы сил в одной плоскости. Поэтому, в статье будем рассматривать векторы, лежащие в одной плоскости — компланарные векторы.

Что такое равнодействующая

Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.

Результат сложения может дать:

вектор, имеющий длину,
или вектор, не имеющий длины.

Примечание: Когда у вектора отсутствует длина, говорят, что вектор равен нулю. На рисунке нулевой вектор можно изобразить одной точкой. Длины у точки нет – т. е. длина нулевая, а направление может быть любым.

Длина вектора содержит сумму квадратов всех его проекций на оси.

Где ( a_ ) и ( a_ ) — это проекции вектора (ссылка) ( vec ) на оси Ox и Oy.

Когда вектор равен нулю, равна нулю каждая его проекция на осях.

Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.

Левая часть силового уравнения

В левой части силового уравнения записываем силы, действующие на тело.

Когда векторы сил направлены вдоль параллельных прямых, проводим на рисунке одну ось. Если векторы сил не параллельные, проводим две оси на плоскости. Раскладываем векторы на проекции по осям. Для каждой оси составляем отдельное уравнение. Количество уравнений совпадает с количеством осей.

Если сила сонаправлена с осью, то она войдет в левую часть уравнения со знаком «+», а если она направлена против оси — то со знаком «минус».

Правая часть силового уравнения

В правой части уравнения записываем равнодействующую. В задаче может присутствовать несколько осей, вдоль каждой оси направляем отдельную проекцию равнодействующей.

Примечание: Тело может вдоль одной оси двигаться с ускорением, а вдоль другой оси двигаться без ускорения, или, вообще, покоиться. Например, тело может двигаться по вертикали под действием силы тяжести, а по горизонтали при этом не смещаться.

Когда проекция равнодействующей вдоль какой-либо оси не равна нулю, тело по оси будет двигаться с ускорением. Это следует из второго закона Ньютона.

Тогда в правой части уравнения запишем:

(ma), если ускорение направлено туда же, куда направлена ось;
(- ma), если ускорение направлено противоположно оси;

А когда проекция равнодействующей на ось нулевая, ускорение вдоль оси отсутствует. Тогда вдоль этой оси тело движется с неизменной скоростью, или же, вдоль этой оси движение отсутствует. Это следует из первого закона Ньютона.

В правой части уравнения запишем ноль (0 = ускорения нет).

Векторы сил параллельны

В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.

Выясним, как выглядит силовое уравнение для задачи, в которой векторы сил направлены вдоль единственной оси. Например, парашютист спускается вертикально вниз (рис. 1) на парашюте под действием силы тяжести.

Проведем на рисунке ось, направим ее вверх.

Примечание: Мы можем направить ось вниз, если захотим. При таком направлении оси знаки проекций векторов изменятся на противоположные, но на конечный ответ это никак не повлияет.

Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:

Сила ( F_<text<сопр>>) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.

В правую часть уравнения поместим равнодействующую.

Размеры парашюта рассчитаны так, что парашютист опускается вниз с постоянной (неизменной, т. е. одной и той же) скоростью. Значит, скорость есть, она не меняется, ускорения нет.

Математики запишут, что ускорение есть, но оно – нулевое (vec=0).

То есть, вдоль вертикальной оси тело движется без ускорения, значит, силы компенсировались. По первому закону Ньютона, равнодействующая равна нулю и, в правой части уравнения запишем ноль.

Примечания:

На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec>). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.

Итоговое силовое уравнение имеет вид:

[large F_<text<сопр>> — m cdot g = 0 ]

Зная массу парашютиста, можно вычислить силу сопротивления воздуха. А зная эту силу, можно рассчитать и размеры парашюта.

Векторы сил не параллельны

Когда векторы направлены вдоль разных прямых, будем проводить две взаимно перпендикулярные оси на плоскости.

Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).

Поверхность шероховатая, это намек на то, что есть сила трения. А если в условии напишут, что поверхность гладкая, значит, силы трения нет.

Движение равнозамедленное (ссылка), значит, скорость тела уменьшается и есть вектор ускорения, который направлен против вектора скорости.

Нарисуем взаимно перпендикулярные оси. Ось Ox проведем горизонтально, а ось Oy – вертикально. Рассмотрим оси и проекции векторов на них по очереди.

Горизонтальная ось. Пусть движение тела происходит в положительном направлении оси Ox. Сила трения всегда направлена против движения, поэтому направим ее влево. Скорость тела направлена вправо и будет уменьшаться, значит, ускорение, так же, направим влево. Вектор ускорения рисуем отдельно от векторов сил.

Наличие ускорения говорит о том, что вдоль оси Ox равнодействующая имеет не нулевую проекцию. Ускорение направлено против оси, запишем (- ma) в правой части уравнения.

Так выглядит уравнение для горизонтальной оси

Вертикальная ось. Вниз направлена сила тяжести, а вверх – сила реакции опоры. Так как поверхность горизонтальная и тело не движется ни вверх, ни вниз, то движения вдоль оси Oy нет. Значит, сила тяжести и реакция опоры компенсировались и нет ускорения вдоль оси Oy. В правой части уравнения для вертикальной оси запишем ноль.

Для вертикальной оси уравнение выглядит так:

[large N — m cdot g = 0 ]

Система, пригодная для решения задачи, состоит из двух уравнений

Куда направить оси

Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).

Силы, действующие на тело в этой задаче, не параллельные, направлены вдоль разных прямых. Поэтому для составления уравнений нужно использовать две взаимно перпендикулярные оси. Попробуем для начала провести ось Oy вертикально, а ось Ox горизонтально.

Из рисунка 3 видно, вдоль оси направлен только один вектор (mg). Остальные векторы сил не параллельны ни одной из осей. Такие векторы придется раскладывать на проекции, это усложнит конечную систему уравнений.

Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.

Попробуем теперь провести оси так, чтобы как можно большее количество векторов оказались параллельными осям (рис. 4). Из рисунка видно, что только один вектор (mg) окажется ненаправленным вдоль какой-либо оси. Остальные векторы сил параллельны осям.

При таком выборе осей раскладывать на проекции придется только один вектор. Это позволит быстрее решить задачу и решать более простые уравнения.

Примечание: Если мы выбререм оси так, как это представлено на рисунке 3, получим более сложные уравнения. Но решив их, мы получим точно такой же ответ, как и в случае выбора осей на рисунке 4.

Выводы:

Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.

Движение по наклонной плоскости

Составим систему уравнений для решения такой задачи:

Велосипедист подъезжает с начальной скоростью к подъему, посыпанному песком и, едет в гору на велосипеде по инерции, не крутя педали. Масса велосипедиста с велосипедом, начальная скорость его, коэффициент сопротивления поверхности и угол наклона известны.

Нужно составить систему силовых уравнений, чтобы найти ускорение велосипедиста. А после, зная начальную скорость и ускорение, найти путь, который велосипедист сможет проехать по инерции в горку.

Выражение для ускорения

Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)

Мы провели оси так, чтобы пришлось разложить на проекции только один вектор и система силовых уравнений оказалась достаточно простой.

Пользуясь осями координат, составляем теперь уравнения в проекциях.

Уравнение для проекций векторов на ось Ox:

[ large — F_<text<трен>> – m cdot g_ = — m cdot a ]

Уравнение для проекций векторов на ось Oy:

[ large N – m cdot g_ = 0 ]

Разложим теперь силу тяжести — вектор (mg) на проекции. Чтобы проделать это разложение, нужно отметить угол (alpha ) межу вектором (mg) и одной из осей. В нашем случае, это угол между вектором (mg) и осью Oy.

[ large begin m cdot g_ = mg cdot cos left(alpha right) \ m cdot g_ = mg cdot sin left(alpha right) end ]

Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений

[ large begin — F_<text<трен>> – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end ]

Дополним эту систему выражением для силы трения.

Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.

[ large begin N = mg cdot cos left(alpha right) \ F_<text<трен>> = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end ]

Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:

[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]

Выражение для пройденного пути

Запишем выражения для связи скоростей и пройденного пути. Велосипедист движется по инерции в гору и его скорость уменьшается из-за силы тяжести и силы сопротивления поверхности, посыпанной песком. Когда скорость велосипедиста обратится в ноль, он, проехав часть пути в гору, остановится. Используем систему двух уравнений, она описывает путь при учете уменьшения скорости до нуля:

[ large begin 0 = v_ <0>— a cdot t \ S = v_ <0>cdot t — a cdot frac <2>end ]

Получим теперь уравнение для пути, в котором будут присутствовать только начальная скорость и ускорение и, будет отсутствовать время.

Упрощенная система для решения задачи теперь включает всего два уравнения

[ large begin mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_ <0>cdot frac> — frac> <2>cdot frac> end ]

Подставив в эту систему известные значения начальной (v_<0>) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

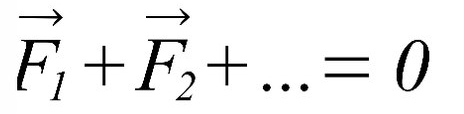
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T – сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM:

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное – понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс – это отношение противолежащего катета к прилежащему:

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Интегрирование дифференциальных уравнений прямолинейного движения материальной точки

Краткое изложение результатов

Здесь мы кратко изложим основные результаты, полученные при интегрировании дифференциальных уравнений прямолинейного движения материальной точки. Далее следует их подробное изложение.

Сила, зависящая от времени

Если на материальную точку действует сила, зависящая от времени , то дифференциальное уравнение прямолинейного движения вдоль оси Ox имеет вид:
.
Вводим ускорение и интегрируем это уравнение.
.
Здесь и далее A и B – произвольные точки на оси Ox . Заменим . Получаем закон изменения скорости от времени:
.
Интегрируя уравнение , получаем закон движения точки :
;
.

Сила, зависящая от скорости

Пусть на точку действует сила, зависящая от скорости . Составляем дифференциальное уравнение движения и интегрируем его:
.
Последнее уравнение дает в неявном виде зависимость . Решаем его. После чего интегрируем уравнение , как описано выше.

Есть второй способ интегрирования уравнения движения в случае зависимости силы от скорости. Для этого переходим от переменных x и t к переменным и x . Считаем, что скорость является функцией от координаты x :
;
.
Последнее уравнение дает в неявном виде зависимость . Далее интегрируем уравнение :
.
Это уравнение дает в неявном виде закон движения точки .

Сила, зависящая от перемещения

Пусть на точку действует сила, зависящая от перемещения . Составляем уравнение движения, переходим от переменных x и t к переменным и x , и интегрируем полученное дифференциальное уравнение:
;
;
.
Это уравнение представляет собой закон сохранения механической энергии для прямолинейного движения. Из него находим зависимость скорости от перемещения . После чего интегрируем уравнение , как это описано выше.

Дифференциальное уравнение движения точки

Рассмотрим прямолинейное движение материальной точки, находящейся под действием постоянных и переменных сил. Направим ось Ox системы координат вдоль линии движения точки. Пусть на нее действуют n сил, проекции которых на ось Ox мы обозначим как . Положение точки, при прямолинейном движении, однозначно определяется ее координатой x . Нам нужно определить закон движения точки , то есть закон изменения ее координаты со временем.

Уравнение движения точки определяется вторым законом Ньютона, который в случае прямолинейного движения имеет вид:
(1) .

Вместо того, чтобы в каждом уравнении выписывать все n сил, введем их равнодействующую, проекция которой, на ось x равна сумме проекций всех сил на эту ось:
.
Тогда задача сведется к движению материальной точки под действием одной силы . При этом уравнение движения примет наиболее простой вид:
(2) .
В дальнейшем, проекцию равнодействующей мы будем называть просто силой, действующей на точку.

Сила может быть как постоянной, так и зависеть от времени t , координаты x и от скорости . К сожалению, если зависит от всех перечисленных факторов, то не всегда возможно решить уравнение (2) аналитически. Поэтому мы рассмотрим те случаи, когда возможно получить аналитическое решение этого уравнения. Заметим, что если сила является постоянной, то уравнение (2) можно решать любыми, приводимыми ниже, способами.

Почему мы обозначаем в виде проекции силы на ось x , хотя рассматриваем только движение вдоль одной оси? – Потому что под обозначением силы R в виде одной буквы, часто подразумевается ее абсолютная величина: . Она имеет неотрицательные значения: . А когда мы пишем силу как проекцию , то подразумеваем, что эта величина может быть как положительной (если сила направлена вдоль оси x ), так и отрицательной (когда она направлена противоположно оси x ). В теоретической механике, в подобных случаях, иногда также говорят, что есть алгебраическое значение силы. Это относится не только к силе, ни и ко всем другим, рассматриваемым далее, векторным величинам.

Интегрирование уравнения движения с силой, зависящей от времени

Вначале рассмотрим случай, когда задан закон изменения силы со временем: . Перепишем уравнение (2), явно указав эту зависимость:
(t1) .

В этом уравнении время t является независимой переменной; координата x – зависимой переменной; – это вторая производная координаты по времени: . Масса m – это постоянная, то есть заданное число. С математической точки зрения, уравнение (t1) есть дифференциальное уравнение второго порядка, не содержащую зависимую переменную x в явном виде.

Решение такого уравнения выполняется с помощью подстановки
.
Тогда
.
Подставляя в (t1), мы получаем дифференциальное уравнение первого порядка:
(t2) .
Выполняя подстановку, мы ввели новую переменную , равную производной координаты x по времени t . Эта производная является проекцией скорости точки на ось Ox . Таким образом, процесс решения разбивается на две части. Сначала мы, решаем уравнение (t2), и находим закон изменения скорости со временем: . Затем, используя уравнение , находим закон изменения координаты .

Упростим уравнение (t2), разделив его на массу m :
(t3) ,
где – ускорение точки. Поскольку зависимость силы от времени известна, то и зависимость ускорения от времени также известна.

Уравнение (t3) является дифференциальным уравнением первого порядка с разделяющимися переменными. Разделяем переменные и интегрируем.
;
(t4) ;
(t5) .
Здесь – постоянная интегрирования. Чтобы ее определить, нужно знать значение скорости в какой-либо момент времени . Если мы сможем выразить интеграл через известные функции, то подставив в (t5) значения времени и значение скорости в этот момент, мы сможем определить постоянную .

Для простых задач, формула (t5) вполне удобна. Но если интеграл не выражается через известные функции, то выполнить численное интегрирование по этой формуле нельзя. Поэтому найдем закон изменения скорости со временем в более удобном виде.

Прямолинейное движение точки M под действием силы R_x.

Пусть нам известно, что в момент времени , точка M находилась в положении A, имела координату и скорость . Рассмотрим произвольный момент времени . Пусть в этот момент времени точка M находится в положении B, с координатой и скоростью . Величины и нам пока не известны. Наша задача их найти.

Перепишем (t4) явно указав, что есть функция от t :
(t6) .
Интегрируем (t6) от момента времени до :
.
Слева – интеграл от полного дифференциала. Поэтому он интегрируется элементарно:
.
Здесь мы учли, что . В результате получаем:
;
.

Этот результат можно получить и несколько иначе, если в интеграле сразу перейти к переменной . Тогда пределы интегрирования станут и . В результате получим тоже самое:
.

Итак, мы нашли значение скорости в произвольный момент времени :
(t7) .
Заменим обозначение момента времени на t . В результате получим закон изменения скорости со временем t :
(t8) .

Интеграл справа записан не вполне корректно, хотя так часто пишут. Рассмотрим пример определенного интеграла . Он зависит от пределов интегрирования a и b , но не зависит от переменной интегрирования t . Можно сказать, что переменная t принимает заданные значения из отрезка , которые применяются только для вычисления интеграла. Поэтому для переменной интегрирования t можно использовать любое обозначение. Например, можно использовать переменную . Тогда .

В (t8) мы использовали одно и то же обозначение, как для верхнего предела интеграла, так и для переменной интегрирования. Это может привести к путанице. Поэтому используем для переменной интегрирования любое другое, не используемое обозначение, например . Тогда формула (t8) примет следующий вид:
(t9) .

Теперь найдем закон изменения координаты x от времени. Интегрируем уравнение
.
Разделяем переменные:
(t10) .
Здесь мы также можем выполнить интегрирование от A до B, но мы продемонстрируем другой способ, как получить результат в удобном виде, применяя неопределенный интеграл. Поскольку неопределенный интеграл определен с точностью до постоянной, то запишем его с нижним пределом интегрирования . Интегрируем (t10):
(t11) .
Найдем значение постоянной интегрирования . Для этого подставим сюда :
.
Далее учитываем, что значение координаты точки в момент времени нам известно: . Также учитываем, что интеграл в правой части имеет равные пределы интегрирования и поэтому равен нулю. В результате получаем:
.
Отсюда находим значение постоянной интегрирования: . В результате получаем закон движения точки:
(t12) .

Итак, мы нашли, что если на точку действует сила , то для определения ее закона движения, нужно сначала определить закон изменения скорости со временем:
(t7) .
А затем определить закон движения:
(t12) .
При этом мы полагаем, что нам известны скорость и координата в некоторый момент времени . Если бы мы проводили интегрирование через неопределенные интегралы в общем виде, то и были бы постоянными интегрирования и .

Постоянная сила

Разберем случай, когда действующая на точку сила имеет постоянное значение: . В этом случае ускорение также постоянно: . Интегрируем, используя таблицу неопределенных интегралов. Из (t7) находим закон изменения скорости со временем:
;
(t14) .
Мы видим, что скорость линейно изменяется со временем.

Подставляем в (t12) и находим закон движения точки:

;
(t15) .

Если в начальный момент времени , скорость точки была , а координата , то . Из (t14) и (t15) получаем:
;
.

Равномерное движение

Если проекция силы на ось Ox равна нулю: , то ускорение также равно нулю: . В этом случае из (t14) находим, что скорость точки постоянна:
.
Из (t15) находим, что координата линейно меняется со временем:
.

Если в начальный момент времени , скорость точки была , а координата , то ;
;
.

Интегрирование уравнения движения с силой, зависящей от скорости

Разберем случай прямолинейного движения материальной точки, когда действующая сила зависит от скорости . Такие задачи встречаются при движении в жидкой или газообразной среде, когда на точку помимо постоянных сил, действует сила трения, зависящая от скорости. В этом случае, уравнение движения имеет вид:
(v1) .
Разделим обе части уравнения на массу m :
(v2) ,
где – ускорение точки. Теперь нам известна зависимость ускорения точки от ее скорости. Уравнение (v2) не содержит в явном виде как зависимую переменную x , так и независимую переменную t . Поэтому его можно решать двумя способами.

Решение уравнения, определяя v_x(t)

Применим к уравнению (v2) метод решения дифференциального уравнения, не содержащего зависимую переменную в явном виде. Для этого, как и в предыдущем случае, делаем подстановку
.
Тогда
.
Подставляя в (v2), мы получаем дифференциальное уравнение первого порядка:
(v3) .

Пусть, как и в предыдущем случае, в момент времени , точка находилась в положении A, имела координату и скорость . И пусть в произвольный момент времени , точка находится в положении B с координатой и скоростью . Нам нужно найти величины и .

Разделяем переменные.
;
.
Перепишем это уравнение, указав, что скорость является функцией от времени:
.
Интегрируем по времени от до :
.
В левой части сделаем замену переменной. От переменной t перейдем к переменной . При этом изменим пределы интегрирования учитывая, что при ; и при :
(v4) .

Заменим обозначения переменных , и переменной интегрирования . Подставим в (v4):
(v5) .
Это уравнение, в неявном виде, дает закон изменения скорости от времени t . Вычислив интеграл, и выполнив преобразование, мы можем выразить через t : .

Далее, по формуле (t12) ⇑ определяем закон движения материальной точки:
(t12) .

Решение уравнения, определяя v_x(x)

Выпишем уравнение (v2) еще раз.
(v2) .
Для применения этого метода, в качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . То есть считаем, что скорость является функцией от координаты: .

Выразим через переменные x и вторую производную координаты по времени:
.
Подставим в (v2) и разделяем переменные:
;
.
В левой части в явном виде запишем как функцию от x , и интегрируем по x от положения A до B:
;
.
В интеграле слева переходим от переменной x к :
(v6) .

Переобозначим переменные:
(v7) .
Это уравнение дает в неявном виде зависимость скорости от координаты:
.
Подставив сюда , получим для x дифференциальное уравнение первого порядка. Решаем его методом разделения переменных:
;
.
Интегрируем от положения A до B:
;
.
Заменим переменные:
(v8) .

Уравнение (v8) дает в неявном виде закон движения материальной точки .

Интегрирование уравнения движения с силой, зависящей от перемещения

Наконец рассмотрим случай прямолинейного движения материальной точки, когда действующая сила зависит от перемещения x . Такие задачи встречаются при движении в потенциальных полях – в гравитационных или электрических. Сюда также относится движение груза, прикрепленного к упругой пружине.

Выписываем уравнение движения для этого случая:
(x1) .
Это дифференциальное уравнение второго порядка. Оно не содержит независимую переменную t в явном виде. Также как и в предыдущем случае, применяем метод решения дифференциального уравнения, не содержащего независимую переменную в явном виде.

Перейдем к новым переменным. В качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . Считаем, что скорость является функцией от координаты: .

Выразим вторую производную координаты по времени через переменные x и :
;
Подставим в (x1) и разделяем переменные:
(x2) ;
.
Интегрируем по x от A до B:
(x3) .
Вычисляем интеграл, используя таблицу неопределенных интегралов:
;
.
Подставляем в (x3):
(x4) . Нетрудно видеть, что слева стоит изменение кинетической энергии материальной точки. Справа – работа, которую совершает сила при перемещении материальной точки из A в B. Само уравнение (x4) представляет собой теорему об изменении кинетической энергии точки для прямолинейного движения.

Вернемся снова к уравнению (x2).
(x2) .
Его можно проинтегрировать и другим способом.

Для этого представим правую часть в виде производной по координате:
,
где – координата произвольной заранее выбранной точки C .
Левую часть также представим в виде производной по координате:
.
Тогда (x2) можно записать в виде:
.

Поскольку производная по x от выражения в скобках равна нулю, то само выражение является постоянной, не зависящей от x величиной:
.
Такая форма записи, когда некоторая функция от переменных приравнивается постоянной, называется интегралом дифференциального уравнения. Перепишем его в следующем виде:
(x5) .
Здесь – кинетическая энергия точки; – потенциальная энергия, отсчитываемая от, произвольным образом выбранной, точки C ; E – постоянная интегрирования, которая в данном случае имеет определенный физический смысл – это полная механическая энергия материальной точки. Поэтому мы ее обозначили привычной для этого случая буквой E . Само уравнение (x5) представляет собой закон сохранения механической энергии. С математической точки зрения, энергия E является интегралом дифференциального уравнения, или, как говорят в механике, интегралом движения точки. То есть величиной, сохраняющей при движении постоянное значение.

Выше мы пришли к выводу, что постоянная интегрирования E не зависит от координаты x , но ничего не сказали о ее зависимости от времени. Однако, для одномерного движения, со временем может изменяться только одна координата x . Поскольку постоянная E от нее не зависит, то она не зависит также и от времени t . Поэтому полная механическая энергия сохраняет постоянное значение и в различные моменты времени.

Нетрудно видеть, что формулировки (x4) ⇑ и (x5) ⇑ эквивалентны. Для доказательства, приравняем механическую энергию точки для двух положений A и B:
;

.
Здесь мы разбили интеграл от до на два интеграла – от до ; и от до . Интегралы от до сократились.

Найдем зависимость скорости точки от координаты. При этом мы считаем, что скорость точки в положении A нам известна. Рассмотрим два положения: A и B. Из (x4) ⇑ имеем:
,
где – работа, которая производит сила при перемещении точки из A в B. Наконец, заменим на x , и на . В результате получим искомую зависимость:
(x6) ,
где – работа, которая производит сила при перемещении материальной точки из A в точку с координатой x . Скорость определена с точностью до знака (плюс или минус). Знак нужно выбирать из начальных условий и исследования движения. Если в точке , то при достаточно малых значениях . Далее точка может остановиться и начать движение в обратную сторону. Тогда нужно выбрать знак минус, чтобы скорость стала отрицательной.

Теперь, зная зависимость , находим закон движения материальной точки. Для этого интегрируем уравнение:
;
;
;
.
Это уравнение дает в неявном виде зависимость координаты x от времени t .

Приложение к движению в пространстве

Приведенные выше результаты могут быть применимы и для некоторых случаев движения материальной точки в двухмерном или трехмерном пространстве.

Пусть нам известно, что в момент времени , материальная точка находилась в точке A, и имела скорость . Выберем трехмерную систему координат Oxyz , и распишем эти начальные условия по компонентам:
При ;
При ;
При .

Сила в пространстве, зависящая от времени

Пусть на материальную точку действует сила, зависящая от времени: . Составим уравнения ее движения:
.

Выпишем уравнение для координаты x с начальными условиями:
; при .
Здесь все необходимые величины известны, и они не зависят от значений других координат. Мы можем найти закон изменения координаты x со временем, применяя интегрирование уравнения движения с силой, зависящей от времени ⇑ для прямолинейного движения.

Выпишем уравнение для координаты y с начальными условиями:
; при .
Здесь также известны все необходимые величины, и они не зависят от значений других координат. Мы также можем найти закон изменения координаты y со временем, применяя интегрирование, как для прямолинейного движения.

Точно также мы можем найти закон изменения координаты z со временем. В этом случае говорят, что переменные разделились. Уравнения движения, составленные для каждой из координат, вместе с начальными условиями, не зависят от значений других координат. Поэтому каждое такое уравнение можно проинтегрировать отдельно. В результате мы получим закон движения материальной точки в трехмерном случае: .

Силы, приводящие к разделению переменных

Пусть теперь на точку действуют три взаимно перпендикулярные силы. И пусть одна из них зависит только от времени; вторая – от проекции скорости на направление силы; третья – от проекции радиус-вектора на направление силы.

Выберем систему координат Oxyz , оси которой направим вдоль направлений действующих сил. Тогда в этой системе координат отличными от нуля будут только три проекции сил: . Составляем уравнения движения:
;
;
.
Мы видим, что и в этом случае переменные разделились. Каждое из этих уравнений зависит только от одной переменной. И мы можем решить его, применяя изложенные выше методы. Все это применимо и к случаю, когда любая из этих сил является постоянной.

И, разумеется, тут могут быть различные вариации, приводящие к разделению переменных. Например, если зависящая от времени сила лежит в плоскости xy , а перпендикулярная ей сила зависит только от координаты z . В этом случае переменные также разделяются.

Автор: Олег Одинцов . Опубликовано: 12-10-2020

[spoiler title=”источники:”]

http://ik-study.ru/ege_po_fizikie/inclined_plane

http://1cov-edu.ru/mehanika/dinamika-tochki/pryamolinejnoe-dvizhenie/

[/spoiler]

Источник

Что такое равнодействующая

Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.

Результат сложения может дать:

вектор, имеющий длину,
или вектор, не имеющий длины.

Длина вектора содержит сумму квадратов всех его проекций на оси.

В частности, для вектора ускорения (vec{a}), лежащего на плоскости xOy, длина вычисляется так

[ large left| vec{a} right| = sqrt{ a_{x}^{2} + a_{y}^{2}} ]

Где ( a_{x} ) и ( a_{y} ) — это проекции вектора (ссылка) ( vec{a} ) на оси Ox и Oy.

Когда вектор равен нулю, равна нулю каждая его проекция на осях.

Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.

Прочитайте подробнее о параметрах векторов.

Левая часть силового уравнения

В левой части силового уравнения записываем силы, действующие на тело.

Правая часть силового уравнения

Тогда в правой части уравнения запишем:

(ma), если ускорение направлено туда же, куда направлена ось;
(- ma), если ускорение направлено противоположно оси;

В правой части уравнения запишем ноль (0 = ускорения нет).

Векторы сил параллельны

В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.

Движение, при котором силы, действующие на тело, направлены вдоль одной оси

Рис. 1. Парашютист спускается на парашюте, векторы сил направлены вдоль единственной оси

Проведем на рисунке ось, направим ее вверх.

Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:

[large F_{text{сопр}} — m cdot g ]

Сила ( F_{text{сопр}}) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.

В правую часть уравнения поместим равнодействующую.

Математики запишут, что ускорение есть, но оно – нулевое (vec{a}=0).

Примечания:

На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec{v_{0}}). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.

Итоговое силовое уравнение имеет вид:

[large F_{text{сопр}} — m cdot g = 0 ]

Векторы сил не параллельны

Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).

Движение, при котором сила трения вызывает замедление двигающегося горизонтально тела

Рис. 2. Равнозамедленное движения тела по горизонтальной шероховатой поверхности

Так выглядит уравнение для горизонтальной оси

[large -F_{text{трен}} = -m cdot a_{x} ]

Для вертикальной оси уравнение выглядит так:

[large N — m cdot g = 0 ]

Система, пригодная для решения задачи, состоит из двух уравнений

[ large boxed{ begin{cases} -F_{text{трен}} = -m cdot a_{x} \ N — m cdot g = 0 end{cases} } ]

Куда направить оси

Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).

Выбор осей произведен так, что большая часть векторов не лежит на осях, такие векторы придется раскладывать на проекции, чтобы составить силовые уравнения

Рис. 3. Большая часть векторов не лежит на осях, такие векторы придется раскладывать на проекции, чтобы составить силовые уравнения

Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.

Выбор осей произведен так, что большая часть векторов лежит на осях, раскладывать на проекции нужно только один вектор, силовые уравнения будут иметь простой вид

Рис. 4. Большая часть векторов лежит на осях, раскладывать на проекции нужно только один вектор, силовые уравнения будут иметь простой вид

Выводы:

Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.

Движение по наклонной плоскости

Составим систему уравнений для решения такой задачи:

Выражение для ускорения

Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)

Велосипедист едет в гору по инерции, отмечены силы, действующие на велосипедиста

Рис. 5. Велосипедист едет в гору по инерции, отмечены силы, действующие на велосипедиста, видно, что при таком выборе осей необходимо разложить вектор mg на проекции

Пользуясь осями координат, составляем теперь уравнения в проекциях.

Уравнение для проекций векторов на ось Ox:

[ large — F_{text{трен}} – m cdot g_{x} = — m cdot a ]

Уравнение для проекций векторов на ось Oy:

[ large N – m cdot g_{y} = 0 ]

[ large begin{cases} m cdot g_{y} = mg cdot cos left(alpha right) \ m cdot g_{x} = mg cdot sin left(alpha right) end{cases} ]

Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений

[ large begin{cases} — F_{text{трен}} – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end{cases} ]

Дополним эту систему выражением для силы трения.

[ large F_{text{трен}} = mu cdot N ]

Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.

[ large begin{cases} N = mg cdot cos left(alpha right) \ F_{text{трен}} = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end{cases} ]

Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:

[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]

Выражение для пройденного пути

[ large begin{cases} 0 = v_{0} — a cdot t \ S = v_{0} cdot t — a cdot frac{t^2}{2} end{cases} ]

[ large begin{cases} t = frac{v_{0}}{a} \ S = v_{0} cdot frac{v_{0}}{a} — a cdot frac{1}{2} cdot frac{v_{0}}{a} cdot frac{v_{0}}{a} end{cases} ]

Упрощенная система для решения задачи теперь включает всего два уравнения

[ large begin{cases} mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_{0} cdot frac{v_{0}}{a} — frac{v_{0}}{2} cdot frac{v_{0}}{a} end{cases} ]

Подставив в эту систему известные значения начальной (v_{0}) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.

Источник

Лекция 10.

Тема 6.

Динамика точки,
механической системы

План:

1. Введение в
динамику. Основные законы классической
механики.

Дифференциальные
уравнения движения материальной точки.
Две
основные задачи динамики. Первая задача
динамики (прямая).
Вторая
(обратная) задача динамики.
Дифференциальные
уравнения прямолинейного движения
материальной точки
Криволинейное
движение материальной точки. Динамика
несвободной материальной точки . Связи
и динамические реакции связи.
Динамика
относительного движения. Случай
относительного покоя.

1. Введение в
динамику. Основные законы классической
механики.

Динамикой
называется раздел механики, в котором
изучается движение твердого тела в
зависимости от действия на них сил.
Понятие и силе как о величине,
характеризующей меру механического
взаимодействия материальных тел было
введено в статике. Но в статике мы
считали, что все силы постоянные, а в
динамике считаем о возможных изменениях
этих сил с течением времени.

Рассмотрим,
инертность тел: сравнивая результаты
действия одной и той же силы на разные
материальные тела.

Если одну и ту же
силу приложить к двум разным телам, то
по истечению одного и того же промежутка
времени эти тела пройдут разные расстояния
и будут иметь разные скорости.

Инертность
– это свойство материальных тел, быстрее
или медленнее изменять скорость своего
движения под действием приложенных
сил.

Количественной
мерой инертности данного тела является
физическая величина, называемой массой
тела.

В механике масса
рассматривается как величина скалярная,
положительная и постоянная для каждого
данного тела.

Основные законы
классической механики.

В основе динамики
лежат законы, впервые введенные Ньютоном.

Если на материальную
точку не действует никакие силы, то
точка находится в состоянии покоя или
движется прямолинейно и равномерно.

;
;

Равномерные
прямолинейное движение называется
движением
по инерции.

Система отсчета,
по отношению к которой выполняются
законы инерции, называется инерциальной
системой отсчёта.

Б) II
закон динамики (основной закон динамики)

Сила, действующая
на материальную точку, сообщает ей
ускорение, которое пропорционально
силе и направлено в сторону её действия.

Это векторное
уравнение устанавливает зависимость
между тремя величинами: F,
m,
a.,
и дает динамический способ определения
модуля и направление силы.

Ускорение, сообщаемое
материальной точке данной силой равно
отношению этой силы к массе точки.

В) Закон равенства
действия и противодействия.

Две материальные
точки действуют друг на друга с силами,
равными по модулю и направленные
в противоположные стороны вдоль прямой,
соединяющих эти точки.

Ускорение,
возникающее при взаимодействии этих
сил, направлены по прямой АВ в
противоположные стороны.

=›

Г) Закон независимости
действия сил.

Если на материальную
точку действует одновременно несколько
сил, то ускорение этой точки равно
геометрической сумме тех ускорений,
которые получает эта точка при действии
каждой из этих сил в отдельности.

2. Дифференциальные
уравнения движения материальной точки.

Используя основной
закон динамики материальной точки в
различных системах координат. Обозначая
равнодействующую всех заданных сил и
сил реакций связей F,
а массу точку m
получаем .
Из кинематики точки известно, что
ускорение выражается через – радиус
вектор :

= .

Дифференциальное
уравнение движения материальной точки
в векторной форме имеет вид

Если спроецировать
обе части уравнений на координатные
оси, то можно получить дифференциальные
уравнения движения точки в проекциях
на эти оси. В декартовой системе координат
в общем случае

Проекции ускорения
на координатные оси можно выразить
через вторые производные по времени от
координат, движущейся точки:

Дифференциальные
уравнения движения материальной точки
в прямоугольной декартовой системе
координат имеет вид:

Используя
дифференциальное уравнения движения
материальной точки в той или иной системе
координат, можно решить 2 основные задачи
динамики точки.

3. Две основные
задачи динамики. Первая задача динамики
(прямая).

Первая задача
динамики.

Зная массу точки
и её закон движения можно найти действующую
на точку силу. Действительно, если заданы
уравнения движения точки в декартовой
системе координат.

то проекции силы
на оси координат определяются из
дифференциальных уравнений движения
точки, т.е

Зная проекции силы
на координатные оси, легко определить
модуль силы и косинусы углов силы с
осями координат.

Пример первой
задачи динамики.

Движение точки
массой m(кг)
в плоскости XY
происходит в соответствии с уравнениями:

Где
– некоторые постоянные величины.

Найдите силу,
вызывающую это движение.

Решение: Движение
точки задано координатным способом,
поэтому применим уравнение

Продифференцируем
два раза исходные уравнения.

Учитывая, что ;

Тогда

Ответ: действующая
сила равна по модулю
и направлена по оси Х.

4. Вторая задача
динамики.

По заданной массе
и действующей на точку силе необходимо
определить движение этой точки. Рассмотрим
решение этой задачи в прямоугольной
декартовой системе координат. В общем
случае сила F,
и её проекции на координатные оси могут
зависеть от времени координат движущейся
точки, её скорости, ускорения и т.д.

Для простоты
ограничимся случаем зависимости силы
и её проекции на оси координат от времени,
координат, скорости. Дифференциальные
уравнения точки имеют вид:

Для случая системы
трех обыкновенных дифференциальных
уравнений 2-го порядка имеется 6
произвольных постоянных

Каждая из координат
x,y,z
движущейся точки после интегрирования
системы уравнений зависит от времени
t
и всех шести произвольных постоянных,
т.е.

Для выделения
конкретного вида движения материальной
точки необходимы дополнительные условия,
позволяющие определить произвольные
постоянные, которых в общем случае будет
6 . В качестве таких условий обычно задают
так называемые начальные условия, т.е
в какой – то определенный момент времени,
например при t=0
задают координаты движущейся точки
и
проекции её скорости .

Пример второй
задачи динамики.

Найти уравнения
движения материальной точки, брошенной
с начальной скоростью
под углом α к горизонту(сопротивлением
воздуха пренебречь)

ешение: на материальную точку
действует единственная сила G,
направленная против оси y.
Тогда дифференциальные уравнения примут
вид:

Интегрируя,
получим:

(*)
(**)

Для определения
постоянных, интегрирования, воспользуемся
начальными условиями, которые с учётом
выбранной системы координат оказываются
следующими:

При =
0

t=0

Подставляя в эти
уравнения функции (*) и (**) находим:

Ответ:
1)

Движение точки
происходит в плоскости XY
по параболе по уравнению из второго
уравнения
подставим в 2)

Дифференциальные
уравнения прямолинейного движения
материальной точки

Если точка движется
по известной траектории, то основное
уравнение динамики удобно записывать
в проекциях на оси естественной системе
координат:

);

;

Правые части этих
уравнений содержат неизвестные силы
реакций связи, т.к. движущаяся точка
несвободна. Исследование такого движения
предполагает одновременное решение 1
и 2 задач динамики при следующих начальных
условиях:

При

7. Динамика
относительного движения. Случай
относительного покоя.

Получим уравнения
движения материальной точки в
неинерциальной системе отсчёта.
Рассмотрим сложное движение точки
одновременно в двух системах координат:

– основной .
(инерциальная система отсчёта)

–

у’

х’

z’

подвижная

Пусть
– равнодействующая сил, действующая
на точку М. В неинерциальной системе
отсчёта:

Воспользуемся
выражением для абсолютного ускорения
точки (т. Кориолиса)

,
тогда

или

Введём обозначения

– переносная сила инерции.
– кориолисовая сила инерции. Тогда
уравнение примет вид:

Основное уравнение
динамики относительного движения.

Уравнения движения
в подвижной системе координат не
совпадает с основным уравнением динамики,
следовательно, система отсчёта не
является инерциальной.

Итак, чтобы получить
уравнение для точки в неинерциальной
системе координат, необходимо добавить
переносную и кориолисову силу инерции.

Дифференциальные
уравнения относительного движения
материальной точки имеют вид:

Если подвижная
система координат движется поступательно,
равномерно и прямолинейно, то переносное
и кориолисова силы инерции равны 0 и
относительное движение описывается
основным уравнением динамики. Это
выражает принцип относительности
классической механики.

В случае, если
материальная точка неподвижна в
неинерциальной системе отсчёта, уравнение
её равновесия (согласно
(*) будет иметь вид:

Условие относительного
покоя материальной точки.

Источник

Содержание:

Определение и формула силы
Второй закон Ньютона
Единицы измерения силы
Примеры решения задач

Определение и формула силы

Определение

Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень»
(интенсивность) воздействия. Направление силы совпадает с направлением ускорения, которое приобретает тело при взаимодействии с другими телами.

Силы способны изменять скорости тел и вызывать их деформации. Примером деформированного тела служит сжатая (растянутая) пружина.

Две силы считают равными по модулю и противоположными по направлению, если они приложены к одному телу, но ускорение такого тела равно нулю.

Второй закон Ньютона

Равнодействующая всех сил приложенных к телу (векторная сумма всех сил)
($bar{F}$) равна производной от импульса тела по времени:

$$bar{F}=sum_{i=1}^{n} bar{F}_{i}=frac{d bar{p}}{d t}(1)$$

где $bar{p}=m bar{v}$ – импульс тела, m–масса рассматриваемого тела,
$bar{v}$ – скорость. Надо отметить, что уравнение (1) строго применимо только относительно
материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.

Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней
(второй закон Ньютона) можно представить в виде:

$$bar{F}=m frac{d bar{v}}{d t}=m bar{a}(2)$$

где $bar{a}$ – ускорение, которое материальная точка приобретает в результате
воздействия на нее силы. Выражение (2) показывает то, что если
$bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.

Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:

$$F=frac{Delta p}{Delta t}=frac{mleft(v_{2}-v_{1}right)}{t_{2}-t_{1}}$$

Единицы измерения силы

Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с²

В СГС: [F]=дин

1Н=10⁵ дин

Примеры решения задач

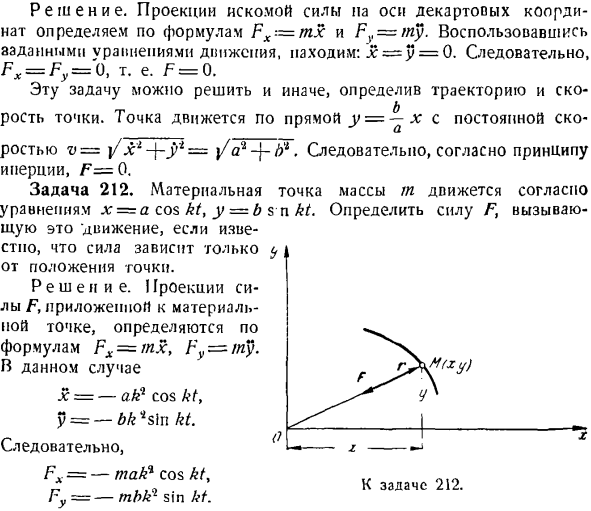
Пример

Задание. Уравнения $x=alpha t^{3}, y=beta t$ ($alpha$ и
$beta$ – постоянные коэффициенты) задают движение материальной точки массы m=const.
Как изменяется по модулю сила, которая действует на точку?

Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:

$bar{F} = mbar{a} (1.1)$

Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения.
Для этого найдем производные по времени от соответствующих координат:

$$
begin{array}{c}
a_{x}=frac{d^{2} x}{d t^{2}}=6 alpha t(1.2) \
a_{y}=frac{d^{2} y}{d t^{2}}=0(1.3)
end{array}
$$

Так как модуль ускорения равен:

$$a=sqrt{a_{x}^{2}+a_{y}^{2}}(1.4)$$

то, учитывая выражения (1.2) и (1.3), получаем:

$a = 6 alpha t (1.5)$

Так как a_y=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили:

$$bar{a}=6 alpha t cdot bar{i}(1.6)$$

где $bar{i}$ – единичный вектор, направленный по оси X.

Исходя из второго закона Ньютона, имеем:

$$F=m cdot 6 alpha t, bar{F}=m 6 alpha t cdot bar{i}$$

Ответ. Так как $F=m cdot 6 alpha t$, то с течением времени сила увеличивается по модулю.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. Масса одного тела равна m₁, второго – m₂. Первое тело толкнули с силой F₀.
Какова сила давления тел друг на друга (F)?

Решение. Сделаем рисунок.

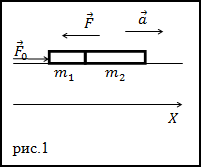
Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:

$$bar{F}_{0}+bar{F}+m_{1} bar{g}+bar{N}=m_{1} bar{a}(2.1)$$

где $m_{1} bar{g}$ – сила тяжести,
$bar{N}$ – реакция опоры,
$bar{a}$ – ускорение тела.

В проекции на ось Xуравнение (2.1) примет вид:

$$F_{0}-F=m_{1} a rightarrow F=F_{0}-m_{1} a(2.2)$$

Рассмотрим силы, приложенные к двум параллелепипедам как системе:

$$bar{F}_{0}+left(m_{1}+m_{2}right) bar{g}+overline{N^{prime}}=left(m_{1}+m_{2}right) bar{a}(2.3)$$

В проекции на ось X уравнение (2.3) примет вид:

$$F_{0}=left(m_{1}+m_{2}right) a(2.4)$$

Из уравнения (2.4) выразим ускорение:

$$a=frac{F_{0}}{m_{1}+m_{2}}$$

Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:

$$F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$$

Ответ. $F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$

Читать дальше: Формула сопротивления.

Источник

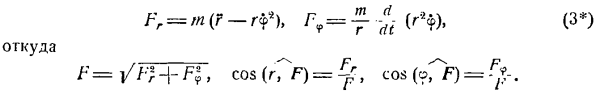
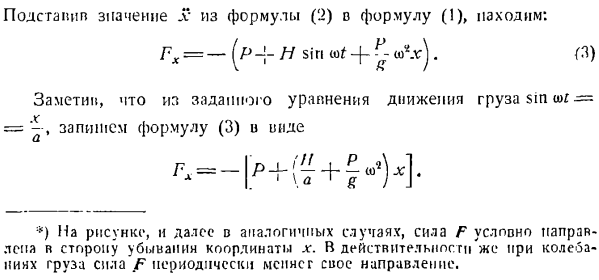
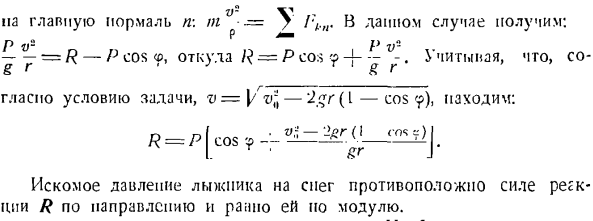
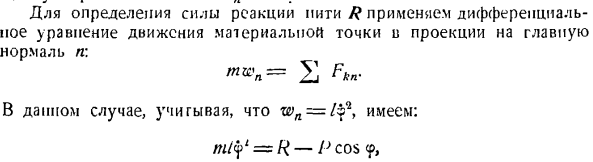
Определение сил по заданному движению

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

Определение сил по заданному движению

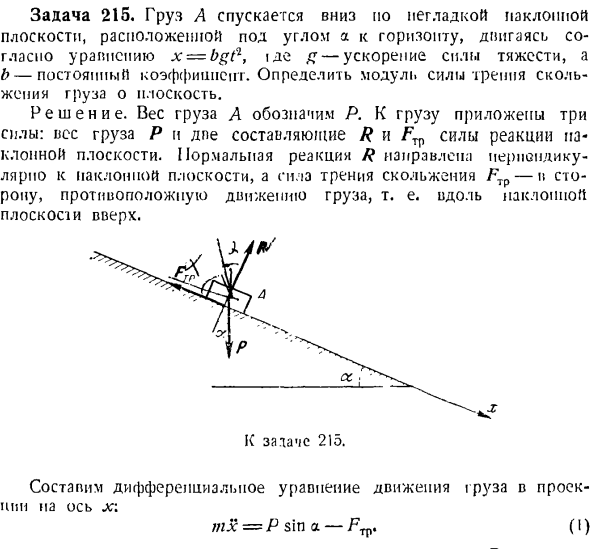
Определение силы по конкретным движениям (Прямая задача динамики важных точек） Если уравнение импульса для точки массы mn задано в декартовых координатах: x -} ( / ), y = / a（/）、= = /、（/）、тогда проекции ΓX, yy и F, силы F-Fxi-j-FJ ^ — Fk для вызова этого движения определяются по формуле. Форекс = MXF и ФЗ = МЗ,(я ） Откуда? Ф = Я / интернет + ТФ-Н-Т、 потому что(ХГ>)=, потому что(г? Ф)= YG может, потому что(Z7 резца-Ф)=.

Поэтому прямая задача динамики важных точек может быть легко решена путем дифференцирования некоторого кинематического уравнения точек. Дано уравнение движения массы точки m вдоль траектории, то есть a = f (), проекции силы F = F Fn и Fh. R «r t-nn+, который вызывает это движение, определяется по формуле: Форекс = Ма£, рН = mvyt ФБ = 0, (2 ） Откуда? F = / F; — rn> cos (Γ>)= y, cos (Г>)=^, cos(0)= 0 В Формуле (2) vx =〜.

Сопротивление движению является функцией скорости лодки.
Людмила Фирмаль

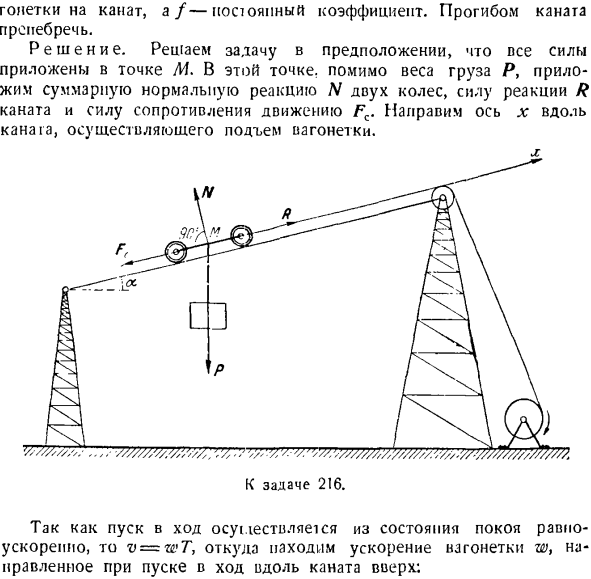
Учитывая уравнение планарного движения точки массы m в полярных координатах r = / 1 ( / ), синоу + ФК +£*. (Да б. Так… = / 7В = ФП потому что А, х = Ш = ^ Г、 Α= Р(синоу + / соз + ^ И я При равномерном движении тележки L * = 0, а Формула(1)принимает вид: Р = р(грех от J — / соз а). Требуемое натяжение каната равно модулю отталкивания R. задача 217.Масса Р определяет сопротивление воды движению лодки. П. С. x = — vQ(1-e p), где x> 0-средняя скорость движения, и- О Фиксированный коэффициент. Н. С. С. Цель 217.

Решение. Сила, приложенная к лодке: P-вес лодки, N-нормальная сила реакции воды, R-сила сопротивления воды движению лодки, а также направлена на противоположную сторону движения. проекция скорости лодки на ось Х — aJLt ЧХ = х * = vQe стр. (Т） Проекция ускорения лодки на ось x = = (2） напишите дифференциальное уравнение для движения лодки, спроецированной на ось X. Р М Л г. Используя формулу(2), можно увидеть следующее: [В] ГХ = — avttc». По условиям, сопротивление jR является функцией скорости лодки, поэтому при приведении Формулы (1) получаем Rx =-avx.

Проблема 218.In в соответствии с Формулой x = a sin +Н грех о) Т—7 а -). (1） Потому что, согласно данному уравнению движения, как x = nut, n = — aui1 sin mt, т. е. х = — » л . (2） Подставляя значение l из Формулы (2) в Формулу (1), получаем: Γχ= — [pI sinЫ+ » Лг)). (3） Из уравнения движения заданной нагрузки sin= запишем Формулу (3) в виде: * ) На рисунке, в дальнейшем аналогичном случае, сила F направлена условно на R-уменьшенную сторону x-coordinate. In дело в том, что даже во время колебаний нагрузки сила F периодически меняется:

x = a, t. in в случае s при самом низком положении нагрузки сила упругости F достигает максимума 31 апексии. То есть, когда нагрузка проходит через положение статического равновесия. когда V = 0, сила упругости пружины равна весу груза. Задача 219.Автомобиль ve и P = 1200 кг движется по дну каньона с постоянным модулем скорости и= 36 км ’ НС. Определите давление автомобиля на дно оврага в наиболее интересующей точке. Радиус кривизны траектории p в этой точке равен 50 м, и мы будем рассматривать транспортное средство как точечную массу. Игнорируйте сопротивление движению.

Примените дифференциальное уравнение движения для массовой точки проекции к главной нормали
Людмила Фирмаль

Решение: используйте естественную трехгранную ось, направив ось m горизонтально вправо, а ось n вертикально вверх. 2 силы приложены к автомобилю и приобретены как масса пункта. Масса P и нормальная реактивная сила R грунта, направленная вертикально вверх вдоль основной законной линии. //： С. С. В этом деле С. С. Откуда? 。 П. В.- С9. Если подставить число, то R = 1445 кг.

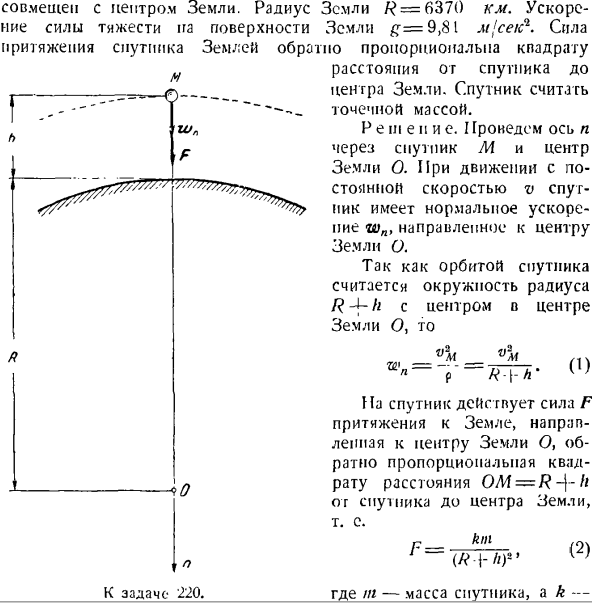
Требуемое давление транспортного средства на дне каньона направлено в противоположную сторону к нормальной силе реакции R, и величина ее равна. Проблема 220.Определите скорость, с которой спутник движется на высоте/ 2 = 900 км, если орбиту спутника можно сделать почти круговой в центре В сочетании с центром Земли. Радиус Земли а? = 6370 км. Гравитация земной поверхности гравитация£= 9.81 м сек спутника обратно пропорциональна квадрату Расстояние от спутника до центра Земли. Спутник считается точечной массой.

Решение. I ось Гройсмана n проходит через центр Земли O со спутником M. При движении с постоянной скоростью v спутник имеет нормальное ускорение wn, которое идет к центру Земли O. Так как орбита спутника представляет собой окружность радиуса R 4-h, центрированную по центру Земли O、 м. / — — — — — О —- То… ш= -^ — = «Го» Третий 0.） Я ’ Спутник находится под влиянием притяжения Земли к Земле, которое направлено в сторону центра Земли O, и обратно пропорционально расстоянию от спутника до центра Земли OM = R-]-H2. п = ._ км(2）

Да. н. К выпуску 220. ’(А * |-а) 2 «в» Где t-масса спутника, к- Ф — М(7-Ф£(Р!Φ), (3 *） Откуда? / ’ = / / .•; + ФДЖ, потому что(Р>)=^, потому что(φГ>)=^ -. Коэффициент пропорциональности. Что находится на поверхности Земли, то есть если h = 0, l:= P = mg, мы узнаем из уравнения (2): k = gR. Следовательно, гравитационное притяжение Далее пишем дифференциальное уравнение движения спутника и, как точку материи, проецируем его на ось N. мзн = Ф Используя Формулы(1)и(3), получаем следующее: , н я nifrR * И затем） IFL 4-NU vM = R j / » = 7,4 км лед k.

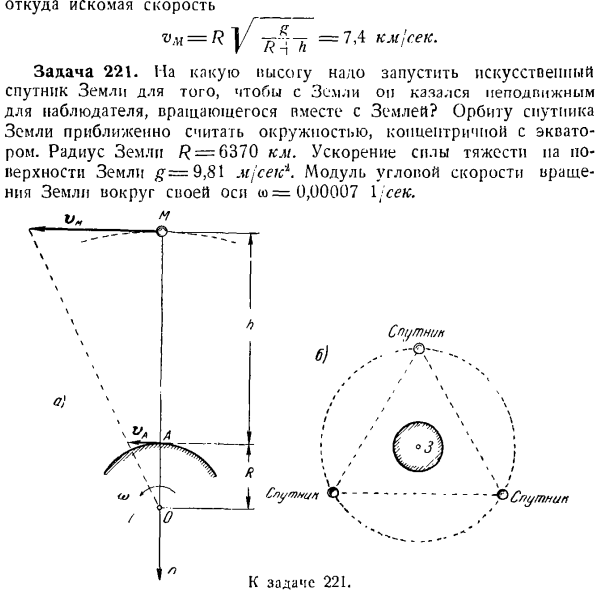
Где находится желаемая скорость Задача 221.At на какой высоте необходимо запустить искусственный спутник Земли, чтобы вращающийся наблюдатель с земли не казался сдвинутым с места искусственным спутником? Приблизительно предполагается, что орбита спутника Земли представляет собой окружность с экватором и концентрическую. Радиус Земли/? = 6370 км. Гравитационное ускорение земной поверхности # = 9.81 Мдж’Сик модуль угловой скорости вокруг земной оси равен= 0.00007 1 сек. Да.

Перейдите к выпуску 221. Спутник ^ Слу / ННК / ТКВ » б.） один.] 「* / / / У СГ / utnip да……. Гравитация спутника Земли обратно пропорциональна квадрату расстояния от спутника до центра Земли. Спутник считается точечной массой. The solution. To сделайте его похожим на искусственный спутник, который движется по экватору и концентрическим орбитам от Земли, пройдите через ось n, проходящую через спутник A, центр Земли O, и наблюдатель A на экваторе, и посмотрите на Землю (см. Рисунок A, схема Земли от Северного полюса).Согласно этому условию, скорости спутника M и наблюдателя

A должны удовлетворять следующему соотношению. _ Ом. ВА ОА ’ поскольку r> d = A> w, t0-отклонение угловой скорости вращения Земли за 1 день вокруг Земли: eV, R = R -/, OA = R, w v. w =(R•!- / / ) быть. Для предыдущего выражения задачи (-1) Это значение V. подставляя вместо ii, мы видим, что: (R-Λ)=^. г / м — / о -’ Где находится нужная высота * == Подставляя цифру, вы найдете нужную! Высота 36800 jc. tf. Существует проект по запуску 3 искусственных спутников на эту высоту, чтобы сформировать равносторонний треугольник, на вершине которого находятся спутники. Подумайте о том, чтобы не двигаться

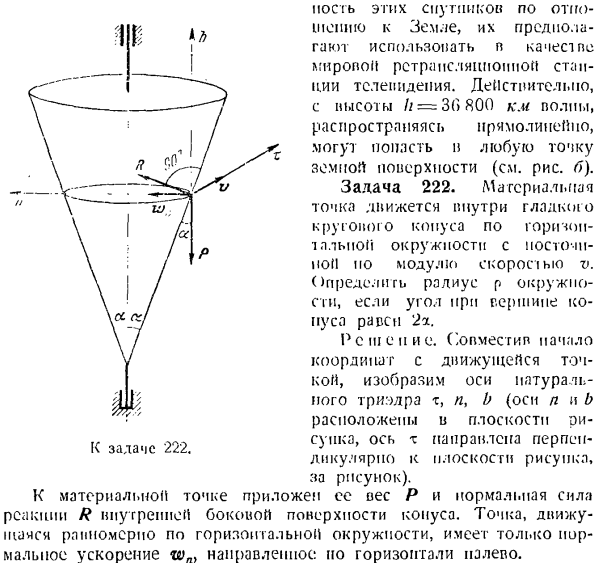
HOC l b этих спутников предполагается использовать в качестве всемирной телевизионной ретрансляционной станции по отношению к Earth. In дело в том, что с высоты// = 3 (>800 км) волны, распространяющиеся по прямой, могут достигать любой точки земной поверхности(см. Рисунок Б). Задача 222.Точка массы является пост-темпом, но движется в гладком конусе вдоль горизонтальной окружности по модулю скорости V. Если угол вершины конуса равен 2a, определите радиус окружности p. R и W E.

выравнивает начало координат до точки движения и изображает естественные трехгранные оси m, n и b (оси n и b «»’ находятся в плоскости 222 на supps ось x направлена на преступника. Особенно на плоскости изображения, для каждого изображения). Вес P и нормальная сила реакции R на внутренней поверхности конуса приложены к точке массы. Только нормальное ускорение wn}направлено к точке, которая равномерно движется по горизонтальной окружности.

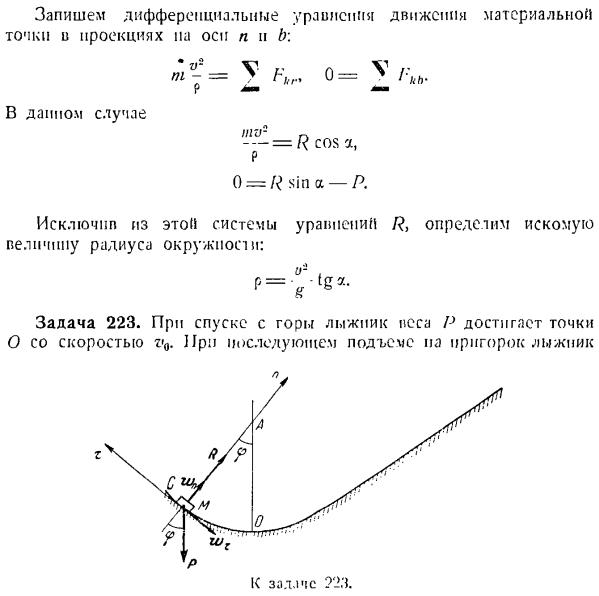
Горизонталь-это олененок. Напишите дифференциальное уравнение движения точки масс в проекции осей n и b. = В 0 = УКБ. В этом деле ИГ — — — = Р потому что, п О = Р грех-Р Исключение R}из этой системы уравнений определяет искомое значение радиуса окружности. Р = vtga- Задача 223.При спуске с горы лыжник с весом P достигает точки O на скорости v0.Затем, когда вы поднимаетесь на холм, лыжник Проблема 72’x. Вдоль дуги окружности OS радиуса r скорость v = Y vij — ’2gt•((где’ f-cos-угол, образованный вертикальной линией и радиусом AM. Считается как точечная масса. Решение.

Траектория катания известна. Изобразим естественное трехгранное естественное по, определив его происхождение в точке А/, занятой текущим лыжником. К лыжнику были приложены следующие усилия. P-лыжная собака, обычная сила реакции снега, которая идет от M к центру L по радиусу дуги R-OS. Представляет нормальную wn и касательную w. компоненты ускорения лыжника. Примените дифференциальное уравнение движения к проекции для определения нормальной силы реакции R В. В.•

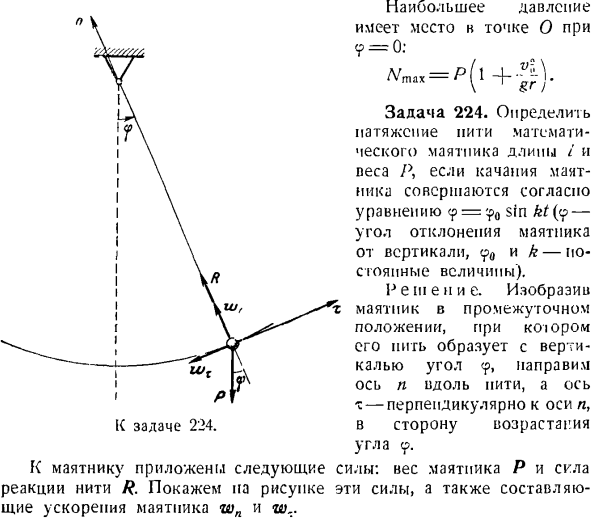
Основной нормальный n t■ -=?В этом случае P v-P v- — г = р-в ^ ОС <р, Где р = р что? — Дж.^—В зависимости от рассматриваемого условия v = [/ rv *-2 gr(I-cos 9）、 г гл•<Г)С Д)| R = P I cos 9—— нет. Требуемое давление лыжника на снег представляет собой модуль с реактивной силой R в обратном направлении. Максимальное давление возникает в точке O, 9 = 0. Задача 224.Когда маятник качается уравнение<? =?0 грех КТ {<?Угол отклонения маятника от вертикали.<p0 и k-постоянные значения.) Решение.

Мы изображаем маятник в среднем положении, и его igi образует вертикальную линию и угол 9, поэтому мы направляем ось n вдоль нити, а ось x перпендикулярна оси n, в направлении, в котором угол 9 увеличивается. К маятнику приложена следующая сила: масса маятника Р и сила реакции нити р. На рисунке показаны компоненты ускорения этих сил и маятников wn и W. Цель 224. Для определения силы реакции нити R используют дифференциальное уравнение движения точки массы в проекции на главную законную линию n В этом случае wn = l $ <it, это выглядит так: млй = р-р с COS <Р、

Если во время движения его линия действия проходит через неподвижную точку, которая называется центром, то сила, приложенная к материальной точке, называется центром. Сила, направленная к неподвижному центру, называется гравитацией. Сила в направлении от неподвижного центра называется разрушающей силе. Движение материальных точек под действием Центральных сил происходит в плоскости через радиус вектора и начальную скорость движения points.

To изучите его, удобно ввести полярные координаты и использовать формулу Bipe. df r J’G 4mC «» Где C-веерообразная скорость точки, которая постоянна при наличии центральной силы. C=—S = y (скорость сечения Называется производной по времени от площади, описываемой вектором радиуса r движущейся точки.） Применение формулы Bipe позволяет определить закон изменения нейтральной силы из некоторого уравнения центральной орбиты (прямая задача). Если Vr положительна, то центральной силой является сила отталкивания, а если она отрицательна, то это сила притяжения.

Рекомендуется решить прямую задачу динамики несвободной материальной точки, где необходимо определить заранее заданную силу и силы реакции, приложенные к точкам l и s и l в следующем порядке. 1) изображающ важные пункты настоящего положения, и силу установки приложенную к напитку. 2) примените принцип высвобождения связи, чтобы изобразить силу реакции соответствующей связи.

Откуда? Так что насчет условия c? = г Необходимое натяжение нити Т направлено в противоположную сторону к силе реакции#, равной модулю силы реакции#. Проблема 225.Точка массы движется под действием центральной силы логарифмической спирали. Форма уравнения: r = ae-x? Как добраться туда, где a и X являются константами. Определяет закон изменения центральной силы. Решение.

Использовать выражение Биазе когда мы получаем 2-ю производную на cf, мы видим, что: / п(). 11й * Г Я А Г Подставляя это значение в венское уравнение и решая уравнение Fr, получаем: Где A = 4 /и C2(1 знак минус-центральная сила、 Перемещение материальной точки по логарифмической спирали является силой притяжения. Эта сила обратно пропорциональна кубу на расстоянии от неподвижного центра.

Напишите уравнение логарифмической спирали в виде: 3) Выберите справочную систему, если она не указана в состоянии проблемы. 4) определить ускорение точки масс по законам заданного движения и найти ее проекцию на выбранную координатную ось. 5) создать дифференциальное уравнение движения точки масс, соответствующее принятой системе отсчета. 6) из системы комбинированных уравнений определить искомое значение. При решении прямой задачи динамики материальной точки необходимо определить результат действия силы, приложенной к этой точке, решение задачи заключается в выделении данного кинетического уравнения точки с помощью

Формулы(1), (2) или плоского движения (3*) уравнения. Задача 211.Точка масс движется по формуле x = at, y = bt. Где A и B-константы. Определите силы, которые вызывают это движение. Решение. Проекция искомой силы на ось декартовых координат определяется по формулам Fx — = mx и Fv = my. Найти Йк = г = 0, используя данное уравнение движения. Итак, Форекс = ФГ = 0, т. е. ф = 0. Эту задачу можно решить и другим способом-определив траекторию и скорость движения точки. Точки движутся по прямой y = — x с постоянной скоростью v = / a2 + b%.So, согласно принципу инерции, F = 0.

Проблема 212.Массовая точка m перемещается по формуле x = A cos kt, y = bsnkt. Если вы знаете, что сила зависит только от расположения точек, определите силу F, которая вызывает это движение. Решение. Проекция силы F, приложенной к точке массы, определяется по формуле Fx = mx, Fy =в этом случае х = — с обеих сторон, потому что КТ、 г = — ьк * СЛН КТ. Так… Форекс = — так * потому, КТ, ФГ = — mbk1 грех КТ. К выпуску 212. По гипотезе, сила F зависит от расположения точки масс, поэтому ее проекции Tx и Fy являются функцией координат x и y. используя уравнение движения точки, оно выглядит так:

Форекс = — mklxy ФВ = — миры. Коэффициент сила F, ф == ^ ф} + ФГ = чернильный * л / х * + У2 = mklr、 Где r-модуль векторного радиуса массовой точки r = OM. Направление силы F определяется с помощью направляющего Косинуса:^ ^ потому что(Л, Ф)== -, cosCv, Ф)=?у =-2. Y и^соответственно, чтобы определить угол, образованный осью В случае X и y радиуса вектора сила направлена от M к O. таким образом, эта материальная точка движется под действием силы притяжения к центру O, которая является модулем с F в качестве закона. Эта сила называется центральной. Задача 213.

Масса вещества m движется по окружности радиуса a по формуле c = bt. Определите силу, которая вызывает это движение(A-координаты дуги, b-постоянная величина). Решение. Использует естественные трехгранные оси N и b. Проекция искомой силы на ось=они определяются по формуле. г Сив. в.- Задача 211. = ФБ = 0. Алгебраическое значение скорости точки- (ЛЗ вы можете видеть, что = v — = b. поэтому： №. Серии WX =:0, ЗП =-=-. .Р б.- Таким образом, Px = 0, Fn = in -,= 0, т. е. сила T7、 Заданным движением материальной точки является рад Б.- Окружность борода находится в центре, а по модулю равна m -. Задача£14.Вес P =Я00кг пассажирский подъемник опускается с ускорением w = $ 0,4.Где g-ускорение свободного падения. Определить натяжение опорного троса, если перемещение резистора F равно 0,2 от веса лифта. Решение.

К лифту прикладывается заранее заданная сила-масса Р, сопротивление движению F, направление, противоположное движению, то есть направленное вертикально вверх. Примените принцип releasable™или сцепления, чтобы мысленно проанализировать кабель и компенсировать поведение секции отходов кабеля с реактивной силой R вертикально вверх. Пойдем по траектории движения лифта, то есть к оси Х в вертикальном направлении.

Запишите производную уравнения движения точки материи, спроецированной на ось lr. н. Техас= В этом случае существуют: — х-Р-Ф-Р、 О том, где Р.- =П-ф-Икс. К Учитывая= o; = 0.4^, a / 7 = 0.2 Р, выглядит так： Р = 0,4 Р = V20 Диск К>.Необходимое натяжение кабеля равно коэффициенту реактивной силы R. Проблема 215.Груз а спускается по гладкой наклонной плоскости, двигаясь по формуле х-БГП, под углом а относительно горизонтальной плоскости.> > де g-ускорение свободного падения, А B-постоянный коэффициент. Определите коэффициент силы трения скользящей нагрузки на плоскость.

Решение. Вес груза A выражается в R. 3 силы прилагаются к грузу. Вес груза P и сила реакции наклонной плоскости составляют 2 составляющие, R и FTr. Нормальная сила реакции R направлена перпендикулярно наклонной плоскости, сила трения скольжения FT?- По направлению, противоположному движению груза, то есть по склону создайте дифференциальное уравнение для движения груза, спроецированного на ось X. = Р ЗША — / в(я）

Смотрите также:

Предмет теоретическая механика

Источник

Как составить силовые уравнения

Что такое равнодействующая

Левая часть силового уравнения

Правая часть силового уравнения

Векторы сил параллельны

Векторы сил не параллельны

Куда направить оси

Движение по наклонной плоскости

Выражение для ускорения

Выражение для пройденного пути