По какой формуле рассчитать силу для поднятия объекта?
Ученик
(99),
закрыт
6 лет назад
Maria ØØØ
Гуру
(3721)
6 лет назад
По формуле F = mg. Вам главное поднять этот груз, чтобы поднять его требуется сила mg Н, а то, что высота есть какая-то чаще всего не имеет значения, вот в нашем случае как раз не имеет. Почему? Да потому, что на высоте один метр ускорение свободного падения, ну, приблизительно равно 9.8, то есть можно сказать, что при поднятии тела ускорение свободного падения не изменяется, так что, чтобы поднять на высоту 1 метр нужно использовать F = mg.
На все тела в воздухе, как и в жидкости, действует выталкивающая, или архимедова сила.
Чтобы найти архимедову (выталкивающую) силу, действующую на тело в газе, надо плотность газа умножить на ускорение свободного падения ((g =) (9,8) Н/кг) и на объём тела, находящегося в газе:
FА=ρгаза⋅g⋅Vтела
.
Обрати внимание!
Для того чтобы летательный аппарат поднялся в воздух, необходимо, чтобы архимедова сила, действующая на шар, была больше силы тяжести.
На этом основано воздухоплавание.
Подъёмная сила воздушного шара зависит от разности архимедовой силы и силы тяжести всей конструкции.
Подъёмная сила увеличивается при увеличении архимедовой силы и уменьшении силы тяжести:
(F=F_A-F_{тяж}).
Плотность газа прямо пропорциональна силе тяжести и обратно пропорциональна подъёмной силе.
Поэтому для увеличения подъёмной силы нужно использовать газы с малой плотностью (меньшей, чем у воздуха). Одним из таких газов является водород. Однако водород взрывоопасен, поэтому его для этой цели не используют. Гелий также имеет небольшую плотность, но, в отличие от водорода, он не горюч. Это способствует тому, что многие аэростаты заполняют именно гелием.
Теплый воздух также имеет меньшую плотность, чем холодный. Поэтому и его можно использовать для создания подъёмной силы.
Чтобы управлять плотностью воздуха, используют газовые горелки. При увеличении пламени газ нагревается сильнее, его плотность уменьшается и шар поднимается выше — подъёмная сила увеличивается. Чтобы снизить высоту воздушного шара, фитиль горелки убавляют, уменьшая скорость нагрева. Воздух внутри шара охлаждается, подъёмная сила уменьшается, шар начинает опускаться вниз.
Таким образом, можно управлять высотой подъёма шара и добиться равенства силы тяжести и силы Архимеда. В этом состоянии шар повисает на одной высоте и будет перемещаться горизонтальными потоками воздуха (ветром).

Плотность атмосферного воздуха изменяется с увеличением высоты. Нагревать газ внутри шара можно до определённого значения. Поэтому при равенстве архимедовой силы и силы тяжести подъём аппарата останавливается.
Единственный выход — уменьшить силу тяжести: уменьшить массу груза. Для этого на воздушные шары берут мешки с песком, которые можно выкинуть или отсыпать часть. При уменьшении массы шара уменьшается сила тяжести, что приводит к продолжению подъёма аэростата.
Если необходимо опустить на меньшую высоту, уменьшают архимедову силу за счёт уменьшения объёма шара. Для этого открывают клапан, и часть газа из шара выходит.
Определение усилий и моментов
-
Через блок А
(рис.2) переброшен трос, к концам которого
подвешен груз массой m=1500
кг. Какую силу нужно приложить к другому
концу троса, чтобы поднимать и опускать
груз с ускорением а=3 м/с2.
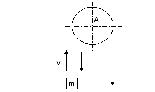
Рисунок 2
Решение.
Для движения груза
необходимо приложить силу:
 (13)
(13)
Сила статических
сопротивлений
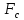 при подъеме груза должна иметь знак
при подъеме груза должна иметь знак
«+», а при опускании – знак «-». Динамическая
же сила при ускорении всегда имеет знак
«+».
При подъеме груза
необходимо приложить движущую силу:
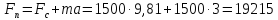 Н (14)
Н (14)
 спуске груза:
спуске груза:
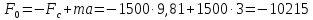 Н (15)
Н (15)
т.е. усилие должно
быть тормозным, следовательно, при
спуске груза необходимо производить
торможение.
-
К концам троса
примера 1 (рис.3) подвешены два груза
массами m1=m2=200
кг. Какую силу необходимо приложить к
окружности шкива, чтобы началось
движение с ускорением а=1,5 м/с2.
Ответ. 600 Н.
-
Через блок А
(рис.3) переброшен трос, к концам которого
подвешены грузы массами m1=150
кг и m2=200
кг. Определить массу груза, которую
нужно добавить к грузу m1,
чтобы началось движение с постоянным
ускорением а=2 м/с2.
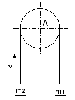
Рисунок 3
Решение.
Обозначим массу
груза, которую нужно добавить к грузу
m1
через х, тогда движение начнется при
условии:
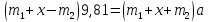 (16)
(16)
откуда добавочный
груз х будет равен:
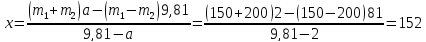 кг
кг
-
Определить силу
необходимую для подъема груза массой
m=1500
кг с ускорением а=1 м/с2,
если масса противовеса m0=750
кг. Потери на трение не учитывать.
Ответ.
F=9600 Н.
-
Определить в
подъемнике (рис.4), какую массу m1
должен иметь груз Q1,
чтобы груз Q2
массой m2=120
кг начал опускаться с ускорением а=0,5
м/с2.

Рисунок 4
Ответ. 133,5 кг
-
Определить
ускорение, с которым начинается движение
грузов массами m1
=200 кг и
m2=500
кг, подвешенных к концам троса (рис.5).
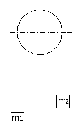
Рисунок 5
Решение.
Для одновременного
подъема и спуска груза m1
и m2
ускорение находим из равенства:
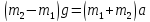 ,
,
(17)
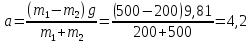 м/с2
м/с2
-
Определить тяговую
силу, которую нужно приложить в период
ускоренного движения вагонетки с
постоянным ускорением а=0,1 м/с2,
если сопротивление движению вагонетки
F=400
Н и приведенная масса вагонетки m=9000
кг.
Ответ. 1300 Н.
-
Определить силу
необходимую для подъема груза массой
m=500
кг вверх по наклонной плоскости с
ускорением а=3м/с2,
если угол наклона плоскости α=45˚, а
коэффициент трения груза о плоскость
μ=0,2.
Решение.
Сила тяжести тела,
равная:
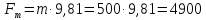 Н (18)
Н (18)
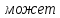 быть разложена на
быть разложена на
две составляющие: (рис.6): первую,
действующую против движения:
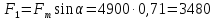 H
H
(19)
вторую, действующую
перпендикулярно движению:
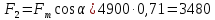 H
H
(20)
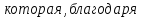 наличию
наличию
трения между грузом и плоскостью, создает
силу трения, равную:
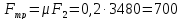 H
H
(21)

Рисунок 6
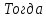 полная статическая
полная статическая
сила, которую нужно преодолеть при
подъеме груза будет равна:
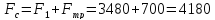 H
H
(22)
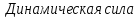 при движении груза
при движении груза
с ускорением а=3 м/с2:
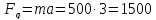 Н
Н
(23)
 сила,
сила,
необходимая при подъеме груза, будет
равна:
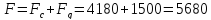 H
H
(24)
-
Определить величину
усилий необходимых:
а) для разгона с
ускорением1м/с2
при подъеме груза массой m=150
кг по наклонной плоскости с углом наклона
α=60˚, одновременном опускании противовеса
массой mп=50
кг, для системы, изображенной на рис.7;
б) для установившегося
движения;
в) для замедления
с ускорением 1 м/с2.
Коэффициент трения
между грузом и наклонной плоскостью
μ=0,2.
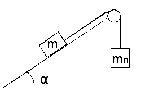
Рисунок 7
Решение.
Уравнение движения
системы может быть представлено:
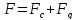 (26)
(26)
В рассматриваемом
случае усилие статических сопротивлений
состоит из разности усилий, создаваемых
грузом m
и противовесом mп.
Сила статических
сопротивлений, которую необходимо
преодолеть при движении груза вверх по
наклонной плоскости, состоит из двух
составляющих сил:
одной, действующей
против направления движения:
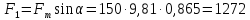 Н (27)
Н (27)
второй, силы
трения, равной:
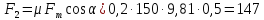 Н (28)
Н (28)
Таким образом,
сила статических сопротивлений груза
буде равна:
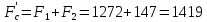 H
H
(29)
Сила статического
сопротивления противовеса равна:
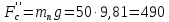 H
H
(30)
Полная сила
статических сопротивлений:
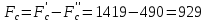 H
H
(31)
Динамическая сила
Fg
всей системы складывается из динамических
сил, создаваемых грузом и противовесом:
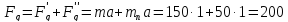 H
H
(32)
Таким образом,
необходимая сила должна быть:
при подъеме
груза с ускорением в 1 м/с2:
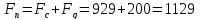 H
H
(33a)
при установившемся
движении:
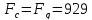 Н
Н
(33б)
при замедлении
с ускорением в 1 м/с2:
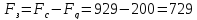 Н (33в)
Н (33в)
-
Определить силу,
необходимую для перемещения вагонетки
по горизонтальной плоскости с постоянной
скоростью, если вес полезного груза
Q=3000
H,
вес вагонетки Q0=252
Н, диаметр колеса d0=20
см, диаметр цапф dц=4
см, коэффициент трения качения f=0,07
см, коэффициент трения скольжения
(цапф) μ=0,08, коэффициент увеличения
трения от реборд α=1,4.
Решение.
Давление, приходящееся
на одно колесо:
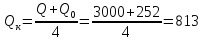 H
H
(34)
Усилие, необходимое
для преодоления трения качения для
одного колеса:
 Н
Н
(35)
Усилие, необходимое
для преодоления трения скольжения в
цапфе:
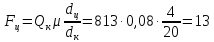 Н (36)
Н (36)
Общее усилие с
учетом трения реборд:
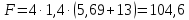 H
H
(37)
Следовательно,
для перемещения вагонетки с постоянной
скоростью необходимо усилие в 104,6 Н.
-
Определить силу,
которую необходимо приложить к вагонетке
примера 10, для того, чтобы затормозить
ее на пути, равном
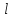 =2
=2
м при равномерно – замедленном движении,
если скорость движения вагонетки перед
торможением равна 0,5 м/с.
Ответ. -83,8 Н.
-
Определить момент,
который нужно приложить к валу барабана
(рис. 8) для поднятия груза массой m=2500
кг с ускорением а=1 м/с2.
Какова должна быть скорость вращения
вала барабана при подъеме груза со
скоростью v=0,75
м/с. Диаметр барабана D=700
мм.

Рисунок 8
Решение.
При равномерно –
ускоренном движении на крюке усилие
будет равно:
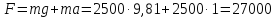 H
H
(38)
Благодаря наличию
блока А это усилие распределится
равномерно (не учитывая потери на трение)
между обеими частями троса, поэтому
барабан воспримет усилие:
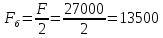 H
H
(39)
Момент на валу
барабана будет равен:
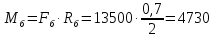 Н·м
Н·м
(40)
Скорость троса на
участке между блоком и барабаном и
равная ей окружная скорость барабана
должны быть в два раза больше скорости
подъема груза, т.е.:
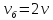 (41)
(41)
откуда скорость
вала барабана:
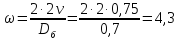 с-1
с-1
(42)
-
Определить в
системе (рис.9) вращающийся момент на
валу двигателя и его мощность, если
статический момент на валу Mp=15000
Н·м, скорость вращения вала np=10
об/мин, передаточное число каждой
ступени k1=k2=10,
а КПД каждой ступени η1=η2=0,95.
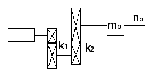
Рисунок 9
Решение.
Вращающийся момент
на валу двигателя при наличии передачи
равен:
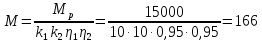 Н·м
Н·м
(43)
Скорость вращения
вала двигателя:
 об/мин
об/мин
(44)
Мощность двигателя:
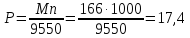 кВт
кВт
(45)
-
Определить
статический момент и статическую
мощность на валу двигателя поворотного
механизма экскаватора ЭШ=4/40, кинематическая
схема которого дана на рис.10. При
равномерном движении платформы со
скоростью n1=0,025
об/с с нагруженным ковшом. Статический
момент на валу колеса А равен Mp=3780
Н·м, КПД каждой пары передачи η=0,95, а
передаточные числа k1=2,7,
k2=2,8,
k3=3,7,
k4=17,5.
Рисунок 10
Решение.
Статический момент
на валу двигателя равен:
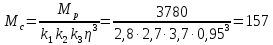 Н·м (46)
Н·м (46)
Скорость вращения
вала двигателя будет равна:
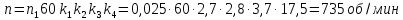 (47)
(47)
Статическая
мощность двигателя:
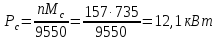 (48)
(48)
-
Определить
статический момент на валу двигателя,
его мощность и скорость вращения,
необходимую для подъема груза массой
m=1000
кг со скоростью 4 м/с. Диаметр барабана
D=2,5
м; передаточное число редуктора k=24;
КПД редуктора ηр=0,9;
КПД барабана ηб=0,85
(рис.11).

Рисунок 11
Решение.
Статическое усилие:
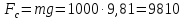 Н (49)
Н (49)
Статический момент
на валу барабана:
 (50)
(50)
Статический момент,
приведенный к валу двигателя:
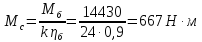 (51)
(51)
Угловая скорость
барабана:
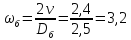 с-1
с-1
(52)
Скорость двигателя:
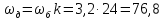 с-1
с-1
(53)
или
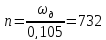 об/мин
об/мин
(54)
Мощность двигателя,
необходимая для подъема груза с заданной
скоростью:
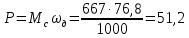 кВт
кВт
(55)
-
Определить
статический момент на валу двигателя
механизма поворота экскаватора (рис.10),
если при равномерном движении на валу
колеса (А) статический момент равен
М=4500 Н·м, КПД редуктора ηр=0,8,
передаточные коэффициенты редуктора
k1=3,
k2=3,
k3=4,
k4=20.
Ответ. 7,85 Н·м.
-
Определить
статический момент на валу двигателя
подъемного крана (рис.12), а также мощность
и скорость двигателя, если масса
поднимаемого груза m=7000
кг, а масса крюка и блока mб=400
кг, передаточные числа k1=7,
k2=4,
k3=4,
КПД передачи η1=η2=
η3 =0,92.
Потери в барабане и блоке не учитываются.
Линейная скорость подъема груза v=0,4
м/с, диаметр барабана Dб=1,2
м.
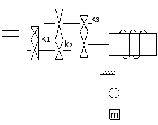
Рисунок 12
Решение.
Статическое усилие
равно:
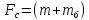 g=(7000+40)9,81=72600
g=(7000+40)9,81=72600
H
(56)
Благодаря наличию
блока это усилие распределяется
равномерно между обеими частями троса,
на которых подвешен блок, поэтому барабан
воспринимает усилие:
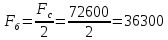 H
H
(57)
Момент на валу
барабана буден равен:
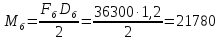 Н·м
Н·м
(58)
Статический момент,
приведенный к валу двигателя:
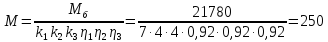 Н·м
Н·м
(59)
Скорость барабана:
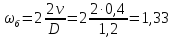 c-1
c-1
(60)
Скорость двигателя:
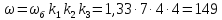 c-1,
c-1,
(61)
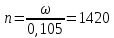 об/мин
об/мин
(62)
Мощность двигателя:
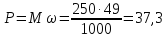
кВт,
(63)
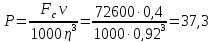 кВт
кВт
(64)
-
По данным задачи
17 определить тормозной момент на валу
двигателя при спуске того же груза.
Ответ. -151,5 Н·м.
-
Определить величину
вращающих моментов на валу двигателя
(рис.13): при подъеме и спуске груза массой
m=
10000 кг, а также при подъеме и опускании
свободного крюка массой m0=
800 кг. КПД подъемного механизма при
передаче номинального момента η= 0,7.
Передаточное число обеих пар зубчатых
колес k=25,
диаметр барабана Dб=0,4
м.
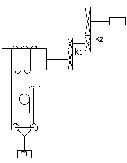
Рисунок 13
Решение.
 g=(10000+800)·9,81=106000
g=(10000+800)·9,81=106000
Н (65)
Благодаря наличию
блока это усилие распределяется
равномерно между четырьмя ветвями
троса, на которых подвешен блок, поэтому
барабан воспринимает усилие:
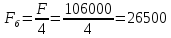 H
H
(66)
Момент на валу
барабана:
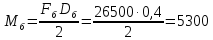 Н·м
Н·м
(67)
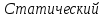 момент
момент
на валу двигателя при полной нагрузке:
 Н·м
Н·м
(68)
Усилие при подъеме
крюка:
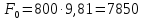 H
H
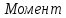 на валу барабана:
на валу барабана:
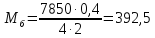 Н·м
Н·м
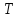 ак
ак
как КПД зубчатой передачи зависит от
загрузки, то при подъеме крюка он будет
другим, поэтому воспользуемся кривыми
(рис.1).
 коэффициент
коэффициент
загрузки передачи:
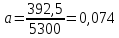
Этому коэффициенту
загрузки соответствует КПД передачи
η1=0,25,
тогда момент на валу двигателя при
подъеме крюка будет равен:
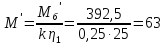 Н·м
Н·м
(69)
Статический момент
на валу двигателя при спуске полного
груза может быть подсчитан по формуле:
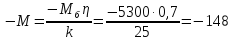 Н·м
Н·м
(70)
или по точной
формуле:
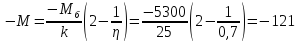 Н·м (71)
Н·м (71)
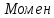 т
т
на валу двигателя при спуске крюка:
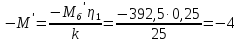 Н·м,
Н·м,
(72)
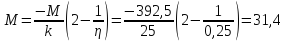 Н·м (73)
Н·м (73)
Таким образом,
статический момент на валу двигателя
при спуске двигателя является тормозным,
но посчитанный по точной формуле
несколько меньший, чем по обычному
выражению, при спуске же порожнего крюка
статический момент на валу двигателя,
подсчитанный по точной формуле, должен
быть двигательным, а по обычному выражению
– тормозным. Это объясняется более
точным учетом потерь в передачах,
подсчитанных по точной формуле.
-
Определить величину
вращающих моментов на валу барабана
(рис.14), необходимых при подъеме вагонетки
вверх по уклону, если: масса полезного
груза m=750
кг; масса пустой вагонетки m0=250
кг. Диаметр колеса вагонетки Dk=35
см, диаметр цапфы dц=5
см; коэффициент трения качения колеса
f=0,05
см; коэффициент трения скольжения цапф
μ=0,08; коэффициент увеличения трения от
реборд a=1,4;
диаметр барабана лебедки Dб=0,5
м; КПД барабана η=0,9; угол наклона
плоскости α=15˚.
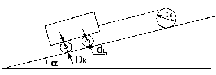
Рисунок 14
Расчет произвести
для случаев:
-
Разгона вагонетки
с ускорением a=1
м/с2; -
Установившегося
движения; -
Замедления с
ускорением 1 м/с2.
Решение.
Сила тяжести
определяется как:
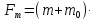 g=(750+250)·9,81=9810
g=(750+250)·9,81=9810
Н (74)
Эту силу раскладываем
на две составляющие: одну, действующую
против движения:
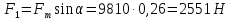 (75)
(75)
и вторую, действующую
перпендикулярно движению:
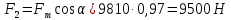 (76)
(76)
Откуда, усилие
необходимое для преодоления трения
качения колес вагонетки, равно:
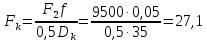 H
H
(77)
Усилие, необходимое
для преодоления трения скольжения в
цапфах:
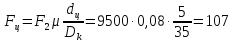 H
H
(78)
Общее усилие, с
учетом трения реборд:
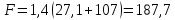 H
H
(79)
Таким образом,
сила статического сопротивления будет
равна:
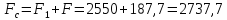 H
H
(80)
Статический момент
на валу барабана с учетом потерь в
барабане:
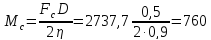 Н·м
Н·м
(81)
Сила динамического
сопротивления:
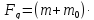 a=(750+250)·1=1000
a=(750+250)·1=1000
H
(82)
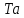 к
к
как ускорение при разгоне и замедлении
принято одинаковым, то динамический
момент на валу барабана в обоих случаях
буден один и то же, но при ускорении
будет складываться со статическим
моментом, а при замедлении – вычитаться.
Динамический
момент на валу барабана с учетом потерь:
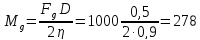 Н·м
Н·м
(83)
Таким образом,
будем иметь момент на валу барабана:
при разгоне:
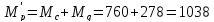 Н·м (84а)
Н·м (84а)
при установившемся
движении:
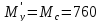 Н·м
Н·м
(84б)
при замедлении:
 Н·м (84в)
Н·м (84в)
-
По данным задачи
20 определить величину вращающих моментов
на валу барабана при спуске пустой
вагонетки, для тех же условий.
Решение.
Сила тяжести равна:
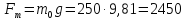 H
H
(85)
Сила, действующая
по направлению движения равна:
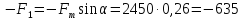 H
H
(86)
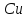 ла
ла
трения равна:
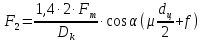 ,
,
(87)
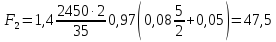 H
H
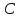 ила
ила
трения всегда препятствует движению,
поэтому сила статических сопротивлений
при спуске пустой вагонетки будет:
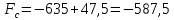 H
H
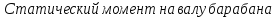 с учетом потерь в
с учетом потерь в
барабане:
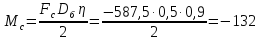 Н·м
Н·м
(88)
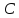 ила
ила
динамического сопротивления:
 H
H
(89)
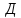 инамический
инамический
момент на валу барабана:
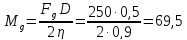 Н·м
Н·м
(90)
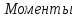 на
на
валу барабана будут равны:
-
при разгоне:
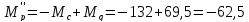 Н·м (91а)
Н·м (91а)
– тормозной режим;
-
при установившейся
скорости:
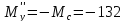 Н·м
Н·м
(91б)
– тормозной режим;
-
при замедлении:
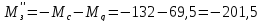 Н·м (91в)
Н·м (91в)
– тормозной режим.
-
На наклонной
плоскости одновременно находятся две
вагонетки, из которых одна идет с грузом
вверх, другая без груза спускается
вниз.
Данные установки
приведены в задаче 20. Определить величины
вращающих моментов, необходимых для
разгона, установившегося движения,
замедления.
Решение.
Для решения
поставленного вопроса используем
полученные результаты задач 20 и 21, тогда
момент на валу барабана:
при разгоне:
 Н·м (92а)
Н·м (92а)
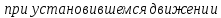 :
:
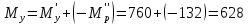 Н·м (92б)
Н·м (92б)
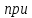 замедлении:
замедлении:
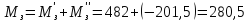 Н·м
Н·м
(92в)
-
По данным задачи
20 определить величину момента на валу
барабана при спуске вниз груженой
вагонетки, для тех же условий.
Ответ. Моменты на
валу барабана будут равны:
-
При разгоне
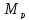 =-271
=-271
Н·м; -
При установившейся
скорости
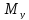 =-529
=-529
Н·м; -
При замедлении
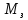 =-787
=-787
Н·м.
-
На наклонной
плоскости одновременно находятся две
вагонетки, одна из которых с грузом
идет вниз, а пустая поднимается вверх.
Данные установки
приведены в задаче 20, но угол наклона
плоскости к горизонту принять α=25˚.
Определить величину момента на валу
барабана.
Ответ. Моменты на
валу барабана будут равны:
-
При разгоне
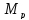 =-247,5
=-247,5
Н·м; -
При установившейся
скорости
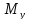 =-595
=-595
Н·м; -
При замедлении
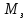 =-942,5
=-942,5
Н·м.
-
Определить:
а) механический
КПД подъемной установки, если при подъеме
груза массой m=
5000 кг за время t=10
с, высота подъема будет равна h=2,5
м, а мощность потребляемая электродвигателем
из сети P1=
20 кВт, КПД двигателя при этом η=0,85;
б) тормозной момент
двигателя при спуске того же груза, если
диаметр барабана лебедки Dб=1
м, а передаточное число зубчатых колес
k1=k2=5,
k3=4.
Решение.
Механический КПД
подъемной установки равен отношению
полезной мощности на барабане, развиваемой
при подъеме груза (Рб),
к мощности, развиваемой на валу двигателя
(Р).
Мощность на барабане
при подъеме груза равна:
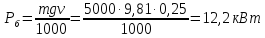 ,
,
(93)
где
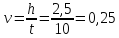 м/с.
м/с.
Мощность на валу
двигателя равна:
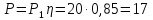 кВт
кВт
(94)
откуда
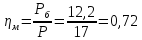 (95)
(95)
Тормозной момент
на валу двигателя при спуске груза
равен:
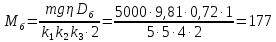 Н·м
Н·м
(96)
-
Подъемная установка
рис.15 имеет следующие данные: масса
поднимаемого груза m=3000
кг, масса порожнего сосуда m0=2500
кг, масса противовеса mп=4000
кг; масса одной ветви каната mк=560
кг; диаметр барабана Dб=3
м, передаточные числа k1=5,
k2=6;
КПД пары передачи η1=
η2=0,94;
скорость поднимаемого груза v=3
м/с. Определить величину статического
момента на валу двигателя для следующих
условий: 1) при подъеме груза: а) груз в
нижнем положении; б) при встрече груза
с противовесом; в) при подходе груза к
верхнему положению; 2) при подъеме
противовеса: а) противовес в нижнем
положении; б) при встрече противовеса
с порожним сосудом; в) противовес
подходит к верхнему положению.
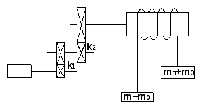
Рисунок 15
Решение.
Усилие на ободе
барабана при подъеме груза:
а) груз внизу:
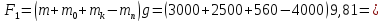
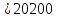 H
H
(97а)
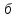 )
)
при встрече груза с противовесом:
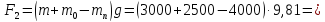
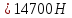 (97б)
(97б)
в) при подходе
груза к верхнему положению:
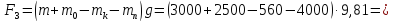
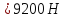 (97в)
(97в)
Усилие на ободе
барабана при подъеме противовеса:
а) противовес
внизу:
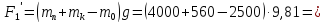
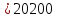 Н
Н
(98а)
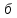 )
)
при встрече противовеса с порожним
сосудом:
 Н (98б)
Н (98б)
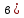 при подходе
при подходе
противовеса к верхнему положению:
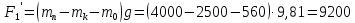 Н (98в)
Н (98в)
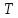 аким
аким
образом, усилие на ободе барабана при
подъеме груза и противовеса при одинаковых
положениях равно, поэтому величины
статических моментов на валу двигателя,
для требуемых положений, будут:
 Н·м, (99)
Н·м, (99)
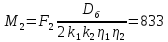 Н·м,
Н·м,
(100)
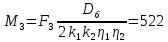 Н·м
Н·м
(101)
-
Определить величину
момента инерции детали приведенной к
валу, вращающемуся со скоростью n=900
об/мин, если при скорости n1=30
об/мин момент инерции равен J0=5
кг·м2.
Решение.
Величина приведенного
момента инерции будет равна:
J=J0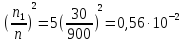
кг·м2
(102)
-
Определить
суммарный момент инерции механизма,
изображенного на рис. 16, приведя его:
а) к валу (А),
вращающемуся со скоростью na=1000
об/мин;
б) к валу (В),
вращающемуся со скоростью nв=100
об/мин.
Исходные данные:
деталь 1 имеет момент инерции J1=40
кг·м2
при скорости вращения n1=250
об/мин, а деталь 2 имеет момент инерции
J2=250
кг·м2
при скорости n2=100
об/мин.
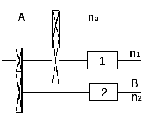
Рисунок 16
Решение.
Момент инерции,
приведенный к валу (А):
JА=J1
кг·м2
(103)
Момент инерции,
приведенный к валу (В):
JВ=J1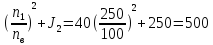
кг·м2
(104)
-
Деталь весом 1500
Н движется поступательно со скоростью
v=50
м/мин. Найти эквивалентный момент
инерции, приведенный к скорости вращения
n=1000
об/мин.
Решение.
Приведенный момент
инерции равен:
J=m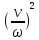 ,
,
(105)
где ω – угловая
скорость вращения, равная:
ω=0,105· n=0,105·1000=105
с-1
(106)
откуда
J=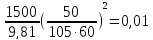
кг·м2
-
Механизм состоит
из детали с моментом инерции J1=50
кг·м2,
вращающейся со скоростью n=300
об/мин, и детали массой m1=30
кг, движущейся поступательно со скоростью
v=2,5
м/с.
Определить:
а) эквивалентный
суммарный момент инерции, отнеся его к
скорости вращения первой детали;
б) эквивалентную
суммарную массу, отнеся ее к поступательно
движущейся детали.
Решение.
Эквивалентный
суммарный момент инерции:
J=m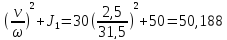
кг·м2,
(107)
где ω=
0,105·n=0,105·300=31,5
c-1.
Эквивалентная
суммарная масса:
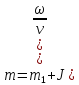 кг (108)
кг (108)
-
Определить
суммарный момент инерции частей
подъемной лебедки, схематически
изображенной на рисунке 17, приведя его
к валу двигателя, если масса поднимаемого
груза m=200
кг, диаметр барабана Dб=
2 м, его момент инерции
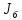 =20
=20
кг·м2,
скорость вращения двигателя nд=730
об/мин, маховый момент ротора двигателя
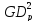 =5,2
=5,2
кг·м2.
Зубчатые колеса
имеют данные, представленные в таблице
1.
Таблица 1
|
№ колеса |
Число |
Маховый |
|
1 |
15 |
1,6 |
|
2 |
60 |
3,6 |
|
3 |
20 |
2 |
|
4 |
50 |
4,8 |
|
5 |
20 |
2 |
|
6 |
55 |
20 |
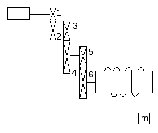
Рисунок 17
Решение.
Находим передаточные
числа:
k1=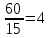 ;
;
k2=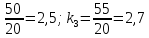
Определяем суммарный
эквивалентный маховый момент зубчатых
колес и ротора двигателя, отнесенного
к скорости вращения двигателя:
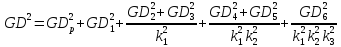 ,
,
(109)
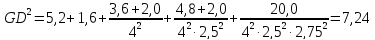 кг·м2
кг·м2
Переводим суммарный
эквивалентный маховый момент в момент
инерции:
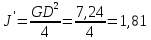 кг·м2
кг·м2
(110)
Для определения
приведенного момента инерции прямолинейно
движущейся массы, необходимо знать
линейную скорость движения массы, для
чего вначале находим скорость барабана:
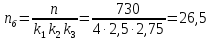 об/мин
об/мин
(111)
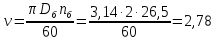 м/с
м/с
(112)
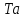 ким
ким
образом, суммарный приведенный момент
движущихся частей подъемной лебедки:
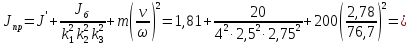
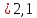 кг·м2
кг·м2
(113)
 ω=0,105n=0,105·730=76,7
ω=0,105n=0,105·730=76,7
c-1.
-
По данным задачи
31 определить суммарный момент инерции,
отнеся его к валу барабана.
Решение.
Момент инерции
системы, приведенный к валу барабана,
может быть определен как произведение
приведенного момента инерции к валу
двигателя на квадраты передаточных
чисел зубчатых колес:
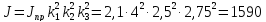 кг·м2
кг·м2
(114)
-
По данным задачи
31 определить массу, приведенную к
окружности барабана.
Ответ. 1590 кг.
-
Определить
приведенный к валу «а» момент инерции
механизма рис.18, если момент инерции
рабочей машины
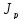 =20
=20
кг·м2,
а скорость вала рабочей машины n=26,2
об/мин. Число зубцов и момент инерции
зубчатых колес имеют значения в
соответствии с таблицей 2.
Таблица 2
|
Zi |
Ji, |
|
|
Колесо |
17 |
0,03 |
|
Колесо |
113 |
0,5 |
|
Колесо |
12 |
0,02 |
|
Колесо |
67 |
0,3 |
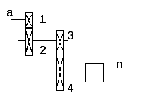
Рисунок 18
Решение.
Определяем
передаточные числа между колесами 1 –
2 (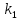 ),
),
и 3 – 4 (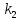 ):
):
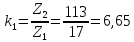 ,
,
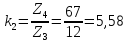 (115)
(115)
Суммарный момент
инерции на валу рабочей машины равен:
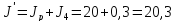 кг·м2
кг·м2
(116)
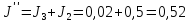 кг·м2
кг·м2
(117)
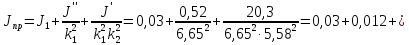
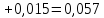 кг·м2
кг·м2
(118)
-
Определить
приведенный к валу двигателя момент
инерции подъемной лебедки, а также
инерционные массы всей системы,
приведенные к канату. Кинематическая
схема показана на рисунке 19. Исходные
данные: массы полезного груза m2=3000
кг, порожнего сосуда m0=560
кг, противовеса mп=4000
кг, одной ветки каната mк=560
кг. Моменты инерции: барабана Jб=950
кг·м2,
первого зубчатого колеса J1=250
кг·м2,
второго J2=70
кг·м2,
третьего J3=150
кг·м2,
четвертого J4=5
кг·м2.
Маховый момент
ротора двигателя
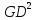 =400
=400
кг·м2.
Передаточное число первой пары колес
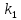 =5,
=5,
второй =6.
=6.
Диаметр барабанаD=3
м. Скорость двигателя n=580
об/мин.
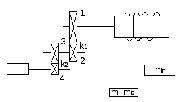
Рисунок 19
Решение.
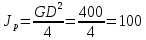 кг·м2
кг·м2
(119)
 гловая
гловая
скорость двигателя: ω=0,105n=0,105·580=60,8
c-1;
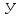 гловая
гловая
скорость барабана:
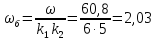 c-1
c-1
(120)
Линейная скорость
каната:
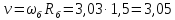 м/с
м/с
(121)
 к
к
валу двигателя момента инерции установки
определяем по формуле:
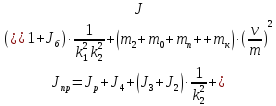 ,
,
(122)
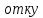 да,
да,
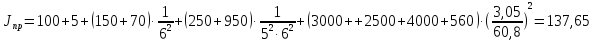 кг·м2
кг·м2
 нерционные
нерционные
массы всей системы, приведенные к
поступательно движущемуся элементу
(канату).
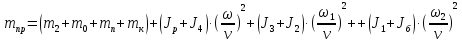 ,
,
(123)
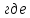
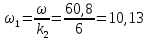 c-1,
c-1,
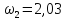 c-1;
c-1;
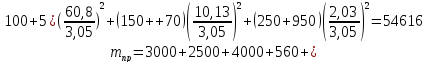 кг
кг
-
Определить на
валу двигателя статический момент,
если скорость вращения вала двигателя
n=980
об/мин, мощность, потребляемая двигателем
из сети, P1=85
кВт и КПД двигателя η=0,85.
Решение.
Полезная мощность
на валу двигателя равна:
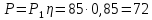 кВт
кВт
(124)
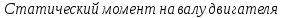 :
:
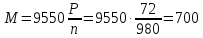 Н·м
Н·м
(125)
-
Определить
статический и динамический моменты на
валу двигателя, когда скорость вращения
двигателя n=739
об/мин, мощность на валу P=240
кВт, а угловое ускорение ротора
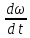 =5,25
=5,25
с-2.
При отключении двигателя от сети за
промежуток времени Δt=2
c
скорость вращения снизится на Δn=200
об/мин при постоянном статическом
моменте.
Решение.
Определяем величину
статического момента на валу двигателя:
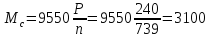 Н·м
Н·м
(126)
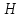 а
а
опыте свободного выбега находим
приведенный момент инерции на валу
двигателя:
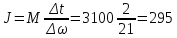 кг·м2,
кг·м2,
(127)
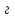 де
де
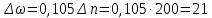 c-1;
c-1;
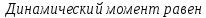 :
:
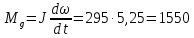 Н·м
Н·м
(128)
-
Определить
вращающий момент двигателя, необходимый
для разгона машины в течение 5 с до
скорости вращения двигателя n=1460
об/мин, если приведенный к валу двигателя
момент инерции J=1,25
кг·м2,
а статический момент на валу двигателя
Mc=50
Н·м.
Решение.
Определяем угловое
ускорение:
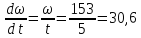 с-2,
с-2,
(129)
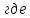
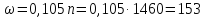 c-1;
c-1;
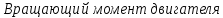 равен:
равен:
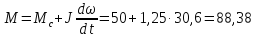 Н·м
Н·м
(130)
-
Одноконцевая
подъемная установка поднимает груз
массой m=600
кг (рис.20). Определить приведенный к
валу двигателя момент инерции и
статический момент, если дано: масса
каната mk=75
кг; передаточное число редуктора k=11,5;
КПД редуктора η=0,95; момент инерции
барабана вместе с зубчатым колесом 1 –
J1=700
кг·м2;
момент инерции ротора двигателя вместе
с зубчатым колесом 2 – J2=100
кг·м2;
скорость вращения двигателя n=475
об/мин; диаметр барабана Dб=3
м.

Рисунок 20
Решение.
Для определения
приведенного момента инерции необходимо
знать линейную скорость груза, для этого
находим скорость вращения барабана:
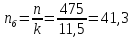 об/мин
об/мин
(131)
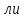 нейная
нейная
скорость груза и каната:
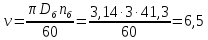 м/с
м/с
(132)
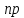 иведенный
иведенный
момент инерции:
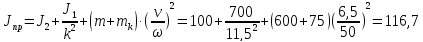 кг·м2,
кг·м2,
(133)
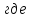
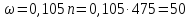 с-1;
с-1;
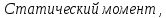 приведенный к валу
приведенный к валу
двигателя:
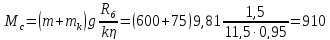 Н·м (134)
Н·м (134)
-
Для установки,
поднимающей груз по наклонной плоскости
рис.21, определить передаточное число
между валом двигателя и валом барабана,
динамический момент и пусковой момент
на валу двигателя, необходимый для
разгона подъемной установки до скорости
v=1,4
м/с, если: время разгона должно быть
равно 2,5 с, вес поднимаемого груза G=9810
Н, момент инерции приводного двигателя
мощностью Р=4,9 кВт при 900 об/мин равен
Jд=0,16
кг·м2,
момент инерции соединительной муфты
Jм=0,3
кг·м2,
момент инерции барабана Jб=110
кг·м2,
диаметр барабана Dб=700
мм, коэффициент трения груза о плоскость
μ=0,15, КПД передачи между валом барабана
и электродвигателя η=0,7, угол наклона
плоскости к горизонту α=5˚.

Рисунок 21
Ответ.
-
Передаточное
число между валом двигателя и валом
барабана k=23,6; -
Динамический
момент постоянный во период разгона
M=33,2
Н·м; -
Пусковой момент
двигателя Mп
=82,3 Н·м.
-
На валу двигателя
скреперной установки средняя мощность
при движении груженного скрепера со
скоростью vг=1,06
м/с составляет Р1=12
кВт, а при движении порожнего скрепера
со скоростью v0=1,67
м/с – Р2=8
кВт.
Определить средний
расчетный момент за цикл на валу
двигателя, а также моменты на валах
грузового и холостого барабанов при
соответствующих режимах работы, если
радиус грузового барабана Rг=210
мм, а холостого R0=225
мм, скорость вращения двигателя n=980
об/мин, КПД редуктора η=0,85.
Решение.
Расчетный момент
на валу двигателя при движении груженого
скрепера:
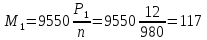 Н·м
Н·м
(135)
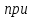 движении порожнего
движении порожнего
скрепера:
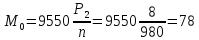 Н·м
Н·м
(136)
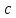 редний
редний
расчетный момент за цикл на валу
двигателя:
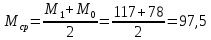 Н·м
Н·м
(137)
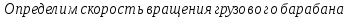 :
:
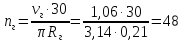 об/мин
об/мин
(138)
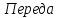 точное
точное
число редуктора лебедки на грузовой
барабан:
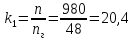 (139)
(139)
 рость
рость
вращения холостого барабана:
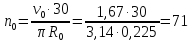 об/мин
об/мин
(140)
Передаточное число
редуктора лебедки на барабан холостого
хода:
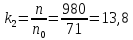 (141)
(141)
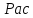 четный
четный
момент на валу лебедки при движении
груженого скрепера:
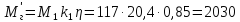 H
H
(142)
 же
же
при движении порожнего скрепера:
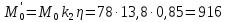 Н·м (143)
Н·м (143)
-
При работе
скреперной установки средняя мощность
на валу двигателя во время движения
груженого скрепера Р2=18,5
кВт при движении со скоростью
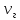 =1
=1
м/с, при движении порожнего Р0=13
кВт со скоростью
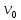 =1,58
=1,58
м/с, скорость вращения двигателяn=980
об/мин, диаметр грузового барабана
Dг=420
мм, холостого D0=450
мм, КПД редуктора η=0,85. Определить момент
на валу двигателя при движении груженого
и порожнего скрепера.
Ответ. Мг=180
Н·м, М0=126,5
Н·м.
-
Подъемная установка
с противовесом (рис.22) поднимает груз
массой m=1500
кг. Определить статический момент на
валу двигателя (при нижнем положении
груза, при встрече груза с противовесом,
при нижнем положении противовеса) и
приведенный к валу двигателя момент
инерции, если дано: масса противовеса
mп=2500
кг, масса порожнего сосуда m0=2000
кг, масса одной ветви каната mк=600
кг, момент инерции барабана с зубчатым
колесом 1 – Jб=7500
кг·м2,
момент инерции ротора двигателя с
зубчатым колесом 4 – Jp=100
кг·м2,
маховый момент зубчатых колес 2 и 3 –
GD2=600
кг·м2,
передаточное число первой пары k1=5,
второй – k2=4,
угловая скорость двигателя ω=76 с-1,
диаметр барабана Dб=3
м, КПД редуктора η=0,8.
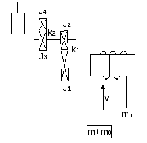
Рисунок 22
Решение.
Определяем
статический момент на валу двигателя
при различных положениях груза:
-
Груз находится в
нижнем положении:
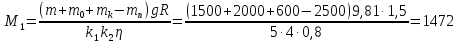 Н·м (144)
Н·м (144)
-
При встрече груза
с противовесом, вес каната уравновешен:
 Н·м (145)
Н·м (145)
При верхнем
положении груза вес каната действует
в направлении противовеса:
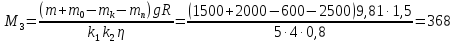 Н·м (146)
Н·м (146)
Для определения
приведенного момента инерции необходимо
знать линейную скорость груза.
Угловая скорость
барабана:
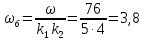 c-1
c-1
(147)
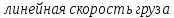 :
:
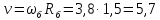 м/с
м/с
(148)
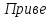 денный
денный
к валу двигателя момент инерции :
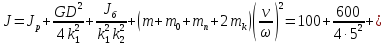
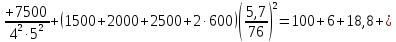
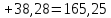 кг·м2
кг·м2
(149)
-
Определить момент
вращения на валу двигателя в период
ускоренного, равномерного и замедленного
движения двухконцевой подъемной
установки (рис.23), если даны: масса
поднимаемого груза m=1200
кг, масса пустого сосуда m0=2000
кг, радиус барабана Rб=1
м, скорость подъема груза v=5
м/с, момент инерции барабана Jб=3000
кг·м2,
момент инерции ротора двигателя Jp=7
кг·м2,
момент инерции редуктора принимаем
15% Jp,
КПД передачи η=0,9, продолжительность
ускорения t1=5
c,
продолжительность замедления t2=4
с, передаточное число редуктора k=15.
При решении задачи не учитывать массу
каната и вредные сопротивления движению
во всех звеньях, кроме редуктора.
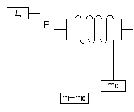
Рисунок 23
Решение.
Для определения
момента вращения на валу двигателя
необходимо знать скорость двигателя.
Угловая скорость
вращения барабана:
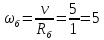 с-1
с-1
(150)
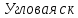 орость
орость
двигателя:
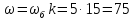 c-1
c-1
(151)
Приведенный к валу
двигателя статический момент:
 Н·м
Н·м
(152)
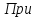 веденный
веденный
к валу двигателя момент инерции:
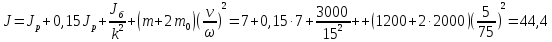 кг·м2
кг·м2
(153)
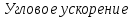 вала двигателя:
вала двигателя:
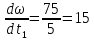 c-2
c-2
(154)
 денный
денный
к валу двигателя динамический момент
при ускорении:
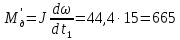 Н·м
Н·м
(155)
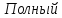 момент на валу
момент на валу
двигателя при ускорении:
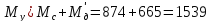 Н·м (156)
Н·м (156)
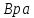 щающий
щающий
момент на валу двигателя в период
равномерного движения:
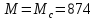 Н·м
Н·м
(157)
Угловое замедление
вала двигателя:
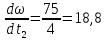 c-2
c-2
(158)
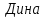 мический
мический
момент, приведенный к валу двигателя
при замедлении:
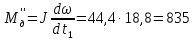 Н·м
Н·м
(159)
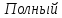 момент двигателя
момент двигателя
при замедлении:
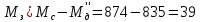 Н·м (160)
Н·м (160)
-
Построить
эквивалентную схему электромеханической
системы, представленной на рис.24, и
определить приведенную жесткость для
этой схемы.
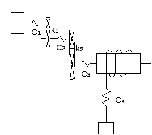
Рисунок 24
Дано: скорость
вращения двигателя n=1000
об/мин, передаточное число редуктора
k1=4,
k2=5,
линейная скорость каната v=2,6
м/с, диаметр каната dк=19
мм, сечение проволок каната S=1,5
см2 (1,5·10-4
м2),
длина каната lк=100
м, диаметры валов: первого d1=75
мм, второго d2=100
мм, третьего d3=150
мм, рабочая длина валов: первого l1=300
мм, второго l2=400
мм, третьего l3=500
мм, радиус навивки барабана Rб=0,25
м.
Решение.
Коэффициент
жесткости каждого вала определяем по
формуле:
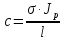 ,
,
(161)
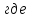
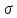 =8,3·106
=8,3·106
– модуль сдвига, Н/см2;
l
– рабочая длина вала, см;
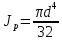 –полярный момент
–полярный момент
инерции сечения вала, см4;
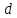 –диаметр вала,
–диаметр вала,
см.
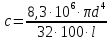 (162)
(162)
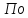 сле
сле
подстановки в указанную формулу величин,
характеризующих вал, получим коэффициенты
жесткости:
Первого вала:
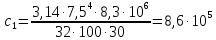 Н·м/рад
Н·м/рад
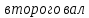 а:
а:
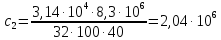 Н·м/рад
Н·м/рад
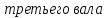 :
:
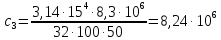 Н·м/рад
Н·м/рад
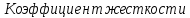 каната
каната
определяем из выражения:
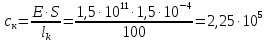 Н/м,
Н/м,
(163)
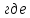 E=
E=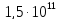 – модуль упругости каната, Н/м2.
– модуль упругости каната, Н/м2.
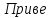 денная
денная
жесткость второго вала к скорости
первого вала:
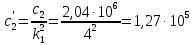 Н·м/рад
Н·м/рад
(164)
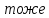 ,
,
третьего вала:
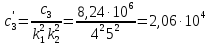 Н·м/рад
Н·м/рад
(165)
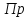 иведенная
иведенная
жесткость каната к скорости первого
вала:
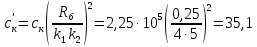 Н·м/рад
Н·м/рад
(166)
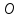 бщий
бщий
приведенный коэффициент жесткости
данной электромеханической системы
будет равен:
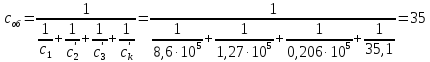 Н·м/рад
Н·м/рад
(167)
-
Определить
эквивалентную жесткость каната
подъемного механизма экскаватора ЭКГ,
представленного на рис.25, приведенную
к валу рабочего двигателя, если жесткость
одного каната с=9·105
Н/м, радиус барабана Rб=0,9
м и общее передаточное число k=k1·k2=46.
Рисунок 25
Решение.
Эквивалентная
жесткость параллельных канатов может
быть определена:
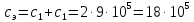 Н/м (168)
Н/м (168)
Приведенная
эквивалентная жесткость канатов к валу
двигателя будет равна:
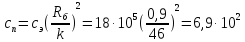 Н·м/рад
Н·м/рад
(169)
-
Определить время
разгона электропривода из неподвижного
состояния до скорости вращения 960 об/мин
при постоянном значении вращающего
момента Мн=360
Н·м и при моменте инерции, приведенном
к валу двигателя, J=5
кг·м2.
Статический момент на валу двигателя
в период разгона равен Мс=100
Н·м.
Решение.
Время разгона
определяется по формуле:
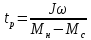 (170)
(170)
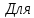 рассматриваемого
рассматриваемого
случая имеем:
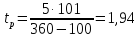 с,
с,
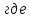
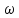 =0,105n=0,105·960=101
=0,105n=0,105·960=101
с-1.
-
Станок, имеющий
скорость вращения приводного вала
n=720
об/мин, момент инерции на валу J=25,5
кг·м2,
приводится в движение асинхронным
двигателем мощностью Р=20,5 кВт. Определить
время разгона для случаев, когда
приводные двигатели имеют скорость
вращения 720 об/мин, 960 об/мин, 1450 об/мин.
При двигателях со скоростью вращения
выше 750 об/мин, предусмотреть промежуточную
зубчатую передачу с η=0,95.
Двигатель при
пуске должен развивать средний пусковой
момент, равный Мп=1,8
Н·м. При пуске момент сопротивления
Мс=270
Н·м. Значения маховых моментов двигателей
представлены в таблице 3.
Таблица 3 – Значения
маховых моментов двигателей
|
Скорость |
Маховый |
|
720 |
25,3 |
|
960 |
16,8 |
|
1450 |
12 |
Решение.
а) Для двигателей
со скоростью вращения 720 об/мин
Номинальный момент
двигателя:
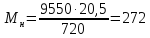 Н·м
Н·м
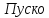 вой
вой
момент двигателя:
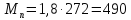 Н·м
Н·м
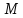 омент
омент
инерции ротора:
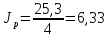 кг·м2
кг·м2
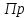 иведенный
иведенный
момент инерции:
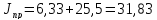 кг·м2
кг·м2
Угловая скорость:
ω=0,105·720=75,5 с-1
Время разгона для
двигателя со скоростью вращения 720
об/мин:
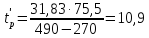 с
с
б) Для двигателя
со скоростью вращения 960 об/мин.
Номинальный момент
двигателя:
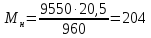 Н·м
Н·м
 вой
вой
момент двигателя:
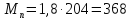 Н·м
Н·м
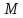 омент
омент
инерции ротора:
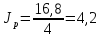 кг·м2
кг·м2
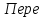 даточное
даточное
число между валом станка и двигателя:
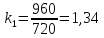
Момент инерции
станка приведенный к валу двигателя:
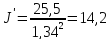 кг·м2
кг·м2
Полный
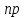 иведенный
иведенный
момент инерции на валу двигателя:
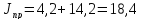 кг·м2
кг·м2
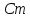 атический
атический
момент приведенный к валу двигателя:
 Н·м
Н·м
Угловая скорость
двигателя:
ω=0,105·960=102 с-1
Время разгона для
двигателя со скоростью вращения 960
об/мин:
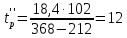 с
с
в) Точно так же
определяем время разгона для двигателя
со скоростью вращения 1450 об/мин:
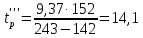 с
с
 примера видно, что
примера видно, что
применение быстроходных двигателей,
ведет к увеличению времени разгона.
-
Определить время
разгона и останова электропривода,
если приведенный к валу двигателя
момент инерции J=85
кг·м2;
скорость вращения двигателя n=725
об/мин; средний пусковой момент Мп=2300
Н·м, статический момент на валу двигателя
Мс=1100
Н·м.
Время останова
определить при свободном выбеге и при
торможении с тормозным моментом Мт=500
Н·м.
Решение.
Время разгона
электропривода будет равно:
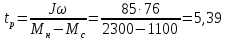 с,
с,
(171)

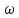 =0,105n=0,105·725=76
=0,105n=0,105·725=76
с-1
 мя
мя
останова при свободном выбеге:
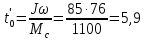 с
с
(172)
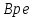 мя
мя
останова при торможении:
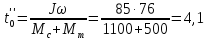 с
с
(173)
-
Двигатель
трехфазного тока 6 кВт, 960 об/мин, Jд=0,3
кг·м2
приводит в движение механизм подъемного
крана. Во время пуска двигатель развивает
вращающий момент, равный 1,8 номинального.
Момент статического сопротивления
равен 0,9 номинального. Общий момент
инерции подъемного крана, отнесенный
к его приводному валу, Jрм=120
кг·м2.
Передаточное отношение между валом
двигателя и рабочей машиной k=10.
Определить угол поворота барабана и
путь, пройденный поднимаемым грузом
за период разгона, если диаметр барабана
равен 0,5 м.
Решение.
Вначале находим
величину номинального момента:
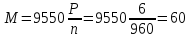 Н·м
Н·м
(174)
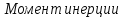 рабочей машины
рабочей машины
приведенный к валу двигателя:
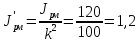 кг·м2
кг·м2
(175)
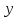 гловая
гловая
скорость вала двигателя:
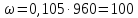 с-1
с-1
 бщий
бщий
момент инерции на валу двигателя:
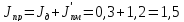 кг·м2
кг·м2
(176)
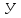 гол
гол
поворота вала двигателя за время пуска:
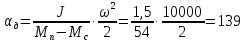 рад (177)
рад (177)
Угол поворота вала
подъемного барабана:
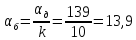 рад
рад
(178)
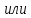 в
в
градусах:
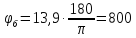 ˚
˚
(179)
что соответствует
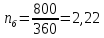 об
об
 уть,
уть,
проходимый грузом за период пуска:
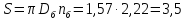 м (180)
м (180)
-
Статический момент
на валу рабочей машины Mc=700
Н·м; средний пусковой момент на валу
двигателя Мп=52
Н·м, маховый момент ротора двигателя
GD2p=4
кг·м2,
момент инерции рабочей машины, приведенный
к валу Jм=200
кг·м2,
средний момент на валу двигателя при
остановке Mт=34
Н·м. Определить наивыгоднейшее
передаточное число редуктора.
Решение.
Для периода пуска,
согласно формуле 12а и 12б:
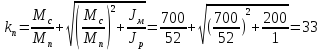 ,
,
(181)

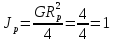 кг·м2.
кг·м2.
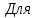 периода замедления:
периода замедления:
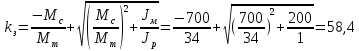 (182)
(182)
Принимаем
передаточное число:
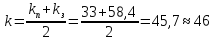 (183)
(183)
-
Определить
наивыгоднейшее передаточное число
редуктора кругового опрокидывателя,
если статический момент на валу
приводного ролика Мс=700
Н·м, пусковой момент двигателя Мп=52
Н·м, момент инерции ротора двигателя
Jд=0,8
кг·м2,
момент инерции опрокидывателя,
приведенный к валу ролика, Jрм=155
кг·м2,
тормозной
момент двигателя при остановке Мт=34
Н·м.
Решение.
Передаточное число
будет равно:
а) для периода
пуска:
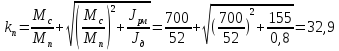 (184)
(184)
б) для периода
останова:
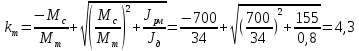 (185)
(185)
Среднее значение
передаточного числа:
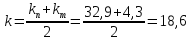 (186)
(186)
-
Для двигателя
постоянного тока независимого возбуждения
построить естественную скоростную
характеристику и выбрать пусковой
реостат (для пуска двигателя в 3 ступени).
Паспортные данные двигателя: Рн=11
кВт, Uн=220
В, Iн=62
А, nн=1000
об/мин.
Примечание. При
решении задачи считать, что ток якоря
равен току двигателя (пренебречь током
возбуждения), момент на валу равен
электромагнитному моменту двигателя
(пренебречь моментом потерь вращения).
Решение.
Номинальное
сопротивление двигателя:
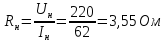 (187)
(187)
Коэффициент
полезного действия двигателя при
номинальной нагрузке:
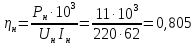 (188)
(188)
Сопротивление
якоря двигателя:
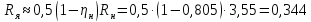 Ом (189)
Ом (189)
Скорость идеального
холостого хода двигателя:
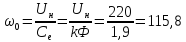 с-1,
с-1,
(190)
где
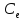 =
=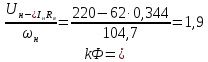 В·с;
В·с;
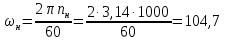 с-1
с-1
(191)
Естественная
характеристика представляет собой
прямую линию, проходящую через точки
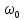 =
=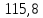 с-1,
с-1,
I=0
и
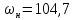 с-1,
с-1,
I=Iн=62
А.
Номинальный момент
двигателя:
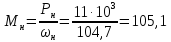 Н·м
Н·м
(192)
Значение максимального
момента и момента переключения
(максимальный и минимальный пусковые
моменты):
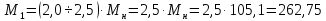 Н·м,
Н·м,
(193)
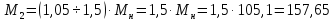 Н·м
Н·м
(194)
По естественной
механической характеристике и найденным
значениям моментов строят пусковую
диаграмму (рис. 26)
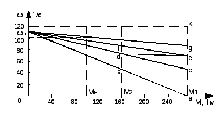
Рисунок 26. Пусковая
диаграмма двигателя
Отрезки на линии
аk
соответствуют
величинам пусковых сопротивлений в
определенном масштабе. Для определения
этого масштаба необходимо найти
сопротивление всей якорной цепи,
соответствующее полному сопротивлению
реостата, включенному в якорь (реостатная
характеристика, проходящая через точку
«а»).
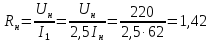 Ом
Ом
(195)
Отсюда масштаб
сопротивлений:
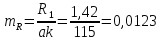 Ом/мм
Ом/мм
(196)
Пусковые сопротивления
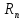 различных ступеней пускового реостата:
различных ступеней пускового реостата:
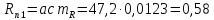 Ом,
Ом,
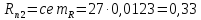 Ом, (197)
Ом, (197)
 Ом
Ом
Полное сопротивление
пускового реостата:
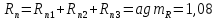 Ом (198)
Ом (198)
-
Для двигателя
последовательного возбуждения с
техническими данными Рн=23
кВт, nн=910
об/мин, Uн=220
В, Iн=122
А, Rя=0,093
Ом, Rв=0,034
Ом, работающего при шунтировании якоря
сопротивлением Rш=1
Ом и введенном добавочном сопротивлении
Rд=0,47
Ом в цепь якоря (рис.27), рассчитать и
построить механическую характеристику.
Потери вращения
при номинальном режиме ΔРвр=1,2
кВт. Данные естественной характеристики
приведены в таблице 4.
Таблица
4 – Расчетные данные естественной
механической характеристики двигателя
|
I=Iв, |
48,8 |
73,2 |
97,6 |
122 |
146,4 |
170,8 |
195,8 |
244,6 |
|
ω, |
143,4 |
114,1 |
103,1 |
95,2 |
88,4 |
85,8 |
81,6 |
68,54 |
|
М, |
65,4 |
120,7 |
176,6 |
241,3 |
309 |
363 |
446,4 |
579,12 |
|
I·Rдв, |
6,2 |
9,3 |
12,4 |
15,5 |
18,6 |
21,7 |
24,8 |
40 |
|
Ед1, |
213,8 |
210,7 |
207,6 |
204,5 |
201,4 |
200,3 |
195 |
189 |
|
kФ, |
1,48 |
1,84 |
2 |
2,14 |
2,27 |
2,33 |
2,39 |
2,54 |
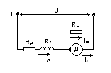
Рисунок 27. Схема
включения двигателя последовательного
возбуждения
Решение.
Определяют
зависимость kФ=f(I),
используя уравнение:
 ,
,
(199)
где
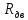 =
=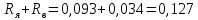 Ом – полное сопротивление обмотки якоря
Ом – полное сопротивление обмотки якоря
и обмотки возбуждения двигателя.
Расчет ведется по
схеме без сопротивления Rш,
задаваясь током двигателя I=Iв.
Результаты расчетов
коэффициентов kФ
сведены в таблицу 2.
Расчет механических
характеристик двигателя производят с
использованием указанных ниже
зависимостей.
Задаваясь током
в обмотке возбуждения I=Iв,
определяют напряжение на зажимах якоря:
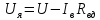 ,
,
(200)
где
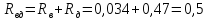 Ом – полное сопротивление обмотки
Ом – полное сопротивление обмотки
возбуждения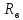 и добавочного сопротивления
и добавочного сопротивления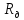 .
.
Ток в шунтирующем
сопротивлении:
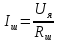 (201)
(201)
Ток в цепи якоря:
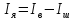 (202)
(202)
ЭДС двигателя:
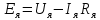 (203)
(203)
Угловая частота
вращения:
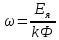 (204)
(204)
Электромагнитный
момент двигателя:
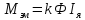 (205)
(205)
Момент холостого
хода двигателя:
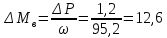 Н·м
Н·м
(206)
Момент на валу
двигателя:
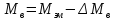 (207)
(207)
Результаты
вычислений сведены в таблицу 5.
Таблица 5 – Расчет
механических характеристик двигателя
при шунтировании якоря
|
|
48,8 |
73,2 |
97,6 |
122 |
146,4 |
170,8 |
195,8 |
244,6 |
|
IвRвд, |
24,4 |
36,6 |
48,8 |
61 |
73,2 |
85,4 |
97,9 |
122 |
|
Uя, |
195,6 |
183,4 |
171,2 |
159 |
146,8 |
134,6 |
122,1 |
98 |
|
Iш, |
195,6 |
183,4 |
171,2 |
159 |
146,8 |
134,6 |
122,1 |
98 |
|
Iя, |
-146,8 |
-110,2 |
-73,6 |
-37 |
-0,4 |
36,2 |
73,7 |
146 |
|
IяRя, |
-13,65 |
-10,25 |
-6,85 |
-3,44 |
-0,037 |
3,37 |
6,85 |
13,6 |
|
Ея, |
-209,3 |
-193,7 |
178,1 |
162,4 |
146,8 |
130,2 |
115,2 |
84,3 |
|
ω, с-1 |
141,4 |
105,2 |
89,03 |
75,9 |
64,7 |
756,3 |
45,18 |
33,2 |
|
Мэм, |
217,3 |
202,8 |
-147,2 |
-79,2 |
-0,9 |
84,3 |
176,1 |
371 |
|
Мв, |
229,9 |
-215,6 |
-159,8 |
-91,8 |
-13,5 |
71,7 |
163,5 |
383 |
|
kФ, |
1,48 |
1,84 |
2 |
2,14 |
2,27 |
2,33 |
2,39 |
2,54 |
По результатам
расчетов строим естественную (кривая
1) и искусственную (кривая 2) механические
характеристики, представленные на
рисунке 28.

Рисунок 28.
Механические характеристики двигателя
при шунтировании якоря
-
Построить
естественную механическую характеристику
для двигательного и генераторного
режимов асинхронного двигателя с фазным
ротором. Паспортные данные двигателя:
Рн=50
кВт, nн=577
об/мин, Uн=380
В, соединение обмоток Y/Y;
ротор: Е2н=253
В, I2н=160
А; обмоточные данные двигателя: R1=0,0549
Ом, R2=0,0332
Ом, x1=0,16
Ом, x2=0,0704
Ом.
Решение.
Коэффициент
трансформации от статора к ротору:
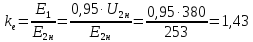 (208)
(208)
Приведенные
сопротивления:
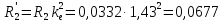 Ом,
Ом,
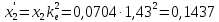 Ом, (209)
Ом, (209)
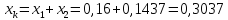 Ом
Ом
Критическое
скольжение двигателя:
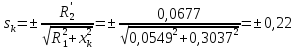 ,
,
(210)
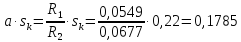 (211)
(211)
Угловая синхронная
частота вращения:
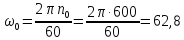 c-1
c-1
(212)
Критический момент
в двигательном режиме:

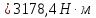 (213)
(213)
Критический момент
в генераторном режиме:
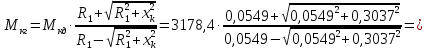
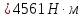 (214)
(214)
Уравнение
естественной механической характеристики:
а) двигательный
режим:
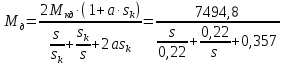 (215)
(215)
б) генераторный
режим:
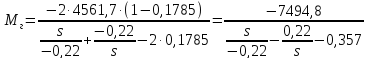 (216)
(216)
Задаваясь
произвольным значением скольжения s,
производят расчет естественной
механической характеристики по полученным
выше уравнениям. Результаты расчетов
сведены в таблицу 6.
Таблица 6 – Расчет
механических характеристик двигателя
|
s |
0 |
0,0383 |
0,1 |
0,18 |
0,22 |
0,25 |
0,4 |
0,75 |
1,0 |
|
Мд,кН·м |
0 |
1,2 |
2,49 |
3,13 |
3,18 |
3,16 |
2,75 |
1,84 |
1,47 |
|
Мг, |
0 |
1,35 |
3,27 |
4,46 |
4,56 |
4,51 |
3,73 |
2,24 |
1,71 |
|
ω, с-1 |
62.8 |
60,4 |
56,52 |
51,5 |
48,98 |
47,1 |
37,68 |
15,7 |
0 |
По данным таблицы
3 строим естественную механическую
характеристику двигателя, представленную
на рисунке 29.
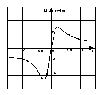
Рисунок 29.
Естественная механическая характеристика
двигателя
-
Расчитать
аналитическим методом пусковой реостат
для асинхронного двигателя со следующими
данными: Рн=280
кВт, nн=985
об/мин, Uн=380
В, λ=1,9,
Е2н=374
В, I2н=465
А. Максимальный момент переключения
принят предварительно М1=1,7·Мн,
минимальный М2=1,2·Мн.
Решение.
Номинальное
скольжение:
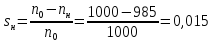 (217)
(217)
Активное сопротивление
фазы ротора:
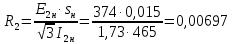 Ом
Ом
(218)
Критическое
скольжение на естественной характеристике:
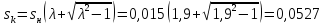 (219)
(219)
Определяем кратности
критического момента по отношению к
моментам переключения:
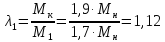 ,
,
(220)
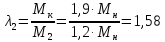
Находим коэффициенты:
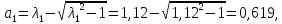 (221)
(221)

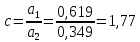 (222)
(222)
Скольжение на
естественной характеристике при моменте
М1:
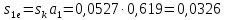 (223)
(223)
Число пусковых
ступеней реостата:
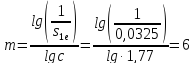 (224)
(224)
Величины пусковых
ступеней реостата:
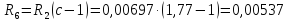 Ом, (225)
Ом, (225)
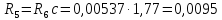 Ом, (226)
Ом, (226)
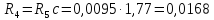 Ом,
Ом,
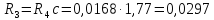 Ом,
Ом,
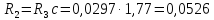 Ом,
Ом,
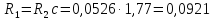 Ом
Ом
Простые механизмы.
-
Рычаг.
-
Неподвижный блок.
-
Подвижный блок.
-
Наклонная плоскость.
-
Золотое правило механики.
-
КПД механизма.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм – это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы – это рычаг и наклонная плоскость.
Рычаг.
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам
и
) приложены силы
и
. Плечи этих сил равны соответственно
и
.
Условие равновесия рычага даётся правилом моментов: , откуда
.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца – это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
к оглавлению ▴
Неподвижный блок.
Важной разновидностью рычага является блок – укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
На правом конце нити в точке закреплён груз весом
. Напомним, что вес тела – это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес
прило жен к точке
, в которой груз крепится к нити.
К левому концу нити в точке приложена сила
.
Плечо силы равно
, где
– радиус блока. Плечо веса
равно
. Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство
, а во-вторых, в процессе движении груза и нити перемещение точки
равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
к оглавлению ▴
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке
и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити
.
 |
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы “перекатывается” через точку
). Говорят ещё, что через точку
проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке
крепления груза к нити. Плечо силы
равно
.
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно
. Соответственно, условием равновесия груза является равенство
(что мы и видим на рис. 3: вектор
в два раза короче вектора
).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) – не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
 |
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
к оглавлению ▴
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость – это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: “наклонная плоскость с углом
“.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом
. Эта сила
, разумеется, направлена вдоль наклонной плоскости (рис. 5).
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что
, поскольку
. Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол
.
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
к оглавлению ▴
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу
. Но для поднятия груза на высоту
большее плечо придётся опустить на
, и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту
над начальным положением, нам нужно пройти путь
вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
к оглавлению ▴
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=Aполезн/Аполн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен
.
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы
из точки
в точку
на высоту
(рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения
.
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
.
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
.
Тогда из (3):
.
Подставляя это в (1), получаем:
.
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Aполн=.
Полезная работа, очевидно, равна:
Аполезн=.
Для искомого КПД получаем:
Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Простые механизмы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Представили эту картину? Впечатляюще, правда? Как вы думаете, механизм, о котором идет речь, действительно волшебный или же его действие основано на физических законах?

Сегодня мы разгадаем эту загадку, а еще узнаем:
-
какие механизмы использовали древние строители;
-
что такое рычаг и где он применяется;
-
что такое плечо рычага и момент силы;
-
закон равновесия рычага и золотое правило механики.
Будет интересно, мы обещаем!
Простые механизмы
Строительство домов, памятников, дворцов и фонтанов — дело не из простых, поэтому еще в древние времена люди изобрели механизмы, которые позволяли упростить процесс.
Простые механизмы — это устройства, которые позволяют изменить величину или направление приложенных к ним сил.
В общем случае простой механизм позволяет затратить меньше усилий для выполнения работы, приложить меньшую силу, получив при этом значительный результат.
К простым механизмам относятся рычаги (на основе которых были созданы блоки и ворот), а также наклонная плоскость, принцип действия которой был заложен в работу клина и винтов.
Обычно простые механизмы — это элементы более сложных устройств, которые используются в быту и промышленности. Без них выполнять такую работу, как поднятие тяжелых предметов на высоту, было бы невозможно.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Рычаг в физике
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.
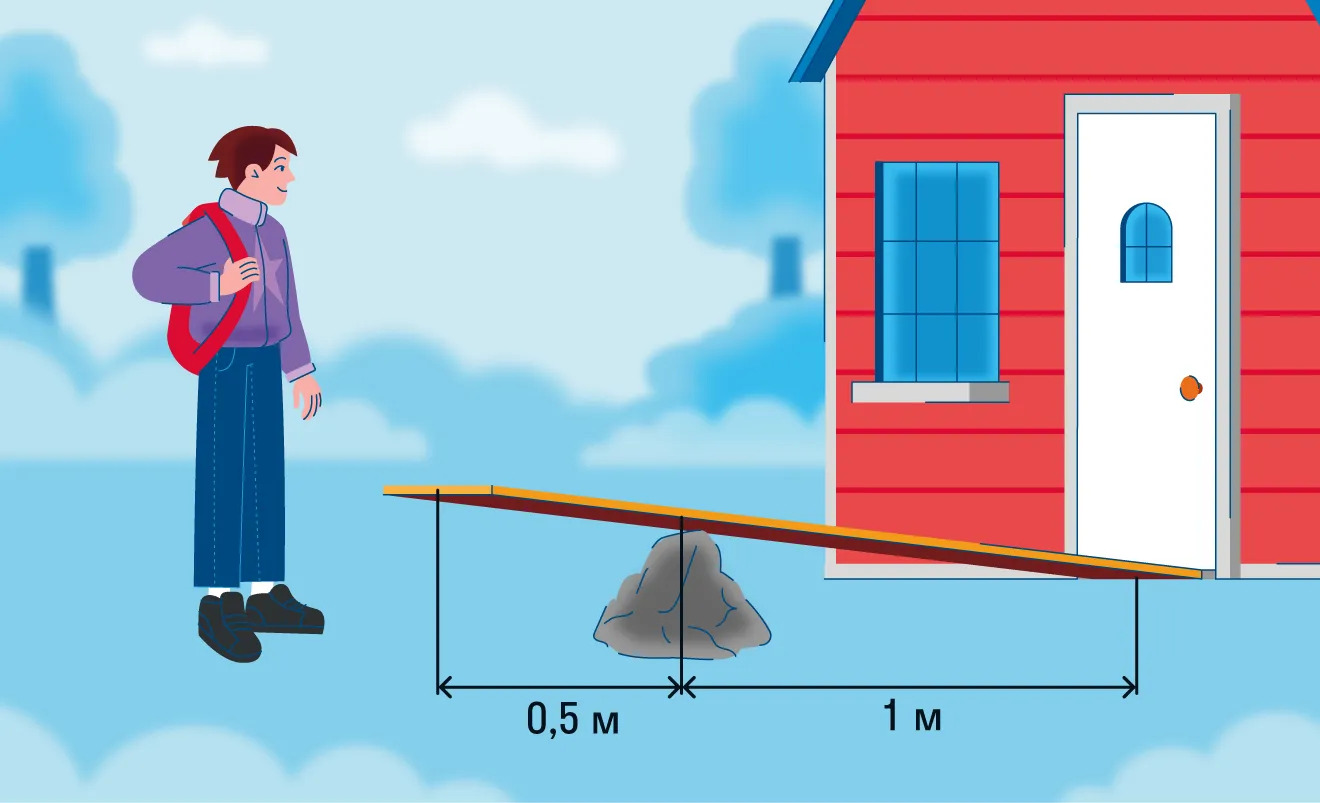
Самый простой пример рычага вы могли видеть в мультфильмах или фильмах: герой подставляет большую доску под камень, опирает ее на бочку или ведро, прикладывает силу к краю доски и… поднимает камень! С помощью такой конструкции можно приподнять любой предмет, весь секрет только в расположении опоры (оси вращения) и правильном распределении усилия.
На рисунке представлен демонстрационный рычаг.
— точка опоры, слева и справа от которой подвешены грузы. Заметим, что количество грузов неравное, но рычаг остается в положении равновесия.
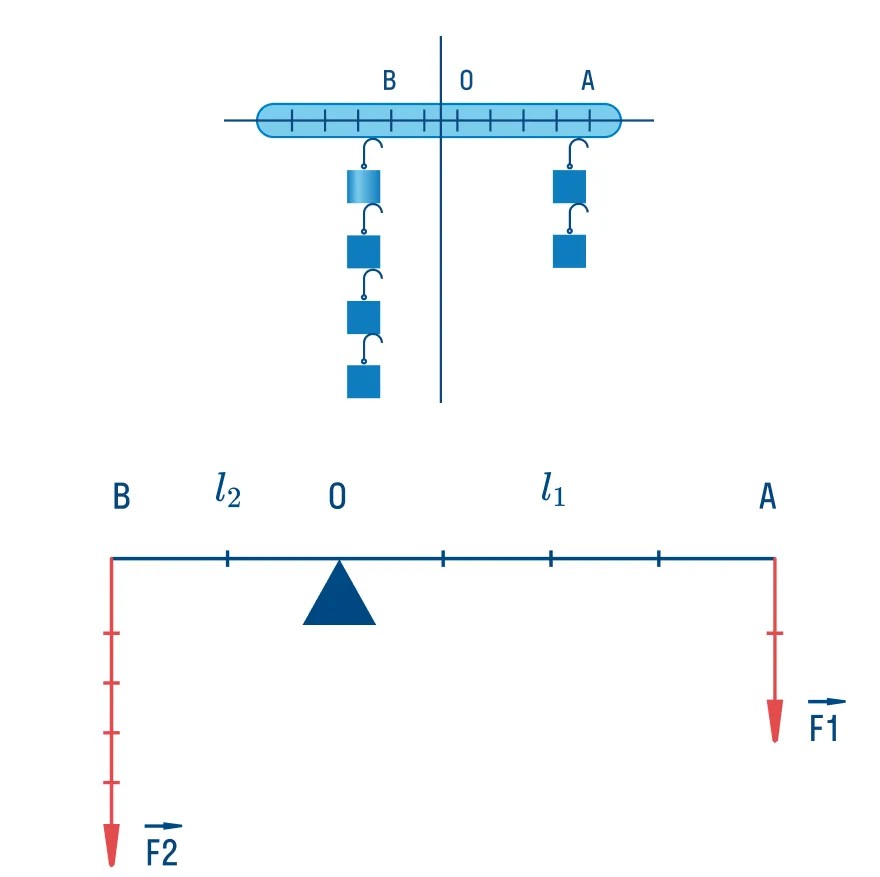
Но главное назначение рычага — не быть в равновесии, а давать выигрыш в силе. Каким образом? Все дело в том, что на рычаг могут действовать разные по величине силы, и точки приложения этих сил располагаются на разном расстоянии от точки опоры. Правильно распределив силы и подобрав расстояние до опоры, можно поднять груз, вес которого намного больше, чем сила, приложенная для его подъёма.
Плечо силы рычага
Плечо силы рычага — это кратчайшее расстояние от точки опоры до точки приложения силы.
На рисунке, который мы рассмотрели, отрезки
и
являются плечом сил
и
соответственно.
Чтобы найти плечо, необходимо из точки опоры опустить перпендикуляр на линию действия силы, длина этого перпендикуляра является плечом данной силы.
Условие равновесия рычага
В каком случае рычаг находится в равновесии? Как необходимо расположить точки приложения сил, чтобы достигнуть этого состояния? Это условие было сформулировано еще много столетий назад.
Рычаг будет находится в равновесии, если силы, действующие на него, обратно пропорциональны плечам этих сил:
, где
и
— приложенные к рычагу силы,
и
— плечи сил
и
соответственно.
Давайте еще раз рассмотрим рисунок:

Предположим, вес одного груза —
, а единичный отрезок равен 1 м. Тогда
м,
м:
Момент силы и рычаги
Правило равновесия рычагов можно переписать, используя понятие «момент силы». Но что это такое?
Момент силы — это произведение величины силы на ее плечо.
В теме 7 класса «Рычаги в физике» вы также можете встретить и другое определение.
Момент силы — физическая величина, характеризующая действие силы на объект, которое вызывает его вращательное движение.

Простыми словами, момент силы — это величина, которая дает характеристику вращательному усилию. Представьте, что вам необходимо закрутить гайку с помощью гаечного ключа. Вы берете ключ, причем автоматически перемещаете руки на его крайнюю часть — так выполнять действие намного проще. Говоря физическим языком, вы увеличиваете плечо силы, чтобы не прикладывать много усилий для закручивания гайки. А еще таким образом вы увеличиваете величину момента вращения.
В физике момент силы обозначается буквой
а измеряется в
Формула момента силы:
Преобразуем условие равновесия рычагов, умножив накрест по основному свойству пропорции:
а так как
то
А значит, сформулировать условие равновесия рычага можно так: рычаг будет находиться в равновесии, когда моменты сил, приложенных к его разным концам, равны.
Задачи
Закрепим пройденный материал, решив парочку задач.
Задача 1
Длина меньшего плеча рычага — 0,05 м, большего — 0,8 м. На меньшее плечо действует 16 H. Какую силу нужно приложить к большему плечу, чтобы уравновесить рычаг (весом рычага можно пренебречь)?
Ответ: 0,012 м.
Золотое правило механики
Как мы видим, рычаги могут дать значительный выигрыш в силе. Этим свойством пользовались древние строители, когда возводили монументальные сооружения. Но помимо выгоды, есть и достаточно плохая новость: чем больший выигрыш в силе нам нужно получить, тем значительнее должны отличаться плечи сил.
Представьте, что вам необходимо поднять камень в тонну при вашей массе 50 кг. Силы отличаются в 200 раз! А значит, и плечи сил должны отличаться во столько же. Если между камнем и точкой опоры будет 0,5 метра, то расстояние от вас до точки опоры должно быть не менее 100 метров. Придется очень потрудиться, чтобы найти доску такой длины.
Золотое правило механики гласит: во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии.
Применение рычагов
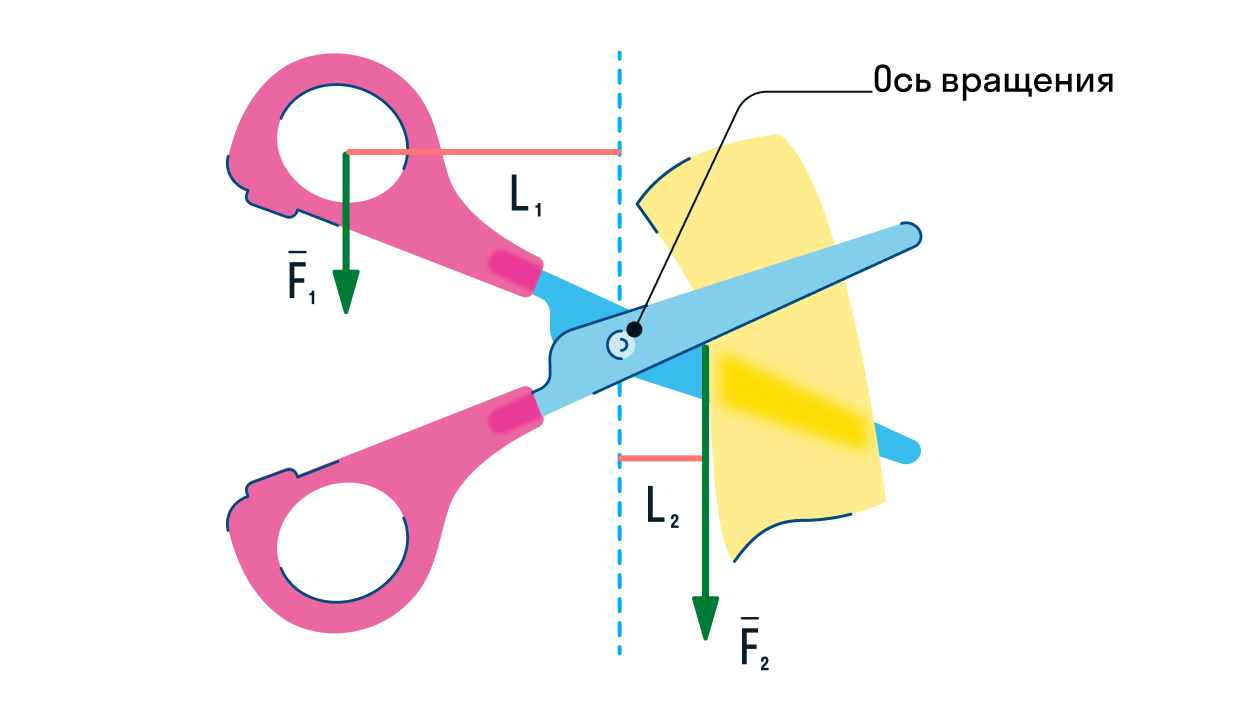
Рычаги встречаются нам ежедневно в обычной жизни, просто до изучения этой темы вы могли их не замечать. Так, ножницы, щипцы для раскалывания орехов, пинцет, механические весы и весло в лодке являются типичными рычагами: у них есть явная точка опоры и плечи сил.
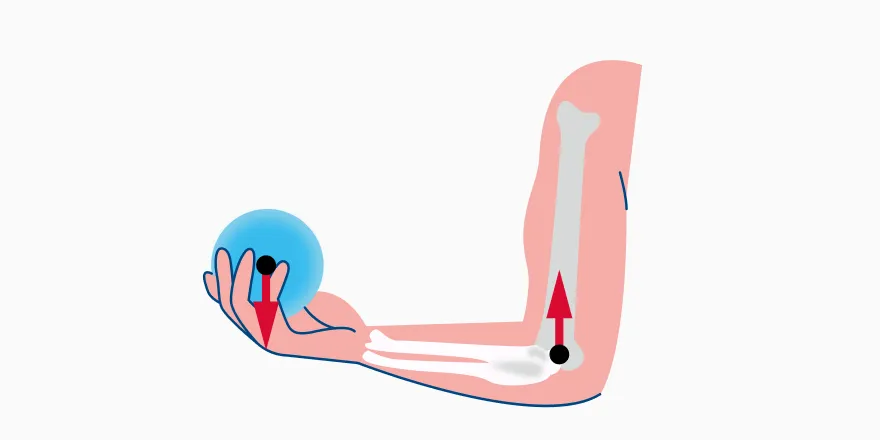
В теле человека тоже есть система рычагов. К ним можно отнести кости рук, ног, пальцев и даже челюсть и череп. Мышцы руки, такие как бицепс и трицепс, тоже можно назвать рычагами: они участвуют во многих движениях, поочередно растягиваясь и сжимаясь.
Виды рычагов
Рычаги делятся на три вида по своему строению. Рассмотрим каждый из них.
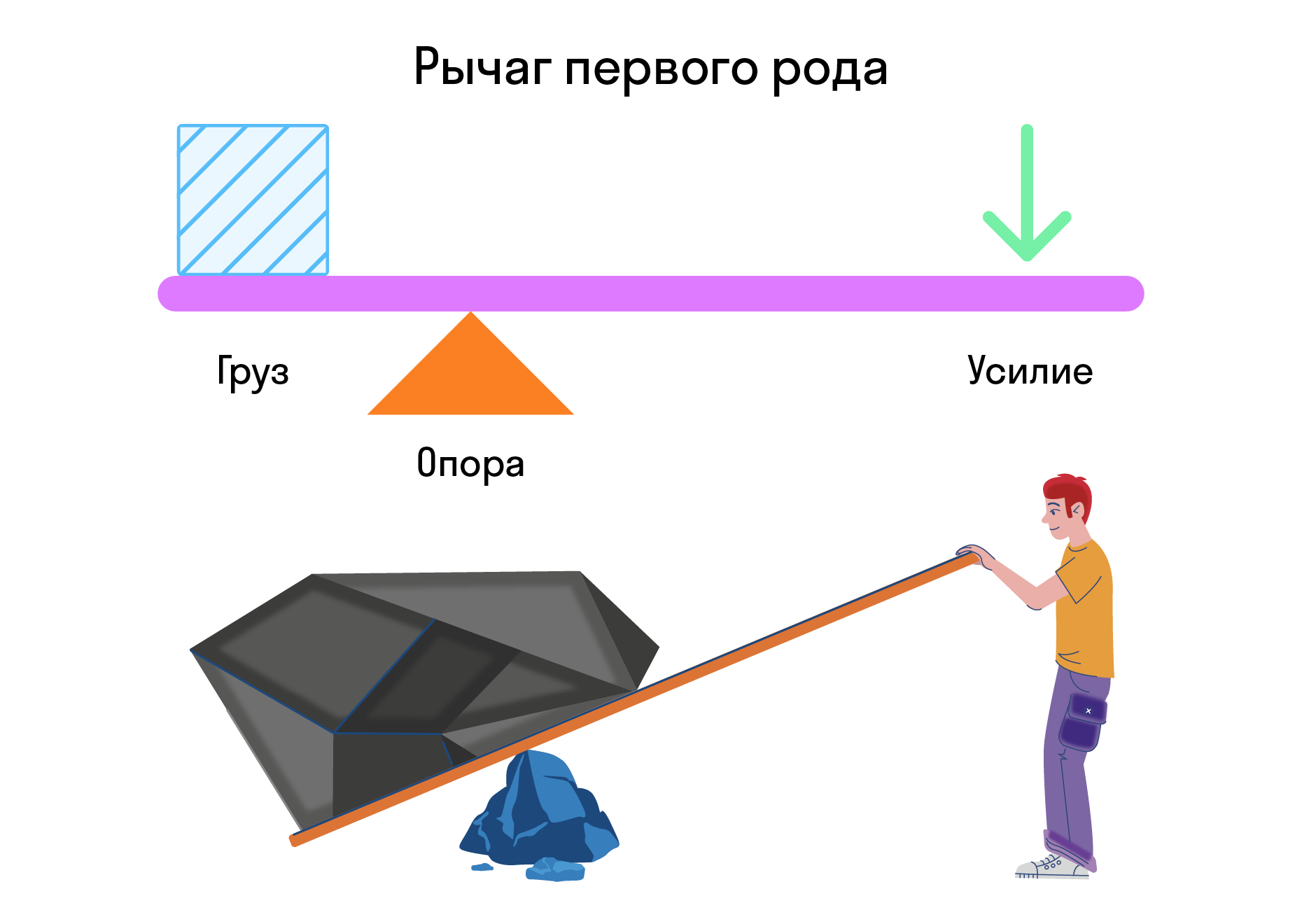
В рычаге первого типа точки приложения сил лежат по разные стороны от точки опоры, силы направлены в одну сторону. Одна из сил стремится повернуть рычаг по часовой стрелке, другая — против часовой стрелки.
Примеры: лом, пила, ножницы, плоскогубцы, детские качели.
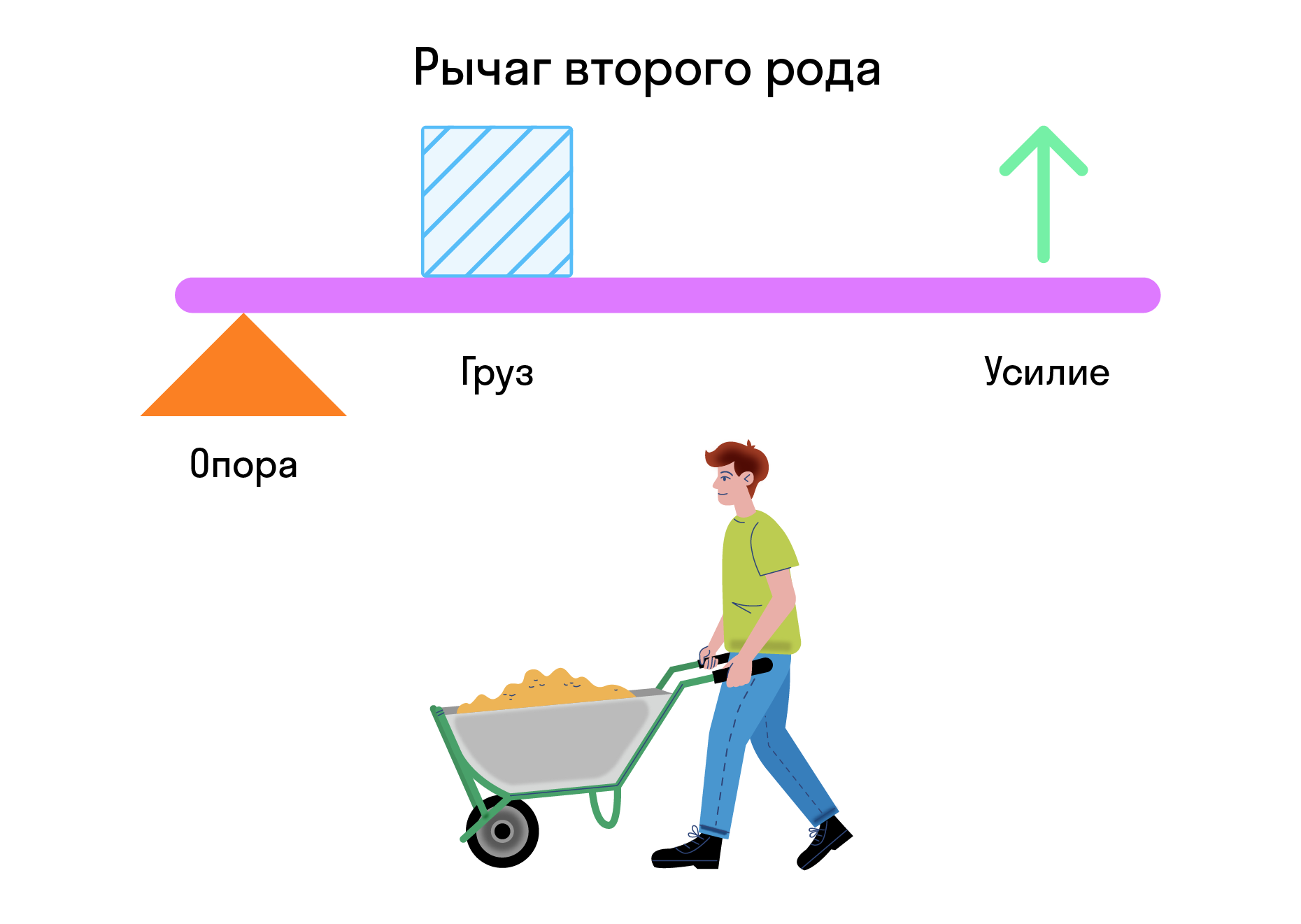
В рычаге второго рода обе точки приложения сил лежат по одну сторону от точки опоры, причем одна из сил имеет меньшее плечо. Примером такого рычага является обычная садовая тачка: чтобы поднять груз, находящийся в ней, необходимо направить нашу силу вверх, чуть приподнимая тачку.
Еще к рычагам второго типа можно отнести щипцы для колки орехов, ключ для открывания бутылок.
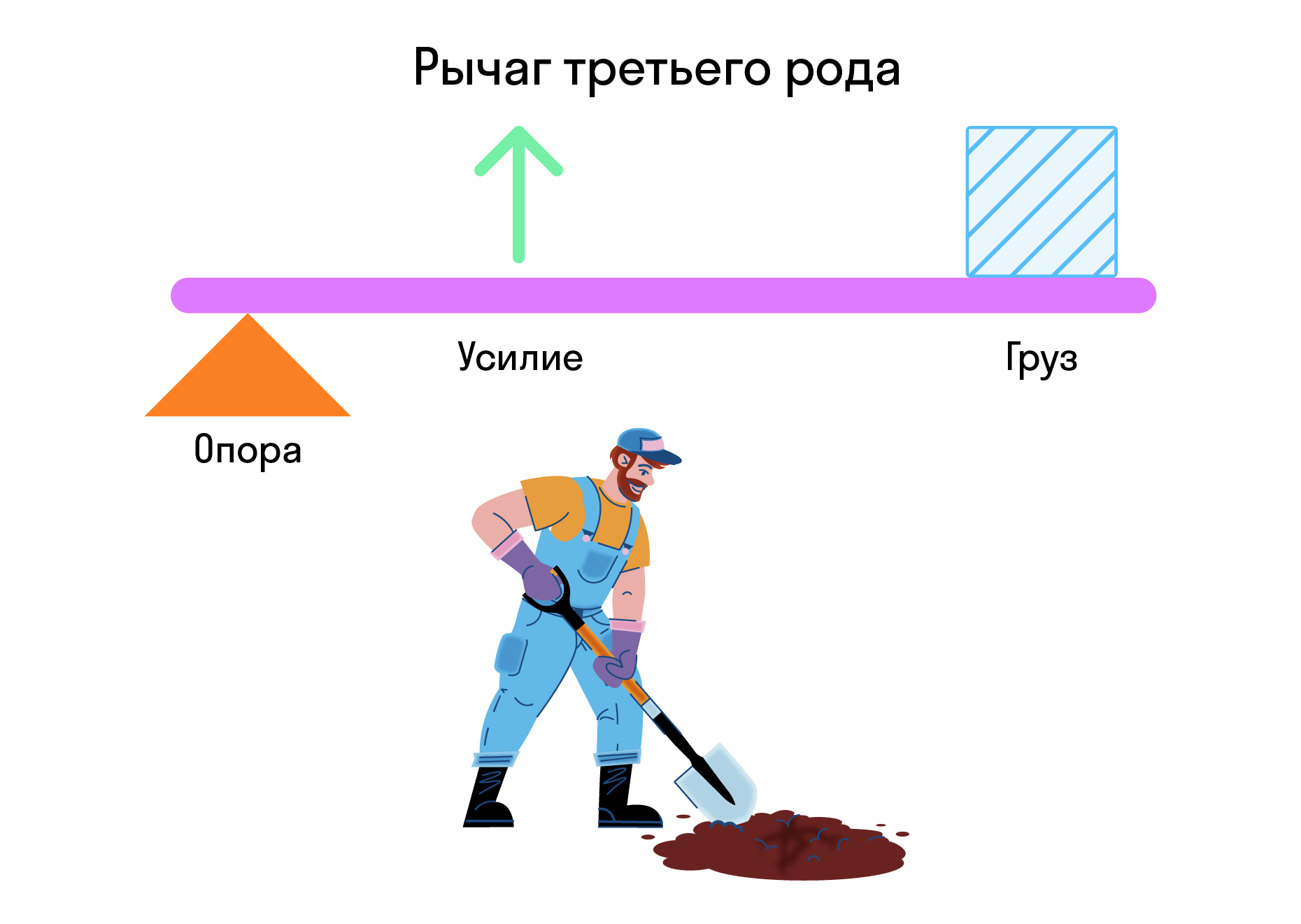
В рычаге третьего типа обе точки приложения сил лежат по одну сторону от точки опоры, но тело, которое необходимо поднять, имеет большее плечо силы. Чтобы поднять такое тело, нам необходимо приложить силу, во много раз превышающую вес груза. К таким рычагам можно отнести ложку, метлу, заднюю дверь багажника и капот легковых автомобилей.
Великий греческий ученый Архимед как-то сказал: «Дайте мне точку опоры, и я сдвину (переверну) Землю!». Имел ли он в виду, что может действительно создать такой масштабный рычаг, сейчас никто не подтвердит. Но мы точно знаем: уверенность в своих силах и знаниях позволит вам справиться с любым сложным делом. Именно такую уверенность дают онлайн-курсы физики в школе Skysmart. Записывайтесь на уроки, и тогда все вам будет нипочем: и школьные уроки физики, и лабораторные работы, и даже олимпиады. И тогда вы, как и Архимед, сможете сказать про себя: я могу сдвинуть даже Землю!💪
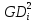
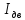 ,
,