Гидравлический пресс в физике, теория и онлайн калькуляторы
Гидравлический пресс
Определение и принцип гидравлического пресса
Определение
Гидравлический пресс – это машина, которая действует на основе законов движения и равновесия жидкостей.
Закон Паскаля лежит в основе принципа действия гидравлического пресса. Название этого устройства происходит от греческого слова гидравликос – водяной. Гидравлическим прессом называют гидравлическую машину, которая используется для прессования (сдавливания). Гидравлический пресс используют там, где необходима большая сила, например, при выдавливании масла из семян. При помощи современных гидравлических прессов можно получать силу до ${10}^8$ньютонов.
Основу гидравлической машины составляют два цилиндра разного радиуса с поршнями (рис.1), которые соединены трубой. Пространство в цилиндрах под поршнями обычно заполняют минеральным маслом.
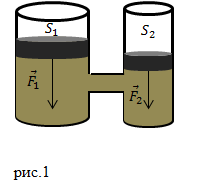
Для того чтобы понять принцип действия гидравлической машины следует вспомнить, что такое сообщающиеся сосуды и в чем смысл закона Паскаля.
Сообщающиеся сосуды
Сообщающимися называют сосуды, соединенные между собой и в которых жидкость может свободно перетекать из одного сосуда в другой. Форма сообщающихся сосудов может быть разной. В сообщающихся сосудах жидкость одной плотности устанавливается на одном уровне, если давления над свободными поверхностями жидкости одинаковы.
Из рис.1 мы видим, что конструктивно гидравлическая машина – это два сообщающихся сосуда разного радиуса. Высоты столбов жидкости в цилиндрах будут одинаковыми, если на поршни не действуют силы.
Закон Паскаля
Закон Паскаля говорит нам о том, что давление, которое оказывают внешние силы на жидкость, передаются ей без изменения во все ее точки. На законе Паскаля основано действие многих гидравлических устройств: прессов, тормозных систем, гидроприводов, гидроусилителей и т.д.
Принцип действия гидравлического пресса
Одним из самых простых и старых устройств основанных на законе Паскаля является гидравлический пресс, в котором небольшая сила $F_1$, прикладываемая к поршню небольшой площади $S_1$, преобразуется в большую силу $F_2$, которая воздействует на площадь большой площади $S_2$.
Давление, которое создает поршень номер один, равно:
[p_1=frac{F_1}{S_1}left(1right).]
Давление второго поршня на жидкость составляет:
[p_2=frac{F_2}{S_2}left(2right).]
Если поршни находятся в равновесии то давления $p_1$ и $p_2$ равны, следовательно, мы можем приравнять правые части выражений (1) и (2):
[frac{F_1}{S_1}=frac{F_2}{S_2}left(3right).]
Определим, каким будет модуль силы, прикладываемой к первому поршню:
[F_1=F_2frac{S_1}{S_2}(4)]
Из формулы (4), видим, что величина $F_1$ больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз.
И так, применяя гидравлический пресс можно небольшой силой уравновесить гораздо большую силу. Отношение $frac{F_1}{F_2}$ показывает выигрыш в силе.
Пресс работает так. Тело, которое необходимо спрессовать, укладывают на платформу, которая лежит на большом поршне. С помощью малого поршня создают высокое давление на жидкость. Большой поршень вместе со сжимаемым телом поднимается, упирается в неподвижную платформу, находящуюся над ними, тело сжимается.
Из малого цилиндра в большой жидкость перекачивают повторным движением поршня малой площади. Делают это следующим образом. Малый поршень поднимается, открывается клапан, при этом в пространство под малым поршнем засасывается жидкость. Когда малый поршень опускается жидкость, оказывая на клапан давление, его закрывает, при этом открывается клапан, который пропускает жидкость в большой сосуд.
Примеры задач с решением
Пример 1
Задание. Каким будет выигрыш в силе у гидравлического пресса, если при действии на малый поршень (площадью $S_1=10 {см}^2$) с силой $F_1=800$ Н, получают силу, воздействия на большой поршень ($S_2=1000 {см}^2$) равной $F_2=72000 $ Н?
Какой выигрыш в силе получался бы у этого пресса, если бы отсутствовали силы трения?
Решение. Выигрышем в силе называют отношение модулей полученной силы к приложенной:
[frac{F_2}{F_1}=frac{72000}{800}=90.]
Используя формулу, полученную для гидравлического пресса:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(1.1right),]
найдем выигрыш в силе при отсутствии сил трения:
[frac{F_2}{F_1}=frac{S_2}{S_1}=frac{1000}{10}=100.]
Ответ. Выигрыш в силе в прессе при наличии сил трения равен $frac{F_2}{F_1}=90.$ Без трения он
был бы равен $frac{F_2}{F_1}=100.$
Пример 2
Задание. Используя гидравлический подъемный механизм, следует поднять груз имеющий массу $m$. Какое число раз ($k$) нужно опустить малый поршень за время $t$, если за один раз он опускается на расстояние $l$? Отношение площадей поршней подъемника равно: $frac{S_1}{S_2}=frac{1}{n}$ ($n>1$). Коэффициент полезного действия машины составляет $eta $ при мощности его двигателя $N$.
Решение. Принципиальная схема работы гидравлического подъемника изображена на рис.2., она аналогична работе гидравлического пресса.
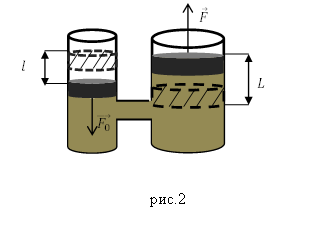
В качестве основы для решения задачи используем выражение, связывающее мощность и работу, но при этом учтем, КПД подъемника, тогда мощность равна:
[N=frac{eta A}{t}to A=eta Ntleft(2.1right).]
Работу производят с целью груз поднять, значит, ее найдем как изменение потенциальной энергии груза, за ноль потенциальной энергии будем считать энергию груза в месте начала его подъема ($E_{p1}$=0), имеем:
[A=E_{p2}-E_{p1}=E_{p2}=mgh left(2.2right),]
где $h$ – высота, на которую подняли груз. Приравняв правые части формул (2.1) и (2.2), найдем высоту, на которую подняли груз:
[eta Nt=mghto h=frac{eta Nt}{mg}left(2.3right).]
Работу, выполняемую силой $F_0$, при перемещении малого поршня найдем как:
[А_1=F_0l left(2.4right),]
Работа силы, которая двигает большой поршень вверх (сжимает гипотетическое тело), равна:
[А_2=FL .]
[А_1=А_2to F_0l=FL]
[frac{F_0}{F}=frac{L}{l}=frac{S_1}{S_2}left(2.5right),]
где $L$ – расстояние, на которое сдвигается большой поршень за один ход. Из (2.5) имеем:
[frac{S_1}{S_2}=frac{L}{l}to L=frac{S_1}{S_2}l left(2.6right).]
Для того чтобы найти количество ходов поршней (число раз которое опустится малый поршень или поднимется большой) следует высоту поднятия груза разделить на расстояние на которое сдвигается большой поршень за один ход:
[k=frac{h}{L}=frac{eta NtS_2}{mgS_1l}=frac{eta Ntn}{mgl}.]
Ответ. $k=frac{eta Ntn}{mgl}$
Читать дальше: закон Архимеда.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Поршневой жидкостный насос. Гидравлический пресс.
«Хотя в мире нет предмета,
который был бы слабее и нежнее воды,
но она может разрушить самый твердый предмет»
Лао-Цзы
В данной теме речь пойдёт о принципах действия поршневого жидкостного насоса и гидравлического пресса.
В прошлых темах говорилось о сообщающихся сосудах — сосуды, которые имеют соединяющую их часть и заполненные покоящейся жидкостью. В открытых сообщающихся сосудах уровень поверхностей однородной жидкости устанавливается на одинаковом уровне (при условии, что давление воздуха над поверхностью жидкости одинаково) и не зависит от формы сосудов.
Также говорилось о законе Паскаля, согласно которому, жидкость или газ передает производимое на нее давление внешней силой по всем направлениям без изменений. Когда Блез Паскаль открыл свой закон, он задумался над тем, как его можно использовать. И придумал устройство гидравлической машиной. Слово «гидравлический» происходит от греческого «гидравликос» — водяной.
Таким образом, гидравлические машины — это машины, работа которых основана на законе Паскаля.
Давайте рассмотрим схему простейшей гидравлической машины.
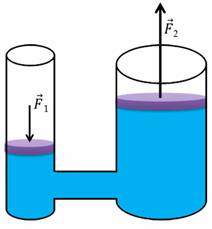
Как видно из рисунка, она состоит из двух сообщающихся сосудов с разными площадями поперечного сечения, заполненных практически несжимаемой жидкостью, обычно маслом, и закрытых подвижными поршнями. Как работает гидравлическая машина? Для этого подействуем на малый поршень небольшой силой. Эта сила будет создавать давление на жидкость, которое по закону Паскаля передается во все точки жидкости. Значит и на большой поршень подействует такое же давление. Тогда сила давления, действующая на большой поршень, будет направлена вверх и равна произведению давления и площади большого поршня. Сравним силы, действующие на малый и большой поршни.
p1 = p2
F1 = p1S1
F2 = p2S2 = p1S2
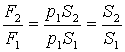
Таким образом, можно сделать вывод о том, что гидравлическая машина дает выигрыш в силе во столько раз, во сколько раз площадь поперечного сечения большого поршня больше площади поперечного сечения малого поршня. Это означает, что с помощью небольшой силы, приложенной к малому поршню гидравлической машины, можно уравновесить существенно большую силу, приложенную к большому поршню.
Гидравлическую машину, служащую для прессования, называют гидравлическим прессом. Он широко применяется в технике для обработки металлов, прессования фанеры, картона, древесностружечных плит. А в сельском хозяйстве гидравлический пресс используется для прессования сена, для выжимки масла из семян подсолнуха, кукурузы и т.д. Современные гидравлические прессы способны развивать силу в десятки и сотни миллионов Ньютонов. Прессуемое тело кладут на платформу, которая соединена с большим поршнем. С помощью малого поршня создается большое давление, которое, согласно закону Паскаля, передается в каждую точку жидкости, заполняющей цилиндры. Тогда и на большой поршень будет действовать такое же давление. Но так как площади поршней отличаются, то сила, действующая на большой поршень, будет больше силы, действующей на малый поршень. Под действием этой силы большой поршень будет подниматься. При его подъеме прессуемое тело упирается в неподвижную платформу и сжимается.
Из малого цилиндра в большой жидкость перекачивается с помощью поршневого жидкостного насоса. Рассмотрим схему и принцип действия такого насоса на примере колонки.
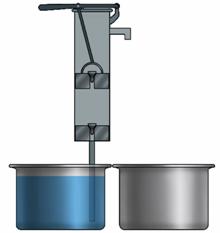
Поршневой жидкостный насос состоит из цилиндра, внутри которого находится плотно прилегающий к стенкам поршень. И в поршне, и в нижней части цилиндра располагаются клапаны, которые открываются только вверх. При движении поршня вверх жидкость под действием атмосферного давления поднимает нижний клапан и, двигаясь вслед за поршнем, входит в трубу. Когда поршень движется вниз, жидкость, находящаяся под поршнем, давит на нижний клапан, и он закрывается. В это же время, под давлением воды, открывается клапан в самом поршне, и жидкость переходит в пространство над поршнем. При следующем движении поршня вверх вместе с ним поднимается и находящаяся над ним жидкость, которая выливается в отводящую трубу. При этом за поршнем поднимается новая порция жидкости, которая при последующем опускании поршня, вновь окажется над ним.
Вернемся опять к гидравлическому прессу.
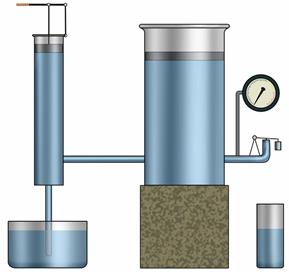
Обратим внимание, поршневой насос в гидравлическом прессе немного отличается от рассмотренного выше. Однако принцип его работы такой же. При подъеме малого поршня открывается клапан, и в пространство, находящееся под поршнем, засасывается жидкость. При опускании малого поршня под действием давления жидкости этот клапан закрывается и открывается клапан, связывающий большой и малый цилиндры, и жидкость переходит в большой сосуд.
Еще одной разновидностью гидравлических машин является гидравлический тормоз. Являющийся важной частью большинства автомобилей, именно он осуществляет быстрое и надежное торможение его колес. Работу гидравлического тормоза можно объяснить, используя упрощенную схему.
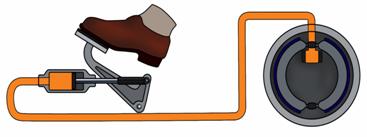
Нога водителя действует на тормозную педаль. Это действие передается на поршень цилиндра, в котором находится тормозная жидкость. Этот поршень создает давление на жидкость, которое согласно закону Паскаля передается в тормозные цилиндры всех колес автомобиля. В тормозном устройстве имеется цилиндр с двумя подвижными поршнями. Под давлением жидкости эти поршни расходятся и прижимают тормозные колодки к тормозным барабанам, что и останавливает вращение колес.
Еще одним эффективным гидравлическим механизмом является гидравлический домкрат, с помощью которого можно поднимать очень тяжелые машины. Принцип действия домкрата такой же, как и гидравлического пресса.

Упражнения.
Задача 1. На малый поршень гидравлического пресса действует сила 150 Н. Определите силу, действующую на большой поршень, если его площадь в 20 раз больше площади малого поршня.

Задача 2. Малый поршень гидравлического пресса за один ход опустился на расстояние 0,2 м, при этом большой поршень поднялся на высоту 0,01 м. С какой силой действует пресс на зажатое в нем тело, если на малый поршень 
Задача 3. Гидравлический пресс, заполненный водой, имеет поршни, площади которых 200 см2 и 20 см2. На большой поршень положили груз массой 60 кг. На какую высоту поднимается после этого малый поршень? Плотность воды примите равной 1000 кг/м3.



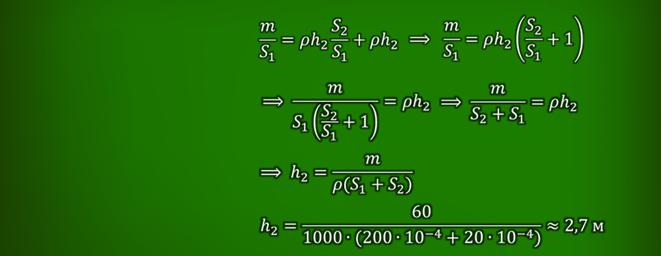
Основные выводы:
– Гидравлическая машина — машина, действие которой основано на законе Паскаля.
– Гидравлический пресс –это гидравлическая машина, служащая для прессования.
– Гидравлический пресс дает выигрыш в силе во столько раз, во сколько раз площадь большого поршня больше площади малого поршня.
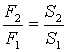
Пройдите тест
Сообщающиеся сосуды. Гидравлический пресс
- Закон сообщающихся сосудов
- Сообщающиеся сосуды с различными жидкостями
- Гидравлический пресс
- Задачи
п.1. Закон сообщающихся сосудов
Как было показано в §31 данного справочника, давление столба жидкости не зависит от формы или размера дна сосуда. На одном и том же уровне (h) давление будет одинаковым.
Поэтому, когда жидкость приходит в равновесие, давление выравнивается, и её поверхность становится горизонтальной.
Второй случай с U-образной трубкой представляет значительный практический интерес, поскольку её колена являются так называемыми сообщающимися сосудами.
Сообщающиеся сосуды – сосуды с общим дном, в которых жидкость может свободно перетекать из одного колена в другое.
 |
Из сказанного выше следует, что при любой форме сообщающихся сосудов жидкость, налитая в них, будет перетекать, пока не установится на одном уровне в каждом из колен. |
Закон сообщающихся сосудов
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне.
п.2. Сообщающиеся сосуды с различными жидкостями
Теперь рассмотрим, какой уровень установится, если в U-образную трубку налить две несмешивающиеся жидкости с различной плотностью, например, керосин и воду.
 |
На рисунке пунктиром обозначен горизонтальный уровень, который проходит под слоем керосина. На этом уровне в обоих коленах трубки находится вода, а значит, давления по закону Паскаля одинаковы. Можем записать $$ rho_2gh_2=rho_1gh_1 Rightarrow frac{h_2}{h_1}=frac{rho_1}{rho_2} $$ Получаем
|
В сообщающихся сосудах с различными жидкостями уровень жидкости выше в сосуде, в котором находится жидкость с меньшей плотностью.
п.3. Гидравлический пресс
Закон Паскаля и закон сообщающихся сосудов позволяет создавать гидравлические механизмы с многократным выигрышем в силе.
Гидравлический пресс состоит из двух сообщающихся цилиндрических сосудов разного диаметра. Сосуды заполняются водой, маслом или другой жидкостью. По закону Паскаля давление одинаково по всем направлениям и передается по всему объему.

Если подействовать на меньший поршень слева силой (F_1), направленной вниз, под поршнем возникнет избыточное давление (p=frac{F_1}{S_1}). Это давление будет передаваться по всему объему в жидкости, и под большим поршнем справа получим (p=frac{F_2}{S_2}). На большой поршень будет действовать сила (F_2=pS_2=F_1frac{S_2}{S_1}), направленная вверх.
За счет разности площади поршней получаем выигрыш в силе $$ k=frac{F_2}{F_1}=frac{S_2}{S_1} $$
Отношение силы давления большого поршня к силе давления малого поршня равно отношению площади большого поршня к площади малого поршня.
Гидравлический пресс был изобретен в 1795 году и с тех пор нашёл множество применений в различных отраслях производства. В современных прессах можно получить силу порядка сотен миллионов ньютонов, что используется для штамповки изделий из металла, прессования картона и хлопка, выдавливания масла из семян и т.д.
п.4. Задачи
Задача 1. Диаметр одного цилиндрического ведра в 1,2 раза больше, чем другого. В оба ведра налили по 5 л воды. В каком ведре давление на дно больше и во сколько раз?
Дано:
(d_1=1,2=d_2)
(V=5 text{л})
__________________
(frac{p_2}{p_1}-?)
Площадь дна каждого из ведер $$ S_1=frac{pi d^2_1}{4}, S_2=frac{pi d^2_2}{4} $$ Найдем высоту столба воды в каждом из ведер $$ V=ShRightarrow h_1=frac{V}{S_1}=frac{4V}{pi d^2_1}, h_2=frac{4V}{pi d^2_2} $$ Давление на дно в каждом из ведер $$ p_1rho gh_1=rho gcdotfrac{4V}{pi d^2_1}, p_2rho gh_2=rho gcdotfrac{4V}{pi d^2_2} $$ Отношение давлений $$ frac{p_2}{p_1}=frac{rho gcdot frac{4V}{pi d^2_2}}{rho gcdot frac{4V}{pi d^2_1}}=frac{d^2_1}{d^2_2}=left(frac{d_1}{d_2}right)^2 $$ Давление больше в узком ведре.
Отношение давлений равно отношению квадратов диаметров. $$ frac{p_2}{p_1}=1,2^2=1,44 $$ Ответ: больше в узком ведре; в 1,44 раза
Задача 2. Горизонтально расположенная труба заполнена водой и имеет два поршня. Площади поршней (S_1=10 text{см}^2, S_2=1 text{дм}^2). На поршень (B) действует сила (10 text{кН}). С какой силой нужно действовать на поршень (A), чтобы уравновесить силу, действующую на поршень (B)?
Дано:
(S_1=10 text{см}^2=0,001 text{м}^2)
(S_2=1 text{дм}^2=0,01 text{м}^2)
(F_2=10 text{кН}=10^4 text{Н})
__________________
(F_1-?)
При действии силы (F_2) на поршень (B) в воде возникает давление $$ p=frac{F_2}{S_2}. $$ По закону Паскаля давление передается во все стороны, и у поршня (A) получаем $$ p=frac{F_1}{S_1}. $$ Для уравновешивающей силы $$ frac{F_1}{S_1}=frac{F_2}{S_2}Rightarrow F-1=F_2frac{S_1}{S_2} $$ Подставляем $$ F_1=10^4cdot frac{0,001}{0,01}=10^3 (text{Н})=1 (text{кН}) $$ Ответ: 1 кН
Задача 3. U-образную трубку частично заполнили водой. В левое колено долили слой керосина высотой 25 см. В каком колене установился уровень выше? Найдите перепад высот (h) между уровнями поверхности воды в правом колене и уровнем керосина в левом колене. Ответ запишите в сантиметрах.
Дано:
(h_2=25 text{см}=0,25 text{м})
(rho_1=1000 text{кг/м}^3)
(rho_2=800 text{кг/м}^3)
__________________
(h-?)
На уровне под слоем керосина в обоих коленах трубки находится вода, а значит, давления на этом уровне по закону Паскаля одинаковы в обоих коленах. Можем записать $$ rho_2gh_2=rho_1gh_1Rightarrow h_1=frac{rho_2}{rho_1}h_2 $$ Поскольку плотность керосина меньше, уровень в левом колене с керосином выше.
Разность уровней begin{gather*} h=h_2-h_1=h_2-frac{rho_2}{rho_1}h_2\[7pt] h=left(1-frac{rho_2}{rho_1}right)h_2 end{gather*} Получаем: $$ h=left(1-frac{800}{1000}right)cdot 0,25=0,05 (text{м})=5 (text{см}) $$ Ответ: в левом колене с керосином; 5 см
Задача 4*. На дно мензурки налита ртуть и в нее опущен конец стеклянной трубки, запаянной сверху. Поверх ртути в мензурку налили слой воды высотой 25 см.
На какую высоту поднимется ртуть в стеклянной трубке?
Примите для расчетов (p_text{атм}=1,013cdot 10^5 text{Па}, g=9,8 text{м/с}^2)
Ответ укажите в миллиметрах.
На какую высоту поднимется ртуть при тех же условиях, если трубка не запаяна сверху?
Дано:
(rho_1=1000 text{кг/м}^3)
(rho_2=13600 text{кг/м}^3)
(h_1=25 text{см}=0,25 text{м})
(gapprox 9,8 text{м/с}^2)
(p_text{атм}=1,013cdot 10^5 text{Па})
__________________
(h_2-?, h’_2-?)
Рассмотрим запаянную трубку. На поверхность ртути, в которую опущен конец трубки, оказывают давление столб воды и атмосфера: $$ p=p_1+p_text{атм}=rho_1gh_1+p_text{атм} $$ Под действием этого давления ртуть в запаянной трубке поднимется на высоту $$ h_2=frac{p}{rho_2g}=frac{rho_1gh_1+p_text{атм}}{rho_2g} $$ Получаем $$ h_2=frac{1000cdot 9,8cdot 0,25+1,013cdot 10^5}{13600cdot 9,8}approx 0,778 (text{м})=778 (text{мм}) $$ Если трубка будет не запаяна, то при подъеме в ней ртути на нее сверху будет действовать атмосферное давление. Высота подъема begin{gather*} h’_2=frac{p-p_text{атм}}{rho_2g}=frac{rho_1gh_1}{rho_2g}=frac{rho_1}{rho_2}h_1\[7pt] h’_2=frac{1000}{13600}cdot 0,25approx 0,018 (text{м})=18 (text{мм}) end{gather*} Ответ: 778 мм; 18 мм
Примечание: заметим, что разность (h_text{атм}=778-18 = 760 text{мм}) – это нормальное атмосферное давление, измеренное в «миллиметрах ртутного столба» (см. §31 данного справочника). Поэтому (h_2=h’_2+h_text{атм}).
Задача 5. Малый поршень гидравлического пресса под действием силы 500 Н опустился на 9 см. При этом большой поршень поднялся на 3 см.
Какая сила действует на большой поршень со стороны жидкости?
Дано:
(F_1=500 text{Н})
(h_1=9 text{см}=0,09 text{м})
(h_2=3 text{см}=0,03 text{м})
__________________
(F_2-?)
Объем воды, вытесняемый при движении малого поршня вниз: (V=h_1S_1).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: (V=h_2S_2).
Получаем для выигрыша в силе: $$ h_1S_1=h_2S_2Rightarrow frac{S_2}{S_1}=frac{h_1}{h_2} $$ Выигрыш в силе равен отношению длин хода малого и большого поршней.
Выигрывая в силе, мы проигрываем в расстоянии.
Сила, действующая на большой поршень: $$ F_2=F_1frac{S_2}{S_1}=F_1frac{h_1}{h_2} $$ Подставляем: $$ F_2=500cdot frac{0,09}{0,03}=1500 (text{Н})=1,5 (text{кН}) $$ Ответ: 1,5 кН
Задача 6. Малый поршень гидравлического пресса площадью 1 м2 под действием силы 2 кН опустился на 24 см. Площадь большего поршня 8 м2. Найдите вес груза, который был поднят большим поршнем и высоту, на которую он был поднят.
Дано:
(S_1=1 text{м}^2)
(F_1=2000 text{Н})
(h_1=24 text{см}=0,24 text{м})
(S_2=8 text{м}^2)
__________________
(P-?, h_2-?)
Вес груза, который можно поднять с помощью пресса, равен силе (F_2), которая действует на большой поршень: $$ P=F_2=F_1frac{S_2}{S_1} $$ Получаем $$ P=2000cdot frac 81=16000 (text{Н})=16 (text{кН}) $$ Объем воды, вытесняемый при движении малого поршня вниз: (V=h_1S_1).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: (V=h_2S_2).
Следовательно $$ h_1S_1=h_2S_2Rightarrow h_2=h_1frac{S_1}{S_2} $$ Получаем begin{gather*} h_2=0,24cdot frac 81=0,03 (text{м})=3 (text{см}) end{gather*} Ответ: 16 кН; 3 см
Задача 7*. На дне аквариума лежал камень массой 390 г, полностью погруженный в воду. Когда его убрали, давление воды на дно аквариума уменьшилось на 25 Па. Найдите плотность камня, если длина аквариума 40 см, а ширина 14 см. ((g=9,8 text{м/с}^2)).
Дано:
(m=390 text{г}=0,39 text{кг})
(Delta p=25 text{Па})
(a=40 text{см}=0,4 text{м})
(b=14 text{см}=0,14 text{м})
(rho_0=1000 text{кг/м}^3)
(g=9,8 text{м/с}^2)
__________________
(rho-?)
Лежа на дне, камень занимал в аквариуме некий объем $$ V_text{к}=frac{m}{rho} $$ Остальной объем занимала вода. Их суммарный объем $$ V=V_text{в}+V_text{к}=Sh=abh $$ Высота слоя воды в аквариуме с камнем $$ h_1=frac{V_text{в}+V_text{к}}{ab} $$ Давление воды на дно в аквариуме с камнем begin{gather*} p_1=rho_0gh_1= rho_0gfrac{V_text{в}+V_text{к}}{ab} end{gather*} Когда камень забрали, в аквариуме осталась только вода объемом (V_text{в}).
Высота слоя воды в аквариуме без камня $$ h_2=frac{V_text{в}}{ab} $$ Давление воды на дно в аквариуме без камня $$ p_2=rho_0gh_2=rho_0gfrac{V_text{в}}{ab} $$ Разность давлений $$ Delta p=p_1-p_2=rho_0 gfrac{V_text{в}+V_text{к}}{ab}-rho_0gfrac{V_text{в}}{ab}=rho_0gfrac{V_text{к}}{ab}=frac{rho_0g}{ab}cdot frac{m}{rho} $$ Откуда плотность камня $$ rho=frac{rho_0g}{ab}cdot frac{m}{Delta p} $$ Подставляем $$ rho=frac{1000cdot 9,8}{0,4cdot 0,14}cdotfrac{0,39}{25}=2730 (text{кг/м}^3) $$ Ответ: 2730 кг/м3
Содержание:
- § 1 Гидравлическая машина
- § 2 Гидравлический пресс
- § 3 Решение задач
- § 4 Важно запомнить
§ 1 Гидравлическая машина
В этом уроке мы изучим устройство и принцип действия гидравлических машин.
В жизни человеку очень часто приходится сталкиваться с такими ситуациями, где нужно поднять груз большой массы на высоту или сжать какое-либо тело. Например, автомобилисту нужно сменить проколотое колесо. Для этого нужно приподнять автомобиль. Поднять 5 кг, 10 кг взрослому человеку не так сложно. Но поднять автомобиль? Или нужно выжать масло из семян подсолнуха, спрессовать бумагу. И вот в таких случаях на помощь приходят разные механизмы, позволяющие получить большую силу, прилагая незначительные усилия.
Одним из таких механизмов является гидравлическая машина.
Гидравлическая машина (от греческого слова гидравликос – водяной) – это машина, действие которой основано на законах движения и равновесия жидкостей. Первая гидравлическая машина была создана Паскалем, который называл ее машиной для увеличения силы.
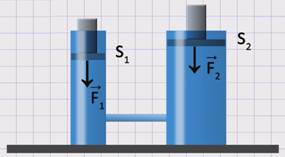
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью (водой или маслом).
Рассмотрим принцип действия гидравлической машины. Обозначим площадь поршня в малом цилиндре S1, площадь поршня в большом цилиндре – S2, F1 и F2 – силы, действующие на поршни.
Если на поршень S1 подействовать с силой F1, то давление в малом цилиндре будет определяться по формуле:
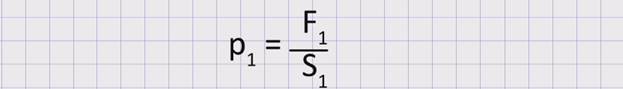
Давление в большом цилиндре:
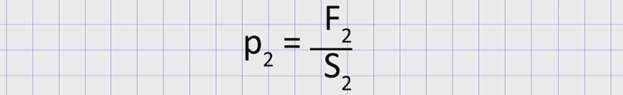
По закону Паскаля давление, производимое на жидкость или газ, передается в каждую точку по всем направлениям одинаково. Значит, давление в обоих цилиндрах будет одинаковым: p1 = p2 . Тогда можем приравнять правые части этих формул:

Читается эта формула так: сила F2, действующая на большой поршень, во столько раз больше силы F1, действующей на малый поршень, во сколько раз площадь большого поршня S2 больше площади малого поршняS1. Отношение F2 к F1показывается выигрышем в силе.
Итак, сделаем вывод. Приложив незначительное усилие F1 к малому поршню, мы можем получить во столько раз большую силу F2 на большом поршне, во сколько раз его площадь превышает площадь малого поршня.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
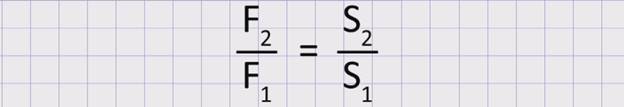
§ 2 Гидравлический пресс
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
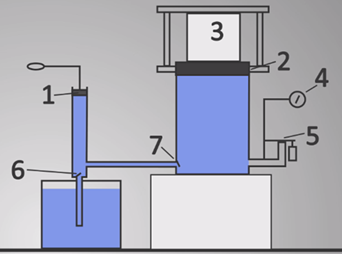
Принцип действия гидравлического пресса таков: на платформу большого поршня 2 кладется прессуемое тело 3. При помощи малого поршня 1 создается давление на жидкость, которое по закону Паскаля передается в каждую точку жидкости, заполняющей цилиндры. Так как площадь большого поршня во много раз больше площади малого, то и действующая на него сила окажется во столько же раз больше. Под действием этой силы большой поршень поднимается и сжимает тело. За значением давления, возникающего в жидкости, следят при помощи деформационного манометра 4, соединенного с предохранительным клапаном 5, который автоматически открывается при превышении допустимого значения давления. Клапаны 6 и 7 служат для перекачивания жидкости: при подъеме малого поршня 1 открывается клапан 6, и жидкость поступает в малый сосуд; при нажатии давление увеличивается, и этот клапан закрывается; открывается клапан 7, и жидкость переходит в большой сосуд.
Гидравлические прессы применяются для выжимания масла на маслобойных заводах, для прессования фанеры, картона, сена. В автомобилях используется гидравлический тормоз, в мастерских и в быту применяют гидравлический домкрат.
§ 3 Решение задач
Рассмотрим решение задачи на расчет выигрыша в силе в гидравлических машинах.

Запишем условие задачи. Нам известны масса m= 1500 кг, площадь малого поршня S1 = 10 см2 = 0, 001 м2, площадь большого поршня S2 = 0,1 м2. Найти F1.
Решение: Запишем формулу выигрыша в силе при помощи гидравлической машины:

Ответ: сила, приложенная к малому поршню,150 Н

Запишем условие задачи: F1= 200 Н, p = 400000 Па, S2 =0,04 м2. Найти показания динамометра, т.е. силу F2 = ? S1 =?

Ответ:F2 = 16 000 Н, S1 = 5 см2
§ 4 Важно запомнить
Гидравлическая машина – это машина, действие которой основано на законе Паскаля.
Гидравлическая машина представляет собой сообщающиеся сосуды – два соединенных друг с другом цилиндра разного диаметра, снабженных поршнями и заполненных жидкостью.
Выигрыш в силе, полученный при помощи гидравлической машины, равен отношению площадей поршней.
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом.
Гидравлические прессы применяются для выжимания масла, для прессования фанеры, картона, сена. В автомашинах используется гидравлический тормоз, для подъема груза предназначен гидравлический домкрат.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября», 2002. – 272 с.
Использованные изображения:
«Важный вопрос, который следует задавать,
приступая к работе, это не вопрос
«Что я получу?»; вместо этого Вы должны
спрашивать себя «Каким я стану?»
Д. Рон
Данная тема будет связана с решением задач на тему «Закон
Паскаля. Гидравлический пресс».
Задача 1. Поршень гидравлического пресса, площадь
сечения которого составляет 200 см2, действует на зажатое в нем тело
силой 20 кН. Определите силу, с которой действует меньший поршень на масло в
прессе, если его площадь сечения 5 см2.
|
ДАНО: |
СИ |
РЕШЕНИЕ: Соотношение сил в гидравлическом прессе: Откуда искомая сила равна |
|
|
Ответ: 500 Н.
Задача 2. Малый поршень гидравлического пресса за один
ход опускается на расстояние 0,2 м, а большой поршень поднимается на 0,01 м. С
какой силой действует пресс на зажатое в нем тело, если на малый поршень
действует сила 500 Н?
|
ДАНО: |
РЕШЕНИЕ: Сила, действующая на малый поршень пресса, создает Сила, действующая на большой поршень: Запишем условие несжимаемости жидкости Согласно закону Паскаля, жидкость передает производимое на Тогда искомая сила |
|
|
Ответ: 10 кН.
Задача 3. Поршни гидравлического пресса, заполненного
водой, находятся на одном уровне. Если на большой поршень площадью 0,1 м2
встанет человек массой 70 кг, то поршень опуститься на 3 см. На какую высоту
при этом поднимется малый поршень, площадь которого 35 см2? Массы
поршней 700 г и 2 кг соответственно.
|
ДАНО: |
СИ |
РЕШЕНИЕ: Давление, которое создает малый поршень, было уравновешено Давление, создаваемое малым поршнем: Давление, создаваемое большим поршнем: Давление, создаваемое человеком: Давление столба воды: По закону Паскаля: Подставляя в закон Паскаля выражения, записанные выше, Преобразуем данную формулу и выразим из неё искомую высоту |
|
|
Ответ: 49 см.
Задача 4. Гидравлический пресс, заполненный водой,
имеет поршни, площади которых 200 см2 и 20 см2. На
большой поршень положили груз массой 60 кг. На какую высоту поднимется после
этого малый поршень? Плотность воды примете равной 1000 кг/м3.
|
ДАНО: |
РЕШЕНИЕ: В данной задаче ничего не говорится о том, с какими Допустим, что в отсутствии груза малый поршень пресса При равновесии жидкости, давление в точках, принадлежащих Давление в точке А: Давление в точке B: Тогда получаем В результате воздействия груза на большой поршень, малый Давление в точке А1: Давление в точке B1: Теперь запишем для этого состояния условие равновесия как Таким образом, получаем систему уравнений Решим систему уравнений методом подстановки Запишем условие несжимаемости жидкости Тогда получим Тогда искомая величина равна |
Ответ: 2,7 м.
Задача 5. С помощью гидравлического пресса с КПД 75%
требуется спрессовать тело массой 80 т так, чтобы максимальная сила давления на
верхнюю площадку пресса достигала величины 1 МН. Считая, что деформация тела по
вертикали подчиняется закону Гука, а тело при этом сжимается на 0,3 м, найти
величину работы, совершенной двигателем. Отношение площадей поршней 1/50.
Определите число ходов малого поршня, если за один ход он опускается на 0,1 м.
|
ДАНО: |
СИ |
РЕШЕНИЕ: Работа переменной силы давления второго поршня на тело Минимальная сила давления большого поршня на тело: Максимальная сила давления большого поршня на тело: Тогда работа равна Коэффициент полезного действия любого механизма Выразим совершенную работу прессом Запишем условие несжимаемости жидкости Объем жидкости, вытесненной малым поршнем: Объем жидкости, поступившей в широкий сосуд: Приравняем последние два выражения и далее выразим искомое |
|
|
Ответ: A1 = 513600 Дж; n = 150.
