Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 января 2023 года; проверки требуют 3 правки.

Монета, лежащая на поверхности воды благодаря силе поверхностного натяжения

Когезия формирует водяные капли, поверхностное натяжение делает их почти сферическими, а адгезия держит их на поверхности другого вещества
| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |
Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.
Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости[1].
Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности

Но более правильно дать определение поверхностному натяжению, как энергии в джоулях на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
В 1983 году было доказано теоретически и подтверждено данными из справочников[2], что понятие поверхностного натяжения жидкости однозначно является частью понятия внутренней энергии (хотя и специфической: для симметричных молекул близких по форме к шарообразным). Приведенные в этой журнальной статье формулы позволяют для некоторых веществ теоретически рассчитывать значения поверхностного натяжения жидкости по другим физико-химическим свойствам, например, по теплоте парообразования или по внутренней энергии[3][4]).
В 1985 году аналогичный взгляд на физическую природу поверхностного натяжения как части внутренней энергии при решении другой физической задачи был опубликован В. Вайскопфом в США[5].
Поверхностное натяжение возникает на границе газообразных, жидких и твёрдых тел. Обычно под термином «поверхностное натяжение» имеется в виду поверхностное натяжение жидких тел на границе жидкость — газ. В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.
Прибор для измерения поверхностного натяжения называется тензиометр.
Проявления[править | править код]

Водомерка на поверхности воды.
Так как увеличение площади поверхности раздела жидкость — газ требует совершения работы, жидкость «стремится» уменьшить площадь своей поверхности:
- в невесомости порция жидкости принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма). То же самое происходит с каплей жидкости, помещаемой внутрь другой, несмешивающейся жидкости с первой жидкостью той же плотности (опыт Плато).
- ламинарная струя воды образует цилиндр, который затем разбивается на шаровидные капли из-за неустойчивости Рэлея — Плато.
- небольшие предметы со средней плотностью большей плотности жидкости способны «плавать» на поверхности жидкости, так как их вес оказывается уравновешенным силой поверхностного натяжения.
- некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
- На многих поверхностях, именуемых несмачиваемыми (гидрофобными), вода (или другая жидкость) собирается в капли.
- Поплавок Ван Дер Месбрюгге – поплавок, имеющий кольцо. Если нажать на поплавок, то он будет удерживаться в нажатом состоянии благодаря силам поверхностного натяжения, они действуют на кольцо, и в свою очередь уравновешивают гидростатические силы, стремящиеся вытолкнуть поплавок из воды.
Теория[править | править код]

Пояснение возникновения силы поверхностного натяжения. Молекулы на границе раздела испытывают силы, стремящиеся втянуть их в жидкость, так как со стороны газа на них не действуют силы притяжения.
Площадь поверхности[править | править код]
Поверхность жидкости обладает свободной энергией:
- где
— коэффициент поверхностного натяжения,
— полная площадь поверхности жидкости[6].
Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля стремится принять форму шара, однако при более сложных начальных условиях задача о форме поверхности жидкости становится математически исключительно сложной.
Формула Лапласа[править | править код]
Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется образование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления поверхностного натяжения плёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и задаётся формулой Лапласа:
Здесь 
Для случая поверхности кругового цилиндра радиуса 
Так как 
Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.
Зависимость от температуры[править | править код]
С увеличением температуры величина поверхностного натяжения уменьшается и равна нулю при критической температуре. Наиболее известная эмпирическая зависимость поверхностного натяжения от температуры была предложена Лорандом Этвёшом, так называемое правило Этвёша. В настоящее время получен вывод теоретической зависимости поверхностного натяжения от температуры в области до критических температур, подтверждающей правило Этвёша[7].
Способы определения[править | править код]
Способы определения поверхностного натяжения делятся на статические и динамические. В статических методах поверхностное натяжение определяется у сформировавшейся поверхности, находящейся в равновесии. Динамические методы связаны с разрушением поверхностного слоя. В случае измерения поверхностного натяжения растворов (особенно полимеров или ПАВ) следует пользоваться статическими методами. В ряде случаев равновесие на поверхности может наступать в течение нескольких часов (например, в случае концентрированных растворов полимеров с высокой вязкостью). Динамические методы могут быть применены для определения равновесного поверхностного натяжения и динамического поверхностного натяжения.
Например, для раствора мыла после перемешивания поверхностное натяжение 58 мДж/м², а после отстаивания — 35 мДж/м². То есть поверхностное натяжение меняется.
До установления равновесного оно будет динамическое.
Статические методы:
- Метод измерения высоты поднятия мениска в капилляре.
- Метод Вильгельми.
- Метод лежачей капли.
- Метод определения по форме висячей капли.
- Метод вращающейся капли.
Динамические методы:
- Метод дю Нуи (метод отрыва кольца).
- Сталагмометрический, или метод счета капель.
- Метод максимального давления пузырька.
- Метод осциллирующей струи.
- Метод стоячих волн.
- Метод бегущих волн.
Методы[править | править код]
Полностью стандартизованные методы измерений описываются в соответствующих ASTM, ГОСТ и т. д.
Метод вращающейся капли[править | править код]
Сущностью метода является измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости[8]. Этот способ измерения годится для измерения низких или сверхнизких значений межфазного натяжения. Он широко применяется для микроэмульсий, измерения эффективности поверхностно-активных веществ (ПАВ) в нефтедобыче, а также для определения адсорбционных свойств.
Метод Дю Нуи (метод отрыва кольца)[править | править код]
Метод является классическим. Сущность метода вытекает из названия. Кольцо из платиновой проволоки плоскость которого параллельна поверхности жидкости медленно поднимают из жидкости, смачивающей его, усилие в момент отрыва кольца от поверхности и есть сила поверхностного натяжения и может быть пересчитано в поверхностную энергию. Метод подходит для измерения поверхностного натяжения ПАВ, трансформаторных масел и т. д.
Метод капиллярных волн[править | править код]
При возмущении жидкости колеблющейся пластиной, лежащей на её поверхности, по поверхности жидкости распространяются капиллярные волны. Если осветить кювету с жидкостью импульсным источником света (стробоскопом) с частотой вспышек равной частоте колебания пластины возмущения, то будет наблюдаться зрительно неподвижная волновая картина. По измеренной длине волны можно рассчитать величину поверхностного натяжения по формуле:
- где
— поверхностное натяжение;
— плотность жидкости;
— длина волны;
— частота колебания пластины;
— ускорение свободного падения.
Поверхностное натяжение некоторых жидкостей на границе с воздухом[править | править код]
| Вещество | Температура °C | Поверхностное натяжение(10−3 Н/м) |
|---|---|---|
| Хлорид натрия 6 M водный раствор | 20 | 82,55 |
| Хлорид натрия | 801 | 115 |
| Глицерин | 30 | 64,7 |
| Олово | 400 | 518 |
| Азотная кислота 70 % | 20 | 59,4 |
| Анилин | 20 | 42,9 |
| Ацетон | 20 | 23,7 |
| Бензол | 20 | 29,0 |
| Вода | 20 | 72,86 |
| Глицерин | 20 | 59,4 |
| Нефть | 20 | 26 |
| Ртуть | 20 | 486,5 |
| Серная кислота 85 % | 20 | 57,4 |
| Спирт этиловый | 20 | 22,8 |
| Уксусная кислота | 20 | 27,8 |
| Эфир этиловый | 20 | 16,9 |
| Раствор мыла | 20 | 43 |
Проявления[править | править код]
-

Мыльный пузырь
-

Маргаритка
-

На фотографии виден эффект, получивший название «слёзы вина»
-

Капля воды на листе
-
Вода набегает на сухую поверхность асфальта
| Видео, демонстрирующее передвижение водомерки по поверхности воды за счёт поверхностного натяжения. |
См. также[править | править код]
- Тензиометр
- Формула Жюрена
Ссылки[править | править код]
- [www.xumuk.ru/colloidchem/19.html Методы определения поверхностного натяжения]
- Видео о физической природе поверхностного натяжения жидкости как части внутренней энергии Архивная копия от 20 декабря 2020 на Wayback Machine (рус.)
Примечания[править | править код]
- ↑ Сумм Б. Д. Основы коллоидной химии
- ↑ (Cтатья: Журнал физической химии. 1983, № 10, с. 2528—2530). Дата обращения: 16 февраля 2014. Архивировано 21 февраля 2014 года.
- ↑ Хайдаров Г. Г., Хайдаров А. Г., Машек А. Ч. Физическая природа поверхностного натяжения жидкости // Вестник Санкт-Петербургского университета. Серия 4 (Физика, химия) 2011. Выпуск 1. с.3-8. Дата обращения: 16 февраля 2014. Архивировано из оригинала 22 февраля 2014 года.
- ↑ Хайдаров Г. Г., Хайдаров А. Г., Машек А. Ч., Майоров Е. Е. Влияние температуры на поверхностное натяжения // Вестник Санкт-Петербургского университета. Серия 4 (Физика, химия). 2012. Выпуск 1. с.24-28. Дата обращения: 16 февраля 2014. Архивировано из оригинала 22 февраля 2014 года.
- ↑ Weisskopf V. F. American Journal of Physics 53 (1985) 19-20.; V. F. Weisskopf, American Journal of Physics 53 (1985) 618—619.
- ↑ Обратите внимание, что плёнка, вроде стенки мыльного пузыря, имеет две стороны, так что площадь поверхности жидкости в два раза больше площади плёнки.
- ↑ Журнал «Вестник Санкт-Петербургского университета», 2012, вып. 1, с. 24—28
- ↑ Тензиометр SITE100. Дата обращения: 19 ноября 2008. Архивировано 3 апреля 2009 года.
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных доменов
|
Содержание:
Поверхностное натяжение жидкости:
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
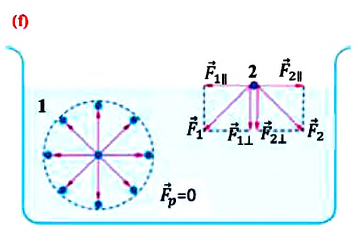
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил 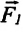
Сила поверхностного натяжения
Сила поверхностного натяжения – это сила, направленная по касательной к поверхности жидкости, перпендикулярно к линии, ограничивающей поверхность жидкости, и стремящаяся сократить площадь поверхности жидкости. Сила поверхностного натяжения прямо пропорциональна длине границы соприкосновения свободной поверхности жидкости с твердым телом:

Здесь 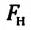 — сила поверхностного натяжения жидкости,
— сила поверхностного натяжения жидкости, 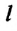 — длина границы соприкосновения свободной поверхности жидкости с твердым телом,
— длина границы соприкосновения свободной поверхности жидкости с твердым телом, 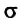 (сигма) – коэффициент поверхностного натяжения:
(сигма) – коэффициент поверхностного натяжения:
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения – численно равен силе поверхностного натяжения, приходящейся на единицу длины линии, ограничивающей поверхность жидкости:

Значение коэффициента поверхностного натяжения зависит от вида жидкости и ее температуры, то есть с увеличением температуры жидкости коэффициент его поверхностного натяжения уменьшается и при критической температуре равен нулю. Единица коэффициента поверхностного натяжения в СИ:
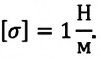
Смачивающая и несмачивающая жидкость. При внимательном рассмотрении можно увидеть искривление поверхности жидкости на границе между жидкостью и твердым телом.
Мениск – это искривление свободной поверхности жидкости в месте ее соприкосновении с поверхностью твердого тела (или другой жидкости). Угол между поверхностью мениска и поверхностью твердого тела называется краевым углом.
Значение краевого угла 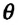 (тетта) зависит от того, является ли жидкость смачивающей или несмачивающей твердое тело:
(тетта) зависит от того, является ли жидкость смачивающей или несмачивающей твердое тело:
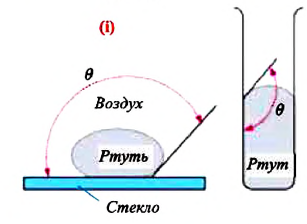
Смачивающая жидкость —это жидкость, у которой краевой угол острый. Сила взаимного притяжения между молекулами смачивающей жидкости и твердого тела больше, чем силы взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде становится вогнутой, например, вода в стеклянном сосуде – смачивающая жидкость (g).
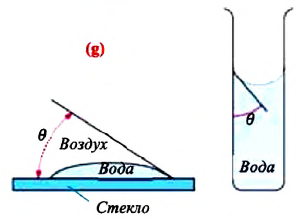
Несмачивающая жидкость — это жидкость, у которой краевой угол тупой. Сила взаимного притяжения между молекулами несмачивающей жидкости и твердого тела меньше, чем сила взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде бывает выпуклой, например, ртуть в стеклянном сосуде — несмачивающая жидкость (i).
Капиллярные явления
В повседневной жизни встречаются и используются тела, с легкостью впитывающие в себя воду, например, полотенце, промокательная бумага, сахар, кирпич, растения и др. Это свойство в телах объясняется существованием в них большого количества очень узких трубочек – капилляров.
Капилляр – это узкая трубка (канал) диаметром меньше 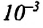 м. Уровень жидкости внутри капилляра, опущенного в жидкость, в зависимости от ее свойств (смачивающая или несмачивающая), отличается от общего уровня жидкости:
м. Уровень жидкости внутри капилляра, опущенного в жидкость, в зависимости от ее свойств (смачивающая или несмачивающая), отличается от общего уровня жидкости:
Капиллярными явлениями называют явления подъема смачивающей и опускания несмачивающей жидкости по капилляру относительно общего уровня жидкости под действием сил поверхностного натяжения (j).
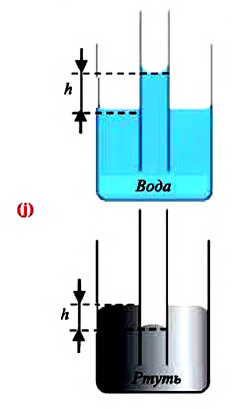
В таблице 6.4 дана зависимость между величинами, характеризующими жидкость, поднимающуюся в капилляре.
Таблица 6.4
|
Характеристики жидкости, поднимающейся в капилляре |
Формула |
| Вес жидкости, поднимающейся в капилляре |
Где |
| Масса жидкости, поднимающейся в капилляре | 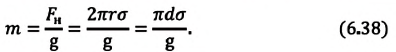 |
| Высота жидкости, поднимающейся в капилляре |
Если жидкость полностью смачиваемая, то получаем в
Где |
| Давление жидкости, поднимающейся в капилляре | 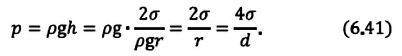 |
Поверхностное натяжение жидкости
Некоторые виды пауков могут передвигаться по поверхности воды не проваливаясь, как будто эта поверхность покрыта невидимой тонкой пленкой. такое же впечатление создается, если наблюдать за вытеканием воды из маленького отверстия — вода течет не тоненькой струйкой, а образует капли. Бумажная салфетка впитывает воду, едва коснувшись ее поверхности. какая сила является причиной всех этих явлений?

Каковы особенности поверхностного слоя жидкости
На свободной поверхности жидкости молекулы находятся в особых условиях, отличающихся от условий, в которых находятся молекулы внутри жидкости. Рассмотрим две молекулы — А и Б (рис. 33.1): молекула А находится внутри жидкости, а молекула Б — на ее поверхности. Молекула А окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу А со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, то есть их равнодействующая равна нулю.
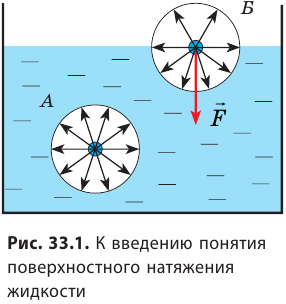
Молекула Б с одной стороны окружена молекулами жидкости, а с другой — молекулами газа. Со стороны жидкости на нее действует гораздо больше молекул, чем со стороны газа, поэтому равнодействующая F межмолекулярных сил направлена в глубь жидкости. Чтобы молекула из глубины попала в поверхностный слой, нужно совершить работу против межмолекулярных сил. Это означает, что молекулы поверхностного слоя жидкости (по сравнению с молекулами внутри жидкости) обладают избыточной потенциальной энергией. Эта избыточная энергия является частью внутренней энергии жидкости и называется поверхностной энергией (Wпов). Очевидно, что чем больше площадь S поверхности жидкости, тем больше поверхностная энергия: W S пов = σ , где σ (сигма) — коэффициент пропорциональности, который называют поверхностным натяжением жидкости.
Поверхностное натяжение жидкости — физическая величина, которая характеризует данную жидкость и равна отношению поверхностной энергии к площади поверхности жидкости:
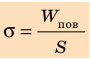
Единица поверхностного натяжения в СИ — ньютон на метр:
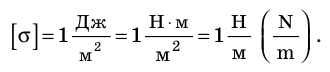
Поверхностное натяжение жидкости определяется силами межмолекулярного взаимодействия, поэтому оно зависит:
- от природы жидкости: у летучих жидкостей (эфир, спирт, бензин) поверхностное натяжение меньше, чем у нелетучих (ртуть, жидкие металлы);
- температуры жидкости: чем выше температура жидкости, тем меньше поверхностное натяжение;
- присутствия в составе жидкости поверхностно активных веществ — их наличие уменьшает поверхностное натяжение;
- свойств газа, с которым жидкость граничит. В таблицах обычно приводят значение поверхностного натяжения на границе жидкости и воздуха при определенной температуре (табл. 1).
Таблица 1
Поверхностное натяжение σ некоторых жидкостей
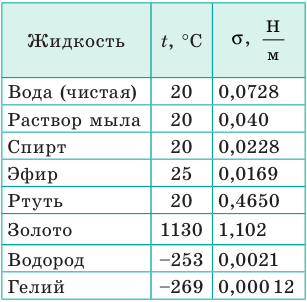
Что такое сила поверхностного натяжения
Поскольку поверхностный слой жидкости обладает избыточной потенциальной энергией (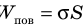 ), а любая система стремится к минимуму потенциальной энергии, то свободная поверхность жидкости стремится уменьшить свою площадь (сжаться). То есть вдоль поверхности жидкости действуют силы, которые пытаются стянуть эту поверхность. Эти силы называют силами поверхностного натяжения.
), а любая система стремится к минимуму потенциальной энергии, то свободная поверхность жидкости стремится уменьшить свою площадь (сжаться). То есть вдоль поверхности жидкости действуют силы, которые пытаются стянуть эту поверхность. Эти силы называют силами поверхностного натяжения.
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на натянутую резиновую пленку, однако упругие силы в резиновой пленке зависят от площади ее поверхности (от того, насколько пленка деформирована), а поверхность жидкости всегда «натянута» одинаково, то есть силы поверхностного натяжения не зависят от площади поверхности жидкости. Наличие сил поверхностного натяжения можно доказать с помощью такого опыта. Если проволочный каркас с закрепленной на нем нитью опустить в мыльный раствор, каркас затянется мыльной пленкой, а нить приобретет произвольную форму (рис. 33.2, а).
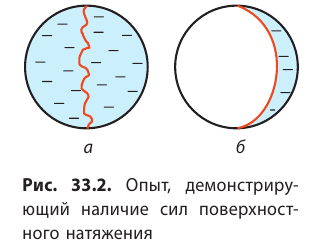
Если осторожно проткнуть иглой мыльную пленку по одну сторону от нити, сила поверхностного натяжения мыльного раствора, действующая с другой стороны, натянет нить (рис. 33.2, б). Опустим в мыльный раствор проволочную рамку, одна из сторон которой подвижна. На рамке образуется мыльная пленка (рис. 33.3). Будем растягивать эту пленку, действуя на перекладину (подвижную сторону рамки) с некоторой силой 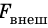 .
.
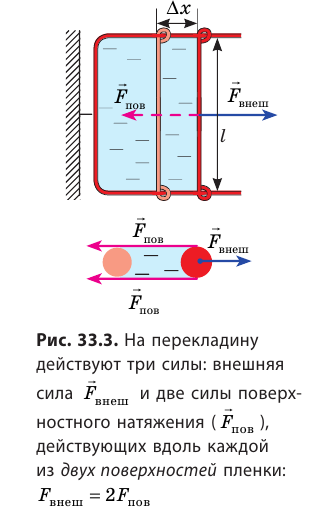
Если под действием этой силы перекладина переместится на ∆x , то внешние силы совершат работу: 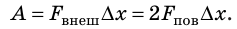 За счет совершения этой работы площади обеих поверхностей пленки увеличатся, а значит, увеличится и поверхностная энергия:
За счет совершения этой работы площади обеих поверхностей пленки увеличатся, а значит, увеличится и поверхностная энергия: 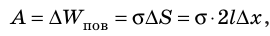 где
где 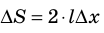 — увеличение площади двух поверхностей мыльной пленки. Приравняв правые части полученных равенств, получим:
— увеличение площади двух поверхностей мыльной пленки. Приравняв правые части полученных равенств, получим: 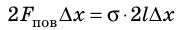 , или:
, или: 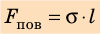
Таким образом, поверхностное натяжение σ численно равно силе поверхностного натяжения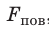 , которая действует на единицу длины l линии, ограничивающей поверхность:
, которая действует на единицу длины l линии, ограничивающей поверхность: 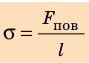
С одним из методов определения поверхностного натяжения жидкости вы ознакомитесь, выполняя лабораторную работу № 7.
- Заказать решение задач по физике
Где проявляется поверхностное натяжение
В жизни вы постоянно сталкиваетесь с проявлениями сил поверхностного натяжения. Так, благодаря ему на поверхности воды удерживаются легкие предметы (рис. 33.4) и некоторые насекомые.

Рис. 33.4. Монетка удерживается на поверхности воды благодаря силе поверхностного натяжения. (Чтобы провести такой опыт, монетку нужно потереть между пальцев и осторожно опустить на поверхность воды.)
Когда вы ныряете, ваши волосы расходятся во все стороны, но как только вы окажетесь над водой, волосы слипнутся, так как в этом случае площадь свободной поверхности воды намного меньше, чем при раздельном расположении прядей в воде. По этой же причине можно лепить фигуры из влажного песка: вода, обволакивая песчинки, прижимает их друг к другу.

Рис. 33.5. Капля удерживается около небольшого отверстия до тех пор, пока сила поверхностного натяжения уравновешивает силу тяжести
Стремлением жидкости уменьшить площадь поверхности объясняется и тот факт, что в условиях невесомости вода принимает форму шара, — при заданном объеме шарообразной форме соответствует наименьшая площадь поверхности. Форму шара приобретают тонкие мыльные пленки (мыльные пузыри). Поверхностным натяжением объясняется образование пены: пузырек газа, достигнув поверхности жидкости, имеет над собой тонкий слой жидкости; если пузырек мал, то архимедовой силы недостаточно, чтобы разорвать двойной поверхностный слой, и пузырек «застревает» вблизи поверхности. Благодаря поверхностному натяжению жидкость не выливается из маленького отверстия тоненькой струйкой, а капает (рис. 33.5), дождь не проливается через ткань зонта или палатки и т. д.
Почему одни жидкости собираются в капли, а другие растекаются
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, в каплях воды, разбегающихся по раскаленной плите, в капельках ртути на поверхности стекла. Однако при соприкосновении с твердым телом сферическая форма капли, как правило, не сохраняется. Форма свободной поверхности жидкости зависит также от сил взаимодействия молекул жидкости с молекулами твердого тела.
Если силы взаимодействия между молекулами жидкости больше, чем силы взаимодействия между молекулами жидкости и твердого тела, жидкость не смачивает поверхность твердого тела (рис. 33.6). Например, ртуть не смачивает стекло, а вода не смачивает покрытую сажей поверхность.

Рис. 33.6. Капля несмачивающей жидкости принимает форму, близкую к сферической, а поверхность жидкости вблизи стенки сосуда является выпуклой
Если же капельку ртути поместить на цинковую пластину, то капелька будет стремиться растечься по поверхности пластины; так же ведет себя и капелька воды на стекле (рис. 33.7). Если силы взаимодействия между молекулами жидкости меньше сил взаимодействия между молекулами жидкости и твердого тела, жидкость смачивает поверхность твердого тела.
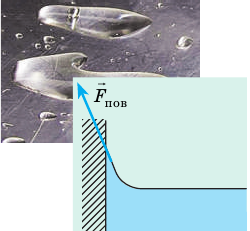
Рис. 33.7. Капля смачивающей жидкости стремится растечься по поверхности твердого тела, а вблизи стенки сосуда поверхность жидкости принимает вогнутую форму
Почему жидкость поднимается в капиллярах
В природе часто встречаются тела, пронизанные многочисленными мелкими капиллярами (от лат. capillaris — волосяной) — узкими каналами произвольной формы. Такую структуру имеют бумага, дерево, почва, многие ткани и строительные материалы. В цилиндрических капиллярах искривленная поверхность жидкости представляет собой часть сферы, которую называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 33.8, а), а у несмачивающей — выпуклый (рис. 33.8, б).
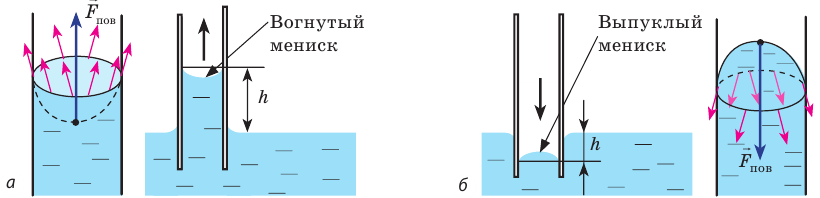
Рис. 33.8. капиллярные явления: а — смачивающая жидкость поднимается по капилляру; б — несмачивающая жидкость опускается в капилляре
Поверхность жидкости стремится к минимуму потенциальной энергии, а искривленная поверхность обладает большей площадью по сравнению с площадью сечения капилляра, поэтому поверхность жидкости стремится выровняться и под ней возникает избыточное (отрицательное или положительное) давление — лапласово давление (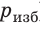 ).
).
Под вогнутой поверхностью (жидкость смачивает капилляр) лапласово давление отрицательное и жидкость втягивается в капилляр. Так поднимаются влага и питательные вещества в стеблях растений, керосин по фитилю, влага в почве. Вследствие лапласового давления салфетки или ткань впитывают воду, брюки в дождливую погоду сильно намокают снизу и т. д. Под выпуклой поверхностью (жидкость не смачивает капилляр) лапласово давление положительное и жидкость в капилляре опускается. Чем меньше радиус капилляра, тем больше высота подъема (или опускания) жидкости (см. задачу ниже).
Пример решения задачи
Капиллярную трубку радиусом r одним концом опустили в жидкость, смачивающую внутреннюю поверхность капилляра. На какую высоту поднимется жидкость в капилляре, если плотность жидкости ρ, а ее поверхностное натяжение σ ? Чему равно лапласово давление под вогнутой поверхностью капилляра? Смачивание считайте полным.
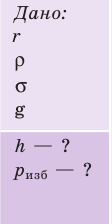
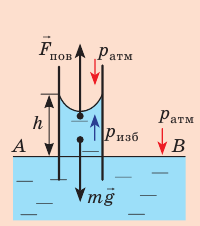
Решение:
На жидкость в капилляре действуют сила тяжести и сила поверхностного натяжения (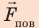 направлена вертикально вверх (по касательной к поверхности мениска). Подъем жидкости в капилляре будет продолжаться до тех пор, пока сила тяжести поднятого столба жидкости не уравновесит силу поверхностного натяжения: mg =
направлена вертикально вверх (по касательной к поверхности мениска). Подъем жидкости в капилляре будет продолжаться до тех пор, пока сила тяжести поднятого столба жидкости не уравновесит силу поверхностного натяжения: mg = 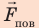 ( *), где m — масса жидкости.
( *), где m — масса жидкости.
Поиск математической модели, решение
Поскольку m V = ρ , а объем воды в цилиндрическом капилляре 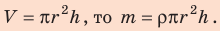 ,
, 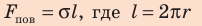 (длина окружности), следовательно,
(длина окружности), следовательно, 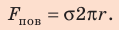 Подставим выражения для m и
Подставим выражения для m и 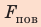 в равенство (*):
в равенство (*):  Для определения лапласова давления
Для определения лапласова давления 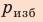 под поверхностью мениска воспользуемся тем фактом, что в однородной неподвижной жидкости давление на одном уровне (у нас — на уровне АВ) одинаково, то есть:
под поверхностью мениска воспользуемся тем фактом, что в однородной неподвижной жидкости давление на одном уровне (у нас — на уровне АВ) одинаково, то есть:
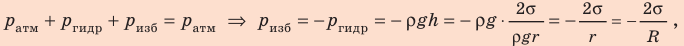
где R — радиус кривизны мениска (при полном смачивании r=R).
Ответ: (Данные выводы следует запомнить!)
- Высота подъема жидкости в капилляре прямо пропорциональна поверхностному натяжению жидкости и обратно пропорциональна плотности жидкости и радиусу капилляра:
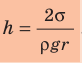 .
. - Лапласово давление (избыточное давление) под сферической поверхностью жидкости прямо пропорционально поверхностному натяжению жидкости и обратно пропорционально радиусу кривизны мениска:
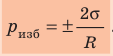 .
.
Выводы:
- Свойства паров в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
В
§ 7.1 были
рассмотрены опыты, свидетельствующие
о стремлении поверхности жидкости к
сокращению. Это сокращение вызывается
силой поверхностного натяжения.
Силу, которая
действует вдоль поверхности жидкости
перпендикулярно линии, ограничивающей
эту поверхность, и стремится сократить
ее до минимума, называют силой
поверхностного натяжения.
Измерение силы поверхностного натяжения
Чтобы
измерить силу поверхностного натяжения,
проделаем следующий опыт. Возьмем
прямоугольную проволочную рамку, одна
сторона которой АВ
длиной
l
может
перемещаться с малым трением в вертикальной
плоскости. Погрузив рамку в сосуд с
мыльным раствором, получим на ней мыльную
пленку (рис. 7.11, а). Как только мы вытащим
рамку из мыльного раствора, проволочка
АВ
сразу
же придет в движение. Мыльная пленка
будет сокращать свою поверхность.
Следовательно, на проволочку АВ
действует
сила, направленная перпендикулярно
проволочке в сторону пленки. Это и есть
сила поверхностного натяжения.

Рис. 7.11
Чтобы
помешать проволочке двигаться, надо к
ней приложить некоторую силу. Для
создания этой силы можно прикрепить к
проволочке мягкую пружину, закрепленную
на основании штатива (см. рис. 7.11, о). Сила
упругости пружины вместе с силой тяжести,
действующей на проволочку, в сумме
составят результирующую силу
![]()
Для
равновесия проволочки необходимо, чтобы
выполнялось равенство
![]() ,
,
где
![]()
—
сила поверхностного натяжения, действующая
на проволочку со стороны одной из
поверхностей пленки (рис. 7.11, б).
Отсюда
![]() .
.
От чего зависит сила поверхностного натяжения?
Если
проволочку переместить вниз на расстояние
h,
то
внешняя сила F1
=
2F
совершит
работу
![]()
(7.4.1)
Согласно
закону сохранения энергии эта работа
равна изменению энергии (в данном случае
поверхностной) пленки. Начальная
поверхностная энергия мыльной пленки
площадью S1
равна Uп1
= =2σS1,
так
как пленка имеет две поверхности
одинаковой площади. Конечная поверхностная
энергия
![]()
где
S2
—
площадь пленки после перемещения
проволочки на расстояние h.
Следовательно,
![]()
Так как
![]()
то
![]()
(7.4.2)
Приравнивая правые
части выражений (7.4.1) и (7.4.2), получим:
![]()
Отсюда
сила поверхностного натяжения, действующая
на границу поверхностного слоя длиной
l,
равна:
![]()
(7.4.3)
Направлена
сила поверхностного натяжения по
касательной к поверхности перпендикулярно
границе поверхностного слоя (перпендикулярно
проволочке АВ
в
данном случае, см. рис. 7.11, а).
Измерение коэффициента поверхностного натяжения
Существует много
способов измерения поверхностного
натяжения жидкостей. Например,
поверхностное натяжение а можно
определить, пользуясь установкой,
изображенной на рисунке 7.11. Мы рассмотрим
другой способ, не претендующий на большую
точность результата измерений.
Прикрепим
к чувствительному динамометру медную
проволочку, изогнутую так, как показано
на рисунке 7.12, a. Подставим под проволочку
сосуд с водой так, чтобы проволочка
коснулась поверхности воды (рис. 7.12, б)
и
«прилипла» к ней. Будем теперь медленно
опускать сосуд с водой (или, что то же,
поднимать динамометр с проволочкой).
Мы увидим, что вместе с проволочкой
поднимается обволакивающая ее водяная
пленка, а показание динамометра при
этом постепенно увеличивается. Оно
достигает максимального значения в
момент разрыва водяной пленки и «отрыва»
проволочки от воды. Если из показаний
динамометра в момент отрыва проволочки
вычесть ее вес, то получится сила F,
равная
удвоенной силе поверхностного натяжения
(у водяной пленки две поверхности):
![]()
где
l
—
длина проволочки.

Рис. 7.12
Отсюда
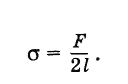
При
длине проволочки 1 = 5 см и температуре
20 °С сила оказывается равной 7,3 · 10-3
Н. Тогда
![]()
Результаты
измерений поверхностных натяжений
некоторых жидкостей приведены в таблице
4.
Таблица 4
|
Жидкость |
Температура, °С |
Поверхностное |
|
Вода(чистая) Раствор мыла Спирт Эфир Ртуть Золото(расплавленное) Жидкий водород Жидкий гелий |
20 20 20 20 20 1130 -253 -269 |
0,073 0,040 0,022 0,017 0,470 1,102 0,0021 0,00012 |
Из таблицы 4 видно,
что у легкоиспаряющихся жидкостей
(эфира, спирта) поверхностное натяжение
меньше, чем у нелетучих жидкостей,
например у ртути. Очень мало поверхностное
натяжение у жидкого водорода и особенно
у жидкого гелия. У жидких металлов
поверхностное натяжение, наоборот,
очень велико.
Различие в
поверхностном натяжении жидкостей
объясняется различием в силах
межмолекулярного взаимодействия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сегодня поверхностно рассматриваем тему поверхностного натяжения и решаем соответствующие задачи по физике.
Даже если вы не большой любитель жидкости, подписывайтесь на наш телеграм-канал, это интересно и полезно для всех.
Поверхностное натяжение, задачи
Задача №1. Поверхностное натяжение
Условие
Для определения коэффициента поверхностного натяжения воды была использована пипетка с диаметром выходного отверстия d=2 мм. Оказалось, что n=40 капель имеют массу m=1,9 г. Каким по этим данным получится коэффициент поверхностного натяжения «сигма»?
Решение
На каплю действует сила тяжести и сила поверхностного натяжения. Эти силы уравновешивают друг друга. Из условия задачи можно найти массу одной капли m0 и длину ее окружности l:
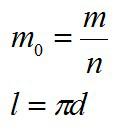
Далее запишем условие равновесия капли:
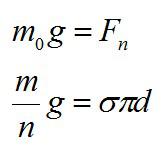
Отсюда находим коэффициент поверхностного натяжения:
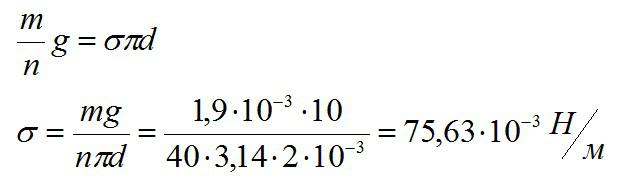
Ответ: 75,63*10^-3 Н/м.
Задача №2. Капиллярные явления
Условие
В капиллярной трубке радиусом 0,5 мм жидкость поднялась на высоту 11 мм. Оценить плотность данной жидкости, если ее коэффициент поверхностного натяжения равен 22 мН/м.
Решение
Для капилляра существует формула:
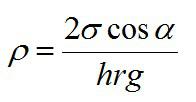
Альфа в этой формуле – угол смачивания стенки капилляра жидкостью. Пример его равным 90 градусов.
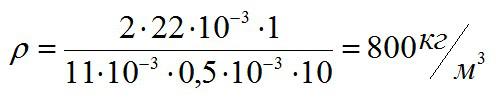
Ответ: 800 килограмм на кубический метр.
Задача №3. Поверхностное натяжение
Условие
В дне сосуда со ртутью имеется круглое отверстие диаметром 70 мкм. При какой максимальной высоте слоя ртути H она не будет вытекать через отверстие?
Решение
Ртуть не будет вытекать до тех пор, пока сила ее давления не превысит силу поверхностного натяжения:
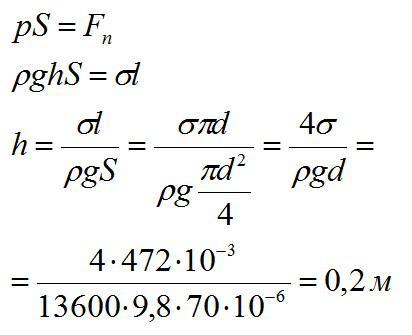
Значения коэффициента поверхностного натяжения разных жидкостей берутся в справочнике.
Ответ: 0,2 м.
Задача №4. Поверхностное натяжение
Условие
Швейная игла имеет длину 3,5 см и массу 0,3 г. Будет ли игла лежать на поверхности воды, если ее положить аккуратно?
Решение
Найдем силу тяжести, которая действует на иглу и сравним ее с силой поверхностного натяжения.
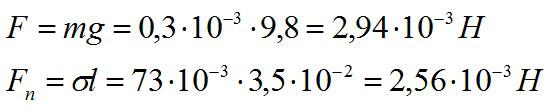
Ответ: Так как сила тяжести больше, игла утонет.
Задача №5. Поверхностное натяжение
Условие
Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г.
Решение
На кольцо действуют силы поверхностного натяжения, сила тяжести и внешняя сила, стремящаяся оторвать кольцо от поверхности. Найдем силу поверхностного натяжения:
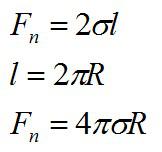
Множитель «2» используется в формуле, так как кольцо взаимодействует с жидкостью двумя своими сторонами.
Теперь запишем условие отрыва кольца:
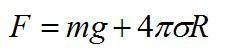
Значение поверхностного натяжения мыльного раствора при комнатной температуре возьмем из таблицы, подставим числа, и получим:
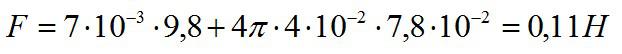
Ответ: 0,11 Н.
Вопросы на тему «Поверхностное натяжение и свойства жидкостей»
Вопрос 1. Что такое жидкость?
Ответ. Жидкость – физическое тело, которое не может самостоятельно сохранять свою форму. Агрегатное состояние вещества между твердым телом и газом.
Вопрос 2. Какие свойства жидкости вы знаете?
Ответ. Среди основных свойств жидкости можно выделить:
- текучесть;
- вязкость;
- сохранение объема;
- поверхностное натяжение.
Вопрос 3. Что такое поверхностное натяжение?
Ответ. Поверхностное натяжение – это явление, при котором жидкость стремиться приобрести форму с наименьшей возможной площадью поверхности.
Примеры поверхностного натяжения в природе:
- Именно благодаря поверхностному натяжению в поле силы тяжести Земли жидкость приобретает форму капли.
- В отсутствие силы тяжести жидкости капля примет шарообразную форму.
- Водомерка удерживается на поверхности воды благодаря силе поверхностного натяжения.
Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью S при постоянной температуре.
Вопрос 4. Что такое капиллярные явления?
Ответ. Капиллярные явления – подъем или опускание жидкости в капиллярах (трубках малого диаметра).
Вопрос 5. Что называется смачиванием?
Ответ. Смачивание – это искривление поверхности жидкости вблизи твердого тела. Возникает из-за взаимодействия молекул жидкости с молекулами твердого тела.
Количественная характеристика этого явления – угол смачивания.
Нужна помощь в решении заданий по учебе? Профессиональный студенческий сервис всегда готов ее оказать! Оформляйте заявку в любое время суток и забудьте о наболевших вопросах.
Поверхностная энергия
Содержание
- 1 Поверхностная энергия
-
2 Поверхностное натяжение
- 2.1 См. также
- 3 Смачивание
- 4 Капиллярные явления
- 5 Литература
Наиболее характерным свойством жидкости, отличающим ее от газа, является то, что на границе с газом жидкость образует свободную поверхность, наличие которой приводит к возникновению явлений особого рода, называемых поверхностными. Своим возникновением они обязаны особым физическим условиям, в которых находятся молекулы вблизи свободной поверхности.
На каждую молекулу жидкости действуют силы притяжения со стороны окружающих ее молекул, расположенных от нее на расстоянии порядка 10-9 м (радиус молекулярного действия). На молекулу M1, расположенную внутри жидкости (рис. 1), действуют силы со стороны таких же молекул, и равнодействующая этих сил близка к нулю.
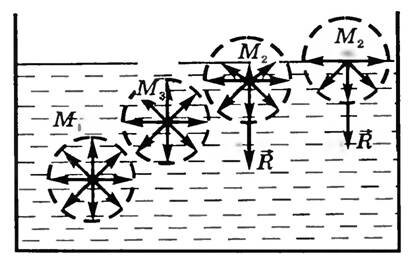
Рис. 1
Для молекул M2 равнодействующие сил отличны от нуля и направлены внутрь жидкости, перпендикулярно к ее поверхности. Таким образом, все молекулы жидкости, находящиеся в поверхностном слое, втягиваются внутрь жидкости. Но пространство внутри жидкости занято другими молекулами, поэтому поверхностный слой создает давление на жидкость (молекулярное давление).
Чтобы переместить молекулу M3, расположенную непосредственно под поверхностным слоем, на поверхность, необходимо совершить работу против сил молекулярного давления. Следовательно, молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией по сравнению с молекулами внутри жидкости. Эту энергию называют поверхностной энергией.
Очевидно, что величина поверхностной энергии тем больше, чем больше площадь свободной поверхности. Пусть площадь свободной поверхности изменилась на ΔS, при этом поверхностная энергия изменилась на (~Delta W_p = sigma cdot Delta S), где σ — коэффициент поверхностного натяжения. Так как для этого изменения необходимо совершить работу
(~A = Delta W_p ,) то (~A = sigma cdot Delta S .)
Отсюда (~sigma = dfrac{A}{Delta S}) .
Единицей коэффициента поверхностного натяжения в СИ является джоуль на квадратный метр (Дж/м2).
Коэффициент поверхностного натяжения — величина, численно равная работе, совершенной молекулярными силами при изменении площади свободной поверхности жидкости на 1 м2 при постоянной температуре .
Так как любая система, предоставленная сама себе, стремится занять такое положение, в котором ее потенциальная энергия наименьшая, то жидкость обнаруживает стремление к сокращению свободной поверхности. Поверхностный слой жидкости ведет себя подобно растянутой резиновой пленке, т.е. все время стремится сократить площадь своей поверхности до минимальных размеров, возможных при данном объеме.
Например, капля жидкости в состоянии невесомости имеет сферическую форму.
Поверхностное натяжение
Свойство поверхности жидкости сокращаться можно истолковать как существование сил, стремящихся сократить эту поверхность. Молекула M1 (рис. 2), расположенная на поверхности жидкости, взаимодействует не только с молекулами, находящимися внутри жидкости, но и с молекулами, находящимися на поверхности жидкости, расположенными в пределах сферы молекулярного действия. Для молекулы M1 равнодействующая (~vec R) молекулярных сил, направленных вдоль свободной поверхности жидкости, равна нулю, а для молекулы M2, расположенной у границы поверхности жидкости, (~vec R ne 0) и (~vec R) направлена по нормали к границам свободной поверхности и по касательной к самой поверхности жидкости.
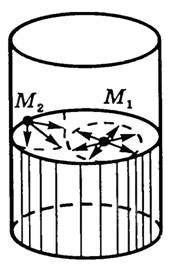
Рис. 2
Равнодействующая сил, действующих на все молекулы, находящиеся на границе свободной поверхности, и есть сила поверхностного натяжения. В целом она действует так, что стремится сократить поверхность жидкости.
Можно предположить, что сила поверхностного натяжения (~vec F) прямо пропорциональна длине l границы поверхностного слоя жидкости, ведь на всех участках поверхностного слоя жидкости молекулы находятся в одинаковых условиях:
(~F sim l .)
Действительно, рассмотрим вертикальный прямоугольный каркас (рис. 3, а, б), подвижная сторона которого уравновешена. После извлечения рамки из раствора мыльной пленки подвижная часть перемещается из положения 1 в положение 2. Учитывая, что пленка представляет собой тонкий слой жидкости и имеет две свободные поверхности, найдем работу, совершаемую при перемещении поперечины на расстояние h = a1 ⋅ a2: A = 2F⋅h, где F — сила, действующая на каркас со стороны каждого поверхностного слоя. С другой стороны, (~A = sigma cdot Delta S = sigma cdot 2l cdot h).
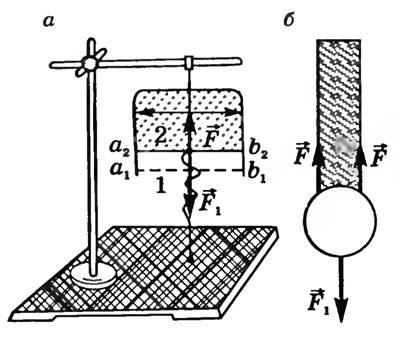
Рис. 3
Следовательно, (~2F cdot h = sigma cdot 2l cdot h Rightarrow F = sigma cdot l), откуда (~sigma = dfrac Fl).
Согласно этой формуле единицей коэффициента поверхностного натяжения в СИ является ньютон на метр (Н/м).
Коэффициент поверхностного натяжения σ численно равен силе поверхностного натяжения, действующей на единицу длины границы свободной поверхности жидкости. Коэффициент поверхностного натяжения зависит от природы жидкости, от температуры и от наличия примесей. При увеличении температуры он уменьшается.
- При критической температуре, когда исчезает различие между жидкостью и паром, σ = 0.
Примеси в основном уменьшают (некоторые увеличивают) коэффициент поверхностного натяжения.
Таким образом, поверхностный слой жидкости представляет собой как бы эластичную растянутую пленку, охватывающую всю жидкость и стремящуюся собрать ее в одну «каплю». Такая модель (эластичная растянутая пленка) позволяет определять направление сил поверхностного натяжения. Например, если пленка под действием внешних сил растягивается, то сила поверхностного натяжения будет направлена вдоль поверхности жидкости против растяжения. Однако это состояние существенно отличается от натяжения упругой резиновой пленки. Упругая пленка растягивается за счет увеличения расстояния между частицами, при этом сила натяжения возрастает, при растяжении же жидкой пленки расстояние между частицами не меняется, а увеличение поверхности достигается в результате перехода молекул из толщи жидкости в поверхностный слой. Поэтому при увеличении поверхности жидкости сила поверхностного натяжения не изменяется (она не зависит от площади поверхности).
См. также
- Кикоин А.К. О силах поверхностного натяжения // Квант. — 1983. — № 12. — С. 27-28
Смачивание
В случае соприкосновения с твердым телом силы сцепления молекул жидкости с молекулами твердого тела начинают играть существенную роль. Поведение жидкости будет зависеть от того, что больше: сцепление между молекулами жидкости или сцепление молекул жидкости с молекулами твердого тела.
Смачивание — явление, возникающее вследствие взаимодействия молекул жидкости с молекулами твердых тел. Если силы притяжения между молекулами жидкости и твердого тела больше сил притяжения между молекулами жидкости, то жидкость называют смачивающей; если силы притяжения жидкости и твердого тела меньше сил притяжения между молекулами жидкости, то жидкость называют несмачивающей это тело.
Одна и та же жидкость может быть смачивающей и несмачивающей по отношению к разным телам. Так, вода смачивает стекло и не смачивает жирную поверхность, ртуть не смачивает стекло, а смачивает медь.
Смачивание или несмачивание жидкостью стенок сосуда, в котором она находится, влияет на форму свободной поверхности жидкости в сосуде. Если большое количество жидкости налито в сосуд, то форма ее поверхности определяется силой тяжести, которая обеспечивает плоскую и горизонтальную поверхность. Однако у самых стенок явление смачивания и несмачивания приводят к искривлению поверхности жидкости, так называемые краевые эффекты.
Количественной характеристикой краевых эффектов служит краевой угол θ – угол между плоскостью касательной к поверхности жидкости и поверхностью твердого тела. Внутри краевого угла всегда находится жидкость (рис. 4, а, б). При смачивании он будет острым (рис. 4, а), а при несмачивании – тупым (рис. 4, б). В школьном курсе физики рассматривают только полное смачивание (θ = 0º) или полное несмачивание (θ = 180º).
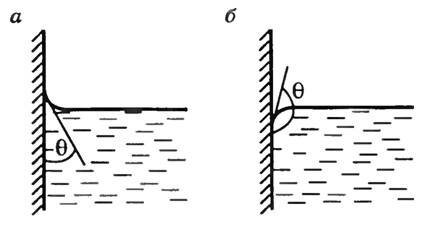
Рис. 4
Силы, связанные с наличием поверхностного натяжения и направленные по касательной к поверхности жидкости, в случае выпуклой поверхности дают результирующую, направленную внутрь жидкости (рис. 5, а). В случае вогнутой поверхности результирующая сила направлена, наоборот, в сторону газа, граничащего с жидкостью (рис. 5, б).
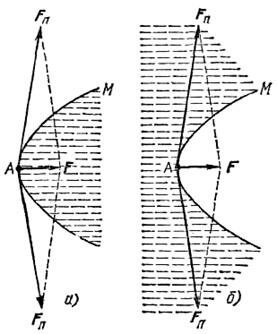
Рис. 5.
Если смачивающая жидкость находится на открытой поверхности твердого тела (рис. 6, а), то происходит ее растекание по этой поверхности. Если на открытой поверхности твердого тела находится несмачивающая жидкость, то она принимает форму, близкую к шаровой (рис. 6, б).
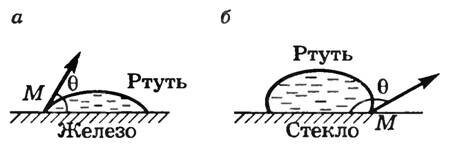
Рис. 6
Смачивание имеет важное значение как в быту, так и в промышленности. Хорошее смачивание необходимо при крашении, стирке, обработке фотоматериалов, нанесении лакокрасочных покрытий, при склеивании материалов, при пайке, во флотационных процессах (обогащение руд ценной породой). И наоборот, при сооружении гидроизоляционных устройств необходимы материалы, не смачиваемые водой.
Капиллярные явления
Искривление поверхности жидкости у краев сосуда особенно отчетливо видно в узких трубках, где искривляется вся свободная поверхность жидкости. В трубках с узким сечением эта поверхность представляет собой часть сферы, ее называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 7, а), а у несмачивающей — выпуклый (рис. 7, б). Так как площадь поверхности мениска больше, чем площадь поперечного сечения трубки, то под действием молекулярных сил искривленная поверхность жидкости стремится выпрямиться.
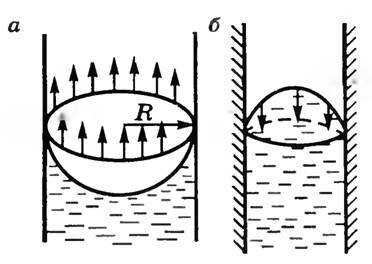
Рис. 7
Силы поверхностного натяжения создают дополнительное (лапласово) давление под искривленной поверхностью жидкости.
Если поверхность жидкости вогнутая, то сила поверхностного натяжения направлена из жидкости (рис. 8, а), и давление под вогнутой поверхностью жидкости меньше, чем под плоской, на (~p = dfrac{2 sigma }{R}). Если поверхность жидкости выпуклая, то сила поверхностного натяжения направлена внутрь жидкости (рис. 8, б), и давление под выпуклой поверхностью жидкости больше, чем под плоской, на ту же величину.
-
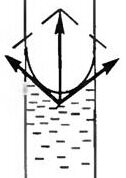
а
-
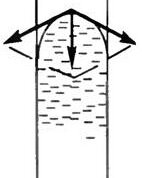
б
Рис. 8
- Эта формула является частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:
(~p = sigma cdot left( dfrac{1}{R_1} + dfrac{1}{R_2} right),)
где R1 и R2 — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости. Для цилиндрической поверхности (R1 = l; R2 = ∞) избыточное давление (~p = dfrac{sigma}{R}) .
Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие наличия силы лапласова давления жидкость в капилляре поднимается (если жидкость смачивающая) или опускается (если жидкость несмачивающая) (рис. 9, а, б), так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.
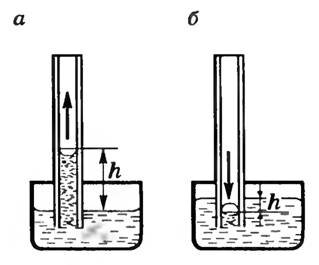
Рис. 9
Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидкости в широких сосудах называются капиллярными явлениями.
Жидкость в капилляре поднимается или опускается на такую высоту h, при которой сила гидростатического давления столба жидкости уравновешивается силой избыточного давления, т.е.
(~dfrac{2 sigma}{R} = rho cdot g cdot h .)
Откуда (~h = dfrac{2 sigma}{rho cdot g cdot R}). Если смачивание не полное θ ≠ 0 (θ ≠ 180°), то, как показывают расчеты, (~h = dfrac{2 sigma}{rho cdot g cdot R} cdot cos theta).
Капиллярные явления весьма распространены. Поднятие воды в почве, система кровеносных сосудов в легких, корневая система у растений, фитиль и промокательная бумага — капиллярные системы.
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 178-184.
- Википедия
- Открытая Физика








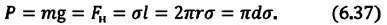
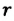 — радиус капилляра,
— радиус капилляра, 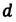 — диаметр капилляра.
— диаметр капилляра.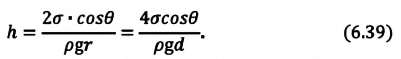
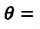
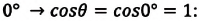

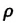 — плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
— плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.