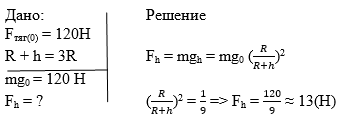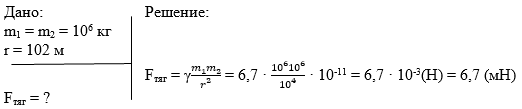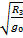Как найти силу притяжения двух планет

Характер и особенности расчета силы притяжения известны еще с древних времен. На основании имеющихся знаний, переданных современному научному сообществу великими исследователями, человек познает не только его окружающий мир, но и Вселенную.

Формула силы притяжения

Со времен Древней Греции философов интересовали явления притяжения тел к земле и свободного падения. К примеру, по утверждениям Аристотеля, из двух камней, брошенных с одинаковой высоты, быстрее достигнет земной поверхности тот, чья масса больше. В IV веке до нашей эры единственными методами научных изысканий служили наблюдения и анализ. К проверке гипотез опытным путем великие мыслители не прибегали. По истечению столетий физик из Италии Галилео Галилей проверил утверждения Аристотеля, используя практические методы исследований.

Итоги проведенных Галилеем опытов были опубликованы в «Беседах и математических доказательствах, касающихся двух новых наук». Ученый использовал псевдоним Сагредо: «пушечное ядро не опередит мушкетной пули при падении с высоты двухсот локтей». Формулировка закона всемирного тяготения была представлена в 1666 году Исааком Ньютоном. В ней фиксировались основные тезисы теоремы Галилея.

Смысл заключался в том, что тела, которые обладают разными массами, падают на землю с одинаковыми ускорениями.  Одно тело притягивает другое и, наоборот, с силой, которая прямо пропорциональна их массам и обратно пропорциональна отрезку пути между ними. Согласно определению гравитации от Ньютона, тела, характеризующиеся массой, обладают свойством, благодаря которому притягиваются друг к другу.

Понятие и определение

Силы взаимного притяжения – это силы, которые притягивают любые тела, обладающие массами.

Корректность выводов Ньютона неоднократно подтверждалась путем практических испытаний. Но в начале ХХ века перед учеными-физиками остро стоял вопрос о природе и характере взаимодействия крупных астрономических тел, включая разные виды планетарных систем и галактик в вакууме. Ньютоновского закона уже было недостаточно, чтобы решить эти задачи. Исключить недочеты позволила новая теория, разработанная Альбертом Эйнштейном в начале ХХ столетия. Общая теория относительности объясняет гравитацию не в качестве силы, а представляет ее в виде искривления пространства и времени в четырех измерениях, которое зависит от массы тел, создающих его.

Гравитация представляет собой свойство тел, которые характеризуются массой, притягивать друг друга. Данное физическое явление можно объяснить, как поле, оказывающее дистанционное воздействие на предметы, не связанные между собой никаким другим способом.

Достижение Эйнштейна не противоречит теоретическому объяснению гравитации от Ньютона. Общая теория относительности рассматривает закон всемирного тяготения, как частный случай, применимый для сравнительно небольших расстояний. Данная закономерность в настоящее время также активно используется для поиска решений задач на практике.

Единицы измерения силы притяжения

В разных системах измерений можно встретить несколько отличающиеся обозначения. Единицы измерения силы притяжения следующие:

• система СИ: ([F]=H);
• система СГС: ([F]=дин).

Формула силы притяжения между телами в космосе

Закономерность гравитации, которую обнаружил Ньютон, можно представить в виде математической формулы. Вычисления выглядят следующим образом:

(F=(Gtimes m1times m2times r)/2),

где (m1,m2) – массы объектов, которые притягиваются друг к другу под действием силы (F),

(r) – расстояние, на которое удалены тела,

(G) – т.н. гравитационная постоянная величина, константа, равная 6,67.

Гравитационное взаимодействие объектов будет слабеть, если тела удаляются друг относительно друга. Сила гравитации пропорциональна величине расстояния в квадрате. При этом для нахождения искомой величины расстояние измеряется от центров тяжести тел, а не от поверхностей.

Гравитация в определенных моментах напоминает другие физические явления. Исходя из зависимости интенсивности силы от расстояния в квадрате, гравитацию можно сравнить с электромагнитным взаимодействием сильного и слабого характера.

Формула силы гравитационного притяжения между двумя телами

Квадратичная связь силы, с которой тела притягиваются друг к другу, с расстоянием между ними объясняет тот факт, что люди, находящиеся на поверхности планеты Земля не притягиваются к Солнцу, хотя масса его велика и превышает земную в миллион раз. Земля и центр Солнечной системы удалены примерно на 150 миллионов километров. Дистанция достаточно велика, чтобы ощущаться человеком. Однако эту силу можно зарегистрировать, используя высокоточные приборы. В рамках планеты Земля сила, с которой тела к ней притягиваются, то есть их вес, измеряется следующим образом:

(P=mtimes g),

где (m) – масса тела, на которое воздействует сила притяжение,

(g) – ускорение свободного падения около Земли (если рассматривать систему в условиях любой другой планеты, данная величина будет отличаться).

На разных географических широтах величина ускорения свободного падения может незначительно отличаться. Производя расчеты, данный показатель принимается за 9,81 метров в секунду в квадрате.

В физике понятия массы и веса тел отличаются. Весом называется сила, определяющее притяжение объекта к планете. Масса представляет собой меру инертности вещества. На нее не влияют другие тела, расположенные рядом.

Формула для силы притяжения тел произвольной формы

Расчеты определяются некоторыми условиями. К ним относятся характеристики исследуемых объектов.

Если сила притяжения измеряется между телами, которые обладают произвольной формой, их считают материальными точками:

(dtimes m1=rho1times dV1)

(dtimes m2=rho2times dV2)

где (rho1, rho2) – обозначают плотность веществ материальных точек, характерных для первого и второго объектов,

(dV1 ,dV2) – элементарные объемы выделенных материальных точек.

Исходя из этого, сила притяжения (doverline F), с которой взаимодействуют объекты, равна:

  (doverline F=-Gtimes frac{rho _{1}timesrho _{2}times dtimes V_{1}times dtimes V_{2}}{r_{12}^{3}} bar{r_{12}})

Таким образом, сила притяжения первого тела вторым рассчитывается следующим образом:

(bar{F}_{12}=-Gtimesint_{V_{1}}^{rho _{1}times dtimes V_{1}}int_{V_{2}}^{frac{rho _{2}}{r_{12}^{3}}times bar{r}_{12}times dtimes V_{2}})

где интегрирование выполняется по всему объему первого ((V1)) и второго ((V2)) тел. Если тела обладают однородностью, то формула корректируется, таким образом:

(bar{F}_{12}=-Gtimesrho1timesrho2timesint_{V_{1}}^{dtimes V_{1}}int_{V_{2}}^{frac{bar{r}_{12}}{r_{12}^{3}}times dtimes V_{2}})

Формула для силы притяжения твердых тел шарообразной формы

В условиях, когда сила притяжения измеряется между телами, представленных в форме шара или близкой к нему, с плотностью, зависящей лишь от удаленности их центров тяжести, применяется следующая формула:

(bar{F}_{12}=-Gtimes(m1times m2)/R^3times R12)

где (m1,m2) – массы шаров,  (R )– радиус – вектор, соединяющий центры шаров.

Пример применения формулы для расчета

Задача. Необходимо рассчитать силу притяжения между двумя идентичными однородными шарами, масса которых составляет по 1 килограмму. При этом их центры тяжести удалены на 1 метр друг от друга.

Решение будет выглядеть следующим образом:

Используя формулу для подсчета силы притяжения между двумя объектами шарообразной формы, получается:

(F_g=6.67times 10^{-11}times frac{1times 1}{1^{2}})

Ответ: (F_g=6.67times 10^{-11})

Выполнить расчет силы притяжения достаточно просто, если правильно выбрать формулу, подходящую под конкретные условия, в которых находятся тела. Если в процессе решения задач по физике или другим дисциплинам возникают проблемы, всегда можно обратиться за помощью к компетентным специалистам портала Феникс.Хелп.

Представим себе, что мы отправляемся в путешествие по Солнечной системе. Какова сила тяжести на других планетах? На каких мы будем легче, чем на Земле, а на каких тяжелее? Пока мы еще не покинули Землю, проделаем такой опыт: мысленно опустимся на один из земных полюсов, а затем представим себе, что мы перенеслись на экватор. Интересно, изменился ли наш вес? Известно, что вес любого тела определяется силой притяжения (силой тяжести). Она прямо пропорциональна массе планеты и обратно пропорциональна квадрату ее радиуса (об этом мы впервые узнали из школьного учебника физики). Следовательно, если бы наша Земля была строго шарообразна, то вес каждого предмета при перемещении по ее поверхности оставался бы неизменным. Но Земля – не шар. Она сплюснута у полюсов и вытянута вдоль экватора. Экваториальный радиус Земли длиннее полярного на 21 км. Выходит, что сила земного притяжения действует на экваторе как бы издалека. Вот почему вес одного и того же тела в разных местах Земли неодинаков. Тяжелее всего предметы должны быть на земных полюсах и легче всего – на экваторе. Здесь они становятся легче на 1/190 по сравнению с их весом на полюсах. Конечно, обнаружить это изменение веса можно только с помощью пружинных весов. Небольшое уменьшение веса предметов на экваторе происходит также за счет центробежной силы, возникающей вследствие вращения Земли. Таким образом, вес взрослого человека, прибывшего с высоких полярных широт на экватор, уменьшится в общей сложности примерно на 0,5 кг. Теперь уместно спросить: а как будет изменяться вес человека, путешествующего по планетам Солнечной системы? Наша первая космическая станция – Марс. Сколько же человек будет весить на Марсе? Сделать такой расчет нетрудно. Для этого необходимо знать массу и радиус Марса. Как известно, масса “красной планеты” в 9,31 раза меньше массы Земли, а радиус в 1,88 раза уступает радиусу земного шара. Следовательно, из-за действия первого фактора сила тяжести на поверхности Марса должна быть в 9,31 раза меньше, а из-за второго – в 3,53 раза больше, чем у нас (1,88 * 1,88 = 3,53). В конечном счете она составляет там немногим более 1/3 части земной силы тяжести (3,53 : 9,31 = 0,38). Таким же образом можно определить напряжение силы тяжести на любом небесном теле. Теперь условимся, что на Земле космонавт-путешественник весит ровно 70 кг. Тогда для других планет получим следующие значения веса (планеты расположены в порядке возрастания веса):

Плутон	4,5
Меркурий	26,5
Марс	26,5
Сатурн	62,7
Уран	63,4
Венера	63,4
Земля	70,0
Нептун	79,6
Юпитер	161,2

Как видим, Земля по напряжению силы тяжести занимает промежуточное положение между планетами-гигантами. На двух из них – Сатурне и Уране – сила тяжести несколько меньше, чем на Земле, а на двух других – Юпитере и Нептуне – больше. Правда, для Юпитера и Сатурна вес дан с учетом действия центробежной силы (они быстро вращаются). Последняя уменьшает вес тела на экваторе на несколько процентов. Следует заметить, что для планет-гигантов значения веса даны на уровне верхнего облачного слоя, а не на уровне твердой поверхности, как у земноподобных планет (Меркурия, Венеры, Земли, Марса) и у Плутона. На поверхности Венеры человек окажется почти на 10% легче, чем на Земле. Зато на Меркурии и на Марсе уменьшение веса произойдет в 2,6 раза. Что же касается Плутона, то на нем человек будет в 2,5 раза легче, чем на Луне, или в 15,5 раза легче, чем в земных условиях. А вот на Солнце гравитация (притяжение) в 28 раз сильнее, чем на Земле. Человеческое тело весило бы там 2 т и было бы мгновенно раздавлено собственной тяжестью. Впрочем, еще не достигнув Солнца, все превратилось бы в раскаленный газ. Другое дело – крошечные небесные тела, такие как спутники Марса и астероиды. На многих из них по легкости можно уподобиться… воробью! Вполне понятно, что путешествовать по другим планетам человек может только в специальном герметичном скафандре, снабженном приборами системы жизнеобеспечения. Вес скафандра американских астронавтов, в котором они выходили на поверхность Луны, равен примерно весу взрослого человека. Поэтому приведенные нами значения веса космического путешественника на других планетах надо по меньшей мере удвоить. Только тогда мы получим весовые величины, близкие к действительным. Коротцев О.Н.

О путешествиях к звездам люди мечтали издревле, начиная с тех времен, когда первые астрономы рассмотрели в примитивные телескопы иные планеты нашей системы и их спутники. С тех пор прошло много веков, но увы, межпланетные и тем более полеты к другим звездам невозможны и сейчас. А единственным внеземным объектом, где побывали исследователи, является Луна. Мы знаем, что силой тяжести называется сила, с которой Земля притягивает различные тела.

Сила тяжести всегда направлена к центру планеты. Сила тяжести сообщает телу ускорение, которое называется ускорением свободного падения и численно равно 9,8м/с. Это значит, что любое тело, независимо от его массы при свободном падении (без сопротивления воздуха) изменяет свою скорость за каждую секунду падения на 9,8 м/с.

Используя формулу для нахождения ускорения свободного падения g = GМ/R2, мы можем рассчитать значения g на поверхности любой планеты. Масса планет M и их радиус R известны благодаря астрономическим наблюдениям и сложным расчетам. а G — гравитационная постоянная (6,6742•10-11 м3с-2кг-1).

Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли (масса М = 5,9736•1024 кг, радиус R = 6,371•106 м), мы получим g=6,6742 * 10 *5,9736 / 6,371*6,371 = 9,822м/сСтандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с2, а в технических расчётах обычно принимают g = 9,81 м/с2.

Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.

Благодаря притяжению к Земле течет вода в реках. Человек, подпрыгнув, опускается на Землю, потому что Земля притягивает его. Земля притягивает к себе все тела: Луну, воду морей и океанов, дома, спутники и т.

п. Благодаря силе тяжести облик нашей планеты непрерывно меняется. Сходят с гор лавины, движутся ледники, обрушиваются камнепады, выпадают дожди, текут реки с холмов на равнины.

Все живые существа на земле чувствуют ее притяжение. Растения также «чувствуют» действие и направление силы тяжести, из-за чего главный корень всегда растет вниз, к центру земли, а стебель вверх.

Земля и все остальные планеты, движущиеся вокруг Солнца, притягиваются к нему и друг к другу. Не только Земля притягивает к себе тела, но и эти тела притягивают к себе Землю. Притягивают друг друга и все тела на Земле.

Например, притяжение со стороны Луны вызывает на Земле приливы и отливы воды, огромные массы которой поднимаются в океанах и морях дважды в сутки на высоту нескольких метров. Притягивают друг друга и все тела на Земле. Поэтому ВЗАИМНОЕ ПРИТЯЖЕНИЕ ВСЕХ ТЕЛ ВСЕЛЕННОЙ НАЗЫВАЕТСЯ ВСЕМИРНЫМ ТЯГОТЕНИЕМ.

Чтобы определить силу тяжести, действующую на тело любой массы, необходимо ускорение свободного падения умножить на массу этого тела. F = g * m,где m-масса тела, g – ускорение свободного падения.

Из формулы видно, что значение силы тяжести увеличивается с увеличением массы тела. Так же видно, что сила тяжести зависит также от величины ускорения свободного падения. Значит, делаем вывод: для тела неизменной массы значение силы тяжести меняется с изменение ускорения свободного падения.

Используя формулу для нахождения ускорения свободного падения g=GМ/R, мы можем рассчитать значения g на поверхности любой планеты. Масса планет M и их радиус R известны благодаря астрономическим наблю¬дениям и сложным расчетам. где G — гравитационная постоянная (6,6742•10-11 м3с-2кг-1).

Планеты издавна делились учеными на две группы. Первая – это планеты земного типа: Меркурий, Венера, Земля, Марс, с недавних пор – Плутон. Для них характерны относительно небольшие размеры, малое количество спутников и твердое состояние.

Оставшиеся – Юпитер, Сатурн, Уран, Нептун – планеты-гиганты, состоящие из газообразного водорода и гелия. Все они движутся вокруг Солнца по эллиптическим орбитам, отклоняясь от заданной траектории, если рядом проходит планета-сосед.

Наша «первая космическая станция» – Марс. Сколько же человек будет весить на Марсе? Сделать такой расчет нетрудно. Для этого необходимо знать массу и радиус Марса.

Как известно, масса “красной планеты” в 9,31 раза меньше массы Земли, а радиус в 1,88 раза уступает радиусу земного шара. Следовательно, из-за действия первого фактора сила тяжести на поверхности Марса должна быть в 9,31 раза меньше, а из-за второго – в 3,53 раза больше, чем у нас (1,88 * 1,88 = 3,53). В конечном счете она составляет там немногим более 1/3 части земной силы тяжести (3,53 : 9,31 = 0,38).

Она составляет 0,38 g от земной, это примерно в два раза меньше. Это значит, что на красной планете можно скакать и прыгать гораздо выше, чем на Земле, и все тяжести весить будут также значительно меньше. Таким же образом можно определить напряжение силы тяжести на любом небесном теле.

Теперь определим, напряжение силы тяжести на Луне. Масса Луны, как мы знаем, в 81 раз меньше массы Земли. Если бы Земля обладала такой маленькой массой, то напряжение силы тяжести на ее поверхности было бы в 81 раз слабее, чем теперь. Но по закону Ньютона шар притягивает так, словно вся его масса сосредоточена в центре. Центр Земли отстоит от ее поверхности на расстоянии земного радиуса, центр Луны – на расстоянии лунного радиуса. Но лунный радиус составляет 27/100 земного, а от уменьшения расстояния в 100/27 раза сила притяжения увеличивается в (100/27) раз. Значит, в конечном итоге напряжение силы тяжести на поверхности Луны составляет1002  /   272 * 81 = 1 / 6 земногоЛюбопытно, что если бы на Луне существовала вода, пловец чувствовал бы себя в лунном водоеме так же, как на Земле. Его вес уменьшился бы в шесть раз, но во столько же раз уменьшился бы и вес вытесняемой им воды; соотношение между ними было бы такое же, как на Земле, и пловец погружался бы в воду Луны ровно на столько же, на сколько погружается он у нас.

ускорение свободного падения на поверхности некоторых небесных тел, м/сСолнце   273,1Меркурий  3,68—3,74 Венера   8,88Земля   9,81 Луна   1,62Церера   0,27 Марс   3,86Юпитер   23,95 Сатурн   10,44Уран   8,86 Нептун   11,09Плутон   0,61Как видно из таблицы, почти идентичное значение ускорения свободного падения присутствует на Венере и составляет 0,906 от земной. Теперь условимся, что на Земле космонавт-путешественник весит ровно 70кг. Тогда для других планет получим следующие значения веса (планеты расположены в порядке возрастания веса):

Плутон – 43 НМеркурий – 260 НМарс – 270 НСатурн -730 НУран 620 НВенера – 622 НЗемля – 786 ННептун – 776 НЮпитер – 1677 НКак видим, Земля по напряжению силы тяжести занимает промежуточное положение между планетами-гигантами. На двух из них – Сатурне и Уране – сила тяжести несколько меньше, чем на Земле, а на двух других – Юпитере и Нептуне – больше. Сила тяжести на Юпитере составляет 2,535 g относительно земной. Правда, для Юпитера и Сатурна вес дан с учетом действия центробежной силы (они быстро вращаются). Последняя уменьшает вес тела на экваторе на несколько процентов.

На поверхности Венеры человек окажется почти на 10% легче, чем на Земле. Зато на Меркурии и на Марсе уменьшение веса произойдет в 2,6 раза. Что же касается Плутона, то на нем человек будет в 2,5 раза легче, чем на Луне, или в 15,5 раза легче, чем в земных условиях.

Самое близкое к нам небесное тело – Луна. Люди там уже побывали и убедились в том, что действительно ускорение свободного падения на Луне в 6 раз меньше земного. А вот на Солнце гравитация (притяжение) в 28 раз сильнее, чем на Земле. Человеческое тело весило бы там 20000 Н и было бы мгновенно раздавлено собственной тяжестью.

Вывод:

Если нам предстоит космическое путешествие по планетам Солнечной системе, то нужно быть готовым к тому, что наш вес будет меняться. Сила притяжения также оказывает различные воздействия на живых существ. Попросту говоря, когда будут открыты другие обитаемые миры, мы увидим, что их обитатели сильно отличаются друг от друга в зависимости от массы их планет. К примеру, будь Луна обитаема, то ее населяли бы очень высокие и хрупкие существа, и наоборот, на планете массой с Юпитер жители были бы очень низкие, крепкие и массивные. А иначе на слабых конечностях в таких условиях попросту не выживешь при всем желании. Сила притяжения сыграет важную роль и при будущей колонизации того же Марса.

До изобретения телескопа было известно лишь семь планет: Меркурий, Венера, Марс, Юпитер, Сатурн, Земля и Луна. Их количество многих устраивало. Поэтому, когда в 1610 г.

вышла книга Галилея «Звездный вестник», в которой он сообщил, что с помощью своей «зрительной трубы» ему удалось обнаружить еще четыре небесных тела, «никем еще не виданные от начала мира до наших дней» (спутники Юпитера), то это вызвало сенсацию. Сторонники Галилея радовались новым открытиям, противники же объявили ученому непримиримую войну.

Уже через год в Венеции вышла книга «Размышления об астрономии, оптике и физике», в которой автор утверждал, что Галилей заблуждается и число планет должно быть обязательно семь, так как, во-первых, в Ветхом Завете упоминается семисвечник (а это означает семь планет), во-вторых, в голове имеется лишь семь отверстий, в-третьих, существует только семь металлов и, в-четвертых, «спутники не видны для простого глаза, а поэтому и не могут оказывать влияние на Землю, следовательно, они не нужны, а поэтому они не существуют».

Однако подобными аргументами нельзя было остановить развитие науки, и теперь мы точно знаем, что спутники Юпитера существуют и число планет вовсе не равно семи. Вокруг Солнца обращаются девять больших планет (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун и Плутон, из которых лишь первые две не обладают спутниками) и свыше трех тысяч малых планет, называемых астероидами.

Спутники обращаются вокруг своих планет под действием их гравитационного поля. Сила тяжести на поверхности каждой из планет может быть найдена по формуле F_T = mg, где g = GM/R — ускорение свободного падения на планете. Подставляя в последнюю формулу массу M и радиус R разных планет, можно рассчитать, чему равно ускорение свободного падения g на каждой из них. Результаты этих расчетов (в виде отношения ускорения свободного падения на данной планете к ускорению свободного падения на поверхности Земли) приведены в таблице 7.

Из этой таблицы видно, что наибольшее ускорение свободного падения и, следовательно, наибольшая сила тяжести на Юпитере. Это самая большая планета Солнечной системы; ее радиус в 11 раз, а масса в 318 раз больше, чем у Земли. Слабее всего притяжение на далеком Плутоне. Эта планета меньше Луны: ее радиус всего лишь 1150 км, а масса в 500 раз меньше, чем у Земли!

Еще меньшей массой обладают малые планеты Солнечной системы. 98% этих небесных тел обращаются вокруг Солнца между орбитами Марса и Юпитера, образуя так называемый пояс астероидов. Первый и самый большой астероид — Церера был открыт в 1801 г. Его радиус около 500 км, а масса примерно 1,2*10 кг (т. е. в 5000 раз меньше, чем у Земли). Нетрудно подсчитать, что ускорение свободного падения на Церере примерно в 32 раза меньше, чем на Земле! Во столько же раз меньше там оказывается и вес любого тела. Поэтому космонавт, оказавшийся на Церере, смог бы поднять груз массой 1,5 т (рис. 110).

На Церере, однако, пока еще никто не был. А вот на Луне люди уже побывали. Впервые это произошло летом 1969 г.

, когда космический корабль «Аполлон-11» доставил на наш естественный спутник трех американских астронавтов: Н. Армстронга, Э. Олдрина и М.

Коллинза. «Конечно, — рассказал потом Армстронг,— в условиях лунного притяжения хочется прыгать вверх. .

. Наибольшая высота прыжка составляла два метра — Олдрин прыгнул до третьей ступеньки лестницы лунной кабины. Падения не имели неприятных последствий.

Ускорение свободного падения на Луне в 6 раз меньше, чем на Земле. Поэтому, прыгая вверх, человек поднимается там на высоту, в 6 раз большую, чем на Земле. Чтобы подпрыгнуть на Луне на 2 м, как это сделал Олдрин, требуется приложить такое же усилие, что и на Земле при прыжке на высоту 33 см. Первые астронавты находились на Луне 21 ч 36 мин. 21 июля они стартовали с Луны, а 24 июля «Аполлон-11» уже приводнился в Тихом океане. Люди покинули Луну, но на ней осталось пять медалей с изображениями пяти погибших космонавтов. Это Ю. А. Гагарин, В. М. Комаров, В. Гриссом, Э. Уайт и R Чаффи.

? ? ?

1. Перечислите все большие планеты, входящие в состав Солнечной системы. 2.

Как называется самая большая из них и самая маленькая? 3. Во сколько раз вес человека на Юпитере превышает вес того же человека на Земле?

4. Во сколько раз сила тяжести на Марсе меньше, чем на Земле? 5.

Что вы знаете о Церере? 6. Почему походка астронавтов на Луне напоминала скорее прыжки, чем обычную ходьбу?

В данной статье мы рассмотрим, если сила тяжести на других планетах нашей Солнечной системы. А также узнаем, какие ее минимальные и максимальные показатели. Ответы на некоторые вопросы, связанные с силой тяжести, интересно узнать не только физикам и астрономам. Даже значительной части обычных людей хотелось бы получить ответы на вопросы о существовании и особенностях силы тяжести на разных планетах.

Но прежде необходимо ознакомиться с базовыми понятиями для этого физического явления. Поэтому давайте рассмотрим именно силу тяжести и ее роль для природы не только на нашей Земле, но и на других планетах Солнечной системы.

Что собой представляет сила тяжести?

Сила тяжести – это довольно удивительная фундаментальная сила. Она является естественным эффектом, в котором все вещи, обладающие массой, притягиваются друг к другу. Будь то астероиды, планеты, звезды, галактики и т. д.

• Чем больше масса объекта, тем большую силу он будет оказывать на объекты вокруг него. Сила объекта также зависит от расстояния — то есть влияние, которое он оказывает на другой объект, уменьшается с увеличением расстояния между ними.
• Силу тяготения называют притягивающей, потому что она всегда пытается объединить массы и никогда не отталкивает их. Фактически, каждый объект живой и неживой природы тянется ко всем другим объектам во Вселенной.
• Сила тяжести также является одной из четырех основных сил, которые регулируют все взаимодействия в природе. Она находится наряду со слабой и сильной ядерной силой, а также электромагнетизмом.
• Из этих сил гравитация является самой слабой. Она слабее примерно в 1038 раз сильной ядерной силы и в 1036 раз слабее электромагнитной силы. Также слабее она и слабой ядерной силы в 1029 раз.
• Лучшим средством описания поведения силы тяжести остается общая теория относительности Эйнштейна. Согласно теории, сила тяготения не является силой. Это следствие кривизны пространства и времени, что вызвана неравномерным распределением массы или энергии.
• С этой теорией согласуются взаимодействия в природе. Энергия и масса эквивалентны, а это значит, что все формы энергии также вызывают силу тяжести и находятся под ее влиянием.
• Однако, большинство способов применения этой силы лучше всего объясняет Закон всемирного тяготения Ньютона. В нем говорится, что сила тяжести существует как притяжение двух тел. Сила этого притяжения может вычисляться математически, где сила тяготения прямо пропорциональна произведению их масс. Также она обратно пропорциональна квадрату расстояния между телами.
• Сила тяготения высчитывается по общепринятой формуле:

None В каждой точке планеты действует сила тяжести, что есть и на других планетах.

[custom_ads_shortcode1]

Какая роль силы тяжести в природе?

Если бы не было силы тяжести, то мы все выплыли в космос. Без нее все наши наземные виды медленно увядали и умирали. В то же время, наши мышцы дегенерировали, кости у людей и животных становились хрупкими и слабыми, а органы переставали функционировать должным образом.

• Поэтому без преувеличений можно сказать, что сила тяготения — это не только факт жизни на Земле, но и предпосылка для этого. Однако порой люди намерены выйти из сферы влияния этой силы.
• Сила тяжести оказывает незначительное влияние на материю в наименьшем из масштабов, то есть на субатомные единицы. Однако она имеет большое значение для развития объектов на макроуровне.
• Поскольку на макроскопическом уровне, то есть на уровне планет, звезд и галактик, она является доминирующей силой, влияющей на взаимодействие материй. Она вызывает формирование и влияет на траекторию астрономических тел, управляя астрономическим поведением. Сила тяготения сыграла важную роль в эволюции ранней Вселенной.
• Именно сила тяжести отвечала за совокупление материи, чтобы образовать облака газа, которые подверглись гравитационному коллапсу. Облака образовывали первые звезды, которые затем формировали первые галактики. Кстати, без нее, например, звезды превращаются в черные дыры.
• В пределах отдельных звездных систем это заставило пыль и газ слиться. В результате образовывались планеты. Сила тяжести управляет движениями орбит планет вокруг звезд, вращением звезд вокруг центра их галактики и слиянием галактик.
• Но нельзя недооценивать всю ее важность – именно сила тяжести и создает необходимую для жизни атмосферу. Именно от нее и зависит атмосферное или гидростатическое давление. А также она закладывает основу нашего скелета и вестибулярного аппарата.

Без силы тяжести мы все бы улетели в космос.

[custom_ads_shortcode2]

Есть ли сила тяжести на других планетах Солнечной системы?

Что на Земле присутствует сила тяготения, знают все жители нашей планеты. Убедиться в этом можно на собственном опыте. Но вот, есть ли эта сила на Юпитере, Марсе, Венере и других планетах, проверить достаточно проблематично.

Возможно, не все пытаются найти ответ на этот вопрос. Но для развития общего кругозора и удовлетворения своего любопытства, предлагаем все же выяснить эту информацию.

Важно: В принципе, гравитация зависит от массы, где все вещи притягиваются друг к другу. Но не забывайте, что размер, масса и плотность объекта также влияют на гравитационную силу. Поэтому расчеты свободного падения для каждой планеты должны проводиться по отдельности за следующей формулой:

g = GM/R2, где M – это масса планеты, а R2 – это ее радиус. Но вот с гравитационной постоянной величиной (G) могут возникнуть некие трудности, а точнее еще одни дополнительные расчеты. С 2014 года ее формула выглядит следующим образом:

G = 6,67408(31)·10−11 м3·с−2·кг−1Теперь можно приступать к расчетам силы тяжести на других планетах. Кстати, не забывайте, что это только математическая и физическая теория.

Юпитер значительно тяжелее Земли, поэтому сила тяжести на нем больше.

• Меркурий — наименьшая и наименее массивная планета, что открывает нашу систему. Выделяется планета, кстати, нестабильными перепадами температуры. Ведь днем она доходит до отметки +350 °C, а ночью превышает даже -150 °C.
  • Сила тяжести такой контрастной планеты среди остальных планет земной группы и, конечно же, газовых гигантов имеет наименьшие показатели – 3,7 м/с².
• Венера немного похожа на Землю, поэтому ее часто называют «близнецом Земли». Правда, только по габаритам. Следовательно, неудивительно, что мощность силы тяготения на Венере очень близка к ее мощности на Земле – 8,88 м/с².
  • Кстати, радиус Венеры от земного меньше лишь на 0,85%. Но вот погулять на такой планете не получится, ведь вас может сдуть ветром с силой в 300 м/с или вы просто сгорите от ее минимальной температуры в 475°C. Но и это еще не все, сверху еще пойдет серный дождь, что будет смешан с хлорным железом.
• Для сравнение приведем средние показатели нашей Земли – 9, 81 м/с².  Кстати, не забывайте, что на полюсе она будет куда выше, нежели на экваторе. А вот на нашем спутнике, для справочной информации, Луна имеет силу тяготения всего лишь 1,62 м/с². Да и всем известно, как космонавты могут бегать по его поверхности.
• Марс более похож на Землю во многих ключевых аспектах. Правда, минусовая температура немного не позволяет появиться там жизни. И вот когда дело доходит до размера, массы и плотности, то он оказывается сравнительно малым. Из-за этого у Марса в 0,38 раза сила тяготения меньше, чем у Земли. И составляет с округлением 3,86 м/с².
  • И вот наглядный пример, когда плотность сыграла свою роль – ведь Марс значительно больше по размерам за Меркурий, но сила тяготения не слишком отличается.

На Марсе наша масса уменьшится на 62%.

• Юпитер — самая большая и самая массивная планета в Солнечной системе. Кстати, это еще и ветреная планета, что характеризуется постоянными штормами и грозами. А будучи газовым гигантом, Юпитер, естественно, менее плотный, чем Земля и другие земные планеты.
  • Более того, его плотность и основной состав из гелия и водорода обеспечили то, что Юпитер не имеет истинной оболочки. Если бы кто-то стоял на нем, он просто тонул бы, пока не достиг твердого ядра. В результате поверхностная сила тяготения Юпитера определяется, как сила на вершинах его облаков. И составляет 24,79 м/с².
• Как и Юпитер, Сатурн — это огромный гигант газа, который значительно больше и массивнее Земли, но менее плотный. В результате, его поверхностная сила тяжести немного больше, чем у Земли.
  • Для сравнения: планета со знаменитым поясом из колец имеет диаметр 57350 км, а вот земля меньше практически в 5 раз — 12742 км. Но вот сила тяжести на Сатурне всего 10,44 м/с². То есть, для таких габаритов это очень мало.
• А площадь Урана примерно в четыре раза больше площади Земли. Однако, как у газового гиганта, его плотность даже ниже земного тяготения. И составляет 8,86 м/с². Ходить по планете можно будет без труда, но вот невероятный холод не даст сделать ни шагу. Ведь температура не поднимается выше -220 ℃.
• Нептун — четвертая по величине планета Солнечной системы. Он в 3,86 раза больше Земли. Кстати, с этой планетой никто не сравнится по мощности штормов — 2100 км/с². Но, будучи газовым гигантом, он имеет низкую плотность и сравнительно небольшую силу тяжести в м/с².
• Стоит еще рассмотреть в качестве дополнительной информации силу тяжести на Плутоне. Хотят с 2006 года космическое тело утратило официальный статус планеты, но даже для карликовой планеты сила тяжести очень мала — всего 0,61 м/с².

Вот так наш вес зависит от силы тяжестиПонимание влияния силы тяжести на организм человека существенно поможет для осуществления космических путешествий, особенно там, где были заданы вопросы о длинных выездных миссиях на орбиту и на Международную космическую станцию. И, конечно же, знание того, насколько сильной является сила тяготения на других планетах, имеет важное значение для пилотируемых миссий. Благодаря этим знаниям возможно даже поселения землян на других планетах.

Важно: Можно сделать вывод, что сила тяжести присутствует на всех планетах Солнечной системы, но не везде ее можно измерить на поверхности планеты. На Юпитере, Сатурне, Уране, Нептуне сила тяжести измеряется на вершинах облаков. Серьезные отличия на разных планетах есть и в мощности этой силы.

[custom_ads_shortcode3]

На какой планете наименьшая сила тяжести?

• Если брать во внимание все астрономические тела в Солнечной системе, где присутствует сила тяготения, то самая маленькая сила тяжести не на поверхности планеты нашей системы. Это астрономическое тело – карликовая планета Цецер с силой тяжести всего в 0,27 м/с².
• Если сравнивать силу тяжести только на поверхности планет, то наименьшая сила на планете Плутоне, что охватывает только 0,61 м/с². Но поскольку его лишили звания планеты, то эта должность снова переходит Меркурию. Напомним, что для Меркурия она составляет 3,7 м/с². Этот факт не вызывает удивления, ведь Меркурий является самой маленькой планетой Солнечной системы.

Наибольшую, просто невероятную силу тяжести имеет Солнце, а среди планет — Юпитер.

[custom_ads_shortcode1]

Планета с наибольшей силой тяжести

• Если изучать силу тяготения на всех астрономических объектах, то наибольшее значение этой силы можно выявить на поверхности звезды. Название этой звезды – Солнце. Сила тяжести на звезде огромная — 274 м/с². Это почти в тридцать раз больше, чем на поверхности Земли.
• Что касается планет, то самая большая сила тяжести на наибольшей из планет. Это гигант – Юпитер. Повторится, что он обладает невероятной силой тяжести — 24,79 м/с². Это почти в 2,53 раза больше того, что мы испытываем на планете Земля. Предмет, который весит 100 грамм на Земле, весил бы 236,4 грамма на Юпитере.

Теперь мы знаем, что на Меркурии и других планетах с малой силой тяжести мы бы улетели в космос. А вот, например, на Юпитере нас бы вдавливало в землю. В данном случае в газ.

Кстати, в первом случае мы бы с вами были высокими и худыми, а во второй вариации — низкими и коренастыми. И, конечно же, вес по-разному бы ощущался. С низкой силой тяжести все предметы были бы до невозможности легкими, а вот при больших показателям даже перышко стало бы весом с грузовую машину.

[custom_ads_shortcode2]

Видео: Есть ли сила тяжести на других планетах Солнечной системы?

Источники:

• prosto-o-slognom.ru
• spishy-u-antoshki.ru
• phscs.ru
• heaclub.ru

Закон всемирного тяготения. Движение планет и спутников

 Закон всемирного тяготения

Со­об­ра­же­ния Нью­то­на со­сто­я­ли в сле­ду­ю­щем.

– Если сила при­тя­же­ния тела к Земле про­пор­ци­о­наль­на массе тела F_тяг = mg, а каж­дой силе дей­ствия есть сила про­ти­во­дей­ствия F_1,2 = F_2,1 и если тело при­тя­ги­ва­ет­ся к Земле, то и Земля при­тя­ги­ва­ет­ся к телу. Тогда сила тя­го­те­ния долж­на быть про­пор­ци­о­наль­на как массе од­но­го тела, так и массе вто­ро­го тела F_тяг ~ m₁m₂, то есть сила тя­го­те­ния про­пор­ци­о­наль­на про­из­ве­де­нию масс, вза­и­мо­дей­ству­ю­щих тел.

– Нью­тон за­ме­тил, что уско­ре­ние на пла­не­те Земля, уско­ре­ние сво­бод­но­го па­де­ния

g = F_тяг / m – это при­мер­но 10 м/с², а уско­ре­ние, с ко­то­рым дви­жет­ся Луна по своей ор­би­те а_л = F_тяг / М_л = g / 3600, – это цен­тро­стре­ми­тель­ное уско­ре­ние, в 3600 раз мень­ше уско­ре­ния сво­бод­но­го па­де­ния. Нью­тон до­га­дал­ся, по­че­му такая раз­ни­ца в чис­лах: дело в том, что рас­сто­я­ние от Земли до Луны со­став­ля­ет при­мер­но ше­сть­де­сят зем­ных ра­ди­у­сов r_з-л ≈ 60R_з. Их, а также уско­ре­ние 3600 Нью­тон объ­еди­нил сле­ду­ю­щим вы­во­дом: сила тя­го­те­ния об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между вза­и­мо­дей­ству­ю­щи­ми те­ла­ми F_тяг ~ 1 / r².

Учи­ты­вая эти два по­сы­ла, Нью­тон дал общую фор­му­ли­ров­ку: сила все­мир­но­го тя­го­те­ния прямо про­пор­ци­о­наль­на мас­сам вза­и­мо­дей­ству­ю­щих тел и об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними.

  = γ (-)

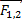
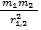
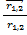
γ – ко­эф­фи­ци­ент про­пор­ци­о­наль­но­сти (гамма), а на­прав­ле­ние силы – это сила при­тя­же­ния друг к другу, и на­прав­ле­ние в этой фор­му­ле да­ет­ся сле­ду­ю­щим об­ра­зом: это еди­нич­ный век­тор, при­ве­ден­ный из пер­во­го тела ко вто­ро­му, то есть от­но­ше­ние са­мо­го век­то­ра к его мо­ду­лю. Знак минус озна­ча­ет, что сила тя­го­те­ния на­прав­ле­на не от пер­во­го тела ко вто­ро­му, а от вто­ро­го тела к пер­во­му.

Ко­эф­фи­ци­ент про­пор­ци­о­наль­но­сти из­ме­рил Ка­вен­диш в своем экс­пе­ри­мен­те:

γ = G = 6,62 · 10^-11 Нм² / кг²

Из за­ко­на все­мир­но­го тя­го­те­ния сле­ду­ют фор­му­лы уско­ре­ния сво­бод­но­го па­де­ния:

1. Уско­ре­ние сво­бод­но­го па­де­ния у по­верх­но­сти пла­не­ты:

g₀ = F_тяг / m = γmМ_з / R²_з · m = γ · М_з / R²_з.

Зная уско­ре­ние на пла­не­те Земля, ра­ди­ус Земли, зна­че­ние гра­ви­та­ци­он­ной по­сто­ян­ной, можно при необ­хо­ди­мо­сти вы­чис­лить массу Земли.

2. Уско­ре­ние сво­бод­но­го па­де­ния на ка­ком-то рас­сто­я­нии h от по­верх­но­сти пла­не­ты:

g_h = γ· М_з / (R_з + h)² = (γ · М_з / R²_з) · R²_з / (R_з + h)².

Так как в такой форме ее труд­но при­ме­нить, то поль­зу­ют­ся при­ве­ден­ной фор­му­лой:

g_h = g₀ · (R_з / R_з + h)²

3. Уско­ре­ние сво­бод­но­го па­де­ния на глу­бине: g_h↓ = g₀ · (R_з – h / R_з).

На ос­но­ве за­ко­на все­мир­но­го тя­го­те­ния можно рас­счи­тать ско­рость спут­ни­ков пла­нет (рис. 1).

Рис. 1. При­мер рас­че­та ско­ро­сти спут­ни­ка

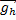
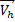
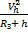
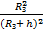
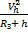
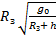
m ┴  => g_h =  ; g₀ = ; V_h =  

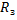
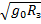
при h <<  V_h =  ≈ 7,9 км/с

В этом слу­чае сила при­тя­же­ния будет пер­пен­ди­ку­ляр­на ско­ро­сти спут­ни­ка при дви­же­нии по кру­го­вой ор­би­те, она вы­зы­ва­ет цен­тро­стре­ми­тель­ное дви­же­ние. Зная уско­ре­ние сво­бод­но­го па­де­ния на вы­со­те h, по­лу­ча­ем фор­му­лу ско­ро­сти спут­ни­ка на вы­со­те h. Оче­вид­но, что с ро­стом вы­со­ты ско­рость будет умень­шать­ся, а у самой по­верх­но­сти Земли при очень малых h по срав­не­нию с ра­ди­у­сом Земли при­ме­ня­ет­ся упро­ще­ние. То есть h пре­не­бре­га­ют, вно­сят ра­ди­ус Земли под ко­рень, про­из­во­дят со­кра­ще­ния и по­лу­ча­ют фор­му­лу пер­вой кос­ми­че­ской ско­ро­сти, ко­то­рая равна 7,9 км/с. При такой ско­ро­сти спут­ник неда­ле­ко от по­верх­но­сти Земли может дви­гать­ся по кру­го­вой ор­би­те.

 Пример решения задачи 1

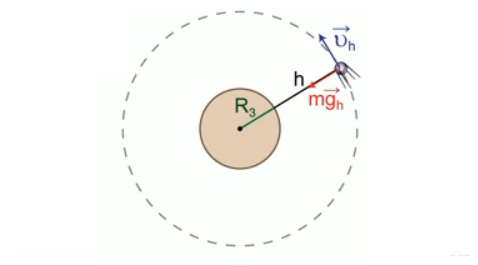
У по­верх­но­сти Луны на кос­мо­нав­та дей­ству­ет сила тя­го­те­ния 120 Н. Какая сила тя­го­те­ния дей­ству­ет со сто­ро­ны Луны на того же кос­мо­нав­та в кос­ми­че­ском ко­раб­ле, дви­жу­щем­ся по кру­го­вой ор­би­те во­круг Луны на рас­сто­я­нии трех лун­ных ра­ди­у­сов от ее цен­тра?

1. 0 Н; 2. 39 Н; 3. 21 Н; 4. 13 Н.

За­пи­шем крат­кое усло­вие за­да­чи и рас­смот­рим ре­ше­ние:

Ответ: ва­ри­ант 4. 13 Н.

 Пример решения задачи 2

Два тела мас­сой по 1000 тонн уда­ле­ны на 0,1 км друг от друга. Найти силу их гра­ви­та­ци­он­но­го при­тя­же­ния.

1. 6,7 мН; 2. 0,67 Н; 3. 6,7 Н; 4. 6,7 кН.

За­пи­сы­ва­ем крат­кое усло­вие за­да­чи, пе­ре­во­дя тонны в ки­ло­грам­мы, рас­сто­я­ние в метры, и ре­ше­ние.

Ответ: ва­ри­ант 1. 6,7 мН.

При­ме­няя закон все­мир­но­го тя­го­те­ния, мы по­лу­ча­ем пра­виль­ный ответ 1.

 Пример решения задачи 3

Чему равна ско­рость спут­ни­ка Земли на кру­го­вой ор­би­те на вы­со­те 500 км от ее по­верх­но­сти? Ра­ди­ус Земли при­нять рав­ным 6400 км.

1. 7,6 км/с; 2. 7,8 км/с; 3. 7,9 км/с; 4. 8,2 км/с.

За­пи­сы­ва­ем крат­кое усло­вие за­да­чи и вы­чис­ле­ния.

Ответ: ва­ри­ант 1. 7,6 км/с.

Ис­поль­зуя фор­му­лу спут­ни­ка на вы­со­те, мы вно­сим ра­ди­ус пла­не­ты под знак ра­ди­ка­ла и раз­би­ва­ем его на два мно­жи­те­ля. У нас под кор­нем по­лу­чи­лась пер­вая кос­ми­че­ская ско­рость, ко­то­рую мы можем вы­не­сти за знак ра­ди­ка­ла и, под­ста­вив зна­че­ния, по­лу­чим, что ско­рость будет равна 7,6 км/с – это со­от­вет­ству­ет 1 от­ве­ту.

 Движение планет и спутников

На ос­но­ве за­ко­на все­мир­но­го тя­го­те­ния рас­счи­ты­ва­ют пе­ри­од об­ра­ще­ния спут­ни­ков, как есте­ствен­ных, так и ис­кус­ствен­ных. Зная пе­ри­од об­ра­ще­ния, мы можем найти массу спут­ни­ков. Пе­ри­од об­ра­ще­ния на­хо­дит­ся по фор­му­ле: Т = 2πR / V, то есть длина окруж­но­сти, де­лен­ная на ско­рость по ор­би­те. При малых вы­со­тах по срав­не­нию с ра­ди­у­сом Земли для вы­чис­ле­ния ско­ро­сти спут­ни­ка, ко­то­рый летит неда­ле­ко от по­верх­но­сти Земли, пе­ри­од мы на­хо­дим по фор­му­ле:

Т_о = 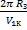 = 2π

Пом­ним о том, что в чис­ли­те­ле у нас длина эк­ва­то­ра, а в зна­ме­на­те­ле пер­вая кос­ми­че­ская ско­рость. Про­из­ве­дя рас­че­ты мы по­лу­чим, что Т_о ≈ 5060 с ≈ 1 ч 24 мин = 1,4 ч – это время, за ко­то­рое ис­кус­ствен­ный спут­ник Земли, дви­га­ю­щий­ся неда­ле­ко от по­верх­но­сти, со­вер­ша­ет пол­ный обо­рот. Если спут­ник летит по ор­би­те, вы­со­та ко­то­рой со­из­ме­ри­ма с ра­ди­у­сом Земли, мы поль­зу­ем­ся фор­му­лой:

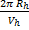
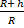
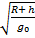
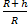
Т_h =  = 2π  = Т_о ( )^3/2

Эту фор­му­лу мы по­лу­чи­ли, внеся (R + h) под знак ра­ди­ка­ла и ис­поль­зуя уже по­лу­чен­ное зна­че­ние Т_о.

Рас­смот­рим за­да­чу, по ко­то­рой была вы­чис­ле­на масса Солн­ца.

Ра­ди­ус зем­ной ор­би­ты со­став­ля­ет 1,5 · 10¹¹ м. Чему равна масса Солн­ца?

Обыч­но эта за­да­ча вы­зы­ва­ет за­труд­не­ние, так как дан всего лишь один па­ра­метр, но нужно пом­нить, что Земля во­круг Солн­ца со­вер­ша­ет один обо­рот за 365 дней, в сут­ках у нас 24 часа и в каж­дом часе 3600 се­кунд, так что нам из­ве­стен пе­ри­од об­ра­ще­ния Земли как спут­ни­ка Солн­ца. По­это­му за­пи­сы­ва­ем крат­кое усло­вие за­да­чи и ре­ше­ние.

Ответ: 2·10³⁰ кг.

Сила, с ко­то­рой Земля при­тя­ги­ва­ет­ся к Солн­цу, при­во­дит к цен­тро­стре­ми­тель­но­му уско­ре­нию, по­это­му при­ме­ня­ем фор­му­лу, ко­то­рая вы­ра­жа­ет­ся через пе­ри­од об­ра­ще­ния. С дру­гой сто­ро­ны, это сила тя­го­те­ния, и по за­ко­ну все­мир­но­го тя­го­те­ния вы­ра­жа­ет­ся через гра­ви­та­ци­он­ную по­сто­ян­ную, массу Земли и массу Солн­ца, де­лен­ные на квад­рат рас­сто­я­ния между ними. Со­кра­ща­ем массу Земли в двух по­след­них чле­нах этого ра­вен­ства, неиз­вест­ным оста­ет­ся толь­ко масса Солн­ца, ко­то­рую мы можем вы­чис­лить, под­став­ляя все дан­ные.

Рас­смот­рим еще одну за­да­чу.

В ре­зуль­та­те пе­ре­хо­да с одной кру­го­вой ор­би­ты на дру­гую цен­тро­стре­ми­тель­ное уско­ре­ние спут­ни­ка Земли умень­ша­ет­ся. Как из­ме­ня­ют­ся в ре­зуль­та­те этого пе­ре­хо­да ра­ди­ус ор­би­ты спут­ни­ка, ско­рость его дви­же­ния по ор­би­те и пе­ри­од об­ра­ще­ния во­круг Земли? Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

1. уве­ли­чи­лась; 2. умень­ши­лась; 3. не из­ме­ни­лась.

При ре­ше­нии задач с вы­бо­ром от­ве­та необ­хо­ди­мо перед ре­ше­ни­ем вы­пи­сать фор­му­лы ве­ли­чин, ко­то­рые фи­гу­ри­ру­ют в усло­вии за­да­чи. Ска­за­но о том, что цен­тро­стре­ми­тель­ное уско­ре­ние умень­ши­лось, а цен­тро­стре­ми­тель­ное уско­ре­ние спут­ни­ка есть не что иное, как уско­ре­ние сво­бод­но­го па­де­ния на его ор­би­те: g_h = g₀ · (R_з / R_з + h)², если g умень­ши­лось, зна­чит, h уве­ли­чи­лось.

Ско­рость спут­ни­ка на ор­би­те, на­хо­дя­ще­го­ся на вы­со­те, – V_h =  , если h уве­ли­чи­ва­ет­ся, то ско­рость умень­ша­ет­ся.

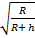
Фор­му­лу для пе­ри­о­да об­ра­ще­ния при­ме­ня­ем Т_h = Т_о (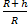)^3/2, по ко­то­рой видно без вы­чис­ле­ний, что про­изо­шли из­ме­не­ния.

Ответ: в ре­зуль­та­те пе­ре­хо­да ра­ди­ус ор­би­ты спут­ни­ка уве­ли­чил­ся, ско­рость его дви­же­ния по ор­би­те умень­ши­лась, пе­ри­од об­ра­ще­ния во­круг Земли уве­ли­чил­ся.

 Заключение

На­ли­чие все­мир­но­го тя­го­те­ния объ­яс­ня­ет устой­чи­вость Сол­неч­ной си­сте­мы, дви­же­ние пла­нет и дру­гих небес­ных тел. С от­кры­ти­ем за­ко­на все­мир­но­го тя­го­те­ния к людям при­шло по­ни­ма­ние прин­ци­па стро­е­ния все­лен­ной. Яр­чай­шим при­ме­ром при­ме­не­ния за­ко­на все­мир­но­го тя­го­те­ния яв­ля­ет­ся за­пуск ис­кус­ствен­но­го спут­ни­ка Земли. Спут­ник все время на­хо­дит­ся на рав­ном рас­сто­я­нии над по­верх­но­стью Земли. Земля при­тя­ги­ва­ет оди­на­ко­во во всех на­прав­ле­ни­ях.

Если кратко, то гравитация и тяготение в теории различения – это проявление подвижной полевой структуры пространства поворотно-вращательного свойства, выражаемое инерционным или свободным движением тел (без воздействия на них других тел). В старой физике гравитационный заряд поля силы тяжести («ускорение» св. падения) «g» выражается зависимым от квадрата расстояния до центра Земли, как от её радиуса плюс высота над поверхностью, т.е. – через произведение «гравитационной постоянной» «G» на «массу» Земли. Но ведь и сама «масса» Земли определена из величины «G» и также из квадрата радиуса земного шара, как выражения того же значения «g» в формуле силы тяжести, т.е. первое выражают через второе, а затем из второго «определяют» первое, что означает физическую тавтологию.

Так и более того, размерность «ускорения» св. падения, определяемая таким образом, не соответствует размерности значения «g» (м/сек^2). Реальное выражение величины «g» потому определяется не «массой» Земли и значением «G», а окружным объёмом земного шара «V» в размерности «м^3», делённым на квадрат периода земного полевого вращения «Т^2» и на квадрат расстояния до центра Земли «Rз», что по полевой физике различения есть отношением окружного (стационарного) и сферического (подвижно-полевого) объёмов Земли, делённым на квадрат земного радиуса. Вблизи земной поверхности такое выражение получает вид «g =4/3 πиRз./Т^2», в котором полевой период образования сферы поля силы тяжести «T» равен 1,59*10^3 сек. или около 25-и минут.

Пространственно-полевое происхождение величины «g», как исходной характеристики структуры частотной воды, говорит о возможности определения на её основе зарядов полей силы тяжести («ускорений» свободных падения) и для других космических тел. Оно, судя по реальному выражению величины «g», исходит из соотношения размеров Земли и космических тел и из периодов (скоростей) их вращения. Отсюда вместо некоей гравитационной «постоянной» необходимо пользоваться величиной «g», как исходной гравитационной величиной.

При этом необходимо различать поля силы тяжести для тел, “доминантно” образующих взаимное вращение (имеющих систему окружных центров), и для тел, обозначающих вращение лишь вокруг их окружного полевого центра, как например, для Луны и других спутников планет (кроме Титана). Тела, “доминантно” образующие взаимное вращение (это Солнце, Земля и планеты) имеют полноценное поворотное поле силы тяжести, кратное земной величине «g».

На Луне и других спутниках планет (как на космических телах, имеющих лишь один окружной центр) образуется спиральное поле силы тяжести (см. 1, стр.155), в котором сила падения и колебание маятника образуется не полным полевым поворотом «πи/2», а «πи/4». Это означает, что величина «g» на Луне и спутниках изначально уменьшается на значение «πи/2», а падение идёт не по поворотной параболе, а – по наклонной или смещённой спирали. Но при контакте тела с опорой величина «g» изначально также становится контурной, уменьшаясь на полное значение «πи» и на величину уменьшения радиуса спутника по отношению к земному радиусу.

Такому соотношению соответствует и высоты поля силы тяжести Земли (высота геостационарной орбиты около 36 тыс. км.) и поля силы тяжести Луны (около 10 тыс. км., что следует из максимальной высоты искусственных спутников вокруг Луны). Соотношение средних радиусов Земли и Луны (6731/1738≈3,6) соответствует отношению высот полей их силы тяжести, а значит, – и такому же отношению их величин «g». Отсюда заряд поля силы тяжести Луны («ускорение» св. падения) будет примерно в 5,7 раз меньше земного (что примерно отвечает данным старой астрономии), а образуемая сила тяжести – меньше примерно в 11,5 раз. Это значит, что на спутниках планет (например, кроме Титана) и на астероидах сила падения больше силы тяжести на величину «πи/2». По этой причине на этих космических телах и не удерживается атмосфера, а космическим аппаратам, запущенным к астероидам легче к ним приземляться, чем удержаться.

Поскольку Солнце образует взаимно-центрическое вращение с Землёй и также имеет оболочковое вращение (систему окружных центров), то при определении силы гравитации Солнца необходимо учитывать не только соотношение его радиуса со средним радиусом Земли, но и скорость вращения, образующую период образования сферы поля силы тяжести, которая примерно в тридцать раз меньше (365/12) и также прямо пропорциональна величине «g». Отсюда заряд поля силы тяжести на Солнце будет примерно лишь в 3,6 раза ((0,695*106/6371)/30) больше земного, а не в 27,9 раз согласно старой астрономии (см. рис. ниже). Внутренние планеты, участвуя в образовании солнечно-земного вращения, находятся в общем солнечно-земном гравитационном поле, а потому при определении величины их гравитации учитывается лишь соотношение их размеров с диаметром Земли.

И величины «g» для Венеры (9,3 м/сек^2) и Меркурия (3,75 м/сек^2) примерно отвечают старой астрономии. Венера имеет движение качения своей полевой сферы вокруг солнечно-земного центра, что образует её большой размер и большой период вращения. И величина «g», примерно равная земной на фоне её медленного движения вокруг оси, приводит потому к вихревому вращению её атмосферы.

Венера и Марс имеют минимально проявленное (в нашей массовой полевой фазе пр-ва) магнитное поле из-за отсутствия у них оболочкового вращения или инротации коры этих планет относительно их мантии. Суточное вращение эти планеты получают не от их магнитного поля, а от нахождения их в едином полевом сцеплении в составе систем «Солнце-Земля» и «Солнце-Марс» («Солнце-Земля-Марс»). Но наличие у Венеры и Марса дальнего окружного центра образует у них полноценное поворотное поле силы тяжести.

Марс также находится в едином с Землёй гравитационном поле, образуя полевую сферу системы «Солнце-Марс», что выражается в периоде его вращения, примерно равном земному. По причине образования движения Марса его увлечением от солнечно-земного вращения он имеет и наклон оси, всего на один градус больший земного. Отсюда величина гравитации Марса также определяется, исходя из соотношения его среднего радиуса с земным размером, и составляет примерно 5,2 м/сек^2. И это уже значительно отличается от расчётов старой астрономии на основе гравитации-притяжения (3,71 м/сек^2).

Поскольку большие планеты или газовые гиганты образуют отдельные гравитационные поля в составе полевых оболочек их взаимно-центрических систем и в центре их газовой оболочки вращаются ядерные системы, подобные Плутону и Харону, то при определении величины «g» их поля силы тяжести учитывается лишь скорость их вращения по отношению к скорости вращения Земли. Для спутников (кроме Титана) больших планет величина «g» (изначально уменьшенная на значение «πи/2») определяется из значения «g» газовых гигантов, уменьшенного также на соотношение диаметра Земли с размерами спутников. Наличие оболочкового вращения у больших планет означает и присутствие у них сильных магнитных полей.

Скорость вращения Юпитера вокруг оси примерно в 2,44 раза выше земного показателя (из соотношения периодов их вращения), а потому на столько же выше и величина «g» для Юпитера, составляя 23,9 м/сек^2, что примерно отвечает данным старой астрономии (24,79 м/сек^2). Скорость вращения Сатурна выше земной окружной скорости в 2,34 раза, а потому величина «g» для него составляет примерно равную с Юпитером величину 22,9 м/сек^2. А явно абсурдное значение старой астрономии гравитации-притяжения, равное лишь 10,44 м/сек^2, подтверждает неверность гравитационный расчётов в этой теории.

Исходя из превышения скорости вращения вокруг оси Урана и Нептуна над земным суточным периодом соответственно в примерно в 2,22 и в 1,52 раза заряд их поля силы тяжести (величина «g») составляет 21,75 м/сек^2 (для Урана) и 14,9 м/сек^2 (для Нептуна). Значения величины «g» для этих планет старой астрономии (8,87 и 11,15 м/сек^2) также подтверждают ошибочность её гравитационных расчётов, тем более, что значение «g» для Нептуна назначается большим несмотря на его меньший размер по сравнению с Ураном.

Ставьте “лайк”, подписывайтесь на канал и оставляйте комментарии (объективные и по существу).

ПОДПИСАТЬСЯ

Филиппов В.В. © Подробнее см.: https://exinworld1.ucoz.ru/blog/zakon_polevogo_tjagotenija_i_realnaja_gravitacija_planet/2020-07-18-89

https://kosmos-x.net.ru/publ/kosmos/zakon_polevogo_tjagotenija_i_realnaja_gravitacija_planet/12-1-0-382

1. Зеркальный космос (Взаимно-оболочковая система мира с комментариями взаимо-центризма). Книга 6-я Теории различения. 2017-2019.
4. Взаимно-центрическое тяготение пространства (Космофизика теории различения), Том I (Книга 5-я Теории различения). Филиппов В.В. 2014-2017.