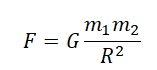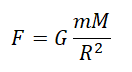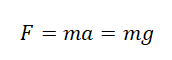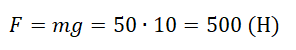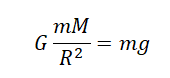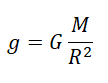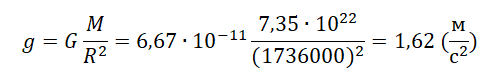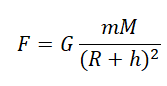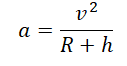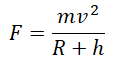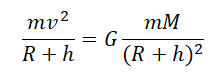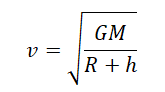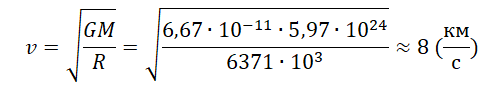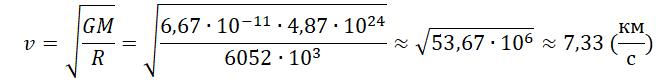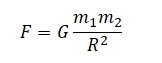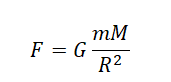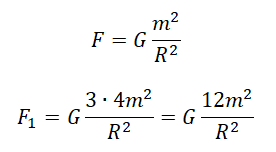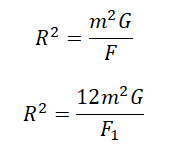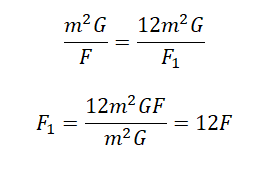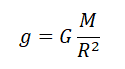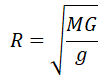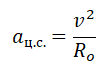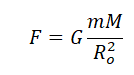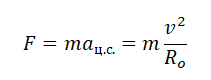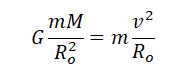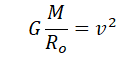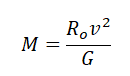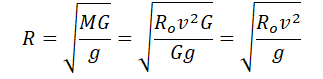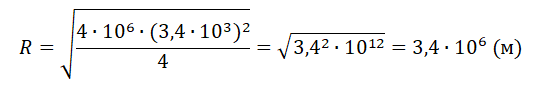Характер и особенности расчета силы притяжения известны еще с древних времен. На основании имеющихся знаний, переданных современному научному сообществу великими исследователями, человек познает не только его окружающий мир, но и Вселенную.
Формула силы притяжения
Со времен Древней Греции философов интересовали явления притяжения тел к земле и свободного падения. К примеру, по утверждениям Аристотеля, из двух камней, брошенных с одинаковой высоты, быстрее достигнет земной поверхности тот, чья масса больше. В IV веке до нашей эры единственными методами научных изысканий служили наблюдения и анализ. К проверке гипотез опытным путем великие мыслители не прибегали. По истечению столетий физик из Италии Галилео Галилей проверил утверждения Аристотеля, используя практические методы исследований.
Итоги проведенных Галилеем опытов были опубликованы в «Беседах и математических доказательствах, касающихся двух новых наук». Ученый использовал псевдоним Сагредо: «пушечное ядро не опередит мушкетной пули при падении с высоты двухсот локтей». Формулировка закона всемирного тяготения была представлена в 1666 году Исааком Ньютоном. В ней фиксировались основные тезисы теоремы Галилея.
Смысл заключался в том, что тела, которые обладают разными массами, падают на землю с одинаковыми ускорениями. Одно тело притягивает другое и, наоборот, с силой, которая прямо пропорциональна их массам и обратно пропорциональна отрезку пути между ними. Согласно определению гравитации от Ньютона, тела, характеризующиеся массой, обладают свойством, благодаря которому притягиваются друг к другу.
Понятие и определение
Силы взаимного притяжения – это силы, которые притягивают любые тела, обладающие массами.
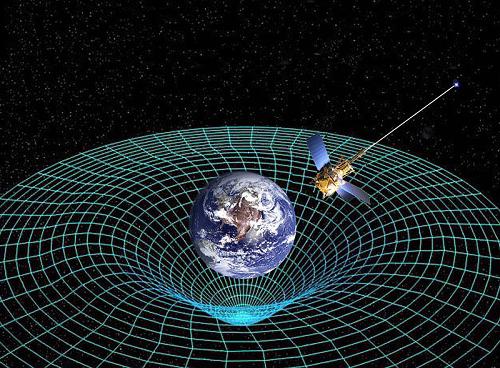
Корректность выводов Ньютона неоднократно подтверждалась путем практических испытаний. Но в начале ХХ века перед учеными-физиками остро стоял вопрос о природе и характере взаимодействия крупных астрономических тел, включая разные виды планетарных систем и галактик в вакууме. Ньютоновского закона уже было недостаточно, чтобы решить эти задачи. Исключить недочеты позволила новая теория, разработанная Альбертом Эйнштейном в начале ХХ столетия. Общая теория относительности объясняет гравитацию не в качестве силы, а представляет ее в виде искривления пространства и времени в четырех измерениях, которое зависит от массы тел, создающих его.
Гравитация представляет собой свойство тел, которые характеризуются массой, притягивать друг друга. Данное физическое явление можно объяснить, как поле, оказывающее дистанционное воздействие на предметы, не связанные между собой никаким другим способом.
Достижение Эйнштейна не противоречит теоретическому объяснению гравитации от Ньютона. Общая теория относительности рассматривает закон всемирного тяготения, как частный случай, применимый для сравнительно небольших расстояний. Данная закономерность в настоящее время также активно используется для поиска решений задач на практике.
Единицы измерения силы притяжения
В разных системах измерений можно встретить несколько отличающиеся обозначения. Единицы измерения силы притяжения следующие:
- система СИ: ([F]=H);
- система СГС: ([F]=дин).
Формула силы притяжения между телами в космосе
Закономерность гравитации, которую обнаружил Ньютон, можно представить в виде математической формулы. Вычисления выглядят следующим образом:
(F=(Gtimes m1times m2times r)/2),
где (m1,m2) – массы объектов, которые притягиваются друг к другу под действием силы (F),
(r) – расстояние, на которое удалены тела,
(G) – т.н. гравитационная постоянная величина, константа, равная 6,67.
Гравитационное взаимодействие объектов будет слабеть, если тела удаляются друг относительно друга. Сила гравитации пропорциональна величине расстояния в квадрате. При этом для нахождения искомой величины расстояние измеряется от центров тяжести тел, а не от поверхностей.
Гравитация в определенных моментах напоминает другие физические явления. Исходя из зависимости интенсивности силы от расстояния в квадрате, гравитацию можно сравнить с электромагнитным взаимодействием сильного и слабого характера.
Формула силы гравитационного притяжения между двумя телами
Квадратичная связь силы, с которой тела притягиваются друг к другу, с расстоянием между ними объясняет тот факт, что люди, находящиеся на поверхности планеты Земля не притягиваются к Солнцу, хотя масса его велика и превышает земную в миллион раз. Земля и центр Солнечной системы удалены примерно на 150 миллионов километров. Дистанция достаточно велика, чтобы ощущаться человеком. Однако эту силу можно зарегистрировать, используя высокоточные приборы. В рамках планеты Земля сила, с которой тела к ней притягиваются, то есть их вес, измеряется следующим образом:
(P=mtimes g),
где (m) – масса тела, на которое воздействует сила притяжение,
(g) – ускорение свободного падения около Земли (если рассматривать систему в условиях любой другой планеты, данная величина будет отличаться).
На разных географических широтах величина ускорения свободного падения может незначительно отличаться. Производя расчеты, данный показатель принимается за 9,81 метров в секунду в квадрате.
В физике понятия массы и веса тел отличаются. Весом называется сила, определяющее притяжение объекта к планете. Масса представляет собой меру инертности вещества. На нее не влияют другие тела, расположенные рядом.
Формула для силы притяжения тел произвольной формы
Расчеты определяются некоторыми условиями. К ним относятся характеристики исследуемых объектов.
Если сила притяжения измеряется между телами, которые обладают произвольной формой, их считают материальными точками:
(dtimes m1=rho1times dV1)
(dtimes m2=rho2times dV2)
где (rho1, rho2) – обозначают плотность веществ материальных точек, характерных для первого и второго объектов,
(dV1 ,dV2) – элементарные объемы выделенных материальных точек.
Исходя из этого, сила притяжения (doverline F), с которой взаимодействуют объекты, равна:
(doverline F=-Gtimes frac{rho _{1}timesrho _{2}times dtimes V_{1}times dtimes V_{2}}{r_{12}^{3}} bar{r_{12}})
Таким образом, сила притяжения первого тела вторым рассчитывается следующим образом:
(bar{F}_{12}=-Gtimesint_{V_{1}}^{rho _{1}times dtimes V_{1}}int_{V_{2}}^{frac{rho _{2}}{r_{12}^{3}}times bar{r}_{12}times dtimes V_{2}})
где интегрирование выполняется по всему объему первого ((V1)) и второго ((V2)) тел. Если тела обладают однородностью, то формула корректируется, таким образом:
(bar{F}_{12}=-Gtimesrho1timesrho2timesint_{V_{1}}^{dtimes V_{1}}int_{V_{2}}^{frac{bar{r}_{12}}{r_{12}^{3}}times dtimes V_{2}})
Формула для силы притяжения твердых тел шарообразной формы
В условиях, когда сила притяжения измеряется между телами, представленных в форме шара или близкой к нему, с плотностью, зависящей лишь от удаленности их центров тяжести, применяется следующая формула:
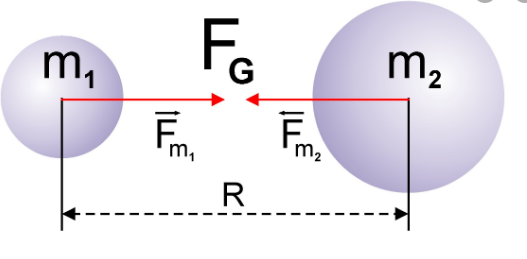
(bar{F}_{12}=-Gtimes(m1times m2)/R^3times R12)
где (m1,m2) – массы шаров, (R )– радиус – вектор, соединяющий центры шаров.
Пример применения формулы для расчета
Задача. Необходимо рассчитать силу притяжения между двумя идентичными однородными шарами, масса которых составляет по 1 килограмму. При этом их центры тяжести удалены на 1 метр друг от друга.
Решение будет выглядеть следующим образом:
Используя формулу для подсчета силы притяжения между двумя объектами шарообразной формы, получается:
(F_g=6.67times 10^{-11}times frac{1times 1}{1^{2}})
Ответ: (F_g=6.67times 10^{-11})
Выполнить расчет силы притяжения достаточно просто, если правильно выбрать формулу, подходящую под конкретные условия, в которых находятся тела. Если в процессе решения задач по физике или другим дисциплинам возникают проблемы, всегда можно обратиться за помощью к компетентным специалистам портала Феникс.Хелп.
Все тела вокруг нас притягиваются друг к другу, причем мы можем рассчитать силу, с которой это происходит. В общем-то, это и есть закон всемерного тяготения.
На этом можно было бы остановиться в его изучении, но таких знаний маловато. Особенно, когда речь идёт об одном из фундаментальных законов физики, который пронизывает нашу жизнь. Это только в школе кажется, что всё это бесполезная и очевидная информация.
Но почему существует гравитация, которая удерживает нас на планете – это работает закон всемирного тяготения. Планета притягивает нас, а мы, как бы это не было странно, притягиваем планету. Почему предметы не рассыпаются в руках, а материал может существовать в нашем пространстве? Потому что тоже работает закон тяготения. Частички в структуре любого материала притягиваются друг к другу. Атомы притягиваются к атомам. Всё это всемирное тяготение.
Всё в мире так или иначе притягивается, а наша вселенная такая, какая она есть благодаря существованию притяжения. Читающий эту статью человек притягивает свой телефон или компьютер, а компьютер притягивает этого человека. Вопрос только в силе, с которой это происходит. Если сила приличная, как сила притяжения нашего тела к земле, то мы её ощущаем и должны преодолевать. Если сила незначительная, то мы её даже не замечаем и эта сила не может превысить силу трения (или другие силы), чтобы притянуть материальный предмет. Очень важно тут осознать именно всеобъемлющую природу гравитационных взаимодействий.
Как был открыт закон всемирного тяготения
Непросвещённый читатель сейчас может сказать, что мол а чего там открывать-то. Бросили что-то на пол и оно упало, вот вам и открытие. Но мало кто понимает истинную сущность и глубину проблемы. Ещё и этот исторически фальсифицированный случай с Ньютоном и яблоком делает из закона не фундаментальный закон физики, а бред мужика в парике, которого подбило яблоком.
Яблоко и правда сыграло свою роль. Но не фундаментальную. Сэр Исаак Ньютон прогуливался в саду родителей и обратил внимание на луну, которая находилась в небе. До этого более 20 лет Ньютон размышлял о природе взаимодействия небесных тел. Одновременно с этим он заметил яблоко, которое падает на землю. Всё это сложилось у него в голове в единую картину и длительная работа получила логическое завершение. Он смог сформулировать закон тяготения в известной нам форме.
До этого момента уже существовали множества догадок о наличии факта притяжения тел. Ньютон сделал свои умозаключения, опираясь на законы Кеплера и поставил логическую точку. Все эти гипотезы строились далеко не на том, что бутерброд упал на пол, а исходили из характера движения планет. Наблюдая за орбитами и особенностями перемещения небесных тел, можно было сделать вывод, что не только яблоко падает на землю, но и все планеты связаны этой единой силой и везде есть гравитация.
Ньютон осмыслил все имеющиеся наработки великих ученых и предложил математическую запись закона. Причем, характерно, что изначально запись эта не содержала гравитационную постоянную.
Формулировка закона всемирного тяготения
В общем-то, мы уже сформулировали этот закон выше 🙂 Все тела притягиваются друг к другу. Но благодаря работам Ньютона мы смогли сказать с какой силой. Поэтому, учебники формулируют закон так:
Сила гравитационного притяжения между двумя материальными точками с массами m1 и m2, расстояние между которыми r, действует вдоль соединяющей их прямой, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния.
То есть:
Где G = 6,67430(15)·10−11 м³/(кг·с²) – гравитационная постоянная. Как мы уже отметили выше, сам Ньютон не закладывал её в формулировку закона, однако последующие опыты показали, что без неё расчёт выходит неверным. Ньютон лишь предполагал, что такой коэффициент есть. Гравитационная постоянная была определена значительно позже, причем методики до сих пор вызывают ряд нареканий в научном сообществе.
Гравитационная постоянная определялась на крутильных весах и логика исходила из того, что мы можем измерить на точном приборе силу взаимодействия между двумя шарами, а потом можем рассчитать её теоретически. Разделив одно на другое, получим недостающий коэффициент. Кстати, изначально то пытались так измерить ускорение свободного падения.
Обычно на канале мы разбираем закон буквально до винтиков. Но тут кажется всё просто. Смотрим на формулу закона и всё понятно.
Разве что, важно отметить – любое тело принимается за материальную точку. Планета тут тоже будет являться материальной точкой 🙂
Если же тело сложной формы, то оно разбивается на фрагменты и каждый из фрагментов считается материальной точкой. Ну а сама точка отсчёта, от которой высчитывается расстояние между телами, ставится в центре объекта.
Так, для того, чтобы рассчитать силу притяжения шарика к земле, нам нужно взять радиус земли и прибавить к нему радиус шарика. Это значение подставим в формулу.
Точность этого закона не вызывает сомнений. Все силы были измерены в том числе и на современном оборудовании. В 2015 году был проведен ряд интересных экспериментов, который подтвердил правильность существования закона тяготения.
Почему тяготение существует
Вот мы и добрались до самого интересного. Начнем с того, что никто из физиков до конца не знает, почему одни тела притягивают другие. Причина ищется в так называемом гравитационном взаимодействии. Это слабое взаимодействие.
Именно существование гравитационного взаимодействия приводит к тяготению, а сама сила этого взаимодействия – это одна из фундаментальных сил в физике. Про гравитацию у нас был большой выпуск и все подробности там расписаны.
Гравитация формирует гравитационное поле. Это гравитационное поле имеет не совсем-таки понятную структуру и не до конца ясно, из чего оно состоит. Логично рассматривать сегодня эту силу как свойство тел в нашей природе.
Современные теории опираются на размышления Эйнштейна, по представлениям которого все тела перемещаются в пространстве и из-за этого перемещения искажают пространство. Чем более массивное тело искажает пространство, тем больше воронка от его движения. Другие тела проваливаются в эту воронку, а мы ощущаем и наблюдаем это как существование гравитационного поля.
Кроме того, некоторые ученые предполагают, что электрическое поле имеет схожую природу с гравитационным полем. Ведь притяжение двух зарядов по закону Кулона высчитывается в итоге также, как и притяжение двух тел. Только роль массы играет величина заряда.
Как использовать закон всемирного тяготения
Мы уже поняли, что закон всемирного тяготения всеобъемлющий. Но обозначим пару значимых примеров, которые позволят ощутить всю глубину этой фразы:
- Ускорение свободного падения, которое мы используем при решении большинства задач физики высчитывается из закона всемирного тяготения. Из него же следует, что для разных планет с разной массой это разные цифры.
- Закон всемирного тяготения позволяет объяснить, почему притяжение на луне имеет меньшие значения, чем на земле. Луна весит меньше вот вам и ответ, подставим в формулу в начале статьи и поймем.
- Закон всемирного тяготения способен объяснить, почему атомы и молекулы притягиваются друг к другу, что в итоге приводит к образованию связей. Это важно для материаловедов. Ну а не слипаются частицы, потому что встречаются уже с силой отталкивания между электронами. Кстати, не путайте гравитационное взаимодействие и внутриатомное взаимодействие. Последнее в много раз превышает гравитацию.
Ну и да, самый интересный пример тут – наше притяжение друг к другу даже на физическом уровне 🙂 Подробнее обо всём этом я написал в своей книге.
Полезная книга от меня по основам физики (механики)
————
Обязательно оцените статью лайком, напишите комментарий и подпишитесь на проект! Это очень важно для развития канала.
————-
Советую также прочитать на нашем канале:
—–
Смотрите нас на YouTube и присоединяйтесь к телеге!
Как найти силу притяжения. Практическое применение ускорения свободного падения. Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Сила тяжести направлена к центру
Гравитационные силы являются одним из четырех основных видов сил, которые проявляются во всем своем многообразии между различными телами как на Земле, так и за ее пределами. Кроме них еще выделяют электромагнитные, слабые и ядерные (сильные). Вероятно, именно их существование человечество осознало в первую очередь. О со стороны Земли было известно еще с самых древних времен. Однако прошли целые столетия, прежде чем человек догадался, что взаимодействие подобного рода происходит не только между Землей и любым телом, но и между разными объектами. Первым, кто понял, как работают был английский физик И. Ньютон. Именно он и вывел всем известный сейчас
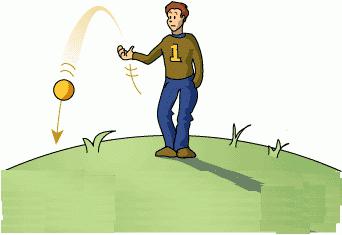
Стреляйте по правильной скорости – скорость все еще очень быстрая – и горизонтальная скорость ее будет такой быстрой, что каждый раз, когда мяч падает к Земле, он также продвинется вперед, достаточно далеко, чтобы поверхность Земли поклонилась в том же сумма.
Именно это происходит с Луной. Когда эта скалистая часть, которая вращается вокруг Земли, возникла, она накопила достаточно энергии, чтобы двигаться в боковом движении через пространство, не падая на Землю, хотя она постоянно падает. Это то, что мы имеем в виду сегодня на орбите, – и Закон гравитации Ньютона позволяет ученым понять, какая боковая энергия необходима для перемещения спутника в этом вращении, вместо того, чтобы возвращаться на Землю.
Формула гравитационной силы
Ньютон решил проанализировать законы, по которым происходит движение планет в системе. В результате он пришел к выводу, что вращение небесных тел вокруг Солнца возможно лишь в том случае, если между ним и самими планетами действуют гравитационные силы. Понимая, что небесные тела от других предметов отличаются всего лишь своими размерами и массой, ученый вывел следующую формулу:
Это может быть удивительно, но одно уравнение дает нашим ученым достаточно информации о спутниках на орбите нашей планеты. Но проанализируйте движение любого из этих спутников, когда они вращаются вокруг Земли, и путь не соответствует предсказанной динамике сил уравнения Ньютона. Но это не потому, что уравнение неверно, потому что каждое тело во вселенной оказывает гравитационную силу на всех остальных. Очевидно, чем больше и ближе они находятся, тем сильнее сила – Ньютон оказывал гораздо меньше сил на яблоко, например, чем Земля, – но это не означает, что каждая проблема может быть решена двумя телами.
F = f x (m 1 x m 2) / r 2 , где:
- m 1 , m 2 – это массы двух тел;
- r – расстояние между ними по прямой;
- f – гравитационная постоянная, значение которой равно 6,668 х 10 -8 см 3 /г х сек 2 .
Таким образом, можно утверждать, что любые два объекта притягиваются друг к другу. Работа гравитационной силы по своей величине прямо пропорциональна массам данных тел и обратно пропорциональна расстоянию между ними, возведенному в квадрат.
Закон Ньютона добавлен к компьютерам
Хорошей новостью является то, что Закон гравитации Ньютона фактически называется Законом о универсальной гравитации Ньютона. Это означает, что вы можете рассчитать все силы, оказываемые различными органами, чтобы выяснить, какие из них действительно важны. Плохая новость заключается в том, что математика, необходимая для вычисления результирующего движения тел на основе этих сил, не является математикой, которая может быть решена на основе.
Гравитация или гравитация – это сила, которая привлекает все объекты друг к другу. Это наиболее легко идентифицируется из четырех основных форм взаимодействия. Ньютон пришел к выводу, что орбита Луны вокруг Земли была обусловлена той же силой, которая заставляет яблоко падать на землю. Это наблюдение побудило его предложить существование силы притяжения между любыми двумя телами, прямо пропорциональными произведению их масс и обратно пропорциональным квадрату расстояния между ними.
Особенности применения формулы
На первый взгляд, кажется, что пользоваться математическим описанием закона притяжения довольно просто. Однако если поразмыслить, данная формула имеет смысл лишь для двух масс, размеры которых по сравнению с расстоянием между ними ничтожно малы. Причем настолько, что их можно принять за две точки. А как же тогда быть, когда расстояние сопоставимо с размерами тел, а сами они имеют неправильную форму? Разделить их на части, определить гравитационные силы между ними и вычислить равнодействующую? Если так, то сколько точек нужно брать для расчета? Как видите, не все так просто.

Развитие теории гравитации было необходимо для вычета законов Кеплера и объяснения приливных явлений и прецессии равноденствий. Благодаря тому, что все эти достижения позволили, открытие Ньютона считается одним из великих достижений науки. Сила тяжести, которая воздействует на объект на поверхности Земли, зависит от места измерения. Это обусловлено главным образом вращением Земли, что вызывает существование центробежной силы, большей на экваторе, где линейная скорость выше и меньше на полюсах, где она будет равна нулю.
Поскольку центробежная сила противостоит силе тяжести, вес одного и того же объекта будет ниже на экваторе. Для выполнения общих расчетов обычно используется среднее значение 9, 8 м с -2. Несколько физиков предложили новые теории гравитации, наиболее известным из которых является случай Эйнштейна с теорией относительности. Хотя он предложил совсем другую теорию по сравнению с теорией Ньютона, он предсказывает очень похожие результаты в системах, в которых гравитационное поле является слабым и скорость намного ниже, чем у света.
- Если тело представляет собой шар (сферу), плотность которого однородна, то оно притягивает к себе любой другой объект так, словно вся его масса сосредоточена в его центре. Поэтому с некоторой погрешностью можно применять этот вывод и для планет.
- Когда для плотности предмета характерна центральная сферическая симметрия, он взаимодействует с другими объектами так, как будто в точке симметрии находится вся его масса. Таким образом, если взять пустотелый шар (например, или несколько вложенных друг в друга шаров (как куклы-матрешки), то они будут притягивать другие тела подобно тому, как это делала бы материальная точка, имеющая их общую массу и расположенная в центре.
На вопрос «Что такое сила?» физика отвечает так: «Сила есть мера взаимодействия вещественных тел между собой или между телами и другими материальными объектами – физическими полями». Все силы в природе могут быть отнесены к четырем фундаментальным видам взаимодействий: сильному, слабому, электромагнитному и гравитационному. Наша статья рассказывает о том, что представляют собой гравитационные силы – мера последнего и, пожалуй, наиболее широко распространенного в природе вида этих взаимодействий.
Теория Эйнштейна позволила нам предсказать, однако, некоторые астрономические явления, такие как кривизна световых лучей под действием солнечного гравитационного поля и изменение частоты электромагнитных волн, подвергнутых сильному гравитационному полю, которое теория Ньютона не которые были позже подтверждены. Почему мы даже изучаем гравитацию? Ну, в основном, чтобы понять законы Кеплера о планетарных орбитах и понять и использовать гравитационную потенциальную энергию.
Очень недавно Николай Коперник опубликовал, что Солнце является центром вселенной, а не Земли. Кроме того, он сказал, что все планеты вращаются вокруг этого Солнца по круговым орбитам. И входит Кеплер, один из первых защитников Коперника. Кеплер работал годами и обнаружил, что орбиты не были кругами, а эллипсами. Тем не менее он также обнаружил, что скорость планеты не постоянна, варьируя в зависимости от ее движения вдоль эллипса.
Начнем с притяжения земли
Всем живущим известно, что существует сила, которая притягивает объекты к земле. Она обычно именуется гравитацией, силой тяжести или земным притяжением. Благодаря ее наличию у человека возникли понятия «верх» и «низ», определяющие направление движения или расположения чего-либо относительно земной поверхности. Так в частном случае, на поверхности земли или вблизи нее, проявляют себя гравитационные силы, которые притягивают объекты, обладающие массой, друг к другу, проявляя свое действие на любых как самых малых, так и очень больших, даже по космическим меркам, расстояниях.
Поясним законы Кеплера, основанные на нашей контекстуализации. Ньютон предложил, чтобы все объекты Вселенной привлекали любые другие объекты с силой, которая. Наоборот пропорционально квадрату расстояния между объектами; Прямо пропорционально произведению масс двух объектов. Мы говорим о гравитационной силе.
Но почему мы не чувствуем эту силу? Гравитационная сила между человеком и телом, даже учитывая небольшое расстояние, очень мала, мы не можем это почувствовать. Сначала мы переходим к некоторым определениям: масса, рассматриваемая в вопросах гравитации, является деноминированной гравитационной массой, а масса, рассматриваемая в вопросах второго закона Ньютона, является инерционной массой.
Сила тяжести и третий закон Ньютона
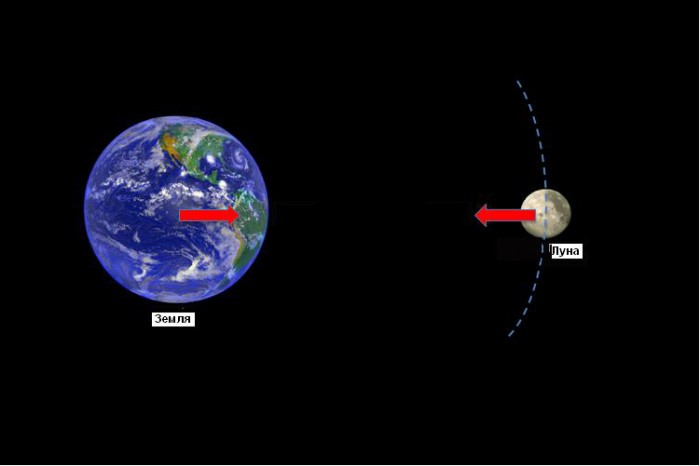
Как известно, любая сила, если она рассматривается как мера взаимодействия физических тел, всегда приложена к какому-нибудь из них. Так и в гравитационном взаимодействии тел друг с другом, каждое из них испытывает такие виды гравитационных сил, которые вызваны влиянием каждого из них. Если тел всего два (предполагается, что действием всех других можно пренебречь), то каждое из них по третьему закону Ньютона будет притягивать другое тело с одинаковой силой. Так Луна и Земля притягивают друг друга, следствием чего являются приливы и отливы земных морей.
Теория гравитации Ньютона
Согласно Ньютону, инерционная масса его второго закона та же самая масса, которая управляет силой гравитационного притяжения между двумя объектами. Вот принцип эквивалентности. Давай, теория – это не просто формула гравитационной силы. Давайте не будем делать эту несправедливость с нашим другом Ньютоном! Можно сказать, что такая теория состоит из.
Конкретный закон силы тяготения; Принцип эквивалентности; Признание того, что три закона движения Ньютона универсальны. Все, что мы узнаем о силах, движении и энергии, имеет отношение к динамике спутников, планет и галактик. Тяговое усилие тела на поверхности планеты Рай.
Каждая планета в Солнечной системе испытывает сразу несколько сил притяжения со стороны Солнца и других планет. Конечно, определяет форму и размеры ее орбиты именно сила притяжения Солнца, но и влияние остальных небесных тел астрономы учитывают в своих расчетах траекторий их движения.
Что быстрее упадет на землю с высоты?
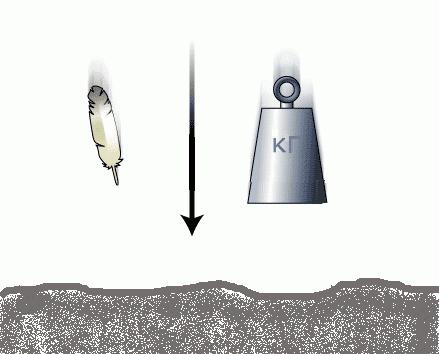
Главной особенностью этой силы является то, что все объекты падают на землю с одной скоростью, независимо от их массы. Когда-то, вплоть до 16-го ст., считалось, что все наоборот – более тяжелые тела должны падать быстрее, чем легкие. Чтобы развеять это заблуждение Галилео Галилею пришлось выполнить свой знаменитый опыт по одновременному сбрасыванию двух пушечных ядер разного веса с наклонной Пизанской башни. Вопреки ожиданиям свидетелей эксперимента оба ядра достигли поверхности одновременно. Сегодня каждый школьник знает, что это произошло благодаря тому, что сила тяжести сообщает любому телу одно и то же ускорение свободного падения g = 9,81 м/с 2 независимо от массы m этого тела, а величина ее по второму закону Ньютона равна F = mg.
Или, используя то, что мы только что узнали. Обобщая, гравитация на поверхности планеты может быть рассчитана на основе ее радиуса и массы. Гравитация – самая слабая из всех фундаментальных сил. Почему все свободные тела тянутся к земле? Как планеты нашей системы вращаются вокруг Солнца? Как мы стоим на поверхности земли? Все это возможно только благодаря силе притяжения, называемой гравитацией.
Гравитационная сила во Вселенной
Когда мы наблюдаем движение небесных тел в пространстве, мы видим, что все они перемещаются по четко определенным орбитам. Это происходит потому, что они подчиняются общим законам, действующим во всей Вселенной. Например, когда мы применяем силу на скале, бросая ее, она неизменно возвращается на поверхность Земли. Эта простая ситуация показывает нам, что Земля оказывает какую-то силу, которая возвращает камень к ней.
Гравитационные силы на Луне и на других планетах имеют разные значения этого ускорения. Однако характер действия силы тяжести на них такой же.
Сила тяжести и вес тела
Если первая сила приложена непосредственно к самому телу, то вторая к его опоре или подвесу. В этой ситуации на тела со стороны опор и подвесов всегда действуют силы упругости. Гравитационные силы, приложенные к тем же телам, действуют им навстречу.
Это тот же тип взаимодействия, который происходит между всеми небесными телами и называется гравитационным взаимодействием. С незапамятных времен человек всегда интересовался движениями небесных тел и возможными последствиями для жизни на Земле. Из наблюдательных данных астронома Тихо Браге Иоганн Кеплер смог обнаружить, что траектории планет вокруг Солнца были эллипсами.
Закон универсальной гравитации Ньютона
Английский ученый отвечал за то, что он показал основы теории гравитации, доказывая наблюдения Кеплера и Тихо Браге. С Законом всеобщей гравитации Исаак Ньютон доказал, что каждая частица материи притягивает другие частицы материи. Закон Универсальной Гравитации Ньютона гласит, что.
Представьте себе груз, подвешенный над землей на пружине. К нему приложены две силы: сила упругости растянутой пружины и сила тяжести. Согласно третьему закону Ньютона груз действует на пружину с силой, равной и противоположной силе упругости. Эта сила и будет его весом. У груза массой 1 кг вес равен Р = 1 кг ∙ 9,81 м/с 2 = 9,81 Н (ньютон).
«Два тела тянуты с силой, пропорциональной их массам и обратно пропорционально квадрату расстояния, разделяющего их центры тяжести». Этот закон представляет следующую формулу. В Законе Универсальной Гравитации есть идея о том, что гравитационная сила между двумя частицами не зависит от присутствия других тел.
Ускорение силы тяжести на поверхности Земли
Гравитация является силой и поэтому может быть описана аналогичным соотношением, являющимся произведением массы т тела ускорением силы тяжести, созданной на ней телом массы М. Согласно Ньютону, масса тел всегда находится в центре центра Земли, и когда гравитационное поле действует на тела, они страдают от изменения скорости, приобретая ускорение.
Гравитационные силы: определение
Первая количественная теория гравитации, основанная на наблюдениях движения планет, была сформулирована Исааком Ньютоном в 1687 году в его знаменитых “Началах натуральной философии”. Он писал, что силы притяжения, которые действуют на Солнце и планеты, зависят от количества вещества, которое они содержат. Онираспространяются на большие расстояния и всегда уменьшаются как величины, обратные квадрату расстояния. Как же можно вычислить эти гравитационные силы? Формула для силы F между двумя объектами с массами m 1 и m 2 , находящимися на расстоянии r, такова:
На все тела на земной поверхности влияет весовая сила, представленная следующим уравнением. Теория Птолемея разумно разрешила астрономические проблемы своего времени. Несколько столетий спустя польский священнослужитель и астроном Николай Коперник, обнаружив неточности в теории Птолемея, сформулировал теорию гелиоцентризма, согласно которой Солнце следует считать центром Вселенной, с Землей, Луной и вращающимися планетами вокруг него. Наконец, немецкий астроном и математик Йоханнес Кеплер, изучив планету Марс около тридцати лет, обнаружил, что ее орбита эллиптична.
- F=Gm 1 m 2 /r 2 ,
где G — константа пропорциональности, гравитационная постоянная.
Физический механизм гравитации
Ньютон был не полностью удовлетворен своей теорией, поскольку она предполагала взаимодействие между притягивающимися телами на расстоянии. Сам великий англичанин был уверен, что должен существовать некий физический агент, ответственный за передачу действия одного тела на другое, о чем он вполне ясно высказался в одном из своих писем. Но время, когда было введено понятие гравитационного поля, которое пронизывает все пространство, наступило лишь через четыре столетия. Сегодня, говоря о гравитации, мы можем говорить о взаимодействии любого (космического) тела с гравитационным полем других тел, мерой которого и служат возникающие между каждой парой тел гравитационные силы. Закон всемирного тяготения, сформулированный Ньютоном в вышеприведенной форме, остается верным и подтверждается множеством фактов.
Этот результат был обобщен на другие планеты. Что касается ученых, цитируемых в тексте, то правильно сказать, что. Закон всемирного тяготения, предложенный Ньютоном, был одним из величайших работ, разработанных по взаимодействию между массами, поскольку он способен объяснить из простейшего явления, такого как падение тела вблизи поверхности Земли, до самого сложного, так как силы обменивались между небесными телами, добросовестно переводили их орбиты и разные движения.
Согласно легенде, Ньютон, наблюдая за падением яблока, задумал, что это будет вызвано притяжением земли. Природа этой силы притяжения такая же, как та, которая должна существовать между Землей и Луной или между Солнцем и планетами; поэтому притяжение среди масс, безусловно, является универсальным явлением.
Теория гравитации и астрономия
Она была очень успешно применена к решению задач небесной механики во время XVIII и начале XIX века. К примеру, математики Д. Адамс и У. Леверье, анализируя нарушения орбиты Урана, предположили, что на него действуют гравитационные силы взаимодействия с еще неизвестной планетой. Ими было указано ее предполагаемое положение, и вскоре астрономом И. Галле там был обнаружен Нептун.
Мы также можем провозгласить закон всемирного тяготения следующим образом: два тела гравитационно притягивают друг друга силой, интенсивность которой прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их телами.
Получив данные, Кавендиш подтвердил значение константы всемирного тяготения. Земля, как и все небесные тела, оказывает силу гравитационного притяжения на тела, расположенные в ее близости. Невзирая на вращательные эффекты нашей планеты, мы можем ассимилировать гравитационное поле следующим образом.
Хотя оставалась одна проблема. Леверье в 1845 году рассчитал, что орбита Меркурия прецессирует на 35″” за столетие, в отличие от нулевого значения этой прецессии, получаемого по теории Ньютона. Последующие измерения дали более точное значение 43″”. (Наблюдаемая прецессия равна действительно 570″”/век, но кропотливый расчет, позволяющий вычесть влияние от всех других планет, дает значение 43″”.)
Только в 1915 г. Альберт Эйнштейн смог объяснить это несоответствие в рамках созданной им теории гравитации. Оказалось, что массивное Солнце, как и любое другое массивное тело, искривляет пространство-время в своей окрестности. Эти эффекты вызывают отклонения в орбитах планет, но у Меркурия, как самой малой и ближайшей к нашей звезде планете, они проявляются сильнее всего.
Инерционная и гравитационная массы
Как уже отмечалось выше, Галилей был первым, кто наблюдал, что объекты падают на землю с одинаковой скоростью, независимо от их массы. В формулах Ньютона понятие массы происходит от двух разных уравнений. Второй его закон говорит, что сила F, приложенная к телу с массой m, дает ускорение по уравнению F = ma.
Однако сила тяжести F, приложенная к телу, удовлетворяет формуле F = mg, где g зависит от другого тела, взаимодействующего с рассматриваемым (земли обычно, когда мы говорим о силе тяжести). В обоих уравнений m есть коэффициент пропорциональности, но в первом случае это инерционная масса, а во втором – гравитационная, и нет никакой очевидной причины, что они должны быть одинаковыми для любого физического объекта.
Однако все эксперименты показывают, что это действительно так.
Теория гравитации Эйнштейна
Он взял факт равенства инерционной и гравитационной масс как отправную точку для своей теории. Ему удалось построить уравнения гравитационного поля, знаменитые уравнения Эйнштейна, и с их помощью вычислить правильное значение для прецессии орбиты Меркурия. Они также дают измеренное значение отклонения световых лучей, которые проходят вблизи Солнца, и нет никаких сомнений в том, что из них следуют правильные результаты для макроскопической гравитации. Теория гравитации Эйнштейна, или общая теория относительности (ОТО), как он сам ее назвал, является одним из величайших триумфов современной науки.
Гравитационные силы – это ускорение?
Если вы не можете отличить инерционную массу от гравитационной, то вы не можете отличить и гравитацию от ускорения. Эксперимент в гравитационном поле вместо этого может быть выполнен в ускоренно движущемся лифте в отсутствии гравитации. Когда космонавт в ракете ускоряется, удаляясь от земли, он испытывает силу тяжести, которая в несколько раз больше земной, причем подавляющая ее часть приходит от ускорения.
Если никто не может отличить гравитацию от ускорения, то первую всегда можно воспроизвести путем ускорения. Система, в которой ускорение заменяет силу тяжести, называется инерциальной. Поэтому Луну на околоземной орбите также можно рассматривать как инерциальную систему. Однако эта система будет отличаться от точки к точке, поскольку изменяется гравитационное поле. (В примере с Луной гравитационное поле изменяет направление из одной точки в другую.) Принцип, согласно которому всегда можно найти инерциальную систему в любой точке пространства и времени, в которой физика подчиняется законам в отсутствии гравитации, называется принципом эквивалентности.
Гравитация как проявление геометрических свойств пространства-времени
Тот факт, что гравитационные силы можно рассматривать как ускорения в инерциальных системах координат, которые отличаются от точки к точке, означает, что гравитация – это геометрическое понятие.
Мы говорим, что пространство-время искривляется. Рассмотрим мяч на плоской поверхности. Он будет покоиться или, если нет никакого трения, равномерно двигаться при отсутствии действия каких-либо сил на него. Если поверхность искривляется, мяч ускорится и будет двигаться до самой низкой точки, выбирая кратчайший путь. Аналогичным образом теория Эйнштейна утверждает, что четырехмерное пространство-время искривлено, и тело движется в этом искривленном пространстве по геодезической линии, которой соответствует кратчайший путь. Поэтому гравитационное поле и действующие в нем на физические тела гравитационные силы – это геометрические величины, зависящие от свойств пространства-времени, которые наиболее сильно изменяются вблизи массивных тел.
Сила тяжести — это свойство тел с массой притягиваться друг к другу. Тела, которые имеют массу, всегда притягиваются друг к другу. Притяжения тел с очень большими массами в астрономических масштабах создает значительные силы, благодаря которым мир является таким, каким мы его знаем.
Сила притяжения является причиной земного притяжения, в результате которого предметы падают на нее. Благодаря силе притяжения Луна вращается вокруг Земли, Земля и другие планеты — вокруг Солнца, Солнечная система — вокруг центра Галактики.
В физике сила тяжести — это сила, с которой тело действует на опору или вертикальный подвес. Эта сила направлена всегда вертикально вниз.
Посчитать, с которой сила притяжения планеты действует на тело очень просто. Вот формула:
F=m*g
- F — сила с которой действует тело. Измеряется в ньютонах (Н).
- m — масса (вес) тела. Измеряется в килограммах (кг)
- g — ускорение свободного падения. Измеряется в ньютонах разделенных на килограмм (Н/кг). Ее величина постоянная и в среднем по земной поверхности равна 9,8 Н/кг.
Как определить силу притяжения?
Пример:
Пусть масса чемодана равна 15 кг, тогда чтобы найти силу притяжения чемодана к Земле воспользуемся формулой:
F= m*g = 15*9,8 = 147 Н.
То есть сила притяжения чемодана составляет 147 ньютонов.
Значение g для планеты Земля неодинаково — на экваторе оно составляет 9,83 Н/кг, а на полюсах 9,78 Н/кг. Поэтому и берут среднее значение, которое мы использовали для расчета. Точные значения для различных регионов планеты используют в авиакосмической отрасли, а также на них обращают внимания в спорте, при тренировках спортсменов для участия в соревнованиях в других странах.
Историческая справка: впервые посчитал g и вывел формулу силы тяжести, а если точнее формулу силы с которой тело действует на другие тела, в 1687 году известный английский физик Исаак Ньютон. Именно в его честь и названа единица измерения силы. Существует легенда, что Ньютон начал исследовать вопрос силы тяжести после того, как ему упало на голову яблоко.
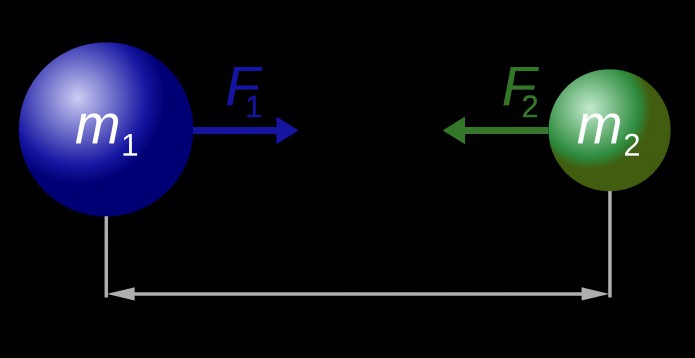
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.
Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
Отсюда:
Формула расчета ускорения свободного падения
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
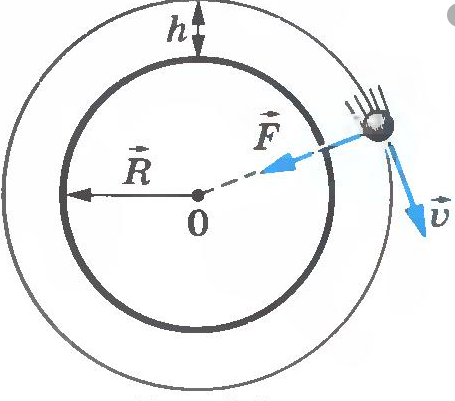
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
Примерим этот закон для первой и второй пары звезд:
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
Приравняем правые части выражений и выразим силу притяжения во втором случае:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
Отсюда радиус равен:
Линейная скорость и радиус орбиты связываются формулой:
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
Отсюда:
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
Из этой формулы выразим массу планеты:
Подставим массу планеты в формулу для нахождения ее радиуса:
Подставляем известные данные и вычисляем:
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 17.8k