Как найти силу притяжения пластин в конденсаторе

Обкладки
конденсатора, заряженные разноимённо,
притягиваются друг к другу.

Механические
силы, действующие на макроскопические
заряженные тела, называют пондеромоторными.

Рассчитаем
пондеромоторные силы, действующие на
обкладки плоского конденсатора. При
этом возможны два варианта:

1. Конденсатор
   заряжен и отключён от заряженной батареи
   ( в этом случае количество зарядов на
   пластинах остаётся постоянным q
   = const).

При
удалении одной обкладки конденсатора
от другой совершается работа

dA=Fdx

за
счёт которой увеличивается потенциальная
энергия системы:

При
этом dA
= dW
. Приравнивая правые части этих выражений,
получаем

(12.67)

В
данном случае при дифференцировании
расстояние между пластинами обозначилось
х.

1. Конденсатор
   заряжен, но не отключён от батареи
   (в этом случае при перемещении одной
   из пластин конденсатора будет сохраняться
   постоянным напряжение (
   U
   =
   const
   ). В этом случае при удалении одной
   пластины от другой потенциальная
   энергия поля конденсатора уменьшается,
   так как происходит «утечка» зарядов с
   пластин, поэтому

Откуда

Но

,
тогда

Полученное
выражение совпадает с формулой
.
Оно может быть представлено и в другом
виде, если вместо зарядаq
ввести поверхностную плотность:

(12.68)

Поле
однородно. Напряжённость поля конденсатора
равна
,
где х – расстояние между пластинами.
Подставив в формулуU²=E²x²,
получим, что сила притяжения пластин
плоского конденсатора

(12.69)

Эти
силы действуют не только на пластины.
Так как пластины, в свою очередь, давят
на диэлектрик, помещённый между ними,
и деформируют его, то в диэлектрике
возникает давление

(S
– площадь каждой пластины).

Давление,
возникающее в диэлектрике, равно

(12.70)

Примеры решения задач

Пример
12. 5. К
пластинам плоского воздушного конденсатора
приложена разность потенциалов 1,5 кВ.
Площадь пластин 150см²
и расстояние между ними 5 мм. После
отключения конденсатора от источника
напряжения в пространство между
пластинами вставили стекло (ε₂=7).Определите:

1)
разность потенциалов между пластинами
после внесения диэлектрика; 2) ёмкость
конденсатора до и после внесения
диэлектрика; 3) поверхностную плотность
заряда на пластинах до и после внесения
диэлектрика.

Дано:
U₁=1,5кВ=1,5∙10³В;
S=150см²=1,5∙10^-2
м²;
ε₁=1;
d=5мм=5∙10^-3
м.

Найти:
1) U₂;
2) С₁
С₂;
3) σ₁,
σ₂

Решение.
Так
как
(σ-
поверхностная плотность зарядов на
обкладках конденсатора), то до внесения
диэлектрика σd=U₁ε₀ε₁
и после внесения диэлектрика σd=U₂ε₀ε₂,
поэтому

Ёмкость
конденсатора до и после внесения
диэлектрика

и

Заряд
пластин после отключения от источника
напряжения не меняется, т.е. q=const.
Поэтому Поверхностная плотность заряда
на пластинах до и после внесения
диэлектрика

Ответ:
1) U₂=214В;
2) С₁=26,5пФ;
С₂=186пФ;
3) σ₁=
σ₂=2.65
мкКл/м².

Пример
12.7. Зазор между обкладками плоского
конденсатора заполнен анизотропным
диэлектриком, проницаемость ε которого
изменяется в перпендикулярном к обкладкам
направлении по линейному законуε =
α + βх от ε₁ до ε₂,
причём ε₂ > ε₁.
Площадь каждой обкладки S,
расстояние между ними d.
Найти ёмкость конденсатора.

Дано:
S;
d;
ε₁;
ε₂

Найти:
С_.

Решение.Диэлектрическая проницаемостьε
изменяется по линейному закону , ε =
α + βх, где х отсчитывается от обкладки,
у которой проницаемость равна ε₁.
Учитывая, что ε (0) = ε₁, ε
(d) = ε₂, получаем
зависимость
.
Найдём разность потенциалов между
обкладками:

Ёмкость конденсатора
будет равна

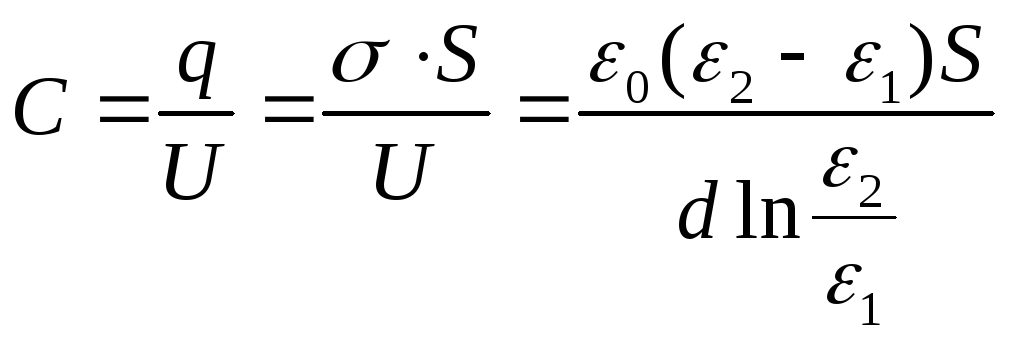
Ответ:

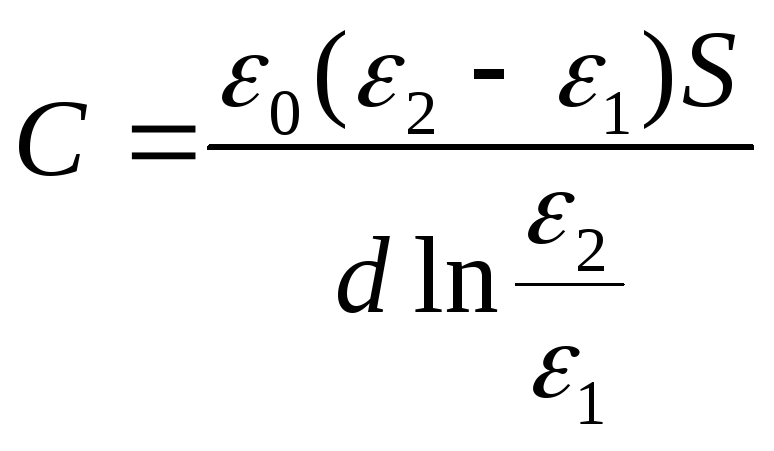
Пример
12.7. Между пластинами плоского конденсатора,
заряженного до разности потенциалов U
, параллельно его обкладкам помещены
два слоя диэлектриков. Толщина слоёв и
диэлектрическая проницаемость
диэлектриков соответственно равны d₁,
d₂,
ε₁, ε₂.
Определите напряжённость электростатических
полей в слоях диэлектриков.

Дано:
U;
d₁,
d₂,
ε₁,
ε₂

Найти:
E₁,
E₂.

Решение.Напряжение на пластинах конденсатора,
учитывая, что поле в пределах каждого
из диэлектрических слоёв однородно,

U=E₁d₁+E₂ d₂.
(1)

Электрическое смещение
в обоих слоях диэлектрика одинаково,
поэтому можем записать

D=D₁=D₂ =
ε₀ ε₁E₁=
ε₀ ε₂E₂
(2)

Из выражения (1) и (2)
найдём искомое

(3)

Из формулы (2) следует,
что

Ответ:;

Пример
12.7. Площадь пластин S
плоского конденсатора равна 100см².
Пространство между пластинами заполнено
вплотную двумя слоями диэлектриков –
слюдяной пластинкой (ε₁=7)
толщиной d₁=3,5
мм и парафина (ε₂=2)
толщиной d₂=5
мм. Определите ёмкость этого конденсатора..

Дано:
S=100см²=10^-2м²;
ε₁=7;
d₁=3,5мм=3.5∙10^-3м;,
ε₁=2;
d₁=3,5мм=5∙10^-3м;

Найти:
С.

Решение.Ёмкость
конденсатора

где
= – заряд на пластинах конденсатора ( –
поверхностная плотность заряда на
пластинах); =- разность потенциалов
пластин, равная сумме напряжений на
слоях диэлектрика: U=U₁+U₂.
Тогда

(1)

Напряжения
U₁
и
U₂
найдём по формулам

;

(2)

где
Е₁
и
Е₂
– напряжённость электростатического
поля в первом и втором слоях диэлектрика;
D
– электрическое смещение в диэлектриках
(в обоих случаях одинаково). Приняв во
внимание, что

D
= σ,

И
учитывая формулу (2), из выражения (1)
найдём искомую ёмкость конденсатора

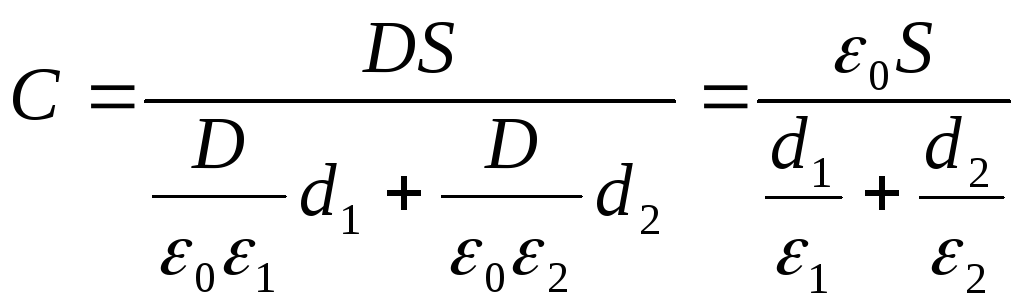
Ответ:
С=29,5пФ.

Пример
12.7. Батарея из трёх последовательно
соединённых конденсаторов С₁=1мкФ;
С₂=2мкФ и С₃=4мкФ
подсоединены к источнику ЭДС. Заряд
батареи конденсаторов
q
=40мкКл. Определите: 1) напряжения U₁,
U₂
и U₃
на каждом конденсаторе; 2) ЭДС источника;
3) ёмкость батареи конденсаторов.

Дано:
С₁=1мкФ=1∙10^-6Ф;
С₂=2мкФ=2∙10^-6Ф
и С₃=4мкФ=4∙10^-6Ф;q=40мкКл=40∙10^-6Ф.

Найти:
1) U₁,
U₂,
U₃
;
2) ξ; 3) С.

Решение.При
последовательном соединении конденсаторов
заряды всех обкладок равны по модулю,
поэтому

q₁=q₂=q₃=q.

Напряжение
на конденсаторах

ЭДС
источника равна сумме напряжений каждого
из последовательно соединённых
конденсаторов:

ξ
=
U₁+
U₂
+U₃

При
последовательном соединении суммируются
величины, обратные ёмкостям каждого из
конденсаторов:

Откуда
искомая ёмкость батареи конденсаторов

Ответ:
1) U₁=
40В; U₂=
20В, U₃
=
10В;
2) Ɛ=
70В;
3) С=
0,571мкФ.

Пример
12.7. Два плоских воздушных конденсатора
одинаковой ёмкости соединены
последовательно и подключены к источнику
ЭДС. Как и во сколько раз изменится заряд
конденсаторов, если один из них погрузить
в масло с диэлектрической проницаемостью
ε=2,2 .

Дано:
С₁=С₂=
С;q=40мкКл=40∙10^-6Ф;
ε₁=1;
ε₂=2,2.

Найти:

.

Решение.
При
последовательном соединении конденсаторов
заряды обоих конденсаторов равны по
модулю. До погружения в диэлектрик (в
масло) заряд каждого конденсатора

где
ξ =
U₁+
U₂
(при последовательном соединении
конденсаторов ЭДС источника равна сумме
напряжений каждого из конденсаторов).

После
погружения одного из конденсаторов в
диэлектрик заряды конденсаторов опять
одинаковы и соответственно на первом
и втором конденсаторах равны

q=
CU₁=ε₂CU₂

(учли,
что ε₁=1),
откуда, если учесть, что ξ
=
U₁+
U₂,
найдём

(2)

Поделив
(2) на (1), найдём искомое отношение

Ответ:

,
т.е. заряд конденсаторов возрастает в
1,37 раз.

Пример
12.7. Конденсаторы ёмкостями С каждый
соединены так, как указано на рис.а.
определите ёмкость С_общ
этого соединения конденсаторов. .

Решение.
Если
отключить от цепи конденсатор С₄,
то получится соединение конденсаторов,
которое легко рассчитывается. Поскольку
ёмкости всех конденсаторов одинаковы
(С₂=С₃
и С₅=С₆),
обе параллельные ветви симметричны,
поэтому потенциалы точек А и В, одинаково
расположенные в ветвях, должны быть
равны. Конденсатор С₄
подключен, таким образом, к точкам с
нулевой разностью потенциалов.
Следовательно, конденсатор С₄
не заряжен, т.е. его можно исключить и
схему, представленную в условии задачи,
упростить (рис.б).

Эта
схема- из трёх параллельных ветвей, две
из которых содержат по два последовательно
включённых конденсаторов

Ответ:
С_общ=2С.

Пример
12.7. Плоский воздушный конденсатор
ёмкостью С₁=4пФ заряжен до
разности потенциалов U₁=100В.
После отключения конденсатора от
источника напряжения расстояние между
обкладками конденсатора увеличили в
два раза. Определите: 1) разность
потенциалов U₂
на обкладках конденсатора после
их раздвижения; 2) работу внешних сил по
раздвижению пластин.

Дано:
С₁=4пФ=4∙10^-12Ф;
U₁=100В;d₂
=2d₁.

Найти:
1)
U₂;2)A.

Решение.
Заряд
обкладок конденсатора после отключения
от источника напряжения не меняется,
т.е. Q=const.
Поэтому

С₁U₁=
С₂U₂,
(1)

где
С₂
и U₂

– соответственно ёмкость и разность
потенциалов на обкладках конденсатора
после их раздвижения.

Учитывая,
что ёмкость плоского конденсатора ,
из формулы (1) получим искомую разность
потенциалов

(2)

После
отключения конденсатора от источника
напряжения систему двух заряженных
обкладок можно рассматривать как
замкнутую, для которой выполняется
закон сохранения энергии: работа А
внешних сил равна изменению энергии
системы

А=
W₂
–
W₁

(3)

где
W₁
и
W₂
– соответственно энергия поля конденсатора
в начальном и конечном состояниях.

Учитывая,
что
и(q
– const),
из формулы (3) получим искомую работу
внешних сил

А=W₂–

[учли,
что q=C₁U₁
и
формулу (2)].

Ответ:
1) U₂=200В;2)A=40нДж.

Пример
12.7. Сплошной шар из диэлектрика
радиусом R=5см
заряжен равномерно с объёмной плотностью
ρ=5нКл/м³. Определите энергию
электростатического поля, заключённую
в окружающем шар пространстве.

Дано:
R=5см=5∙10^-2м;
ρ=5нКл/м³=5∙10^-9
Кл/м³.

Найти:
W.

Решение.
Поле
заряженного шара сферически симметрично,
поэтому объёмная плотность заряда
одинакова во всех точках, расположенных
на равных расстояниях от центра шара.

Энергия
в элементарном сферическом слое (он
выбран за пределами диэлектрика, где
следует определить энергию) объёмомdV
(см. рисунок)

dW=ωdV,
(1)

где
dV=4πr²dr
(r
– радиус элементарного сферического
слоя; dr
– его толщина);
(ε=1
– поле в вакууме; Е – напряженность
электростатического поля).

Напряжённость
Е найдём по теореме Гаусса для поля в
вакууме, причём в качестве замкнутой
поверхности мысленно выберем сферу
радиусом r
(см. рисунок). В данном случае внутрь
поверхности попадает весь заряд шара,
создающий рассматриваемое поле, и, по
теореме Гаусса,

Откуда

Подставив
найденные выражения в формулу (1), получим

Энергия,
заключённая в окружающем шар пространстве,

Ответ:
W=6,16∙10^-13Дж.

Пример
12.7. Плоскому конденсатору с
площадью обкладок S
и расстоянием между ними ℓ сообщён
заряд q , после
чего конденсатор отключён от источника
напряжения. Определите силу притяжения
F между обкладками
конденсатора, если диэлектрическая
проницаемость среды между обкладками
равна ε.

Дано:
S;
ℓ;
q;
ε.

Найти:
F.

Решение.
Заряд
обкладок конденсатора после отключения
от источника напряжения не меняется,
т.е. q=const.
Предположим, что под действием силы
притяжения F
расстояние между обкладками конденсатора
изменилось на d
ℓ.
Тогда сила F
совершает
работу

dA=Fdℓ
(1)

Согласно
закону сохранения энергии, эта работа
равна убыли энергии конденсатора, т.е.

dA=-dW,
(2)

откуда,
исходя из выражений (1) и (2), получим

.
(3)

Подставив
в формулу для энергии заряженного
конденсатора
выражение для ёмкости плоского
конденсатора,
получим

(4)

Подставив
в формулу (3) значение энергии (4) и выполнив
дифференцирование, найдём искомую силу
притяжения между обкладками конденсатора

где
знак «-» указывает на то, что сила F
является силой притяжения.

Ответ:

Пример
12.7. Плоский конденсатор площадью
обкладок S и
расстоянием между ними ℓ подключен к
источнику постоянного напряжения U.
Определите силу притяжения F
между обкладками конденсатора, если
диэлектрическая проницаемость среды
между обкладками равна ε.

Дано:
S;
ℓ;
U;
ε.

Найти:
F.

Решение.
Согласно
условию задачи, на обкладках конденсатора
поддерживается постоянное напряжение,
т.е. U=const.
Предположим, что под действием силы
притяжения F
расстояние между обкладками конденсатора
изменилось на dℓ.
Тогда сила
F
совершает работу

dA=Fdℓ
(1)

Согласно
закону сохранения энергии, эта работа
в данном случае идёт на увеличение
энергии конденсатора (сравните с
предыдущей задачей), т.е.

dA=dW
(2)

откуда,
исходя из выражений (1) и (2), получим

(3)

Подставив
в формулу для энергии конденсатора
выражение
для ёмкости плоского конденсатора,
получим

(4)

Подставив
в формулу (3) значение энергии (4) и выполнив
дифференцирование, найдём искомую силу
притяжения между обкладками конденсатора

.

где
знак «-» указывает на то, что сила F
является силой притяжения.

Ответ:

Для школьников.

Когда говорят фразу “воздушный конденсатор“, то имеют ввиду, что пространство между его обкладками заполнено воздухом, диэлектрическая проницаемость которого принята равной единице.

Если же это пространство заполнить стеклом, с диэлектрической проницаемостью

равной пяти, то стекло уменьшит напряжённость поля в 5 раз, увеличив этим в 5 раз ёмкость конденсатора.

Иначе, в присутствии стекла конденсатор при том же напряжении между обкладками накопит в 5 раз больший заряд и, значит, сможет отдать в электрическую цепь в 5 раз больший заряд при разрядке.

О возможности диэлектрика ослаблять внутри себя электрическое поле см. Занятие 51.

Задача.

Пояснение.

Вывод формулы для нахождения напряжённости электрического поля, создаваемого заряженной плоскостью (в нашем случае электрическое поле создаётся одной обкладкой конденсатора в месте нахождения второй обкладки) дан в Занятии 48.

Учтём, что заряд обкладки поделённый на её площадь даёт плотность заряда на обкладке.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Действие рентгеновских лучей, направленных на одну обкладку незаряженного плоского конденсатора.

Следующая запись: Какую работу надо совершить, чтобы раздвинуть обкладки плоского заряженного конденсатора на некоторое расстояние?

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия (статьи), начиная с электростатики, даны в Занятии 45 (в конце занятия).

Рассчитать силу притяжения двух электрически заряженных пластин конденсатора, имея из параметров только площадь или емкость и напряжение на пластинах?

На  заряженное тело, помещенное в
электрическое поле, действует пондеромоторная
сила. Пондеромоторными называются
силы, действующие со стороны электрического
поля на макроскопические заряженные
тела.

Определим силу
взаимного притяжения между разноименно
заряженными пластинами плоского
конденсатора (пондеромоторную силу)
двумя способами.

Эту силу можно определить,
как силу F₂
, действующую на вторую пластину со
стороны первой

где Q₂
– величина заряда на второй пластине,
E₁–
напряженность поля первой пластины.

где σ₁
– поверхностная плотность заряда на
первой пластине.

$frac{F}{S}=frac{varepsilon_0varepsilon E^2}{2}$.              (5)

Работа
по изменению расстояния между пластинами
заряженного конденсатора на величину
dx определяется
формулой

где F
– сила взаимодействия между обкладками
(пондеромоторная сила).

 Сила,
действующая на единицу площади пластины

Конденсаторы: сила притяжения пластин, напряжения, эквивалентные емкости.

В этой статье рассматриваются задачи на определение напряжения на конденсаторе и в схеме с конденсаторами, между точками этих схем. Также мы рассмотрим задачи, связанные с силой притяжения пластин. В конце будет рассмотрен сложный (для запоминания) перерасчет звезды из конденсаторов в треугольник.

Задача 1. В плоский конденсатор, подключенный к источнику с постоянной ЭДС, помещена плоская пластина, имеющая заряд . Расстояние от пластины до обкладок и . Площадь пластины . Определите силу, действующую на пластину со стороны электрического поля.

Запишем силу как произведение заряда пластины на напряженность поля:

Обозначим потенциал пластины , примем потенциал левой пластины конденсатора равным нулю, а правой – .

Составим систему уравнений. Запишем разности потенциалов между левой обкладкой и пластиной и между правой и пластиной, учтем наложение поля конденсатора на поле, создаваемое пластиной:

Сложим уравнения:

Откуда

Тогда сила равна

Задача 2.

  Когда к батарее, изображенной на рисунке, подвели напряжение , заряд среднего конденсатора оказался равным нулю. Какова емкость Сх?

Так как заряд равен нулю, то . Следовательно, потенциалы точек и – равны. А это означает, что разности потенциалов и . Также известно, что при последовательном соединении заряд на всех конденсаторах одинаков, поэтому

Тогда отношение напряжений равно отношению емкостей:

И во второй ветви будет соблюдаться то же отношение:

Откуда .

Задача 3.

  В цепи известны емкости и ЭДС . Кроме того, известно, что заряд первого конденсатора равен . Найдите ЭДС второго элемента.

Зная заряд первого конденсатора и его емкость, найдем напряжение между точками и :

Напряжение это мы еще можем записать для каждой ветви так:

Или:

Так как обкладки конденсаторов соединены в точке , то алгебраическая сумма зарядов на этих обкладках равна нулю:

Домножим на емкость и разделим на :

Тогда

Определяем ЭДС:

Ответ:

Задача 4.

Найдите разность потенциалов между точками и .

Запишем напряжение между точками и с двух сторон, и в прямом, и в переносном смысле:

Напряжение на параллельно включенных конденсаторах и равно:

Так как конденсаторы соединены в одной точке – точке , то алгебраическая сумма зарядов на этих обкладках равна 0:

Напряжение на тогда

Напряжение на :

Тогда заряд равен:

Тогда

Подставим найденный заряд:

Ответ:

Задача 5.

Найдите разность потенциалов между точками и в этой цепи.

Запишем напряжение между точками и :

Для точки :

Где – напряжение на .

Отсюда получим, что

Для точки :

Где – напряжение на .

Отсюда получим, что

Тогда для получим:

Ответ:

Задача 6.

Найдите разность потенциалов между точками и в этой цепи.

Запишем уравнение Кирхгофа (по 2-му закону) для обоих контуров (справа и слева):

Вычтем из первого второе:

Так как конденсаторы соединены последовательно, то заряды на них равны:

Тогда :

Или:

Подставим (2) в (1):

Подставим (3) в (1):

Наконец,

Можно было также воспользоваться (4) и найти .

Ответ:

Задача 7.

Найдите силу притяжения между пластинами плоского конденсатора в схеме, изображенной на рисунке, если , , , ,  а расстояние между пластинами конденсатора равно .

Конденсаторы в схеме, по сути, соединены последовательно, поэтому их заряды одинаковы. Напряжение на первом тогда

А на втором

Сумма напряжений в контуре по второму закону равна сумме ЭДС:

Сила притяжения пластин будет равна:

Ответ:

Задача 8.

В схеме, изображенной на рисунке, сила притяжения между пластинами плоского конденсатора равна . Найдите расстояние между пластинами этого конденсатора, если ,, , .

Напряжение на первом конденсаторе тогда

А на втором

Сумма напряжений в контуре по второму закону равна сумме ЭДС:

Сила притяжения пластин будет равна:

Откуда

Ответ:

Задача 9.

Найдите емкость батареи. Емкость каждого конденсатора равна .

Чтобы было проще решить эту задачу, применим перерасчет (переход) от треугольника емкостей к звезде и обратно. Нам понадобится как раз обратный: от звезды к треугольнику. Выполняются оба перехода так:

Треугольник – звезда:

Звезда – треугольник:

Тогда у нас

Теперь оказывается, что каждый из конденсаторов , и соединен параллельно с . При параллельном соединении, как известно, емкости складываются:

Получим:

Таким образом, емкости и соединены последовательно, и это последовательное соединение – параллельно конденсатору . Тогда

Окончательно, складывая и , получаем:

Ответ:

Решение. Заряд одной пластины конденсатора –q₁, находится в поле действия другой пластины +q₂ (рис).  На первый заряд действует сила которая определяется по формуле:

[ F=qcdot E (1). ]

Где: Е – напряженность поля создаваемое зарядом одной из пластин.

[ E=frac{sigma }{2cdot {{varepsilon }_{0}}}=frac{q}{2cdot {{varepsilon }_{0}}cdot S} (2), ]

где: σ – поверхностная плотность одной из пластин, ε₀ = 8,854∙10-12 Ф/м – электрическая постоянная.
Подставим (2) в (1) найдем F:

[ F=frac{{{q}^{2}}}{2cdot {{varepsilon }_{0}}cdot S}, ]

F = 9,4∙10^-3 Н.
Запишем формулу для вычисления объемной плотности энергии поля конденсатора:

[ omega =frac{varepsilon cdot {{varepsilon }_{0}}cdot {{E}^{2}}}{2} (3).  ]

Подставим (2) в (3):

[ omega =frac{varepsilon cdot {{q}^{2}}}{4cdot {{varepsilon }_{0}}cdot {{S}^{2}}}, ]

ε = 1, диэлектрическая проницаемость воздуха.
ω = 0,3 Дж/м³.
Ответ: 9,4∙10^-3 Н, 0,3 Дж/м³.