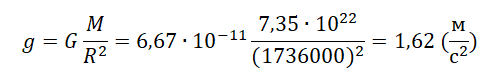Содержание
- Как найти силу притяжения спутника к планете
- Что такое сила притяжения?
- Как найти силу притяжения спутника к планете?
- Как определить массу планеты и спутника?
- Как определить расстояние между планетой и спутником?
- Итог
- Как найти силу притяжения спутника к планете
- Определение силы притяжения
- Найти расстояние между спутником и планетой
- Расчет силы притяжения
- Итог
- Как найти силу притяжения спутника к планете
- 1. Понимание базовой физики
- 2. Определение силы притяжения между планетой и спутником
- 3. Учет других факторов
- 4. Пример расчета силы притяжения между планетой и спутником
- Итог
Как найти силу притяжения спутника к планете

Притяжение является одной из наиболее фундаментальных сил в нашей вселенной. Эта сила ответственна за то, что все тела в природе притягиваются друг к другу. В этой статье мы рассмотрим, как найти силу притяжения спутника к планете.
Что такое сила притяжения?
Сила притяжения — это сила, которая притягивает одно тело к другому. Эта сила обычно обусловлена наличием массы в теле, которое оказывает притяжение. Кроме того, существует и так называемая гравитационная постоянная — константа, которая определяет силу притяжения.
Как найти силу притяжения спутника к планете?
Для того чтобы найти силу притяжения спутника к планете, необходимо знать массу планеты, массу спутника, а также расстояние между ними. Формула для расчета силы притяжения имеет вид:
F = G * (m1 * m2) / r^2

Здесь G — гравитационная постоянная, m1 и m2 — массы планеты и спутника, а r — расстояние между ними.
Как определить массу планеты и спутника?
Массу планеты можно определить на основе орбиты ее спутника. Для этого нужно измерить период обращения спутника вокруг планеты и расстояние между ними. Формула, позволяющая определить массу планеты, имеет вид:
m1 = (4 * pi^2 * r^3) / (G * T^2)
Здесь r — расстояние между планетой и спутником, Т — период обращения спутника.
Массу спутника можно определить на основе его гравитации. Для этого спутник должен иметь на своей поверхности какой-либо объект, который можно сбросить на планету. Эта операция позволяет измерить гравитацию спутника, а затем на основе этой информации можно вычислить массу спутника с использованием формулы:
m2 = a^3 / (G * P^2)
Здесь а — радиус спутника, а Р — период обращения спутника.
Как определить расстояние между планетой и спутником?
Расстояние между планетой и спутником можно измерить на основе времени, которое требуется спутнику для прохождения по своей орбите. Если известен период обращения спутника (Т), то расстояние между ним и планетой можно рассчитать по формуле:
r = (G * m1 * T^2 / 4 * Pi^2)
Итог
Таким образом, сила притяжения спутника к планете зависит от их массы и расстояния между ними. Для того чтобы рассчитать эту силу, необходимо знать массу планеты и спутника, а также расстояние между ними. Расчеты проводятся с использованием формул, которые позволяют точно определить силу притяжения.
Как найти силу притяжения спутника к планете
Притяжение является одним из фундаментальных законов вселенной. Без нее не было бы звезд, планет, спутников и галактик. Сила, которая удерживает спутник на орбите планеты, называется силой притяжения. В этой статье мы расскажем, как найти силу притяжения между спутником и планетой.
Определение силы притяжения
Сила притяжения, также известная как гравитация, является силой, которая действует между двумя объектами с массой. Она обратно пропорциональна квадрату расстояния между объектами и прямо пропорциональна их массам.
Формула для расчета силы притяжения выглядит следующим образом:
F = G * (m1 * m2) / r2
где:
- F — сила притяжения;
- G — гравитационная постоянная;
- m1 и m2 — массы двух объектов;
- r — расстояние между объектами.
Найти расстояние между спутником и планетой
Для расчета силы притяжения между спутником и планетой нужно сначала найти расстояние между ними. Расстояние можно найти, используя закон Кеплера, который устанавливает, что период обращения спутника вокруг планеты пропорционален радиусу орбиты в степени 3/2:
T2 = 4 * π2 * a3 / GM
где:
- T — период обращения;
- a — радиус орбиты;
- G — гравитационная постоянная;
- M — масса планеты.
После того как радиус орбиты найден, расстояние между спутником и планетой можно определить, используя формулу:
r = a — R
где:
- R — радиус планеты.
Расчет силы притяжения

После того как найдено расстояние между спутником и планетой, можно приступить к расчету силы притяжения с помощью формулы, описанной выше:
F = G * (m1 * m2) / r2

где:
- m1 — масса спутника;
- m2 — масса планеты.
Также учтите, что для расчета силы притяжения нужно использовать единицы измерения, которые соответствуют системе СИ. В противном случае расчеты могут быть неточными.
Итог
Сила притяжения является важным понятием в физике и астрономии. Расчет силы притяжения между спутником и планетой может быть выполнен, используя закон Кеплера и формулу для силы притяжения. Используйте систему СИ для единиц измерения, чтобы получить точные результаты.
Как найти силу притяжения спутника к планете
Определение силы притяжения между телами — задача, которая всегда возникает при решении любых космических вопросов. Особенно важен этот параметр в случае, когда речь идет о спутниках планет. Именно сила притяжения определяет, на какой орбите будет находиться спутник, сколько времени он будет проводить на своей орбите и какие будут условия для его существования в пространстве. В этой статье будет описан способ определения силы притяжения спутника к планете.
1. Понимание базовой физики

Перед тем, как приступать к определению силы притяжения, необходимо иметь базовое понимание физики. Необходимо знать, что каждое тело во Вселенной обладает массой и что масса оказывает влияние на силу притяжения между телами. Сила притяжения тела зависит от его массы, а также от массы другого тела, которое находится рядом с ним. Если два тела находятся близко друг к другу, то сила притяжения будет большой, если же тела находятся на большом расстоянии, то и сила притяжения будет значительно меньше.
2. Определение силы притяжения между планетой и спутником
Для определения силы притяжения между планетой и спутником необходимо знать массу планеты, массу спутника и расстояние между ними. Если не известна масса планеты или спутника, то ее можно определить посредством наблюдений других параметров, таких как гравитационное взаимодействие тел в системе или скорость движения спутника по орбите. Для определения расстояния между телами, необходимо провести комплексные наблюдения посредством телескопов, радиолокационных устройств и других инструментов.
3. Учет других факторов
Определение силы притяжения между планетой и спутником не является простой математической задачей. Необходимо учитывать множество других факторов, таких как вращение земли, затмения, искривление пространства, гравитационное поле планеты и атмосферные явления. Все эти факторы оказывают влияние на силу притяжения между телами и должны учитываться при решении задачи.
4. Пример расчета силы притяжения между планетой и спутником
Пример расчета силы притяжения между планетой и спутником:
- Масса планеты: 5.97 x 10^24 кг
- Масса спутника: 3500 кг
- Расстояние между телами: 384 400 км
Сила притяжения между планетой и спутником можно рассчитать по формуле:
F = G * ((m1 * m2) / r^2)
Где:
- F — сила притяжения
- G — гравитационная постоянная (6,674 x 10^-11)
- m1 — масса планеты
- m2 — масса спутника
- r — расстояние между телами

Подставляя значения в формулу, получаем:
F = 6,674 x 10^-11 * ((5.97 x 10^24 кг * 3500 кг) / (384 400 км)^2) = 196 Н
Следовательно, сила притяжения между планетой и спутником составляет 196 Н.
Итог
Определение силы притяжения между телами — важная задача, которая играет ключевую роль при решении задач космической отрасли. Для определения силы притяжения между планетой и спутником необходимо знать массу планеты, массу спутника, расстояние между ними и учитывать другие факторы, которые могут повлиять на итоговый результат. Эта задача является сложной и требует базового понимания физики и математики. Однако, благодаря ее решению, мы можем лучше понимать космические процессы и развивать новые технологии для исследования Вселенной.
Сила всемирного тяготения. Искусственные спутники
- Гравитационное взаимодействие
- Закон всемирного тяготения
- Ускорение свободного падения на поверхности для различных планет
- Космические скорости
- Искусственные спутники Земли
- Задачи
п.1. Гравитационное взаимодействие
Согласно современным представлениям, все тела, обладающие массой, притягиваются друг к другу. Это взаимодействие называется гравитационным.
Таким образом, масса проявляется в природе двумя качественно разными способами.
Инертная масса – мера инертности тел (второй закон Ньютона), дающая связь между силой и вызываемым ею ускорением.
Гравитационная масса – мера гравитационного взаимодействия тел (закон всемирного тяготения), определяющая силу взаимного притяжения.
Нужно подчеркнуть, что инертная масса и гравитационная масса возникают в механике при рассмотрении совершенно разных явлений, и ниоткуда не следует, что они должны быть равны.
Тем не менее, уже сам Ньютон доказал равенство этих масс с точностью 10-3.
На сегодняшний день (эксперимент 2009 г.) этот факт подтвержден с точностью 10-13.
Принцип эквивалентности
Значения инертной и гравитационной массы одного и того же тела равны.
п.2. Закон всемирного тяготения
Закон всемирного тяготения
Две материальные точки массами (m_1) и (m_2) притягиваются по направлению друг к другу с силой (F), прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния (r) между ними: $$ F=Gfrac{m_1m_2}{r^2} $$ Коэффициент пропорциональности называется гравитационной постоянной;
она одинакова для всех тел природы и в системе СИ равна $$ G=6,67cdot 10^{-11}frac{text{Н}cdot text{м}^2}{text{кг}^2} $$
Физический смысл гравитационной постоянной
Если два тела массой по 1 кг находятся на расстоянии 1 м друг от друга, сила гравитационного взаимодействия между ними равна $$ F=Gcdot 1frac{text{кг}^2}{text{м}^2}=6,67cdot 10^{-11} text{Н} $$
Закон всемирного тяготения выполняется для тел, размерами которых можно пренебречь, т.е. для материальных точек. Но его применение можно расширить.
При рассмотрении небесных тел (Солнца, планет и их спутников) в первом приближении их можно считать однородными идеальными сферами с одинаковой плотностью вещества внутри. Как показывает теория, в такой модели небесное тело можно заменить материальной точкой, совпадающей с его центром, с массой полностью сосредоточенной в этом центре.
В этом случае для применения закона всемирного тяготения открываются дополнительные возможности. Например, можно описывать движение небольшого тела на поверхности планеты, «сжимая» всю планету в материальную точку, от которой тело удалено на расстояние, равное радиусу планеты.
п.3. Ускорение свободного падения на поверхности для различных планет
Найдем силу, с которой Земля притягивает небольшое тело массой m, расположенное на её поверхности.
 |
Будем считать Землю сферическим однородным телом. Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), радиус Земли (R_oplus=6370 text{км}). Допущение об однородности позволяет перейти к модели, в которой вся масса Земли сосредоточена в её центре. Расстояние от центра до поверхности, на которой находится тело, – это радиус Земли. |
Получаем, что сила притяжения между Землей и телом: $$ F=Gfrac{M_oplus m}{R^2_oplus} $$
По своей природе, полученная сила является ничем иным, как силой тяжести (F=mg), с которой мы уже знакомы (см. §22 данного справочника).
Значит, (Gfrac{M_oplus m}{R^2_oplus}=mg), и ускорение свободного падения begin{gather*} g=Gfrac{M_oplus}{R^2_oplus}\[6pt] g=6,67cdot 10^{-11}cdot frac{5,97cdot 10^{24}}{(6,37cdot 10^6)^2}approx 9,81 (text{м/с}^2) end{gather*} Что полностью согласуется с многочисленными экспериментами.
Полученный результат можно обобщить и применить к любому другому небесному телу.
Ускорение свободного падения на поверхности сферической однородной планеты или звезды массой (M) и радиусом (R) прямо пропорционально массе и обратно пропорционально квадрату радиуса: $$ g=Gfrac{M}{R^2} $$
Например, для Луны (g_{text{Л}}=1,62frac{text{м}}{text{с}^2}approx 0,165g_0); для Юпитера (g_{text{Ю}}=23,95frac{text{м}}{text{с}^2}approx 2,442g_0); для Солнца (g_{text{С}}=273,1frac{text{м}}{text{с}^2}approx 27,85g_0). Здесь, (g_0) – ускорение свободного падения у поверхности Земли.
Заметим, что в задачах на гравитационное взаимодействие часто оказывается полезной замена (GM=gR^2).
п.4. Космические скорости
Если тело находится на поверхности Земли, то расстояние между центром планеты, где сосредоточена вся масса, и этим телом равно радиусу Земли (R_oplus).
Если подняться над поверхностью на некоторую высоту (h), расстояние станет равным ((R_oplus+h)). Сила всемирного тяготения (она же – сила тяжести) на этой высоте: $$ F_h=Gfrac{M_oplus m}{(R_oplus+h)^2} $$
Т.к. (GM_oplus=gR^2_oplus), где (g=9,81 (text{м/с})^2), можем также записать удобное на практике выражение: $$ F_h=mgleft(frac{R_oplus}{(R_oplus+h)}right)^2 $$
Пусть мы хотим запустить спутник, который будет летать на высоте (h) по круговой орбите с постоянной скоростью (v). При равномерном движении по окружности ускорение равно отношению квадрата скорости к радиусу орбиты. Получаем: $$ F_h=Gfrac{M_oplus m}{(R_oplus +h)^2}=ma=mfrac{v^2_h}{(R_oplus + h)} $$
Скорость вращения спутника на высоте (h): $$ v_h=sqrt{frac{GM_oplus}{R_oplus + h}} $$
Зная ускорение свободного падения у поверхности Земли (g), можем также записать: $$ v_h=sqrt{frac{gR^2_oplus}{R_oplus + h}} $$
В общем случае:
Чтобы запустить тело на круговую орбиту на высоте (h) над поверхностью сферической однородной планеты или звезды массой (M) и радиусом (R), нужно на этой высоте сообщить телу в горизонтальном направлении скорость $$ v_h=sqrt{frac{GM}{R+h}} $$
Скорости, достаточные для запуска околоземного спутника, межпланетной станции и вылета за пределы Солнечной системы, называют космическими скоростями для Земли.
Первая космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), стало её искусственным спутником, равна $$ v_1=sqrt{frac{GM_oplus}{R_oplus}}=sqrt{gR_oplus}approx 7,92 text{км/с} $$
Вторая космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), преодолело земное притяжение и смогло осуществить межпланетный полет в пределах Солнечной системы, равна $$ v_2=sqrt{frac{2GM_oplus}{R_oplus}}=sqrt{2gR_oplus}approx 11,18 text{км/с} $$
Аналогичные формулы для первой и второй космических скоростей можно получить для любой планеты, как в Солнечной системе, так и за ее пределами.
Нужно только знать массу и радиус планеты.
Можно также рассчитать скорость, необходимую для межзвездных полетов при старте с Земли. Это задача непростая, т.к. необходимо учесть относительное движение трех тел: космического корабля, Земли и Солнца.
Третья космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), преодолело притяжение Земли и Солнца и смогло осуществить межзвездный полет за пределы Солнечной системы, равна $$ v_3=sqrt{(sqrt{2}-1)^2frac{GM_odot}{R_odot}+frac{2GM_oplus}{R_oplus}} approx 16,65 text{км/с} $$
В этой формуле, (M_odot) – масса Солнца, (R_odot) – радиус орбиты вращения Земли вокруг Солнца.
п.5. Искусственные спутники Земли
Искусственный спутник Земли – это космический летательный аппарат, вращающийся вокруг Земли по геоцентрической орбите (эллипсу, в одном из фокусов которого находится Земля).
Круговая орбита спутника в плоскости экватора Земли, двигаясь по которой он находится всё время над одной и той же точкой экватора, называется геостационарной. Такие спутники имеет большое значение для создания систем связи.
Чтобы запустить спутник на орбиту, ему необходимо сообщить скорость, больше чем первая космическая, но меньше чем вторая космическая: $$ 7,92frac{text{км}}{text{с}}lt vlt 11,18frac{text{км}}{text{с}} $$
На практике, получение соответствующей силы тяги ракетного двигателя, способного разогнать ракету до таких скоростей, является сложной технической проблемой.
Вывод спутников на орбиту осуществляется с помощью многоступенчатых ракет-носителей в несколько этапов. На первом этапе ракета стартует и, двигаясь вертикально вверх, проходит плотные слои атмосферы на относительно небольшой скорости, после чего отработавшие двигатели первой ступени отделяются (у Илона Маска – аккуратно возвращаются на Землю). На втором этапе ракета постепенно разворачивается параллельно к поверхности Земли и начинает ускоряться. Когда скорость достигает определенной величины и направления, работа двигателей прекращается, отделяется вторая ступень. Спутник начинает самостоятельное движение по расчетной орбите.
Искусственные спутники Земли используются для решения разнообразных научных и прикладных задач.
В апреле 2020 года на орбите находилось 1388 спутников США, 356 Китая, 167 России, 138 Британии, 78 Японии и 627 других стран. Из них: 1007 спутников связи, 446 спутников для исследования Земли, 97 спутников навигации и GPS, 87 научно-исследовательских спутников и другие космические аппараты.
п.6. Задачи
Задача 1. С какой силой Земля притягивает Луну? Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), масса Луны (m_{text{л}}=7,36cdot 10^{22} text{кг}), средний радиус лунной орбиты (R=384 text{тыс.км}). А с какой силой Луна притягивает Землю?
Дано:
(M_oplus=5,97cdot 10^{24} text{кг})
(m_{text{л}}=7,36cdot 10^{22} text{кг})
(R=384 text{тыс.км}=3,84cdot 10^8 text{м})
__________________
(F_{text{ЗЛ}}, F_{text{ЛЗ}}-?)
По закону всемирного тяготения $$ F_{text{ЗЛ}}=Gfrac{M_oplus m_{text{л}}}{R^2} $$ Получаем begin{gather*} F_{text{ЗЛ}}=6,67cdot 10^{-11}cdot frac{5,97cdot 10^{24}cdot 7,36cdot 10^{22}}{(3,84cdot 10^8)^2}approx \[6pt] approx 19,9cdot 10^{-11+24+22-16}=1,99cdot 10^{20} (text{Н}) end{gather*} Эта сила направлена от центра Луны к центру Земли. 
По третьему закону Ньютона, Луна притягивает Землю с такой же по величине силой, которая направлена противоположно, от центра Земли к центру Луны: $$ overrightarrow{F_{text{ЗЛ}}}=-overrightarrow{F_{text{ЛЗ}}} $$ Ответ: 1,99·1020 Н
Задача 2. Самая высокая гора на Земле – Эверест (8848 м). Во сколько раз сила тяжести на уровне моря больше силы тяжести на вершине Эвереста? Радиус Земли (R_oplus=6370 text{км}).
Дано:
(R_oplus=6370 text{км}=6,37cdot 10^6 text{м})
(h=8848 text{м})
__________________
(frac{F}{F_h}-?)
Сила тяжести для тела массой (m) на уровне моря begin{gather*} F=Gfrac{M_oplus m}{R_oplus^2} end{gather*} На вершине Эвереста begin{gather*} F_h=Gfrac{M_oplus m}{(R_oplus +h)^2} end{gather*} Отношение сил: begin{gather*} frac{F}{F_h}=Gfrac{M_oplus m}{R_oplus^2}:Gfrac{M_oplus m}{(R_oplus +h)^2}= frac{(R_oplus+h)^2}{R^2_oplus}=left(frac{R_oplus+h}{R_oplus}right)^2 =left(1+frac{h}{R_oplus}right)^2 end{gather*} Получаем: begin{gather*} frac{F}{F_h}=left(1+frac{8848}{6,37cdot 10^6}right)^2approx 1,003 end{gather*} Ответ: в 1,003 раза
Задача 3. На поверхности Земли на тело действует силы тяжести (F=54 text{Н}).
Чему будет равна сила тяжести, действующая на это тело на высоте, равной двум радиусам Земли?
Дано:
(F=54 text{Н})
(h=2R_oplus )
__________________
(F_h-?)
Сила тяжести на поверхности Земли begin{gather*} F=Gfrac{M_oplus m}{R_oplus^2} end{gather*} Сила тяжести на высоте (h) begin{gather*} F_h=Gfrac{M_oplus m}{(R_oplus +h)^2}=Gfrac{M_oplus m}{(R_oplus+2R_oplus)^2}=Gfrac{M_oplus m}{9R^2_oplus} end{gather*} Отношение сил: begin{gather*} frac{F}{F_h}=Gfrac{M_oplus m}{R_oplus^2}:Gfrac{M_oplus m}{9R^2_oplus}=9, F_h=frac{F}{9}\[6pt] F_h=frac{54}{9}=6 (text{Н}) end{gather*} Ответ: 6 Н
Задача 4*. Чему равны первая и вторая космические скорости вблизи поверхности Луны? Сравните их со значениями первой и второй космических скоростей у поверхности Земли.
Радиус Луны (R=1740 text{км}), масса Луны (M=7,36cdot 10^{22} text{кг}).
Дано:
(R=1740 text{км}=1,74cdot 10^6 text{м})
(M=7,36cdot 10^{22} text{кг})
__________________
(v_1, v_2-?)
(frac{v_{text{1З}}}{v_{text{1Л}}}, frac{v_{text{2З}}}{v_{text{2Л}}}-?)
Первая и вторая космические скорости $$ v_1=sqrt{frac{GM}{R}}, v_2=sqrt{frac{2GM}{R}}=sqrt{2}v_1 $$ Получаем: begin{gather*} v_1=sqrt{frac{6,67cdot 10^{-11}cdot 7,36cdot 10^{22}}{1,74cdot 10^6}}approx sqrt{2,82cdot 10^6}approx\[6pt] approx 1,68cdot 10^3frac{text{м}}{text{с}}=1,68frac{text{км}}{text{с}}\[6pt] v_2=sqrt{2}cdot 1,68approx 2,37frac{text{км}}{text{с}} end{gather*} Сравним со скоростями для Земли: begin{gather*} frac{v_{text{1З}}}{v_{text{1Л}}}=frac{7,92}{1,68}approx 4,7 text{раз}, frac{v_{text{2З}}}{v_{text{2Л}}}=frac{sqrt{2}v_{text{1З}}}{sqrt{2}v_{text{1Л}}}=frac{v_{text{1З}}}{v_{text{1Л}}}approx 4,7 text{раз} end{gather*} Космические скорости для Луны в 4,7 раз меньше земных.
Ответ: 1,68 км/с; 2,37 км/с; в 4,7 раз меньше
Задача 5*. Рассчитайте радиус геостационарной орбиты спутника и высоту такого спутника над Землей. Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), радиус Земли (R_oplus =6400 text{км}).
Ответ запишите в км.
Дано:
(M_oplus=5,97cdot 10^{24} text{кг})
(T=24 text{ч}=8,64cdot 10^4 text{с})
(R_oplus =6400 text{км}=6,4cdot 10^6 text{м})
__________________
(R, h-?)
На геостационарной орбите спутник «зависает» над Землей, его линейная скорость равна отношению длины окружности орбиты к периоду вращения (сутки): begin{gather*} v=frac{2pi R}{T}=sqrt{frac{GM_oplus}{R}}Rightarrow frac{4pi ^2R^2}{T^2}=frac{GM_oplus}{R}Rightarrow R^3=frac{GM_oplus T^2}{4pi ^2}\[6pt] R=sqrt[{3}]{frac{GMT^2}{4pi ^2}} end{gather*} Получаем: begin{gather*} R=sqrt[{3}]{frac{6,67cdot 10^{-11}cdot 5,97cdot 10^{24}cdot (8,64cdot 10^4)^2}{4pi ^2}}approx sqrt[{3}]{75,3cdot 10^{-11+24+8}}approx\[6pt] approx 4,22cdot 10^7 (text{м})=42200 (text{км})\[6pt] h=R-R_oplus=42200-6400=35800 (text{км}) end{gather*} Ответ: 42200 км; 35800 км
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
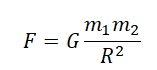
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
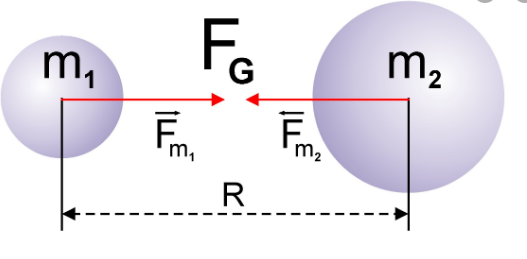
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.

Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
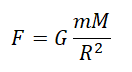
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
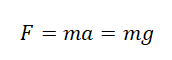
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
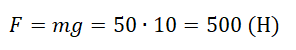
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
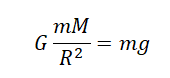
Отсюда:
Формула расчета ускорения свободного падения
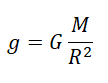
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
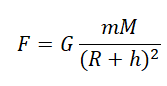
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
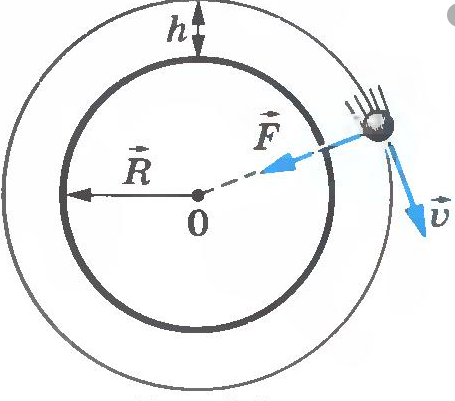
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
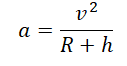
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
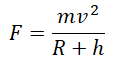
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
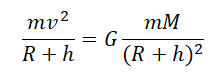
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
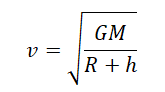
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
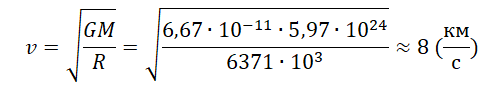
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
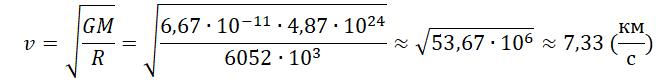
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
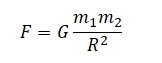
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
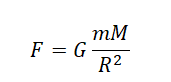
Примерим этот закон для первой и второй пары звезд:
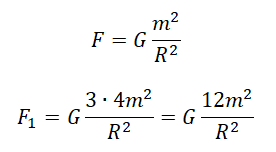
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
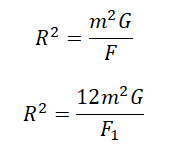
Приравняем правые части выражений и выразим силу притяжения во втором случае:
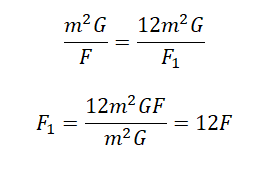
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
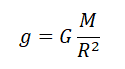
Отсюда радиус равен:
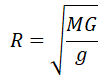
Линейная скорость и радиус орбиты связываются формулой:
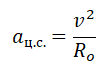
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
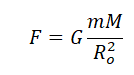
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
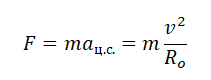
Отсюда:
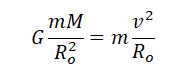
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
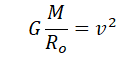
Из этой формулы выразим массу планеты:
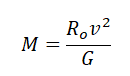
Подставим массу планеты в формулу для нахождения ее радиуса:
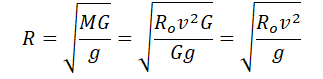
Подставляем известные данные и вычисляем:
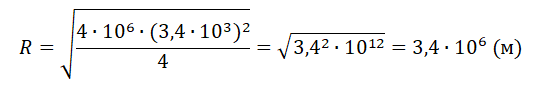
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 17.9k
Исходя из трактовки второго закона Ньютона, можно сделать вывод, что изменение движения происходит посредствам силы. Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.
Закон всемирного тяготения. Формулы
В 1862 году был открыт закон всемирного тяготения И. Ньютоном. Он предположил, что силы, удерживающие Луну, той же природы, что и силы, заставляющие яблоко падать на Землю. Смысл гипотезы состоит в наличии действия сил притяжения, направленных по линии и соединяющих центры масс, как изображено на рисунке 1.10.1. Шаровидное тело имеет центр массы, совпадающий с центром шара.
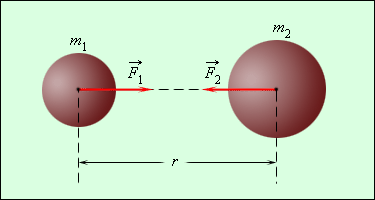
Рисунок 1.10.1. Гравитационные силы притяжения между телами. F1→=-F2→.
Далее, Ньютон искал физическое объяснение законам движения планет, которые открыл И. Кеплер в начале XVII века, и давал количественное выражение для гравитационных сил.
При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики.
Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача). Обратная же выполняется с определением действующих сил на тело с известным его направлением. Такие задачи привели ученого к открытию определения закона всемирного тяготения.
Ускорение свободного падения
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
F=Gm1m2r2.
Значение G определяет коэффициент пропорциональности всех тел в природе, называемое гравитационной постоянной и обозначаемое по формуле G=6,67·10-11 Н·м2/кг2 (СИ).
Большинство явлений в природе объясняются наличием действия силы всемирного тяготения. Движение планет, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все объясняется законом тяготения и динамики.
Проявлении силы тяготения характеризуется наличием силы тяжести. Так называется сила притяжения тел к Земле и вблизи ее поверхности.
Когда М обозначается как масса Земли, RЗ– радиус, m – масса тела, то формула силы тяжести принимает вид:
F=GMRЗ2m=mg.
Где g – ускорение свободного падения, равняющееся g=GMRЗ2.
Сила тяжести направлена к центру Земли, как показано в примере Луна-Земля. При отсутствии действия других сил тело движется с ускорением свободного падения. Его среднее значение равняется 9,81 м/с2. При известном G и радиусе R3=6,38·106 м производятся вычисления массы Земли М по формуле:
M=gR32G=5,98·1024 кг.
Если тело удаляется от поверхности Земли, тогда действие силы тяготения и ускорения свободного падения меняются обратно пропорционально квадрату расстояния r к центру. Рисунок 1.10.2 показывает, как изменяется сила тяготения, действующая на космонавта корабля, при удалении от Земли. Очевидно, что F притягивания его к Земле равняется 700 Н.
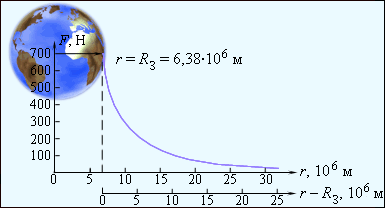
Рисунок 1.10.2. Изменение силы тяготения, действующей на космонавта при удалении от Земли.
Земля-Луна подходит в качестве примера взаимодействия системы двух тел.
Расстояние до Луны – rЛ=3,84·106 м. Оно в 60 раз больше радиуса Земли RЗ. Значит, при наличии земного притяжения, ускорение свободного падения αЛ орбиты Луны составит αЛ=gRЗrЛ2=9,81 м/с2602=0,0027 м/с2.
Оно направлено к центру Земли и получило название центростремительного. Расчет производится по формуле aЛ=υ2rЛ=4π2rЛT2=0,0027 м/с2, где Т =27,3 суток – период обращения Луны вокруг Земли. Результаты и расчеты, выполненные разными способами, говорят о том, что Ньютон был прав в своем предположении единой природы силы, удерживающей Луну на орбите, и силы тяжести.
Луна имеет собственное гравитационное поле, которое определяет ускорение свободного падения gЛ на поверхности. Масса Луны в 81 раз меньше массы Земли, а радиус в 3,7 раза. Отсюда видно, что ускорение gЛ следует определять из выражения:
gЛ=GMЛRЛ2=GMЗ3,72T32=0,17 g=1,66 м/с2.
Такая слабая гравитация характерна для космонавтов, находящихся на Луне. Поэтому можно совершать огромные прыжки и шаги. Прыжок вверх на метр на Земле соответствует семиметровому на Луне.
Искусственные спутники Земли
Движение искусственных спутников зафиксировано за пределами земной атмосферы, поэтому на них оказывают действие силы тяготения Земли. Траектория космического тела может изменяться в зависимости от начальной скорости. Движение искусственного спутника по околоземной орбите приближенно принимается в качестве расстояния до центра Земли, равняющемуся радиусу RЗ. Они летают на высотах 200-300 км.
Отсюда следует, что центростремительное ускорение спутника, которое сообщается силами тяготения, равняется ускорению свободного падения g. Скорость спутника примет обозначение υ1. Ее называют первой космической скоростью.
Применив кинематическую формулу для центростремительного ускорения, получаем
an=υ12RЗ=g, υ1=gRЗ=7, 91·103 м/с.
При такой скорости спутник смог облететь Землю за время, равное T1=2πRЗυ1=84 мин 12 с.
Но период обращения спутника по круговой орбите вблизи Земли намного больше, чем указано выше, так как существует различие между радиусом реальной орбиты и радиусом Земли.
Спутник движется по принципу свободного падения, отдаленно похожее на траекторию снаряда или баллистической ракеты. Разница заключается в большой скорости спутника, причем радиус кривизны его траектории достигает длины радиуса Земли.
Спутники, которые движутся по круговым траекториям на больших расстояниях, имеют ослабленное земное притяжение, обратно пропорциональное квадрату радиуса r траектории. Тогда нахождение скорости спутника следует по условию:
υ2к=gR32r2, υ=gR3RЗr=υ1R3r.
Поэтому, наличие спутников на высоких орбитах говорит о меньшей скорости их движения, чем с околоземной орбиты. Формула периода обращения равняется:
T=2πrυ=2πrυ1rRЗ=2πRзυ1rR33/2=T12πRЗ.
T1 принимает значение периода обращения спутника по околоземной орбите. Т возрастает с размерами радиуса орбиты. Если r имеет значение 6,6 R3 то Т спутника равняется 24 часам. При его запуске в плоскости экватора, будет наблюдаться, как висит над некоторой точкой земной поверхности. Применение таких спутников известно в системе космической радиосвязи. Орбиту, имеющую радиус r=6,6 RЗ, называют геостационарной.
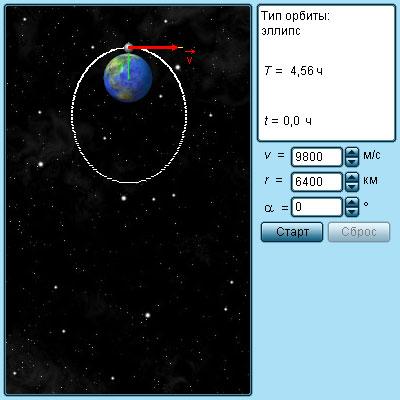
Рисунок 1.10.3. Модель движения спутников.
Характер и особенности расчета силы притяжения известны еще с древних времен. На основании имеющихся знаний, переданных современному научному сообществу великими исследователями, человек познает не только его окружающий мир, но и Вселенную.
Формула силы притяжения
Со времен Древней Греции философов интересовали явления притяжения тел к земле и свободного падения. К примеру, по утверждениям Аристотеля, из двух камней, брошенных с одинаковой высоты, быстрее достигнет земной поверхности тот, чья масса больше. В IV веке до нашей эры единственными методами научных изысканий служили наблюдения и анализ. К проверке гипотез опытным путем великие мыслители не прибегали. По истечению столетий физик из Италии Галилео Галилей проверил утверждения Аристотеля, используя практические методы исследований.
Итоги проведенных Галилеем опытов были опубликованы в «Беседах и математических доказательствах, касающихся двух новых наук». Ученый использовал псевдоним Сагредо: «пушечное ядро не опередит мушкетной пули при падении с высоты двухсот локтей». Формулировка закона всемирного тяготения была представлена в 1666 году Исааком Ньютоном. В ней фиксировались основные тезисы теоремы Галилея.
Смысл заключался в том, что тела, которые обладают разными массами, падают на землю с одинаковыми ускорениями. Одно тело притягивает другое и, наоборот, с силой, которая прямо пропорциональна их массам и обратно пропорциональна отрезку пути между ними. Согласно определению гравитации от Ньютона, тела, характеризующиеся массой, обладают свойством, благодаря которому притягиваются друг к другу.
Понятие и определение
Силы взаимного притяжения – это силы, которые притягивают любые тела, обладающие массами.
Корректность выводов Ньютона неоднократно подтверждалась путем практических испытаний. Но в начале ХХ века перед учеными-физиками остро стоял вопрос о природе и характере взаимодействия крупных астрономических тел, включая разные виды планетарных систем и галактик в вакууме. Ньютоновского закона уже было недостаточно, чтобы решить эти задачи. Исключить недочеты позволила новая теория, разработанная Альбертом Эйнштейном в начале ХХ столетия. Общая теория относительности объясняет гравитацию не в качестве силы, а представляет ее в виде искривления пространства и времени в четырех измерениях, которое зависит от массы тел, создающих его.
Гравитация представляет собой свойство тел, которые характеризуются массой, притягивать друг друга. Данное физическое явление можно объяснить, как поле, оказывающее дистанционное воздействие на предметы, не связанные между собой никаким другим способом.
Достижение Эйнштейна не противоречит теоретическому объяснению гравитации от Ньютона. Общая теория относительности рассматривает закон всемирного тяготения, как частный случай, применимый для сравнительно небольших расстояний. Данная закономерность в настоящее время также активно используется для поиска решений задач на практике.
Единицы измерения силы притяжения
В разных системах измерений можно встретить несколько отличающиеся обозначения. Единицы измерения силы притяжения следующие:
- система СИ: ([F]=H);
- система СГС: ([F]=дин).
Формула силы притяжения между телами в космосе
Закономерность гравитации, которую обнаружил Ньютон, можно представить в виде математической формулы. Вычисления выглядят следующим образом:
(F=(Gtimes m1times m2times r)/2),
где (m1,m2) – массы объектов, которые притягиваются друг к другу под действием силы (F),
(r) – расстояние, на которое удалены тела,
(G) – т.н. гравитационная постоянная величина, константа, равная 6,67.
Гравитационное взаимодействие объектов будет слабеть, если тела удаляются друг относительно друга. Сила гравитации пропорциональна величине расстояния в квадрате. При этом для нахождения искомой величины расстояние измеряется от центров тяжести тел, а не от поверхностей.
Гравитация в определенных моментах напоминает другие физические явления. Исходя из зависимости интенсивности силы от расстояния в квадрате, гравитацию можно сравнить с электромагнитным взаимодействием сильного и слабого характера.
Формула силы гравитационного притяжения между двумя телами
Квадратичная связь силы, с которой тела притягиваются друг к другу, с расстоянием между ними объясняет тот факт, что люди, находящиеся на поверхности планеты Земля не притягиваются к Солнцу, хотя масса его велика и превышает земную в миллион раз. Земля и центр Солнечной системы удалены примерно на 150 миллионов километров. Дистанция достаточно велика, чтобы ощущаться человеком. Однако эту силу можно зарегистрировать, используя высокоточные приборы. В рамках планеты Земля сила, с которой тела к ней притягиваются, то есть их вес, измеряется следующим образом:
(P=mtimes g),
где (m) – масса тела, на которое воздействует сила притяжение,
(g) – ускорение свободного падения около Земли (если рассматривать систему в условиях любой другой планеты, данная величина будет отличаться).
На разных географических широтах величина ускорения свободного падения может незначительно отличаться. Производя расчеты, данный показатель принимается за 9,81 метров в секунду в квадрате.
В физике понятия массы и веса тел отличаются. Весом называется сила, определяющее притяжение объекта к планете. Масса представляет собой меру инертности вещества. На нее не влияют другие тела, расположенные рядом.
Формула для силы притяжения тел произвольной формы
Расчеты определяются некоторыми условиями. К ним относятся характеристики исследуемых объектов.
Если сила притяжения измеряется между телами, которые обладают произвольной формой, их считают материальными точками:
(dtimes m1=rho1times dV1)
(dtimes m2=rho2times dV2)
где (rho1, rho2) – обозначают плотность веществ материальных точек, характерных для первого и второго объектов,
(dV1 ,dV2) – элементарные объемы выделенных материальных точек.
Исходя из этого, сила притяжения (doverline F), с которой взаимодействуют объекты, равна:
(doverline F=-Gtimes frac{rho _{1}timesrho _{2}times dtimes V_{1}times dtimes V_{2}}{r_{12}^{3}} bar{r_{12}})
Таким образом, сила притяжения первого тела вторым рассчитывается следующим образом:
(bar{F}_{12}=-Gtimesint_{V_{1}}^{rho _{1}times dtimes V_{1}}int_{V_{2}}^{frac{rho _{2}}{r_{12}^{3}}times bar{r}_{12}times dtimes V_{2}})
где интегрирование выполняется по всему объему первого ((V1)) и второго ((V2)) тел. Если тела обладают однородностью, то формула корректируется, таким образом:
(bar{F}_{12}=-Gtimesrho1timesrho2timesint_{V_{1}}^{dtimes V_{1}}int_{V_{2}}^{frac{bar{r}_{12}}{r_{12}^{3}}times dtimes V_{2}})
Формула для силы притяжения твердых тел шарообразной формы
В условиях, когда сила притяжения измеряется между телами, представленных в форме шара или близкой к нему, с плотностью, зависящей лишь от удаленности их центров тяжести, применяется следующая формула:
(bar{F}_{12}=-Gtimes(m1times m2)/R^3times R12)
где (m1,m2) – массы шаров, (R )– радиус – вектор, соединяющий центры шаров.
Пример применения формулы для расчета
Задача. Необходимо рассчитать силу притяжения между двумя идентичными однородными шарами, масса которых составляет по 1 килограмму. При этом их центры тяжести удалены на 1 метр друг от друга.
Решение будет выглядеть следующим образом:
Используя формулу для подсчета силы притяжения между двумя объектами шарообразной формы, получается:
(F_g=6.67times 10^{-11}times frac{1times 1}{1^{2}})
Ответ: (F_g=6.67times 10^{-11})
Выполнить расчет силы притяжения достаточно просто, если правильно выбрать формулу, подходящую под конкретные условия, в которых находятся тела. Если в процессе решения задач по физике или другим дисциплинам возникают проблемы, всегда можно обратиться за помощью к компетентным специалистам портала Феникс.Хелп.