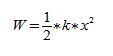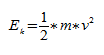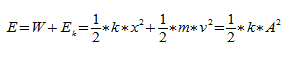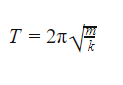Формулы пружинного маятника в физике
Формулы пружинного маятника
Определение и формулы пружинного маятника
Определение
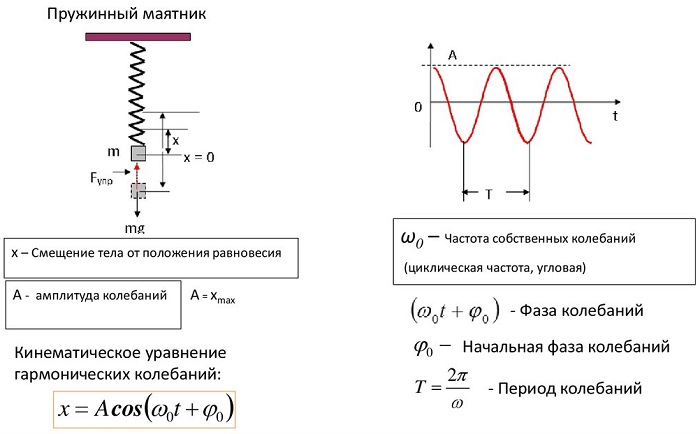
Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.
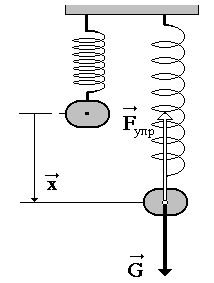
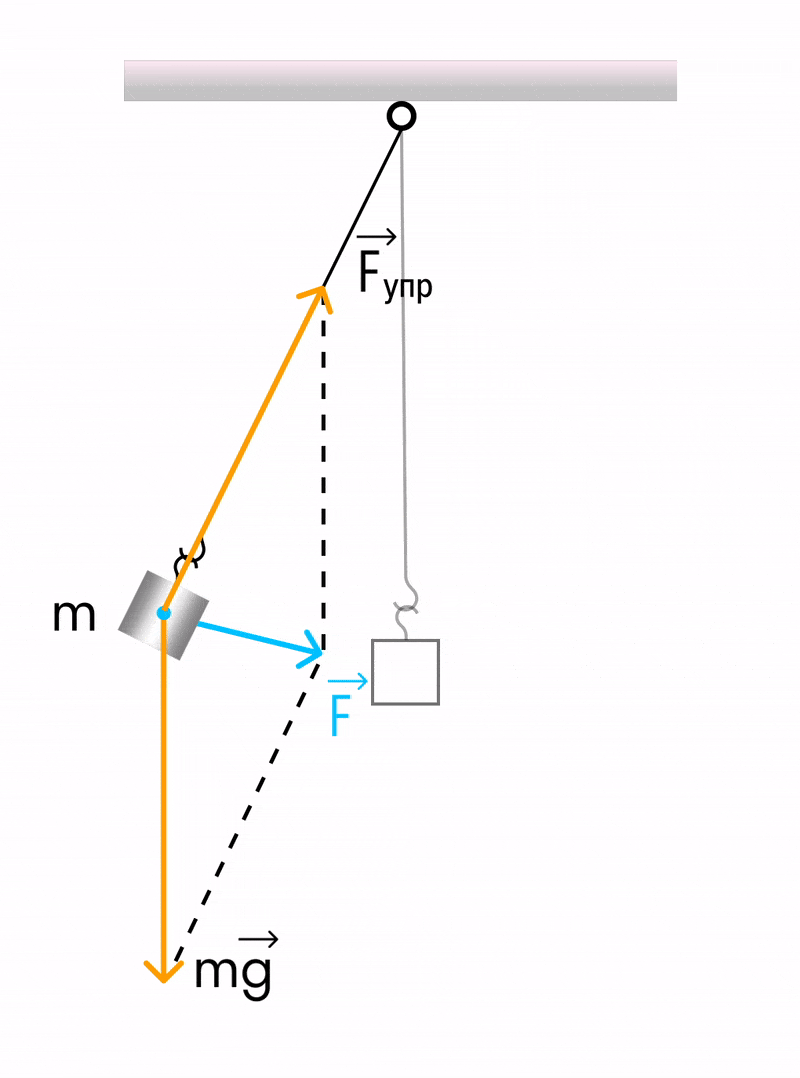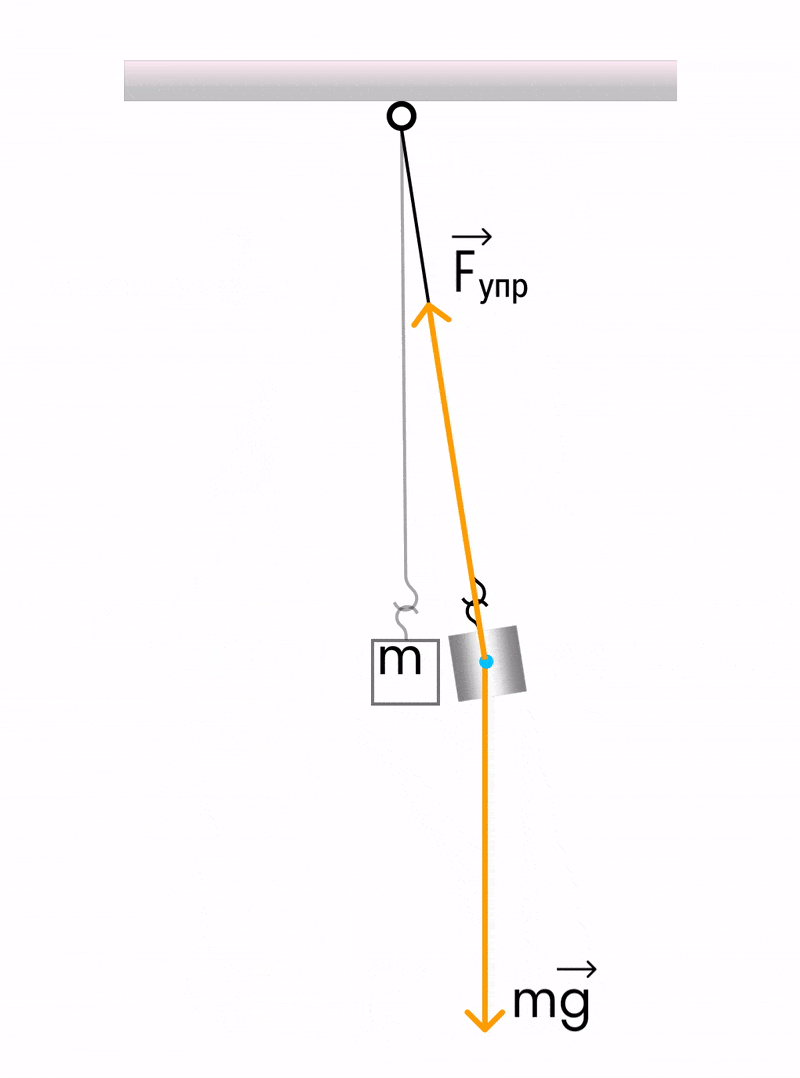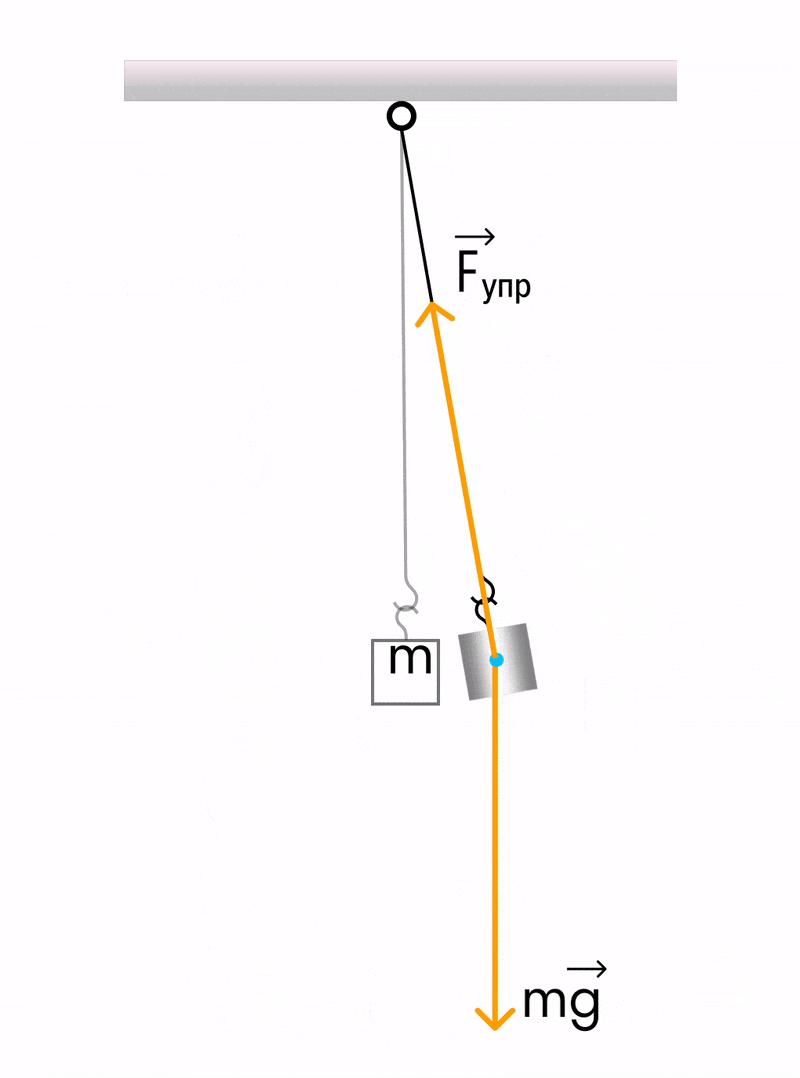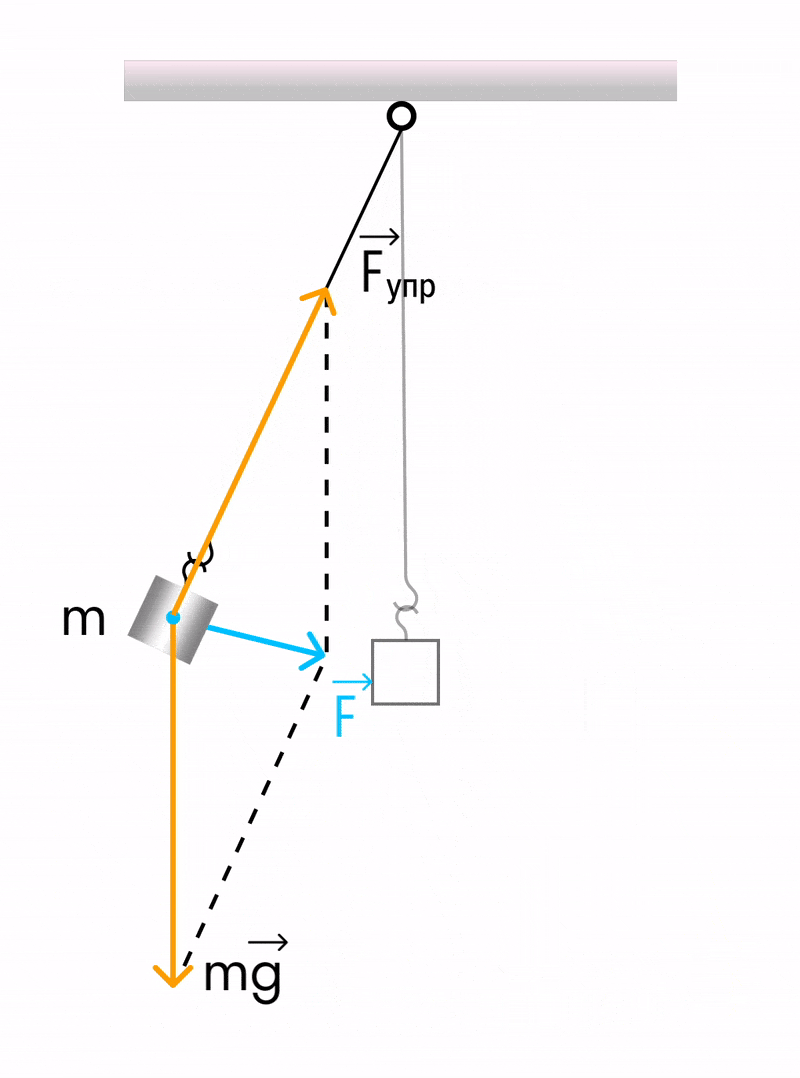
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.
Уравнения колебаний пружинного маятника
Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${щu}^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
В экспоненциальном виде колебания пружинного маятника можно записать как:
[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]
Формулы периода и частоты колебаний пружинного маятника
Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:
[T=2pi sqrt{frac{m}{k}}left(4right).]
Так как частота колебаний ($nu $) – величина обратная к периоду, то:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]
Формулы амплитуды и начальной фазы пружинного маятника
Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).
Амплитуду можно найти как:
[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]
начальная фаза при этом:
[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]
где $v_0$ – скорость груза при $t=0 c$, когда координата груза равна $x_0$.
Энергия колебаний пружинного маятника
При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:
[E_p=-frac{dF}{dx}(8)]
учитывая, что для пружинного маятника $F=-kx$,
тогда потенциальная энергия ($E_p$) пружинного маятника равна:
[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]
Закон сохранения энергии для пружинного маятника запишем как:
[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]
где $dot{x}=v$ – скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ – кинетическая энергия маятника.
Из формулы (10) можно сделать следующие выводы:
- Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
- Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.
Примеры задач с решением
Пример 1
Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac{м}{с}$?
Решение. Сделаем рисунок.
По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:
[E_{pmax}=E_{kmax }left(1.1right),]
где $E_{pmax}$ – потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax }$ – кинетическая энергия шарика, в момент прохождения положения равновесия.
[E_{kmax }=frac{mv^2}{2}left(1.2right).]
Потенциальная энергия равна:
[E_{pmax}=frac{k{x_0}^2}{2}left(1.3right).]
В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:
[frac{mv^2}{2}=frac{k{x_0}^2}{2}left(1.4right).]
Из (1.4) выразим искомую величину:
[x_0=vsqrt{frac{m}{k}}.]
Вычислим начальное (максимальное) смещение груза от положения равновесия:
[x_0=1cdot sqrt{frac{0,36}{1600}}=1,5 cdot {10}^{-3}(м).]
Ответ. $x_0=1,5$ мм
Пример 2
Задание. Пружинный маятник совершает колебания по закону: $x=A{cos left(omega tright), } $где $A$ и $omega $ – постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_{p0}$.
В какой момент времени это произойдет?
Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:
[F=-kx=-kA{cos left(omega tright)left(2.1right). }]
Потенциальную энергию колебаний груза найдем как:
[E_p=frac{kx^2}{2}=frac{kA^2{{cos }^2 left(omega tright) }}{2}left(2.2right).]
В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:
[frac{E_{p0}}{F_0}=-frac{A}{2}{cos left(omega tright) }to t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }.]
Ответ. $t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }$
Читать дальше: формулы равноускоренного прямолинейного движения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
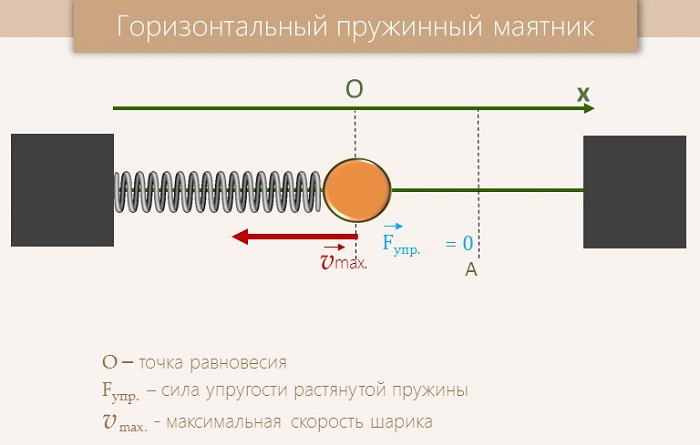
Пружинный маятник – колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.
Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.
В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.
Что такое пружинный маятник
Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.
Приняты следующие обозначения:
-
m – масса тела;
-
k – коэффициент жесткости пружины.
Общий вид маятника:
Особенностями пружинных маятников являются:
-
Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;
-
У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;
-
Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;
-
Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;
-
От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.
Виды пружинных маятников
Существует два типа данной системы:
-
Вертикальный маятник – на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.
-
Горизонтальный – в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.
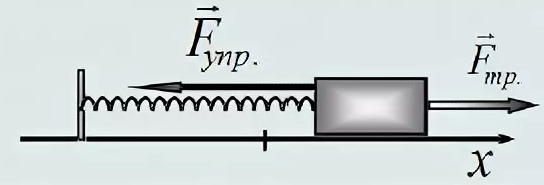
Сила упругости в пружинном маятнике
До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.
Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.
Расчёт силы упругости может быть проведен таким образом:
Fупр = – k*x
где k — коэффициент жесткости пружины (Нм),
x – смещение (м).
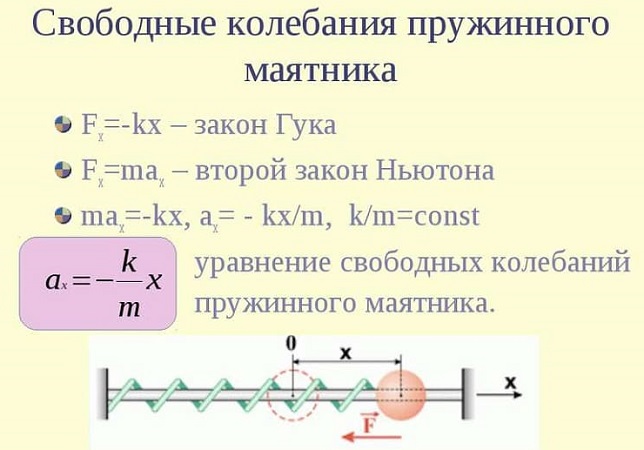
Уравнения колебаний пружинного маятника
Свободные колебания пружинного маятника описываются с помощью гармонического закона.
Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:
F(t) = ma(t) = – mw2x(t),
где w – радиальная частота гармонического колебания.
Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:
Период и частота свободных колебаний пружинного маятника
При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.
Изменение циклической частоты покажет формула, приведенная на рисунке:
Факторы, от которых зависит частота:
-
Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.
-
Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.
Амплитуда и начальная фаза пружинного маятника
Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.
В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).
Энергия пружинного маятника
При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.
Потенциальная энергия:
Кинетическая энергия:
Полная энергия:
Расчет имеет особенности. При его проведении нужно учитывать несколько условий:
-
Колебания проходят в двух плоскостях: вертикальной и горизонтальной.
-
В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.
-
Влияние силы трения при расчете не учитывают.
Дифференциальное уравнение гармонических колебаний пружинного маятника
Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.
Если
колебательная система совершает
гармонические колебания, имея одну
степень свободы, то она называется
линейным классическим гармоническим
осциллятором.
Примерами
классического линейного осциллятора
являются пружинный маятник, математический,
физический маятники и др.
Рассмотрим
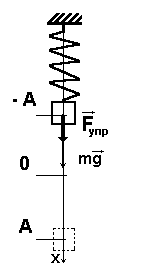
колебания пружинного маятника.
Пружинный
маятник представляет собой некоторый
груз массой m,
закрепленный на пружине с коэффициентом
жесткости
k,
совершающий свободные гармонические
колебания (рис. 2.2).
Гармонические
колебания называют свободными, если
они совершаются только под действием
сил, вызывающих эти колебания.
Частоту
свободных гармонических колебаний
называют собственной частотой (0),
так как она зависит только от свойств
самой физической системы.
Найдем
дифференциальное уравнение свободных
гармонических колебаний пружинного
маятника. На маятник действует сила
тяжести
G = mg
и
сила упругости (закон Гука, рис. 2.2)
Fупр
=
–
кх,
Рис. 2.2
где
х –
смещение ; k –
коэффициент жесткости (упругости)
пружины.
Эти
силы в состоянии покоя равны по величине,
но противоположны по направлению
(третий закон Ньютона).
Однако
при колебаниях сила упругости изменяется
периодически по величине и по направлению.
Значит,
силой, вызывающей колебания пружинного
маятника, является сила упругости.
При этом выполняется
следующее соотношение:
maх
= –
kx,
где
,
тогда

(2.1)
Последнее выражение
приведем к нормальному виду однородного
дифференциального уравнения второго
порядка, описывающего одномерное (с
одной степенью свободы) движение
пружинного маятника, например, вдоль
оси Х:

(2.2)
Решением данного
дифференциального уравнения является
функция
х
= Асos (оt
+ o).
(2.3)
Выразим
k
в уравнении (2.2) через собственную
круговую частоту 0
и смещение х.
Для этого достаточно
вспомнить, что ускорение
.
(2.4)
Используя выражения (2.1) и (2.4), запишем, что
F
= ma =
m о2х.
(2.5)
С
другой стороны, при колебаниях пружинного
маятника роль действующей силы выполняет
сила упругости (речь о ней шла выше)
Fупр
= –
кх.
(2.6)
Из соотношений
(2.5) и (2.6) имеем
m
о2х
= –
кх.
После несложных
преобразований получим
k
= m о2.
(2.7)
Дифференциальное
уравнение (6.24) принимает следующий
вид:
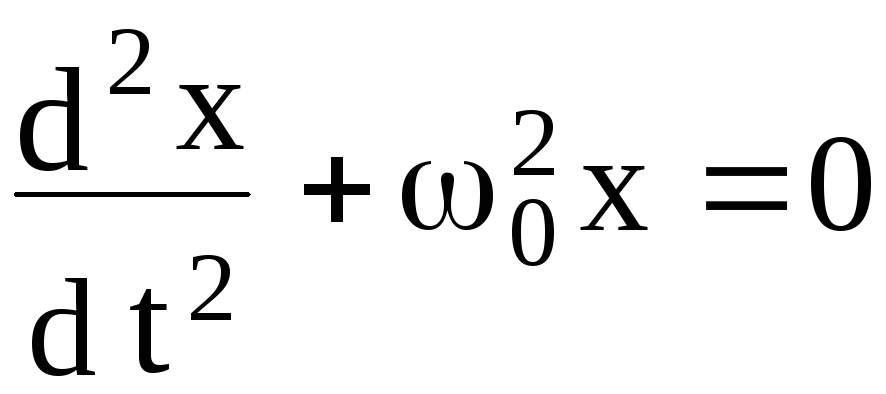
(2.8)
Напомним,
что уравнение вида (2.8) является общим
для всех физических систем различной
природы, совершающих свободные
гармонические колебания, только вместо
смещения
х
используется величина, характеризующая
колебания данной системы, например,
колебание заряда (q), тока (I) и т. д.
Сравнивая общее дифференциальное
уравнение гармонических колебаний
(2.8) и дифференциальное уравнение
колебаний пружинного маятника (2.2),
приходим к заключению, что квадрат
круговой частоты прямо пропорционален
коэффициенту жесткости пружины и обратно
пропорционален его массе:
(2.9)
Найдем период
колебаний пружинного маятника.
Из
кинематики вращательного движения
известно, что период и угловая скорость
(круговая частота) связаны соотношением
T
=
.
Следовательно,
период колебаний пружинного маятника
.
(2.10)
Вывод:
Период колебаний пружинного маятника
прямо пропорционален квадратному корню
массы маятника и обратно пропорционален
квадратному корню коэффициента жесткости
пружины.
Замечание:
Выводы, полученные при рассмотрении
колебаний пружинного маятника, можно
использовать в задачах, связанных с
колебаниями атомов и молекул различных
физических систем.
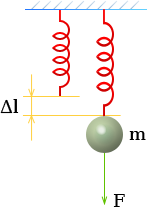
Колебания пружины, формула
При колебаниях пружины восстанавливающая сила обусловлена ее упругостью.
В определенных пределах, согласно закону Гука, вызванная деформацией сила пропорциональна величине деформации.
Поэтому упругие колебания являются гармоническими.
В случае пружин величина жесткости обычно обозначается через k
и именуется коэффициентом упругости пружины.
Если
| k | коэффициент упругости пружины, | Ньютон / метр |
|---|---|---|
| F | сила, вызывающая деформацию Δl, | Ньютон |
| Δl | удлинение, прогиб или другое изменение формы, | метр |
| ω | угловая частота, | радиан / секунда |
| f | линейная частота, | Герц |
| T | период, длительность полного колебания, | секунда |
| m | масса колебательной системы, обычно тела, укрепленного на пружине, | кг |
то
[
ω = 2πf = frac{2π}{T}
]
[
k = frac{F}{Δl}
]
И в соответствии с (9)
[
ω = sqrt{frac{k}{m}}
]
[
f = frac{1}{2π} sqrt{frac{k}{m}}
]
[
T = 2π sqrt{frac{m}{k}}
]
[
m = frac{1}{3}m_{пружины} + m_{тела}
]
Колебания пружины |
стр. 543 |
|---|
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
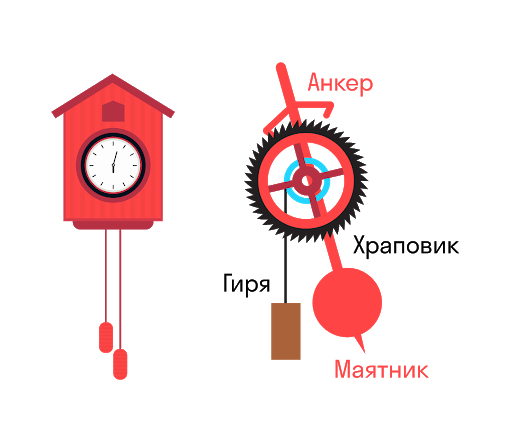
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
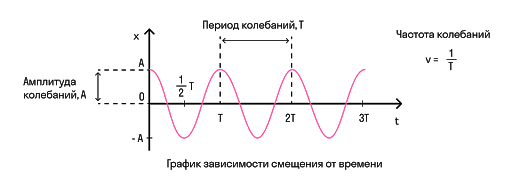
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний
T = t/N
T — период [с]
t — время [с]
N — количество колебаний [—]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
ν — частота [Гц]
t — время [с]
T — период [с]
N — количество колебаний [—]
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x = xmaxcos(2πνt)
x — координата в момент времени t [м]
xmax — амплитуда [м]
ν — частота [Гц]
t — момент времени [с]
π = 3,14
(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
φ = 2πνt
φ — фаза [рад]
ν — частота [Гц]
t — момент времени [с]
π = 3,14
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:
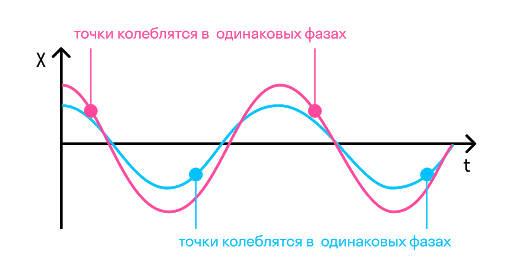
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
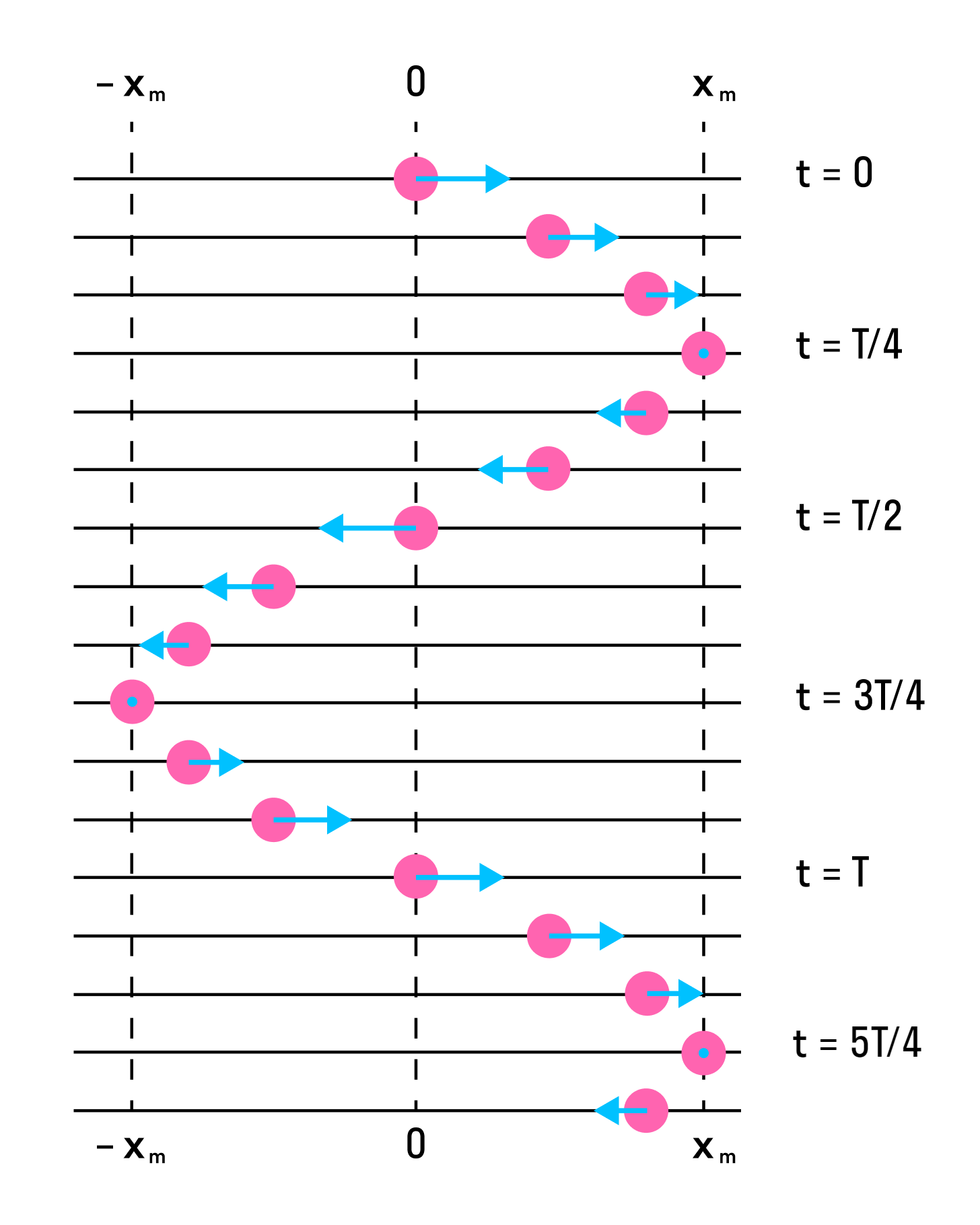
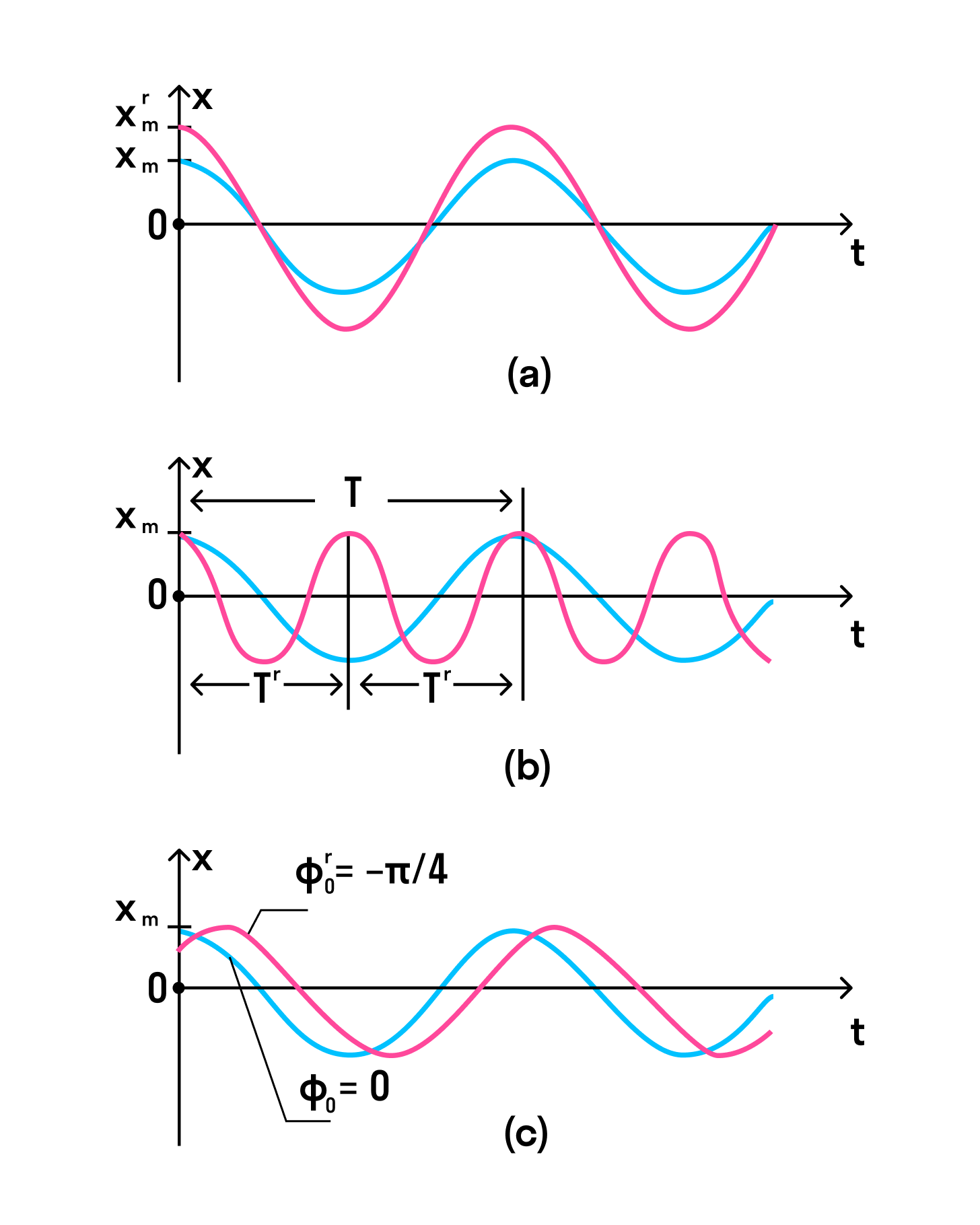
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
-
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
-
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
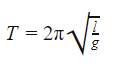
T — период [с]
l — длина нити [м]
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с2
π = 3,14
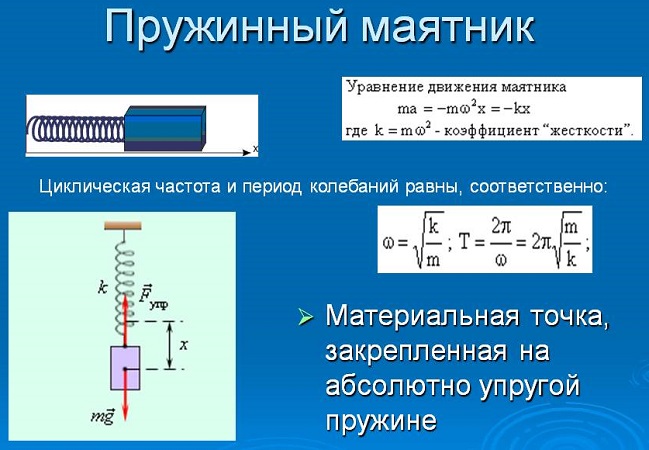
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника
T — период [с]
m — масса маятника [кг]
k — жесткость пружины [Н/м]
π = 3,14
Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
Рассмотрим его на примере математического маятника.
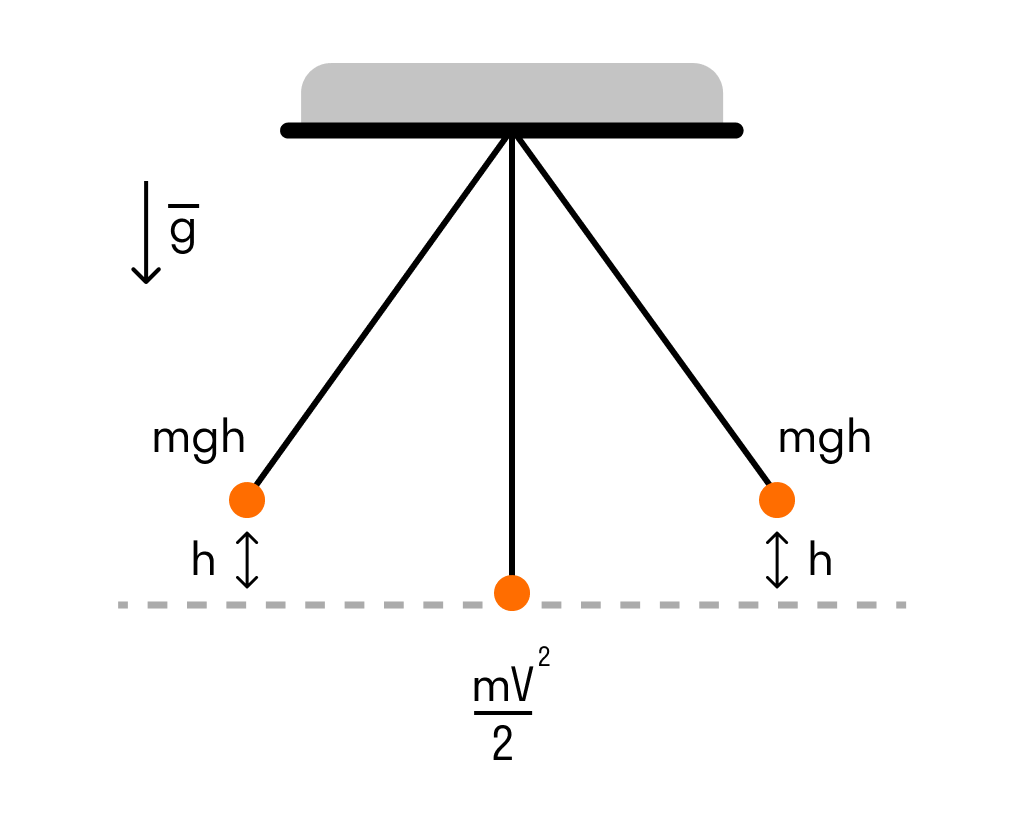
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!