Время на прочтение
3 мин
Количество просмотров 9.6K
Немного теории.
Для начала разберемся с тем, что такое лошадиные силы и устроим небольшой экскурс в школьную физику.
1 л.с. – это мощность, затрачиваемая при вертикальном подъёме груза массой 75 кг со скоростью 1 м/с.
Как известно, мощность показывает, какую работу совершает тело в единицу времени:
Работа равна произведению силы на перемещение: A = F*S. Учитывая, что скорость V=S/t, получим:
Получаем формулу для перевода лошадиных сил в принятую в международной системе СИ единицу измерения мощности – Ватт:
Перейдем к основной части, а именно – к техническим характеристикам автомобиля.
Некоторые характеристики и расчёты будут приводиться приближенно, поскольку мы не претендуем на умопомрачительную точность расчетов, важнее понять физику и математику процесса.
m = 2 тонны = 2000 кг – масса автомобиля (масса авто 1940 кг, считаем что в ней водитель массой 60 кг и больше ничего/никого).
P = 670 л.с. (по паспорту 625 л.с., но реально мощность выше – измерено на динамометрическом стенде в ролике DSC OFF https://www.youtube.com/watch?v=ysg0Depmyjc. В этой статье мы ещё обратимся к замерам отсюда.)
Разгон 0-100 км/ч: 3.2-3.3 с (по паспорту, замерам)
Разгон 100-200 км/ч: 7.5-7.6 с (по паспорту, замерам)
Мощность двигателя генерируется на маховике, потом через сцепление передается в КПП, далее через дифференциалы, привода, карданный вал передается на колёса. В результате эти механизмы поглощают часть мощности и итоговая мощность, поставляемая к колесам, оказывается меньше на 18-28%. Именно мощность на колесах определяет динамические характеристики автомобиля.
У меня нет сомнений в гениальности инженеров БМВ, но, для начала, возьмем для удобства потери мощности 20%.
Вернемся к нашим физическим баранам. Для вычисления разгона нам нужно связать мощность со скоростью и временем разгона. Для этого воспользуемся вторым законом Ньютона:
Вооружившись этими знаниями, получим конечную формулу:
Выражая отсюда t, получим итоговую формулу для вычисления разгона:
На самом деле в паспорте автомобиля указывается максимальная мощность, достигаемая двигателем при определенном числе оборотов. Ниже приведена зависимость мощности двигателя от числа оборотов (синяя линия). Строго говоря, параметры этой кривой зависят от номера передачи, так что для определенности скажем, что график для 5й передачи.
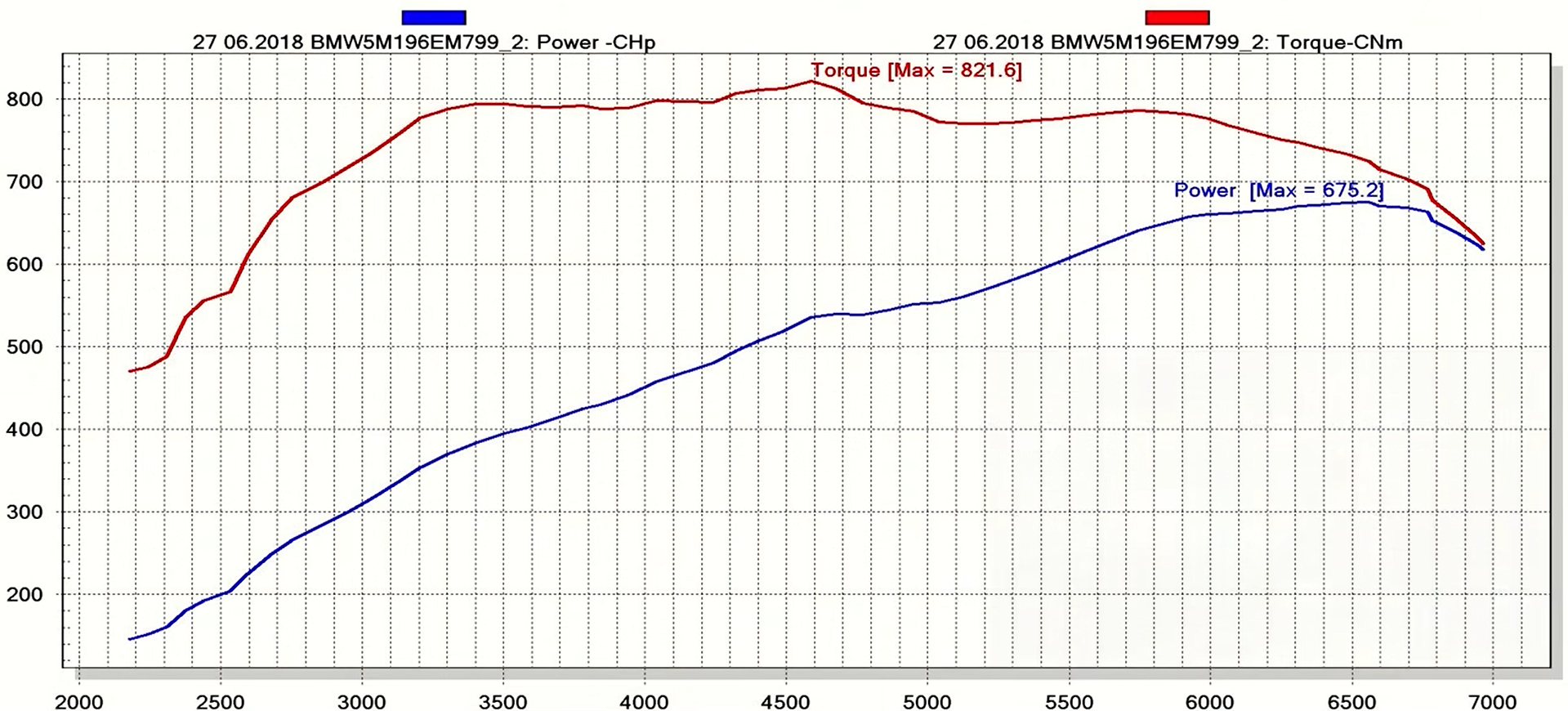
Главное, что мы должны усвоить из этого графика – мощность автомобиля не постоянна во время движения, а увеличивается по мере роста оборотов двигателя.
Перейдем к расчету разгона от 0 до 100 км/ч. Переведем скорость в м/с:
При разгоне от 0 до 100 км/ч автомобиль практически сразу переключается с первой передачи на вторую, и при достижении около 90 км/ч переключается на третью. Будем считать, что на всём протяжении разгона автомобиль разгоняется на второй передаче, причем максимальная мощность будет меньше 670 л.с., поскольку передача ниже пятой. Возьмём в качестве начальной мощности при 0 км/ч мощность 150 л.с. (при 2000 об/мин), конечную – 600 л.с. (7000 об/мин):
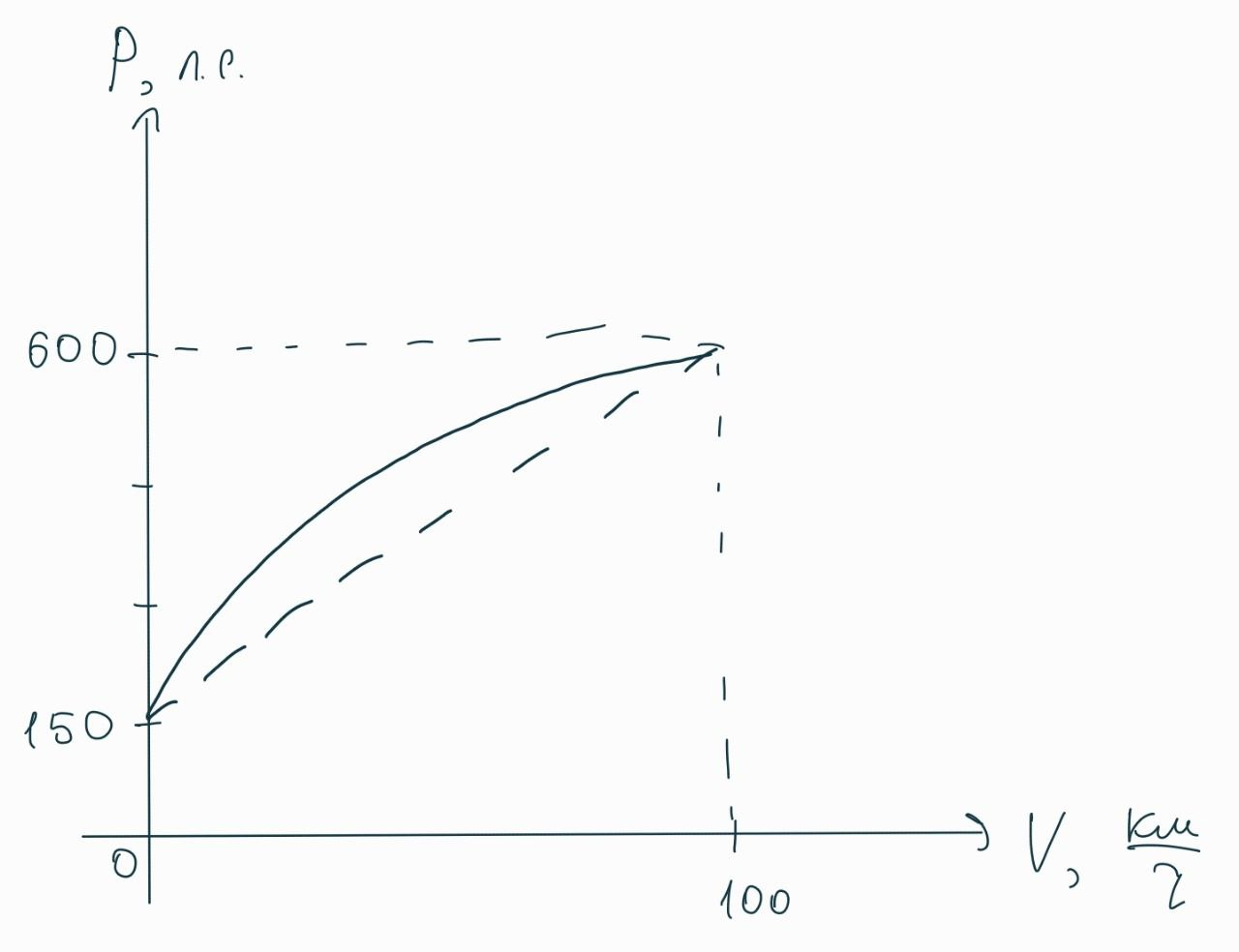
Чтобы не считать сложные интегралы для вычисления средней мощности, скажем следующие слова: учитывая приближенный характер наших расчетов, проскальзывание авто при ускорении, а также сопротивление воздуха (хотя при разгоне от 0 до 100 оно играет не такую большую роль, как при разгоне до 200 км/ч), будем считать, что мощность зависит от скорости линейно, тогда средняя мощность при разгоне от 0 до 100 км/ч составляет:
Пришло время учесть потери мощности, о которых было сказано ранее, а заодно перевести мощность в кВт (1 кВт = 1000 Вт) для удобства. Потери мощности 20%, значит эффективность 80%=0.8:
Теперь подставляем всё в конечную формулу:
Получили довольно близкий к “паспортным” 3.3 с результат, ура! Специально не стал ничего дополнительно подгонять, дабы подчеркнуть приближенный характер расчёта, хотя это было довольно просто сделать, взяв, например, чуть больше мощность.
Теперь, ради интереса и проверки самих себя, вычислим разгон 100-200 км/ч.
С ростом скорости растёт трение воздуха, для движения используются более высокие передачи КПП (3-я, 4-я, 5-я), но при этом уменьшается проскальзывание колес. Так что оставим среднюю мощность 375 л.с.
Так делать конечно же нельзя! После 2-й передачи двигатель работает на “комфортных” для себя оборотах 4000-7000 об/мин, поэтому средняя мощность будет гораздо выше, поскольку выше будет начальная мощность для каждой передачи. Здесь уже не получится считать, что автомобиль едет только на 4-й передаче на всем протяжении разгона, но можно считать, что он проехал одинаковые промежутки времени на 3-й, 4-й и 5-й передаче, и пусть график зависимости мощности от числа оборотов для них одинаков, поэтому построим общую условную кривую зависимости мощности от скорости:
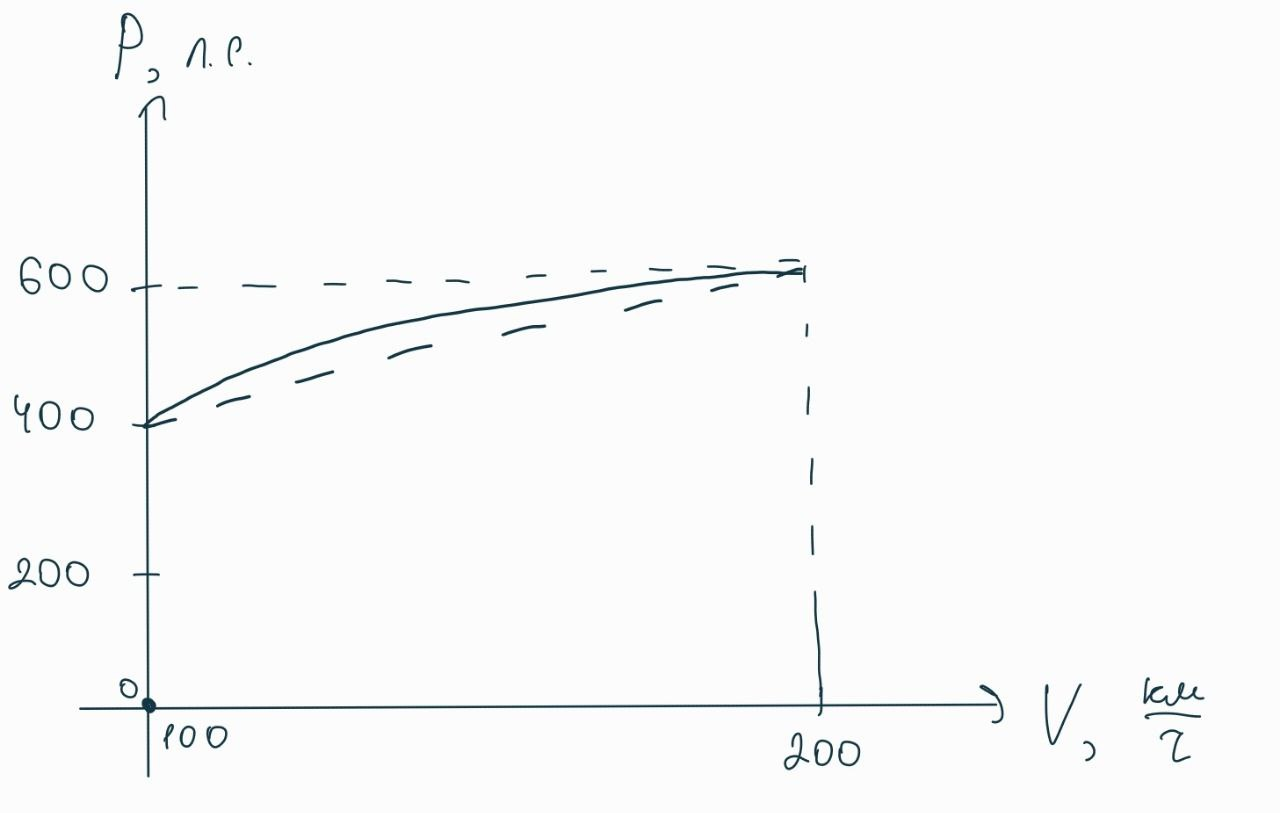
Опять же, считаем для простоты зависимость мощности от скорости линейной, тогда получаем среднюю и реальную мощность:
Тогда итоговое время разгона 100-200 км/ч:
Время разгона “по паспорту” 7.6 с. И снова мы оказались близко к истине!
P.S. не хочу объяснять, откуда взялось (V^2 – V_0^2), можете повыводить на досуге 🙂
Ну и в общем-то всё. Приведенные рассуждения и вычисления не претендуют на истину в последней инстанции и большую точность, но показывают, что зная “школьные” формулы по физике, можно решать такие интересные задачки, связанные с жизнью.
Сила сопротивления разгону
Сила
сопротивления разгону возникает
вследствие затрат энергии на раскручивание
вращающихся частей двигателя и
трансмиссии, а также колес при движении
автомобиля с ускорением.
Сила сопротивления
разгону, Н:
![]()
где
G
— вес
автомобиля, Н; g
— ускорение
силы тяжести, м/с2;
δвр
— коэффициент учета вращающихся масс
автомобиля; j
—
ускорение автомобиля, м/с2.
Мощность, кВт,
затрачиваемая на разгон:
![]()
Зависимости
силы сопротивления разгону Ри
и мощности NИ,
необходимой для преодоления этого
сопротивления, от скорости автомобиля
v
представлены
на рис. 3.20.
Коэффициент учета вращающихся масс
Этот коэффициент
учитывает дополнительное сопротивление
разгону автомобиля, вызванное
раскручиванием вращающихся частей
двигателя, трансмиссии и колес.
Коэффициент учета
вращающихся масс показывает, во сколько
раз мощность, затрачиваемая на разгон
автомобиля, больше мощности, не
обходимой для
установившегося движения:

где
Jм
— момент инерции маховика; uT,
ηтр
— передаточное число и КПД трансмиссии;
Jсум
— суммарный момент инерции всех колес
автомобиля.
Коэффициент учета
вращающихся масс для автомобиля с
полной нагрузкой можно приближенно
рассчитать по формуле
![]()
47
где
uк,
uд
— передаточные числа основной и
дополнительной коробок передач.
Условие равномерного
движения при отсутствии буксования
ведущих колес записывается в вид
3.12. Уравнение движения автомобиля
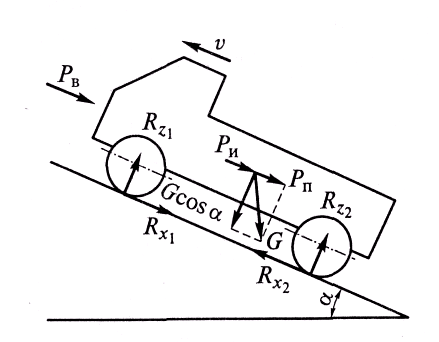
Для вывода уравнения
движения рассмотрим разгон автомобиля
на подъеме (рис. 3.21).
Спроецируем все
силы, действующие на автомобиль, на
поверхность дороги:
![]() (3.19)
(3.19)
Подставим
в формулу (3.19) касательные реакции дороги
Rx1,
и Rx2,
объединим
члены с коэффициентом сопротивления
качению ƒ и члены с ускорением j
и, принимая во внимание соотношения
ƒ(Rz2+Rz1
) = РK,
и
jk1
+ jk2
= jk
, а также коэффициент учета вращающихся
масс, получим уравнение движения
автомобиля в общем виде:
![]()
Или
![]() (3.20)
(3.20)
Уравнение движения
автомобиля выражает связь между
движущими силами и силами сопротивления
Рис.
3.21. Схема сил, действующих
на автомобиль на подъеме
движению.
Оно позволяет определить режим движения
автомобиля в любой момент.
Так, например, при
установившемся (равномерном) движении
![]()
Из уравнения (3.20)
следует, что безостановочное движение
автомобиля возможно только при условии
![]()
р
гв-
Данное неравенство
связывает конструктивные параметры
автомобиля с эксплуатационными
факторами, обусловливающими сопротивление
движению. Однако оно не гарантирует
отсутствия буксования ведущих колес.
Безостановочное движение автомобиля
без буксования ведущих колес возможно
лишь при соблюдении условия
![]()
Условия
равномерного движения при отсутствии
буксования ведущих колёс записывается
в виде
![]()
3.13. Силовой баланс автомобиля
Представим
уравнение движения автомобиля в следующем
виде:
![]() (3.21)
(3.21)
В такой форме оно
называется уравнением силового баланса
автомобиля и выражает соотношение между
тяговой силой на ведущих колесах и
силами сопротивления движению.
На основании
уравнения (3.21) строится график силового
баланса, позволяющий оценивать
тягово-скоростные свойства автомобиля.
 При
При
построении графика силового баланса
(рис. 3.22) сначала строят тяговую
характеристику автомобиля. Затем наносят
зависимость силы сопротивления
дороги от скорости. Если коэффициент
сопротивления дороги — постоянная
величина, то указанная зависимость
представляет собой прямую линию,
параллельную оси абсцисс, а при
непостоянном коэффициенте сопротивления
дороги — кривую параболической формы.
После этого от кривой, характеризующей
силу сопротивления дороги, откладывают
вверх значения силы сопротивления
воздуха при различных скоростях движения.
Полученная зависимость
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основное понятие силы тяги в физике
Определение 1
Сила тяги — это показатель силы, которую прикладывают к некоторому телу.
Она служит для обеспечения нахождения данного тела в состоянии равновесия.
Когда сила тяги прекращает свое действие — это может привести к следующим последствиям:
- остановка, которая связана с силой трения;
- состояние вязкости окружающей среды;
- множество других сопутствующих факторов и сил.
Для тела, на которое оказывает свое воздействие сила тяги, характерно постоянное движение. И обозначается следующим значение, а именно: [(v=operatorname{cons} t)]
Особым, частным случаем данного движения является состояние покоя.
При котором, скорость равна нулевому значению.
Определение 2
Состояние инерции — характер движения, при котором соблюдается постоянная скорость движения тела.
Чтобы тело поменяло свое состояние, и изменило скорость своего движения, необходимо приложить к нему силу тяги. При данных условиях скорость тела будет изменяться, причиной этого является получаемое ускорение. Также ускорение может быть отрицательным, в таком случае будет наблюдаться замедление скорости.
Показатель величины ускорения по закону физики обратно пропорционален массе тела.
Из состояния инерции труднее всего вывести тело более массивное и тяжелое.
Также величина ускорения прямо пропорциональна значению интенсивности силы, которая оказывает воздействие на тело.
Данное утверждение можно преобразовать и вывести в виде формулы:
Формула
[mathrm{F}=mathrm{m} cdot mathrm{a}]
Где: F — сила тяги, m — масса тела, которая оказывает воздействие на тело, a — ускорение.
Данная формула наглядно характеризует второй закон Ньютона.
Основные формулы для расчета силы тяги
Наглядно силу тяги можно рассмотреть на примере спортсмена штангиста.
Именно на данном примере можно подробно понять, как приложенная сила, может вывести тело из состояния равновесия.
Распишем все операции, выполняемые спортсменам поэтапно:
- первоначально штанга находится в состоянии инерции, иными словами имеет состояние покоя;
- при отрыве от поверхности земли штанги, все мышцы спортсмена имеют способность сокращаться, с силой которая не превышает вес самой штанги (иначе это звучит как: величина силы с которой ее к себе притягивает гравитация Земли);
- при отрыве от пола, штанги на определенную высоту, происходит процесс ускорения;
Силой тяги для снаряда, который осуществляет движение будет являться величина силы с которой сокращаются мышцы спортсмена.
Для данного случая, обязательно должно соблюдаться следующее условие:
[F_{M}>F_{T} text {. то есть } F_{M}>m times g]
Где:
- [F_{m}] — сила, с которой происходит сокращение мышечной массы (сила тяги для данного случая);
- [F_{т}] сила тяжести или гравитационная;
- m — масса, которая оказывает воздействие на тело;
- g — показатель ускорение свободного падения.
Характер движения тела по инерции всегда нужно уметь отличать от движения, которое совершается равномерно. Следовательно, в случае, когда сила тяги имеет способность уравновешиваться сторонними силами (противодействующими).
Например:
Автомобиль совершает движение и его двигатель находится в состоянии работы. Работающий двигатель придает силу на колеса, через трансмиссию, проделывая следующие операции:
- преодолевает силу трения, которая возникает внутри всего механизма;
- сопротивление воздуха;
- процесс трения колес о любую поверхность.
Для определения силы тяги, необходимо знать следующие данные:
- t — время, за которое происходит разгон транспортного средства;
- [v] — необходимая скорость;
- m — непосредственная масса автомобиля.
Сила определяется по формуле:
[F=m times frac{V}{t}]
Из формулы видно, что ускорение выражено как: деление скорости на время разгона транспортного средства:
[a=frac{V}{t}]
Через мощность можно выразить силу.
Определение 3
Мощность — это совершенная работа, любым источником энергии.
Если высокая мощность, то следует что, время за которое источник развивает силу будет уменьшаться. А именно: способность разогнать тело определенной массы равной m до необходимой величины скорости движения.
Значение совершаемой работы прямо пропорционально силе и вычисляется по формуле:
[A=F times s]
Где: S — расстояние, на которое при помощи силы, перемещается тело;
Расстояние можно определить по формуле, выразив его через скорость тела и время движения:
[s=v cdot t]
Затем определяется мощность, которая должна выполнять в единицу времени и выражается следующей формулой:
[mathrm{N}=frac{d}{t}]
Окончательное уравнение выражает так:
[frac{A}{t}=frac{F cdot V cdot t}{t} Rightarrow N=F cdot V Rightarrow F=frac{N}{V}]
Нет времени решать самому?
Наши эксперты помогут!
Пример решения задачи на определение силы тяги
Нужно определить показатель силы тяги транспортного средства. Оно движется с ускорением равным a. Масса автомобиля равна 1,5 тонны и сила трения составляет 10 процентов от всей силы тяжести.
Сила тяги будет определяться как сумма двух основных сил:
- Автомобиль, который разгоняется с заданным значением ускорения: [F_{1}=m cdot a]
Где: m — масса автомобиля, a — показатель ускорения.
- Преодоление силы трения:
[F_{2}=mu cdot m cdot g]
Где: [mu] — коэффициент, который характеризует силу трения, g — значение ускорения свободного падения.
Все числовые известные значения подставим в формулу, и вычислим нужное нам значение силы. В процессе вычисления все единицы измерения переводятся в единицы системы СИ, а именно: килограммы.
[F=F_{1}+F_{2}=m cdot a+mu cdot m cdot g]
[mathrm{F}=1500 cdot 3+0.1 cdot 9.8 cdot 1500=1500 cdot(3+0.98)=5970]
Ответ: 5970.
Что такое сила тяги и по какой формуле её находить ?
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.

Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- силы трения (покоя, качения, скольжения),
- сопротивления воздуха (газа),
- сопротивления воды и др.
Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т.е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).

Примеры из жизни
Насколько вы сильны?
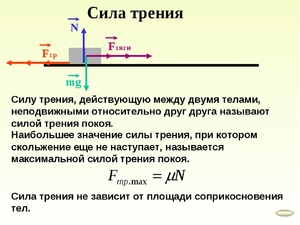
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н
2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)
0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Сила как мера взаимодействия тел. Равнодействующая сил
Согласно закону инерции (см. §17 данного справочника), если на тело не действуют другие тела, оно, либо покоится, либо движется прямолинейно и равномерно.
Чтобы сдвинуть тело с места или остановить его движение, каким-то образом изменить его скорость по величине или направлению, необходимо подействовать на него другими телами. Т.е., для изменения скорости необходимо взаимодействие тел.
Примеры изменения скорости при взаимодействии тел
Для количественного описания взаимодействия тел в физике вводят понятие «силы».
Напомним, что вектор – это направленный отрезок. Характеристиками вектора являются его величина и направление. Подробней о векторных величинах – см. §6 данного справочника.
п.2. Зависимость ускорения тела от приложенной силы
Сила является причиной изменения скорости тела. А само изменение скорости тела за единицу времени описывается физической величиной, которую называют ускорением (см. §11 данного справочника).
Чем больше приложенная к телу сила, тем большим будет изменение скорости, т.е. ускорение. Многочисленные опыты доказывают, что величина ускорения прямо пропорциональна величине силы: $$ asim F $$
С другой стороны, если одну и ту же силу прикладывать к телам разной массы, ускорение будет разным. Чем больше масса, тем меньше полученное ускорение. Опыты подтверждают, что величина ускорения обратно пропорциональна массе тела: $$ asim frac 1m $$
Этот результат согласуется с понятием массы как меры инертности тел.
п.3. Единицы измерения силы
Чтобы перейти в зависимости между ускорением, силой и массой от знака пропорциональности (
) к знаку равенства (=), условимся измерять силу в ньютонах: $$ 1text=1textcdotfrac>^2>=1fraccdot text>^2> $$
Получаем формулу для расчета силы.
п.4. Сила как векторная величина. Равнодействующая сил
В формулу для расчета силы входит масса (скалярная величина, имеющая некоторое значение) и ускорение (векторная величина, имеющая не только некоторое значение, но и направление). Значит, сила – также векторная величина, причем направления векторов силы и ускорения совпадают.
При этом направление векторов скорости (overrightarrow) и перемещения (overrightarrow) может, как совпадать, так и отличаться от направления вектора силы (overrightarrow).
На чертежах силу изображают в виде вектора, т.е. направленного отрезка.
Начало вектора – это точка приложения силы. Длина вектора в заданном масштабе соответствует модулю значения силы.
Результат действия силы зависит от её модуля, направления и точки приложения.
п.5. Задачи
Задача 1. Найдите величину равнодействующей двух сил 6 Н и 8 Н, если силы действуют: а) в одном направлении; б) в противоположных направлениях; в) перпендикулярно друг другу.
a)
Если силы действуют в одном направлении, их равнодействующая будет направлена в том же направлении. Величина равнодействующей будет равна сумме: $$ F=F_1+F_2, F=6+8=14 (text) $$
б)
Если силы действуют в противоположных направлениях, их равнодействующая будет направлена в сторону большей силы, т.е. (overrightarrow). Величина равнодействующей будет равна разности: $$ F=F_2-F_1, F=8-6=2 (text) $$
в)
Если силы действуют перпендикулярно, их равнодействующая равна диагонали прямоугольника, построенного на векторах (overrightarrow) и (overrightarrow), и направлена, как показано на рисунке.
По теореме Пифагора: $$ F=sqrt, F=sqrt=10 (text) $$
Задача 2. Компьютерную мышку тянут по столу. Изобразите на рисунке все силы, действующие на мышку. Как будет выглядеть рисунок, если размерами мышки пренебречь и считать её материальной точкой?

(overrightarrow) — сила тяги
(overrightarrow) — сила реакции опоры (стола)
(moverrightarrow) — сила тяжести
(moverrightarrow_>) — сила трения
Если считать мышку материальной точкой, все силы будут приложены в этой точке.
Задача 3. Под действием какой силы тело массой 100 г приобретает ускорение 2 м/с 2 ?
$$ F=ma, F=0,1cdot 2=0,2 text $$ Ответ: 0,2 Н
Задача 4. Автомобиль массой 1,5 т трогается с места и за 10 с набирает скорость 36 км/ч.
Найдите силу тяги, действующую на автомобиль.
Ускорение автомобиля $$ a=frac=frac vt $$ Сила тяги $$ F=ma=frac$$ $$ F=frac=1500 (text)=1,5 (text) $$ Ответ: 1,5 кН
Задача 5*. На тело действуют четыре силы: 120 Н вертикально вверх, 60 Н вертикально вниз, 140 Н горизонтально влево, 60 Н горизонтально вправо. Чему равна равнодействующая эти сил? 
Горизонтальная составляющая направлена влево и равна $$ 140-60=80 text $$ Вертикальная составляющая направлена вверх и равна $$ 120-60=60 text $$ По теореме Пифагора равнодействующая равна $$ sqrt=100 text $$ Направление равнодействующей – влево вверх, как показано на рисунке.
Ответ: 100 H
Как найти ускорение — определение и формулы расчета в физике
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( beginaend=frac м)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;fract) , где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;fract) , где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
Максимальное ускорение
(a_=omega v_,) где (a_) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow>=frac) , где (overrightarrow>) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х) :
(a_x=frac>t) , где где (a_x) — проекция ускорения на ось (х) , (V_x) — проекция текущей скорости на ось (х) , (V_) — проекция начальной скорости на ось (х) , (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Загрузить PDF
Загрузить PDF
Ускорение характеризует быстроту изменения скорости движущегося тела.[1]
Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. [2]
Ускорение измеряется в метрах в секунду за секунду (м/с2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.
-

1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с2.
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.[4]
Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
-

2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = vк – vн и Δt = tк – tн, где vк – конечная скорость, vн – начальная скорость, tк – конечное время, tн – начальное время.[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что tн = 0.
-

3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (vк – vн)/(tк – tн). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк – vн)/(tк – tн)
- Напишите переменные: vк = 46,1 м/с, vн = 18,5 м/с, tк = 2,47 с, tн = 0 с.
- Вычисление: a = (46,1 – 18,5)/2,47 = 11,17 м/с2.
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк – vн)/(tк – tн)
- Напишите переменные: vк = 0 м/с, vн = 22,4 м/с, tк = 2,55 с, tн = 0 с.
- Вычисление: а = (0 – 22,4)/2,55 = -8,78 м/с2.
Реклама
-

1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.[6]
Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.- Второй закон Ньютона описывается формулой: Fрез = m x a, где Fрез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с2).
-

2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
-

3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.[7]
Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с2.[8]
-

4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
-

5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с2
Реклама
-
1
Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Движение автомобиля Изменение скорости Значение и направление ускорения Движется вправо (+) и ускоряется + → ++ (более положительное) Положительное Движется вправо (+) и замедляется ++ → + (менее положительное) Отрицательное Движется влево (-) и ускоряется – → — (более отрицательное) Отрицательное Движется влево (-) и замедляется — → – (менее отрицательное) Положительное Движется с постоянной скоростью Не меняется Равно 0 -

2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с2. Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с2.
-

3
Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
Реклама
- Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
- Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 – 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с2.
Об этой статье
Эту страницу просматривали 190 101 раз.

