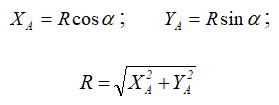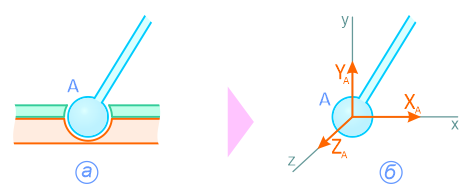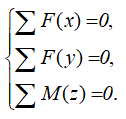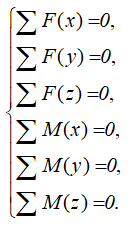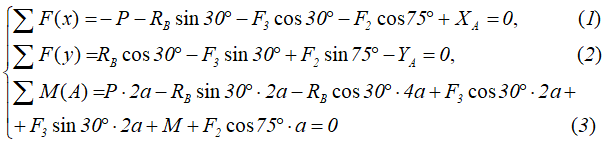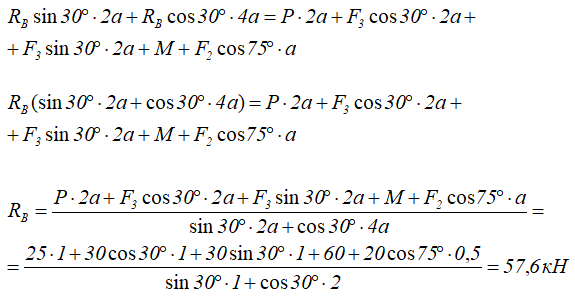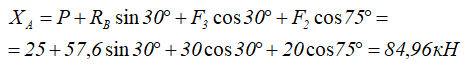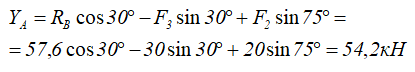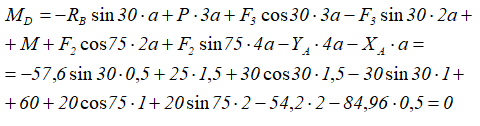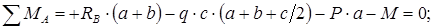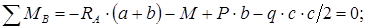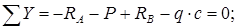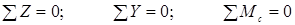Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
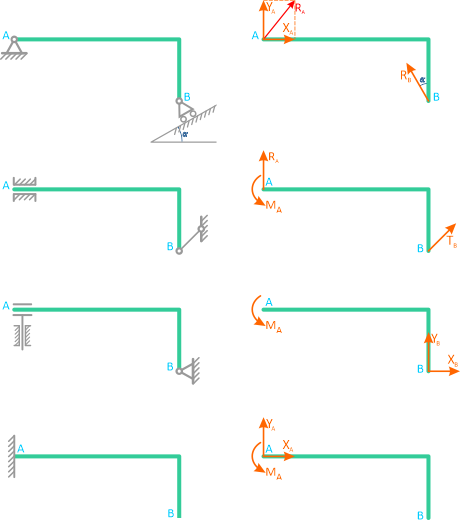
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
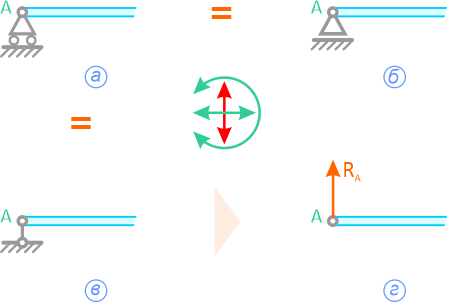
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
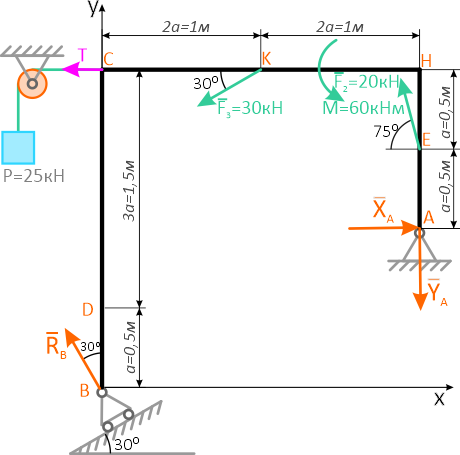
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
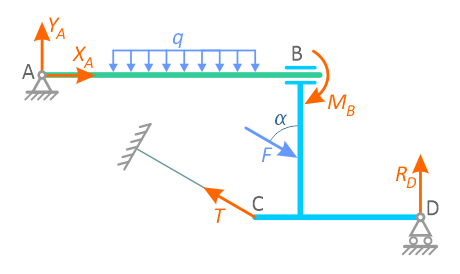
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.
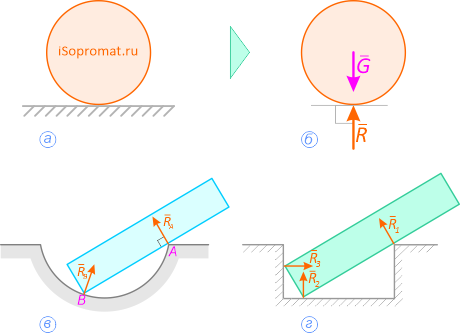
Тело находится на выпуклой или вогнутой поверхности
Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой (vec{N}). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.
Примечания:
- Нормаль – значит, перпендикуляр.
- Искривленную, т.е., выпуклую, или вогнутую поверхность, можно считать частью сферы. Центр сферы – точка, она находится внутри сферы, от этой точки к поверхности сферы можно провести радиус.
(vec{N} left( H right) ) – сила, с которой опора действует на тело.
Рис. 1. Тело (шар) опирается на выпуклую – а) и вогнутую – б) поверхность. А поверхность реагирует на вес тела силой нормальной реакции
Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.
Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция (vec{N}) направлена по радиусу внутрь сферической поверхности к ее центру.
Тело опирается на поверхность в двух точках
На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.
Рис. 2. Однородный стержень опирается на поверхность двумя точками, в каждой из точек сила реакции располагается перпендикулярно поверхности
В точках соприкосновения поверхность отвечает телу силой (vec{N}) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.
Cилы реакции (vec{N_{1}}) и (vec{N_{2}}) имеют различные направления и в общем случае не равны по модулю.
[large vec{N_{1}} ne vec{N_{2}}]
Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.
Как рассчитать силу нормальной реакции
Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.
Примечание: Сила реакции (vec{N}) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.
Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.
На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.
Рис. 3. Тело опирается на поверхность горизонтальную – а) и наклонную – б), составляя силовые уравнения для сил, расположенных перпендикулярно соприкасающимся поверхностям, рассчитывают силу реакции опоры
Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.
По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.
[large boxed{ N = m cdot g }]
(m vec{g} left( H right) ) – сила, с которой тело действует на опору;
(vec{N} left( H right) ) – сила, с которой опора отвечает телу;
Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы (m vec{g}) на ось — это (mg_{y}), она будет направлена противоположно реакции опоры (vec{N}) и численно равна ей.
Примечание: Выражение «численно равна» нужно понимать, как «длины векторов равны».
[large boxed{ N = m cdot g cdot cos(alpha) }]
(alpha left(text{рад} right) ) – угол между силой (mg) и осью Oy.
Итоги
- Сила, с которой опора сопротивляется воздействию тела, называется силой реакции опоры, она имеет электромагнитную природу.
- Ее, как и любую силу, измеряют в Ньютонах, обозначают так: (vec{N}).
- Реакция опоры направлена перпендикулярно поверхности, поэтому ее называют силой нормальной реакции.
- Сила (vec{N}) распределена по площади соприкосновения, но для удобства ее обычно считают сосредоточенной силой. Ее изображают исходящей из точки, расположенной под центром масс тела на границах между поверхностями тела и опоры.
- Чтобы рассчитать силу реакции, нужно знать законы Ньютона, уметь составлять силовые уравнения и понимать, что такое равнодействующая.
Представьте учебник по какой-либо дисциплине, лежащий на деревянной парте.
Книга покоится, и это, по первому закону Ньютона, означает, что силы, действующие на нее, уравновешены либо вовсе отсутствуют.
Одна сила на книгу точно действует. Это сила тяжести. Сила тяжести действует на все тела, находящиеся в гравитационном поле Земли. Обозначается она обычно вот так: ,mvec{g},. Эта сила всегда тянет предметы вниз, к центру Земли. Обозначим ее на нашем рисунке.
Мы знаем, что книжка покоится, значит, должна существовать сила, противостоящая силе тяжести. Что же это за сила? Сила реакции опоры.
Сила реакции опоры – это сила, действующая на тело со стороны поверхности, на которой оно находится. Обычно она обозначается вот так: vec{N}. Направлена она всегда перпендикулярно к поверхности соприкосновения.
В нашем случае сила реакции опоры препятствует движению предмета вниз, поэтому вектор этой силы направлен вверх. Важно понимать, что он может быть направлен иначе.
Например, представим скалолаза, карабкающегося по отвесной стене с помощью каната.
Мне удалось нарисовать только один его ботинок, и в принципе этого достаточно. Скалолаз будет давить на стену с некоторой силой, а стена будет давить на него в ответ, не давая его ноге перемещаться в горизонтальном направлении. Сила реакции опоры будет действовать в направлении, показанном на рисунке.
Чтобы найти величину силу реакции опоры, обычно применяют второй закон Ньютона. В случае с книгой его нужно использовать для оси y:
vec{a}_y=dfrac{varSigmavec{F}_y}{m}
Ускорение учебника равно нулю, он покоится. Сила реакции опоры направлена вверх, сила тяжести направлена вниз. Укажем это с помощью знаков:
0=dfrac{N-mg}{m}
Если мы умножим обе части уравнения на массу, то получим очень незамысловатый ответ:
0=N-mg
N=mg
Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.
Реакции связей — это усилия, с которыми связи действуют на данное тело.
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными.
Рассмотрим реакции связей основных типов, встречающихся при решении задач: гладкой поверхности, ребра, гибкой нити, стержня, шарнирных опор и заделок, а также примеры замены связей их реакциями.
Реакции гладкой поверхности и ребра
Ниже приведены примеры замены связей гладкой поверхности и ребра их реакциями.
На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.
а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям
Рисунок 1.1
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1).
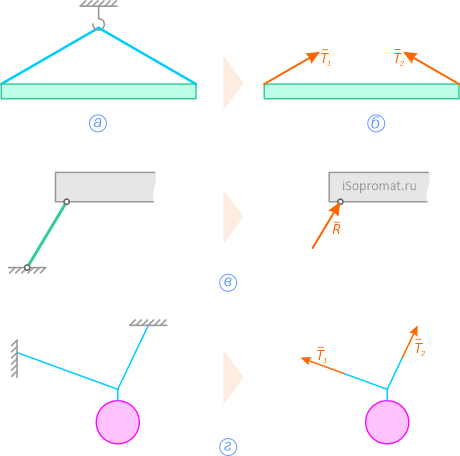
Реакции связей нити и стержня
Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня) (рисунок 1.2).
а – балка висит на двух тросах;
б – действие тросов заменено силами Т1 и Т2;
в – связь «идеальный стержень»;
г – связь «идеальная нить»
Рисунок 1.2
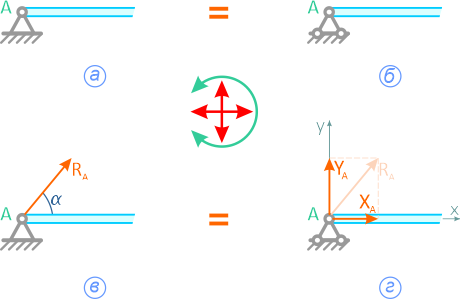
Реакции связей шарнирных опор
Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3,а или 1.3,б). Она может быть заменена либо силой R с углом α (рисунок 1.3,в), либо двумя силами, например, XA и YA (рисунок 1.3,г).
Рисунок 1.3
Всегда можно перейти от R и α к XA и YA (и наоборот):
Шарнирно-подвижная опора (рисунок 1.4,а, б, в) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное.
Реакция R может быть направлена только по нормали к опорной поверхности (рисунок 1.4, г).
Рисунок 1.4
В следующем примере, связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), а их действие заменено силами XA, YA и RB.
Рисунок 1.5
Подробнее про связи и реакции связей смотрите в нашем видео:
Другие видео
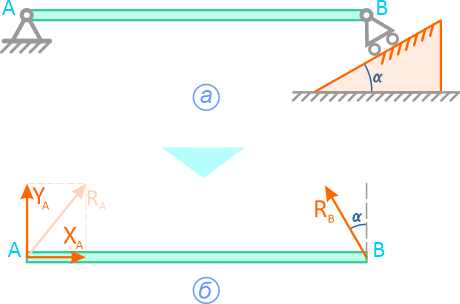
Реакции связи в заделках
Все виды заделок исключают поворот, поэтому в них всегда возникает связь «момент».
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросив втулку – получаем действие на стержень силы RD и момента MD.
Рисунок 1.6
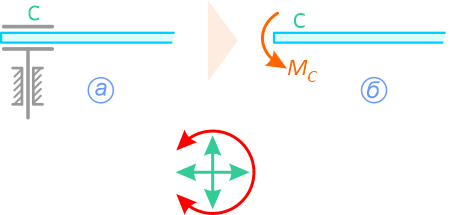
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет только момент MC (рисунок 1.7, б).
Рисунок 1.7
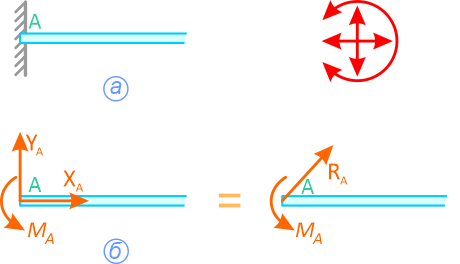
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA) и момент ΜA (рисунок 1.8).
Рисунок 1.8
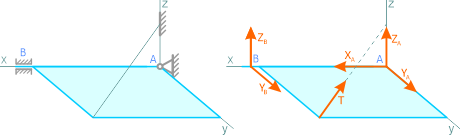
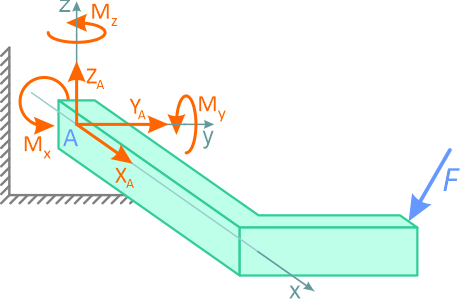
Реакции пространственных связей
Трехмерная шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменяется системой сил (рисунок 1.9, б) XA, YA и ZA, т.е. силой, неизвестной по величине и направлению.
Рисунок 1.9
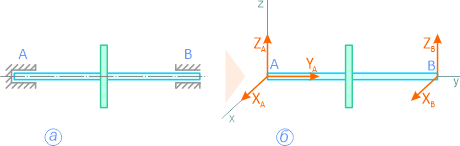
На рисунке 1.10, а показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA, YA, ZA и XB, ZB (рисунок 1.10, б).
Рисунок 1.10
На следующих рисунках показаны примеры замены различных типов связей их реакциями.
Рисунок 1.11
Трехмерная система удерживаемая в равновесии тремя типами связей: скользящей заделкой, шарнирно неподвижной опорой и тросом.
Рисунок 1.12
В общем случае пространственного нагружения, в глухой заделке может возникать до шести реакций связей: три силы и три момента.
Рисунок 1.13
Величина и истинное направление сил реакций связей определяются из уравнений равновесия рассматриваемой системы.
Для плоской системы сил составляется 3 уравнения
Для пространственной системы — до шести уравнений статики.
Из которых выражаются и рассчитываются искомые реакции.
Пример определения сил реакций связей
Задача
Жесткая рама закреплена в точке A шарнирной связью, а в точке B удерживается в состоянии статического равновесия опорой на катках, с упором в наклонную плоскость под углом 30°.
В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25кН.
На раму действует пара сил с моментом M=60кНм и две силы F2 и F3 приложенные в точках K и E и расположенные под углами 30° и 75° к горизонтальной оси.
Требуется определить реакции связей в точках A и B, вызываемые заданными действующими нагрузками.
При расчетах, принять размер a=0,5м.
Решение
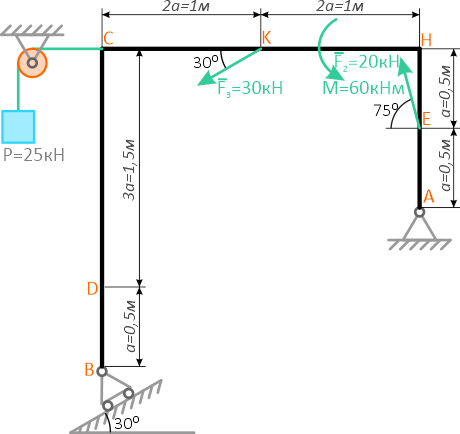
Рассмотрим равновесие рамной пластины.
Проведем координатные оси x-y и изобразим действующие на пластину внешние нагрузки: силы F, пару сил с моментом M, натяжение троса T (по модулю T=P) и реакции связей XA, YA, RB.
Реакцию неподвижной шарнирной опоры A изображаем двумя составляющими её связями. Реакция на катке направлена перпендикулярно опорной плоскости.
Для полученной плоской системы сил составим три уравнения равновесия системы.
При вычислении моментов сил F относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие Fx=Fcosα и Fy=Fsinα и учтём что mA(F)=mA(Fx)+mA(Fy).
Запишем уравнения сумм проекций сил на оси x и y, а также суммы моментов относительно любой точки системы, например, точки A.
Решая полученную систему уравнений, определяем неизвестные реакции связей катка и шарнирно-неподвижной опоры.
Из уравнения (3) находим реакцию катка
Из уравнения (1) горизонтальную реакцию в точке A
Из уравнения (2) — вертикальную.
Положительные значения найденных реакций говорят о том, что направление связей было выбрано, верно.
Проверку можно выполнить, составив уравнение суммы моментов, в котором будут записаны все искомые реакции, например, относительно точки D:
Ноль, полученный в ответе, означает правильность составления и решения уравнений
Ответ: Получены следующие значения сил реакций связей: в катке RB=57,6кН, в шарнирной опоре XA=84,96кН и YA=54,2кН.
Другие примеры решения задач >
Проекция силы на ось >
Определение опорных реакций
Способы определения опорных реакций изучаются в курсе теоретической механики. Остановимся только практических вопросах методики вычисления опорных реакций, в частности для шарнирно опертой балки с консолью (рис. 7.4).

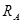
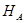
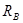
Нахождение и проверка опорных реакций в шарнирной опоре
Для вычисления значений реакций опор составим уравнения статики:
Сумма проекций всех сил (активных и реактивных) на ось z равна нулю: 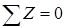
Поскольку на балку действуют только вертикальные нагрузки (перпендикулярные к оси балки), то из этого уравнения находим: горизонтальная реакция неподвижной шарнирной опоры 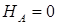
Сумма моментов всех сил относительно опоры А равна нулю: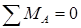
Правило знаков для момента силы: считаем момент силы положительным, если он вращает балку относительно точки против хода часовой стрелки.
Необходимо найти равнодействующую распределенной погонной нагрузки. Распределенная погонная нагрузка равна площади эпюры распределенной нагрузки 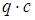
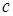
Тогда
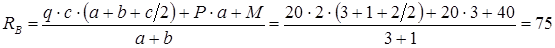
Сумма моментов всех сил относительно опоры B равна нулю:
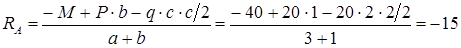
Знак «минус» в результате говорит: предварительное направление опорной реакции 
Проверка опорных реакций
Сумма проекций всех сил на ось y должна быть равна нулю: 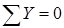
Силы, направление которых совпадает с положительным направлением оси y, проектируются на нее со знаком «плюс»:
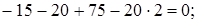
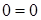
Нахождение опорных реакций в жесткой заделке
Найдем реакции опор в жесткой заделке. Для определения опорных реакций составляются уравнения статики:
Из первого уравнения определяется реакция 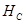
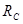
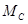
Проверка, как правило, не производится.