Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.
Тело находится на выпуклой или вогнутой поверхности
Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой (vec{N}). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.
Примечания:
- Нормаль – значит, перпендикуляр.
- Искривленную, т.е., выпуклую, или вогнутую поверхность, можно считать частью сферы. Центр сферы – точка, она находится внутри сферы, от этой точки к поверхности сферы можно провести радиус.
(vec{N} left( H right) ) – сила, с которой опора действует на тело.

Рис. 1. Тело (шар) опирается на выпуклую – а) и вогнутую – б) поверхность. А поверхность реагирует на вес тела силой нормальной реакции
Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.
Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция (vec{N}) направлена по радиусу внутрь сферической поверхности к ее центру.
Тело опирается на поверхность в двух точках
На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.

Рис. 2. Однородный стержень опирается на поверхность двумя точками, в каждой из точек сила реакции располагается перпендикулярно поверхности
В точках соприкосновения поверхность отвечает телу силой (vec{N}) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.
Cилы реакции (vec{N_{1}}) и (vec{N_{2}}) имеют различные направления и в общем случае не равны по модулю.
[large vec{N_{1}} ne vec{N_{2}}]
Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.
Как рассчитать силу нормальной реакции
Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.
Примечание: Сила реакции (vec{N}) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.
Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.
На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.

Рис. 3. Тело опирается на поверхность горизонтальную – а) и наклонную – б), составляя силовые уравнения для сил, расположенных перпендикулярно соприкасающимся поверхностям, рассчитывают силу реакции опоры
Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.
По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.
[large boxed{ N = m cdot g }]
(m vec{g} left( H right) ) – сила, с которой тело действует на опору;
(vec{N} left( H right) ) – сила, с которой опора отвечает телу;
Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы (m vec{g}) на ось — это (mg_{y}), она будет направлена противоположно реакции опоры (vec{N}) и численно равна ей.
Примечание: Выражение «численно равна» нужно понимать, как «длины векторов равны».
[large boxed{ N = m cdot g cdot cos(alpha) }]
(alpha left(text{рад} right) ) – угол между силой (mg) и осью Oy.
Итоги
- Сила, с которой опора сопротивляется воздействию тела, называется силой реакции опоры, она имеет электромагнитную природу.
- Ее, как и любую силу, измеряют в Ньютонах, обозначают так: (vec{N}).
- Реакция опоры направлена перпендикулярно поверхности, поэтому ее называют силой нормальной реакции.
- Сила (vec{N}) распределена по площади соприкосновения, но для удобства ее обычно считают сосредоточенной силой. Ее изображают исходящей из точки, расположенной под центром масс тела на границах между поверхностями тела и опоры.
- Чтобы рассчитать силу реакции, нужно знать законы Ньютона, уметь составлять силовые уравнения и понимать, что такое равнодействующая.
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
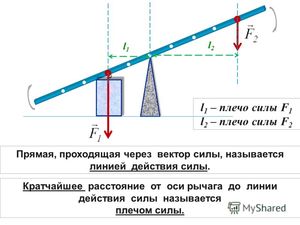
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:



Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
![]()
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:


Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Статика – один из разделов современной физики, который изучает условия нахождения тел и систем в механическом равновесии. Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.
Второй и третий законы Ньютона
Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.
Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:
F = m*a
Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.
Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:
F1¯ = -F2¯
Эта запись является математическим выражением для третьего ньютоновского закона.
При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.
Сила реакции опоры
Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.
Сила N – это контактная величина. Если имеется контакт между телами, то она появляется всегда. В примере выше значение величины N равно по модулю весу тела. Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела – это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.
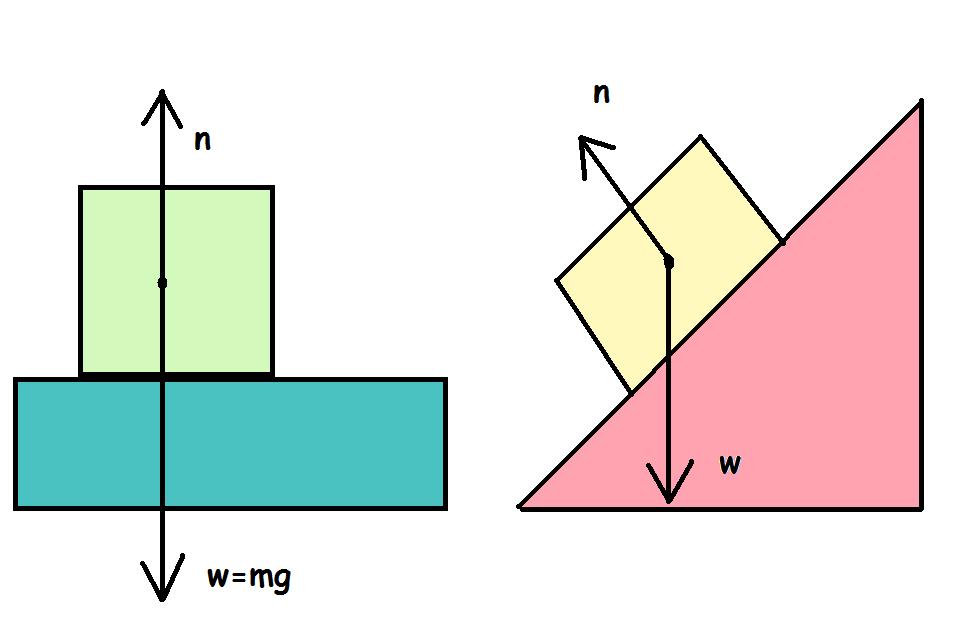
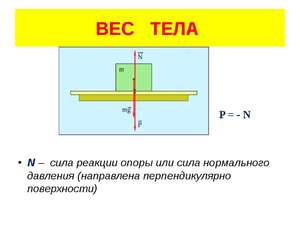
Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.
Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).
Физическая причина появления силы N
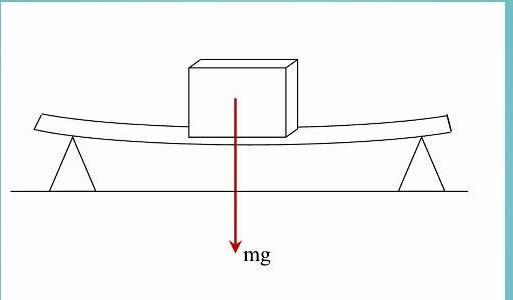
Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.
Если рассматривать вопрос на атомном уровне, то появление величины N – это результат действия принципа Паули. При небольшом сближении атомов их электронные оболочки начинают перекрываться, что приводит к появлению силы отталкивания.
Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.
Как вычислять силу N?
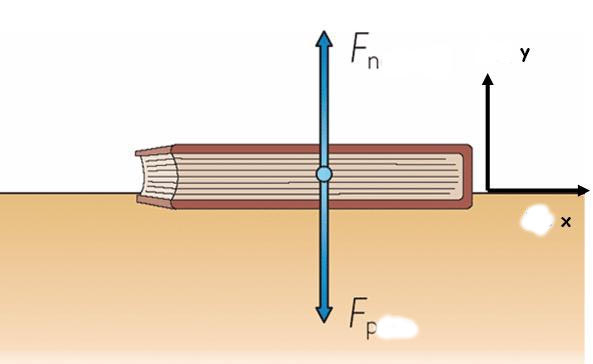
Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.
Методика определения величины N заключается в следующем:
- сначала записывают второй закон Ньютона для данной системы, учитывая все действующие в ней силы;
- находят результирующую проекцию всех сил на направление действия реакции опоры;
- решение полученного уравнения Ньютона на отмеченное направление приведет к искомому значению N.
При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.
Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.
Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.
Задача со стаканом на столе
Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?
Запишем динамическое уравнение. Имеем:
m*a = P1 + P2 – N
Здесь P1 и P2 – вес стакана с водой и книги соответственно. Поскольку система находится в равновесии, то a=0. Учитывая, что вес тела равен силе тяжести, а также пренебрегая массой пластикового стакана, получаем:
m1*g + m2*g – N = 0 =>
N = (m1 + m2)*g
Учитывая, что плотность воды равна 1 г/см3, и 1 мл равен 1 см3, получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.
Задача с доской, двумя опорами и грузом

Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?
Прежде чем переходить к решению задачи, следует ввести понятие момента силы. В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.
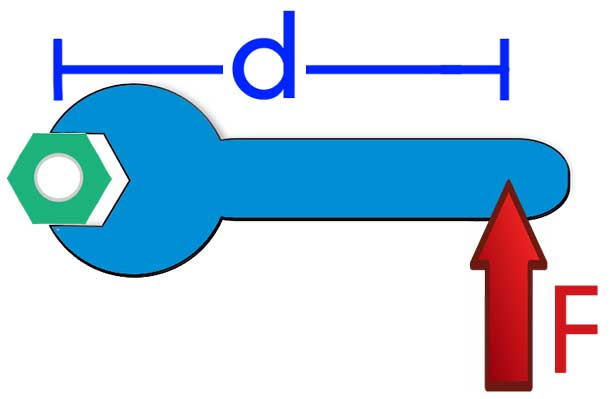
Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:
M1 = -m*g*L/2
Здесь L/2 – рычаг действия силы тяжести. Знак минус появился потому, что момент M1 осуществляет вращение против часовой стрелки.
Момент силы реакции опоры будет равен:
M2 = N*L
Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:
M1 + M2 = 0 =>
N*L + (-m*g*L/2) = 0 =>
N = m*g/2 = 3*9,81/2 = 14,7 Н
Заметим, что от длины доски сила N не зависит.
Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.
Некоторые физические явления сложны для понимания школьников. К таковым относится и сила реакция опоры. Скорее всего причина тут кроется в том, что этот тип взаимодействия между физическими предметами и телами противоречит житейской логике.
Между тем, достаточно немного усидчивости и терпения, чтобы убедиться, что это совсем не так.
Что такое сила реакции опоры
Прежде всего дадим определение данной силе. Сила реакции опоры (N) представляет собой взаимодействие на молекулярном уровне.
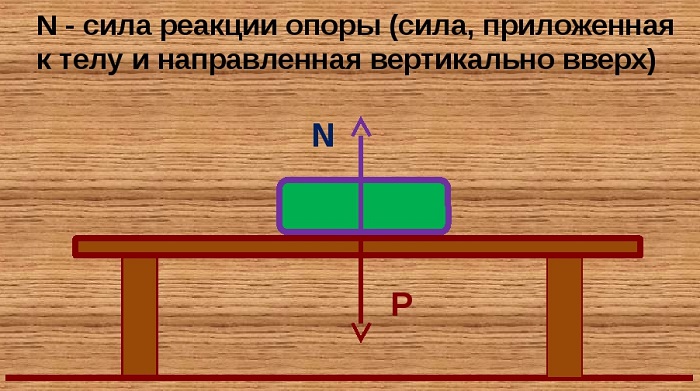
Это сила, приложенная к телу и направленная вертикально вверх.
Сила реакции опоры — сила упругости, возникающая при малых деформациях опоры, всегда перпендикулярна опоре, N = P.
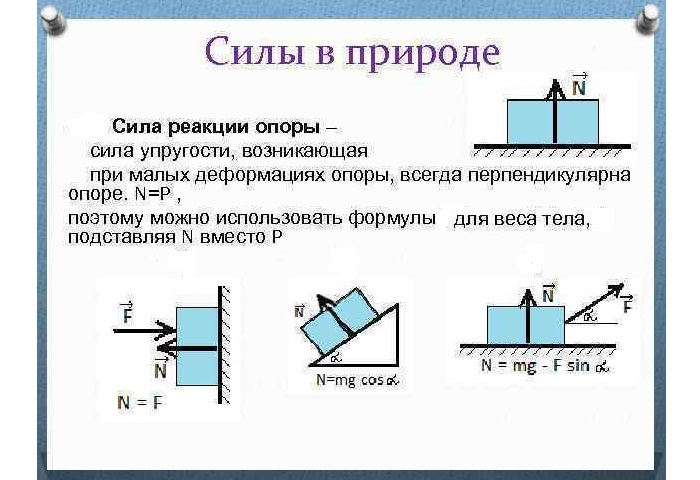
Книга, положенная на стол, давит на ее поверхность с определенной нагрузкой, но молекулы, сжатые ею, хотят снова прийти в равновесие и поэтому давят на книгу ровно с такой же силой. Если бы в природе не существовало этого взаимодействия, то тела не выдерживали бы нагрузки. Из этого можно заключить, что сила реакции опоры представляет собой разновидность силы упругости.
Единица измерения, как и для всех силы (упругости, трения и др.), – Н (Ньютоны).
Примеры решения задач
Задача 1
Определить реакции опор горизонтальной балки от заданной нагрузки.
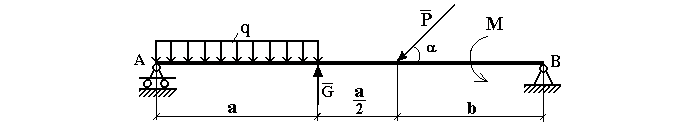
Рис. 1
Дано:
-
P = 20 кН;
-
G = 10 кН;
-
М = 4 кНм;
-
q = 2 кН/м;
-
a = 2 м;
-
b = 3 м;
-
α = 300.
Решение:
Перед тем, как начать составлять систему уравнений, необходимо несколько преобразовать систему балки:
-
Опора А покоится на подвижной опоре, которая может двигаться в горизонтальной плоскости, поэтому имеет только вертикальную составляющую реакции опоры – RA.
-
Опора В абсолютно неподвижна, и ее реакция опоры состоит из двух взаимодействий, направленных вдоль линий оси: XB и YB.
-
Распределенную нагрузку q для простоты можно заменить одиночной нагрузкой Q. Она будет располагаться ровно посередине отрезка. Находится по формуле: Q = (q × a). Делаем расчет и узнаем, чему равна Q = 2 × 2 = 4 кН.
-
Сила P не принадлежит ни к одной из плоскостей, а находится как бы между ними. Поэтому ее раскладывают на две составляющие: Px и Py. Это не значит, что они делят ее пополам. Для ее разложения понадобится вспомнить закон Пифагора. Px = P × cos α, Py = P × sin α.
После всех этих преобразований схема балки примет следующий вид:
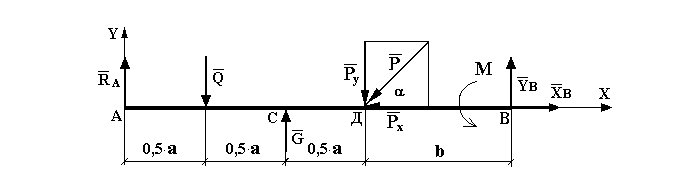
Рис. 2
Теперь можно выписывать силы по принадлежности:
∑Fx = XB – P × cos α = 0;
∑Fy = RA – Q + G – P × sin α + YB = 0;
∑МВ = М + P × sin α × b – G × (b + 0,5 × a) + Q × (a + b) – RA × (1,5 × a + b) = 0.
Как видно из уравнения момента сил, за точку вращения балки принята опора B. Поэтому значение воздействия в килоньютонах умножается на расстояние до этой точки в метрах.
Теперь в каждом уравнении есть одна неизвестная, поэтому, подставив известные значения, можно их найти:
XB = P × cos α = 20 × cos 300 = 20 × 0,866 = 17,32 кН;
RA + YB = Q – G + P × sin α = 4 – 10 + 20 × sin 300
= 4 кН;
RA = М + P × sin α × b – G × (b + 0,5 × a) + Q × (a + b) × (1,5 × a + b) = 4 + 20 × sin 300 × 3 – 10 × (3 + 0,5 × 2) + 4 × (2 + 3) × (1,5 × 2 + 3) = 2,33 кН;
Отсюда YB = 4 – RA = 4 – 2,33 = 1,77 кН.
Задача 2
Для заданной плоской рамы определить реакции опор. Значения сил возьмем из задачи №1, несколько изменим их распределение. Схема балки показана на рис. 3.
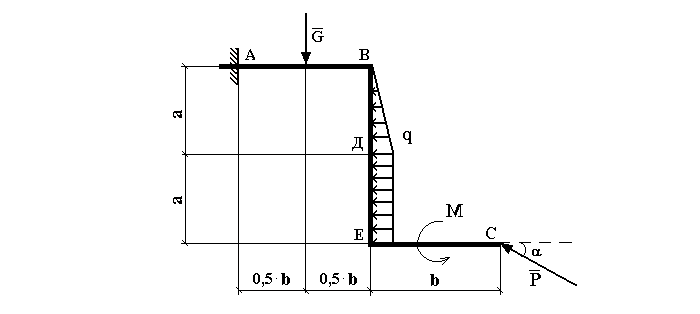
Рис. 3
В этом примере существует только одна опора в точке А, распределенная нагрузка имеет сложную форму. Остальные силы, а точнее их проекции на оси х и у не претерпевают каких-либо изменений.
Чтобы правильно разложить нагрузку q, ее разделяют на две: Q1 в виде треугольника от В до Д и на Q2, представляющей собой прямоугольник.
Соответственно, определяться они тоже будут по-разному:
Q1 = (q × a) / 2 = (2 × 2) / 2 = 2 кН;
Q2 = q × a = 2 × 2 = 4 кН.
Обе эти силы будут расположены посередине своих отрезков (Q1 из характера нагрузки на 1/3 от точки Д).
В предыдущем примере шаровая опора могла вращать балку вокруг себя, поэтому не имела момента вращения. В данном случае опора представляет собой жестко закрепленную опору, поэтому имеет ко всему прочему еще и момент МА.
После всех преобразований схема балки будет следующей:
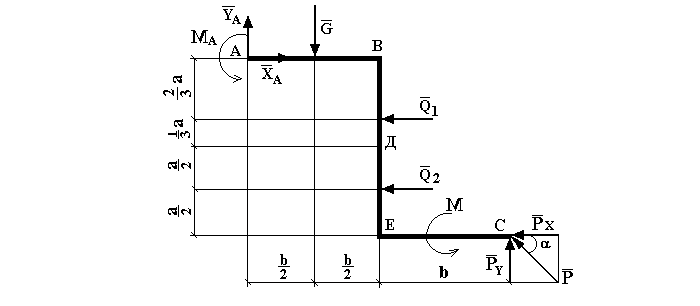
Рис. 4
Теперь можно приступать к выписыванию сил:
∑Fx = XA – Q1 – Q2 – P × cos α = 0;
∑Fy = YA – G + P × sin α = 0;
∑МВ = MA – G × 0.5 × b – Q1 × 2/3 × a – Q2 ×1,5 × a + M + P × sin α × 2b – P × cos α × 2a.
Две силы Р в последнем уравнении связаны с формой самой балки, которая может испытывать момент вращения от каждой из них.
Теперь можно подставлять уже известные значения:
XA – 2 – 4 – 20 × cos 300 = 0 → XA = 23,32 кН;
YA – 10 + 20 × sin 300 = 0 → YA = 0 кН;
MA – 10 × 0,5 × 3 – 2 × 2/3 × 2 – 4 ×1,5 × 2 + 4 + 20 × sin 300 × 2 × 3 – P × cos 300 × 2 × 2 = 0 → MA = 34,95 кН.
Задача решена.
Расчет реакций относится к разделу физики с названием “Статика”, которая рассматривает структуру и системы, находящиеся в покое.
Силой реакции опоры называется усилие противодействия опоры действующему на нее объекту, при этом она равна по модулю и противоположна по направлению усилию, с которым объект действует на опору, согласно третьему закону Ньютона.
Система между некоторой структурой и опорой, которая препятствует линейному или угловому перемещению этой структуры, называется системой опоры. Существует несколько типов опор:
- Шарнир (валик) — опора первого порядка, ограничивающая смещение в пространстве в одном измерении и обладающее реакцией опоры перпендикулярной основанию.
- Плоская опора — опора второго порядка, которая ограничивает перемещение в пространстве в двух измерениях (горизонтальном и вертикальном) и разрешает только движение вращения структуры.
Расчет равновесных систем связан с вычислением результирующего динамического момента. В ньютоновской (классической) механике момент силы определяется как векторное произведение усилия, действующего на опору, на вектор, образованный между точкой опоры и точкой приложения этого усилия. Момент силы также называют динамическим моментом или просто моментом.
Далее в статье приводится пример расчета реакции для наиболее распространенной задачи: балки с двумя опорами.
Содержание:
- Решение задачи о реакции опоры балки
- Первый способ: через моменты
- Второй способ: через силы
- Видео
Решение задачи о реакции опоры балки
Как было сказано выше, балка с двумя опорами является типичной и наиболее простой задачей статики. Задача состоит в расчете реакций в точках А и В ввиду действующих на балку усилий.
Знание этих величин необходимо для правильного понимания диаграмм моментов и диаграмм сил данной системы, и является важной частью статики в школьных и университетских курсах. Существует компьютерная программа SkyCiv, которая предоставляет мощный инструмент по расчету таких реакций для различных равновесных систем.
Возвращаясь к поставленной выше задаче, напомним, что основным ее условием является статическое состояние, то есть отсутствие каких-либо линейных перемещений и вращений объектов. В простой физике последний факт означает, что сумма векторов всех усилий равна нулю (то есть сумма усилий, направленных вверх, равна таковым, направленным вниз). Вторым условием равновесия системы является равенство нулю динамических моментов, приложенных относительно определенной точки опоры.
Чтобы определить реакции подпорок балки, следуйте нижеизложенным двум способам решения задачи:
- используя равенство нулю суммы динамических моментов;
- используя равенство нулю суммы действующих усилий.
Первый способ: через моменты
Для начала нужно положить, что сумма всех моментов относительно точки реакции равна нулю, то есть ΣMi = 0, где Мi – момент усилия. Расчет таких моментов для нашей задачи очень прост, и состоит в перемножении действующих усилий на расстояния от точки их приложения до точки реакции.
Будем считать, что наша балка имеет длину 4 метра и расположена на двух подпорках А и В. Посредине балки вертикально вниз действует усилие в 20 кН, и нужно рассчитать реакции каждой подпорки, то есть Ay и By . Описанная задача представлена на рисунке.
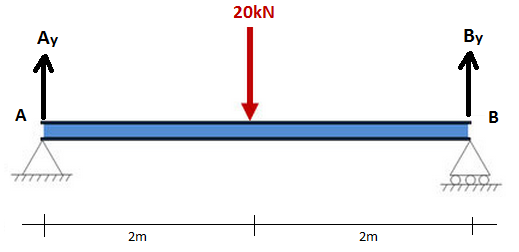
Например, рассчитаем сумму всех динамических моментов относительно точки реакции В, учитывая ее равенство нулю в равновесии. Выбор точки В, относительно которой будет проводиться расчет, является произвольным, точно так же можно выбрать точку А. Таким образом, просуммируем все динамические моменты относительно точки В, полагая эту сумму равной нулю:
ΣMв = 0 = 20*2 – A y * 4 ==> A y = 10 кН.
Отметим, что в формуле выше мы выбрали положительное направление для моментов, действующих против часовой стрелки, и отрицательное направление для моментов, действующих по часовой стрелке. Такой выбор знаков моментом является наиболее общим, однако, вы можете выбрать и наоборот. Необходимо помнить, что всегда нужно использовать одно и то же соглашение на знак моментов, начиная сначала и следуя ему на протяжении всего решения конкретной задачи.
Таким образом, мы получили нашу первую формулу, из которой определили силу реакции опоры в точке А. Аналогичная формула запишется для определения реакции в точке В. В нашем случае, ввиду симметричности действующего вертикально вниз усилия в 20 кН относительно точек подпорок, реакция в точке В будет равна таковой в точке А, то есть 10 кН.
Второй способ: через силы
Для существования равновесия сумма всех вертикальных сил должна быть равна нулю, то есть ΣF y = 0, где индекс Y определяет конкретную вертикальную силу в системе. Помните, что в данном случае мы должны включать в расчет все действующие в системе силы. Принимая во внимание последний факт, проводим суммирование всех вертикальных сил, в итоге получаем следующую формулу:
ΣF y = 0 = A y + В y – 20 кН, откуда 0 = 10 кН + В y – 20 кН, и В y = 10 кН.
Так же, как и в случае моментов сил, силы являются векторными величинами и имеют знак, здесь мы приняли за положительные силы те, которые действуют вверх, и за отрицательные те, которые действуют вниз. Выбор знака остается за вами, однако, напоминаем, что этот выбор не должен изменяться в процессе решения задачи. Отметим, что в формуле выше мы использовали результат, полученный в предыдущем пункте, когда вычислили силу реакции Ay.
Таким образом, мы решили, поставленную в начале этого параграфа задачу о расчете сил реакций опоры балки, используя при этом две системы уравнений, уравнения момента силы и уравнения силы, и получили ответы: силы реакции в точках А и В равны между собой и составляют 10 кН. Напоминаем, что физический смысл полученного равенства заключается в том, что действующая на балку внешняя сила приложена точно посередине балки. В случае ее приложения в другой точке, приведенные формулы также будут действительны и процесс расчета остается тем же самым.
Видео
Эта видеоподборка поможет вам лучше разобраться в теме и закрепить полученные знания.
