Как найти силу сцепления

1 Трение покоя (сцепления)

Исследованием
явления трения впервые занимался
Леонардо да Винчи. В конце XVII в. французский
физик Амонтон
(1663-1705) уста­новил независимость силы
трения от величины поверхности
соприка­сания тел. Законы трения были
сформулированы французским физиком
Кулоном
(1736-1806).

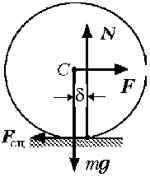
Если
к твердому телу, покоящемуся на шероховатой
горизонтальной плоскости (рис. 6.1),
приложить горизонтальную силу

,
то действие этой

Рис.
6.1 Рис. 6.2

силы
вызовет появление силы сцепления

,
представляющей со­бой силу противодействия
плоскости смещению тела. Благодаря
сцепле­нию тело остается в покое при
изменении модуля силы

от нуля до некоторого значения

.
Это значит,
что модуль силы сцепления тоже изменяется
от

до

в момент начала движения.

Модуль
максимальной силы сцепления, как
показывает опыт, про­порционален
нормальному давлению N
тела на плоскость. В рассматри­ваемом
случае N
= G.
Тогда

.

Коэффициент
пропорциональности

является
отвлеченным числом и называется
коэффициентом
сцепления.

Коэффициент
сцепления зависит от материала и
физического состоя­ния соприкасающихся
тел и определяется экспериментально.
Его величина для материалов, используемых
в технике, обычно меньше единицы. Так
как максимальное значение силы сцепления
равно

,
то модуль силы сцепления всегда
удовлетворяет условию

.

Направление
силы сцепления противоположно направлению
того движения, которое возникло бы под
действием приложенных к телу сил при
отсутствии сцепления.

При
скольжении тела по шероховатой поверхности
к нему
прила­жена
сила трения скольжения.
Направление этой силы, противодей­ствующей
скольжению, противоположно направлению
скорости тела (рис. 6.2).

Модуль
силы трения скольжения пропорционален
нормальному давлению N:

.

Коэффициент
пропорциональности f
называется коэффициентом
трения скольжения и
определяется опытным путем.

Коэффициент
трения скольжения является отвлеченной
величиной и зависит от материала и
физического состояния трущихся
поверхностей, а также от скорости
движения тела и удельного давления.

Однако в
элементарных расчетах зависимость
коэффициента трения скольжения от
скорости и удельного давления часто не
учитывается.

Экспериментально установлено, что

.

Реакция
R
реальной (шероховатой) поверхности в
отличие от реак­ция идеальной (гладкой)
поверхности имеет две составляющие:
нор­мальную реакцию

и силу сцепления


(или силу трения

при дви­жении тела).

Угол
φ_сц,
образованный реакцией шероховатой
поверхности с нормалью к поверхности
в предельном состоянии покоя при

называется углом
сцепления
(рис. 6.3). Тангенс угла сцепления равен
коэффициенту сцепления:

,

или

.

Рис.
6.3 Рис.
6.4

Угол,
тангенс которого равен коэффициенту
трения скольжения, называется углом
трения.

Угол
сцепления можно определить опытным
путем. Прибор для определения угла
сцепления очень прост. Он представляет
собой наклонную плоскость, угол наклона
которой α
можно
изменять (рис. 6.4, а).

Зафиксируем
угол наклона α плоскости ОА, при
котором помещен­ное на ней тело
находится в предельном состоянии покоя
и сила сцепления достигает максимального
значения. Построим замкнутый треугольник
сил, действующих на тело, и определим
угол α (рисунок 6.4, б):

т.е.
угол наклона плоскости α, при котором
тело находится в предельном состоянии
покоя, равен углу сцепления φ_сц.

Значение
коэффициента сцепления для соответствующих
материалов (тело – плоскость) можно
определить по таблице тангенсов углов,
так как

.

Конус
с вершиной в точке касания тел, образующая
которого составляет угол сцепления с
нормалью к поверхностям тел, называется
конусом
сцепления
(рис. 6.5). Поверхность конуса сцепления
представляет собой геометрическое
место максимальных реакций опорной
поверхности. Действительно, максимальная
реакция поверхности может занимать
различные положения на поверхности
этого конуса, зависящие от направления
силы

,
стремящейся сдвинуть тело (рис. 6.3).
Пространство внутри конуса, представляет
собой совокупность возможных положений
реакций опорной поверхности в состоянии
покоя. Пусть к покоящемуся телу приложены
силы (в том числе вес тела), линия действия
равнодействующей

которых лежит внутри конуса сцепления
(рис. 6.5). Эти силы не приведут тело в
движение, так как сила

будет уравновешена реакцией поверхности.

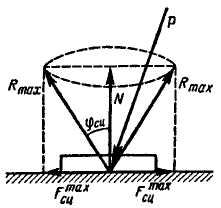
Рис.
6.5 Рис.
6.6

Рассмотрим
равновесие сил, действующих на тяжелый
брусок, опирающийся на две шероховатые
плоскости (рис. 6.6). В точках
А
и В
возникают
реакции опор, линии действия которых
не выходят за пределы конусов сцепления.
Проведя линии А—I,А—II,В—III
и
В — IV, составляющие
углы сцепления φ_1сц,
и φ_2сц
с перпендикулярами к опорным плоскостям,
восставленными в точках А
и
В, получаем
границы конусов сцепления. Четырехугольник,
образованный этими линиями, внутри
которого могут пересекаться линии
действия реакций опор А
и
В, называется
областью
равновесия.

Брусок
АВ
находится под действием трех сил: его
веса

и двух реакций
опор

и

.
При равновесии линия действия этих трех
сил пересекутся в одной точке.

Так
как любая точка площадки klmn
может являться точкой пере­сечения
линий действия реакций опор

и

,
то брусок
находится в состоянии покоя, если линия
действия силы веса бруска пересекает
об­ласть равновесия.

В
случае если линия действия силы веса
проходит через точку k
области
равновесия, брусок находится в предельном
состоянии покоя.

Брусок
не может удержаться в указанном на
рисунке положении, если линия действия
силы веса проходит вне области равновесия.
Если на брусок действует несколько
задаваемых сил и они приводятся к
равнодействующей силе, установленным
условиям должна удовлетво­рять эта
равнодействующая.

Задача
1. Определить
модуль силы

,
при которой начнется движение блока
(рис. 6.7, а).
Вес блока Q
= 2 кН,
высота h
= 0,8 м,
ширина b
= 0,6 м.
Сила

,
приложенная в точке В,
образует угол 30° с горизонтом. Коэффициент
трения между блоком и горизон­тальным
полом f
= 0,2.

Решение.
Движение блока может начаться в двух
случаях: а) если начнется скольжение
блока по плоскости вправо (рис. 6.7, б)
и б) если
блок начнет опрокидываться вокруг ребра
(рис. 6.7, в).

Рассмотрим
первый случай.
В этом случае точка приложения реакции
пола

неизвестна. Составим уравнения равновесия
— при­равняем суммы проекций всех
сил на оси координат (рис. 6.7, б)
нулю

Рис.
6.7

,

.

Кроме
того, учтем зависимость силы трения от
нормального дав­ления

.

Определим
из данной системы уравнений силу

.
Исключая силы


и

,
находим

кН.

Если
величина силы

станет больше
этого значения,
то блок
нач­нет скользить вправо.

Рассмотрим
второй случай.
В случае возможного опрокидыва­ния
блока вокруг ребра А
нормальная реакция

и сила трения

будут
приложены в точке А
(рис. 6.7, в).

Составим
три уравнения равновесия и четвертое
уравнение-зависимость силы трения от
нормального давления:

,
(6.1)

,
(6.2)

.
(7.3)

.

(6.4)

Для
нахождения величины силы

достаточно найти
ее значение
из (6.3):

кН.

Если
модуль силы

станет больше этого значения, то блок
начнет опрокидываться около ребра А.

Уравнения
(6.1), (6.2), (6.4) смогут быть использованы
для опре­деления нормальной реакции
и силы трения.

Сопоставляя
значения модуля силы

в первом и во втором случаях, заключаем,
что так как величина силы

при скольже­нии меньше ее величины
при опрокидывании, то при возрастании
модуля силы

от нуля до максимума блок начнет
сначала
скользить, а не опрокидываться.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сцепление и трение скольжения

Рассмотрим равновесие тела лежащего на горизонтальной шероховатой поверхности OXY (рис. 1.73).

На тело действуют сила тяжести G и нормальная реакция N этой поверхности. Нетрудно видеть, что: G = – N; G = N. При этом реакция N перпендикулярна опорной поверхности OXY.

Если к телу, покоящемуся на шероховатой горизонтальной поверхности приложить горизонтальную силу S , то действие этой силы вызовет отклонение реакции R от нормали к этой поверхности на угол φ_ss (рис. 1.74).

Угол φ_SS называют углом сцепления. Реакцию R шероховатой поверхности раскладывают на горизонтальную F_ss и вертикальную N составляющие.

R = F_ss + N,

где F_ss – сила сцепления; N – нормальная реакция.

Сила F_ss противодействует смещению тела по шероховатой поверхности.

Модули F_ss, N сил F_ss, N связаны соотношением

Как правило, в технических расчётах используют понятие коэффициент сцепления f_ss = tg(φ_ss). Тогда имеем

Из условия равновесия тела на шероховатой поверхности получим F_ss = S.

Благодаря сцеплению тело остается в покое при изменении модуля силы S от нуля до некоторого значения S_max. При значении S_max тело начинает двигаться по шероховатой поверхности. В инженерной практике говорят, что тело в этот момент времени находится в состоянии предельного равновесия.

Угол φ_ss сцепления, а следовательно, и коэффициент сцепления зависят от материала и физического состояния соприкасающихся тел и определяется экспериментально при предельном равновесии тела на шероховатой поверхности. В справочной литературе коэффициент сцепления φ_ss имеет максимальное значение. Его величина для материалов, используемых в технике, обычно меньше единицы. Зачастую в технической литературе коэффициент f_ss называют коэффициентом трения в покое.

Так как максимальное значение силы сцепления F_ssmax равно f_ss·N, то модуль силы сцепления всегда удовлетворяет условию

Направление силы сцепления противоположно направлению того движения, которое возникло бы под действием приложенных к телу сил при отсутствии сцепления.

При скольжении тела по шероховатой поверхности её реакция отклоняется от нормали на угол φ_tr ( рис. 1.75), который называют углом трения.

Как правило, реакцию шероховатой поверхности раскладывают на горизонтальную и вертикальную составляющие.

R = F_tr + N,

где F_tr – сила трения скольжения; N – нормальная реакция.

Сила F_tr противодействует перемещению тела по шероховатой поверхности, поэтому её направление противоположно направлению скорости V_C. Модуль F_tr силы трения скольжения F_tr пропорционален модулю N нормальной реакции N.

где f_tr = tg(φ_tr) – коэффициент трения скольжения.

Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления. Однако в элементарных расчётах зависимость коэффициента трения скольжения от скорости и удельного давления часто не учитывается. Экспериментально установлено, что f_tr

Таким образом, при решении задач статики предельного состояния механической системы к уравнениям равновесия добавляют уравнение: F_ss = f_ss·N.

В частности, для плоской произвольной системы сил имеем:

Σ 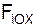+ Σ = 0; (1)

Σ + Σ = 0; (2)

Σ M_A(F_i E ) + Σ M_A(R_i E ) = 0; (3)

где 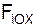Σ , Σ 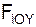– соответственно суммы проекций активных сил на координатные оси OX, OY; Σ , Σ 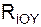– суммы проекций реакций внешних связей на координатные оси OX, OY; Σ M_A(F_i E ) – сумма алгебраических моментов активных сил F_i E относительно точки А; Σ M_A(R_i E ) – сумма алгебраических моментов реакций R_i E внешних связей относительно точки А.

Выполнение курсовых заданий на сцепление и трение скольжения для заочной и дистанционной форм обучения не предусмотрено. Однако задачи такого типа включены в дидактические единицы интернет-экзамена. Рассмотрим один из примеров решения задачи на предельное равновесие механической системы.

Тело весом G = 20 Н удерживается в равновесии на шероховатой наклонной поверхности с углом наклона α = 30 о силой S. Коэффициент сцепления f_ss = 0,3 (рис. 1.76).

Определить минимальное S_min значение силы S_min для перемещения тела вверх по наклонной плоскости.

Приложим к телу активные силы G , S_min и реакции N , F_ss шероховатой поверхности (рис. 1.77).

Модули F_ss, N сил F_ss, N связаны соотношением

Запишем уравнения предельного равновесия для тела, на которое действует система сил (G , S_min, N, F_ss).

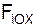Σ + Σ = 0 = G·cos(α) + N = 0; (1)

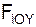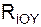Σ + Σ = 0 =

Из уравнения (1) имеем N = G·cos(α). Тогда F_ss = f_ss·G·cos(α).

Из уравнения (2) определим S_min.

Ответ: S_min = 15,196 H.

1.30. Центр тяжести твёрдого тела

В инженерной практике часто требуется определить положение центра тяжести тела или механической системы. Рассмотрим методику решения таких задач.

В теоретической механике тело рассматривают как непрерывную совокупность материальных точек. Если тело находится вблизи земной поверхности, то к каждой материальной точке C_i этого тела приложена её сила тяжести G_Ci. Эти силы тяжести приближенно образуют систему параллельных сил (линии действия сил тяжести двух материальных точек, находящихся на земной поверхности и отстоящих друг от друга на расстоянии 31 м, образуют угол, равный одной секунде).

Исходя из этого, в технических расчётах принято силы тяжести точек считать системой параллельных сил (рис. 1.78).

На рис. 1.78 использованы следующие обозначения: С – центр тяжести тела; C_i, C_i+n – материальные точки тела; X_Ci, Y_Ci, Z_Ci, X_Ci+n, Y_Ci+n, Z_Ci+n – координаты материальных точек в системе отсчёта OXYZ; r_Ci, r_Ci+n – радиус-векторы материальных точек; r_C – радиус-вектор центра тяжести тела; X_C, Y_C, Z_C – координаты центра тяжести тела; G – сила тяжести тела; – радиус-вектор i-й точки тела (начало радиус-вектора находится в центре С тяжести тела).

Силу G = Σ G_Ci прикладывают в точке, которую называют центром тяжести тела. Определим это понятие.

Центр тяжести твёрдого тела – геометрическая точка С, для которой сумма произведений весов G_Ci всех материальных точек, образующих твёрдое тело, на их радиус-векторы , проведенные из этой точки, равна нулю.

Согласно определению имеем:

= 0,

где G = Σ G_Ci – вес тела, равный сумме весов G_Ci материальных точек этого тела.

Радиус-вектор центра С тяжести тела и его координаты определяют по формулам:

;

;

;

.

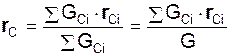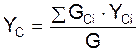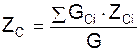Рассмотрим механическую систему, находящуюся в однородном поле сил тяжести (рис. 1.79). Под механической системой условимся понимать систему материальных тел, соединенных между собой недеформируемыми связями.

Силу тяжести G_C и вес G_C механической системы определяют по формулам:

где G_Ci, G_Ci – соответственно сила тяжести и вес i-го тела, входящего в механическую систему.

Силу тяжести G_C прикладывают в центре С тяжести механической системы. Введем это понятие.

Центр тяжести механической системы – геометрическая точка С, для которой сумма произведений весов G_Ci всех материальных тел, входящих в механическую систему, на их радиус-векторы , проведённые из этой точки, равна нулю.

Исходя из этого определения, имеем

= 0.

Очевидно, что центр тяжести тела и центр тяжести механической системы определяют по одной методике.

Радиус-вектор r_C и координаты X_C, Y_C, Z_C центра тяжести механической системы определяют по формулам:

;

;

;

,

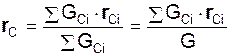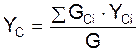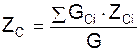где G_Ci – вес i-го тела механической системы; r_Ci – радиус-вектор центра тяжести i-го тела; X_Ci, Y_Ci, Z_Ci – координаты центра тяжести i-го тела механической системы.

В динамике используют понятие центр масс механической системы. Положения центра тяжести механической системы и её центра масс совпадают. Понятие центр масс механической системы более широкое по сравнению с понятием центр тяжести механической системы. Понятие центр масс применимо для любой системы материальных точек независимо от того, находится ли она под действием каких-либо сил или нет, тогда как понятие центр тяжести применяется лишь для системы тел, находящихся в однородном поле сил тяжести.

Центр тяжести однородного тела, заполняющего некоторый объём, называется центром тяжести объёма. Его координаты находят по формулам:

;

;

,

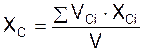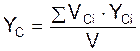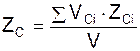где V_Ci – элементарный объём тела; V – полный объём тела; X_Ci, Y_Ci, Z_Ci – координаты центра тяжести i-го элементарного объёма тела.

Таким образом, для определения положения центра тяжести однородного тела, находящегося в некотором объёме, этот объём необходимо разбить на элементарные объёмы V_Ci (куб, параллелепипед, призма и т. д., положения центров тяжести которых приведено в справочной документации).

Однородное тело, имеющее форму тонкой пластинки, рассматривают как материальную плоскую фигуру. Координаты центра тяжести плоской фигуры определяют по формулам:

;

,

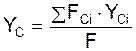где F_Ci – элементарная площадь плоской фигуры; X_Ci, Y_Ci – координаты центра тяжести элементарной площади; F – площадь плоской фигуры.

Для определения положения центра тяжести плоской фигуры эту фигуру разбивают на элементарные участки площадью F_Ci (квадрат, прямоугольник, треугольник и т. д., положения центров тяжестей которых известны).

Аналогичным образом определяют положения центров тяжестей однородных тел, имеющих большую протяженность при сравнительно малой площади поперечного сечения (например, проволока).

;

;

,

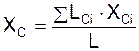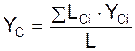где L_Ci – элементарная длина тела; L – полная длина тела, вытянутого в одну линию; X_Ci, Y_Ci, Z_Ci – координаты центра тяжести i-го участка элементарной длины тела.

При определении положения центра тяжести широко используют следующие рекомендации:

1) если однородное тело имеет ось симметрии, то его центр тяжести лежит на этой оси;

2) если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости;

3) если плоская фигура или линия имеет ось симметрии, то её центр тяжести лежит на этой оси.

При решении некоторых задач используют методы отрицательных площадей и объёмов. Поясним это примером.

Определить положение центра тяжести однородного диска радиусом R с круглым отверстием, радиус которого r = R/2 (рис. 1.80)

Заштрихованная фигура имеет ось симметрии, поэтому центр С её тяжести находится на оси ОХ. Отсюда имеем Y_C = 0. Координату Х_С находим по формуле

,

где F_Ci – элементарная площадь плоской фигуры; X_Ci – абсцисса центра тяжести элементарной площади; F – площадь плоской фигуры.

Расчленим исходную фигуру на две составные части. Первая фигура – сплошной круг радиусом R. Вторая фигура – круг радиусом r. Для двух тел последняя формула принимает вид

.

Дата добавления: 2015-05-30 ; просмотров: 1162 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Тре́ние поко́я, трение сцепления — сила, возникающая между двумя неподвижными контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Трение покоя наблюдается до перехода к движению на макроуровне, когда начинает действовать сила трения качения или скольжения. Действует в направлении, противоположном направлению возможного относительного движения. Максимальная сила трения покоя обычно несколько выше, чем сила трения скольжения.

В 1779 году французский физик Кулон установил, от чего зависит максимальная сила трения покоя. Оказалось, что сила трения покоя зависит от того, с какой силой прижимаются друг к другу соприкасающиеся предметы. Также было установлено, что трение покоя зависит от материала соприкасающихся поверхностей.

Примером силы трения покоя может служить эскалатор со стоящим на нем человеком. Также эта сила проявляется в забитом в доску гвозде, завязанном банте или шнурке и т.д.

Максимальная сила трения покоя в простейшем приближении^[1]:
,
где  — коэффициент трения покоя,  — сила нормальной реакции опоры.

Примечания[править | править код]

Ссылки[править | править код]

• Таблица коэффициентов трения покоя (коэффициентов сцепления) для различных пар материалов (большая).
• Таблица коэффициентов трения покоя (коэффициентов сцепления) сплавов по стали без смазки.
• Таблица коэффициентов трения покоя (коэффициентов сцепления) смазанных металлов по стали.
• Таблица коэффициентов трения покоя (коэффициентов сцепления) водяного льда по льду в зависимости от температуры.

Научные статьи на тему «Сила сцепления»

Повышение качества дорожного покрытия

Но в силу многих обстоятельств, среди которых и короткий сезон проведения работ, и экстремальные нагрузки…
Коэффициент сцепления
Сцепные качества покрытия являются одними из важнейших, поэтому эксплуатационные…
Определение 1

Коэффициент сцепления – это величина, которая показывает соотношение между максимально…
возможным значением силы сцепления между шинами и поверхностью дороги и весом транспортного средства…
Коэффициент сцепления может меняться от 0 до 1, где 1 является самым высоким показателем.

Статья от экспертов

Исследование силы сцепления различных адгезивных систем с тканями зубов

Недостаточное освещение вопросов применения адгезивных систем в стоматологии в зависимости от витальности, функциональной принадлежности зуба и возраста пациента определили актуальность и цель настоящего исследования.

Хромосомная теория наследования. Кроссинговер

Сцепленное наследование….
Оно характеризирует силу сцепления и выражается в процентах рекомбинации кроссинговера или в морганидах…
Есть гены, имеющие высокий процент сцепления и такие, где почти не выявляется это сцепление….
Каждая пара хромосом представляет собой группу сцепления генов, благодаря чему происходит сцепленное…
Сила сцепления между генами обратно пропорциональна расстоянию между ними.

Статья от экспертов

Экспериментальное исследование сил сцепления некоторых метилметакрилатов с костью при остеопорозе

Две трупные женские бедренные кости с остеопорозом пересечены в области истмуса. Их костномозговые каналы разработаны разверткой в проксимальном направлении, включая межвертельную область. В одну кость ретроградно шприцом введен низковязкостный цемент Lima, в другую антеградно высоковязкостный цемент Symplex. Из первой кости получены 14 образцов для испытаний на машине ZWICK-1464, из второй 13. Таким образом, проведены 27 испытаний прочности связи двух цементов с остеопорозной костью. Полученные результаты свидетельствуют, что силы связи цемента с кортикальной костью не зависят от его вязкости. При сохранении эндоста в костномозговом канале эти силы возрастают с уменьшением вязкости цемента.



Трение скольжения и трение качения

П.Ф.Севрюков,
СКрИПКРО, г. Ставрополь

Трение скольжения и трение качения

Если к твёрдому телу, покоящемуся на
шероховатой горизонтальной поверхности,
приложить горизонтальную силу F, то
действие этой силы вызовет появление силы
сцепления F_cц = –F,
представляющей собой силу противодействия
смещению тела со стороны поверхности. Благодаря
сцеплению тело остаётся в покое при изменении
модуля силы F от нуля до некоторого
значения F_max. Это означает, что модуль
силы сцепления тоже изменяется от нуля до F_сц
max в момент начала движения. Как показывает
опыт, |F_max| пропорционален
модулю силы нормального давления |N|
со стороны плоскости: F_max = f_сц
• N. Коэффициент f_сц является
безразмерной величиной и называется
коэффициентом сцепления. Этот коэффициент
зависит от физических свойств соприкасающихся
поверхностей и определяется экспериментально.
Его величина для материалов, используемых в
технике, обычно меньше единицы. Таким образом,
всегда выполняется условие а направление силы сцепления
противоположно направлению того движения,
которое возникло бы под действием приложенных
сил при отсутствии сцепления.

При скольжении тела по шероховатой
поверхности к нему приложена сила трения
скольжения. Направление этой силы,
противодействующей скольжению, противоположно
вектору скорости тела. Модуль силы трения
скольжения пропорционален модулю силы
нормального давления N: F_ск = f_ск
• N. Коэффициент пропорциональности f_ск
называется коэффициентом трения скольжения и
определяется опытным путём. Этот коэффициент
является также безразмерной величиной и зависит
от материалов, состояния и свойств трущихся
поверхностей (так, коэффициент трения скольжения
между двумя деревянными брусками зависит от
того, вдоль или поперёк волокна эти бруски
перемещаются относительно друг друга;
существенно облегчает скольжение наличие
смазки, но при этом уже нельзя говорить о
скольжении одного тела по другому), а также от
давления и скорости относительного движения
тела. Экспериментально установлено, что f_ск
< f_сц.

Сила реакции R реальной
(шероховатой) поверхности в отличие от идеальной
(гладкой) имеет две составляющие: силу
нормального давления (нормальную реакцию) N
и силу сцепления F_cц (или силу
трения F_ск при движении тела).

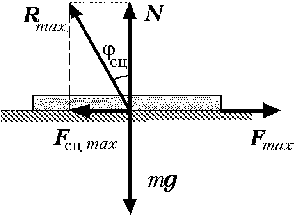
Угол _cц,
образованный силой реакции шероховатой
поверхности с нормалью к этой поверхности в
предельном состоянии покоя, т.е. при F_cц
= F_max, называется углом сцепления. Через
mg здесь и далее обозначается сила
тяжести. Тангенс угла сцепления равен
коэффициенту сцепления:

tg_cц
= = f_cц,
или _cц = arctg f_cц.

Угол, тангенс которого равен
коэффициенту трения скольжения, называется
углом трения.

Угол сцепления можно определить
опытным путём с помощью очень простого прибора.
Он представляет собой наклонную плоскость, угол
наклона которой можно измерить (для расчётов
достаточно знать длину наклонной плоскости и
высоту подъёма её верхнего конца). Поднимая один
конец плоскости и измеряя угол её наклона в
момент, когда тело начнёт скользить по плоскости,
мы получаем значение угла сцепления _cц.

Конус с вершиной в точке касания тел
(поверхность, на которой находится тело, может
быть и криволинейной), образующая которого
составляет угол сцепления с нормалью к
поверхности тел, называется конусом сцепления.
Поверхность конуса сцепления представляет собой
геометрическое место максимальных сил реакции
опорной поверхности при заданной нормальной
составляющей N. Действительно,
максимальная сила реакции поверхности может
занимать различные положения на поверхности
этого конуса, в зависимости от направления силы F,
стремящейся сдвинуть тело. Пространство внутри
конуса представляет собой совокупность
возможных положений сил реакции опорной
поверхности в состоянии покоя.

Статья подготовлена при поддержке учебного центра «НП МАЭБ». Если вы решили приобрести качественные знания в области подъемных механизмов, то оптимальным решением станет обратиться в учебный центр «НП МАЭБ». На сайте, расположенном по адресу www.maeb.ru, вы сможете, не отходя от экрана монитора, записаться на курсы в области промышленной безопасности. Более подробную информацию о ценах и акциях действующих на данный момент вы сможете найти на сайте www.maeb.ru.

Пусть к покоящемуся телу, помимо силы
реакции опоры, приложены силы (в том числе и сила
тяжести), линия действия равнодействующей Р
которых лежит внутри конуса сцепления. Эти силы
не приведут тело в движение, т.к. сила Р
будет уравновешена силой реакции поверхности.

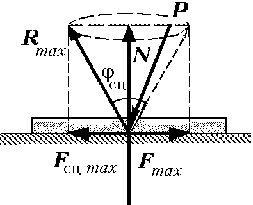
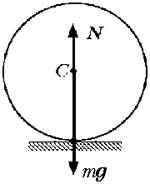
Рассмотрим цилиндрический каток,
покоящийся на горизонтальной плоскости. На каток
действуют две взаимно уравновешивающие силы:
сила тяжести mg и нормальная
реакция плоскости N = –mg.
Если под действием горизонтальной силы F,
приложенной к центру катка С, он катится по
плоскости без скольжения, то силы mg
и N образуют пару сил,
препятствующую качению катка. Возникновение
этой пары сил обусловлено неабсолютной
твёрдостью материалов катка и опорной плоскости.
Под действием силы давления катка происходит
деформация соприкасающихся поверхностей, и
каток соприкасается с плоскостью не по линии, а
по некоторой малой площадке. В этом случае
обозначенная на рисунке сила реакции N
является нормальной составляющей
равнодействующей сил реакции, распределённых по
этой площадке. Её линия действия оказывается
сдвинутой в сторону движения катка на некоторое
расстояние от
линии действия силы mg, так что
нормальная реакция плоскости N и
сила тяжести катка mg образуют пару
сил сопротивления качению с плечом . Момент этой пары сил
называется моментом сопротивления качению. Его
величина равна произведению модуля силы
нормальной реакции на плечо пары , называемое
коэффициентом трения качения: М_сопр = N.

Коэффициент трения качения выражается в единицах
длины. Его значения (в 10^–5 м) для некоторых
пар материалов приведены ниже:

Мягкая сталь по мягкой
стали…………………………….. 5
Стальной бандаж по стальному рельсу………………… 50
Дерево по стали……………………………………………….
30–40
Дерево по дереву……………………………………………..
50–60

Определим наименьшую горизонтальную
силу F, приложенную к центру
цилиндрического катка радиуса R,
находящегося на горизонтальной плоскости,
которая может вывести каток из состояния покоя.
Чтобы каток начал катиться, момент силы F
относительно точки опоры катка должен быть
больше момента сопротивления (момент силы
сцепления F_сц, приложенной в
точке опоры, равен нулю), т.е. FR > N, откуда F > . Так как в
рассматриваемом случае N = mg, то

 

Это выражение показывает, что модуль
силы F, приводящей цилиндрический
каток в движение, обратно пропорционален радиусу
катка R. (Поэтому, как правило, круглое тело
катить легче, чем волочить. – Ред.) Если действие
силы F прекращается, качение
замедляется вплоть до полной остановки
вследствие действия пары сил сопротивления.

Довольно часто можно встретить в
литературе (в том числе и в школьных учебниках)
термин «сила трения качения». Эта величина
введена по аналогии с силой трения скольжения.
Объясним её появление. Пусть под действием силы F
происходит качение так, что центр катка С
переместился на расстояние s. Работа момента
сил сопротивления M при этом равна А = М, где – угол поворота тела в
радианах. В нашем случае тело вращается по
часовой стрелке, а пара сил стремится развернуть
тело в противоположном направлении, поэтому пара
сил совершает отрицательную работу.

Если центр катка переместилcя на
расстояние s, то каток при этом повернулся на
угол тогда
работа, совершаемая моментом сил сопротивления:

По аналогии с силой трения скольжения
(тело скользит по горизонтальной поверхности, А_тр=
–F_скs = –f_скmgs), все
символы, стоящие между «минусом» и буквой s,
объединяют как «силу трения качения» При этом и учащиеся, и
даже учителя забывают о том, что коэффициент
трения скольжения является величиной
безразмерной, а коэффициент трения качения имеет
размерность длины. На вопрос «Если по одной и той
же поверхности тело сначала прокатить, а потом
протащить, то какой из коэффициентов трения –
скольжения или качения – будет больше?» редко
можно получить ответ, что величины, имеющие
разные размерности, сравнивать нельзя! Ведь
никакому здравомыслящему человеку не придёт в
голову мысль сравнивать 5 мин и 7 см.

---

КОММЕНТАРИЙ РЕДАКЦИИ. В статье вводятся
термины, не употребляемые в школьных учебниках и,
на наш взгляд, не вносящие большой ясности в
понимание вопроса. Так, введённую П.Ф.Севрюковым
силу трения сцепления обычно называют силой
трения покоя, а коэффициент сцепления –
коэффициентом трения покоя. Далее, при
обсуждении трения качения говорится, что
реальное тело, катящееся по плоскости,
соприкасается с ней не по одной линии, а по
некоторой площадке. В статье К.Ю.Богданова «Всё о
силе трения» (см. № 21/05) приводится рисунок, из
которого ясно, что эта малая площадка
ориентирована под некоторым отнюдь не
постоянным углом к рассматриваемой плоскости,
так что и результирующая сила её нормальной
реакции также составляет некоторый угол с этой
плоскостью. П.Ф.Севрюков совершенно правильно
рассматривает её вертикальную составляющую. Но
ведь можно рассматривать и горизонтальную – и
тогда сравнивать коэффициент трения скольжения
с коэффициентом трения качения вполне допустимо:
они оба – безразмерные величины.