Силы сопротивления движению поезда.
Сопротивления
движению поезда делятся на две
составляющие:
I.
Основное,действуют при движении
поезда всегда:
1.Сопротивление
пути:
а)
трение качения колес по рельсам из-за
деформации опорных поверхностей (сила
обратно пропорциональна диаметру колес
и зависит от твердости материалов);
б)
трение скольжения из-за проскальзывания
и из-за трения между гребнями бандажей
и рельсами, которые уменьшаются при
натяжке в режиме тяги;
в)
от ударов при движении по неровностям
пути (зависит от скорости, нагрузки на
ось, зазора в стыке).
2.Сопротивление
подвижного состава:
трение
в подшипниках (сила прямо пропорциональна
диаметру оси, обратно пропорциональна
диаметру колеса, зависит от коэффициента
трения, площади соприкосновения,
смазки).
3.Сопротивление
внешней среды:
а)
впереди происходит сжатие воздуха;
б)
боковые поверхности и крыша соприкасаются
с воздухом;
в)
в промежутках между вагонами и за
составом происходит разряжение,
завихрение воздуха (конструктивно
выполняют более обтекаемую форму
подвижного состава).
II.
Дополнительные− возникают при
движении по отдельным участкам пути и
в отдельные периоды времени:
1.От
уклонов:
эта
сила создается составляющей веса
поезда, действующая на подъеме против
движения поезда, а на спусках – по
направлению движения поезда.
Уклон
характеризуется крутизной i,
измеряется в тысячных и размерность
обозначается «‰», и показывает
разницу по высоте подъема в метрах на
каждую 1000 метров пути.
Дополнительное
удельное сопротивление от подъема в
Н/кНчисленно равно величине
подъема в‰.
2.От
кривых:
а)
под действием центробежной силы гребни
бандажей колесных пар прижимаются к
наружному рельсу и появляется трение;
б)
колесо, идущее по внутреннему рельсу,
имеет проскальзывание;
в)
трение в центральных и боковых опорах
кузова.
Из-за
большого числа факторов и сложных
зависимостей дополнительное удельное
сопротивление от кривой определяется
по эмпирической формуле:
![]() ,
,
где
R– радиус кривой вм.
3.При
трогании с места:
а)
повышенное трение в подшипниках (смазка
выдавлена из-под трущихся поверхностей
и получается полусухое трение);
б)
большая деформация рельса и колеса.
Дополнительное
удельное сопротивление при трогании
с места определяются по эмпирическим
формулам:
для
подшипников скольжения:
![]()
![]() ;
;
![]()
для
подшипников качения:
![]() ,
,
где
mвo– масса вагона в тоннах, приходящаяся
на одну ось.
4.При
низких температурах окружающего
воздуха:
а)
возрастает вязкость смазки, а значит
и коэффициент трения;
б)
возрастает сопротивление воздушной
среды (увеличивается давление воздуха);
Дополнительное
удельное сопротивление при низких
температурах окружающего воздуха
определяется по формуле:
wнт
= wo(Кнт
-1) .
Значение
коэффициента низких температур Кнт
берется из таблицы вПТРпри
различных значениях низких температур
и скоростях движения для грузовых и
пассажирских вагонов.
5.От
ветра:
а)
встречный и боковой ветер увеличивают
сопротивление из-за трения;
б)
увеличения сопротивления воздушного
потока.
Дополнительное
удельное сопротивление от ветра
определяется по формуле:
wв
= w0 (Кв
−1) .
Значение
коэффициента ветра Кв
берется из таблицы вПТР.
6.От
подвагонных генераторов для пассажирских
вагонов.
7.От
движения в тоннелях.
Общее
сопротивление движению поезда Wкопределяется алгебраической суммой
основного и дополнительного
сопротивлений:
WК
= W0 + Wд,
в Н.
Почти
все виды сопротивлений пропорциональны
весу поезда, поэтому рассматривают
удельные сопротивления движению
поезда:
wк
= w0
+ wд,вН/кН.
Основное
удельное сопротивление определяется
по эмпирическим формулам в зависимости
от скорости движения:
а)для
различных серий локомотивов;
б)
при движении под током;
в)
при движении без тока;
г)
в зависимости от подшипников качения
или скольжения;
д)
в зависимости от количества осей вагона;
е)
для груженых или порожних вагонов;
ж)
для стыкового или бесстыкового пути.
Общее
основное удельное сопротивление
определяется как:
 .
.
Образование
силы торможения.
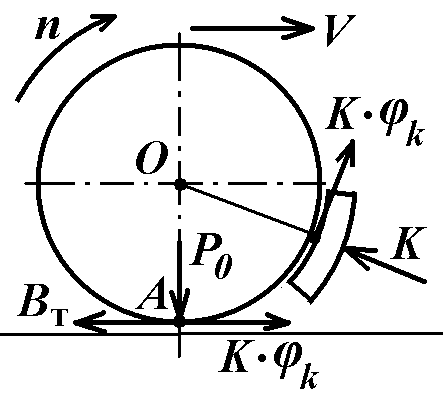 При
При
механическом торможении подается
сжатый воздух в тормозные цилиндры.
Поршень в цилиндре перемещается, через
шток, тяги и рычаги прижимая тормозную
колодку к колесу с усилением К. В
месте контакта колеса с тормозной
колодкой возникает сила тренияK×φк,
направленная навстречу вращению колеса.
φк
− это коэффициент трения колодки
о колесо. Перенесем силу тренияK×φк
в точкуАкасания колеса с рельсом.
Колесо прижато к рельсу силойР0.
Обе эти силы внутренние по отношению
к поезду и не могут повлиять на характер
движения.
Если
колесо прижато к рельсу с силой Р0,
то в результате сцепления колеса с
рельсом силаK×φкстремится сдвинуть рельс по
направлению движения. Но рельс закреплен
и вызывается реакция рельса по третьему
закону НьютонаВт, равнаяK×φк и противоположно направленная.
Эта сила по отношению к поезду является
внешней и называетсятормозной
силой.Она действует против
движения и создает колесу упор.
Тормозная
сила одного колеса:Bт= K×φк.
Усилие
прижатия тормозной колодки к колесу«К» зависит от интенсивности
торможения, от диаметра тормозного
цилиндра, от давления воздуха в нем, от
передаточного отношения рычажной
передачи, от силы оттормаживающей
пружины в тормозном цилиндре.
Коэффициент
трения
φк зависит
от материала колодок, скорости движения
и удельных сил нажатия колодок на
колеса.
С
увеличением скорости движения и
удельного нажатия колодок коэффициент
трения снижается, так как за счет тепла
металл размягчается, в тонком слое
может оплавиться. Для повышения
коэффициента трения применяют
двухстороннее нажатие колодок.
Коэффициент
трения рассчитывают по эмпирическим
формулам, которые можно найти в «Правилах
тяговых расчетов для поездной работы».
Применяются
тормозные колодки чугунные, чугунные
с повышенным содержанием фосфора (до
1,0÷1,4 %) и композиционные.
С
увеличением скорости движения у чугунных
колодок коэффициент трения более резко
снижается. Чугунные колодки имеют
больший износ. У композиционных колодок
коэффициент трения выше и с увеличением
скорости движения он в меньшей степени
снижается. У чугунных колодок с повышенным
содержанием фосфора коэффициент трения
имеет промежуточное значение, но ближе
к значениям чугунных колодок.
Тормозная
сила Вт
не должна
превышать силу сцепления колеса с
рельсом. Вт≤
Fк
сцеп .
В противном
случае колесо прекращает вращение и
будетдвигаться
«юзом» по рельсу. На поверхности катания
колеса образуется площадка (ползун),
который во время дальнейшего движения
будет разрушать рельсы.
Режимы
движения поезда.
Поезд
может находиться в трех режимах движения:
в режиме тяги, когда у локомотива
создается сила тяги; в режиме выбега,
когда у локомотива нет силы тяги, и
поезд движется за счет запасенной
кинетической энергии (по инерции); в
режиме торможения, когда создается
тормозная сила.
Если
силу тяги Fк,
силы сопротивления Wк,
силу торможения Вт
поделить на вес поезда (масса, умноженная
на ускорение свободного падения m×g),
то получим, соответственно, удельную
силу тяги
![]() ,
,
удельную силу сопротивления![]() ,
,
удельную тормозную силу![]() .
.
Удельная
ускоряющая сила в общем случае
fy=fк−wk−bm.
Для режима тяги fy=fк−wk;
для режима выбега fy=
−wk;
для режима торможения
fy=
−wk−bm..
При
движении поезда ускоряющая сила
изменяется в связи с изменением режимов
работы локомотива, плана и профиля
пути. Наиболее общим случаем является
ускоренное или замедленное движение
и только в частных случаях – равномерное.
Ускоренное
движение можно получить как в режиме
тяги, так и в режиме выбега или торможения
при следовании на спусках, когда
составляющие от веса поезда окажутся
больше сил сопротивления движению или
суммы сил сопротивления движению и
тормозной силы.
Равномерное
движение наступает при равенстве этих
сил.
Замедленное
движение может быть и в режиме тяги при
следовании по подъему, когда сила тяги
окажется меньше сил основного и
дополнительного сопротивлений движению.
При
fy > 0– ускоренное
движение,приfy =
const > 0равноускоренное.
При
fy < 0– замедленное
движение, приfy = const
< 0равнозамедленное.
При
fy = 0 – равномерное
движение.
Определение
массы состава.
Масса
состава – один из важнейших показателей
работы железнодорожного транспорта.
Увеличение массы состава позволяет
повысить провозную способность
железнодорожных линий, уменьшить расход
топлива и электрической энергии, снизить
себестоимость перевозок.
Наибольшая
масса поезда ограничивается возможностью
проведения поезда локомотивом по
наиболее тяжелому (расчетному) подъему,
условиями трогания поезда с места на
станции и длиной приемо отправочных
путей.
Расчетный
подъем – это наиболее трудный для
движения в данном направлении элемент
профиля пути, на котором достигается
расчетная скорость, соответствующая
расчетной силе тяги локомотива. Наиболее
крутой подъем участка достаточно
длинный принимается за расчетный. Если
же наиболее крутой подъем заданного
участка имеет небольшую протяженность
и ему предшествуют «легкие» элементы
профиля (спуски, площадки), на которых
поезд может развить высокую скорость,
то такой подъем не может быть принят
за расчетный, так как поезд его
преодолевает за счет запасенной
кинетической энергии, по инерции. И
такие подъемы называются инерционными.
И за расчетный подъем принимается
подъем меньшей крутизны, но большей
протяженности, на котором может быть
достигнута равномерная скорость
движения при выравнивании силы тяги с
общим сопротивлением движению поезда
(Fk
=Wk)
Средне
– эксплуатационный КПД
локомотивной тяги.
Для
электрической
тяги КПД
определяется произведением:
![]() ,
,
где
![]() –КПД
–КПД
электростанции (тепловая, атомная,
гидравлическая); у гидроэлектростанции
КПД
выше;
![]() –КПД
–КПД
повышающего трансформатора, установленного
на электростанции;
![]() –КПД
–КПД
линии
высоковольтной передачи (ЛЭП);
![]() –КПД
–КПД
тяговой подстанции;
![]() –КПД
–КПД
контактной сети;
![]() –КПД
–КПД
электровоза.
Наибольшее
влияние на величину КПД
электрической тяги оказывает значение
КПД
электростанции.
Для
тепловой
тяги КПД
определяется произведением:
![]() ,
,
где
![]() =
=
0,35![]() 0,40–КПД
0,40–КПД
дизеля;
![]() =
=
0,94
![]() 0,95– КПД
0,95– КПД
генератора;
![]() 0,99– КПД
0,99– КПД
выпрямительной установки (только для
тепловозов с генератором переменного
тока и тяговыми электродвигателями
постоянного тока);
![]() =
=
0,915– КПД
тяговых электродвигателей;
![]() =
=
0,975–
КПД зубчатой
передачи;
![]() =
=
0,88
![]() 0,92– КПД
0,92– КПД
вспомогательных
затрат.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет сил действующие на поезд
Страницы работы
Содержание работы
Силы действующие на
поезд.
В тяговых расчетах изучают
характер и режим движения поезда под действием приложенных к нему внешних сил,
кгс;
–
силы тяги локомотива (F)
–
силы сопротивления движению поезда
(W)
–
силы торможения (B)
В
большинстве случаев в расчетах пользуются значением удельных сил, кгс/т, т.е.
отнесенных к единице массы поезда:
f, w, b.
При
выполнении расчетов могут быть приняты различные модели поезда и которая
расположена в середине поезда. Такого упрощенного представления в большинстве
случаев вполне достаточно для решения практических задач, возникающих в
практике проектирования железных дорог, в частности, определения:
массы состава (Q), скорости движения в зависимостти от характеристики
пути (V(S)), времени хода поезда (t(S)), расхода
электрической энергии (А) или дизельного топлива (Е), механической работы силы
тяги локомотива (Rм), работы
сил сопротивления движению (Rc) и др.
Расчет
удельных сил сопротивления движению поезда.
Определение основного
удельного сопротивления вагонов при движении по звеньевому пути
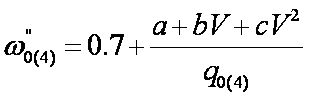
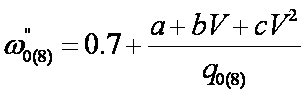
где q0(4) = 18,35 т и q0(8) = 20,80 т.
(см. ранее) – осевые нагрузки.
V– скорость, км/ч.
Основное
удельное сопротивление движению локомотива.
В режиме тяги ![]()
В режиме холостого хода ![]()
Вычисления произведем для скоростей V от 10 до 100
км/ч (через 10 км/ч) и для V = 43.5 км/ч.
Основное средневзвешенное удельное
сопротивление движению состава.
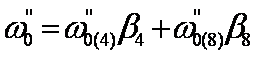 , где
, где
b4 – доля по массе 4х осных вагонов = 0.74
b8 – доля по массе 8х осных вагонов = 0.26
И тогда основное средневзвешенное удельное сопротивление
движению поезда, кгс/т
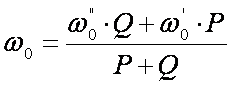
где Q – масса состава брутто, т;
Масса состава поезда
Масса состава, т, определяется из условия равномерного
движения поезда по руководящему уклону с минимальной расчетной скоростью по
формуле
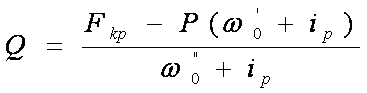
Fkp – сила тяги локомотива при расчетной
скорости, кгс.
P – масса локомотива, кгс.
ip – руководящий уклон линии ip = 15%o
w 0’ – основное удельное сопротивление локомотива в
режиме тяги при расчетной скорости.
w 0” – – основное удельное сопротивление состава при
расчетной скорости.
Для 2М62 : Q = 2238,5 т.
Для ВЛ80 : Q = 2930 т.
P – масса
локомотива, т.
Результаты расчетов по определению основного удельного
сопротивлению движению поезда представлены в таблице.
|
V |
W0″ |
W0′ |
W0’x |
W0 |
W0x |
||
|
2М62 |
ВЛ80 |
2М62 |
ВЛ81 |
||||
|
10 |
0,9501 |
2,03 |
2,545 |
1,0539 |
1,0165 |
1,1034 |
1,0482 |
|
20 |
1,0318 |
2,22 |
2,76 |
1,1460 |
1,1049 |
1,1979 |
1,1381 |
|
30 |
1,1385 |
2,47 |
3,045 |
1,2665 |
1,2204 |
1,3217 |
1,2557 |
|
40 |
1,2702 |
2,78 |
3,4 |
1,4153 |
1,3631 |
1,4749 |
1,4012 |
|
43,5 |
1,3221 |
2,90 |
3,5408 |
1,4740 |
1,4193 |
1,5353 |
1,4585 |
|
50 |
1,4268 |
3,15 |
3,825 |
1,5924 |
1,5328 |
1,6573 |
1,5743 |
|
60 |
1,6084 |
3,58 |
4,32 |
1,7979 |
1,7297 |
1,8690 |
1,7752 |
|
70 |
1,815 |
4,07 |
4,885 |
2,0317 |
1,9537 |
2,1100 |
2,0038 |
|
80 |
2,0466 |
4,62 |
5,52 |
2,2939 |
2,2049 |
2,3804 |
2,2602 |
|
90 |
2,3032 |
5,23 |
6,225 |
2,5845 |
2,4832 |
2,6801 |
2,5444 |
|
100 |
2,5848 |
5,90 |
7 |
2,9034 |
2,7887 |
3,0091 |
2,8563 |
|
110 |
2,929 |
6,63 |
7,85 |
3,2847 |
3,1566 |
3,4019 |
3,2316 |
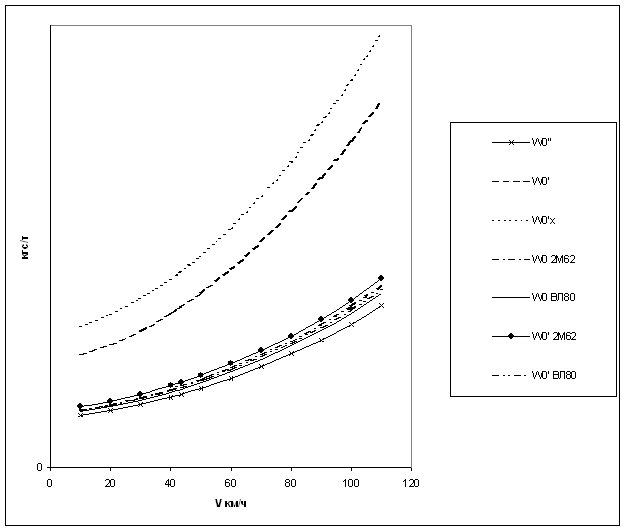
На
основании расчетов
Построение
тяговой характеристики локомотивов и определение массы состава по силе тяга.
Зависимость силы тяги локомотива от скорости движения
поезда называется тяговой характеристикой. Тяговые характеристики приведены в
Правилах тяговых расчетов. При производстве тяговых расчетов для заданных
локомотивов необходимо построить расчетную кривую Fк(V) c учетом
ограничения силы тяги по сцеплению колес с рельсами.
Общая масса состава называется массой брутто Q, а масса
груза в вагонах – массой нетто Qн, т.
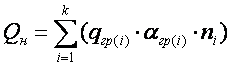
где qгр(i) –
грузоподъемность вагона i – го типа, т.
aгр(i) – коэффициент
использования грузоподъемности вагона i – ого типа = 0.71.
ni
– количество
вагонов i – ого типа.
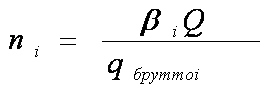 –
–
количество вагонов.
Для локомотива 2М62:
n4 = 22.7 шт. Примем n4 =23 шт. n8 = 3.22 шт. Примем n8 = 3 шт.
Для локомотива ВЛ80:
n4 = 29,9 шт. Примем n4 =30 шт. n8 = 4,6 шт. Примем n8 = 4 шт.
Тогда Для 2М62:
Qн = 1579.4 т.
Для ВЛ80: Qн
= 2188,5т.
Общая длина поезда, м, может быть определена из выражения
ln =
lсостава
+ lлокоматива;
lсостава = l4 n4 + l8 n8 , где
li – длина вагона i –ого типа, м.
l4 = 14 м, l8 = 20 м.
Для 2М62: lп
= 418 м.
Для ВЛ80: lп
= 553 м.
Проверка при трогании с места :
![]()
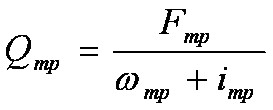
Примем iтр = 12 %o (
максимально допустимый уклон линии на станции или раздельном пункте );
Fтр – сила тяги
локомотива при трогании с места, кгс.
Для 2М62: Fт = 71400 кгс.
Для ВЛ80: Fт = 69000 кгс.
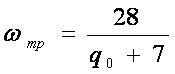 ,
,
где q0 = b4 q0(4)
+ b8 q0(8)
q0
=19.2 т.
wтр = 1.067
Для 2М62: 5492,3 т
Для ВЛ80: 5280,5 т.
Окончательно получаем состав из 3 восьмиосных и 23
четырехосных вагонов для локомотива 2М62 и 5 восьмиосных и 30 четырехосных
вагонов для локомотива ВЛ80.
Согласно
полученной длине поезда и СНиПу принимаем длину приемо-отправочных путей lпо
=850 м.
Проверка: Q по=
qп (lпо –50)
где
qп =Q/lп – погонная нагрузка поезда.
Для 2М62: qп = 5.23 т/м.
Для ВЛ80: qп = 5,31т/м.
Для 2М62: Q по = 4184.1 т >
Q = 2238,5 т.
Для ВЛ80: Q по = 4245,9 т >
Q = 2935 т. -> длина приемо-отправочных путей достаточна.
На ж/д наиболее распространены механические и электрические
способы торможения.
Основным является механическое торможение, которое может
осуществлятся при любом виде тяги.
При механическом торможении удельная тормозная сила поезда,
кгс/т, определяется по формуле
![]()
где
jкр –
расчетный коэффициент трения тормозной колодки о колесо.
Для
стандартных тормозных колодок
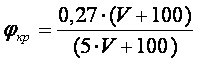
![]() – расчетный тормозной коэффициент
– расчетный тормозной коэффициент
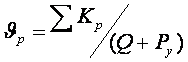
SКр –
суммарное расчетное нажатие на тормозные оси состава, тс.
Рy
– учетная масса локомотива равная массе локомотива Р.
![]()
где
n4 и n8 – количество осей вагона данного типа, шт.
K0(i)
– расчетное нажатие на тормозную ось вагона i – ого типа = 7.0 тс.
Окончательно
получим :
|
V |
bт |
||
|
jкр |
2М62 |
ВЛ80 |
|
|
10 |
0,1485 |
35,64 |
38,61 |
|
20 |
0,1296 |
31,10 |
33,70 |
|
30 |
0,1170 |
28,08 |
30,42 |
|
40 |
0,1191 |
28,57 |
30,95 |
|
43,5 |
0,1107 |
26,57 |
28,78 |
|
50 |
0,1013 |
24,30 |
26,33 |
|
60 |
0,0960 |
23,04 |
24,96 |
|
70 |
0,0918 |
22,03 |
23,87 |
|
80 |
0,0884 |
21,21 |
22,97 |
|
90 |
0,0855 |
20,52 |
22,23 |
|
100 |
0,0831 |
19,94 |
21,60 |
|
|
0,5670 |
136,08 |
147,42 |
Построение
диаграмм удельных равнодействующих сил.
Похожие материалы
- Расчет удельных сил сопротивления состава. Определение массы состава. Тормозная сила поезда
- Реконструкция участка существующей железной дороги с технико-экономическим анализом овладения перевозками и выбором средств этапного усиления мощности
- Реконструкция участка существующей железной дороги с технико-экономическим обоснованием проектных решений
Информация о работе
Тяговые расчёты — прикладная часть теории тяги поездов, в которой рассматриваются условия движения поезда и решаются задачи, связанные с определением сил, действующих на поезд, и законов движения поезда под воздействием этих сил.
История тяговых расчётов[править | править код]
В 1814 г. в Англии Уильям Гедли и Тимоти Гакуорд провели первые опыты по экспериментальной оценке сил сцепления колёс паровоза с рельсами. В 1818 г. Джордж Стефенсон провёл первые опыты по определению сил сопротивления движению вагонов. В 1825—1830 гг. чешский инженер Франтишек Антонин Герстнер, строивший в Австро-Венгрии конно-рельсовую дорогу, определил, что по рельсам лошадь может перевести в семь раз больший груз, чем по грунтовой дороге.
В 1858 г. профессор Института Корпуса инженеров путей сообщения А. Г. Добронравов опубликовал свой труд «Общая теория паровых машин и теория паровозов», где дал уравнение движения поезда и подробно рассмотрел элементы сил сопротивления движению. В 1869 г. профессор М. Ф. Окатов ставил опыты «на скольжение», то есть определял величину силы тяги по сцеплению. В 1877—1879 гг. конструктор паровозов инженер В. И. Лопушинский проводил на разных дорогах опыты по измерению сопротивления движению паровоза и вагонов с применением динамометров.
В 1877 г. профессор Л. А. Ермаков в своём труде «Определение расходования топлива паровозами» научно разработал основы тяговых расчётов для определения веса состава, времени хода, допускаемой скорости поездов по тормозным средствам, расхода топлива и воды. В 1883 г. Л. А. Ермаков рассмотрел природу сопротивления движению на горизонтальном и прямом пути, на подъёмах и в кривых участках пути.
В 1880 г. инженер А. П. Бородин в Киевских железнодорожных мастерских создал стенд для испытаний паровозов. Ведущая колёсная пара паровоза типа 1-2-0 отделялась от спаренной и приподнималась над рельсами, один из бандажей обтачивался под шкив ремённой передачи. Нагрузкой паровозу служило станочное оборудование мастерских. Недостатком стенда было ограничение по нагрузке — 65—70 кВт при 100 об/мин ведущих колёс, что соответствовало скорости движения 30 км/ч.
В 1889 г. был издан труд профессора Петербургского технологического института Н. П. Петрова «Сопротивление поездов на железных дорогах», в котором теоретически рассмотрены составляющие сил сопротивления движению поезда и влияние различных факторов на их величину. В 1892 г. им были предложены расчётные формулы для определения сопротивления движению подвижного состава.
В 1903—1904 гг. на путиловском заводе в Петербурге построена катковая испытательная станция. Каждая ведущая ось локомотива устанавливалась на каток, обод которого имел профиль головки рельса, направляющие и поддерживающие колёсные пары опирались на рельсы. Локомотив сцепкой через динамометр присоединялся к массивной стойке. Торможением катков создавалось требуемая постоянная нагрузка локомотива.
В 1898 г. инженер Ю. В. Ломоносов начал проводить эксплуатационные испытания паровозов в составе поездов по поручению службы тяги Харьково-Николаевской железной дороги. С1908 г. на всех железных дорогах тягово-теплотехнические испытания паровозов проводились по предложенной им методике. В 1912 г. при министерстве путей сообщения создана «Контора опытов над типами паровозов», возглавляемая Ю. В. Ломоносовым. Министерством путей сообщения были утверждены «Правила производства сравнительных опытов над типами паровозов», обязательные для испытания паровозов на казённых железных дорогах. На основе проведённых испытаний были созданы технические паспорта паровозов почти всех серий, работающих на железных дорогах России. В 1917 г. Министерство путей сообщения утвердило «Временные правила о производстве тяговых расчётов», созданные на основе работы «Конторы опытов».
В 1932 г. вблизи станции Бутово построено «Опытное железнодорожное кольцо» диаметром 1912 м, предназначенное для испытаний подвижного состава. В 1935 г. кольцо было электрифицировано, что позволило испытать первые электровозы серий ВЛ19 и С11. Все новые типы локомотивов проходят испытания на кольце с целью определения их тяговых характеристик.
Тяговые расчёты[править | править код]
Тяговые расчёты используются:
- при проектировании железных дорог;
- при проектировании подвижного состава;
- при организации эксплуатации локомотивов;
- при организации движения поездов.
Упрощения, используемые при расчётах[править | править код]
- Поезд принимается за материальную точку, условно располагаемую в середине поезда. При вычислениях с использованием ЭВМ масса поезда считается равномерно распределённой по его длине.
- Железнодорожный путь в плане считается состоящим из прямых участков и дуг окружностей постоянного радиуса. Длина переходных кривых включается в общую длину криволинейного участка.
- Продольный профиль железнодорожного пути считается состоящим из прямолинейных отрезков, расположенных либо горизонтально, либо под углом к горизонту. Наличие между ними сопряжений не учитывается.
В случае если путь не состоит из прямолинейных участков, прибегают к спрямлению профиля пути.
Спрямление профиля пути и определение расчетного скоростного подъема и наибольшего спуска[править | править код]
Для повышения точности результатов тяговых расчетов, а также сокращения объема их и, времени на их выполнение, необходимо спрямить профиль пути заданного участка.
В основе спрямления профиля пути лежит равенство механических работ на спрямленном профиле и на действительном профиле.
Спрямление профиля состоит в замене двух или нескольких смежных элементов продольного пути одним элементом, длина которого sс равна сумме длин спрямляемых элементов ( s1, s2, . . . . , sn ) т. е.
![]()
где i1, i2,…in – крутизна элементов спрямляемого участка.
sС= s1+s2+….+sn ,
крутизна i”c вычисляется по формуле
Чтобы расчеты скорости и времени движения поезда по участку были достаточно точными, необходимо выполнить проверку возможности спрямления
группы элементов профиля по формуле :

где si– длина спрямляемого участка, м;
Δi – абсолютная величина разности между уклоном спрямленного участка и уклоном проверяемого элемента, 0/00 ,
Данной проверке подлежит каждый элемент спрямляемой группы. Чем короче элементы спрямленной группы и чем ближе они по крутизне, тем более вероятно, что проверка их на удовлетворение условию окажется положительной.
Кривые на спрямленном участке заменяются фиктивным подъемом, крутизна которого определяется по формуле

где Sкрi и Ri – длина и радиус кривой в пределах спрямленного участка, м.
Крутизна спрямленного участка с учетом фиктивного подъема от кривой

Принимаем для движения туда значения i’c положительным, а значения обратного движения i’c отрицательным, т.е. подъем становится спуском.
Нельзя спрямлять следующие элементы: расчётный подъём, крутой подъем, наикрутейший спуск. Площадки на перегоне между элементами разного знака также нельзя включать в спрямление. Спрямленный профиль должен сохранять все особенности действительного профиля в смысле относительного расположения повышенных и пониженных точек.
После спрямления профиля пути производим его анализ с целью выявления расчетного подъёма, скоростного подъема и наикрутейшего спуска.
Расчетным подъемом называют такой подъем, на котором устанавливается расчетная скорость, данный подъем является наиболее труднопреодолимым участком. iрасч= 8,0 ‰.
Короткий подъем крутизной больше расчетного – это такой подъем, при котором iрасч<iкр, но протяженность его меньше чем расчетного и поэтому поезд преодолевает его достаточно легко iкр= 8,0 ‰.
Крутой спуск – это самый крутой спуск, при котором поезду необходимо переходить на холостой ход и при этом пользоваться тормозом iспу= -6,8 ‰
Расчет массы состава[править | править код]
Расчет массы производим по формуле:

где Fкр– расчетная сила тяги локомотива, кгс;
значение расчетной скорости равно Vр
iр – крутизна расчетного подъема,
P- расчетная масса локомотива, m
w,0 – основное удельное сопротивление локомотива, кгс/т
Зависит от скорости и определяется по формуле:

w,,0 – основное удельное сопротивление состава в кгс/т, рассчитываем соответственно тоже для расчетной скорости по формуле

где альфы,бетта и гамма – соответственно доли 4-х, 6 -ти и 8-ми осных вагонов в составе по массе заданные
Проверка массы состава[править | править код]
Учитываем что перед преодолением крутого участка, составу предшествуют легкие элементы профиля. При этом путь, крутизна которого равна 8,0 0/00, проходимый поездом с учетом кинетической энергии

где Vн –скорость в начале проверяемого подъема, т.е. эта та скорость которая была развита на предшествующем элементе
Vк – скорость в конце проверяемого подъема
(fк – wк)ср –удельная сила, рассчитываем для среднего значения скорости

Значение средней скорости равно:

Проверка массы состава по длине приемо-отправочных путей станции[править | править код]
Чтобы выполнить проверку массы состава по длине приемо-отправочных путей, необходимо вначале определить число вагонов в составе и длину поезда.
Число вагонов в составе поезда:
4-х-осных:

8-х-осных :

Найдем общую длину поезда по формуле:

где Ll – длина локомотива
Расчет и построение кривых ускоряющих и замедляющих усилий[править | править код]
Расчет диаграммы удельных равнодействующих сил выполняется для трех режимов ведения поезда по горизонтальному участку:
1) для режима тяги 
2) для режима холостого хода 
3) для режима торможения:
при служебном регулировочном торможении

при экстренном торможении

Расчет ведем относительно скоростей от 0 до конструкционной , а так же для скоростей расчетных и скорости выхода на автоматическую характеристику
Силы, действующие на поезд[править | править код]
Сила тяги[править | править код]
Сила тяги локомотива в зависимости от скорости определяется по тяговым характеристикам, которые строятся для новых бандажей в соответствии с характеристиками тяговых двигателей, снятыми на стенде или при эксплуатационных испытаниях.
Сила тяги локомотива не может превосходить силы сцепления ведущих колёс локомотива с рельсами.
,
где FK — сила тяги;
P — «сцепной» вес локомотива (сумма нагрузок на рельсы от всех ведущих колёс);
ψ — коэффициент сцепления.
Коэффициент сцепления колеса с рельсом максимален на стоянке и убывает по мере увеличения скорости движения локомотива. Поскольку реальный коэффициент сцепления зависит от случайных факторов, таких как состояние пути и атмосферные условия, его заменяют расчётным коэффициентом сцепления ψK, величину которого определяют по эмпирическим формулам, основанным на результатах многочисленных опытов в условиях реальной эксплуатации. В простейшем случае, для паровозов:
,
где v — скорость движения, км/ч.
Сопротивление движению[править | править код]
Сопротивлением движению поезда называют силу, приложенную в точках касания колёс с рельсами, на преодоление которой затрачивается такая же работа, как на преодоление всех неуправляемых сил, препятствующих движению. Удельное сопротивление — сила сопротивления каждой единицы веса поезда.
,
где w — удельное сопротивление;
W — полное сопротивление, Н;
P — вес локомотива, кН;
Q — вес вагонов поезда, кН.
Основным сопротивлением называют силы, препятствующие движению подвижного состава по прямому горизонтальному пути на открытой местности при нормальных метеоусловиях с любой допустимой скоростью. Основное сопротивление складывается из:
- сопротивления от трения в буксовых подшипниках;
- сопротивление от трения качения колёс по рельсам;
- сопротивление от трения скольжения колёс по рельсам;
- рассеяния энергии при взаимодействии колёс с рельсами (потеря энергии на стыках и неровностях пути, упругая деформация рельсов и шпал);
- сопротивления воздушной среды;
- рассеяния энергии в окружающую среду при вертикальных колебаниях подрессоренных частей подвижного состава и рывках по длине поезда.
Из-за влияния многочисленных факторов, установить аналитические зависимости для расчёта основного удельного сопротивления практически невозможно, его значение получают исключительно экспериментальным путём. В результате обработки экспериментальных данных получают эмпирические формулы или графики. Например, для четырёхосного вагона на роликовых подшипниках, движущегося по звеньевому пути
,
где q0 — нагрузка от колёсной пары на рельсы.
Дополнительными сопротивлениями называют временно действующие силы, возникающие в конкретных условиях эксплуатации подвижного состава:
- от уклона профиля пути;
- от кривизны пути;
- от ветра;
- от низкой температуры;
- от тоннелей;
- от подвагонных генераторов пассажирских вагонов.
Дополнительное удельное сопротивление движению от уклона принимают равным величине уклона в промилле.
.
Дополнительное удельное сопротивление движению в кривых участках пути возникает по следующим причинам:
- колёса одной колёсной пары проходят разный путь по наружному и внутреннему рельсу (конусность бандажей уменьшает эту разницу), что приводит к увеличению проскальзывания колёс;
- за счёт действия центробежной силы гребни колёс прижимаются к внутренней боковой грани наружного рельса, что увеличивает силу трения скольжения;
- тележки подвижного состава поворачиваются относительно оси кузова, в результате чего в опорах, шкворневых устройствах и буксах возникают силы трения скольжения.
Дополнительное удельное сопротивление движению от кривой рассчитывается по эмпирическим формулам, при длине поезда более длины кривой
,
где R — радиус кривой;
sKP — длина кривой;
lП — длина поезда.
При длине поезда менее или равной длине кривой
.
При проведении расчётов, требующих повышенной точности учитывается также скорость движения поезда и возвышение наружного рельса.
Дополнительное удельное сопротивление движению, вызванное действием лобового или бокового ветра определяется в долях от основного удельного сопротивления при помощи коэффициента КB.
.
Коэффициент КB определяется по таблицам или номограммам и зависит от скорости ветра, скорости движения подвижного состава и плотности воздуха. Перечень участков, для которых используется поправка на ветер и скорости ветра для каждого периода устанавливается по результатам многолетних метеорологических наблюдений.
При низких температурах наружного воздуха повышается его плотность, увеличивая аэродинамическое сопротивление движению, повышается вязкость смазки в буксовых и моторно-осевых подшипниках, увеличивая силы трения в них. Дополнительное удельное сопротивление движению от низкой температуры наружного воздуха учитывается при температурах ниже −25 °C при помощи коэффициента КHT
.
Коэффициент КHT определяется по таблицам в зависимости от скорости движения поезда и температуры наружного воздуха.
Дополнительное удельное сопротивление от движения в тоннелях возникает вследствие увеличения лобового сопротивления, эффекта разрежения в хвостовой части поезда и возникновения турбулентности между стенками тоннеля и поездом.
.
Коэффициент КT зависит от скорости движения поезда и числа путей в тоннеле. В двухпутном тоннели сопротивление движению воздушной среды значительно меньше, чем в однопутном.
Дополнительное сопротивление от подвагонных генераторов пассажирских вагонов учитывают при скоростях движения 20 км/ч и выше.
,
где P’ — средняя условная мощность подвагонного генератора.
Подвагонные генераторы отсутствуют в скоростных поездах, имеющих централизованное электроснабжение от локомотива или вагона-электростанции.
Процесс трогания с места подвижного состава после длительных стоянок (20 мин и более) происходит в условиях полусухого и сухого трения. За время стоянки разрушается масляный клин между трущимися деталями буксового подшипника, снижается температура и повышается вязкость смазки. Стоянка сопровождается значительным смятием металла в зоне контактной площадки, что увеличивает потери от трения качения по рельсам. Добавочное сопротивление при трогании с места для подвижного состава на подшипниках качения
.
Тормозная сила[править | править код]
Тормозная сила поезда определяется как сумма произведений действительных сил нажатия тормозных колодок К на действительные коэффициенты трения колодок φK или как произведение суммы расчётных (приведённых) сил нажатия КP на расчётный коэффициент трения колодок φKP.
.
С увеличением скорости и удельного нажатия колодок, количество тепла, выделяемое при трении колодки о колесо возрастает, повышается температура металла колеса и колодки, поверхностный слой становится более пластичным, в результате чего коэффициент трения уменьшается. Коэффициент трения рассчитывается по эмпирическим формулам, например, для стандартных чугунных тормозных колодок
.
Действительная сила нажатия определяется давлением воздуха в тормозном цилиндре (тормозные цилиндры имеют отверстия для подключения манометра), площадью поршня, усилием отпускной пружины, передаточным отношением тормозной рычажной передачи, количеством колодок, работающих от одного цилиндра, КПД цилиндра и рычажной передачи. Для упрощения расчётов используют расчётную силу нажатия и расчётный коэффициент трения. Формула для определения расчётного коэффициента трения для чугунных колодок имеет вид
.
Расчётные силы нажатия определяют по нормативам, устанавливаемым для каждого типа локомотива, вагона и величины его загрузки. Для предотвращения юза тормозная сила, создаваемая тормозными средствами каждой колёсной пары, не должна превышать силу сцепления колёсной пары с рельсами.
Расчётным тормозным коэффициентом называют отношение суммы расчётных сил нажатия к весу поезда
.
В расчётах, где учитывается применение экстренного торможения, расчётный тормозной коэффициент принимается равным его полному значению, при применении полного служебного торможения, расчётный тормозной коэффициент принимается равным 0,8 от его полного значения. При регулировочных торможениях значение расчётного тормозного коэффициента, в зависимости от ступени торможения определяется по таблицам.
Расчёт веса состава[править | править код]
Вес состава и скорость движения поезда определяется из условия полного использования мощности локомотива и кинетической энергии поезда. Вес состава определяется исходя из условия движения по расчётному (руководящему) подъёму с равномерной скоростью и по труднейшему подъёму с неравномерной скоростью с использованием кинетической энергии поезда.
Вес поезда при условии движения с равномерной скоростью на расчётном подъёме определяют из условия равенства сил тяги и сопротивления движению поезда по формуле
,
где w’0 — основное удельное сопротивление локомотива;
w”0 — основное удельное сопротивление вагонов.
Вес состава для прохождения труднейшего подъёма с использованием кинетической энергии определяется методом подбора. Для этого определяется вес состава для расчётного подъёма и проверяется возможность прохождения труднейшего подъёма. Если скорость в конце проверяемого элемента меньше расчётной (минимально допустимой), вес состава уменьшают и повторяют расчёт.
Вес состава проверяется также на условие трогания на подъёме, при этом результирующая ускоряющая сила должна быть больше нуля.
Решение тормозных задач[править | править код]
Тормозными задачами называются задачи определения тормозных средств, которые обеспечивают снижение скорости или полную остановку поезда на требуемом расстоянии и задачи определения расстояния, на котором поезд с известными тормозными средствами может остановиться или снизить скорость до заданного значения. Из-за инерционности тормозной системы нарастание тормозной силы в разных вагонах происходит не одновременно. Для упрощения расчётов считается, что тормозная сила нарастает мгновенно до установившегося значения через некоторый отрезок времени tп, который называют временем подготовки тормозов к действию. Время подготовки тормозов к действию увеличивается при увеличении длины состава, так же при расчётах используются поправки на уклон и на величину тормозной силы.
Тормозной путь равен сумме подготовительного тормозного пути (расстояния, пройденного за время подготовки тормозов) и действительного пути торможения. Величина действительного пути торможения обычно определяется численным интегрированием уравнения движения по интервалам скоростей.
Определение максимально допустимой скорости по расчетному тормозному нажатию в зависимости от величины уклона[править | править код]
Поиск производится для наиболее крутого спуска при заданных тормозных средствах и принятом полном тормозном пути равным . Метод решения- графоаналитический. Полный тормозной путь равен:

где Sp –путь подготовки тормозов к действию, на протяжении которого тормоза поезда условно принимаются недействующими (от момента установки ручки крана машиниста в тормозное положение до включения тормозов поезда).
Sd –действительный тормозной путь, на протяжении которого поезд движется с действующими в полную силу тормозами
Расчет времени хода методом Дегтярёва[править | править код]
Для построения необходимо изготовить шаблон в виде равнобедренного треугольника. Для нашего масштаба размеры треугольника следующие: основание равно 60 мм, высота 180 мм. После изготовления шаблона начинаем построение. При начале движения поезда со станции «А» его скорость растет соответственно должна расти кривая времени, прикладываем основание шаблона так, что угол одной из его сторон и основания упирался в начало станции «А», проводим линию по шаблону от нуля до точки пересечения со скоростью. От полученной точки проводим линию по другой равнобедренной стороне до основания. Рядом строим такой же треугольник, который так же ограничиваем уже построенной кривой скорости.
Далее продолжаем строить треугольники один рядом с другим. В итоге получаем, что чем выше скорость, тем больше треугольник, а один треугольник равен одной минуте. Подсчитываем эти треугольники путем построения кривой времени, для этого абсциссу, на которой заканчивается треугольник, равный минуте, проектируем на абсциссу, которая соответствует значению 1 минуте, а точку, которая соответствует этой минуте, соединяем со следующей минутой. Таким образом, получаем кривую с интервалами от минуты до другой минуты, т.е. от конца одного треугольника до конца другого треугольника. Следует иметь ввиду, что кривая времени нарастающая, поэтому при достижении ординаты равной 10 мин, кривую обрываем, а точку обрыва переносим вниз. Таким образом, кривую обрываем каждые 10 мин. В нашем случае, исходя из масштаба, один треугольник равен 0,1 минуте.
Построение кривой скорости движения[править | править код]
Кривой скорости движения называют график зависимости скорости движения поезда от пройденного пути. Ниже оси абсцисс условно изображают профиль пути. Обычно строят кривую скорости движения для состава расчётного веса при определении наименьшего времени хода поезда по заданному участку. Расчёт производится графическим методом, используя диаграммы ускоряющих и замедляющих сил, или интегрированием уравнения движения поезда. Результат расчёта используется при составлении графика движения поездов.
Литература[править | править код]
- Астахов П. Н. «Сопротивление движению железнодорожного подвижного состава» Труды ЦНИИ МПС. Выпуск 311. — Москва: Транспорт, 1966. — 178 с.
- Деев В. В., Ильин Г. А., Афонин Г. С. «Тяга поездов» Учебное пособие. — Москва: Транспорт, 1987. — 264 с.
- Правила тяговых расчётов для поездной работы. — М.: Транспорт, 1985. 287 с.
Расчет сопротивления движения поезда, расхода и стоимости электроэнергии на движение поезда
Расчёт сопротивления
движения поезда, расхода и стоимости электроэнергии на движение поезда
Введение
Целью курсовой работы является исследование зависимости
расхода электрической энергии при равномерном движении грузового поезда с
различными скоростями на участке пути, состоящем из четырех элементов различной
крутизны.
Для достижения цели необходимо выполнить следующие задачи:
рассчитать массу, вес и длину поезда при заданной загрузке вагонов, рассчитать
вес поезда при максимальной загрузке вагонов, определить эквивалентный уклон,
рассчитать основное сопротивление движению поезда заданном значении скорости,
рассчитать основное сопротивление движению поезда для скоростей 20,40,60,80,100
км/ч и построить графики, рассчитать мощность, развиваемую поездом при с
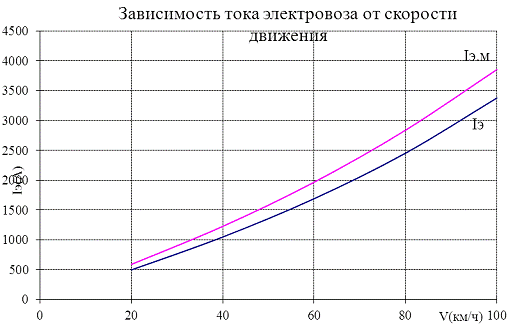
скорости 20,40,60,80,100 км/ч и построить графики, рассчитать ток электровоза
для скоростей 20,40,60,80,100 км/ч и построить графики, рассчитать расход
энергии для заданной скорости движения, рассчитать потери напряжения и мощности
в тяговой сети, построить графики, определить стоимость электроэнергии.
1. Расчёт массы, веса и длины поезда при заданной
загрузке вагонов
1.1 Масса поезда
Масса поезда определена по формуле, Т:
mп = mэ + mв. (1.1)
где mэ – масса электровоза, Т;
mв – масса вагонов, Т.
Масса гружёных вагонов определена по формуле, Т:
mв = Nв (mт + mгр · α2). (1.2)
где Nв – количество вагонов в поезде;
mт – тара вагона, т.е. масса порожнего вагона; Т;
mгр – грузоподъёмность вагона, т.е. наибольшая масса
груза, которую можно перевозить в вагоне данного типа, Т;
α2 – коэффициент
использования грузоподъёмности вагона, зависящий от рода груза и его размещения
в вагоне.
mв = 50 (23+ 64 · 0,75) = 3550 (Т).
mп = 186 + 3550 = 3736 (Т).
1.2 Масса вагона, отнесённая к колёсной паре
Масса вагона, отнесённая к колёсной паре определена из
уравнения, Т:
qо =![]() . (1.3)
. (1.3)
где Nо – число осей вагона.
qо = ![]() = 17,75 (Т).
= 17,75 (Т).
1.3 Вес поезда
Вес поезда, Qп в кН складывается из веса электровоза и веса
вагонов
G = mэ · g. (1.5)
Q = mв · g. (1.4)
где g – 9,81 м/с2 – ускорение силы тяжести.
G = 186 · 9,81 = 1824,6 (кН).
Q = 3550 · 9,81 = 34825,5 (кН).
Qп = Q + G = (mэ · g,) + (mв · g,) = 1824,6 + 34825,5 = 36650,1 (кН).
1.4 Длина поезда
Длина поезда найдена по формуле, м:
lп = lэ + Nв · lв. (1.6)
где lэ – длина электровоза, можно принять lэ=30 м;
lв – длина вагона, м.п = 30 + 50 · 15 =
780 (м).
Полученное значение lп необходимо сопоставить с
полезной длиной приёмоотправочных путей.п = 780, длина
приёмоотправочных путей равна 1200 м. из этого следует, что размещение поезда
возможно.
2. Расчёт веса поезда при максимальной загрузке
вагонов
2.1 Масса поезда
Масса поезда определяется из массы электровоза и массы
вагонов при максимальной загрузке вагонов.
mп,м = mэ + mв,м. (2.1)
mв,м = Nв (mт + mгр·α2). (2.2)
mв,м = 50 (23 + 64·1) = 4350 (Т).
mп,м = 186 + 4350 = 4536 (Т).
2.2 Масса вагона, отнесённая к колёсной паре
Масса вагона, отнесённая к колёсной паре, находится из
формулы, Т:
qо.м =![]() (Т). (2.3)
(Т). (2.3)
qо.м = ![]() = 21,75 (Т).
= 21,75 (Т).
2.3 Вес поезда
Вес поезда рассчитан по формуле:
Qп.м = G + Qм = (mэ · g) + (mв.м · g). (2.4)
Qп.м = (186 · 9,81) + (4350·9,81) = 1824,6 + 42673,5 =
44498,1 (Т)
3. Определение эквивалентного уклона
3.1 Эквивалентный уклон (с учётом сопротивления
от кривых)
Эквивалентный уклон (с учётом сопротивления от кривых)
рассчитан по формуле, ‰;
iэ = ![]() (3.1)
(3.1)
где n – число элементов профиля;
![]() Sj – длина элементов профиля, м;
Sj – длина элементов профиля, м;
ij – уклон элемента
профиля, ‰;
wRj – сопротивление движению
по кривой, Н/кН;
Sкрj – длина кривой, м.
Расчёт iэ производим в виде табл. 1.
Таблица 1. Расчёт эквивалентного уклона
|
№ элемента |
Длина элемента |
Уклон элемента ij |
ij |
Радиус кривой Rj, м |
Длина кривой Sкрj, м |
wRj |
|
|
1 |
1400 |
1,4 |
1960 |
– |
– |
– |
– |
|
2 |
3600 |
5,5 |
1980 |
– |
– |
– |
– |
|
3 |
4600 |
4,0 |
18400 |
500 |
900 |
1,4 |
1260 |
|
4 |
1400 |
1,0 |
1400 |
600 |
400 |
0,85 |
340 |
|
|
|
|
3.2 Сопротивление движению на кривом участке пути
Сопротивление движению на кривом участке пути определяется по
формуле, Н/кН;
w = ![]() . (3.2)
. (3.2)
для участка на котором поезд полностью расположен в кривой,
т.е. lп ![]() Sкр
Sкр
На третьем участке lп = 780 м ![]() Sкр3 = 900 м, следовательно:
Sкр3 = 900 м, следовательно:
W3 = ![]() =
= ![]() = 1,4 (Н/кН).
= 1,4 (Н/кН).
W = ![]() ·
· ![]() .
.
(3.3)
для участка где длинна поезда lп превышает
длину кривой Sкр, т.е. lп ![]() Sкр
Sкр
На четвертом участке lп = 780 м ![]() Sкр2 = 400 м, следовательно:
Sкр2 = 400 м, следовательно:
W4 = ![]() ·
· ![]() =
= ![]() ·
· ![]() = 1,7· 0,5 = 0,85 (Н /
= 1,7· 0,5 = 0,85 (Н /
Кн).
Эквивалентный уклон
iэ = ![]() =
= ![]() = 3,9 (‰).
= 3,9 (‰).
4. Расчёт основного удельного сопротивления
движению электровоза и вагонов при заданном значении скорости
4.1 Основное удельное сопротивление движению
электровоза
Основное удельное сопротивление движению электровоза найдено
из формулы, Н/кН:
w′о = 1,9 + 0.01U + 0,0003 U 2. (4.1)
где U – скорость движения поезда, км/ч.
w′о = 1,9 + 0,01· 56 + 0,0003 · (56)2 =
1,9 + 0,56 + 0,9408 = 3,4 (Н/кН).
4.2 Основное удельное сопротивление движению
вагонов
Зависит от типа вагонов и типа подшипников. Для грузовых
четырехосных вагонов на подшипниках скольжения рассчитано по формуле, Н/кН:
w′′о = 0,7 + ![]() . (4.2)
. (4.2)
w′′о = 0,7 + ![]() = 0,7 +
= 0,7 + ![]() = 0,7 +
= 0,7 + ![]() = 1,9 (Н/кН).
= 1,9 (Н/кН).
4.3 Дополнительное удельное сопротивление
движению поезда на эквивалентном уклоне
Дополнительное удельное сопротивление движению поезда на
эквивалентном уклоне численно равно уклону в Н/кН:
wi = iэ
5. Расчёт основного сопротивления движению поезда
и мощности, развиваемой поездом
5.1 Полное сопротивление движению поезда
Полное сопротивление движению поезда зависит от типа
подвижного состава и веса поезда, от профиля и плана железнодорожной линии и
рассчитано по формуле, Н:
W = G · w′о + Q · w′′о + (G + Q) iэ. (5.1)
W = 1824,6 · 3,4 +
34825,5 · 1,9 + (1824,6 + 34825,5)· 3,9 = 6203,6 + 66168,4 +
(36650,1)·3,9 = 215307,4 (Н)
5.2 Основное сопротивление движению поезда
Основное сопротивление движению поезда найдено из первых двух
членов выражения (5.1)
Wо = G · w′о + Q · w′′о. (5.2)
Wо = 1824,6 ·
3,4 + 34825,5 · 1,9 = 6203,6 + 66168,4 = 72372,05 (Н)
5.3 Расчёт сопротивления движению поезда
Расчёт сопротивления движению поезда необходимо выполнить при
скорости движения 20, 40, 60, 80 и 100 км/ч для двух режимов загрузки вагонов.
Сами вычисления удобно представлены в виде табл. 2. По данным табл. 2
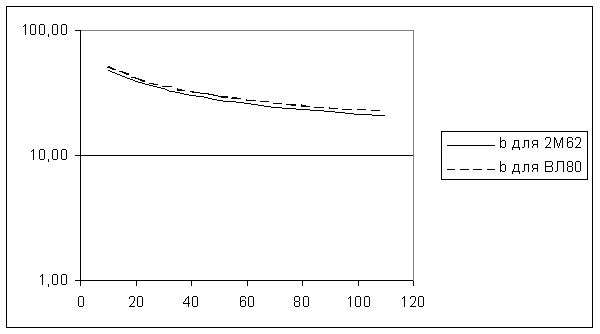
необходимо построить четыре графических зависимости W(v) и Wо(v) заданного и
максимального использования грузоподъёмности вагонов. Все четыре кривые следует
построить в одних и тех же координатах (рис. 2).
5.4 Мощность электровоза
Мощность электровоза Рэ, развиваемая электровозом
при движении поезда по рассматриваемому участку с заданной скоростью, равна
произведению его силы тяги Fк на скорость v:
Pэ = Fк · v
При равномерном движении поезда сила тяги электровоза
уравновешивается силой полного сопротивления движению поезда W.
Поэтому мощность, развиваемая электровозом при равномерном
движении, численно равна произведению силы полного сопротивления движению W и скорости v:
Pэ = W · v (5.3)
Произведен расчет сопротивления движения поезда и
потребляемой мощности по формуле:
G · w′о =1824,6![]() 3,4=6205 (Н).
3,4=6205 (Н).
Загрузка вагонов по заданию
Q · w′′о= 34825,5![]() 1,9=66443,13 (Н).
1,9=66443,13 (Н).
Wо= G·w′о+Q·w′′о=
6203,6+66168,45=72372,05 (Н).
W =Wо+(G+Q)
iэ=
72372,05+(1824,6+34825,5) ![]() 3,9 = 215307,4 (Н).
3,9 = 215307,4 (Н).
Pэ=![]() =
= ![]() = 3349 (кВт).
= 3349 (кВт).
масса поезд сопротивление мощность
Полная загрузка вагонов
w′′о.м = 0,7 + ![]() = 0,7+
= 0,7+![]() = 1,5 (Н/кН).
= 1,5 (Н/кН).
Qм · w′′о,м = 42673,5 ![]() 1,5 = 62126,7 (Н).
1,5 = 62126,7 (Н).
Wо,м=G·w′о+Qм·w′′о,м = 6205 + 62126,7 = 68331,7 (Н).
Wм =Wо,м+(G+Qм) iэ = 68331,7 + (1824,6 + 42673,5) ![]() 3,9 = 241874,3 (Н)
3,9 = 241874,3 (Н)
Pэ,м=![]() =
= ![]() = 3762,5 (кВт)
= 3762,5 (кВт)
Таблица 2. Расчет сопротивления движению поезда и
потребляемой мощности
|
Вычисляемые величины |
Значение величины при скоростях движения, км/ч |
||||||
|
20 |
40 |
56 |
60 |
80 |
100 |
||
|
Электровоз |
w′о, Н/кН |
2,22 |
2,78 |
3,4 |
3,58 |
4,62 |
6 |
|
G · w′о, Н |
4050,6 |
5072,4 |
6205 |
6532 |
8429,6 |
10947,6 |
|
|
Загрузка вагонов по заданию |
w′′о, Н/кН |
1,3 |
1,6 |
1,9 |
2 |
2,5 |
3,12 |
|
Q · w′′о, Н |
45959,8 |
55769,8 |
66443,13 |
69651 |
87161,8 |
108743,8 |
|
|
Wо=G·w′о+Q·w′′о, Н |
50010,4 |
72648,1 |
76183 |
95591,4 |
119691,4 |
||
|
W =Wо+(G+Q) iэ, Н |
192945,8 |
203728,6 |
215583,5 |
219118,4 |
238526,8 |
262626,8 |
|
|
Pэ= |
1072 |
2264 |
3354 |
3652 |
5300 |
7295 |
|
|
Полная загрузка вагонов |
w′′о,м, Н/кН |
1,2 |
1,4 |
1,5 |
1,75 |
2,2 |
2,7 |
|
Qм · w′′о,м, Н |
51453,4 |
59742,9 |
62126,7 |
74678,6 |
93881,7 |
115218,4 |
|
|
Wо,м=G·w′о+Qм·w′′о,м, Н |
55504,05 |
64815,3 |
68331,7 |
81210,6 |
102311,3 |
126166 |
|
|
Wм =Wо,м+(G+Qм) iэ, Н |
229046,6 |
238357,9 |
241874,3 |
254750,8 |
275854 |
299708,6 |
|
|
Pэ,м= |
1272,5 |
2648,4 |
3762,5 |
4245,8 |
6130 |
8325,2 |
Мощность электровоза подсчитывается для всех значений
скорости, указанных в табл. 2, для заданного и максимального использования
грузоподъемности вагонов. По данным табл. 2 строятся четыре графических
зависимости W(v) и Wo(v) для заданного и
максимального использования грузоподъёмности вагонов. Графические зависимости W(v) и Wo(v) приведены на рис. 1
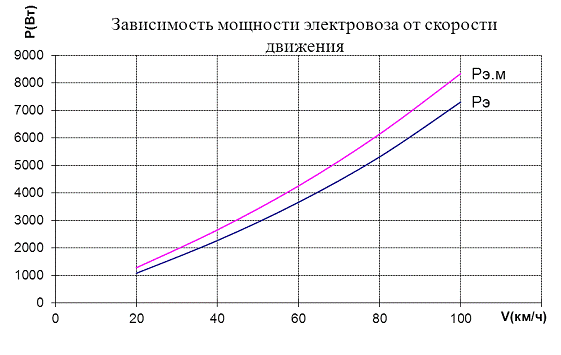
По рассчитанным в табл. 2 значениям мощности электровоза
строится график зависимости Рэ (v) для двух значений
загрузки вагонов (рис. 2).
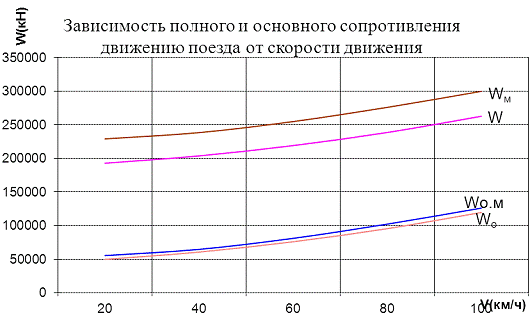
Рис. 1
6. Расчёт тока электровоза, полного и удельного
расхода энергии
6.1 Ток, потребляемый из контактной сети
Ток, потребляемый из контактной сети определён по мощности
электровоза.
Электровоз преобразует электрическую мощность Рэл,
потребляемую из контактной сети, в механическую мощность Рэ = W · v.
Электрическая мощность Рэл при постоянном токе
равна произведению напряжения контактной сети Uc на ток электровоза Iэ:
Iэ = ![]() =
= ![]() . (6.1)
. (6.1)
где ŋэ – коэффициент полезного действия
электровоза постоянного тока.
При движении с постоянной скоростью можно принять равным 0,9.
Uc – напряжение контактной сети В.
Iэ = ![]() =1553 (А)
=1553 (А)
Таблица 3. Расчет тока электровоза
|
Вычисляемые величины |
Значения величины при скоростях движения, км/ч |
|||||
|
20 |
40 |
56 |
60 |
80 |
100 |
|
|
Iэ, А |
496,3 |
1048 |
1553 |
1690 |
2453 |
3377 |
|
Iэ,м, А |
589,1 |
1226,1 |
1742 |
1966 |
2838 |
3854,3 |
6.2 Полный расход энергии электровозом
Полный расход энергии электровозом рассчитан по формуле, Вт·с:
Wэ = ![]() (G + Q) (wo +
(G + Q) (wo +
iэ) S.
(6.2)
где: wo – удельное основное сопротивление движению;
S – длина участка.
wo = Wо /(G + Q) = 72648,1 / (1824,6 + 34825,5) = 1,2 (Н/кН)
Wэ = ![]() (1824,6 + 34825,5)
(1824,6 + 34825,5)
(1,2+3,9) 11000 = 1,28·36650,1·5,1·11000 =2,631 · 109 (Вт·с).
.3 Удельный расход электроэнергии
Удельный расход электроэнергии определяется по формуле,
Вт·с/ткм:
wэ = ![]() =
= ![]() . (6.3)
. (6.3)
wэ = ![]() = 64020 (Вт·с/ткм).
= 64020 (Вт·с/ткм).
Для перехода к Вт·ч/ткм выражение (6.4) следовало разделить
на 3600
wэ = ![]() = 17,78 (Вт·ч/ткм).
= 17,78 (Вт·ч/ткм).
7. Расчёт потерь напряжения и мощности в тяговой
сети, стоимости электрической энергии
Расчёт производится для поезда, движущегося с заданной
скоростью и при заданном использовании грузоподъёмности вагонов, т.е.
принимается равномерное движение поезда со скоростью v и постоянном токе
электровоза Iэ, который находится для заданного значения v.
.1 Сопротивление тяговой сети постоянного тока
Сопротивление тяговой сети постоянного тока определено из
выражения, Ом/км:
ro = rэп + rэр. (7.1)
где rэп – эквивалентное сопротивление проводов
контактной подвески;
rэр – эквивалентное сопротивление рельсов.
rэп = ![]() . (7.2)
. (7.2)
rэр = ![]() . (7.3)
. (7.3)
здесь: 𝒫м – здесь сопротивление
меди, равное 18,6 · 10-9 Ом·м;
Sм – сечение медных проводов подвески, м2;
Sa – сечение алюминиевых проводов подвески, мм2;
Nр – число ниток рельсов, для однопутного участка;
mр – масса рельса длиной 1 м, кг.
rэп = ![]() =0,03 (Ом/км).
=0,03 (Ом/км).
rэр = ![]() = 0,01 (Ом/км).
= 0,01 (Ом/км).
ro = 0,03 + 0,01 = 0,04 (Ом/км).
7.2 Мгновенные потери напряжения до поезда
Мгновенные потери напряжения до поезда Δuп зависят от потребляемого тока, положения электровоза и схемы
питания тяговой сети. При схеме двустороннего питания определяются по формуле,
В:
Δuп = Iп,ср · ro(х – ![]() . (7.4)
. (7.4)
здесь Iп,ср = Iп – средний ток поезда;
x – расстояние от поезда до тяговой подстанции А;
L = S – длина рассматриваемого участка.
Вычисляем Δuп и напряжение на поезде uп для значений х равных 0,
![]() . Расчёт производится в
. Расчёт производится в
табл. 4.
Таблица 4. Мгновенные значения потерь напряжения до поезда,
напряжений на поезде и потерь мощности в тяговой сети
|
Вычисляемые величины |
Значения величины при расстояниях, км |
||||||
|
0 |
|
|
|
|
L |
||
|
Δuп, В |
0 |
128,6 |
150 |
170,83 |
155,3 |
128,6 |
0 |
|
uп, В |
3400 |
3271,4 |
3250 |
3229,2 |
3244,7 |
3271,4 |
3400 |
|
Δp, кВт |
0 |
199,7 |
231,5 |
265,3 |
237,3 |
199,7 |
0 |
7.3 Средняя потеря напряжения до поезда
Средняя потеря напряжения до поезда ΔUп,ср также зависит от схемы питания поезда.
При схеме двустороннего питания определена по формуле, В:
ΔUп,ср = ![]() . (7.5)
. (7.5)
ΔUп,ср = ![]() = 113,9 (В).
= 113,9 (В).
7.4 Мгновенные потери мощности в тяговой сети
Мгновенные потери мощности в сети зависят от схемы питания.
При схеме двустороннего питания определены по формуле, Вт:
Δp = I2п,ср · ro
· (x – ![]() . (7.6)
. (7.6)
Эти значения внесены в табл. 4 и построена зависимость Δp(х) для двусторонней схемы питания аналогично построению Δuп(x)
и uп (x) при тех же значениях х.
7.5 Средние потери мощности
Средние потери мощности в сети зависят от схемы питания. При
схеме двустороннего питания определены по формуле, Вт:
ΔPср = ![]() . (7.7)
. (7.7)
ΔPср = ![]() = 176866 (Вт).
= 176866 (Вт).
7.6 Расход энергии на компенсацию потерь мощности
за время движения по участку длиной S
Расход энергии на компенсацию потерь мощности за время
движения по участку длиной S рассчитан по формуле, Вт·ч:
ΔW = ΔPcp ![]() . (7.8)
. (7.8)
ΔW = 176866 ![]() = 34741 (Вт/ч) = 34,74
= 34741 (Вт/ч) = 34,74
(кВт·ч).
7.7 Полный расход энергии на движение поезда с
учётом потерь энергии в тяговой сети
Полный расход энергии на движение поезда с учётом потерь в
тяговой сети определён по формуле, кВт/ч:
Wтп = Wэ + ΔW. (7.9)
Wтп = 731,05 + 34,74 = 765,8 (кВт/ч).
7.8 Стоимость электрической энергии, потребляемой
поездом при движении по участку
Стоимость электрической энергии потребляемой поездом при
движении по участку рассчитана по формуле, руб.:
Сэ = сэ · Wтп. (7.10)
где: сэ – цена 1 кВт/ч, руб.
Сэ = 2 · 765,8 = 1531,6 (руб.).
Библиографический список
1.
Расчёт сопротивления движению поезда, расхода и стоимости электрической энергии
на движение поезда: Метод. Указ. К курсовой работе. / Сост. В.С. Лиокумович,
Э.П. Селедцов, Б.П. Сорин.-Л.:ЛИИЖТ. 1988. – 25 с.
.
А.В. Плакс, В.В. Привалов. Введение в теорию движения поезда и принципы
управления электроподвижным составом. М.:ВЗИИЖТ. 1981. – 94 с.
.
Оформление текстовых документов: Метод. Указ. /Сост. В.А. Болотин, В.В. Ефимов,
В.П. Игнатьева, Н.В. Фролова.-Л.: ПГУПС-ЛИИЖТ, 2002. – 44 с.
21. Сопротивления движению поезда.
Силы, действующие вдоль оси пути по направлению движения поезда называются движущими силами, а силы встречного направления – силами сопротивления движения поезда.
Сопротивления движению поезда делятся на две составляющие:
I. Основное, действует при движении поезда всегда:
1). Сопротивление пути – трение качения колес по рельсам из-за деформации опорных поверхностей (сила обратно пропорциональна диаметру колес и зависит от твердости материалов); трение скольжения из-за проскальзывания и из-за трения между гребнями бандажей и рельсами, которые уменьшаются при натяжке в режиме тяги; от ударов на неровностях пути (зависит от скорости, нагрузки на ось, зазора в стыке).
2). Сопротивление подвижного состава – трение в подшипниках (сила прямо пропорциональна диаметру оси, обратно пропорциональна диаметру колеса, зависит от коэффициента трения, площади соприкосновения, смазки).
3). Сопротивление внешней среды – впереди сжатие воздуха, боковые поверхности и крыша соприкасаются с воздухом, в промежутках между вагонами и за составом происходит разряжение, завихрение воздуха (конструктивно выполнять более обтекаемую форму).
II. Дополнительное – возникает при движении по отдельным участкам пути и в отдельные периоды времени.
1). От уклонов – эти силы создаются составляющей веса поезда, действующая на подъеме против движения поезда, а на спусках – по направлению движения.
Рекомендуемые материалы
Уклон характеризуется крутизной i, в – тысячных долях и показывает высоту подъема в метрах на каждый километр пути.
Удельная сила дополнительного сопротивления от подъема численно равна величине подъема и измеряется в ньютонах на килоньютон.
2). От кривых – под действием центробежной силы гребни бандажей колесных пар прижимаются к рельсам и появляется трение. Колесо, идущее по внутреннему рельсу, имеет проскальзывание; трение в опорах кузова, в боковых опорах. Из-за большого числа факторов и сложных зависимостей удельное дополнительное сопротивление от кривой определяется по эмпирической формуле ωR = 700 / R, где R – радиус кривой в м.
3). При трогании с места – повышенное трение в подшипниках (смазка выдавлена, полусухое трение), большая деформация рельса и колеса.
Силы удельного дополнительного сопротивления при трогании с места определяются по эмпирическим формулам:
для подшипников скольжения  ;
;
для подшипников качения  .
.
mBo – масса вагона, приходящаяся на одну ось.
4). При низких температурах окружающего воздуха – возрастает вязкость смазки, а значит и коэффициент трения; возрастает так же и сопротивление воздушной среды; определяется по формуле ωНТ = ω0 (КНТ -1), а значение коэффициента КНТ берется из таблицы при различных низких температурах и скоростях движения для грузовых и пассажирских вагонов.
5). От ветра – встречный и боковой ветер увеличивают сопротивление из-за трения и увеличения сопротивления воздушного потока. По таблице берется коэффициент ветра КВ и дополнительное сопротивление от ветра ωВ = ω0 (КВ -1).
6). От подвагонных генераторов для пассажирских вагонов.
7). От движения в тоннелях.
Общее сопротивление движения поезда WК определяется алгебраической суммой основного и дополнительного сопротивлений. WК = W0 + Wд, в Н. Почти все виды сопротивлений пропорциональны весу поезда, поэтому рассматривают удельное сопротивление движения поезда ωН = ω0 + ωд в Н/кН.
Основное удельное сопротивление определяется по эмпирическим формулам в зависимости от скорости движения:
– для различных серий локомотивов;
– при движении под током;
Если Вам понравилась эта лекция, то понравится и эта – Монтаж и эксплуатация устьевого оборудования на скважинах ЭЦН.
– при движении без тока;
– в зависимости от подшипников качения или скольжения;
– в зависимости от количества осей вагона;
– для груженых или порожних вагонов;
– для стыкового или бесстыкового пути.
Общее основное удельное сопротивление определяется как  .
.