Отличие вязкого трения от сухого заключается в том, что оно способно обращаться в ноль одновременно со скоростью. Даже при малой внешней силе может быть сообщена относительная скорость слоям вязкой среды.
Сила сопротивления при движении в вязкой среде
Кроме сил трения при движении в жидких и газообразных средах возникают силы сопротивления среды, которые проявляются намного значительней, чем силы трения.
Поведение жидкости и газа по отношению к проявлениям сил трения не отличаются. Поэтому, приведенные ниже характеристики, относят к обоим состояниям.
Действие силы сопротивления, возникающей при движении тела в вязкой среде, обусловлено ее свойствами:
- отсутствие трения покоя, то есть передвижение плавающего многотонного корабля при помощи каната;
- зависимость силы сопротивления от формы движущегося тела, иначе говоря, от ее обтекаемости для уменьшения сил сопротивления;
- зависимость абсолютной величины силы сопротивления от скорости.
Сила вязкого трения
Существуют определенные закономерности, которым подчинены и силы трения и сопротивления среды с условным обозначением суммарной силы силой трения. Ее величина находится в зависимости от:
- формы и размеров тела;
- состояния его поверхности;
- скорости относительно среды и ее свойства, называемого вязкостью.
Для изображения зависимости силы трения от скорости тела по отношению к среде используют график рисунка 1.
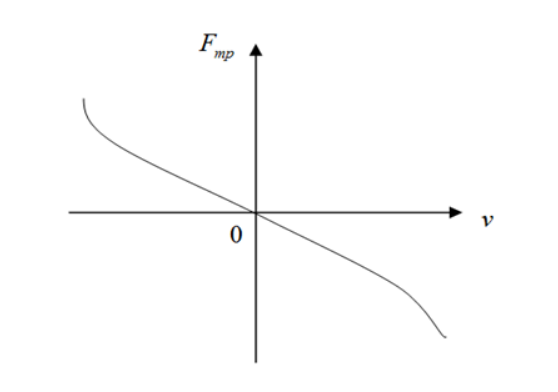
Рисунок 1. График зависимости силы трения от скорости по отношению к среде
Если значение скорости мало, то сила сопротивления прямо пропорциональна относительно υ, а сила трения линейно увеличивается со скоростью:
Fтр=-k1υ (1).
Наличие минуса означает направление силы трения в противоположную сторону относительно направления скорости.
При большом значении скорости происходит переход линейного закона в квадратичный, то есть рост силы трения пропорционально квадрату скорости:
Fтр=-k2υ2 (2).
Если в воздухе уменьшается зависимость силы сопротивления от квадрата скорости, говорят о скоростях со значениями нескольких метров в секунду.
Величина коэффициентов трения k1 и k2 находится в зависимости от формы, размера и состояния поверхности тела и вязких свойств среды.
Если рассматривать затяжной прыжок парашютиста, то его скорость не может постоянно увеличиваться, в определенный момент начнется ее спад, при котором сила сопротивления приравняется к силе тяжести.
Значение скорости, при котором закон (1) производит переход в (2), зависит от тех же причин.
Происходит падение двух различных по массе металлических шариков с одной и той же высоты с отсутствующей начальной скоростью. Какой из шаров упадет быстрее?
Дано: m1, m2, m1>m2
Решение
Во время падения оба тела набирают скорость. В определенный момент движение вниз производится с установившейся скоростью, при которой значение силы сопротивления (2) приравнивается силе тяжести:
Fтр=k2υ2=mg.
Получаем установившуюся скорость по формуле:
υ2=mgk2.
Следовательно, тяжелый шарик обладает большей установившейся скоростью падения, чем легкий. Поэтому достижение земной поверхности произойдет быстрее.
Ответ: тяжелый шарик быстрее достигнет земли.
Парашютист летит со скоростью 35 м/с до раскрытия парашюта, а после – со скоростью 8 м/с. Определить силу натяжения строп при раскрытии парашюта. Масса парашютиста 65 кг, ускорение свободного падения 10 м/с2. Обозначить пропорциональность Fтр относительно υ.
Дано: m1=65 кг, υ1=35 м/с, υ2=8 м/с.
Найти: T – ?
Решение
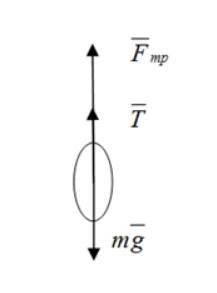
Рисунок 2
Перед раскрытием парашютист обладал скоростью υ1=35 м/с, то есть его ускорение было равным нулю.
По второму закону Ньютона получаем:
0=mg-kυ1.
Очевидно, что
k=mgυ1.
После того, как парашют раскрылся, его υ меняется и становится равной υ2=8 м/с. Отсюда второй закон Ньютона примет вид:
0-mg-kυ2-T.
Для нахождения силы натяжения строп необходимо преобразовать формулу и подставить значения:
T=mg1-υ2υ1≈500 Н.
Ответ: T=500 Н.
| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |

Поведение жидкости с малой (сверху) и с большой (снизу) вязкостью
Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате макроскопическая работа, затрачиваемая на это перемещение, рассеивается в виде тепла. Твёрдые тела (стекло, металлы, полупроводники, диэлектрики, ферромагнетики)[1] также могут обладать вязкостью, но внутреннее трение в твёрдых телах в силу специфики явления обычно рассматривается отдельно в теории упругости и пластичности.
Механизм внутреннего трения в жидкостях и газах заключается в том, что движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Вязкость газов и жидкостей характеризуют динамическим коэффициентом вязкости (единица измерения в Международной системе единиц (СИ) — паскаль-секунда, Па·с, в системе СГС — пуаз, П; 1 Па·с = 10 П, 1 сП = 10−3 Па·с = 1 мПа·с) или кинематическим коэффициентом вязкости (единица измерения в СИ — м2/c, в СГС — стокс, Ст; 1 Ст = см2/с = 10−4 м2/с, 1 сСт = 1 мм2/с = 10−6 м2/с; внесистемная единица — градус Энглера). Кинематический коэффициент вязкости — отношение динамического коэффициента к плотности вещества. Классические методы измерения вязкости включают, например, измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.
Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 1011—1012 Па·с.
Сила вязкого трения[править | править код]
Если параллельные плоские тела площадью S каждое, находящиеся на малом расстоянии h, движутся в той же плоскости со скоростью 

Коэффициент пропорциональности, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости. Этот закон был предложен Исааком Ньютоном в 1687 году и носит его имя (закон вязкости Ньютона). Экспериментальное подтверждение закона было получено в начале XIX века в опытах Кулона с крутильными весами и в экспериментах Хагена и Пуазёйля с течением воды в капиллярах[2].
Эта сила называется силой вязкого трения. Её качественное отличие от сухого трения, кроме прочего, в том, что она пропорциональна скорости. Следовательно, при наличии только вязкого трения и сколь угодно малой внешней силы тело обязательно придёт в движение, то есть для вязкого трения не существует трения покоя.
Вторая вязкость[править | править код]
Вторая вязкость, или объёмная вязкость, — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и (или) при учёте неоднородности коэффициента второй вязкости по пространству.
Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.
Объёмная вязкость играет большую роль в затухании звука и ударных волн и экспериментально определяется путём измерения этого затухания.
Вязкость газов[править | править код]
В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле
где 



С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа 

Влияние температуры на вязкость газов[править | править код]
В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).
Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:[3]
где
— динамическая вязкость (в Па·с) при заданной температуре
;
— контрольная вязкость (в Па·с) при некоторой контрольной температуре
;
— заданная температура в кельвинах;
— контрольная температура в кельвинах;
— постоянная Сазерленда для того газа, вязкость которого требуется определить.
Эту формулу можно применять для температур в диапазоне 0 < 
Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже:
| Газ |  , K , K
|
 , K , K
|
 , мкПа·с , мкПа·с
|
|---|---|---|---|
| Воздух | 120 | 291,15 | 18,27 |
| Азот | 111 | 300,55 | 17,81 |
| Кислород | 127 | 292,25 | 20,18 |
| Углекислый газ | 240 | 293,15 | 14,8 |
| Угарный газ | 118 | 288,15 | 17,2 |
| Водород | 72 | 293,85 | 8,76 |
| Аммиак | 370 | 293,15 | 9,82 |
| Оксид серы(IV) | 416 | 293,65 | 12,54 |
| Гелий | 79,4[4] | 273 | 19[5] |
Вязкость жидкостей[править | править код]
Динамическая вязкость[править | править код]
Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Для так называемых ньютоновских жидкостей (которых вокруг нас большинство) справедлив общий закон внутреннего трения — закон Ньютона:
Коэффициент вязкости 

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским[6]. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества 
где:
— константа, характерная для определённой жидкости;
— собственный объём, занимаемый частицами жидкости.
Динамическая вязкость жидкостей уменьшается с увеличением температуры и растёт с увеличением давления.
Кинематическая вязкость[править | править код]
В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной
и эта величина получила название кинематической вязкости[7].
Здесь 

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом: 1 сСт = 1 мм2/c = 10−6 м2/c.
Условная вязкость[править | править код]
Условная вязкость — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма раствора через вертикальную трубку (определённого диаметра). Измеряют в градусах Энглера (по имени немецкого химика К. О. Энглера), обозначают — °ВУ. Определяется отношением времени истечения 200 мл испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 мл дистиллированной воды из того же прибора при 20 °С. Условную вязкость до 16 °ВУ переводят в кинематическую по таблице ГОСТ, а условную вязкость, превышающую 16 °ВУ, по формуле
где 

Ньютоновские и неньютоновские жидкости[править | править код]
Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье — Стокса[8]):
где 
Среди неньютоновских жидкостей по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.
С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.[источник не указан 996 дней]
Вязкость аморфных материалов[править | править код]
Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс[9]:
где
— энергия активации вязкости (Дж/моль);
— температура (К);
— универсальная газовая постоянная (8,31 Дж/моль·К);
— некоторая постоянная.
Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости 







Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением[10]
с постоянными 




В узких температурных интервалах недалеко от температуры стеклования 
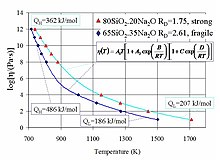
Если температура существенно ниже температуры стеклования, 
с высокой энергией активации 



При 
но с низкой энергией активации 

Относительная вязкость[править | править код]
В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:
где
- μ — динамическая вязкость раствора;
- μ0 — динамическая вязкость растворителя.
Вязкость некоторых веществ[править | править код]
Для авиастроения и судостроения наиболее важно знать вязкости воздуха и воды.
Вязкость воздуха[править | править код]

Зависимость вязкости сухого воздуха от давления при температурах 300, 400 и 500 K
Вязкость воздуха зависит в основном от температуры.
При 15,0 °C вязкость воздуха составляет 1,78⋅10−5 кг/(м·с) = 17,8 мкПа·с = 1,78⋅10−5 Па·с. Можно найти вязкость воздуха как функцию температуры с помощью программ расчёта вязкостей газов[11].
Вязкость воды[править | править код]

Зависимость динамической вязкости воды от температуры в жидком состоянии (Liquid Water) и в виде пара (Vapor)
Динамическая вязкость воды составляет 8,90·10−4 Па·с при температуре около 25 °C. Как функция температуры: T = A × 10B/(T−C), где A = 2,414·10−5 Па·с, B = 247,8 K, C = 140 K.
Значения динамической вязкости жидкой воды при разных температурах вплоть до точки кипения приведены в таблице:
| Температура, °C | Вязкость, мПа·с |
|---|---|
| 10 | 1,308 |
| 20 | 1,002 |
| 30 | 0,7978 |
| 40 | 0,6531 |
| 50 | 0,5471 |
| 60 | 0,4668 |
| 70 | 0,4044 |
| 80 | 0,3550 |
| 90 | 0,3150 |
| 100 | 0,2822 |
Динамическая вязкость разных веществ[править | править код]
Ниже приведены значения коэффициента динамической вязкости некоторых ньютоновских жидкостей:
| Газ | при 0 °C (273 K), мкПа·с | при 27 °C (300 K), мкПа·с |
|---|---|---|
| воздух | 17,4 | 18,6 |
| водород | 8,4 | 9,0 |
| гелий | 20,0 | |
| аргон | 22,9 | |
| ксенон | 21,2 | 23,2 |
| углекислый газ | 15,0 | |
| метан | 11,2 | |
| этан | 9,5 |
| Жидкость | Вязкость, Па·с | Вязкость, мПа·с |
|---|---|---|
| ацетон | 3,06·10−4 | 0,306 |
| бензол | 6,04·10−4 | 0,604 |
| кровь (при 37 °C) | (3—4)·10−3 | 3—4 |
| касторовое масло | 0,985 | 985 |
| кукурузный сироп | 1,3806 | 1380,6 |
| этиловый спирт | 1.074·10−3 | 1.074 |
| этиленгликоль | 1,61·10−2 | 16,1 |
| глицерин (при 20 °C) | 1,49 | 1490 |
| мазут | 2,022 | 2022 |
| ртуть | 1,526·10−3 | 1,526 |
| метиловый спирт | 5,44·10−4 | 0,544 |
| моторное масло SAE 10 (при 20 °C) | 0,065 | 65 |
| моторное масло SAE 40 (при 20 °C) | 0,319 | 319 |
| нитробензол | 1,863·10−3 | 1,863 |
| жидкий азот (при 77K) | 1,58·10−4 | 0,158 |
| пропанол | 1,945·10−3 | 1,945 |
| оливковое масло | 0,081 | 81 |
| пек | 2,3·108 | 2,3·1011 |
| серная кислота | 2,42·10−2 | 24,2 |
| вода | 8,94·10−4 | 0,894 |
Примечания[править | править код]
- ↑ Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках: Сб. статей / Под ред. Ф. Н. Тавадзе. — М.: Наука, 1978. — 235 с.
- ↑ О некоторых ошибках в курсах гидродинамики Архивная копия от 22 декабря 2015 на Wayback Machine, с. 3—4.
- ↑ Alexander J. Smits, Jean-Paul Dussauge Turbulent shear layers in supersonic flow Архивная копия от 17 июля 2017 на Wayback Machine. — Birkhäuser, 2006. — P. 46. — ISBN 0-387-26140-0.
- ↑ Data constants for Sutherland’s formula Архивная копия от 6 марта 2018 на Wayback Machine.
- ↑ Viscosity of liquids and gases Архивная копия от 3 октября 2017 на Wayback Machine.
- ↑ Хмельницкий Р. А. Физическая и коллоидная химия: Учебних для сельскохозяйственных спец. вузов. — М.: Высшая школа, 1988. — С. 40. — 400 с. — ISBN 5-06-001257-3.
- ↑ Попов Д. Н. Динамика и регулирование гидро- и превмосистем : Учеб. для машиностроительных вузов. — М. : Машиностроение, 176. — С. 175. — 424 с.
- ↑ Седов Л. И. Механика сплошной среды Архивная копия от 28 ноября 2014 на Wayback Machine. Т. 1. — М.: Наука, 1970. — С. 166.
- ↑ Френкель Я. И. Кинетическая теория жидкостей. — Ленинград, Наука, 1975. — с. 226.
- ↑ Ojovan M. Viscous flow and the viscosity of melts and glasses. Physics and Chemistry of Glasses, 53 (4) 143—150 (2012).
- ↑ Gas Viscosity Calculator Архивная копия от 21 июля 2011 на Wayback Machine.
Литература[править | править код]
- R. H. Doremus. J. Appl. Phys., 92, 7619—7629 (2002).
- M. I. Ojovan, W. E. Lee. J. Appl. Phys., 95, 3803—3810 (2004).
- M. I. Ojovan, K. P. Travis, R. J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
- Л. И. Седов. Механика сплошной среды. Т. 1. — М.: Наука, 1970. — 492 с.
- П. Н. Гедык, М. И. Калашникова. Смазка металлургического оборудования. — М.: Металлургия, 1976. — 380 с.
- И. Ф. Голубев. Вязкость газов и газовых смесей. — М.: Физматлит, 1959.
- Ред. Ф. Н. Тавадзе Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках. — М., Наука, 1978. — 235 c.
Ссылки[править | править код]
- Аринштейн А. Сравнительный вискозиметр Жуковского // Квант, № 9, 1983.
- Измерение вязкости нефтепродуктов
- Булкин П. С. Попова И. И., Общий физический практикум. Молекулярная физика
- Градус условной вязкости // Большой энциклопедический политехнический словарь. — 2004.
- Вязкость воды
8.7.1 Определение общего вида формулы сопротивления воды движению полупогруженного тела
В современной гидромеханике аналитическое выражение для определения силы полного сопротивления движению тела в воздушной или водной среде, отвечающее принципам гидродинамического подобия, имеет вид
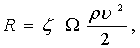 (8.54)
(8.54)
где R – полная сила сопротивления воды движению тела;
ζ – безразмерный коэффициент сопротивления;
ρ – плотность среды;
Ω – характерная площадь тела;
υ – относительная скорость движения тела.
Требуется установить зависимость для определения силы сопротивления движению тела, используя метод показателей.
1. Записываем функциональную зависимость для определения силы сопротивления
R = f (ρ, l, υ, μ, g) (8.55)
где l – длина тела;
μ – динамическая вязкость;
g – ускорение свободного падения.
Размерность входящих в зависимость (8.55) параметров является сочетанием трех основных единиц измерения [ М ],[ L ] и[Т].
2. Возведем в соответствующую степень каждый из определяющих параметров зависимости (8.55)
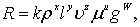 (8.56)
(8.56)
где k – безразмерный коэффициент пропорциональности;
x, y, z, u, w– пять неизвестных показателей степени.
3. Подставим размерности входящих в равенство параметров, пользуясь принятой системой основных единиц измерения (таблица 8.1),
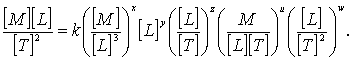 (8.57)
(8.57)
4. Независимо от системы единиц измерения, в которой выраже ны все входящие в уравнение (8.57) параметры, размерность левой части и итоговая размерность произведения правой части уравнения (8.57) должна быть одной и той же.
Условие однородности требует, чтобы показатели степени для каждой из трех единиц измерения [М], [L], [Т] были одинаковы и в левой и в правой частях уравнения (8.57), т.е.
|
для массы [М] |
|
|
для длины [L] |
|
|
для времени [Т] |
Из системы уравнений (8.58) получим
х = 1 – u; y = 2 – u + w; z = 2 – u – 3w.
Подставив найденные значения показателей х, у ,z в формулу (8.56), получим
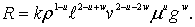
Произведя перегруппировку множителей по показателям, получим
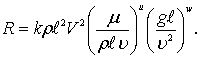 (8.59)
(8.59)
В этой формуле
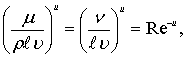
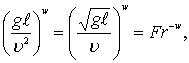
где Re – число Рейнольдса;
Fr – число Фруда.
В формуле (8.59) произведение Re–u, Fr–w можно записать в виде некоторой функции f(Re, Fr) тогда окончательное выражение для определения сопротивления воды движению тела примет вид
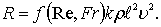
Обозначим f(Re, Fr) = ζ, ![]() 2 = Ω, принимая значения к = 0,5, получим
2 = Ω, принимая значения к = 0,5, получим
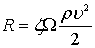 .
.
Общий вид формулы для определения сил сопротивления, полученной на основе теории размерности, идентичен зависимости, отвечающей принципам гидродинамического подобия (8.54). В этих формулах безразмерный коэффициент ζ называется коэффициентом сопротивления тела. Коэффициент сопротивления является сложной функцией, зависящей одновременно от чисел Рейнольдса и Фруда.
Таким образом, величина полной гидродинамической силы, действующей на тело, т.е. силы сопротивления воды движению тела, пропорциональна безразмерному коэффициенту сопротивления ζ, скоростному напору ρυ2/2 и характерной площади Ω.
Выше были представлены
простейшие законы движения жидкости
(газа). Теперь рассмотрим особенности
движения тел в жидкостях (газах).
Как установил
Стокс,
на тело шарообразной формы, движущееся
с небольшой скоростью в жидкости,
действует сила сопротивления, равная
![]()
,
где
–
коэффициент вязкости,
–
радиус шарика,
–
его скорость движения.
Эта формула часто
используется для расчета стационарной
скорости падения шарообразного тела в
вязкой среде (![]()
).
Определим эту скорость. При равномерном
движении тел все действующие на него
силы уравновешивают друг друга. Для
рассматриваемого случая
![]()
,
где
![]()
– сила тяжести,
– плотность материала
шарика,
![]()
–
сила вязкого трения Стокса,
![]()
– сила Архимеда,
![]()
– плотность среды.
Решение этого
уравнения относительно
имеет вид:
![]()
.
Более детальное
рассмотрение этой задачи, позволяет
найти динамику движения тела сферической
формы в вязкой среде. В соответствии со
вторым законом Ньютона, предполагая,
что движение происходит в направлении
оси
,
запишем:
![]()
.
Это
уравнение может быть преобразовано к
виду:
![]()
,
где
![]()
,
![]()
,
![]()
.
Решением
выше представленного уравнения является:
![]()
.
Величина постоянной
интегрирования находится из условия,
что в начальный момент времени скорость
тела была равной
,
поэтому
![]()
.
В результате
получаем:
![]()
или
![]()
.
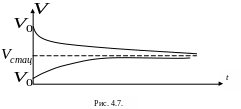
Анализ представленного
решения показывает, что в зависимости
от начальных условий, соотношения
плотностей материалов шарика и среды
движение тела будет различным. На рис.
4.7 представлен характер изменения
скорости шарообразного тела, плотность
которого выше плотности среды, для двух
значений начальной скорости.
При больших
скоростях
движения тел в жидкостях или газах
возникают завихрения, энергия затрачивается
на их образование при этом сила
сопротивления становится пропорциональной
![]()
и площади сечения тела
,
перпендикулярной скорости движения.
Для этого случая Ньютоном была получена
формула для силы трения, которая имеет
вид:
![]()
,
где
![]()
– плотность среды,
![]()
–
коэффициент лобового сопротивления,
который зависит от формы тела, определяющей
характер вихрей:
–
квадратная пластинка, перпендикулярная
потоку газа (жидкости).
![]()
,
–
диск, перпендикулярный потоку газа
(жидкости).
![]()
,
–
шар,
![]()
,
–
сигарообразное тело (длина = 4 диаметрам).
![]()
.
Физический смысл
формулы Ньютона состоит в том, что тело,
при своем движении, оттесняет за 1 секунду
массу жидкости (газа), равную
![]()
.
Скорость, сообщаемая телом частицам
оттесненной среды, в среднем равна
скорости самого тела, поэтому, количество
движения, теряемое телом за одну секунду,
будет равно
![]()
.
Эта величина определяет возникающую
силу сопротивления движению, силу,
обусловленную инерционными свойствами
частиц среды.
4.5. Кинематическая вязкость. Число Рейнольдса
Опыт подтверждает
представленные выше выражения для сил
сопротивления движению тел в вязких
средах, а именно, то, что при малых
скоростях сила трения пропорциональна
скорости движения тела, а при больших
– квадрату ее величины.
Если предположить,
что формула Ньютона более универсальна,
чем формула Стокса, то следует
констатировать, что значение
является функцией
![]()
,
где
–
характерный размер тела, причем их
комбинация должна быть безразмерной.
Такой комбинацией является величина:
![]()
,
называемая
числом
Рейнольдса.
(![]()
).
Число Рейнольдса
имеет важный физический смысл. Оно
пропорционально отношению силы трения,
связанной с инерционными свойствами
частиц среды (~
![]()
),
к силе трения, обусловленной вязкостью
среды (![]()
).
Величина
![]()
называется кинематической
вязкостью.
![]()
.
Из представленных
в таблице значений видно,
|
Среда |
Кинематическая ) |
|
Вода при 20 |
O,01 |
|
Воздух при 20 |
0,15 |
|
Воздух при 0 , |
13,3 |
|
Глицирин при 20 |
6,8 |
что
кинематическая вязкость воды может
быть меньше кинематической вязкости
воздуха – это следствие того, что
плотность воздуха меньше плотности
воды.
Число Рейнольдса
– главная характеристика обтекаемости
тел. При малых значениях
![]()
– течение имеет ламинарный характер,
при больших – турбулентный.
При моделировании
потоков (строительство каналов, различных
гидросооружений и т.д.) проводят
макетирование, при этом важно не только
повторить геометрию, но и реализовать
в эксперименте соответствующее реальности
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Макеты страниц
При движении тела в жидкости или газе с небольшой скоростью сопротивление движению обусловлено силами трения и, как установил Стоке, пропорционально произведению вязкости среды на линейные размеры тела и первую степень скорости. Для тел шарообразной формы сопротивление вязкости равно

где  коэффициент вязкости,
коэффициент вязкости,  скорость
скорость  радиус тела.
радиус тела.
Формула Стокса имеет много применений. В частности, формулу Стокса применяют для вычисления скорости равномерного свободного падения тела в вязкой среде. Очевидно, что равномерное падение должно наблюдаться в том случае, если сопротивление движению равно кажущемуся весу тела в среде (т. е. его истинному весу  плотность тела за вычетом веса вытесненной среды
плотность тела за вычетом веса вытесненной среды  где
где  плотность среды):
плотность среды):

Отсюда скорость равномерного падения тела в вязкой среде равна: 

Часто эту формулу используют для вычисления радиуса капелек или пылинок по наблюденной скорости их равномерного падения в воздухе или в жидкости.
Если в указанную формулу подставить вязкость и плотность воздуха при нормальных условиях, то для вычисления скорости равномерного падения водяных капелек в воздухе получается такое соотношение:

где  выражено в сантиметрах,
выражено в сантиметрах, 
При больших скоростях движения сопротивление жидкости и газа обусловлено в основном затратой работы на образование вихрей, В этих случаях сопротивление (его часто называют лобовым сопротивлением) по закону, открытому Ньютоном, пропорционально квадрату скорости движения и площади проекции тела на плоскость, перпендикулярную к направлению движения («миделево сечение» 

Здесь  плотность среды и
плотность среды и  числовой коэффициент, различный для тел разных форм, называемый коэффициентом лобового сопротивления.
числовой коэффициент, различный для тел разных форм, называемый коэффициентом лобового сопротивления.
Учитывая, что лобовое сопротивление вызывается главным образом возникающими в среде вихрями, мы можем получить
вышеприведенную формулу из следующего (нестрогого) рассуждения. Пусть тело, движущееся в жидкости, оттесняет на своем пути в каждую секунду массу жидкости, равную произведению плотности жидкости  на объем
на объем  Если считать, что всем частицам этой оттесняемой жидкости сообщается скорость, в среднем пропорциональная скорости движения тела
Если считать, что всем частицам этой оттесняемой жидкости сообщается скорость, в среднем пропорциональная скорости движения тела  то, стало быть, оттесняемой жидкости сообщается в каждую секунду количество движения, пропорциональное
то, стало быть, оттесняемой жидкости сообщается в каждую секунду количество движения, пропорциональное  по закону равенства действия и противодействия жидкость должна оказывать телу сопротивление, равное приращению количества движения жидкости за 1 сек., т. е. сопротивление, пропорциональное
по закону равенства действия и противодействия жидкость должна оказывать телу сопротивление, равное приращению количества движения жидкости за 1 сек., т. е. сопротивление, пропорциональное 
Если бы не происходило вихреобразования, то при равномерном движении тела в жидкости сопротивление движению определялось бы только силами трения, а инерция среды никак не сказывалась бы на величине сопротивления. В идеальной невязкой жидкости относительные скорости частиц жидкости на некотором расстоянии позади тела должны были бы оставаться такими же, как перед ним.

Рис. 108. К пояснению парадокса Эйлера.
Встречаясь с поверхностью тела в точке А (рис. 108), частицы жидкости вынуждены изменить первоначальное прямолинейное направление движения на криволинейное. В связи с этим они действуют на поверхность тела с некоторой силой, поэтому в пространстве А В давление на поверхность тела повышается. На рис. 108 области повышенного давления обозначены знаками плюс. На участке  направление частиц жидкости вновь меняется: теперь частицы жидкости стремятся по инерции уйти от тела. На этом участке давление понижается. На рис. 108 области пониженного давления обозначены знаком минус. На участке
направление частиц жидкости вновь меняется: теперь частицы жидкости стремятся по инерции уйти от тела. На этом участке давление понижается. На рис. 108 области пониженного давления обозначены знаком минус. На участке  частицы жидкости опять будут оказывать давление на поверхность тела. Аналогичное распределение сил имеет место и на нижней поверхности тела. Вследствие симметричного распределения давлений равнодействующая сила равна нулю.
частицы жидкости опять будут оказывать давление на поверхность тела. Аналогичное распределение сил имеет место и на нижней поверхности тела. Вследствие симметричного распределения давлений равнодействующая сила равна нулю.
Сказанное приводит к парадоксальному выводу, который находится в противоречии с повседневным опытом и формулой (10): в невязкой жидкости при равномерном движении тело не должно было бы испытывать никакого сопротивления движению (парадокс Эйлера).
Сопротивление движению по формуле (10), вызываемое инерциальными силами жидкости, создается вследствие отрыва пограничного слоя, что приводит к вихреобразованию и к той реальной картине обтекания, которая, в отличие от изображенной на рис. 108, показана на рис. 109 и 110.
Вблизи участков поверхности  жидкость движется с большей скоростью, чем в невозмущенном потоке; давление здесь понижается. Под действием разности давлений течение в пограничном слое направлено от
жидкость движется с большей скоростью, чем в невозмущенном потоке; давление здесь понижается. Под действием разности давлений течение в пограничном слое направлено от  к
к  (по направлению потока) и от
(по направлению потока) и от  к
к  (против потока). Эти встречные течения пограничного слоя и потока сталкиваются друг с другом у точек
(против потока). Эти встречные течения пограничного слоя и потока сталкиваются друг с другом у точек  На пограничном слое создается выступ, который закручивается набегающим потоком, отрывается от поверхности тела и уносится в виде вихря.
На пограничном слое создается выступ, который закручивается набегающим потоком, отрывается от поверхности тела и уносится в виде вихря.

Рис. 109. Поток, обтекающий цилиндр небольшое время.

Рис. 110. Схема движений жидкости за цилиндрическим телом.
Вихревая область постепенно перемешивается с окружающей жидкостью, образуя позади тела расширяющуюся турбулентную зону, или вихревую пелену.
В связи со сказанным ясно, почему коэффициент пропорциональности  входящий в формулу (10), — коэффициент лобового сопротивления — зависит от формы тела: форма тела может облегчать или же, наоборот, затруднять возникновение вихрей.
входящий в формулу (10), — коэффициент лобового сопротивления — зависит от формы тела: форма тела может облегчать или же, наоборот, затруднять возникновение вихрей.

Рис. 111. Различные тела, обладающие одинаковым лобовым сопротивлением.

Рис. 112. Тело удобообтекаемой формы.
Если тело имеет удобообтекаемую форму, то разности давлений в различных участках его поверхности, вызванные различием скорости, будут незначительны; встречное движение слоев жидкости близ поверхности будет выражено слабо; срыва струй и завихрения жидкости почти не будет, и испытываемое телом сопротивление движению будет невелико. Напротив, если тело ограничено острыми углами, как, например, плоская пластинка, поставленная перпендикулярно к потоку, то разности давлений, вызванные изменением скорости при
обтекании острых углов, будут большими, вихрей образуется много, и лобовое сопротивление окажется значительным.
На рис. 111 изображены тела различных размеров и форм, обладающие одним и тем же лобовым сопротивлением. Наиболее удобо – обтекаемой оказывается вытянутая, каплеобразная форма, такая, какую придают всем фюзеляжам самолетов. Тело подобной формы почти совсем не создает в потоке вихрей (рис. 112); сопротивление движению такого тела вызывается главным образом силами трения.
Ниже даны коэффициенты лобового сопротивления  для некоторых тел:
для некоторых тел:
(см. скан)
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ И АКУСТИКА
- § 1. О взаимосвязи явлений и допустимых границах их схематизации в физике
- § 2. Система ориентировки. Материальная точка и ее перемещение
- § 3. Элементарное перемещение. Векторы скорости и ускорения
- § 4. Тангенциальное и центростремительное ускорения
- § 5. Угловая скорость и угловое ускорение
- § 6. Абсолютное, переносное и относительное движения
- § 7. Закон сложения ускорений
- ГЛАВА II. ЗАКОНЫ НЬЮТОНА
- § 9. Первый ньютонов закон механики (закон инерции)
- § 10. О понятиях «покоя» и «равномерности»
- § 11. Инерциальная система. Принцип относительности
- § 12. Второй ньютонов закон механики
- § 13. Различные понимания второго закона механики
- § 14. Движение под действием постоянной силы
- § 15. Третий ньютонов закон механики
- § 16. Статическое и динамическое проявления сил
- § 17. Силы инерции. Центробежная сила
- ГЛАВА III. РАБОТА И ЭНЕРГИЯ
- § 18. Работа, энергия, мощность. Элемент и интеграл работы
- § 19. Кинетическая энергия и потенциальная энергия
- § 20. Системы мер и размерность механических величин
- ГЛАВА IV. ДИНАМИКА СИСТЕМЫ
- § 21. Механическая система. Внутренние и внешние силы. Центр масс
- § 22. Закон сохранения количества движения и теорема о движении центра масс
- § 23. Закон сохранения энергии в консервативных системах. Минимум потенциальной энергии при равновесии
- § 24. Число степеней свободы и работа сил связи. Принцип возможных перемещений
- § 25. Принцип Даламбера и релятивистское понимание инерции
- ГЛАВА V. МЕХАНИЧЕСКАЯ ПЕРЕДАЧА СИЛ И ЭНЕРГИИ (ТРЕНИЕ, УДАР, ТЯГА)
- § 26. Трение. Тяга
- § 27. Удар
- ГЛАВА VI. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ И ЭЛЕМЕНТЫ НЕБЕСНОЙ МЕХАНИКИ
- § 28. Законы Кеплера
- § 29. Ньютонов закон тяготения
- § 30. Зависимость веса и ускорения силы тяжести от высоты и географической широты местности
- § 31. Вычисление массы Солнца, Земли и планет
- § 32. Потенциальная энергия и потенциал тяготения
- § 33. Некоторые теоремы о потенциале тяготения
- § 34. Потенциальная энергия системы частиц
- ГЛАВА VII. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДЫХ ТЕЛ
- § 35. Момент силы
- § 36. Кинетическая энергия вращательного движения. Момент инерции
- § 37. Основное уравнение динамики вращательного движения
- § 38. Закон сохранения момента количества движения
- § 39. Проявление поворотных (кориолисовых) сил инерции
- ГЛАВА VIII. ЭЛЕМЕНТЫ ТЕОРИИ УПРУГОСТИ И МЕХАНИЧЕСКИЕ СВОЙСТВА ТЕЛ
- § 40. Упругие свойства тел
- § 41. Закон Гуна. Энергия деформированного тела
- § 42. Модуль объемной упругости. Сжимаемость
- § 43. Модуль Юнга, коэффициент Пуассона, модуль сдвига и соотношение между ними
- § 44. Характеристика механических свойств твердого тела по диаграмме растяжения. Явление наклепа
- § 45. Пластичность
- § 46. Прочность и твердость
- § 47. Механические свойства важнейших материалов
- ГЛАВА IX. ОСНОВЫ ГИДРОДИНАМИКИ И АЭРОДИНАМИКИ
- § 48. Основные понятия и направления гидродинамики
- § 49. Уравнение Бернулли
- § 50. Гидравлическая энергия
- § 51. Вязкость и течение жидкости при трении
- § 52. Пограничный слой и вихреобразование. Строение турбулентного потока
- § 53. Сопротивление движению тел в жидкостях и газах
- § 54. Числа Рейнольдса. Кинематическая вязкость
- § 55. Аэродинамические силы. Подъемная сила крыла и тяга самолета
- ГЛАВА X. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 56. Гармоническое колебание
- § 57. Энергия и собственная частота гармонических колебаний
- § 58. Сложение колебаний одинаковой частоты и одинакового направления (интерференция колебаний)
- § 59. Другие случаи сложения колебаний
- § 60. Затухающие колебания
- § 61. Вынужденные колебания. Резонанс
- § 62. Связанные колебания
- ГЛАВА XI. УЧЕНИЕ О ВОЛНАХ
- § 63. Волновой процесс. Уравнение волн. Виды волн
- § 64. Интерференция волн. Стоячие волны
- § 65. Фазовая и групповая скорости волн
- ГЛАВА XII. АКУСТИКА
- § 66. Звук как физическое явление. Распространение звуковых волн
- § 67. Интенсивность звука
- § 68. Частота и состав звуков
- § 69. Явление Допплера
- § 70. Звук как психофизиологическое явление. Механизм звукового восприятия
- § 71. Высота и тембр звука
- § 72. Ультразвуки
- ЧАСТЬ ВТОРАЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 73. Исторические сведения. Картина молекулярного движения
- § 74. Статистический метод в физике
- § 75. Термодинамический метод
- § 76. Термодинамическая характеристика состояния тел и термодинамические процессы
- § 77. Уравнение Клапейрона
- § 78. Внутренняя энергия. Теплота и работа. Уравнение первого начала
- § 79. Изобарная и изотермическая работа газа
- § 80. Термохимические уравнения
- ГЛАВА XIV. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 81. Схематизация явлений («модели» в молекулярной физике)
- § 82. Максвеллов закон распределения молекулярных скоростей в газе
- § 83. Основное уравнение кинетической теории газов
- § 84. Молекулярно-кинетическое понимание абсолютной температуры
- § 85. Об уточненном (термодинамическом) понимании абсолютной температуры
- § 86. Тепловое равновесие и распределение энергии по степеням свободы
- § 87. Максвеллова теория газовых теплоемкостей
- § 88. Молекулярно-кинетическое пояснение работы расширения газа
- § 89. Средний свободный пробег газовых молекул
- ГЛАВА XV. ТЕПЛОПЕРЕДАЧА, ДИФФУЗИЯ И ВЯЗКОСТЬ. ВАКУУМ
- § 90. Тепловое излучение (законы Стефана и Ньютона)
- § 91. Теплопроводность (закон Фурье)
- § 92. Диффузия (закон Фика)
- § 93. Молекулярная теория теплопроводности газов
- § 94. Молекулярная теория вязкости газов
- § 95. Сопоставление явлений диффузии, теплопроводности и вязкости газов
- § 96. Вакуум. Манометры
- § 97. Вакуумные насосы
- ГЛАВА XVI. ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ И ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- § 98. Термодинамическое равновесие и e-положение Больцмана
- § 99. Ограничения, налагаемые вторым началом термодинамики на циклические превращения тепла в работу
- § 100. Уравнение Пуассона. Адиабатная работа газа
- § 101. Цикл Карно и теорема о сумме приведенных теплот
- § 102. Энтропия. Основное уравнение термодинамики
- § 103. Процессы обратимые и необратимые. Теорема о возрастании энтропии
- § 104. Статистический смысл энтропии
- § 105. Теоремы о термодинамическом равновесии. Свободная энергия и термодинамический потенциал
- § 106. О так называемой «тепловой смерти» мира
- § 107. Уравнения Гиббса — Гельмгольца и Клапейрона—Клаузиуса
- ГЛАВА XVII. ФИЗИКА РЕАЛЬНЫХ ГАЗОВ И ПАРОВ. УРАВНЕНИЕ ВАН-ДЕР-ВАЛЬСА
- § 108. Пары насыщенные и перегретые. Диаграмма Эндрюса
- § 109. Конденсация газов
- § 110. Уравнение Ван-дер-Вальса
- § 111. Учение о соответственных состояниях
- § 112. О качественных превращениях при тепловых процессах
- ГЛАВА XVIII. ФИЗИКА ЖИДКОСТЕЙ
- § 113. Механические и термодинамические свойства жидкостей
- § 114. Поверхностное натяжение
- § 115. Формула Лапласа. Явления капиллярности и смачивания
- § 116. Поверхностноактивные вещества
- § 117. Строение жидкостей
- § 118. Кинетика испарения. Зависимость давления насыщенного пара от кривизны поверхности жидкости. Формула Томсона — Шиллера
- § 119. Понижение давления пара над раствором и повышение температуры кипения растворов. Законы Рауля
- § 120. Осмотическое давление. Закон Вант-Гоффа
- § 121. Электролитическая диссоциация. Закон Оствальда
- § 122. Абсорбция. Закон Генри
- § 123. О столкновении противоположных процессов в молекулярно-тепловых явлениях
- ГЛАВА XIX. ФИЗИКА ТВЕРДЫХ ТЕЛ
- § 124. Строение кристаллов
- § 125. Понятие о кристаллохимии
- § 126. Форма и рост кристаллов
- § 127. Теплоемкость твердых тел
- § 128. Сублимация твердых тел. Тройная точка
- § 129. Кристаллизация растворов. Диаграмма плавкости
- § 130. Силы связи в кристаллах
- § 131. Адсорбция
- ГЛАВА XX. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ В ДВИГАТЕЛЯХ И СВЕРХЗВУКОВОЕ ДВИЖЕНИЕ
- § 132. Основное уравнение газодинамики. Адиабатный теплоперепад
- § 133. Адиабатное течение газа
- § 134. Ударные волны и скачки уплотнения. Адиабата Гюгонио
- § 135. Процессы в двигателях внутреннего сгорания
- § 136. Процессы в паровых машинах и паровых турбинах
- § 137. Реактивные двигатели














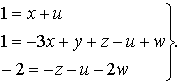 (8.58)
(8.58) 
