Начнём с определения:
Удар — кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер.
Сила удара, как и любая другая сила, измеряется в Ньютонах (Н) и килограмм-силах (кгс).
Один Ньютон – это сила, благодаря которой тело массой 1 кг получает ускорение 1 м/с2. Одна кгс – это сила, которая сообщает телу массой 1 кг ускорение 1 g = 9,81 м/с2 (g – ускорение свободного падения). Поэтому 1 кгс = 9,81 Н.
Вес тела массой m определяется силой притяжения Р, с которой он давит на опору: P = mg.
Если масса Вашего тела 80 кг, то Ваш вес, определяемый силой тяжести или притяжением, P = 80 кгс. Но в просторечье говорят «мой вес 80 кг», и всем всё понятно.
Поэтому часто о силе удара тоже говорят, что он составляет сколько-то кг, а подразумевается кгс.
Согласно Второго закона динамики, силу удара спортсмена определяют по формуле:
F = V0 m k1 k2 / t
где V0 – скорость ударной массы в момент соударения, мс:
m – собственно ударная масса, кг.
k1 – коэффициент, учитывающий жесткость кинематической цепи звеньев тела и жёсткости мишени .
k2 – коэффициент, учитывающий форму ударного движения..
t – время взаимодействия (соударения) ударной поверхности и мишени.
Таким образом на величину силы удара спортсмена-единоборца влияют следующие факторы:
1. СКОРОСТЬ ДВИЖЕНИЯ УДАРНОЙ МАССЫ.
Спортсмены-ударники, стараются увеличивать силу удара конечностей, придавая им максимальное ускорение (взрывная сила), а также максимально быстро перемещая тело (быстрая сила). Ударная масса обратно пропорциональна скорости – с увеличением ударной массы уменьшается скорость ее перемещения и наоборот.
2. ВЕЛИЧИНА УДАРНОЙ МАССЫ. Чем выше весовая категория спортсмена-единоборца, тем больше его ударная масса. Вот почему бойцы при нанесении ударов стремятся увеличивать ударную массу используя максимально массу всех звеньев тела. Это необходимо для увеличения силы толчка или удара.
3. ЖЕСТКОСТЬ КИНЕМАТИЧЕСКОЙ ЦЕПИ. Чем больше жесткость соударяющихся тел, тем выше сила удара. По этому сила удара по мешку весом в 100 кг будет выше чем по мешку в 20кг. Понятно, что, ударив по воздушному шарику, какой-либо значительной величины мы вообще не получим.
В момент касания цели необходимо создать максимальную жесткость в кинематической цепи суставов тела (структура) путем кратковременной фиксации звеньев тела, участвующих в этом движении (структура тела). Это так же увеличит и ударную массу в момент контакта с мишенью.
Каждое движение выполняется по схеме «расслабление-напряжение». Фаза расслабления должна занимать 99% времени всего движения, именно за счет ее появляется «хлесткость» удара.
4. ФОРМА УДАРНОГО ДВИЖЕНИЯ. Классическая механика исходит из того, что при ударе кинетическая энергия ударной массы полностью переходит в кинетическую энергию ударяемого тела. Передача энергии улучшается в том случае, когда центры масс звеньев ударной цепи в момент удара находятся на одной линии. При этом, чем резче и акцентированней остановка ударной поверхности в конечной фазе удара, тем больший выброс энергии следует. Энергия удара зависит и от правильной координации движения то есть – от правильной техники исполнения удара.
5. ВРЕМЯ СОУДАРЕНИЯ обратно пропорционально силе удара и не зависит от конечной скорости ударной массы. Это время растет с увеличением масс соударяющихся тел и уменьшением жесткости суставных соединений (ослабление стутуры тела) .
Отсюда исходит важность правильного выстраивания структуры тела.
Оптимальное время контакта ударной поверхности с целью составляет 0,014-0,018 с, при увеличении времени до 0,3 с удар превращается в толчок.
Все пять указанных факторов связаны между собой “принципом одновременности окончания”. То есть, все движения, составляющие удар (вращение бедер, шаг, разгибание ударной или блокирующей конечности), а также концентрация физической силы в момент нанесения удара должны происходить и заканчиваться одновременно.
Но сила удара сама по себе еще не гарантирует эффективное поражение. Его поражающее воздействие зависит и от следующих дополнительных факторов:
– Подготовка ударной поверхности.
Сила удара так же зависит от подготовленности ударной поверхности. Чем выше сила удара, тем большей нагрузке подвергается тело бьющего бойца. По этому, подготовка к ударным нагрузкам (набивка) – важный этап обучения.
– Точность направления удара к поверхности тела.
Удары по прямой линии к оси вращения противника позволяют наиболее полно реализовать разрушительную силу удара.
– Восприимчивости уязвимого места.
Легче всего вывести противника из строя, воздействуя на его болевые точки (расположенные близко к поверхности тепа нервные центры, жизненно важные органы, оголения костей, сухожильные связки и прочее).
Подводя итог – если мы хотим сделать наши удары по настоящему грозным оружием – мы должны учитывать все факторы рассмотренные в статье.
Успехов в практике!
по какой формуле можно найти силу удара?
Дмитрий Сударчиков
Ученик
(214),
на голосовании
12 лет назад
условие задачи:
стальной шарик массой m падет с высоты Н на стальную плитуюПосле столкновения от плиты шарик отскакивает с той же скоростью. Время соударения t(передним еще теругольник). Найти силу соударения.
Голосование за лучший ответ
Константин
Гуру
(4662)
12 лет назад
По второму закону Ньютона, сила равна скорости изменения импульса. При отскоке импульс изменился на 2*m*v, поскольку сохранил величину, но изменил направление на противоположное. Скорость этого изменения равна изменению величины импульса, делённому на время, за которое это изменение произошло. Скорость шарика, упавшего с высоты Н равна корню из 2*g*H. Т. о. , Ваша сила равна
F = 2*m*v / dt = 2*m*sqrt{ 2*g*H } / dt
где sqrt обозначает корень квадратный, dt — заданное в задаче время
Содержание:
Столкновения:
Наиболее общим явлением, наблюдаемым в природе, является взаимодействие материальных тел. Бильярдные шары, сближаясь, в момент соприкосновения взаимодействуют друг с другом. В результате этого меняются скорости шаров, их кинетические энергии. О таком взаимодействии шаров говорят как об их столкновениях.
Но понятие «столкновение» относится не только к взаимодействиям, происходящим в результате соприкосновения материальных тел. Комета, прилетевшая из отдаленных областей пространства и прошедшая в окрестности Солнца, меняет свою скорость и удаляется. Этот процесс также является столкновением. хотя непосредственного соприкосновения между кометой и Солнцем не произошло, а осуществлено оно было посредством сил тяготения.
Характерная особенность этого взаимодействия, дающая нам возможность рассматривать его как столкновение, заключается в том, что область пространства, в котором оно произошло, относительно мала. Заметное изменение скорости кометы происходит вблизи Солнца (рис. 129).
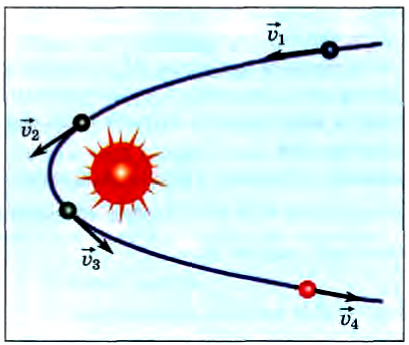
Приведенные примеры позволяют нам дать следующее определение столкновения.
Что такое столкновение
Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени. Вне этого промежутка времени можно говорить о начальных и конечных импульсах тел, когда тела можно считать невзаимодействующими.
Столкновение материальных тел часто называется ударом. Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений. Это частный случай столкновения, например столкновение шаров, шайб, автомобилей и т. п.
Процессы столкновения являются чрезвычайно сложными. Например, при столкновении двух шаров в момент их соприкосновения начинается деформация шаров. В результате часть кинетической энергии переходит в потенциальную энергию деформации. Затем энергия деформации снова превращается в кинетическую, однако не полностью — часть энергии превращается во внутреннюю. Кроме того, после столкновения шары будут вращаться по иному, чем до столкновения.
Главный интерес при рассмотрении столкновений заключается в знании не самого процесса, а результата. Ситуация до столкновения называется начальным состоянием, а после — конечным. Между величинами, характеризующими начальное и конечное состояния, соблюдаются определенные соотношения. независящие от детального характера взаимодействия. Такими величинами. в частности, являются импульс и энергия системы тел.
В зависимости от характера изменения кинетической энергии тел все столкновения делятся на упругие и неупругие.
Если при столкновении кинетическая энергия тел сохраняется, то столкновение называется упругим, если же не сохраняется — неупругим.
Рассмотрим вначале абсолютно неупругое столкновение (абсолютно неупругий удар). Это частный случай неупругого столкновения, при котором после столкновения тела «слипаются» и движутся вместе.
Пусть в некоторой инерциальной системе отсчета первое тело массой m1 движется до столкновения со скоростью υ1, а второе тело массой m2 — со скоростью υ2. Следовательно, импульсы тел до столкновения равны соответственно: 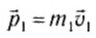
Процесс столкновения обычно наглядно представляют с помощью векторной диаграммы импульсов (рис. 130). Нетрудно убедиться, что кинетическая энергия системы не сохраняется. До столкновения она составляет:
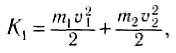
после столкновения —
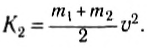
Изменение кинетической энергии:
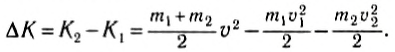 (2)
(2)
Для расчета выберем оси координат так, как показано на рисунке 130, и спроектируем на них равенство (1). B результате получим:
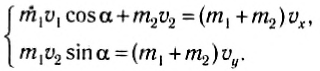
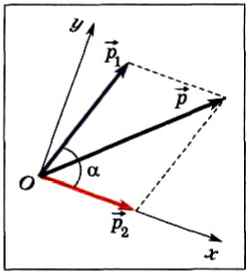
Рис. 130
Отсюда легко находится квадрат скорости тел после столкновения:
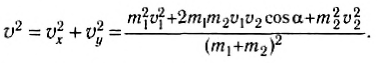
Подставив полученное выражение в (2), получим после несложных преобразований:
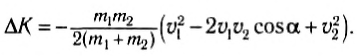
Как видно, кинетическая энергия системы уменьшилась. Часть кинетической энергии превратилась в теплоту.
Если тела при столкновении не «слипаются», то скорости тел после столкновения можно найти из закона сохранения импульса:
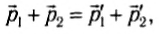
где штрихом отмечены импульсы тел после столкновения.
При этом кинетическая энергия может как уменьшаться, так и увеличиваться. Последнее происходит, например, при различных взрывах. В этом случае часть внутренней энергии превращается в кинетическую энергию осколков.
Как уже отмечалось, при упругом столкновении выполняется закон сохранения импульса и механической энергии.
Рассмотрим вначале лобовое столкновение, т. е. такое столкновение, при котором импульсы тел до и после столкновения параллельны некоторой прямой. Эту прямую мы примем за ось Ox (рис. 131). Закон сохранения импульса в этом случае примет вид:
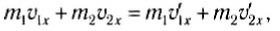
а закон сохранения кинетической энергии –
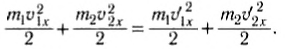
Из этих уравнений найдем скорости тел после удара. Для этого перепишем (3) и (4) следующим образом:
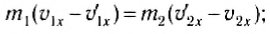
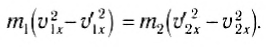
Воспользовавшись тем, что a2 – b2 = (a-b)(a + b), из выражений (5) и (6) легко получить:
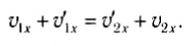
Выразив отсюда, например, 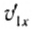 и подставив его в (5), после несложных преобразований находим:
и подставив его в (5), после несложных преобразований находим:
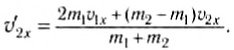
Аналогично:
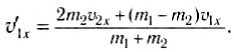
Проекции импульсов тел после столкновения равны соответственно:
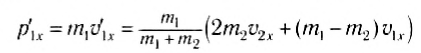
и
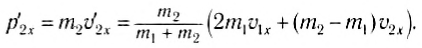
Проанализируем полученные выражения для некоторых частных случаев.
Предположим, что тело 2 до столкновения покоилось, т. е. 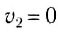 .
.
Тогда
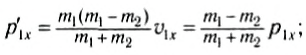
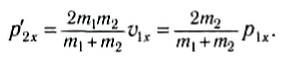
При равных массах тел m1 = m2 получим:
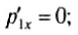
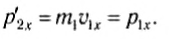
Значит, первое тело остановится, а второе придет в движение с таким же импульсом.
Теперь предположим, что масса второго тела намного больше массы первого. Тогда, пренебрегая m1 по сравнению с m2 , получим:
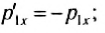
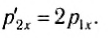
Значит, первое тело отскочит назад с таким же по модулю импульсом, а тело 2 получит импульс, равный удвоенному значению импульса первого тела.
Найдем кинетическую энергию тел после столкновения для случая, когда 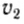 = 0:
= 0:
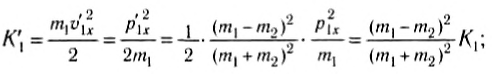 (10)
(10)
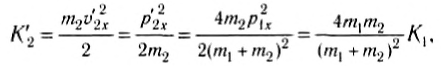 (10)
(10)
где K1 — кинетическая энергия первого тела до столкновения.
Из полученных выражений следует, что при m1 = m2 первое тело останавливается, а второе приобретает ту же энергию. Если масса второго тела m2 намного больше массы первого m1 то из (10) и (11) следует, что 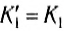 ,
, 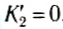 . Значит, кинетическая энергия первого тела не изменяется, а второе тело получает импульс, но его энергия не изменяется.
. Значит, кинетическая энергия первого тела не изменяется, а второе тело получает импульс, но его энергия не изменяется.
- Заказать решение задач по физике
Главные выводы:
- Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени.
- Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений.
- Столкновение тел называется упругим, если кинетическая энергия тел сохраняется. При неупругом столкновении кинетическая энергия тел не сохраняется.
- При столкновениях тел выполняется закон сохранения импульса.
Определение столкновения
Законы сохранения энергии и импульса позволяют провести теоретическое исследование процессов столкновения тел без описания сил, действующих между ними.
Под столкновениями понимают механические процессы взаимодействия между телами, происходящие за очень короткий промежуток времени. При этом силы взаимодействия между сталкивающимися телами настолько велики, что внешними силами, действующими на систему, можно пренебречь.
Вследствие того, что длительность столкновения мала по сравнению со временем наблюдения, различают механические состояния до и после столкновения, причем тела, находящиеся на большом расстоянии друг от друга, считают свободными.
Длительность столкновения бильярдных шаров 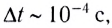 что намного меньше характерного времени движения шаров по столу
что намного меньше характерного времени движения шаров по столу 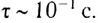
Различают упругие (абсолютно упругие) и неупругие столкновения. В первом случае не происходит выделения теплоты, и механическая энергия сохраняется. Во втором случае выделяется некоторое количество теплоты, поэтому механическая энергия после столкновения уменьшается.
Примером упругих столкновений служат столкновения металлических шаров, а примером неупругих — столкновения пластилиновых шаров, которые при этом слипаются и продолжают движение как одно целое.
Для макроскопических тел в большей степени характерными являются неупругие столкновения, в то время как для физики элементарных частиц, ядер атомов, молекул определяющую роль играет упругое взаимодействие.
Если в процессе столкновения тел на них не действуют внешние силы, то к телам применим закон сохранения импульса, а во многих случаях — и закон сохранения механической энергии. Именно эти законы позволяют, зная скорости тел до столкновения, определить их скорости после столкновения, совершенно не интересуясь тем, что происходило во время него.
При абсолютно неупругом столкновении скорости обоих взаимодействующих тел оказываются одинаковыми. Примером таких тел являются тела из различных пластичных веществ. Такое столкновение можно наблюдать, если подвесить тары из пластилина, развести их в разные стороны и отпустить. После столкновения они оба будут двигаться вместе с одинаковой скоростью.
При абсолютно упругом столкновении в обоих телах не остается никаких деформаций. Кроме того, вся кинетическая энергия, которой тела обладали до столкновения, снова превращается в кинетическую энергию. Примерами таких тел являются шары из стали или слоновой кости.
Рассмотрим простейшее столкновение — центральное, когда скорости тел находятся на линии, соединяющей их центры. Очень часто такое столкновение называют лобовым.
Скорость движения 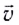 после абсолютно неупругого столкновения тел массами
после абсолютно неупругого столкновения тел массами 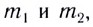 движущихся до столкновения со скоростями
движущихся до столкновения со скоростями 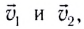 можно определить из закона сохранения импульса:
можно определить из закона сохранения импульса:
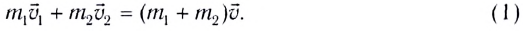
Откуда находим
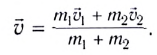
Определим «потери» механической энергии, найдя кинетическую энергию
тел до столкновения:
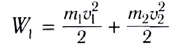
и после столкновения:
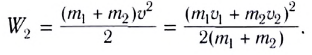
Тогда часть механической энергии, перешедшая во внутреннюю, определяется выражением:
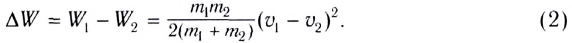
Следовательно, она зависит от масс сталкивающихся тел и относительной скорости 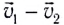 их движения до столкновения.
их движения до столкновения.
Задача о центральном абсолютно неупругом столкновении впервые была решена Дж. Валлисом в 1669 г.
При абсолютно упругом столкновении двух тел массами 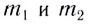 на основании закона сохранения импульса и закона сохранения энергии можно записать
на основании закона сохранения импульса и закона сохранения энергии можно записать
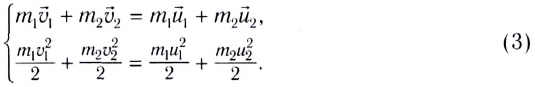
Здесь 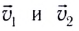 — скорости тел до столкновения,
— скорости тел до столкновения, 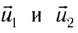 — после столкновения.
— после столкновения.
Преобразуем систему уравнений (3), перенеся в правую часть все величины, относящиеся к первому телу, а в левую — ко второму:
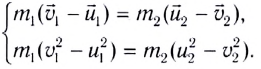
Разделив второе уравнение на первое, получим

Перепишем это уравнение в виде 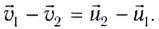 .
.
Из него следует, что при центральном абсолютно упругом столкновении тел любой массы их относительная скорость до и после столкновения не изменяется.
Теперь можно дать еще одно определение неупругого столкновения: если относительная скорость тел при центральном столкновении изменяется, то такое столкновение называется неупругим.
Меру неупругости k можно определить как отношение относительных скоростей сталкивающихся тел после и до столкновения: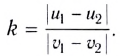
Она называется коэффициентом восстановления и впервые была измерена Ньютоном в 1687 г. В частности, Ньютон получил значения коэффициента для стали k = 0,55 и стекла k = 0,94, которые приводят и современные справочники.
Абсолютно неупругим является столкновение, при котором скорости тел после столкновения равны 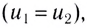 т. е. k = 0.
т. е. k = 0.
Решая уравнение (4) совместно с первым уравнением системы (3), находим скорости тел после столкновения:
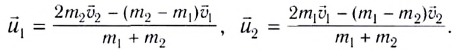
На самом деле при столкновении всегда происходят «потери» механической энергии, т. е. переход части ее в теплоту. Но при малых «потерях» действительный процесс достаточно хорошо описывается абсолютно упругим столкновением.
Задача о центральном абсолютно упругом столкновении впервые была решена X. Гюйгенсом и К. Реном в 1669 г.
Отметим, что осуществить центральное, или лобовое, столкновение на практике очень трудно. Подавляющее число столкновений являются нецентральными.
Основные формулы
Импульс тела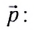
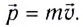
Закон изменения импульса системы тел:
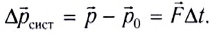
Закон сохранения импульса системы тел:
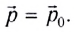
Работа: 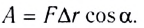
Средняя мощность: 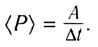
Мгновенная мощность: 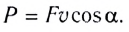
Кинетическая энергия: 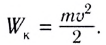
Теорема о кинетической энергии:
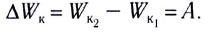
Потенциальная энергия: 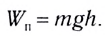
Потенциальная энергия упруго деформированного тела:
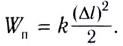
Закон сохранения механической энергии:
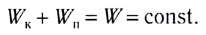
- Рычаг в физике
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
Impact force is defined as a situation when some work is done to move an object a specific distance. It can be interpreted as the force produced when two items collide. An object collision occurs when one object collides with another. The impact force has a huge impact on an object in a short period of time. It is denoted by the symbol F. it is unit of measurement is Newtons (N) and the dimensional formula is given by [M1L1T-2]. Its formula equals the product of mass and velocity of a body to the twice time taken. In other words, it is the ratio of kinetic energy possessed by a body to the distance traveled by it.
Impact Force Formula
F = mv/2t
where,
F is the impact force,
m is the mass of the body,
v is the velocity of the body,
t is the time taken.
Derivation
Consider an object of mass m which moves with a velocity v when some work W is done on it. The force applied is F and it moves the object to a distance of d units for t seconds.
We know the work done equals the product of force applied and distance travelled.
W = Fd ⇢ (1)
Also, the work done equals the kinetic energy of the body.
W = K.E. = 1/2 mv2 ⇢ (2)
From (1) and (2) we get,
Fd = 1/2 mv2
F = mv2/2d
Putting d = vt, we get,
F = mv2/2vt
F = mv/2t
This derives the formula for impact force acting on a body.
Sample problems
Problem 1: Calculate the impact force acting on an object of mass 2 kg, velocity 4 m/s for 2 seconds.
Solution:
m = 2
v = 4
t = 2
Using the formula we get,
F = mv/2t
= 2 (4) / 2 (2)
= 8/4
= 2 N
Problem 2: Calculate the impact force acting on an object of mass 3 kg, velocity 8 m/s for 3 seconds.
Solution:
m = 3
v = 8
t = 3
Using the formula we get,
F = mv/2t
= 3 (8) / 2 (3)
= 24/6
= 4 N
Problem 3: Calculate the mass of the body if the impact force acting on an object is 10 N, and velocity is 5 m/s for 4 seconds.
Solution:
F = 10
v = 5
t = 4
Using the formula we get,
F = mv/2t
=> m = 2Ft/v
= 2 (10) (4) / 5
= 16 kg
Problem 4: Calculate the velocity of the body if the impact force acting on an object is 14 N mass is 2 kg for 2 seconds.
Solution:
We have,
F = 14
m = 2
t = 2
Using the formula we get,
F = mv/2t
=> v = 2Ft/m
= 2 (14) (2) / 2
= 28 m/s
Problem 5: Calculate the time taken by the body if the impact force acting on an object is 30 N, mass is 4 kg, and velocity is 15 m/s.
Solution:
F = 30
m = 4
v = 15
Using the formula we get,
F = mv/2t
=> t = mv/2F
= 4 (15) / 2 (30)
= 60/60
= 1 s
Problem 6: Calculate the impact force acting on an object of kinetic energy 20 J if the distance traveled is 2 m.
Solution:
E = 20
d = 2
Using the formula we get,
F = E/d
= 20/2
= 10 N
Problem 7: Calculate the kinetic energy of a body if the impact force acting on an object is 40 N and the distance traveled is 4 m.
Solution:
F = 40
d = 4
Using the formula we get,
F = E/d
=> E = Fd
= 40 (4)
= 160 J
Last Updated :
15 May, 2022
Like Article
Save Article
Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.
Применение такого вида задач используется в технике и физике элементарных частиц.
Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.
При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.
Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.
Абсолютно неупругий удар. Скорость
Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.
Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.
Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1.21.1, m – горизонтально летящая пуля с v→ скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.
Если скорость ящика с пулей обозначить как u→, тогда, используя формулу сохранения импульса, получаем:
mv=(M+m)u; u=mM+mv.
Когда пуля застревает в песке, то механическая энергия теряется:
∆E=mv22-(M+m)u22=MM+m·mv22.
M (M + m) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда
∆EE0=MM+m=11+mM.
Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.
Когда m << М ∆EE0→12, тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆EE0→0, только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим (m>>М), отношение принимает вид ∆EE0→0.
Расчет движения маятника производится по закону сохранения механической энергии. Получаем
(M+m)u22=(M+m)gh; u2=2gh.
В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что
v=M+mm2gh.
При известной высоте h возможно определение скорости пули v.
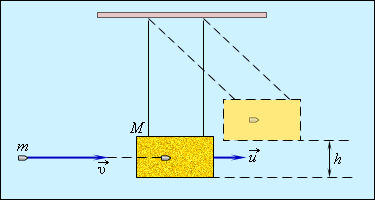
Рисунок 1.21.1. Баллистический маятник.
Абсолютно упругий удар
Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.
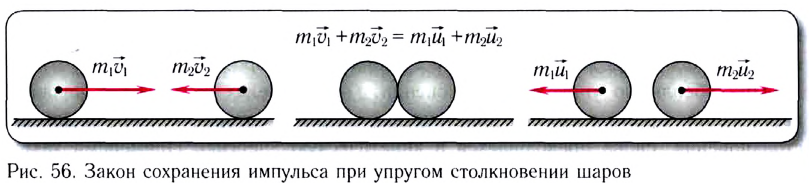
Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1.21.2.
Центральный удар – это соударение, когда скорости шаров направлены по линии центра.
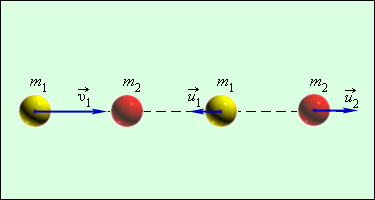
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров.
Встречаются случаи, когда массы m1 и m2 не равны. Тогда, используя закон сохранения механической энергии, получаем
m1v122=m1v122+m2v222.
За v1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v2=0 скорость второго шара, u1 и u2 – скорости после столкновения.
Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:
m1v1=m1u1+m2u2.
Полученная система из двух уравнений позволяет найти неизвестные скорости u1 и u2 шаров после столкновения.
u1=m1-m2v1m1+m2; u2=2m1v1m1+m2.
Если массы равны, то есть, тогда происходит остановка первого шара (u1=0), а второй продолжает движение u2=v1. происходит обмен скоростями и импульсами.
При наличии нулевой скорости второго шара (v2≠0), задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v1’=v1–v2. После определения скорости шаров v1 и v2 производится переход к «неподвижной» системе.
С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.
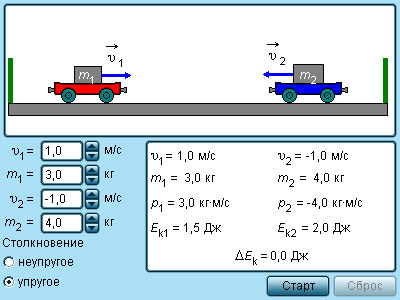
Рисунок 1.21.3. Модель упругие и неупругие соударения.
При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.
Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1.21.4.
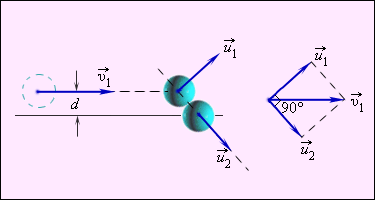
Рисунок 1.21.4. Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.
Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v1 и v2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d, изображенное на рисунке 1.21.4.
Предельное расстояние
Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v1→ летящего шара.
При одинаковых массах шаров векторы v1→ и v2→ имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m1=m2=m, тогда определение примет вид
v1→=u1→+u2→; v12=u12+u22.
Первое равенство значит, что векторы v1→, u1→, u2→ образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u1→ и u2→, равняется 90 градусов.
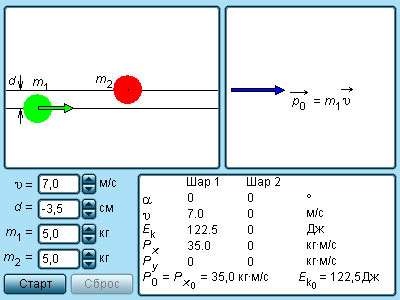
Рисунок 1.21.5. Модель соударения упругих шаров
