Содержание
- – Как узнать ускорение свободного падения 7 класс?
- – Чему равна сила падения?
- – Чему равен вес тела при свободном падении?
- – Что нужно сделать чтобы найти силу тяжести?
- – Как найти мощность Формула 7 класс?
- – Как определить ускорение свободного падения?
- – Как рассчитать скорость падения тела?
- – Чему равна сила в физике?
- – Чему равна сила притяжения тела к Земле?
- – Как узнать вес при падении?
- – Чему равен вес тела в физике?
- – Что такое сила тяжести и вес тела?
- – Как найти силу F в физике?
- – Как найти силу тяжести на высоте?
- – Какая сила притяжения Земли?
Силу, с которой Земля притягивает тела, можно рассчитать по формуле F = m ⋅ g , где m — масса тела, а g — ускорение свободного падения. Ускорение свободного падения — это ускорение, которое вблизи Земли приобретает тело, падающее свободно и беспрепятственно.
Чему равна сила падения?
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с².
Чему равен вес тела при свободном падении?
Вес, сила, с которой тело, покоящееся в поле сил тяжести, действует на подвес или горизонтальную опору, препятствующую свободному падению тела. Численно В. тела Р равен действующей на него силе тяжести, то есть Р = mg, где m — масса тела, g — ускорение свободного падения (или ускорение силы тяжести).
Что нужно сделать чтобы найти силу тяжести?
Формула силы тяжести Fт=m*g, где m-масса тела, g-ускорение свободного падения.
Как найти мощность Формула 7 класс?
Чтобы вычислить мощность, надо работу разделить на время, в течение которого совершена эта работа. мощность = работа/время. N = A/t, где N – мощность, A – работа, t – время выполненной работы.
Как определить ускорение свободного падения?
Величина ускорения свободного падения на расстоянии h от поверхности Земли вычисляется при помощи формулы: g=γM(R+h)2(6).
Как рассчитать скорость падения тела?
Ускорение и скорость при свободном падении
g=γM(R+h)2(1), где γ=6,67⋅10−11Н⋅м2кг2- гравитационная постоянная; M – масса Земли; R – радиус Земли. Если расстояние, с которого падает тело много меньше, чем радиус Земли ( h≪R), то ускорение свободного падения считают постоянной величиной, равной: g=γMR2≈9,8 (мс2)(2).
Чему равна сила в физике?
Сила равна массе тела, умноженной на его ускорение.
Чему равна сила притяжения тела к Земле?
Стандартное («нормальное») значение, принятое при построении систем единиц, составляет g = 9,80665 м/с². Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
Как узнать вес при падении?
Вес человека до падения будет равен m*g (где m – масса человека, а g – ускорение свободного падения (обычно берут 9.8 м/c^2); g в общем случае зависит от высоты, но в данном случае разница в g на 10 этаже и на уровне земли будет пренебрежимо мала).
Чему равен вес тела в физике?
Сила, с которой тело давит на опору или растягивает подвес, называют весом. Вес тела обозначают P и измеряют в ньютонах (H). Вес неподвижного тела равен P = mg .
Что такое сила тяжести и вес тела?
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Как найти силу F в физике?
Формула Умножьте массу на ускорение. Сила F, необходимая для того, чтобы придать объекту массой m ускорение a, определяется по следующей формуле: F = m x a. То есть сила равна массе, умноженной на ускорение.
Как найти силу тяжести на высоте?
Если тело находится на высоте h над поверхностью планеты, то для силы тяжести получаем: mg(h) = G Mm (R + h)2 . Здесь g(h) ускорение свободного падения на высоте h: g(h) = G M (R + h)2 = gR2 (R + h)2 .
Какая сила притяжения Земли?
9,807 м/с²
Интересные материалы:
Как назывался авангард в армии Тимура?
Как назывался Донецк до Юзовки?
Как назывался дракон в Гарри Поттере?
Как назывался его полк Петра 1?
Как назывался главный вход во дворец в Коломенском?
Как назывался город из Алых парусов?
Как назывался город Костанай раньше?
Как назывался город Ульяновск раньше?
Как назывался Ханты Мансийский округ?
Как назывался художественный фильм который прославил окуджаву как автора и композитора?
Общие сведения
Основоположником создания учения о движении стал Аристотель. Он утверждал, что скорость падения тела зависит от его веса. Значит, тяжёлый предмет сможет долететь до Земли быстрее, чем лёгкий. Если же на объект не будут воздействовать какие-либо силы, его движение невозможно.

Но Галилео Галилей, известный итальянский изобретатель и физик, изучая падение различных предметов и их инерцию, смог опровергнуть догадки Аристотеля. Результаты его исследований были революционными в науке. При этом даже была выпущена книга «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению», в которой были изложены основные размышления Галилея.
За дату рождения кинематики как науки можно принять 20 января 1700 года. В это время проходило заседание Академии наук, на котором Пьер Вариньона не только дал определения понятиям скорость, ускорение, но и описал их в дифференциальном виде. Уже после Ампер использовал для изучения процессов вариационное исчисление. Наглядные опыты провёл Лейбниц, а потом. профессор МГУ Н. А. Любимов смог продемонстрировать появление невесомости при свободном падении.
Под невесомостью понимают состояние тела, при котором силы взаимодействия с опорой, существующие из-за гравитационного притяжения, не оказывают никакого влияния. Такое положение имеет место, когда воздействующие на тело внешние силы можно охарактеризовать массовостью, например, тяготения.
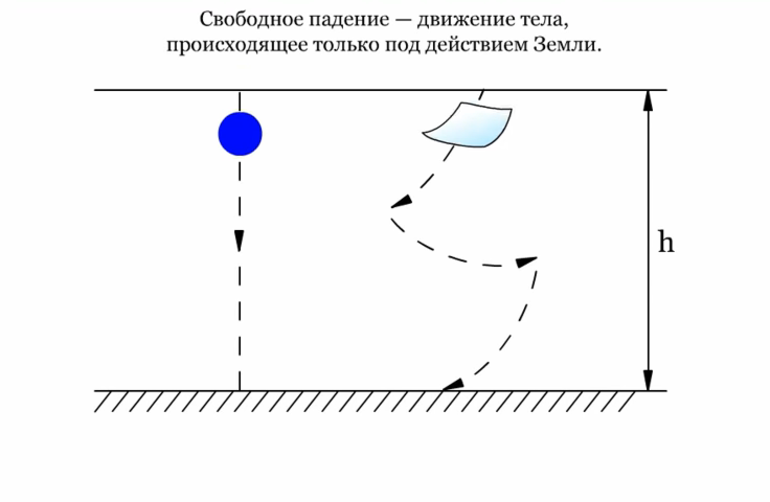
В этом случае силы поля сообщают всем частицам предмета в любом из его положений равные по модулю и направлению ускорения, либо при движении возникают одинаковые по модулю скорости всех частиц тела. Например, поступательное движение. Состояние невесомости особо ярко проявляется в начальный момент при падении тела в атмосфере. Это связано с тем, что сопротивление воздуха ещё невелико.
Таким образом, для существования свободного падения нужно выполнение как минимум двух условий:
- малость или отсутствие сопротивления среды;
- действие лишь одной силы тяжести.
Что интересно, движение вверх тоже считается свободным падением, несмотря на обратное интуитивное восприятие, поэтому траектория движения может иметь форму как участка параболы, так и отрезка прямой. Например, камень, брошенный с небольшой высоты или поверхности под любым углом.
Опыт Галилея
Падение относится к реальному движению. Любое взаимодействие с Землёй приводит к изменению скорости из-за чего возникает ускорение. В 1553 году итальянец Джованни Бенедетти заявил, что 2 тела с разной массой, но одинаковой формы, брошенные в одной среде за одинаковое время пролетят равные расстояния. Это утверждение нуждалось в доказательстве, так как противоречило общепринятому на тот момент времени пониманию процессов. В частности, высказываниям Аристотеля.

Одним из экспериментаторов стал Галилей. Для проведения опыта учёному понадобилось:
- стофунтовое ядро;
- однофунтовый шар.
Существует мнение, что вместо шара учёный использовал мушкетную пулю. Эксперимент заключался в следующем. Подняв 2 предмета на Пизанскую башню, Галилей сбросил их одновременно. Наблюдающие люди воочию смогли убедиться, что 2 тела упали на землю одновременно. Когда же один из учеников Аристотеля упрекнул итальянца, что на такой малой высоте невозможно оценить достоверно разницу, экспериментатор ответил: «Проделайте опыт самостоятельно, вы найдёте, что более тяжёлый предмет опередит тот, что легче на 2 пальца, поэтому, когда первый упадёт на землю, то второй будет от него на расстоянии толщины двух пальцев».

В своих работах Галилей рассуждал, что если связать верёвкой 2 тела разной тяжести, то с большим весом, по мнению Аристотеля, предмет будет лететь быстрее. Причём лёгкий объект начнёт замедлять падение тяжёлого. Но так как система в целом тяжелее, чем отдельно взятые тела, падать она должна быстрее самого тяжёлого тела. Другими словами, возникает противоречие, значит, предположение о влиянии веса на скорость падения неверно.
Сегодня эксперимент, подтверждающий доводы Галилея, может провести самостоятельно, пожалуй, каждый интересующийся. Такой опыт часто демонстрируют в средних классах общеобразовательной школы. Для этого нужно взять 2 трубки, длиной более метра и поместить в них 2 шарика разной массы. Затем создать внутри вакуум и одновременно их перевернуть. Если все условия соблюдены верно, то 2 тела опустятся на дно ёмкостей одновременно.
Если же опыт повторить не в вакууме, на шары будет действовать сила сопротивления, поэтому время падения уже не будет совпадать. Причём зависеть оно будет от формы предмета и его плотности.
Закон ускорения
Формула для свободного падения была выведена из выражения, определяющего силу тяжести: F = m * g. В соответствии с законом, падение предметов выполняется с одним и тем же ускорением вне зависимости от массы тела. По сути, это частный случай равноускоренного движения, обусловленное силой тяжести.
Для количественного анализа нужно ввести систему координат, взяв начало у поверхности Земли. Тогда можно рассмотреть падение тела массой m с высоты y0. Причём вращением планеты и сопротивлением воздушной среды нужно пренебречь.
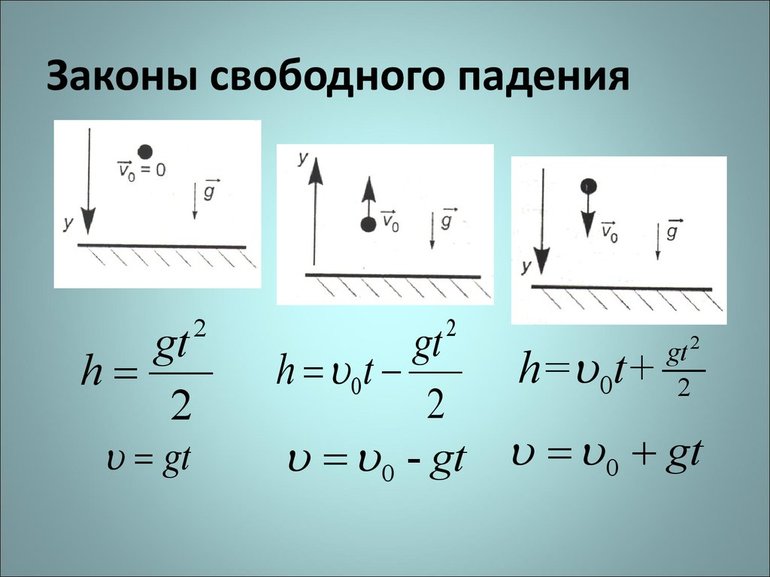
Дифференциальное уравнение будет иметь вид: my = – mg, где: g — ускорение свободного падения. Само же дифференцирование выполняется по времени. При заданных начальных условиях y = y0 и беря во внимание проекцию скорости на вертикальную ось после интегрирования, зависимость переменных от t примет вид:
- v = v0 + gt;
- y = y0 + v0t — (gt2 / 2).
Из полученных формул становится понятно, почему свободное падение не зависит от массы тела. При этом если начальная скорость будет равна нулю, то есть при падении предмету не сообщается импульс, текущее движение пропорционально времени, а пройденный путь определяется его квадратом.
Как показали эксперименты, если сопротивления воздуха нет, ускорение для любых летящих предметов по отношению к Земле составит 9,8 м / с2. Формулы, которые используются при расчёте величин, совпадают с выражениями, справедливыми для любого равноускоренного движения. Например, если тело падает без начальной скорости, его скорость можно найти по формуле: V2 = g * t, а высоту падения определить так: h = (gt2 / 2).
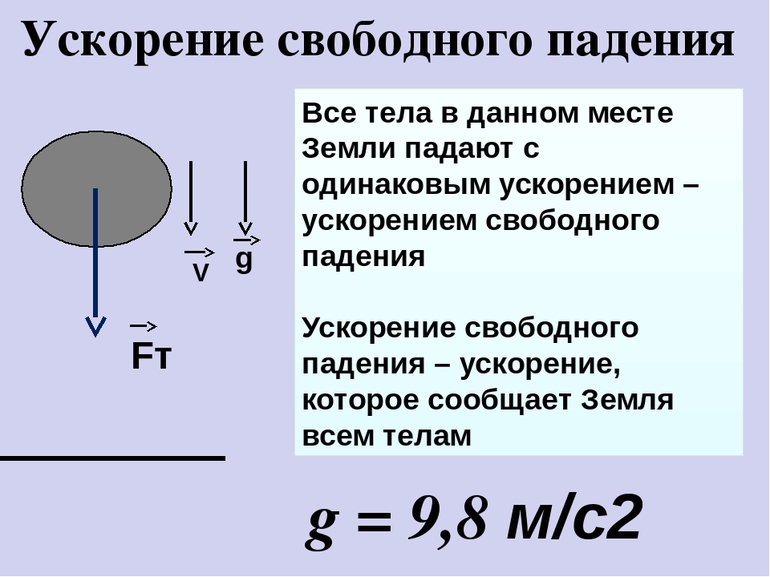
Следует отметить, что при удалении предмета от Земли значение свободного движения уменьшается. Причём из-за формы планеты на экваторе оно будет составлять 9,78 м / с2, а с противоположной стороны — 9,832 м / с2. Чтобы определить значение в любом месте, используют нитяной маятник. Его период колебаний определяется по формуле: T = 2p√(l / g), где l — длина нити.
Значения силы тяжести также зависит от строения земной коры и содержащихся в недрах полезных ископаемых. С учётом этого рассчитываются гравитационные аномалии: Δg = g — gср. Например, если g > gcp, то с большой вероятностью в земле содержатся залежи железной руды, в ином случае — нефти или газа.
Решение задач
Свободно двигаться, то есть не испытывать действие сторонних сил, могут любые тела в вакууме. Но в реальности на них оказывается воздействие как атмосферными явлениями, так и сопротивлением среды. При решении задач учитывается только сила тяжести, а вот остальными явлениями пренебрегают, считая их ничтожно малыми.
Вот некоторые из типовых задач, используемые при обучении в среднеобразовательных школах:

- Деревянная бочка падает с 30 метров. Какова будет её скорость перед столкновением с Землёй? Так как рассматривается свободное падение, для решения нужно использовать формулу: v2 = 2 * g * h. Отсюда, v = √(2 * g * h) = (2 * 9,81 м / с2 * 30 м) = 24,26 м/с.
-
Тело вылетает вертикально вверх со скоростью 45 м/с. Какой высоты оно достигнет перед изменением направления полёта и сколько для этого понадобится времени. Для начала следует записать формулу скорости: v = v0 — gt. Отсюда можно рассчитать время полёта: t = v0 / g = 45 / 9,8 = 4,6 c. Теперь можно определить максимальную высоту: h = vot — (gt 2 / 2) = 45 м / с * 4,6 с — 9,8 м / с2 * (4,6 c)2 / 2 = 207 м — 103,7 м = 103,3 м.
-
Камень летит со скоростью 30 м/с. Найти время, за которое он достигнет 25 метров. Система уравнений, описывающая движение, будет выглядеть так: h = v0t — (gt2 / 2); 25 = 30t — 5t2. Полученные уравнения в системе называются квадратными, поэтому нужно выразить одно из другого и определить корни: t2 — 6t + 5 = 0. В результате должно получиться время, равное одной секунде.
Рассмотренные задания довольно простые. Но есть и повышенной сложности, требующие не только знания формул, но и умения выполнять анализ. Вот одно из таких.
Мяч бросили с горки под углом к горизонту. Через время, равное t = 0,5 c он достигнет наибольшей высоты, а t2 = 2,5 он упадёт. Определить высоту горки, ускорение падения принять равное g = 10 м / с2. Скорость движущегося предмета можно представить в координатной плоскости x и y. В горизонтальном направлении сил, оказывающих воздействие, нет. Движение равномерное. Наибольшая высота будет достигнута при h = H + v0y * t1 — (gt21 / 2).
Вертикальную составляющую можно вычислить, руководствуясь геометрическими принципами: v0y = v0 * sin (a). Учитывая, что h = (gt2 / 2), для высоты горки можно записать: H = (g * (t21 + t22) / 2) — t1 * v0 sin (a). Так как gt1 = v0 sin (a), то рабочая формула примет вид: H = (g * (t21 + t22) / 2) — gt21. После подстановки данных в ответе должна получиться высота равная 30 метров. Задача решена.
Силу гравитации, с которой Земля притягивает тело, находящееся на её поверхности или вблизи неё, называют силой тяжести. Эта сила направлена к центру Земли.
Сила гравитации Земли для нас является самой важной, поэтому ей и дано особое название.
Земля притягивает всё, что находится вокруг неё: твёрдые тела, жидкости, газы.
Из-за того что есть сила тяжести, возможно существование атмосферы (молекулы газа не улетают в космос), воды морей и океанов удерживаются на своих местах, если какой-либо предмет приподнимают и роняют, этот предмет падает вниз — в направлении Земли.
Силу, с которой Земля притягивает тела, можно рассчитать по формуле:
F=m⋅g
, где (m) — масса тела, а (g) — ускорение свободного падения.
Ускорение свободного падения — это ускорение, которое вблизи Земли приобретает тело, падающее свободно и беспрепятственно. Вблизи поверхности Земли значение (g) равно примерно (9,81)
мс2
, для приблизительных расчётов можно использовать значение (10)
мс2
.
Что означает эта единица измерения?

Скорость свободно падающего тела каждую секунду увеличивается на (9,81) метра в секунду (
м/с
).
Если предмет падает, например, в течение (4) секунд, то скорость его падения в самом начале равна (0)
м/с
;
за (1)-ю секунду он достигает скорости (9,81)
м/с
;
за (2)-ю секунду он достигает скорости: (9,81), умноженное на (2), т.е. модуль скорости (v) (=) (19,62)
м/с
;
за (3)-ю секунду он достигает скорости: (9,81), умноженное на (3), т.е. модуль скорости (v) (=) (29,43)
м/с
;
за (4)-ю секунду тело достигает скорости: (9,81), умноженное на (4), т.е. модуль скорости (v) (=) (39,24)
м/с
, что приблизительно составляет (141) км/ч.
Обрати внимание!
Интересно, что кирпич и яблоко падают с одинаковой скоростью. Только падение лёгких предметов сопротивление воздуха замедляет сильнее, например, птичье перо из-за сопротивления воздуха будет падать медленнее.
Ускорение свободного падения на поверхности Луны составляет только (1,62)
мс2
.
На Юпитере значение (g) приблизительно равно (26,2)
мс2
, это примерно так же, как если бы человек в дополнение к своим (60) кг веса взвалил бы на плечи ещё примерно (102) кг.
Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря – падение в пустоте. Конечно, отсутствие сопротивления воздуха – это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного падения – ускорение, с которым все тела падают на Землю.
Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.
Земля – не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения – на полюсах (≈9,83 мс2), а самое малое – на экваторе (≈9,78 мс2).
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.
h=v0+gt22.
Так как начальна скорость равна нулю, перепишем:
h=gt22.
Отсюда находится выражение для времени падения тела с высоты h:
t=2hg.
Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:
v=2hg·g=2hg.
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
v=v0-gt.
Подставив v=0, найдем время подъема тела на максимальную высоту:
t=v0g.
Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.
Максимальная высота подъема тела, брошенного вертикально:
h=v022g.
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
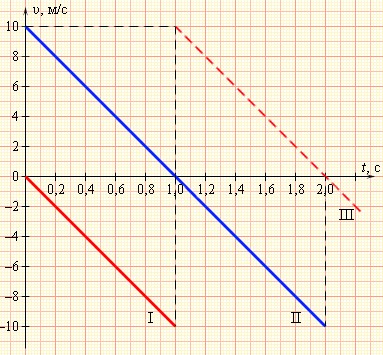
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.
Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
Движение тела, брошенного под углом к горизонту
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.
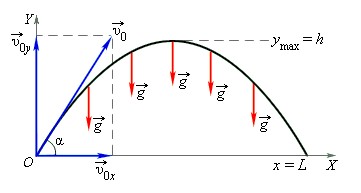
Условия для движения вдоль оси ОХ:
x0=0; v0x=v0cosα; ax=0.
Условия для движения вдоль оси OY:
y0=0; v0y=v0sinα; ay=-g.
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t=2v0sinαg.
Дальность полета тела:
L=v02sin2αg.
Максимальная дальность полета достигается при угле α=45°.
Lmax=v02g.
Максимальная высота подъема:
h=v02sin2α2g.
Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 августа 2022 года; проверки требуют 4 правки.
| Земля | 9,81 м/с2 | 1,00 g | Солнце | 273,1 м/с2 | 27,85 g |
| Луна | 1,62 м/с2 | 0,165 g | Меркурий | 3,70 м/с2 | 0,378 g |
| Венера | 8,88 м/с2 | 0,906 g | Марс | 3,86 м/с2 | 0,394 g |
| Юпитер | 24,79 м/с2 | 2,528 g | Сатурн | 10,44 м/с2 | 1,065 g |
| Уран | 8,86 м/с2 | 0,903 g | Нептун | 11,09 м/с2 | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с2 | 0,084 ± 0,002 g | Плутон | 0,617 м/с2 | 0,063 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении взаимодействия с другими телами.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или более грубо 10 м/с².
Физическая сущность[править | править код]
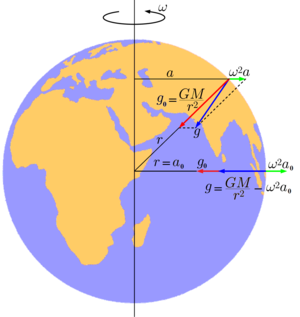
Две компоненты ускорения свободного падения на Земле
g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна
GM/r2 и центробежная, равная
ω2a, где
a — расстояние до земной оси,
ω — угловая скорость вращения Земли.
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центростремительное ускорение[править | править код]
Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с2, причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение[править | править код]
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:
,
где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
,
- где M — масса планеты.
Ускорение свободного падения на Земле[править | править код]
Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:
- где
— широта рассматриваемого места,
— высота над уровнем моря в метрах.
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение[править | править код]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
См. также[править | править код]
- Свободное падение
- Гравиметрия
- Гравиразведка
- Перегрузка (летательные аппараты)
Примечания[править | править код]
- ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
- ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
- ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М. : Изд-во стандартов, 1990. — С. 237.
- ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
- ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
- ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
- ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
- ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.
Литература[править | править код]
- Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.

