Как найти силу тесла

Как найти силу тесла

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 декабря 2020 года; проверки требуют 11 правок.

У этого термина существуют и другие значения, см. Тесла.

Тесла
Тл, T
Inductor for experiments PNr°0016.jpg
Величина индукция магнитного поля
Система СИ
Тип производная

Те́сла (русское обозначение: Тл; международное обозначение: T) — единица индукции магнитного поля в Международной системе единиц (СИ), равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, расположенного по нормали вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.

Через основные единицы СИ тесла выражается следующим образом:

  • кг·с−2·А−1

Через производные единицы СИ тесла выражается соотношениями:

  • Вб / м2
  • В·с / м2
  • Н·А−1·м−1

В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы измерения «тесла» пишется со строчной буквы, а её обозначение «Тл» — с заглавной.

Соотношения с другими единицами измерения магнитной индукции:

  • 1 Тл = 10 000 гаусс (единица СГС)
  • 1 Тл = 1⋅109 гамма (единица, применяемая в геофизике)

Единица названа в честь изобретателя Николы Теслы. В Международную систему единиц (СИ) тесла введён решением XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием СИ в целом[1].

Характерные значения[править | править код]

  • В космическом пространстве магнитная индукция составляет от 0,1 до 10 нанотесл (от 10−10 до 10−8 Тл).
  • Магнитное поле Земли значительно варьируется во времени и пространстве. На широте 50° магнитная индукция в среднем составляет 5⋅10−5 Тл, а на экваторе (широта 0°) — 3,1⋅10−5 Тл.
  • В солнечных пятнах — 0,3 Тл[2].
  • Стандартное значение магнитной индукции, создаваемой высокопольным магнитно-резонансным томографом, — 1,5 Тл.
  • Отклоняющие дипольные магниты Большого адронного коллайдера — от 0,54 до 8,3 Тл.
  • В белых карликах — 100 Тл.
  • Рекордное значение постоянного магнитного поля, достигнутое людьми без разрушения установки — 1200 Тл[3].
  • Рекордное значение импульсного магнитного поля, когда-либо наблюдавшегося в лаборатории — 2800 Тл[4].
  • Магнитные поля в атомах — от 1 до 10 килотесл (103 — 104 Тл).
  • На нейтронных звёздах — от 1 до 100 мегатесл (106 — 108 Тл).
  • На магнетарах — от 0,1 до 100 гигатесл (108 — 1011 Тл).
  • Рекордное значение, зафиксированное в природе — ~1,6 гигатесл (109 Тл), зарегистрировано на пульсаре Swift J0243.6+6124[5].

Кратные и дольные единицы[править | править код]

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Кратные Дольные
величина название обозначение величина название обозначение
101 Тл декатесла даТл daT 10−1 Тл децитесла дТл dT
102 Тл гектотесла гТл hT 10−2 Тл сантитесла сТл cT
103 Тл килотесла кТл kT 10−3 Тл миллитесла мТл mT
106 Тл мегатесла МТл MT 10−6 Тл микротесла мкТл µT
109 Тл гигатесла ГТл GT 10−9 Тл нанотесла нТл nT
1012 Тл тератесла ТТл TT 10−12 Тл пикотесла пТл pT
1015 Тл петатесла ПТл PT 10−15 Тл фемтотесла фТл fT
1018 Тл эксатесла ЭТл ET 10−18 Тл аттотесла аТл aT
1021 Тл зеттатесла ЗТл ZT 10−21 Тл зептотесла зТл zT
1024 Тл иоттатесла ИТл YT 10−24 Тл иоктотесла иТл yT
1027 Тл роннатесла РТл RT 10−27 Тл ронтотесла рТл rT
1030 Тл кветтатесла КвТл QT 10−30 Тл квектотесла квТл qT
     рекомендовано к применению      применять не рекомендуется

Примечания[править | править код]

  1. ↑ Resolution 12 of the 11th meeting of the CGPM (1960) Архивная копия от 14 мая 2013 на Wayback Machine (англ.) на сайте Международного бюро мер и весов
  2. ↑ Kenneth R. Lang. A Magnetic Star: The photosphere and its magnetism (англ.). NASA’s Cosmos (2010). Дата обращения: 25 августа 2020. Архивировано 10 декабря 2015 года.
  3. ↑ D. Nakamura, A. Ikeda, H. Sawabe, Y. H. Matsuda, and S. Takeyama. Record indoor magnetic field of 1200 T generated by electromagnetic flux-compression (англ.) // AIP. Архивировано 5 июня 2019 года.
  4. ↑ Boyko, B. A. et al. With record magnetic fields to the 21st Century (англ.) // 12th IEEE International Pulsed Power Conference, 1999. Digest of Technical Papers.. — 1999. — P. 746—749. — doi:10.1109/PPC.1999.823621. Архивировано 23 августа 2009 года.
  5. ↑ Astronomers Have Spotted a Record-Breaking Magnetic Field in Space, and It’s Epic. Дата обращения: 15 июля 2022. Архивировано 17 августа 2022 года.
Источник
Идеальный трансформатор
Идеальный трансформатор

Если заговорить о Формуле Николы Тесла, то первое что вспомнят все это то что Тесла – единица измерения плотности магнитного потока
Эту формулу преподают давно и всем
✔️ Тл = кг / (с2 · А) = Н / (А · м) = Вб / м2.
✔️ 1 Тл = 1 кг / (1 с2 · 1 А) = 1 Н / (1 А · 1 м) = 1 Вб / 1 м2.

И мало кто вспоминает, среди сказок и легенд про патенты и изобретения Тесла, что Никола Тесла , в попытках понять и осмыслить теорию трансформации переменного тока в напряжение и обратно, сочинил некоторые не всем известные формулы увязывающие силу тока и напряжение в проводниках трансформаторов с МАССОЙ МЕДИ в этих проводниках. Да именно с Массой меди.

В упрощенном виде Формула Токовой Трансформации Тесла выглядит следующим образом:

U(преобразования ) = Nп(количество витков провода)* Mп(масса меди провода)/ Nв(количество витков провода)* Mв(масса меди провода)

Где Мп и Мв – это масса меди первичной и вторичной обмоток соответственно, а Nп Nв количество витков.

Одновременно с этой Формулой уже существовала Формула расчета Тока и Напряжения в трансформаторах учитывающая не количество Меди а геометрию проводника – его Сечение и Диаметр витков.
В общем расчеты по массе и объему близки по смыслу, но , увы, Формула Тесла не смотря на все мифы о гениальных изобретениях на практике не удалась.

Тесла – единица измерения плотности магнитного потока, напряжённости и индукции магнитного поля в Международной системе единиц (СИ), названная в честь изобретателя Николы Теслы.
Тесла как единица измерения имеет русское обозначение – Тл и международное обозначение – T.
1 тесла равен индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон. Другими словами, один тесла равен напряжённости поля, действующего на проводник с силой один ньютон на метр проводника при силе тока на каждый ампер тока.
Аналогично, один тесла представляет собой плотность магнитного потока в один вебер на квадратный метр площади.
Тл = кг / (с2 · А) = Н / (А · м) = Вб / м2.
1 Тл = 1 кг / (1 с2 · 1 А) = 1 Н / (1 А · 1 м) = 1 Вб / 1 м2.

Тесла работал инженером-электриком в Венгерской правительственной телеграфной компании в Будапеште и даже сумел исправить ряд ошибок и недоработок при постройке электростанции для железнодорожного вокзала в Страсбурге.
После этого Тесла получил огромное множество патентов на всевозможные технологии, широко используемые в наше время, однако дело всей жизни — эффективная передача энергии по воздуху — так и не получило дальнейшего развития И такое утверждение более чем странно учитывая развитую сеть радиотрансляционных станций и СТК передающие мощность с помощью радиоволн.
Ученый добился успехов в экспериментах с переменным током, создал высокочастотный электромеханический генератор и высокочастотный трансформатор, разработал правила техники безопасности при работе с током. Как ни странно но паралельно все эти открытия и изобретения уже применялись в Европе и Америке.
Кроме того, Тесла проводил эксперименты и на своем организме: он выяснил, что болевое воздействие тока перестает ощущаться при частоте свыше 700 Гц, и на основе этого открытия разработал электротехнические аппараты для медицинских исследований.
Многие изобретения используемые в те годы теперь приписываются трудам Николы Тесла, так к работам Теслы относят и эксперименты с высокочастотными токами большого напряжения, которые позволяют чистить поверхность кожи — убирают мелкую сыпь, очищают поры, уничтожают микробов (в наше время данный метод используется в электротерапии).

В Международную систему единиц тесла введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы «тесла» пишется со строчной буквы, а её обозначение — с заглавной (Тл). Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием теслы.

Источник

Тесла.

Тесла – единица измерения плотности магнитного потока, напряжённости и индукции магнитного поля в Международной системе единиц (СИ). Тесла как единица измерения имеет русское обозначение – Тл и международное обозначение – T.

Тесла, как единица измерения

Применение тесла

Представление тесла в других единицах измерения – формулы

Перевод тесла в другие единицы измерения

Кратные и дольные единицы тесла

Интересные примеры

Другие единицы измерения

Тесла, как единица измерения:

Тесла – единица измерения плотности магнитного потока, напряжённости и индукции магнитного поля в Международной системе единиц (СИ), названная в честь изобретателя Николы Теслы.

Тесла как единица измерения имеет русское обозначение – Тл и международное обозначение – T.

1 тесла равен индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон. Другими словами, один тесла равен напряжённости поля, действующего на проводник с силой один ньютон на метр проводника при силе тока на каждый ампер тока.

Аналогично, один тесла представляет собой плотность магнитного потока в один вебер на квадратный метр площади.

Тл = кг / (с2 · А) = Н / (А · м) = Вб / м2.

1 Тл = 1 кг / (1 с2 · 1 А) = 1 Н / (1 А · 1 м) = 1 Вб / 1 м2.

В Международную систему единиц тесла введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы «тесла» пишется со строчной буквы, а её обозначение — с заглавной (Тл). Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием теслы.

Тесла включен в первый раздел Общероссийский классификатор единиц измерения (ОКЕИ) – “Национальные единицы измерения, включенные в ОКЕИ“.

Применение тесла:

В теслах измеряют плотность магнитного потока, напряжённость и индукцию магнитного поля.

Представление тесла в других единицах измерения – формулы:

Через основные и производные единицы системы СИ тесла выражается следующим образом:

Тл = кг / (с2 · А).

Тл = Н / (А · м).

Тл = Вб / м2.

Тл = В · с / м2.

где  Тл – тесла, А – ампер, В – вольт, Вб – вебер, Н – ньютон, м – метр, с – секунда, кг – килограмм.

Перевод тесла в другие единицы измерения:

1 Тл = 10 000 гаусс.

1 Тл = 1⋅109 гамма.

Кратные и дольные единицы тесла:

Кратные и дольные единицы образуются с помощью стандартных приставок СИ.

Кратные Дольные
величина название обозначение величина название обозначение
101 Тл декатесла даТл daT 10−1 Тл децитесла дТл dT
102 Тл гектотесла гТл hT 10−2 Тл сантитесла сТл cT
103 Тл килотесла кТл kT 10−3 Тл миллитесла мТл mT
106 Тл мегатесла МТл MT 10−6 Тл микротесла мкТл µT
109 Тл гигатесла ГТл GT 10−9 Тл нанотесла нТл nT
1012 Тл тератесла ТТл TT 10−12 Тл пикотесла пТл pT
1015 Тл петатесла ПТл PT 10−15 Тл фемтотесла фТл fT
1018 Тл эксатесла ЭТл ET 10−18 Тл аттотесла аТл aT
1021 Тл зеттатесла ЗТл ZT 10−21 Тл зептотесла зТл zT
1024 Тл иоттатесла ИТл YT 10−24 Тл иоктотесла иТл yT

Интересные примеры:

Во внешнем космосе магнитная индукция составляет от 0,1 до 10 нанотесла (от 10−10 Тл до 10−8 Тл).

Магнитное поле Земли значительно варьируется во времени и пространстве. На широте 50° магнитная индукция в среднем составляет 5⋅10−5 Тл, а на экваторе (широта 0°) — 3,1⋅10−5 Тл.

Сувенирный магнит на холодильнике создает поле около 5 миллитесла (5⋅10−3 Тл).

В солнечных пятнах магнитная индукция составляет 10 Тл.

Рекордное значение импульсного магнитного поля, когда-либо наблюдавшегося в лаборатории – 2,8⋅103 Тл.

Магнитные поля в атомах составляют от 1 до 10 килотесла (103 – 104 Тл).

Источник: https://ru.wikipedia.org/wiki/Тесла_(единица_измерения)

Примечание: © Фото https://www.pexels.com, https://pixabay.com

тл тесла физическая единица измерения си магнитной индукции физическая величина физика википедия
какая физическая величина имеет единицу 1 тесла

Коэффициент востребованности
4 796

Источник

From Wikipedia, the free encyclopedia

tesla
Unit system SI
Unit of magnetic flux density
Symbol T
Named after Nikola Tesla
Conversions
1 T in … … is equal to …
   SI base units    1 kg⋅s−2⋅A−1
   Gaussian units    ≘ 104 G

The tesla (symbol: T) is the unit of magnetic flux density (also called magnetic B-field strength) in the International System of Units (SI).

One tesla is equal to one weber per square metre. The unit was announced during the General Conference on Weights and Measures in 1960 and is named[1] in honour of Serbian-American electrical and mechanical engineer Nikola Tesla, upon the proposal of the Slovenian electrical engineer France Avčin.

Definition[edit]

A particle, carrying a charge of one coulomb (C), and moving perpendicularly through a magnetic field of one tesla, at a speed of one metre per second (m/s), experiences a force with magnitude one newton (N), according to the Lorentz force law. That is,

{displaystyle {text{T}}={dfrac {{text{N}}{cdot }{text{s}}}{{text{C}}{cdot }{text{m}}}}.}

As an SI derived unit, the tesla can also be expressed in terms of other units. For example, a magnetic flux of 1 weber (Wb) through a surface of one square meter is equal to a magnetic flux density of 1 tesla.[2] That is,

{displaystyle {text{T}}={dfrac {text{Wb}}{{text{m}}^{2}}}.}

Expressed only in SI base units, 1 tesla is:

{displaystyle {text{T}}={dfrac {text{kg}}{{text{A}}{cdot }{text{s}}^{2}}},}[2]

where A = ampere, kg = kilogram, and s = second.

Additional equivalences result from the derivation of coulombs from amperes (A), {displaystyle {text{C}}={text{A}}cdot {text{s}}}:

{displaystyle {text{T}}={dfrac {text{N}}{{text{A}}{cdot }{text{m}}}},}

the relationship between newtons and joules (J), {displaystyle {text{J}}={text{N}}cdot {text{m}}}:

{displaystyle {text{T}}={dfrac {text{J}}{{text{A}}{cdot }{text{m}}^{2}}},}

and the derivation of the weber from volts (V), {displaystyle {text{Wb}}={text{V}}cdot {text{s}}}:

{displaystyle {text{T}}={dfrac {{text{V}}{cdot }{text{s}}}{{text{m}}^{2}}}.}

The tesla is named after Nikola Tesla. As with every SI unit named for a person, its symbol starts with an upper case letter (T), but when written in full it follows the rules for capitalisation of a common noun; i.e., “tesla” becomes capitalised at the beginning of a sentence and in titles, but is otherwise in lower case.

Electric vs. magnetic field[edit]

In the production of the Lorentz force, the difference between electric fields and magnetic fields is that a force from a magnetic field on a charged particle is generally due to the charged particle’s movement,[3] while the force imparted by an electric field on a charged particle is not due to the charged particle’s movement. This may be appreciated by looking at the units for each. The unit of electric field in the MKS system of units is newtons per coulomb, N/C, while the magnetic field (in teslas) can be written as N/(C⋅m/s). The dividing factor between the two types of field is metres per second (m/s), which is velocity. This relationship immediately highlights the fact that whether a static electromagnetic field is seen as purely magnetic, or purely electric, or some combination of these, is dependent upon one’s reference frame (that is, one’s velocity relative to the field).[4][5]

In ferromagnets, the movement creating the magnetic field is the electron spin[6] (and to a lesser extent electron orbital angular momentum). In a current-carrying wire (electromagnets) the movement is due to electrons moving through the wire (whether the wire is straight or circular).

Conversion to non-SI units[edit]

One tesla is equivalent to:[7][page needed]

10,000 (or 104) G (gauss), used in the CGS system. Thus, 1 G = 10−4 T = 100 μT (microtesla).
1,000,000,000 (or 109) γ (gamma), used in geophysics.[8][failed verification] Thus, 1 γ = 1 nT (nanotesla).

For the relation to the units of the magnetising field (ampere per metre or Oersted), see the article on permeability.

Examples[edit]

The following examples are listed in the ascending order of the magnetic-field strength.

  • 3.2 × 10−5 T (31.869 μT) – strength of Earth’s magnetic field at 0° latitude, 0° longitude
  • 4 × 10−5 T (40 μT) – walking under a high-voltage power line[9]
  • 5 × 10−3 T (5 mT) – the strength of a typical refrigerator magnet
  • 0.3 T – the strength of solar sunspots
  • 1.25 T – magnetic flux density at the surface of a neodymium magnet
  • 1 T to 2.4 T – coil gap of a typical loudspeaker magnet
  • 1.5 T to 3 T – strength of medical magnetic resonance imaging systems in practice, experimentally up to 17 T[10]
  • 4 T – strength of the superconducting magnet built around the CMS detector at CERN[11]
  • 5.16 T – the strength of a specially designed room temperature Halbach array[12]
  • 8 T – the strength of LHC magnets
  • 11.75 T – the strength of INUMAC magnets, largest MRI scanner[13]
  • 13 T – strength of the superconducting ITER magnet system[14]
  • 14.5 T – highest magnetic field strength ever recorded for an accelerator steering magnet at Fermilab[15]
  • 16 T – magnetic field strength required to levitate a frog[16] (by diamagnetic levitation of the water in its body tissues) according to the 2000 Ig Nobel Prize in Physics[17]
  • 17.6 T – strongest field trapped in a superconductor in a lab as of July 2014[18]
  • 27 T – maximal field strengths of superconducting electromagnets at cryogenic temperatures
  • 35.4 T – the current (2009) world record for a superconducting electromagnet in a background magnetic field[19]
  • 45 T – the current (2015) world record for continuous field magnets[19]
  • 97.4 T – strongest magnetic field produced by a “non-destructive” magnet [20]
  • 100 T – approximate magnetic field strength of a typical white dwarf star
  • 1200 T – the field, lasting for about 100 microseconds, formed using the electromagnetic flux-compression technique[21]
  • 109 T – Schwinger limit above which the electromagnetic field itself is expected to become nonlinear
  • 108 – 1011 T (100 MT – 100 GT) – magnetic strength range of magnetar neutron stars

Notes and references[edit]

  1. ^ “Details of SI units”. sizes.com. 2011-07-01. Retrieved 2011-10-04.
  2. ^ a b The International System of Units (SI), 8th edition, BIPM, eds. (2006), ISBN 92-822-2213-6, Table 3. Coherent derived units in the SI with special names and symbols Archived 2007-06-18 at the Wayback Machine
  3. ^ Gregory, Frederick (2003). History of Science 1700 to Present. The Teaching Company.
  4. ^ Parker, Eugene (2007). Conversations on electric and magnetic fields in the cosmos. Princeton University press. p. 65. ISBN 978-0691128412.
  5. ^ Kurt, Oughstun (2006). Electromagnetic and optical pulse propagation. Springer. p. 81. ISBN 9780387345994.
  6. ^ Herman, Stephen (2003). Delmar’s standard textbook of electricity. Delmar Publishers. p. 97. ISBN 978-1401825652.
  7. ^ McGraw Hill Encyclopaedia of Physics (2nd Edition), C.B. Parker, 1994, ISBN 0-07-051400-3
  8. ^ “Geomagnetism Frequently Asked Questions”. National Geophysical Data Center. Retrieved 21 October 2013.
  9. ^ “EMF: 7. Extremely low frequency fields like those from power lines and household appliances”. ec.europa.eu. Archived from the original on 2021-02-24. Retrieved 2022-05-13.
  10. ^ “Ultra-High Field”. Bruker BioSpin. Archived from the original on 21 July 2012. Retrieved 4 October 2011.
  11. ^ “Superconducting Magnet in CMS”. Retrieved 9 February 2013.
  12. ^ “The Strongest Permanent Dipole Magnet” (PDF). Retrieved 2 May 2020.
  13. ^ “ISEULT – INUMAC”. Retrieved 17 February 2014.
  14. ^ “ITER – the way to new energy”. Retrieved 19 April 2012.
  15. ^ Hesla, Leah (13 July 2020). “Fermilab achieves 14.5-tesla field for accelerator magnet, setting new world record”. Retrieved 13 July 2020.
  16. ^ Berry, M. V.; Geim, A. K. (1997). “Of Flying Frogs and Levitrons” by M. V. Berry and A. K. Geim, European Journal of Physics, v. 18, 1997, p. 307–13″ (PDF). European Journal of Physics. 18 (4): 307–313. doi:10.1088/0143-0807/18/4/012. S2CID 1499061. Archived from the original (PDF) on 8 October 2020. Retrieved 4 October 2020.
  17. ^ “The 2000 Ig Nobel Prize Winners”. August 2006. Retrieved 12 May 2013.)
  18. ^ “Superconductor Traps The Strongest Magnetic Field Yet”. 2 July 2014. Retrieved 2 July 2014.
  19. ^ a b “Mag Lab World Records”. Media Center. National High Magnetic Field Laboratory, USA. 2008. Retrieved 24 October 2015.
  20. ^ “World record pulsed magnetic field”. Physics World. 31 August 2011. Retrieved 26 January 2022.)
  21. ^ D. Nakamura, A. Ikeda, H. Sawabe, Y. H. Matsuda, and S. Takeyama (2018), Magnetic field milestone

External links[edit]

Look up tesla in Wiktionary, the free dictionary.

  • Gauss ↔ Tesla Conversion Tool
Источник

Что такое магнитная индукция и магнитный поток

Магнитное поле, так же как и электрическое поле, является одной из сторон электромагнитного поля и представляет собой один из видов материи. Оно возникает, например, при движении электрических зарядов и, в частности, вокруг проводов с током.

Магнитное поле обладает энергией называемой энергией магнитного поля, которая проявляет себя различным образом, например в действии одного провода с током на другой провод с током, находящийся в магнитном поле первого, или в действии магнитного поля проводника с током на магнитную стрелку.

Физический смысл магнитной индукции

Прежде, чем перейти к рассмотрению формулы магнитной индукции, нужно выяснить, чем объясняется возникновение самого явления в системе. Соленоид не является плоским элементом и включает в себя спираль из проводника (металла). При отсутствии воздействующих на него магнитных явлений находящиеся в кристаллической решетке материала спирали электрозаряды ведут себя статично. Когда в соленоиде движется постоянный магнитный элемент, формирующий поле, под его влиянием движутся и заряженные частицы, тогда в индуктивном элементе появляется электрический ток, сила которого определяется характеристиками магнитного и спирального элемента и тем, как быстро происходит движение.

Важно! Имеющие одинаковую ориентацию поля суммируются, образуя общее поле. Когда передвижение заряженных частиц в соленоиде прекращается, сердечник перестает проявлять магнитные характеристики, если он выполнен из мягкого металла (к стальным изделиям это правило не относится).

Чем характеризуется магнитная индукция

Более мелкой единицей магнитного потока, не относящейся к системе СИ, является максвелл

1 мкс = 10-8вб = 1 гс•см2.

Так как магнитная индукция характеризуется числом магнитных линий, проходящих через единицу площади поверхности, перпендикулярной направлению поля, то магнитный поток будет характеризоваться числом линий, проходящих через площадь S.

Единицы измерения магнитной индукции

В международной системе единиц (СИ) сила измеряется в ньютонах, ток — в амперах, длина — в метрах, поэтому единица измерения магнитной индукции

[B] = [F : (Il)] = н : (a • м) = дж/м : (a • м) = (в • k) : (a • м2) = (в • а • сек) : (a • м2) = (в • сек) : м2

Единица вольт-секунда называется вебер (вб), а вебер, деленный на квадратный метр, — тесла (тл),

таким образом:

[B] = вб : м2 = тл

Кроме единицы тесла, иногда применяется гаусс (гс) — единица магнитной индукции, не принадлежащая к системе СИ, при этом

1 гс — 10-4 тл, или 1 тл = 104 гс.

Провод с током в магнитном поле

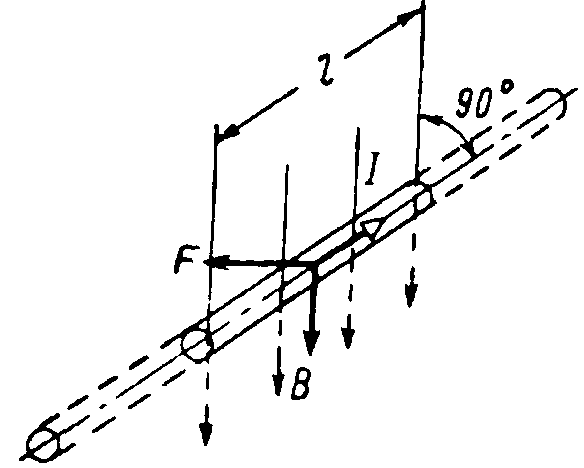
Рис. 3. Провод с током в магнитном поле.

Магнитная индукция — векторная величина. Направление вектора магнитной индукции совпадает с направлением поля в данной точке.

Магнитное поле, во всех точках которого векторы магнитной индукции одинаковы по величине и параллельны друг другу, называется однородным.

Линии магнитной индукции можно использовать не только для указания направления поля, но и для характеристики его интенсивности.

Для этого условно через единичную площадку, перпендикулярную к направлению поля, проводят число линий, равное или пропорциональное величине магнитной индукции в данном месте поля.

Произведение магнитной индукции В на площадь S, перпендикулярную к вектору магнитной индукции, называется магнитным потоком, т. е.

Ф = BS.

Формула магнитной индукции:

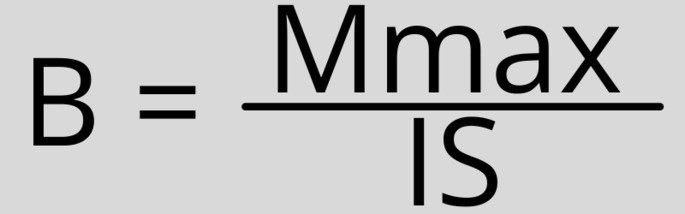
Формулы вычисления магнитной индукции B = Mmax/IS
Формула магнитной индукции: B = Mmax/IS

Где:

  • B — индукция магнитного поля (в Тл)
  • Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
  • l — длина проводника (в м)
  • S — площадь рамки (в м²)

Формула для определения модуля магнитной индукции

Если проводник расположен перпендикулярно линиям магнитной индукции 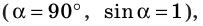Сила и закон Ампера - формулы и определение с примерами
поле действует на проводник с максимальной силой:

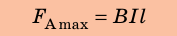
Сила и закон Ампера - формулы и определение с примерами

Отсюда получаем формулу для определения модуля магнитной индукции:

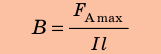
Сила и закон Ампера - формулы и определение с примерами

Обратите внимание! Значение магнитной индукции не зависит ни от силы тока в проводнике, ни от длины проводника, а зависит только от свойств магнитного поля.

Например, если уменьшить силу тока в проводнике, то уменьшится и сила Ампера, с которой магнитное поле действует на проводник, а вот значение магнитной индукции останется неизменным.

В СИ единица магнитной индукции — тесла (Тл), единица силы — ньютон (Н), силы тока — ампер (А), длины — метр (м), поэтому:

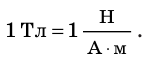
Сила и закон Ампера - формулы и определение с примерами

1 Тл — это индукция такого однородного магнитного поля, которое действует с максимальной силой 1 Н на проводник длиной 1 м, в котором течет ток силой 1 А.

  • Заказать решение задач по физике

Пример №3

Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.

Анализ физической проблемы. Около любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как будут вести себя проводники.

Решение

Решая задачу, выполним пояснительные рисунки: изобразим проводники А и В, покажем направления тока в них и т. д.

Выясним направление силы Ампера, которая действует на проводник А, находящийся в магнитном поле проводника В.

  1. С помощью правила буравчика найдем направление линий магнитной индукции магнитного поля, созданного проводником В(рис. 1, а). Выясняется, что вблизи проводника А магнитные линии направлены к нам (обозначено «•»).
  2. Воспользовавшись правилом левой руки, определим направление силы Ампера, действующей на проводник А со стороны магнитного поля проводника В (рис. 1, б).

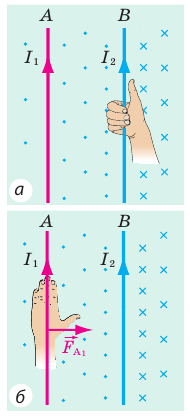
Сила и закон Ампера - формулы и определение с примерами

Рис. 1

3. Приходим к выводу: проводник А притягивается к проводнику В.

Теперь выясним направление силы Ампера, которая действует на проводник В, находящийся в магнитном поле проводника А.

1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рис. 2, а). Выясняется, что вблизи проводника В магнитные линии направлены от нас (обозначено 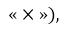Сила и закон Ампера - формулы и определение с примерами

2) Определим направление силы Ампера, действующей на проводник В (рис. 2, б).

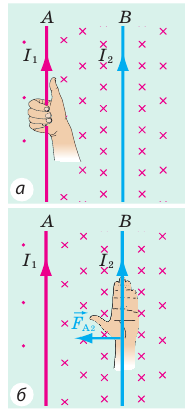
Сила и закон Ампера - формулы и определение с примерами

Рис. 2

3) Приходим к выводу: проводник В притягивается к проводнику А.

Ответ: два параллельных проводника, в которых текут токи одного направления, притягиваются.

Пример №4

Прямой проводник (стержень) длиной 0,1 м и массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитным линиям поля (рис. 3).

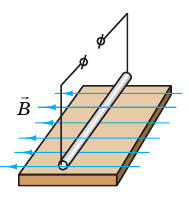
Сила и закон Ампера - формулы и определение с примерами

Рис. 3

Ток какой силы и в каком направлении следует пропустить по стержню, чтобы стержень не давил на опору (завис в магнитном поле)?

Анализ физической проблемы. Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при условиях: 1) сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх); 2) значение силы Ампера будет равно значению силы тяжести: 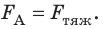Сила и закон Ампера - формулы и определение с примерами

Дано:

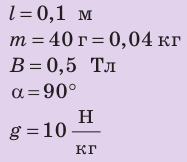
Сила и закон Ампера - формулы и определение с примерами

Найти:

Сила и закон Ампера - формулы и определение с примерами

Поиск математической модели, решение

1. Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90° большой палец был направлен вертикально вверх. Четыре вытянутых пальца укажут направление от нас. Следовательно, ток в проводнике нужно направить от нас.

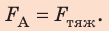
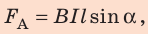
2. Учитываем, что Сила и закон Ампера - формулы и определение с примерами

Сила и закон Ампера - формулы и определение с примерами
где 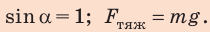Сила и закон Ампера - формулы и определение с примерами

Следовательно, 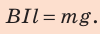Сила и закон Ампера - формулы и определение с примерами

Из последнего выражения найдем силу тока: 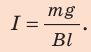Сила и закон Ампера - формулы и определение с примерами

Проверим единицу, найдем значение искомой величины.

Вспомним: 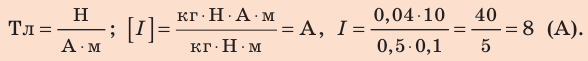Сила и закон Ампера - формулы и определение с примерами

Ответ: 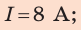Сила и закон Ампера - формулы и определение с примерами
от нас.

Подводим итоги:

Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера находят по формуле: 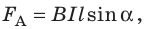Сила и закон Ампера - формулы и определение с примерами
где В — индукция магнитного поля; I — сила тока в проводнике; 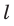Сила и закон Ампера - формулы и определение с примерами
— длина активной части проводника; 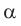Сила и закон Ампера - формулы и определение с примерами
— угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяют по правилу левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера.

Другие формулы, где встречается B

Эти формулы также можно использовать для её расчёта.

Сила Ампера

Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:

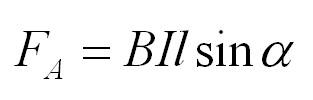
основные формулы электричество и магнетизм

Это и есть сила Ампера. Угол альфа– угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.

Правило левой руки для силы Ампера

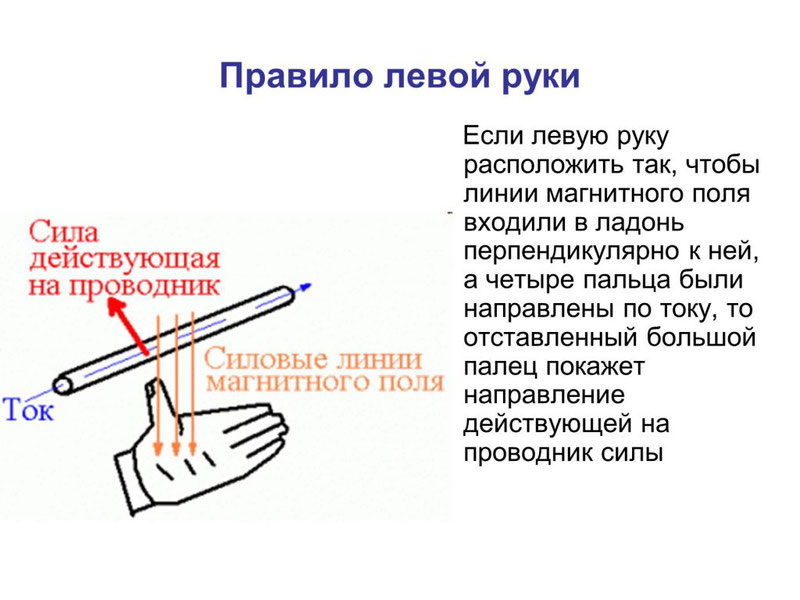
Характеристика силы действующей на проводник с током

Между полюсами подковообразного постоянного магнита подвесим на тонких и гибких проводах прямой алюминиевый проводник (рис. 4.1, а). Если через проводник пропустить ток, проводник отклонится от положения равновесия (рис. 4.1, б). Причина такого отклонения — сила, действующая на проводник с током со стороны магнитного поля. Доказал наличие этой силы и выяснил, от чего зависят ее значение и направление, А. Ампер. Именно потому эту силу называют силой Ампера.

Рис. 4.1. Опыт, демонстрирующий действие магнитного поля на алюминиевый проводник: при отсутствии тока магнитное поле на проводник не действует (а); если в проводнике течет ток, на проводник действует магнитное поле и проводник отклоняется (б)

Сила Ампера — это сила, с которой магнитное поле действует на проводник с током.

Сила Ампера прямо пропорциональна силе тока в проводнике и длине активной части проводника (то есть части, расположенной в магнитном поле). Сила Ампера увеличивается с увеличением индукции магнитного поля и зависит от того, под каким углом к линиям магнитной индукции расположен проводник.

Значение силы Ампера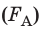Сила и закон Ампера - формулы и определение с примерами
вычисляют по формуле:

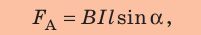
Сила и закон Ампера - формулы и определение с примерами

где 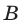Сила и закон Ампера - формулы и определение с примерами
— магнитная индукция магнитного поля; Сила и закон Ампера - формулы и определение с примерами
— сила тока в проводнике; 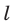Сила и закон Ампера - формулы и определение с примерами
— длина активной части проводника; 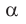Сила и закон Ампера - формулы и определение с примерами
— угол между направлением вектора магнитной индукции и направлением тока в проводнике (рис. 4.2).

Обратите внимание! Магнитное поле не будет действовать на проводник с током 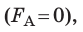Сила и закон Ампера - формулы и определение с примерами
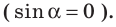
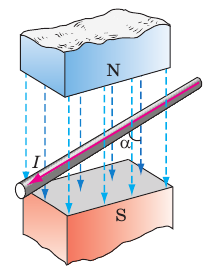
если проводник расположен параллельно магнитным линиям поля Сила и закон Ампера - формулы и определение с примерами

Сила и закон Ампера - формулы и определение с примерами

Рис. 4.2. Угол 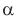Сила и закон Ампера - формулы и определение с примерами
— это угол между направлением вектора магнитной индукции и направлением тока в проводнике

Чтобы определить направление силы Ампера, используютправило левой руки:

Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера (рис. 4.3).

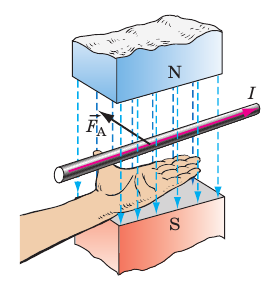
Сила и закон Ампера - формулы и определение с примерами

Рис. 4.3. Определение направления силы Ампера по правилу левой руки

Сила Лоренца

Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.

Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа– это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:

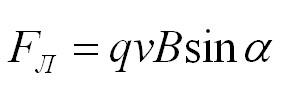
магнетизм основные понятия и формулы

Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.

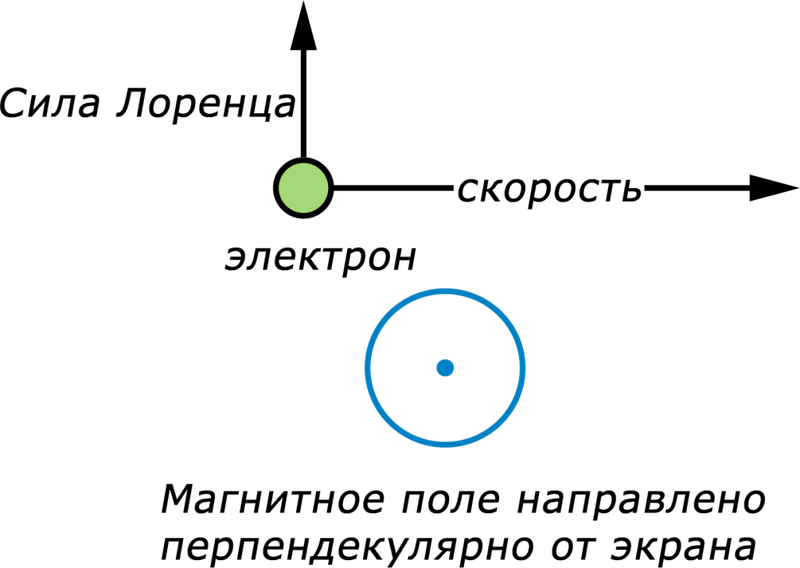
Определение направления силы Лоренца

Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:

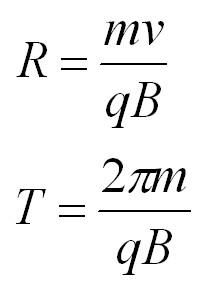
формулы по теме магнетизм

Магнитный поток

Формулы вычисления магнитной индукции Ф = BS cosα
Магнитный поток: Ф = BS cosα

Где:

  • Ф — магнитный поток (в Вб — вебер)
  • B — индукция (в Тл)
  • S — площадь рамки (в м²)
  • α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

Вектор магнитной индукции

Определение

Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как →B. Единица измерения — Тесла (Тл).

За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.

Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:

B=FAmaxIl..

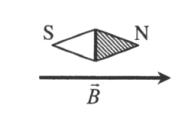
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.

Сила магнитной индукции (формулы единицы)

Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.

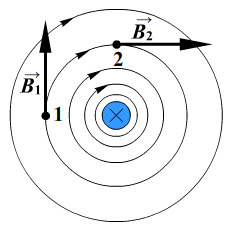
Сила магнитной индукции (формулы единицы)

Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.

Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.

Частные случаи формул для вычисления величины вектора магнитной индукции

Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):

[B=frac{{mu }_0mu }{2}frac{I}{R} qquad(6)]

где R – радиус витка.

Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:

[B=frac{{mu }_0mu }{2pi }frac{I}{r} qquad(7)]

где r – расстояние от оси проводника до точки, в которой рассматривается поле.

В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:

[B={mu }_0mu nI qquad(8)]

где n – количество витков соленоида на единицу длины; I – сила тока в витке.

Действие магнитного поля на рамку с током

Когда в наружное поле помещают рамку из проводникового материала (проволоки), и в ней создается электроток, со стороны поля на нее будет воздействовать сила Ампера. При однородности поля равнодействующая амперовых сил получится нулевой. При этом их момент таковым не будет. Вследствие этого рамка будет поворачиваться вокруг своей оси. Индукционный вектор будет образовывать прямой угол с рамочной плоскостью.

Зависимость магнитной индукции

На электромагнитную индукцию абсолютно не влияют, ни сила тока, ни длина проводника. Она находится в прямой зависимости и связи, только с магнитным полем. Таким образом, при уменьшении силы тока в проводнике, без изменения каких-либо других показателей, происходит уменьшение не индукции, прямо пропорционально связанной с силой тока, а той силы, с которой магнитное поле воздействует на проводник. При этом, значение самой магнитной индукции остается постоянным. Благодаря этим качествам, электромагнитная индукция выступает в роли количественной характеристики магнитного поля.
Индукция магнитного поля
Измерение магнитной индукции производится в теслах, по формуле: 1 Тл=1 Н/(А*м). Физическую зависимость этой величины от различных факторов, можно определить в ходе проведения несложного эксперимента. Необходимо взять весы, где на одной стороне прикрепляется проводник, а на другой стороне расположены гири. Проводник находится в постоянном электромагнитном поле, при этом, его масса и вес гирь имеют одинаковое значение.

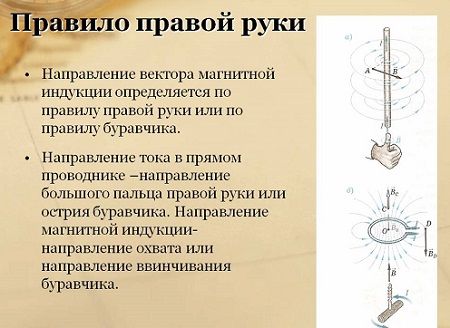
Сила магнитной индукции (формулы единицы)

После уравновешивания весов, по проводнику пропускается электрический ток. Вокруг него происходит образование магнитного поля, определяемое в соответствии с правилом правой руки. В результате, наблюдается взаимодействие полей постоянного магнита и самого проводника. При этом, равновесие весов будет нарушено. Из-за протекания тока, сторона весов с проводником начинает опускаться. Для того, чтобы вычислить силу воздействия поля на этот проводник, нужно уравновесить его с помощью гирь. Сила их тяжести рассчитывается по специальной формуле, и будет равняться силе магнитного поля, воздействующей на проводник с током. Соотношение этой силы с длиной проводника и силой тока является постоянной величиной. Данная количественная характеристика находится в зависимости только от поля и представляет собой ни что иное, как модуль вектора магнитной индукции.

Изменения в магнитосфере Земли

Характеристики земного МП меняются, в основном, вследствие того, что оно смещается относительно земного шара. Люди привыкли, что северный конец стрелы должен устремляться к северу. При обратной намагниченности диполя планеты ситуация будет противоположной. В обсерваториях фиксируются данные о состоянии МП планеты, и на их основе создаются геомагнитные карты. Они демонстрируют наличие отклонений в напряженности МП и положении силовых линий в некоторых уголках Земли. Эти явления называют магнитными аномалиями. Иногда их используют как индикаторы местоположения определенных ископаемых ресурсов.

Связь между индукцией и степенью напряженности поля широко используется в расчетах. Она позволяет вывести выражения для нахождения значения индукции в проводниках разных форм, сделанных из материалов с различными показателями магнитной проницаемости.

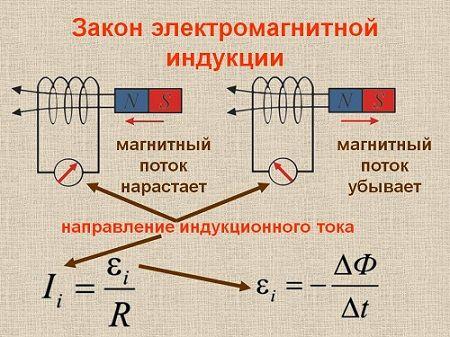
Явление электромагнитной индукции

Явление электромагнитной индукции было открыто английским ученым.

Электромагнитная индукция и магнитная индукция: какая между ними разница?

Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.

Магнитная индукция может производить постоянный магнит, но может и не производить.

Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.

В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.

Пример определения магнитного поля

Поместим в магнитное поле перпендикулярно его направлению участок прямолинейного провода длиной l, по которому проходит ток I (рис. 3).

Правило буравчика для кольцевого тока

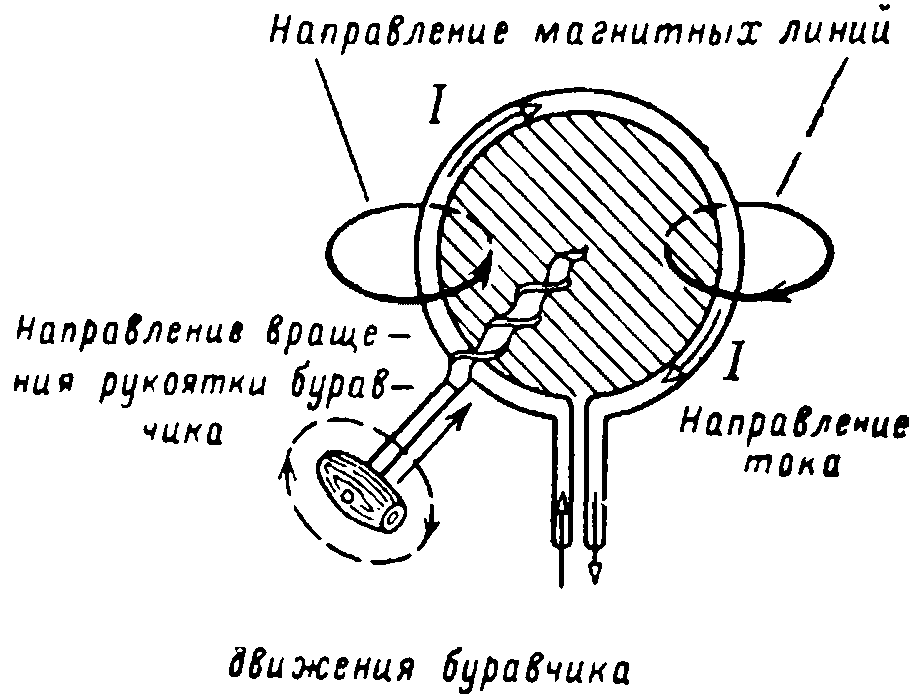
Из опыта можно убедиться, что на участок провода будет действовать сила F, по величине пропорциональная току, длине участка проводника и интенсивности магнитного поля, которая характеризуется величиной магнитной индукции В.

Таким образом, сила

F = IBl

Рис. 2. Правило буравчика для кольцевого тока.

Из написанного следует, что

B = F : (Il)

т. е. магнитная индукция измеряется отношением механической силы, действующей на участок провода, по которому проходит ток, к произведению тока и длины участка провода, причем провод должен быть расположен перпендикулярно направлению поля.

Предыдущая

ТеорияВатт – единица измерения мощности

Следующая

ТеорияЧто такое чередование фаз по цвету и как его проверить?

Источник

Добавить комментарий