Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
![]()
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Онлайн калькулятор закона Ома позволяет определять связь между силой тока, электрическим напряжением и сопротивлением проводника в электрических цепях.
Для расчета, вам понадобится воспользоваться отдельными графами:
– сила тока вычисляется в Ампер, исходя из данных напряжения (Вольт) и сопротивления (Ом);
– напряжение вычисляется в Вольт, исходя из данных силы тока (Ампер) и электрического сопротивления (Ом);
– электрическое сопротивление вычисляется в Ом, исходя из данных силы тока (Ампер) и напряжения (Вольт);
– мощность вычисляется в Ватт, исходя из данных силы тока (Ампер) и напряжения (Вольт).
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

{I = dfrac{U}{R}}
На этой странице вы можете рассчитать силу тока, напряжение и сопротивление по закону Ома для участка цепи с помощью удобного калькулятора онлайн
Закон Ома – один из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Он был открыт эмпирическим путем Георгом Омом в 1826 году.
Содержание:
- калькулятор закона Ома
- закон Ома для участка цепи
- формула силы тока
- формула напряжения
- формула сопротивления
- примеры задач
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи I= dfrac{U}{R}
Формула силы тока
Формула позволяет найти силу тока I через напряжение U и сопротивление R по закону Ома для участка цепи.
{I = dfrac{U}{R}}
I – сила тока
U – напряжение
R – сопротивление
Сила тока (I) в проводнике прямо пропорциональна напряжению (U) на его концах и обратно пропорциональна его сопротивлению (R).
Формула напряжения
Формула позволяет найти напряжение U через силу тока I и сопротивление R по закону Ома для участка цепи.

{U = I cdot R}
U – напряжение
I – сила тока
R – сопротивление
Падение напряжение на проводнике равно произведению сопротивления проводника на силу тока в нем.
Формула сопротивления
Формула позволяет найти сопротивление R через силу тока I и напряжение U по закону Ома для участка цепи.

{R = dfrac{U}{I}}
R – сопротивление
U – напряжение
I – сила тока
Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него.
Примеры задач на нахождение силы тока, напряжения и сопротивления по закону Ома
Задача 1
Найдите силу тока в участке цепи, если его сопротивление 40 Ом, а напряжение на его концах 4 В.
Решение
Воспользуемся формулой силы тока. Подставим в нее значения напряжения и сопротивления, после чего останется произвести простейший математический расчет.
I = dfrac{U}{R} = dfrac{4}{40} = 0.1 А
Ответ: 0.1 А
На этой странице есть калькулятор, который поможет проверить полученный ответ.
Задача 2
Найдите напряжение на концах нагревательного элемента, если его сопротивление 40 Ом, а сила тока 2А.
Решение
Для решения этой задачи нам пригодится формула напряжения.
U = I cdot R = 2 cdot 40 = 80 В
Ответ: 80 В
Проверим получившийся результат с помощью калькулятора .
Задача 3
Найдите сопротивление спирали, сила тока в которой 0.5 А, а напряжение на ее концах 120 В.
Решение
Чтобы найти сопротивление спирали нам потребуется формула сопротивления.
R = dfrac{U}{I} = dfrac{120}{0.5} = 240 Ом
Ответ: 240 Ом
Проверка .
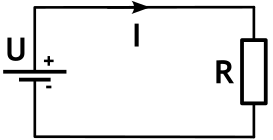
Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
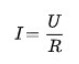
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
Общие схемы типов соединений представлены на рисунке 1.
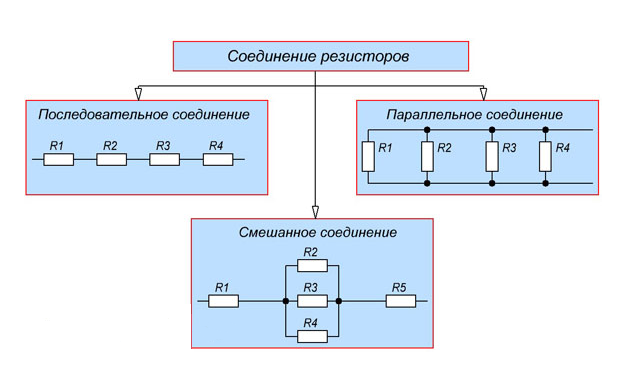
Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
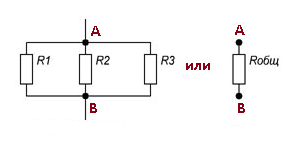
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
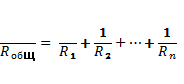
и рассчитывается по формуле:
![]()
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
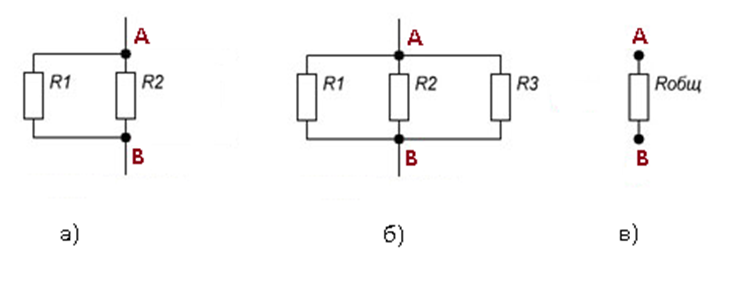
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
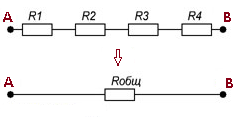
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
![]()
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
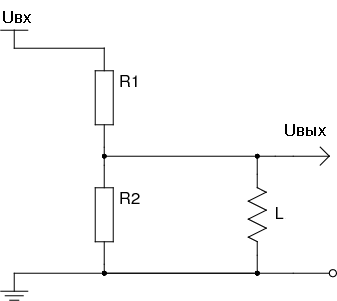
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
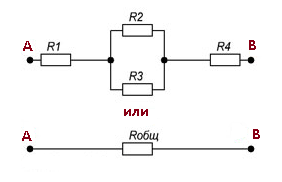
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
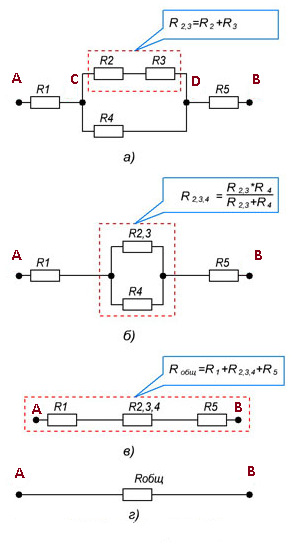
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Закон Ома
- Главная
- /
- Физика
- /
- Закон Ома
Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:
Закон Ома для участка цепи
Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).
Онлайн калькулятор
Найти силу тока
Напряжение: U =В
Сопротивление: R =Ом
Сила тока: I =
0
А

Формула
I = U/R
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока на этом участке I = 12/2= 6 А
Найти напряжение
Сила тока: I =A
Сопротивление: R =Ом
Напряжение: U =
0
В

Формула
U = I ⋅ R
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U =В
Сила тока: I =A
Сопротивление: R =
0
Ом
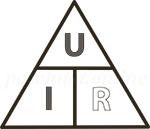
Формула
R = U/I
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление на этом участке R = 12/6 = 2 Ом
Закон Ома для полной цепи
Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Онлайн калькулятор
Найти силу тока
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
Сила тока: I =
0
А
Формула
I = ε/R+r
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока I = 12/4+2 = 2 А
Найти ЭДС
Сила тока: I =А
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
ЭДС: ε =
0
В
Формула
ε = I ⋅ (R+r)
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I =А
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =
0
Ом
Формула
r = ε/I – R
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Внутреннее сопротивление источника напряжения r = 12/2 – 4 = 2 Ом
Найти сопротивление всех внешних элементов цепи
Сила тока: I =А
ЭДС: ε =В
Внутреннее сопротивление источника напряжения: r =Ом
Сопротивление всех внешних элементов цепи: R =
0
Ом
Формула
R = ε/I – r
Пример
Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:
Сопротивление всех внешних элементов цепи: R = 12/2 – 2 = 4 Ом
