Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.
Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.
Определение
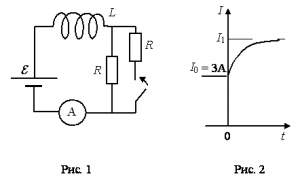
Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.
Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.
Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.
Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.
Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.
Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.
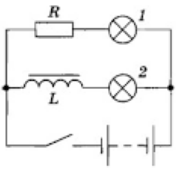
Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).
Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.
На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.
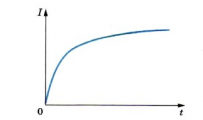
График на рисунке 4 красноречиво объясняет эффект задержки.
Обратите внимание на нелинейность изменения силы тока по времени.
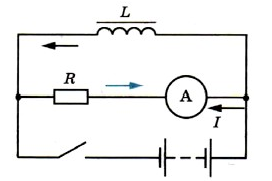
Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.
Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.
В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.
Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.
Формулы
Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.
При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:
где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.
Индуктивность
Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.
Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.
Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.
Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.
Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.
Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: Wм = LI2/2.
Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.
Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.
Примеры использования на практике
Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.
Работает этот важный узел следующим образом:
- На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
- Электрическая цепь резко обрывается специальным прерывателем.
- Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
- Искровой разряд зажигает топливную смесь, приводя в движение поршень.
В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.
Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.
В блоках питания электронной аппаратуры таким же способом убирают:
- шумы:
- пульсации;
- нежелательные частоты.
Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.
Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.
В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.
В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.
Видео в помощь
Самоиндукция
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.
Самоиндукция является частным случаем электромагнитной индукции. Оказывается, что электрический ток в контуре, меняющийся со временем, определённым образом воздействует сам на себя.
Ситуация 1 .Предположим, что сила тока в контуре возрастает. Пусть ток течёт против часовой стрелки; тогда магнитное поле этого тока направлено вверх и увеличивается (рис. 1).
Рис. 1. Вихревое поле препятствует увеличению тока
Таким образом, наш контур оказывается в переменном магнитном поле своего собственного тока. Магнитное поле в данном случае возрастает (вместе с током) и потому порождает вихревое электрическое поле, линии которого направлены по часовой стрелке в соответствии с правилом Ленца.
Как видим, вихревое электрическое поле направлено против тока, препятствуя его возрастанию; оно как бы «тормозит» ток. Поэтому при замыкании любой цепи ток устанавливается не мгновенно — требуется некоторое время, чтобы преодолеть тормозящее действие возникающего вихревого электрического поля.
Ситуация 2 . Предположим теперь, что сила тока в контуре уменьшается. Магнитное поле тока также убывает и порождает вихревое электрическое поле, направленное против часовой стрелки (рис. 2).
Рис. 2. Вихревое поле поддерживает убывающий ток
Теперь вихревое электрическое поле направлено в ту же сторону, что и ток; оно поддерживает ток, препятствуя его убыванию.
Как мы знаем, работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура — это ЭДС индукции. Поэтому мы можем дать такое определение.
Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре.
При возрастании силы тока (в ситуации 1) вихревое электрическое поле совершает отрицательную работу, тормозя свободные заряды. Стало быть, ЭДС индукции в этом случае отрицательна.
При убывании силы тока (в ситуации 2) вихревое электрическое поле совершает положительную работу, «подталкивая» свободные заряды и препятствуя убыванию тока. ЭДС индукции в этом случае также положительна (нетрудно убедиться в том, что знак ЭДС индукции, определённый таким образом, согласуется с правилом выбора знака для ЭДС индукции, сформулированным в листке «Электромагнитная индукция»).
Индуктивность
Мы знаем, что магнитный поток, пронизывающий контур, пропорционален индукции магнитного поля: . Кроме того, опыт показывает, что величина индукции магнитного поля контура с током пропорциональна силе тока:
. Стало быть, магнитный поток через поверхность контура, создаваемый магнитным полем тока в этом самом контуре, пропорционален силе тока:
.
Коэффициент пропорциональности обозначается и называется индуктивностью контура:
(1)
Индуктивность зависит от геометрических свойств контура (формы и размеров), а также от магнитных свойств среды, в которую помещён контур (Улавливаете аналогию? Ёмкость конденсатора зависит от его геометрических характеристик, а также от диэлектрической проницаемости среды между обкладками конденсатора). Единицей измерения индуктивности служит генри (Гн).
Допустим, что форма контура, его размеры и магнитные свойства среды остаются постоянными (например, наш контур — это катушка, в которую не вводится сердечник); изменение магнитного потока через контур вызвано только изменением силы тока. Тогда , и закон Фарадея
приобретает вид:
(2)
Благодаря знаку «минус» в (2) ЭДС индукции оказывается отрицательной при возрастании тока и положительной при убывании тока, что мы и видели выше.
Рассмотрим два опыта, демонстрирующих явление самоиндукции при замыкании и размыкании цепи.
Рис. 3. Самоиндукция при замыкании цепи
В первом опыте к батарейке подключены параллельно две лампочки, причём вторая — последовательно с катушкой достаточно большой индуктивности (рис. 3).
Ключ вначале разомкнут.
При замыкании ключа лампочка 1 загорается сразу, а лампочка 2 — постепенно. Дело в том, что в катушке возникает ЭДС индукции, препятствующая возрастанию тока. Поэтому максимальное значение тока во второй лампочке устанавливается лишь спустя некоторое заметное время после вспыхивания первой лампочки.
Это время запаздывания тем больше, чем больше индуктивность катушки. Объяснение простое: ведь тогда больше будет напряжённость вихревого электрического поля, возникающего в катушке, и потому батарейке придётся совершить большую работу по преодолению вихревого поля, тормозящего заряженные частицы.
Во втором опыте к батарейке подключены параллельно катушка и лампочка (рис. 4). Сопротивление катушки много меньше сопротивления лампочки.
Рис. 4. Самоиндукция при размыкании цепи
Ключ вначале замкнут. Лампочка не горит — напряжение на ней близко к нулю из-за малости сопротивления катушки. Почти весь ток, идущий в неразветвлённой цепи, проходит через катушку.
При размыкании ключа лампочка ярко вспыхивает! Почему? Ток через катушку начинает резко убывать, и возникает значительная ЭДС индукции, поддерживающая убывающий ток (ведь ЭДС индукции, как видно из (2), пропорциональна скорости изменения тока).
Иными словами, при размыкании ключа в катушке появляется весьма большое вихревое электрическое поле, разгоняющее свободные заряды. Под действием этого вихревого поля через лампочку пробегает импульс тока, и мы видим яркую вспышку. При достаточно большой индуктивности катушки ЭДС индукции может стать существенно больше ЭДС батарейки, и лампочка вовсе перегорит.
Лампочку-то, может, и не жалко, но в промышленности и энергетике данный эффект является серьёзной проблемой. Так как при размыкании цепи ток начинает уменьшаться очень быстро, возникающая в цепи ЭДС индукции может значительно превышать номинальные напряжения и достигать опасно больших величин. Поэтому в агрегатах, потребляющих большой ток, предусмотрены специальные аппаратные меры предосторожности (например, масляные выключатели на электростанциях), препятствующие моментальному размыканию цепи.
Электромеханическая аналогия
Нетрудно заметить определённую аналогию между индуктивностью в электродинамике и массой
в механике.
1. Чтобы разогнать тело до заданной скорости, требуется некоторое время — мгновенно изменить скорость тела не получается. При неизменной силе, приложенной к телу, это время тем больше, чем больше масса тела.
Чтобы ток в катушке достиг своего максимального значения, требуется некоторое время; мгновенно ток не устанавливается. Время установления тока тем больше, чем больше индуктивность катушки.
2. Если тело налетает на неподвижную стену, то скорость тела уменьшается очень быстро. Стена принимает на себя удар, и его разрушительное действие тем сильнее, чем больше масса тела.
При размыкании цепи с катушкой ток уменьшается очень быстро. Цепь принимает на себя «удар» в виде вихревого электрического поля, порождаемого убывающим магнитным полем тока, и этот «удар» тем сильнее, чем больше индуктивность катушки. ЭДС индукции может достичь столь больших величин, что пробой воздушного промежутка выведет из строя оборудование.
На самом деле эти электромеханические аналогии простираются довольно далеко; они касаются не только индуктивности и массы, но и других величин, и оказываются весьма полезными на практике. Мы ещё поговорим об этом в листке про электромагнитные колебания.
Энергия магнитного поля
Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?
Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.
Чтобы разогнать тело массы из состояния покоя до скорости
, внешняя сила должна совершить работу
. Тело приобретает кинетическую энергию, которая равна затраченной работе:
.
Чтобы после замыкания цепи ток в катушке индуктивности достиг величины
, источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).
Индуктивность служит аналогом массы
; сила тока
является очевидным аналогом скорости
. Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:
(3)
(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).
Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.
Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени
. В течение этого промежутка приращение силы тока равно
; величина
считается настолько малой, что
много меньше, чем
.
За время по цепи проходит заряд
. Вихревое электрическое поле совершает при этом отрицательную работу:
Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):
Интегрируя это от нуля до , найдем работу источника
, которая затрачивается на создание тока
:
Эта работа превращается в энергию магнитного поля созданного тока, и мы приходим к формуле (3).
Разберем задачи ЕГЭ по физике по темам: “Самоиндукция”, “Магнитный поток”, “Индуктивность”, “Электромагнитная индукция”.
Задача 1. На катушке сопротивлением 8,2 Ом и индуктивностью 25 мГн поддерживается постоянное напряжение 55 В. Сколько энергии выделится при размыкании цепи? Какая средняя ЭДС самоиндукции появится при этом в катушке, если энергия будет выделяться в течение 12 мс?
Дано:
R = 8,2 Ом;
L= 25 мГн = Гн;
t = 12 мс = 12;
Найти:
Wм – ? Eis – ?
Решение:
Решение любой задачи по физике должно начинаться с создания модели, которая поясняет ситуацию, описанную в данной задачи. В качестве модели может выступать чертеж, пояснительный рисунок, электрическая схема.
Для этой задачи необходимо начертить электрическую схему.
На схеме изображены катушка индуктивности, источник тока, поддерживающий на ней постоянное напряжение, ключ.
При замкнутом ключе через катушку протекает постоянный электрический ток, величину которого можно рассчитать, используя закон Ома для участка цепи. Катушка аналогична резистору, подключенному в эту цепь.
Энергия магнитного поля рассчитывается по формуле:
(Дж).
Стоит обратить внимание, что эта формула аналогична формуле кинетической энергии в механике:
При размыкании ключа, через катушку начинает протекать уже переменный ток. Поэтому магнитный поток, пронизывающий катушку, меняется. В самой катушке возникает ЭДС индукции, так как в ней течёт переменный ток. Тем самым, возникает явление самоиндукции.
Используя закон электромагнитной индукции в виде приходим к расчету второй неизвестной величины этой задачи:
(B).
В этих расчетах мы не учитывали знак (-), который указан в законе электромагнитной индукции. Смысл этого знака заключен в учёте правила Ленца, определяющего направление индукционного тока. Но так как о направлении индукционного тока речь в задаче не идет, то в расчетах именно получено значение модуля ЭДС самоиндукции.
Ответ: 0,56 Дж, 14 В.
Задача 2. На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 5 до 15 с. Ответ выразите в мкВ.
Решение
Решение любых графических задач необходимо начинать с «чтения» самого графика. В этой задаче рассматривается зависимость силы тока от времени в цепи, содержащей катушку индуктивности. Необходимо обратить внимание на те интервалы времени, в течение которых происходит изменение силы тока. С изменением этой величины связано изменение магнитного потока и, как следствие, возникновение ЭДС самоиндукции. Сила тока меняется в интервале от 0 до 5 с, от 5 до 10 с и от 15 до 20 с. В интервале от 10 до 15 с сила тока постоянна, изменение магнитного потока не происходит, поэтому . Для участка от 5 до 10 с надо применить закон электромагнитной индукции
.
Для модуля ЭДС самоиндукции, т.е. без учета направления индукционного тока, этот закон будет иметь вид:
.
Данные для расчета необходимо взять из графической зависимости, учитывая при этом перевод в систему «СИ».
(мкВ).
Ответ: 2 мкВ.
Задача 3. Катушка, обладающая индуктивностью , соединена с источником питания с ЭДС
и двумя одинаковыми резисторами
. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.
В момент времени ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения –
Определите значение силы тока
Внутренним сопротивлением источника тока пренебречь.
Решение
В данной задаче необходимо рассмотреть две ситуации, которые происходят до и после замыкания ключа.
- До замыкания ключа в цепи устанавливается постоянная сила тока, которая определяется законом Ома для полной цепи
. Так как по условию внутренним сопротивлением источника можно пренебречь, то
(A).
- После замыкания ключа параллельно к первому резистору подключается второй, имеющий такое же сопротивление. Тогда общее сопротивление цепи можно рассчитать, как
Таким образом, внешнее сопротивление цепи уменьшается в 2 раза.
Наличие в цепи катушки индуктивности, в которой возникает ЭДС самоиндукции, препятствует мгновенному нарастанию силы тока (по аналогии с механикой – тело большой массы не может быстро изменить свою скорость). Поэтому сила тока плавно увеличивается до некоторого значения - Так как ЭДС самоиндукции с течением времени уменьшается до нулевого значения, то ток в цепи будет возрастать в 2 раза, так как общее сопротивление уменьшается также в 2 раза.
(A).
Ответ: 6 А.
Задача 4. Катушка Проволочная рамка площадью 60 см2 помещена в однородное магнитное поле так, что плоскость рамки перпендикулярна вектору индукции . Проекция
индукции магнитного поля на нормаль к плоскости рамки изменяется во времени t согласно графику на рисунке.
Из приведенного ниже списка выберите все верные утверждения о процессах, происходящих в рамке.
- Модуль ЭДС электромагнитной индукции, возникающий в рамке, максимален в интервале от 0 до 1мс.
Ответ. Согласно закону электромагнитной индукции
Т.е. максимальное значение ЭДС индукции будет наблюдаться на интервале максимального измененияс течением времени. В интервале от 0 до 1 мс скорость изменения проекции
наибольшая.
Утверждение верное. - Магнитный поток через рамку в интервале от 2 до 4 мс равен 12 мВб.
Ответ. Формула для расчета магнитного потока имеет вид
В данном временном интервале проекцияпостоянна и равна 2 Тл.
(Вб) = 12 (мВб).
Утверждение верное. - Модуль ЭДС электромагнитной индукции, возникающей в рамке, в интервале от 4 до 6 мс равен 6 В.
Ответ. Согласно закону электромагнитной индукции
(B).
Утверждение неверное. - Модуль скорости изменения магнитного потока через рамку минимален в интервале от 0 до 1 мс.
Ответ. В той задаче изменение магнитного потока связано с изменением проекциииндукции магнитного поля. В интервале от 0 до 1 мс проекция
меняется быстрее всего, потому и изменение магнитного потока максимальное.
Утверждение неверное. - Модуль ЭДС электромагнитной индукции, возникающей в рамке, равен нулю в интервале времени от 2 до 4 мс.
Ответ. Согласно закону электромагнитной индукции
В интервале от 2 до 4 мс проекцияне изменяется, потому
и
.
Тогда в проволочной рамке ЭДС индукции не возникает.
Утверждение верное.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Самоиндукция» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
20.1. Индуктивность контура
Контур с электрическим
током I
создает магнитное поле с индукцией
.
Площадь, охватываемая контуром, равна
S.
Магнитный поток, сцепленный с этим
контуром, равен
.
Индукция
магнитного поля проводника с током
пропорциональна силе тока
.
Таким образом,
магнитный поток контура с током
пропорционален силе тока в нем
.
(20.1.1)
Коэффициент
пропорциональности называют индуктивностью
контура. Определим индуктивность контура
из формулы (20.1.1)
.
Физический смысл
индуктивности: индуктивность показывает
магнитный поток, сцепленный с контуром
при единичной силе тока в нем.
Единица измерения индуктивности в СИ:
=
=
1 Гн.
1 Генри
– индуктивность такого контура, магнитный
поток которого равен 1 вебер при силе
тока в контуре 1 ампер. Индуктивность
контура зависит от формы, размеров
контура и магнитных свойств среды.
20.2. Самоиндукция
Самоиндукция –
один из видов электромагнитной индукции.
Самоиндукция –
явление возникновения ЭДС индукции в
проводнике при изменении силы тока в
нем. С
увеличением силы тока
I
в проводнике (рис. 20.2.1) вокруг появляется
переменное магнитное поле.
Оно порождает
индукционный ток Is
(ток самоиндукции), мешающий увеличению
силы тока в цепи, т.е. направленный
противоположно току I.
Если бы ток самоиндукции был сонаправлен
с током I,
это привело бы к увеличению силы тока
I
и к возникновению нового индукционного
тока Is,
который опять увеличил бы силу тока в
цепи, и т.д. Таким образом, сила тока в
цепи должна возрастать до бесконечности
и приводить к нарушению закона сохранения
энергии.
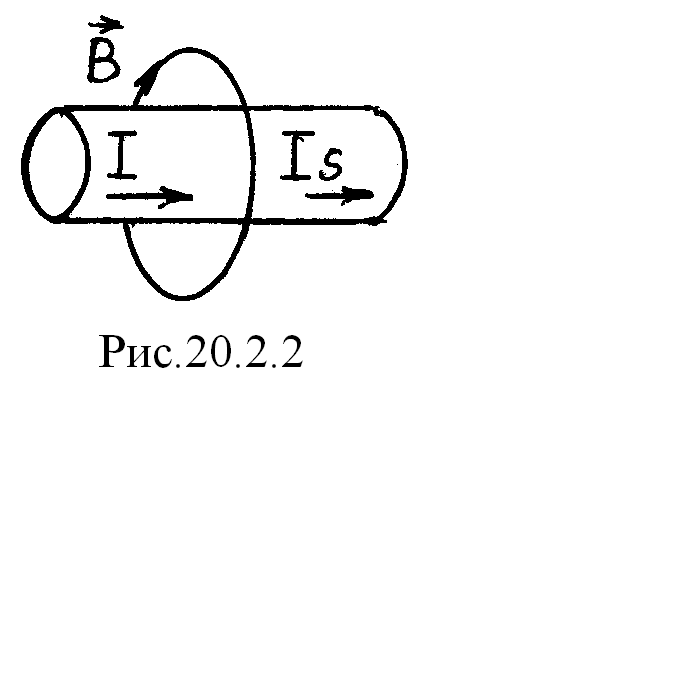
С
уменьшением силы тока в цепи
I
(рис. 20.2.2) возникает переменное магнитное
поле с индукцией
.
Оно приводит к возникновению индукционного
тока Is,
мешающего уменьшению тока
I,
поэтому ток I
в цепи и индукционный ток Is
сонаправлены.
Запишем основной
закон электромагнитной индукции
применительно к самоиндукции. В формулу
ЭДС самоиндукции
подставим выражение
магнитного потока
,
получим
.
Если контур не
деформируется, и нет ферромагнетиков,
то индуктивность L
можно считать
постоянной и вынести из-под дифференциала
.
ЭДС самоиндукции
пропорциональна
скорости изменения силы тока в цепи.
Минус в
формуле показывает, что индуктивность
контура приводит к замедлению изменения
тока в контуре. Для среднего значения
ЭДС самоиндукции можно записать выражение
.
Явление
самоиндукции противодействует изменению
магнитного потока
в проводнике с током увеличением или
уменьшение силы тока в нем.
20.3. Индуктивность катушки
Катушка длиной l
и площадью поперечного сечения S
содержит N
витков (рис. 20.3.1). Потокосцеплением ψ
катушки называют
магнитный
поток,
сцепленный
со всеми N
витками.
Свяжем потокосцепление с магнитным
потоком одного витка Фm
.
С другой стороны
для потокосцепления можно записать
формулу в виде
.
Сравнивая обе
формулы, находим выражение индуктивности
катушки
.
Магнитный
поток витка равен
,
где угол
,
т.к. вектор магнитной индукции и нормаль
к плоскости витка сонаправлены.
Учитывая, что
магнитная индукция связана с напряженностью
магнитного поля соотношением
,
а
напряженность катушки равна
,
получаем
формулу индуктивности катушки
.
Плотность витков
равна
,
тогда
индуктивность катушки можно записать
в виде
.
Объем катушки
цилиндрической формы равен
.
Окончательно
получаем формулу
индуктивности катушки
.
(20.3.1)
Из выражения
(20.3.1.) следует, что индуктивность зависит
от размеров катушки, плотности витков
и магнитных свойств среды.
Соседние файлы в предмете Физика
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 мая 2020 года; проверки требуют 7 правок.
Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре[1] (в цепи) при изменении протекающего через контур тока.
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Это явление и называется самоиндукцией. Стоит отметить, что данное понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем.
Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока[4].
При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы (переменного) тока 
.
Коэффициент пропорциональности 
Самоиндукция и синусоидальный ток[править | править код]
В случае синусоидальной зависимости тока, текущего через катушку, от времени, ЭДС самоиндукции в катушке отстаёт от тока по фазе на 


Для расчёта более или менее сложных схем, содержащих индуктивные элементы, то есть витки, катушки и т. п. устройства, в которых наблюдается самоиндукция, (особенно, полностью линейных, то есть не содержащих нелинейных элементов[5]) в случае синусоидальных токов и напряжений применяют метод комплексных импедансов или, в более простых случаях, менее мощный, но более наглядный его вариант — метод векторных диаграмм.
Заметим, что всё описанное применимо не только непосредственно к синусоидальным токам и напряжениям, но и практически к произвольным, поскольку последние могут быть практически всегда разложены в ряд или интеграл Фурье и таким образом сведены к синусоидальным.
В более или менее непосредственной связи с этим можно упомянуть о применении явления самоиндукции (и, соответственно, катушек индуктивности) в разнообразных колебательных контурах, фильтрах, линиях задержки и других разнообразных схемах электроники и электротехники.
Самоиндукция и скачок тока[править | править код]
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом (при резком размыкании) величина ЭДС самоиндукции может в этот момент значительно превышать ЭДС источника.
Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение зажигания при напряжении питающей батареи 12 В составляет 7-25 кВ. Впрочем, превышение ЭДС в выходной цепи над ЭДС батареи здесь обусловлено не только резким прерыванием тока, но и коэффициентом трансформации, поскольку чаще всего используется не простая катушка индуктивности, а катушка-трансформатор, вторичная обмотка которой как правило имеет во много раз большее количество витков (то есть, в большинстве случаев схема несколько более сложная, чем та, работа которой полностью объяснялось бы через самоиндукцию; однако физика её работы и в таком варианте отчасти совпадает с физикой работы схемы с простой катушкой).
Это явление применяется и для поджига люминесцентных ламп в стандартной традиционной схеме (здесь речь идёт именно о схеме с простой катушкой индуктивности — дросселем).
Кроме того, явление самоиндукции надо учитывать всегда при размыкании контактов, если ток течёт по нагрузке с заметной индуктивностью: возникающий скачок ЭДС может приводить к пробою промежутка между контактами и/или другим нежелательным эффектам, для подавления которых в этом случае, как правило, необходимо принимать разнообразные специальные меры, например устанавливать диод в обратном включении параллельно выводам катушки (дросселя).
См. также[править | править код]
- Взаимоиндукция
- Электрический генератор
- Катушка индуктивности
Примечания[править | править код]
- ↑ Контур может быть и многовитковым — в частности, катушкой. В этом случае, так же как и в случае одиночного контура, строго говоря, контур должен быть замкнутым (например, через вольтметр, измеряющий ЭДС), но на практике при (очень) большом количестве витков различие ЭДС в полностью замкнутом контуре и в контуре с разрывом (геометрически даже большим по сравнению с размером катушки) может быть пренебрежимо малым.
- ↑ Поскольку магнитный поток через контур пропорционален току в контуре. Для тонкого жёсткого контура (для случая которого, это утверждение и является точным) точная пропорциональность очевидна исходя из закона Био-Савара, так как согласно этому закону вектор магнитной индукции прямо пропорционален току, а поток этого вектора (что и называется магнитным потоком) через фиксированную (она не меняется при жёстком контуре) поверхность тогда тоже пропорционален току. Формально это записывается в виде равенства:
, где
— магнитный поток,
— коэффициент самоиндукции,
— ток в контуре.
- ↑ В случае сложной формы контура, например, если контур многовитковый (катушка), поверхность, ограниченная контуром (или, как говорят, «натянутая на контур») оказывается достаточно сложной, что ничуть не меняет сути описываемого явления. Для упрощения понимания случая многовитковых контуров (катушек) можно (приближённо) считать поверхность, натянутую на такой контур, состоящей из множества (стопки) поверхностей, каждая из которых натянута на свой отдельный единичный виток.
- ↑ Калашников С. Г., Электричество, М., ГИТТЛ, 1956, гл. IX «Электромагнитная индукция», п. 107 «Исчезновение и установление тока», с. 221 – 224;
- ↑ Сами индуктивные элементы являются линейными, то есть подчиняются линейному дифференциальному уравнению, приведённому в статье выше. Впрочем, это уравнение в реальности выполняется лишь приближённо, так что индуктивные элементы являются линейными также лишь приближённо (хотя иногда и с крайне хорошей точностью). Также в реальности встречаются отклонения от идеального уравнения, носящие линейный характер (например, связанные с упругими деформациями катушки в линейном приближении).
Ссылки[править | править код]
- Про самоиндукцию и взаимоиндукцию из «Школы для электрика»
Если по катушке идет переменный ток, то магнитный поток, пронизывающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идет переменный ток. Это явление называют самоиндукцией.
При самоиндукции проводящий контур выполняет двойную роль. С одной стороны, переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, появляется ЭДС индукции εis. По правилу Ленца в момент нарастания тока напряженность вихревого электрического поля направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.
Явление самоиндукции можно наблюдать в простых опытах. На рисунке представлена схема параллельного соединения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L, снабженной железным сердечником.
При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (см. график ниже).
Появление ЭДС самоиндукции при размыкании можно наблюдать в опыте с цепью, схематически показанной на следующем рисунке. При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания через гальванометр идет ток (цветная стрелка), направленный против начального тока до размыкания (черная стрелка). Сила тока при размыкании цепи может превышать силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции εis больше ЭДС ε батареи элементов.
Самоиндукция и инерция
Явление самоиндукции проще понять, проведя аналогию с инерцией в механике. Инерция приводит к тому, что под действием силы тело не мгновенно приобретает скорость, а постепенно. Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила. Точно так же за счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы не прекращаем ток сразу. Самоиндукция его поддерживает некоторое время, несмотря на сопротивление цепи.
Чтобы увеличить скорость тела, согласно законам механики нужно совершить работу. При торможении тело само совершает работу. Точно так же для создания тока нужно совершить работу против вихревого электрического поля, а при исчезновении тока это поле совершает положительную работу.
Индуктивность
Модуль вектора индукции В магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф ~ В~ I. Это дает право утверждать, что:
Φ=LI
L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком, пронизывающим этот контур. Эту величину также называют индуктивностью контура, или его коэффициентом самоиндукции.
Применив закон электромагнитной индукции, а также считая, что форма контура остается неизменной, и поток меняется только за счет изменения силы тока, получим:
εis=−ΔΦΔt=−LΔIΔt
Эта формула позволяет дать такую формулировку L, которая точно отражает суть этой величины.
Определение
Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Единица измерения индуктивности — генри (Гн). Индуктивность проводника равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции в 1 В.
Индуктивность подобна электроемкости. Она зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Пример №1. При равномерном изменении силы тока в катушке на 10 А за 0,02 с в ней возникает ЭДС самоиндукции, равная 200 В. Чему равна индуктивность катушки?
Выразим индуктивность из формулы для ЭДС самоиндукции:
L=−ΔtεisΔI=0,02·20010=−0,4 (Гн)
Знак «минус» означает, что ЭДС самоиндукции действует так, что индукционный ток препятствует изменению магнитного потока. Поэтому само значение индуктивности мы можем принять за модуль полученного результата — 0,4 Гн.
Задание EF17686
Катушка, обладающая индуктивностью L, соединена с источником питания с ЭДС ε и двумя одинаковыми резисторами R. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.
В момент времени t=0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните, почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения – I1. Определите значение силы тока I1. Внутренним сопротивлением источника тока пренебречь.
Алгоритм решения
1.Установить, какими физическими законами можно описать эксперимент.
2.Описать, что происходит до замыкания ключа.
3.Определить, что произойдет после замыкания ключа.
4.Вычислить силу тока в катушке.
Решение
На рисунке 1 изображена схема, в которой катушка индуктивности подключена последовательно к двум параллельно соединенным резистором и источнику тока. Амперметр тоже соединен с катушкой последовательно, следовательно, он определяет силу тока, проходящую через нее.
Для описания процесса можно подходит закон Ома для полной цепи и формула ЭДС самоиндукции, которая будет возникать при изменении силы тока в цепи:
IRобщ=ε+εis
εis=−LΔIΔt
До замыкания ключа общее сопротивление цепи равно сопротивлению одного резистора — R. Так как ток в этом случае постоянный, ЭДС самоиндукции отсутствует. Тогда закон Ома принимает вид:
I0=εR
Когда ключ замыкается, сопротивление в цепи уменьшается вдвое, так как подключается второй резистор:
1Rобщ=1R+1R=2R
Rобщ=0,5R
Изменение сопротивления в цепи вызывает изменение силы тока. В результате возникает ЭДС самоиндукции. Она препятствует изменению силы тока через катушку в соответствии с правилом Ленца. Поэтому сила тока через катушку при замыкании ключа не претерпевает скачка.
Постепенно ЭДС самоиндукции уменьшается до нуля, а сила тока через катушку плавно возрастает до значения:
I1=ε0,5R=2I0
На рисунке 2 начальная сила тока равна 3 А. Следовательно:
I1=3·2=6 (А)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17724
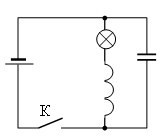
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Установить величину электромагнитного поля катушки и электрического поля конденсатора.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: r = 1 Ом.
• Емкость конденсатора: C = 2 мФ.
• Индуктивность катушки: L = 36 мГн.
• Сопротивление лампы: R = 5 Ом.
2 мФ = 2∙10–3 Ф
36 мГн = 36∙10–3 Гн
Пока ключ замкнут, через катушку L течёт ток определяемый внутренним сопротивлением источника и сопротивлением лампочки. Его можно вычислить, используя закон Ома для полной цепи:
I=εR+r
При этом конденсатор будет заряжен до напряжения U, которое определяется законом Ома для участка цепи:
U=IR
Подставив в это выражение закон Ома для полной цепи, получим:
U=εRR+r
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22=C2(εRR+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR+r)2
После размыкания ключа начинаются затухающие электромагнитные колебания, и вся энергия, запасённая в конденсаторе и катушке, выделится на лампе:
E=Wкон+Wкат=C2(εRR+r)2+L2(εR+r)2
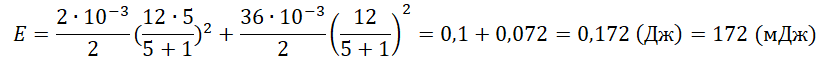
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18478
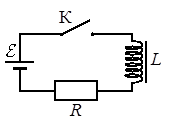
с точностью 0,01 А, представлены в таблице.
Выберите два верных утверждения о процессах, происходящих в цепи.
Ответ:
- Напряжение на резисторе в момент времени t= 1,0 c равно 1,9 В.
- Энергия катушки максимальна в момент времени t= 0 c.
- ЭДС источника тока равна 18 В.
- Напряжение на катушке максимально в момент времени t= 6,0 c.
- Модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В.
Алгоритм решения
1.Проверить истинность каждого утверждения.
2.Выбрать 2 верных утверждения.
Решение
Согласно утверждению 1, напряжение на резисторе в момент времени t = 1,0 c равно 1,9 В. Так как сила тока еще не установилась, а сопротивление источника тока пренебрежимо мало, вычислить напряжение на резисторе можно с помощью закона Ома для полной цепи:
I=ε−εisR
U=ε−εis=IR=0,19·60=11,4 (В)
Следовательно, утверждение 1 — неверно.
Согласно утверждению 2, энергия катушки максимальна в момент времени t = 0 c. Энергия катушки определяется формулой:
Wкат=LI22
Так как сила тока в начальный момент времени равна нулю, то энергия катушки в это время тоже нулевая.
Следовательно, утверждение 2 — неверно.
Согласно утверждению 3, ЭДС источника тока равна 18 В. Вычислить ЭДС источника тока можно, используя закон Ома для полной цепи в момент, когда сила тока в цепи достигнет максимального значения. В этом случае ЭДС самоиндукции будет равна 0. Тогда:
I=εR
ε=IR=0,3·60=18 (В).
Это действительно так. Следовательно, утверждение 3 — верно.
Согласно утверждению 4, напряжение на катушке максимально в момент времени t = 6,0 c. Напряжение на катушке равно разности напряжения ЭДС источника тока и напряжения на резисторе (так как они соединены последовательно):
U=ε−IR
Так как значение силы тока в момент времени t = 6,0 с максимально, то напряжение на катушке. Следовательно, утверждение 4 — неверно.
Согласно утверждению 5, модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В. Проверяя истинность утверждения 3, мы выяснили, что ЭДС источника тока равна 18 В. Следовательно, ЭДС самоиндукции равна:
εis=ε−IR
Для вычислений используем значения из таблицы для момента времени t = 2,0 с:
εis=18−0,26·60=2,4 (В)
Следовательно, утверждение 5 — верно.
Ответ: 35
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.1k