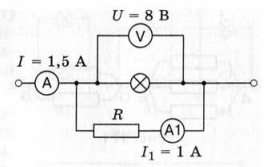
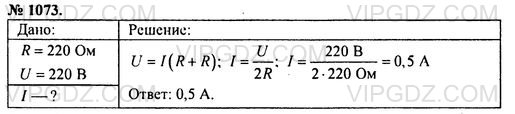Рассчитайте силу тока в лампе и её сопротивление по схеме, изображённой на рисунке 174.
рис. 174
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Параллельное соединение проводников. Номер №1122
Решение
Дано:
I = 1,5 А;
U
л
=
8
В;
I
1
=
1
А.
Найти:
R
л
− ?
I
л
− ?
Решение:
При параллельном соединении сила тока в подводящих проводах равна сумме сил тока в лампе и проводнике:
I
=
I
1
+
I
л
;
I
л
=
I
−
I
1
;
I
л
=
1
,
5
−
1
=
0
,
5
А;
Напряжение на лампе и на проводнике равно напряжению сети, т.к. лампа и проводник соединены параллельно.
U
л
=
U
1
=
U
=
8
В;
Найдем сопротивление лампы по закону Ома:
R
л
=
U
I
л
;
R
л
=
8
0
,
5
=
16
Ом.
Ответ: 0,5 А; 16 Ом.
Светило науки – 78 ответов – 1540 раз оказано помощи
P1 = 40 Вт
P2 = 75 Вт – это мощности лампочек.
Воспользуемся формулой для нахождения можности P = I*U
Т.е. P1 = I1 * U
P2 = I2 * U
Выразим I1 и I2.
I1 = P1/U
I2 = P2/U
I1 = 40/120 = 1/3 A
I2 = 75/120 = 0.625 A
У нас два неизвестных. Это I и R. Но нам дано напряжение. Существует формула, связывающая эти три характеристики. I = U/R. Отсюда R = U / I.
Вернемся к нашим основным уравнениям и вместо R будем подставлять U / I
P1 = I1^2 * U/I1 = I1*U.
P2 = I2^2 * U/I2 = I2*U.
Теперь выразим I1 и I2.
I1 = P1/U
I2 = P2/U
Отсюда I1 = 40/120 = 1/3 А
I2 = 75/120 = 0.625 А
На один вопрос задачи мы ответили. Т.е. мы нашли силу тока в каждой лампе. Теперь найдем их сопротивления.
R1 = U/ I1
R2 = U/ I2
R1 = 120 / 1/3 = 360 Ом
R2 = 120 / 0.625 = 192 Ом
Ответ: I1 = 1/3A; I2 = 0,625 A; R1 = 360 Om; R2 = 192 Om.
Смешанное соединение проводников. Расчёт электрических цепей
Повторение. Факты про последовательное и параллельное соединение проводников.
1. При последовательном соединении проводников общее сопротивление участка равно сумме сопротивлений проводников:
2. При последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи:
3. При последовательном соединении проводников сумма напряжений равна общему напряжению на участке цепи:
4. При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:
5. При параллельном соединении проводников сумма сил токов равна общей силе тока на участке цепи:
6. При параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи:
Задача 1
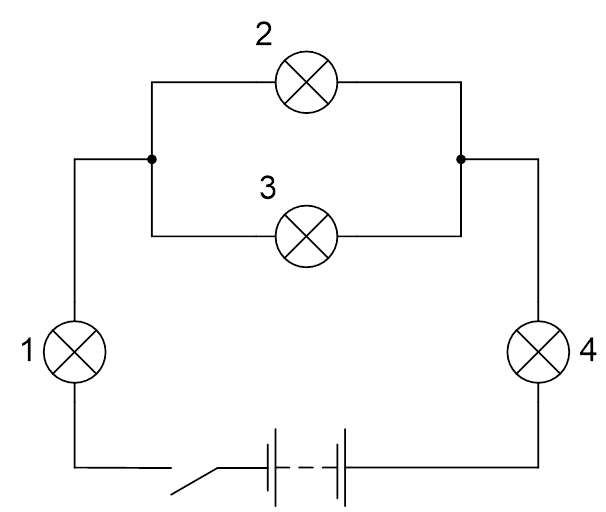
Четыре одинаковые лампы подключены к источнику постоянного напряжения (см. Рис. 1). Определите силу тока в каждой лампе, если напряжение на источнике составляет 30 В.
Дано: ;
Найти: ,
,
,
Решение
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображена электрическая цепь со смешанным соединением проводников: лампы 2 и 3 соединены параллельно, а лампы 2 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3.
Проводимость участка цепи, состоящего из ламп 2 и 3, равна:
Следовательно, сопротивление этого участка равно:
Так как лампы 1 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3, то общее сопротивление ламп будет равно:
Согласно закону Ома, сила тока всей цепи равна:
Так как при последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи, то:
Необходимо найти силу тока на лампах 2 и 3. Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:
Так как лампы 2 и 3 соединены параллельно, то напряжения на этих лампах равны:
Отсюда сила тока в каждой лампе равна:
Ответ: ;
Задача 2
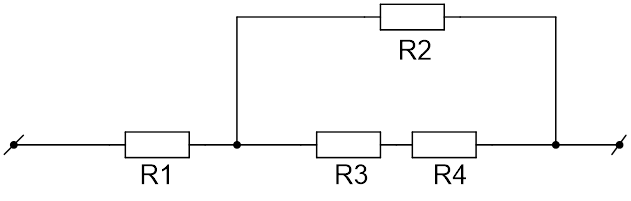
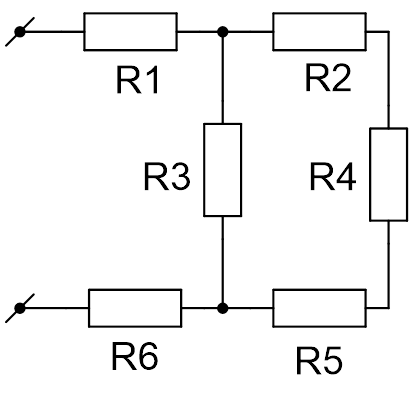
Участок цепи, который состоит из четырёх резисторов, подключён к источнику с напряжением 40 В (см. Рис. 2). Вычислите силу тока в резисторах 1 и 2, напряжение на резисторе 3. Сопротивление первого резистора равно 2,5 Ом, второго и третьего – по 10 Ом, четвёртого – 20 Ом.
Дано: ;
;
;
Найти: ,
,
Решение
Рис. 2. Иллюстрация к задаче
Через резистор течёт такой же ток, как и через весь участок (
), следовательно, согласно закону Ома:
То есть для нахождения нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором
, другая часть с резисторами
:
Резистор соединён параллельно резисторам
и
, следовательно:
Резисторы и
соединены последовательно, поэтому:
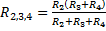
Следовательно, сопротивление всей цепи равно:
Подставим данное значение в формулу для нахождения тока в резисторе :
Так как при параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи, то:
Отсюда:
При последовательном соединении силы тока одинаковы, поэтому:
Получили систему уравнений:
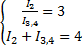
Решив эту систему получим, что:
Так как и
соединены последовательно:
Напряжение на резисторе равно:
Ответ: ;
;
Задача 3
Найдите полное сопротивление цепи (см. Рис. 3), если сопротивление резисторов ,
,
. Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
Дано: ;
;
;
Найти: ,
, ,
,
,
,
;
Решение
Рис. 3. Иллюстрация к задаче
Резисторы ,
,
соединены последовательно, поэтому сопротивление на этом участке равно:
Резистор подключён параллельно участку с резисторами
,
,
, поэтому сопротивление на участке с резисторами
,
,
,
равно:
Резисторы и
соединены с участком цепи с резисторами
,
,
,
последовательно, то есть общее сопротивление цепи равно:
Через резистор и
(
) неразветвлённой цепи течёт весь ток цепи, поэтому:
По закону Ома этот ток равен:
Общее напряжение цепи будет состоять из напряжений , так как
,
,
соединены последовательно (
, потому что
и
параллельны):
Согласно закону Ома:
Резисторы ,
,
соединены последовательно, следовательно:
Ответ: ;
;
;
Разветвление: Задача на бесконечную электрическую цепь
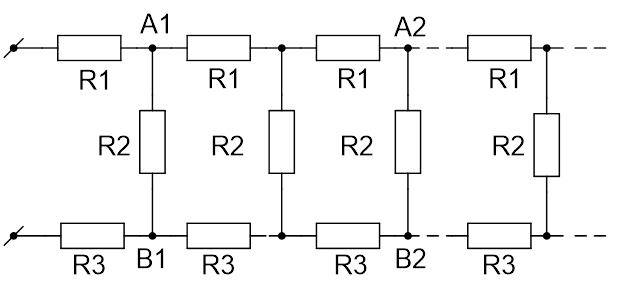
Найдите сопротивление R бесконечной цепи, показанной на рисунке 4.
Рис. 4. Иллюстрация к задаче
Решение
Поскольку рассматриваемая в задаче цепь бесконечна, удаление одной «ячейки», состоящей из резисторов и
, не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена
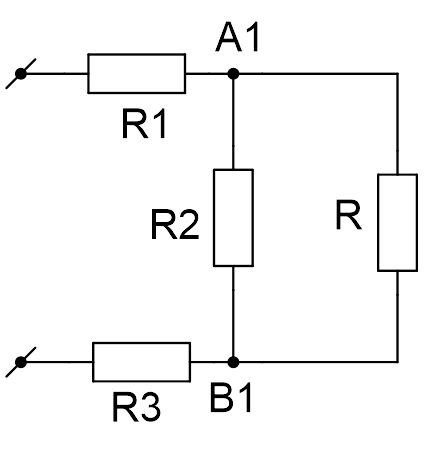
, тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. Рис. 5) и записать для неё уравнение.
Рис. 5. Иллюстрация к задаче
Получили квадратное уравнение относительно R. Решая это уравнение и отбрасывая отрицательный корень (отрицательного сопротивления не существует), получаем формулу для общего сопротивления цепи:
Проанализировав данную формулу, можно заметить, что если , то общее сопротивление цепи
. То есть резистор с малым сопротивление
практически закоротит всю последующую бесконечную цепь.
Ответ:
Итоги
Мы рассмотрели различные задачи на смешанное сопротивление проводников, а также на расчёт электрических цепей.
Разветвление: Задача из ЕГЭ
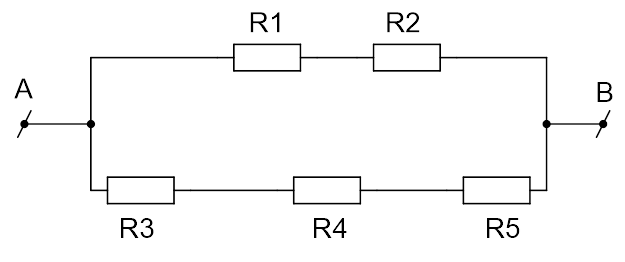
Сопротивление каждого резистора в цепи (см. Рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами AиB. Напряжение на резисторе равно 12 В. Найти напряжение между выводами схемы на участке A–B(варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В.
Дано: ;
Найти:
Решение
Рис. 6. Иллюстрация к задаче
Резисторы расположены последовательно, значит, силы тока на этих резисторах равны:
Так как, по условию, 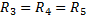
Следовательно, общее напряжения на участке, состоящем из резисторов , будет равно:
Так как участок с резисторами соединён с участком с резисторами
параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:
Ответ: г) 36 В
Данную задачу, как видим, можно решить, не зная значений сопротивления, а зная только то, что они равны. Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.
Вопросы к конспектам
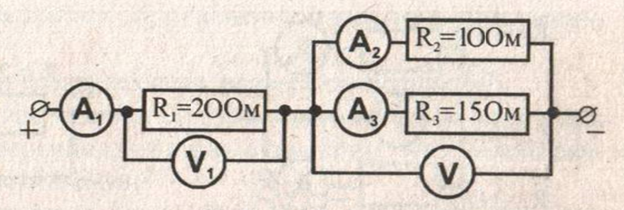
Участок электрической цепи состоит из трех сопротивлений: ;
;
(см. Рис. 7). Определите показания вольтметров
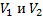
, если амперметр
показывает силу тока 2 А.
Рис. 7. Иллюстрация к задаче
Как нужно соединить четыре резистора, сопротивления которых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее сопротивление было 1 Ом?
Классы
Все классы
- 7
- 8
- 9
Предметы
Все предметы
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
войтирегистрация
- Ответкин
- Решебники
- 7 класс
- Физика
- Пёрышкин (сборник задач)
- Номер задания №1073
Назад к содержанию
ГДЗ (готовое домашние задание из решебника) на Номер задания №1073 по учебнику Физика. 7-9 классы. Сборник задач к учебникам / А.В. Перышкин – 9ое издание. Экзамен, 2013-2017г.
Условие
К сети напряжением 220 В последовательно подсоединены две лампы сопротивлением 220 Ом каждая. Найти силу тока в каждой лампе.
Решение 1
Другие задачи из этого учебника
Популярные решебники

Издатель: А. В. Перышкин, Дрофа, 2013-2019г

Издатель: А. В. Перышкин, Экзамен, 2013-2017г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО
ГДЗ и решебники
вип уровня
Условие
К сети напряжением 220 В последовательно подсоединены две лампы сопротивлением 220 Ом каждая. Найти силу тока в каждой лампе.