леня
Ученик
(189),
закрыт
7 лет назад

АС
Высший разум
(140966)
7 лет назад
Ты не поверешь, но исключительно на основе Закона О М Я: I=U/Rобщ как для всей цепи, так и для каждой ветви. Готов проверить Т В О Е решение, т. к. задача устная I1=I2=2A, I3=1.2A, I4=0.8A
леняУченик (189)
7 лет назад
R общее = 100 ом сила тока = 2 ампера. Но это общее значение.
АС
Высший разум
(140966)
Верно, но а дальше -то? Через R1 и R2 протекает ток равный 2 А, через R3 протекает равный 1.2А, а через R4 – 0.8А. Теперь тебе осталось это доказать с мощью законов физики (раздел электричество) и арифметики.
леняУченик (189)
7 лет назад
Должно получится 3 разных тока
АС
Высший разум
(140966)
Так я и их тебе и представил.
Направления
токов в ветвях выбираются произвольно
(рис. 2.5), а их величины определяются
согласно закону Ома для активного или
пассивного участков цепи:
I1
=
(E1+Uab)/R1
=
(60+120)/60 = 3 A;
I2
=
(E2
–Uab)/R2
=
(240–120)/8 = 15 A;
I3
=
– Uab/R3
=
– 120/60 = -2 A;
I4
=
Uab/R4
=
120/30 = 4 A;
I5
= Uab/R5
=
120/20 = 6 A.
3. Проверкой служит
уравнение, составленное по первому
закону Кирхгофа, при подстановке в нее
рассчитанных числовых значений токов:
– I1
+
I3
+
I2
–
I4
–
I5
=
0 или
– 3 + (-2) + 15 – 4 – 6 = 0.
Задача
2.4. Определить
показание вольтметра в электрической
цепи (рис. 2.6), используя данные таблицы
2.4.
Р ешение
ешение
С
учетом того, что ЭДС источника питания
всегда направлена от минуса к плюсу, а
заземленные узлы равно потенциальны,
предлагаемая схема может быть изображена
следующим образом (рис. 2.7)

Показание
вольтметра в такой схеме, как известно,
определяется методом междуузлового
напряжения как модуль напряжения между
двумя узлами a
и b
:

Задача
2.5. Для
электрической цепи определить ток в
ветви с резистором R4
методом активного двухполюсника (рис.
2.8), используя данные таблицы 2.5.
Р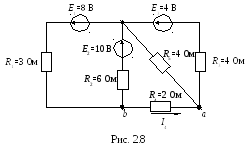 ешение
ешение
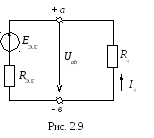
Согласно методу
активного двухполюсника (или эквивалентного
генератора МЭГ) воздействие всех
источников питания на ветвь с неизвестным
током заменяется воздействием одного,
так называемого «эквивалентного»,
генератора, который на эквивалентной
схеме замещения (рис.2.9) соединяется
последовательно с исследуемой ветвью:
![]()
+
–
![]() ,
,
где
![]() –
–
напряжение между зажимами эквивалентного
генератора а
и b
в режиме холостого хода;
![]() –
–
сопротивление между зажимами а
и b
пассивного двухполюсника, полученного
из схемы, соответствующей холостому
ходу эквивалентного генератора.
В
рассматриваемом случае схема,
соответствующая холостому ходу
эквивалентного генератора, выглядит
так (рис. 2.10.)
Пассивный
двухполюсник (рис. 2.11) образуется при
исключении источников питания, по
сохранения их внутренних сопротивлений
(в данном случае нулевых).
1.
Определение ЭДС эквивалентного генератора
(рис. 2.10). В двухконтурной схеме
определяются токи в ветвях и далее на
основе двух законов Кирхгофа в контуре
aсb
расcчитывается
![]() :
:
I1хх
= (-E1
–
E2)/(R1
+ R2)
= ( – 6 – 10)/(3 + 6)= -2 A,
I3хх=
– E3
/(R3
+ R5)
= – 4/(4 + 4)= – 0,5 A,
–E2
= R5I3хх
+ R2I1хх
–![]()
или
![]()
= E2
+ R5I3хх
+ R2I1хх
=10 + 4(-0,5) + 6(-2) = – 4 В.
Таким
образом,
![]() =
=
– 4 В.
2.
Определение внутреннего сопротивления
эквивалентного генератора (рис. 2.11). Как
видно, R1
и R2
соединены параллельно друг другу, R5
и R3
–аналогично,
между собой они соединены последовательно,
поэтому:
![]()
 =
=
R1R2/(R1
+
R2)
+R3R5/(R3
+
R5)
= 36/(3+6)
+ 44/(4+4)
= 4 Ом,
или RЭ.Г.
=
![]()
= 4 Ом.
3. Определение тока
в исследуемой ветви (рис. 2.9)
I4
= –EЭ.Г.
/(RЭ.Г.
+ R4)
= – (–4) /(4 + 2) = 2/3 A.
Задача
2.6. В
электрической цепи (рис.2.12) определить
ток в ветви с линейным элементом R5,
используя данные таблицы 2.6. Вольтамперная
характеристика (ВАХ) нелинейного элемента
(НЭ) приведена на рис. 2.13.

Решение
1
 .
.
Определение параметров эквивалентного
генератора
Для
определения тока в одной ветви схемы
(в рассматриваемом случае, в ветви с
НЭ) используется метод эквивалентного
генератора. Эквивалентная схема замещения
исходной цепи, а так же схемы эквивалентного
генератора на холостом ходу и пассивного
двухполюсника приводится на рис. 2.14,
2.15 и 2.16.

А налогично
налогично
решению предыдущей задачи ЭДС
эквивалентного генератора (рис. 2.14)
ЕЭ.Г.
=![]() ,
,
причем (рис. 2.15)
–![]() +
+
R2![]() –
–
R4![]() =
=
0,
то есть EЭ.Г.=
![]() =+
=+
R2![]() –
–
R4![]() .
.
Токи
![]()
и
![]() определяются
определяются
любым известным методом, например,
![]() =
=
– E
/
(R1
+ R2)
= -120 / (20 + 30) = -2,4 A;
![]() =
=
–E
/ (R3
+ R4)
= -120 / (10 + 40) = -2,4 A.
Тогда
EЭ.Г.
=![]() =
=
30(-2.4)
– 40
(-2,4) = 24 В, внутреннее сопротивление
эквивалентного генератора (рис. 2.16)
![]() .
.
Т аким
аким
образом, внешняя характеристика
эквивалентного генератора
Uab
=
EЭ.Г.–RЭ.Г.I
=24 – 20I
имеет вид (рис. 2.17)
Соседние файлы в папке Примеры решения задач
- #
- #
- #
- #
- #
- #
- #
Расчет электрических цепей
Содержание
- 1 Категории элементов и устройств электрической цепи
- 2 Метод расчета по законам Ома и Кирхгофа
- 2.1 Закон Ома для участка цепи
- 2.2 Закон Ома для полной цепи
- 2.3 Первый закон Кирхгофа
- 2.4 Второй закон Кирхгофа
- 3 Метод преобразования электрической цепи
- 3.1 Расчет цепи с одним источником питания
- 3.2 Расчет разветвленной электрической цепи с несколькими источниками питания
- 4 Дополнительные методы расчета цепей
- 4.1 Метод узлового напряжения
- 4.2 Метод эквивалентного генератора
- 5 Видео
Для вычисления рабочих параметров радиотехнических устройств и отдельных схем применяют специальные методики. После изучения соответствующих технологий результат можно узнать быстро, без сложных практических экспериментов. Корректный расчет электрических цепей пригодится на стадии проектирования и для выполнения ремонтных работ.
Задачи на расчет электрических цепей решают с применением типовых алгоритмов
Категории элементов и устройств электрической цепи
Для условного изображения определенной цепи применяют специальную схему. Кроме отдельных физических компонентов, она содержит сведения о направлении (силе) токов, уровнях напряжения и другую информацию. Качественная модель показывает реальные процессы с высокой точностью.
Компоненты электрической цепи:
- источник постоянного или переменного тока (Е) – аккумулятор или генератор, соответственно;
- пассивные элементы (R) – резисторы;
- компоненты с индуктивными (L) и емкостными (С) характеристиками;
- соединительные провода.
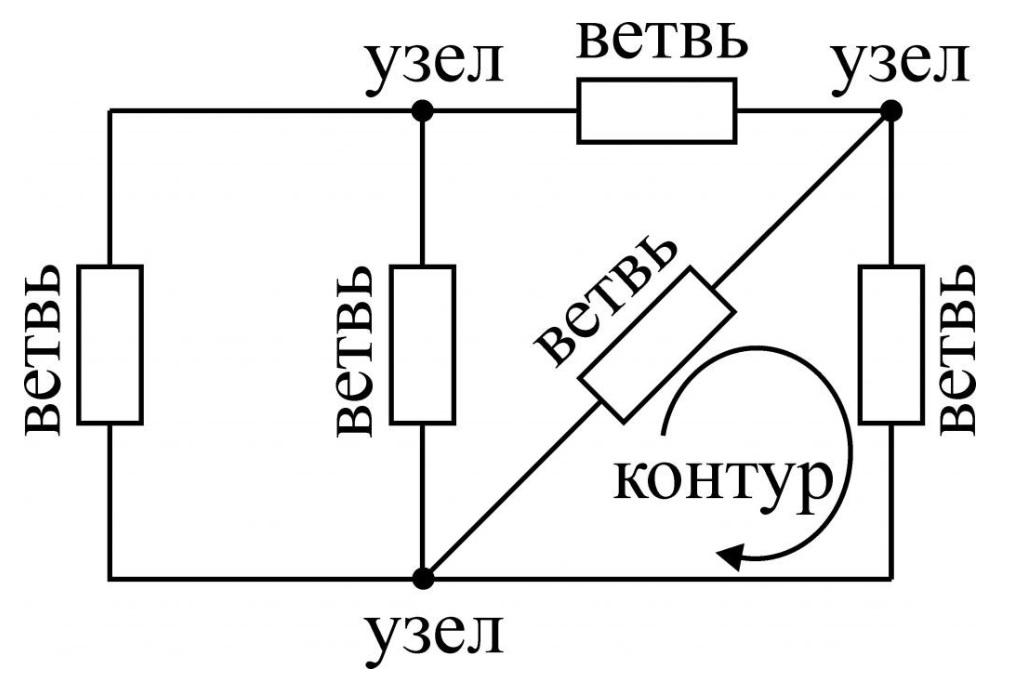
Типовые названия
На рисунке обозначены:
- ветви – участки цепи с одним током;
- узлы – точки соединения нескольких ветвей;
- контур – замкнутый путь прохождения тока.
При решении практических задач выясняют, как узнать силу тока в отдельных ветвях. Полученные значения используют для анализа электрических параметров. В частности, можно определять падение напряжения на резисторе, мощность потребления подключенной нагрузки. При расчете цепей переменного тока приходится учитывать переходные энергетические процессы, влияние частоты.
Метод расчета по законам Ома и Кирхгофа
До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:
- последовательное – увеличивает общее сопротивление;
- параллельное – распределяет токи по нескольким ветвям, что улучшает проводимость.
Закон Ома для участка цепи
Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (< 1 мм), высокая плотность тока в соответствующем поперечном сечении быстро увеличит температуру вплоть до теплового разрушения материала с разрывом цепи. Этот пример демонстрирует функциональность обычного плавкого предохранителя.
Подключив нагрузку, можно мультиметром проверить напряжение. Значение этого параметра остается неизменным. Если известно сопротивление (пример – R = 50 Ом), применение закона Ома (I = U/ R) поможет рассчитать ток:
I = 12/ 50 = 0,24 А.
По вычисленному значению с использованием формулы быстро определяется мощность:
P = I2 *R = U2/ R = 0,0576 * 50 = 2,88 Вт.
К сведению. Результат показанного расчета пригодится для поиска подходящего резистора. Следует делать запас в сторону увеличения. По стандарту серийных изделий подойдет элемент с паспортной номинальной мощностью 5 Вт.
На практике приходится решать более сложные задачи. Так, при значительной длине линии нужно учесть влияние соединительных ветвей цепи. Через стальной проводник ток будет протекать хуже, по сравнению с медным аналогом. Следовательно, надо в расчете учитывать удельное сопротивление материала. Короткий провод можно исключить из расчета. Однако в нагрузке может быть два элемента. В любом случае общий показатель эквивалентен определенному сопротивлению цепи. При последовательном соединении Rэкв = R1 + R2 +…+ Rn. Данный метод пригоден, если применяется постоянный ток.
Закон Ома для полной цепи
Для вычисления такой схемы следует добавить внутреннее сопротивление (Rвн) источника. Как найти ток, показывает следующая формула:
I = U/ (Rэкв + Rвн).
Вместо напряжения (U) при расчетах часто используют типовое обозначение электродвижущей силы (ЭДС) – E.
Первый закон Кирхгофа
По классической формулировке этого постулата алгебраическая сумма токов, которые входят и выходят из одного узла, равна нулю:
I1 + I2 + … + In = 0.
Это правило действительно для любой точки соединения ветвей электрической схемы. Следует подчеркнуть, что в данном случае не учитывают характеристики отдельных элементов (пассивные, реактивные). Можно не обращать внимания на полярность источников питания, включенных в отдельные контуры.
Чтобы исключить путаницу при работе с крупными схемами, предполагается следующее использование знаков отдельных токов:
- входящие – положительные (+I);
- выходящие – отрицательные (-I).
Второй закон Кирхгофа
Этим правилом установлено суммарное равенство источников тока (ЭДС), которые включены в рассматриваемый контур. Для наглядности можно посмотреть, как происходит распределение контрольных параметров при последовательном подключении двух резисторов (R1 = 50 Ом, R2 = 10 Ом) к аккумуляторной батарее (Uакб = 12 V). Для проверки измеряют разницу потенциалов на выводах пассивных элементов:
- UR1 = 10 V;
- UR1 = 2 V;
- Uакб = 12 V = UR1 + UR2 = 10 + 2;
- ток в цепи определяют по закону Ома: I = 12/(50+10) = 0,2 А;
- при необходимости вычисляют мощность: P = I2 *R = 0,04 * (50+10) = 2,4 Вт.
Второе правило Кирхгофа действительно для любых комбинаций пассивных компонентов в отдельных ветвях. Его часто применяют для итоговой проверки. Чтобы уточнить корректность выполненных действий, складывают падения напряжений на отдельных элементах. Следует не забывать о том, что дополнительные источники ЭДС делают результат отличным от нуля.
Метод преобразования электрической цепи
Как определить силу тока в отдельных контурах сложных схем? Для решения практических задач не всегда нужно уточнение электрических параметров на каждом элементе. Чтобы упростить вычисления, используют специальные методики преобразования.
Расчет цепи с одним источником питания
Для последовательного соединения пользуются рассмотренным в примере суммированием электрических сопротивлений:
Rэкв = R1 + R2 + … + Rn.
Контурный ток – одинаковый в любой точке цепи. Проверять его можно в разрыве контрольного участка мультиметром. Однако на каждом отдельном элементе (при отличающихся номиналах) прибор покажет разное напряжение. По второму закону Кирхгофа можно уточнить результат вычислений:
E = Ur1 + Ur2 + Urn.
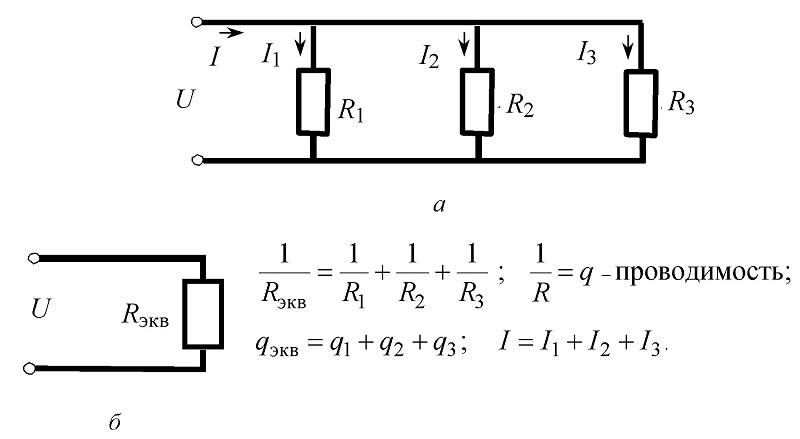
Параллельное соединение резисторов, схемотехника и формулы для расчетов
В этом варианте в полном соответствии с первым постулатом Кирхгофа токи разделяются и соединяются во входных и выходных узлах. Показанное на схеме направление выбрано с учетом полярности подключенного аккумулятора. По рассмотренным выше принципам сохраняется базовое определение равенства напряжений на отдельных компонентах схемы.
Как найти ток в отдельных ветвях, демонстрирует следующий пример. Для расчета приняты следующие исходные значения:
- R1 = 10 Ом;
- R2 = 20 Ом;
- R3= 15 Ом;
- U = 12 V.
По следующему алгоритму будут определяться характеристики цепи:
- базовая формула для трех элементов:
Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.
- подставив данные, вычисляют Rобщ = 10 * 20 * 15 / (10*20 + 20*15 +10*15) = 3000 /(200+300+150) = 4,615 Ом;
- I = 12/ 4,615 ≈ 2,6 А;
- I1 = 12/ 10 = 1,2 А;
- I2 = 12/20 = 0,6 А;
- I3 = 12/15 = 0,8 А.
Как и в предыдущем примере, рекомендуется проверить результат вычислений. При параллельном соединении компонентов должно соблюдаться равенство токов на входе и суммарного значения:
I = 1,2 + 0,6 + 0,8 = 2,6 А.
Если применяется синусоидальный сигнал источника, вычисления усложняются. При включении в однофазную розетку 220V трансформатора придется учитывать потери (утечку) в режиме холостого хода. В этом случае существенное значение имеют индуктивные характеристики обмоток и коэффициент связи (трансформации). Электрическое сопротивление (ХL) зависит от следующих параметров:
- частоты сигнала (f);
- индуктивности (L).
Вычисляют ХL по формуле:
ХL = 2π * f * L.
Чтобы находить сопротивление емкостной нагрузки, подойдет выражение:
Хc = 1/ 2π * f * C.
Следует не забывать о том, что в цепях с реактивными компонентами сдвигаются фазы тока и напряжения.
Расчет разветвленной электрической цепи с несколькими источниками питания
Пользуясь рассмотренными принципами, вычисляют характеристики сложных схем. Ниже показано, как найти ток в цепи при наличии двух источников:
- обозначают компоненты и базовые параметры во всех контурах;
- составляют уравнения для отдельных узлов: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
- в соответствии со вторым постулатом Кирхгофа, можно записать следующие выражения для контуров: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=-I5*(R02+R5+R6)-I4*R4;
- проверка: d) I3+I6-I1=0, внешний контур E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.
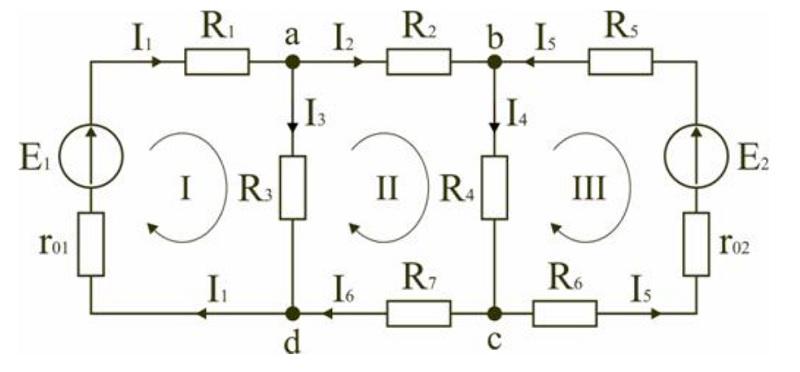
Пояснительная схема к расчету с двумя источниками
Дополнительные методы расчета цепей
В зависимости от сложности устройства (электрической схемы), выбирают оптимальную технологию вычислений.
Метод узлового напряжения
Основные принципы этого способа базируются на законе Ома и постулатах Кирхгофа. На первом этапе определяют потенциалы в каждом узле. Далее вычисляют токи в отдельных ветвях с учетом соответствующих электрических сопротивлений (отдельных компонентов или эквивалентных значений). Проверку делают по рассмотренным правилам.
Метод эквивалентного генератора
Эта технология подходит для быстрого расчета тока в одной или нескольких контрольных ветвях.

Графическое пояснение
В данной методике общую цепь представляют в виде источника тока с определенным напряжением и внутренним сопротивлением. Далее выполняют вычисления по контрольной ветви с применением стандартного алгоритма.
Видео


Первый и второй законы Кирхгофа
Содержание
- 1 Первый закон Кирхгофа
- 2 Второй закон Кирхгофа
- 3 Значение правил Кирхгофа
- 4 Законы для магнитного поля
- 5 Видео по теме
Некоторые электрические цепи можно изобразить в виде простого контура, содержащего источник питания и небольшое количество деталей — резисторов, конденсаторов или других. Но существуют и большие схемы, включающие в себя несколько замкнутых ветвей. В этих случаях важно точно рассчитать электрические параметры на любом рассматриваемом участке. Законы Кирхгофа позволяют их определить путём составления и решения нескольких простых уравнений.

Первый закон Кирхгофа
Закон Ома описывает взаимосвязь между напряжением, сопротивлением и силой тока в простых одноконтурных цепях. На практике чаще встречаются сложные разветвленные цепи, состоящие из нескольких контуров и многих узлов, которые невозможно описать, применяя стандартные правила для расчета последовательных и параллельных цепей.

Определить напряжение и силу тока в разветвленных цепях позволяют правила Кирхгофа, которые в технической литературе обычно называют законами Кирхгофа. Хотя более корректным следует считать название «правила», поскольку они не являются фундаментальными законами природы. Например, первое правило Кирхгофа вытекает из закона сохранения заряда. Оно гласит, что сумма всех токов в каждом узле электроцепи равна нулю.

Формулировка закона требует уточнения следующих терминов:
- Узел — это определённое место на схеме, в котором сходится 3 или большее количество проводов. Узлами можно назвать точки, расположенные на протяжении 1 провода, если в этих местах подсоединены ещё провода.
- Движение тока, направленного к определённому узлу, условно называют положительным, противоположное — отрицательным.

Закон Кирхгофа, если говорить простыми словами, может быть сформулирован так: сколько токов втекает в узел, столько же и вытекает. Это свидетельствует о непрерывности тока для электрической цепи. Поэтому существует ещё одна формула, выражающая первое правило Кирхгофа:

Здесь с одной стороны знака равенства рассматриваются токи, входящие в определённый узел, а с другой — выходящие.
При использовании первого закона Кирхгофа для цепи переменного тока применяются мгновенные значения напряжений, которые принято обозначать буквой İ. Расчеты в этом случае проводятся по уравнению, представленному в комплексной форме.

Второй закон Кирхгофа
Когда рассматривается электрическая цепь, подключённая к источнику тока, в каждой её точке имеется определённый потенциал. Разность между ними создаёт электрическое поле, которое вызывает перемещение зарядов.
Цепь представляет собой замкнутый контур, по которому движутся электроны. Электрическое поле выполняет определённую работу по их перемещению. Каждый заряд перемещается по цепи, а затем под действием ЭДС источника замыкает круг.
Второй закон Кирхгофа гласит, что работа по перемещению заряда вдоль любого контура электроцепи с возвратом в начальную точку равна нулю. В этой формулировке подразумевается любой замкнутый контур, причем как тот, который включает источник питания, так и о тот, где его нет.
Работа электрического поля при перемещении заряда в рассматриваемом случае представляет собой сумму падений напряжения для каждого из участков контура. Таким образом, второе правило или закон Кирхгофа гласит, что сумма напряжений всех ветвей в контуре равняется нулю. Это можно выразить в виде следующего уравнения:

Если напряжение и направление обхода контура совпадают, то U записывают со знаком плюс, в противном случае — со знаком минус. Направление обхода выбранного контура может быть определено произвольным образом. Второе правило Густава Кирхгофа его не регламентирует.
Если в контуре есть один или несколько источников питания, то формулу можно выразить следующим образом:

Здесь имеется p источников питания, q участков контура. Сумма всех ЭДС имеющихся источников питания равна сумме падений напряжения.
Значение правил Кирхгофа
Законы Кирхгофа выражают фундаментальные принципы физики. Их формулировки кажутся очень простыми и очевидными. Но на самом деле они представляют собой метод, позволяющий рассчитать электрические параметры сетей очень сложной конфигурации.
С помощью законов Кирхгофа можно составить систему независимых уравнений для расчета параметров электрической цепи. Важно, чтобы их количество было не меньше, чем число параметров, которые необходимо определить.

На приведённом рисунке представлена электроцепь, для которой будет проводиться расчёт. Используя первый закон или правило Кирхгофа, для узла A можно записать:
I = I1 + I2.
В этот узел входят два тока, а выходит один. Далее необходимо применить второе правило. Для этого можно выбрать внешний контур. Видно, что здесь имеется два источника тока и два резистора. Поэтому будут получены уравнения:

Здесь приведены 2 эквивалентные формулы. В левой части равенства учтены электродвижущие силы двух источников тока, в правой — падение напряжения на обоих резисторах с учётом направления токов. Ещё одно уравнение можно получить из 2 закона при обходе по правому внутреннему контуру:

В результате получена система, включающая в себя три уравнения с тремя неизвестными:

Используя конкретные данные, можно подставить в систему уравнений численные значения и найти, чему равна сила тока для каждой ветви, относящейся к узлу A. При расчётах важно понимать, что при достаточно сложной конфигурации электроцепи иногда бывает непросто определить направление силы тока для каждой ветви.
Первый и второй законы Густава Кирхгофа позволяют точно определить не только величину тока, но и его знак. Если в приведённом примере после вычисления искомых значений с помощью представленной системы уравнений окажется, что ток с индексом 2 принимает отрицательное значение, то это означает, что на самом деле он имеет направление, противоположное указанному на рисунке.
Законы для магнитного поля
Правила Кирхгофа нашли свое применение и при расчете магнитных цепей. Первый закон Кирхгофа для магнитной цепи выглядит так:

Проще говоря, сумма всех магнитных потоков, проходящих через узел, равняется нулю.
Второй закон в применении к магнитным полям звучит следующим образом: «Сумма магнитодвижущих сил в контуре равняется сумме магнитных напряжений». Формула выглядит так:

Кирхгофом выведены правила, имеющие абсолютный прикладной характер. С их помощью можно решать практические вопросы в электротехнике. Широкое применение этих правил объясняется простотой формулировки уравнений и возможностью их решения с применением стандартных способов линейной алгебры.
Видео по теме
Если же
известно падение напряжения в какой-нибудь части цепи и известно ее сопротивление, то, разделив падение напряжения на сопротивление этой части цепи, мы получим силу тока
в амперах. Например, если по части цепи с сопротивлением в 5 ом
проходит ток силою в 10 ампер, то падение напряжения в этой части цепи равно:
1Х£= ЮХ5==50 вольт.
И
наоборот, если “известно, что падение напряжения па какой-нибудь части
цепи равно 50 вольт, а сопротивление этой части цепи равно 5 омам, то не трудно
найти и силу тока в цепи:
/= 50 : 5 = 10
ампер.
Пример 28.
Имеется разветвление (рис. 93), состоящее из двух ветвей, причем сопротивление
одной ветви равно 7 омам, а другой 3 омам. Найти силу тока в каждой ветви, если сила тока до разветвления равна 20
амперам.
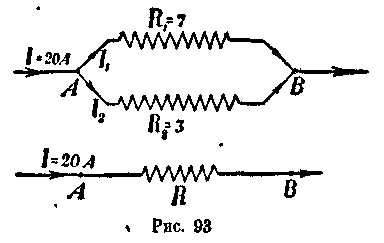 Решение. Дано: Я,=7 омам. й, = 3 омам и / = 20
Решение. Дано: Я,=7 омам. й, = 3 омам и / = 20
амперам.
Найти ток?, ltи /,.
Заменим
обе ветви с сопротивлениями Riи Яа одной ветвью ‘ с сопротивлением Я, равным сопротивлению разветвления.
При этом
сопротивление разветвления
равно (см. § 32):
Д,ХЙ^7ХЗ 21
I
Ток такой
же силы проходит по проводнику R(рис. 9°,
внизу), и следовательно, падение
напряжения в этом проводнике между точками А и В равно:
/ х R — 20 X 2,1 = 42 вольта.
Но проводник Rзаменяет собой разветвление;
следовательно, напряжение
между точками А и В (рис. 93, вверху) также должно быть равно 42 вольтам. А потому
падение напряжения в проводнике Я, равно 42 вольтам и падение напряжения в
проводнике й, также равно 42 вольтам.
Теперь нам
известно падение напряжения в проводнике Rtи известно его сопротивление; следовательно, сила тока в этом проводнике равна:
It=42:7 = 6 ампер.
Падение напряжения
в другой ветви, равно 42 вольта и сопротивление ее равно 3 омам, а потому сила
тока в этой ветви равна;
/* = 42.:3 = 14
ампер.
Для проверки следует взять сумму токов,
проходящих по ветвям, которая
должна равняться
силе тока в неразветвленной части цепи.
В нашем примере эта
сумма равна-
6 +14 = 20 ампер.
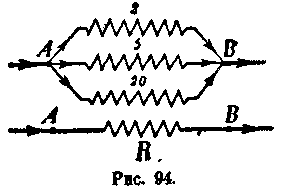 -Пример 29. Имеется разветвление, состоящее из трех ветвей
-Пример 29. Имеется разветвление, состоящее из трех ветвей
(рис. 94); сопротивление одной ветви равно 2 омам, второй — 5 омам третьей — 20
омам. Найти сумму тока в каждой из трех
ветвей, если до разветвления сила тока равна 15 амперам.
Решение. Проводимость первой ветви
равна-проводимость второй ветвиравна-4-и проводимость третьей ветвя равна
Общая проводимость
разветвления равна сумме проводимости ветвей;)
Общее сопротивление
разветвления равно:
R= 1- 3/4- ома. Падение напряжения между точками А ж В равно:
/ X R=15 X 1 1/3- = 15 х4 =20 вольт.
Сила тока в первой
ветви будет равна:
/=20:2 = 10 амперам.
Сила тока во второй ветви будет равна:
/2=20/5 = 4
амперам. Сила тока в третьей ветви будет
равна:
/= 20:20 = 1 амперу.
Вопросы для
повторения 2-й главы.
Что принято считать
за направление электрического тока?
1.
Как
устроен гальванический элемент?
2.
Какими единицами измеряются электродвижущая сила сила тока и электрическое сопротивление проводника?
3.
Что
называют силой тока?
4.
Что
называется падением напряжения в проводнике?
5.
Как
выражается закон Ома для участка электрической цепи?
6.
Как
выражается закон Ома для всей цепи?
7.
Указать
зависимость между электродвижущей силой и напряжением на зажимах элемента.
8.
Чему
равна электродвижущая сила батареи и ее внутреннею сопротивление, если элементы
соединены друг с другом последовательно?
10.Определить
электродвижущую силу батареи элементов, соединенных между собой параллельно, если дано значение
электродвижущей силы каждого отдельного элемента.
11.Определить
электродвижущую силу батареи элементов, соодиионных в группы.
12.Объяснит причину
появления электродвижущей силы поляризации электродов.
13.Определить общее сопротивление, состоящее
из нескольких Сопротивлений, соединенных
между собой последовательно?
14.Что называется электрической проводимостью
проводника?
15.Что называется сопротивлением разветвления?
16.Как войти значения
силы тока в ветвях, если дано значение тока в неразветвленной части цепи? j
ГЛАВA3
. ЭЛЕКТРИЧЕСКОЕ
СОПРОТИВЛЕНИЕ.
§ 34. Зависимость сопротивления от
размеров я материала
проводника.
Чем длиннее проводник, тем больше препятствие оказывает он прохождению
электрического тока, а потому и электрическое сопротивление его будет больше. Если ваять
несколько медных проводников одинакового поперечного сечения, но разной длины,
например, води длина одного проводника будет больше длины другого в 2 раза, то и
сопротивление его будет больше также в 2 раза; если же один проводник будет
длиннее другого в 10 раз, то и сопротивление его будет в 10 раз больше.
Сопротивление проводника зависит не только от его длины, но также и от площади
его поперечного сечения. Если взять несколько проводников одинаковой длины, но разной толщины, то
электрическое сопротивление их будет
неодинаково: чем тоньше проводник, тем большее
препятствие оказывает он прохождению электрического тока, а потому и электрическое сопротивление его будет
больше. И если’ один проводник имеет
площадь поперечного сечения в два раза большую другого, то электрическое сопротивление его будет в два раза меньше.
Итак, электрическое сопротивление проводника одного и того же материала будет тем
больше, чем больше его длина и чем меньше площадь его поперечного сечения. Или,
другими словами, электрическое сопротивление проводника увеличивается с
увеличением его длины он
уменьшается с увеличением площади его поперечного сечения.
Не трудно понять,
что кусок медной проволоки, длиною в 100 м и сечением в 1 кв. мм, будет иметь
одинаковое сопротивление с другим куском .проволоки, длиною 400 м и сечением 4
кв. мм.
Но электрическое сопротивление проводников зависит не только от их длины и площади
поперечного сечения, но оно зависит также от материала, из которого они сделаны.
Для того чтобы было удобнее сравнивать между собой проволоки, изготовленные из
разных материалов, введено понятие об удельном сопротивлении, причем удельным
сопротивлением проводника из Какого-нибудь материала называется
сопротивление в омах проводника
длиной в 1 метр и поперечным сечением в 1 кв. мм. Например, говорят, что удельное сопротивление медного проводника равно
