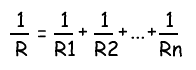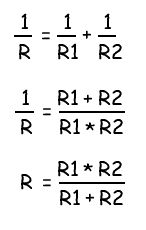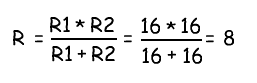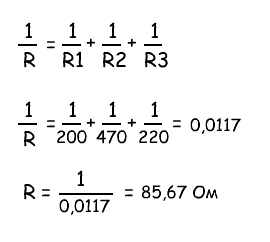Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
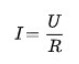
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
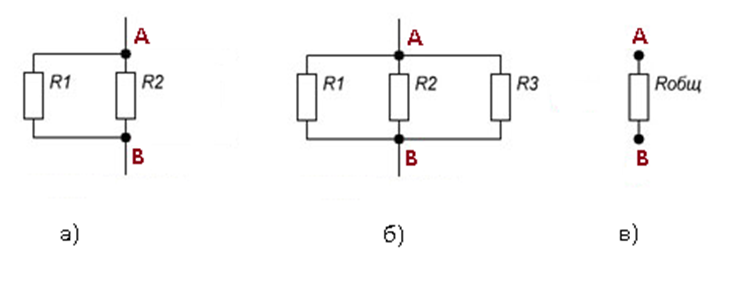
Общие схемы типов соединений представлены на рисунке 1.
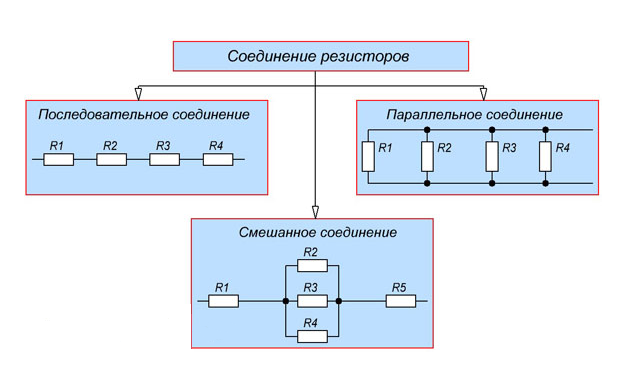
Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
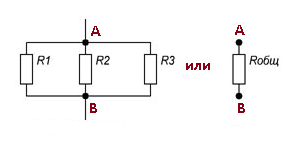
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
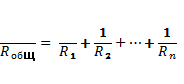
и рассчитывается по формуле:
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
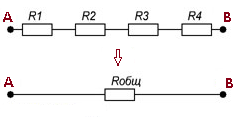
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
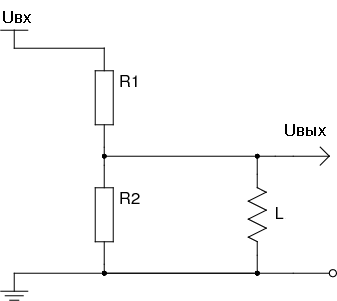
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
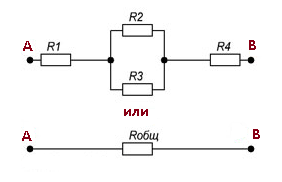
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
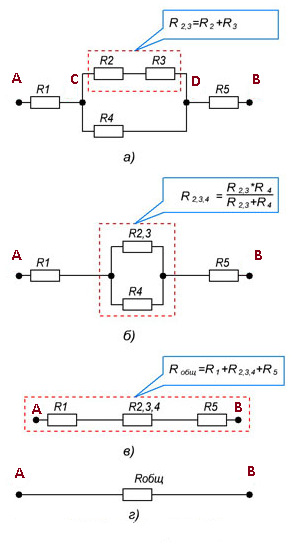
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.
Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.
Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
В этом случае, сила тока в цепи будет равна:
Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.
Решение
Воспользуемся формулами, которые приводили выше.
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
Следовательно,
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой
чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
I=U/Rобщее
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Подробное объяснение на видео:
Прикольный набор радиолюбителя по ссылке <<<
Похожие статьи по теме «последовательное и параллельное соединение»
Закон Ома
Проводник (электрический проводник)
Что такое резистор
Делитель напряжения
Делитель тока
Что такое напряжение
Что такое сила тока
Загрузить PDF
Загрузить PDF
В параллельной цепи резисторы соединены таким образом, что электрический ток в цепи делится между резисторами и проходит через них одновременно (сравните это с автодорогой, которая разделяется на две параллельные дороги и делит поток машин на два потока, движущихся параллельно друг другу). В этой статье мы расскажет вам, как вычислить напряжение, силу тока и сопротивление в параллельной цепи.
Шпаргалка
- Формула для вычисления общего сопротивления RT в параллельной цепи: 1/RT = 1/R1 + 1/R2 + 1/R3 + …
- Напряжение в параллельной цепи одинаковое на каждом ее элементе: VT = V1 = V2 = V3 = …
- Формула для вычисления общей силы тока в параллельной цепи: IT = I1 + I2 + I3 + …
- Закон Ома: V = IR
-
1
Определение. Параллельная цепь — это цепь, в которой ток течет из точки А в точку В одновременно по нескольким элементам цепи (то есть поток электронов разбивается на несколько потоков, которые на конечном участке цепи вновь объединяются в единый поток). В большинстве задач, в которых присутствует параллельная цепь, нужно вычислить напряжение, сопротивление и силу тока.
- Элементы, подключенные параллельно, находятся на отдельных ветвях цепи.
-
2
Сила тока и сопротивление в параллельных цепях. Представьте себе автостраду с несколькими полосами, на каждой из которых установлен пункт пропуска, замедляющий движение автомобилей. Построив новую полосу, вы увеличите скорость движения (даже если и на этой полосе вы поставите пункт пропуска). Аналогично с параллельной цепью — добавив новую ветвь, вы уменьшите общее сопротивление цепи и увеличите силу тока.
-
3
Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть, если известна сила тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + …
-
4
Общее сопротивление в параллельной цепи. Оно вычисляется по формуле: 1/RT = 1/R1 + 1/R2 + 1/R3 + …, где R1, R2 и так далее — это сопротивление соответствующих элементов (резисторов) этой цепи.
- Например, параллельная цепь включает два резистора и сопротивление каждого равно 4 Ом. 1/RT = 1/4 + 1/4 → 1/RT = 1/2 → RT = 2 Ом. То есть общее сопротивление параллельной цепи с двумя элементами, сопротивления которых равны, в два раза меньше сопротивления каждого резистора.
- Если какая-либо ветвь параллельной цепи не имеет сопротивления (0 Ом), то весь ток пройдет именно через эту ветвь.[1]
-
5
Напряжение. Напряжение — это разность электрических потенциалов между двумя точками электрической цепи. Так как здесь рассматриваются две точки без учета пути движения тока по цепи, напряжение в параллельной цепи одинаково на каждом элементе этой цепи, то есть: VT = V1 = V2 = V3 = …
-
6
Вычислите значения неизвестных величин по закону Ома. Закон Ома описывает взаимосвязь между напряжением V, силой током I и сопротивлением R: V = IR. Если вам известны значения двух величин из этой формулы, вы можете найти значение третьей величины.
- Вы можете применить закон Ома для всей цепи (V = ITRT) или для одной ветви этой цепи (V = I1R1).
Реклама
-
1
Нарисуйте таблицу, чтобы облегчить решение задачи, особенно если неизвестны значения сразу нескольких величин в данной параллельной цепи.[2]
Рассмотрим пример электрической цепи с тремя параллельными ветвями. Обратите внимание, что здесь под ветвями подразумеваются резисторы с сопротивлениями R1, R2, R3.R1 R2 R3 Общее Единицы измерения V В I А R Ом -
2
Внесите в таблицу данные вам значения. Например, к электрической цепи подключена батарея, напряжение которой равно 12 В. Цепь включает три параллельные ветви с сопротивлениями 2 Ом, 4 Ом, 9 Ом.
R1 R2 R3 Общее Единицы измерения V 12 В I А R 2 4 9 Ом -
3
Заполните значения напряжения для каждого элемента цепи. Помните, что общее напряжение в параллельной цепи и напряжение на каждом резисторе этой цепи равны.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I А R 2 4 9 Ом -
4
Вычислите силу тока на каждом резисторе по закону Ома. Так как теперь в каждом столбце вашей таблицы есть значения двух величин, вы с легкостью вычислите значение третей величины при помощи закона Ома: V = IR. В нашем примере нужно найти силу тока, поэтому перепишите формулу закона Ома следующим образом: I = V/R
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 12/2 = 6 12/4 = 3 12/9 = ~1,33 А R 2 4 9 Ом -
5
Вычислите общую силу тока. Помните, что общая сила тока в параллельной цепи равна сумме сил тока на каждом элементе этой цепи.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1,33 6 + 3 + 1,33 = 10,33 А R 2 4 9 Ом -
6
Вычислите общее сопротивление. Сделайте это одним из двух способов. Либо используйте формулу
1/RT = 1/R1 + 1/R2 + 1/R3, либо формулу закона Ома: R = V/I.R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1.33 10,33 А R 2 4 9 12 / 10,33 = ~1,17 Ом Реклама
-
1
Вычислите мощность тока по формуле: P = IV. Если вам дана мощность тока на каждом участке цепи, то общая мощность вычисляется по формуле: PT = P1 + P2 + P3 + ….
-
2
Вычислите общее сопротивление в параллельной цепи, состоящей из двух ветвей (двух резисторов).
- RT = R1R2 / (R1 + R2)
-
3
Найдите общее сопротивление в параллельной цепи, если сопротивление всех резисторов одинаково: RT = R1 / N, где N — количество резисторов в цепи.[3]
- Например, если в параллельной цепи два резистора с одинаковым сопротивлением, то общее сопротивление цепи будет вдвое меньше сопротивления одного резистора. Если в цепи восемь одинаковых резисторов, то общее сопротивление будет в восемь раз меньше сопротивления одного резистора.
-
4
Вычислите силу тока на каждом резисторе, если напряжение неизвестно. Это можно сделать, воспользовавшись правилом Кирхгофа.[4]
Вам необходимо вычислить сопротивление каждого резистора и общую силу тока в цепи.- Два резистора в параллельной цепи: I1 = ITR2 / (R1 + R2)
- Несколько (более двух) резисторов в параллельной цепи. В этом случае для вычисления I1 найдите общее сопротивление всех резисторов за исключением R1. Для этого воспользуйтесь формулой для вычисления общего сопротивления в параллельной цепи. Затем используйте правило Кирхгофа, заменив R2 полученным значением.
Реклама
Советы
- В параллельной цепи напряжение одинаково на всех резисторах.
- Возможно, в вашем учебнике закон Ома представлен следующей формулой: E = IR или V = AR. Здесь присутствуют другие обозначения величин, но суть закона Ома не меняется.
- Общее сопротивление часто именуется эквивалентным сопротивлением.
- Если у вас нет калькулятора, найти общее сопротивление, используя значения R1, R2 и так далее, довольно проблематично. Поэтому воспользуйтесь законом Ома.
- Если в задаче дана параллельно-последовательная цепь, сделайте вычисления для ее параллельного участка, а затем для полученной последовательной цепи.
Реклама
Об этой статье
Эту страницу просматривали 172 510 раз.
Была ли эта статья полезной?
В статье подробно рассмотрим, как параллельно соединять резисторы и научимся легко считать сопротивление тока в электрической цепи и узнаем, для чего вообще нужно параллельное соединение резисторов.
Понятие и определение
Параллельное соединение резисторов имеет некоторый принцип, согласно которому, выводы одного изделия подключены и работают с аналогичными выводами другого. Создаются подобные решения, чтобы специально формировать более трудные по своему составу и компоновке схемы.
Что ещё нужно учитывать
Параллельное соединение определяет принцип, согласно которому величина, установленная обратной общему показателю цепи, будет равна непосредственно сумме величин, обратных значению включённых проводников. Такая же ситуация будет отмечена при значительно большем количестве проводниковых элементов.
Особенности включения
Параллельное соединение резисторов предусматривает, что показатель напряжения везде будет одинаковым, но ток фиксируется пропорциональным.
Отличия от иных вариантов подключения
В данной схеме, исключается подключение к источнику различных наименований реактивных компонентов. Исключаются проблемные процессы колебания, сопряжённые ранее с фиксируемыми циклами смены уровня получения энергии в контексте подачи нагрузки.
Формула
Формула, согласно которой проводится расчёт и составляется схема резисторов в параллельном соединении:
[ 1/Rобщ=1/R1+1/R2 ]
[ Rобщ=1/(1/R1+1/R2) ]
[ Rобщ=(R1*R2)/(R1+R2) ]
Онлайн-калькулятор расчета параллельного соединения резисторов
Как выполняется расчёт
Проводя расчёт сопротивления для рассматриваемого соединения резисторов, нужно учесть факт, общий параметр всегда будет несколько ниже, нежели параметр наименьшего в приведённом сочетании.
Пример №1
Потребуется включить резистор, имеющий сопротивление 8 Ом. Рассматривая номенклатуру изделий, отмечаем, резистор с подобным параметром в базовых наименованиях отсутствует. Необходимо использовать параллельную схему. В дальнейшем, расчёт выполняется:
[ 1/R=1/R1+1/R2 ]
[ 1/R=(R1+R2)/(R1*R2) ]
[ R=(R1*R2)/(R1+R2) ]
В данном случае можно увидеть, что если оба значения равны между собой, то итог будет соответствовать половине одного из используемых двух резисторов. Если ставится задача подобрать сопротивление 8 Ом, то значение 2*8=16 Ом.
[ R=(R1*R2)/(R1+R2)=(16*16)/(16+16)=8 ]
Таким образом, чтобы получить значение равное 8 Ом, соединяем два резистора по 16 Ом параллельно.
Пример расчёта №2
Есть три элемента: R1=200, R2=470, R=220
Общее значение выводится по формуле:
[ 1/R=1/R1+1/R2/1/R3 ]
[ 1/R=1/200+1/470+1/220=0,0117 ]
[ R=1/0,0117=85,67 Ом ]
Данный метод без проблем актуален для выполнения расчёта практически любой численности включённых в конструкцию элементов.
Ток в цепи параллельно соединенных резисторов
При параллельном соединении отмечается, что ток, приравнивается сумме из отдельных составляющих. Показатель в каждом ответвлении, не фиксируется идентичным значению в соседних ответвлениях. К отдельному резистору прикладывается идентичное напряжение.
Сила тока
Актуально выполнить расчёт для всех ветвей. Общий показатель силы тока составляет 8А, тогда предстоит распределить напряжения, показатель замеряется на отдельно рассмотренных участках.
[ U12=I*Rэкв1=0,8*((2*4)/(2+4))=0,8*1,3=1,04 V ]
[ I1=U12/R1=0,52 А ]
[ I2=U12/R2=0,26 А ]
Корректность выполненных вычислений определяется:
[ I=I1+I2=0,52+0,26≈0,8 А ]
Мощность
Для корректного выбора резисторов учитывается и мощность рассеивания. Данный показатель можно рассчитывать так:
[ P=U*I ]
U — напряжение, В
I — сила тока, А
Показатель косвенным образом определяет некоторое количество энергии, она будет потребляться на выделение тепла.
Как найти сопротивление
Определение сопротивления выполняется по формулам:
[ 1/G ]
[ U/I ]
[ U2/P ]
[ P/I2 ]
Выбор параллельного подключения резисторов определяется с учётом входных параметров. Стоит только помнить о том, что показатель напряжения и уровень тока в отдельных ответвлениях идентичны.
Примеры применения при параллельном соединении
Конструктивно, каждый резистор рассчитан на некоторый рабочий диапазон температурного воздействия. Увеличение порога вызовет разрушение места пайки, соединения, самой детали, даже расположенных соседних блоков. Стоит помнить, что существуют одновременные соединения резисторов, приведённая компоновка способна нарушить функциональность и исправное состояние.
Благодаря использованию автоматических схем определения рабочих показателей можно переставлять резисторы, устанавливать в конкретном месте различные светодиоды, корректировать уровень сигнала на выходе.
Видео
Главная » Справочник » Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…