При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.
Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:
A=ΔqU
Но сила тока равна:
I=ΔqΔt
Выразим заряд:
Δq=IΔt
Тогда работа тока равна:
A=IUΔt
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.
Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:
A=I2RΔt=U2RΔt
Работа тока измеряется в Джоулях (Дж).
Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.
A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Закон Джоуля—Ленца
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
Q=I2RΔt
Количество теплоты измеряется в Джоулях (Дж).
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Используем закон Ома и закон Джоуля—Ленца:
Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Определение
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
P=AΔt
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P=IU=I2R=U2R
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P=I2R=0,32·10=0,9 (Вт)
Выразив силу тока через заряд, прошедший за единицу времени, получим:
P=qUt
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P=(εR+r)2R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
Pmax=(εr+r)2r=ε24r
Мощность тока внутренней цепи:
Pвнутр=I2r=(εR+r)2r
Полная мощность:
Pполн=I2(R+r)=ε2R+r
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P=(εR+r)2R
Применим закон Ома для полной цепи:
I=εR+r
Выразим сопротивление внешней цепи:
R=εI−r
Отсюда:
P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
rI2−Iε+P=0
I2−1I+0,75=0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
| Объем проводника цилиндрической формы |
V=Sl |
| Масса проводника цилиндрической формы |
m=ρV=ρSl |
| Количество теплоты и изменение температуры |
Q=cmΔT |
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
| Электроемкость, заряд и напряжение |
C=qU |
| Напряженность и напряжение |
E=Ud |
| Энергия конденсатора |
W=q22C=CU22 |
| Количество теплоты |
Q=ΔW |
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
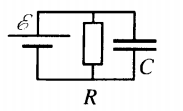
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
I=εR+r
Применим закон Ома:
I=UR
Приравняем правые части выражений и получим:
εR+r=UR
Отсюда напряжение на конденсаторе равно:
U=εRR+r
Напряженность электрического поля равна:
E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)
Задание EF17564
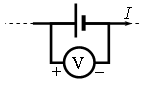 Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?
Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?
Ответ:
а) 5 Дж
б) 4 Дж
в) 3 Дж
г) 1 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для нахождения количества теплоты, выделенной внутри источника тока.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 3 В.
• Внутреннее сопротивление источника тока: r = 1 Ом.
• Сила тока в цепи: I = 2 А.
• Напряжение на внешней цепи: U = 5 В.
Количество теплоты, выделенной внутри источника тока, равно:
Q=I2rt=22·1·1=4 (Дж)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17573
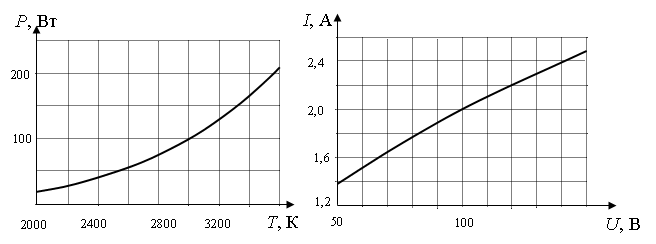
При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали P=P(T) и силы тока от приложенного напряжения I=I(U). При помощи этих графиков определите примерную температуру спирали лампы при силе тока I=2 A.
Ответ:
Алгоритм решения
1.Записать исходные данные.
2.С помощью графика зависимости силы тока от напряжения вычислить мощность.
3.С помощью графика зависимости мощности от температуры спирали определить ее температуру.
Решение
Нас интересует сила тока, равная 2 А. По графику зависимости силы тока от напряжения этому значение соответствует U = 100 В. Мощность определяется формулой:
P=IU=2·100=200 (Вт)
Этой мощности соответствует температура, равная около 3600 К.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17608
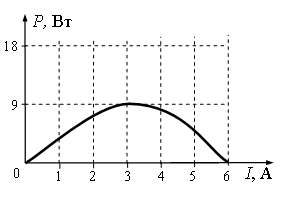 Ученик исследовал зависимость тепловой мощности Р, выделяющейся на реостате R, от силы тока в цепи. При проведении опыта реостат был подключён к источнику постоянного тока. График полученной зависимости приведён на рисунке.
Ученик исследовал зависимость тепловой мощности Р, выделяющейся на реостате R, от силы тока в цепи. При проведении опыта реостат был подключён к источнику постоянного тока. График полученной зависимости приведён на рисунке.
Какое из утверждений соответствует результатам опыта?
А. При коротком замыкании в цепи сила тока будет равна 6 А.
Б. При силе тока в цепи 3 А на реостате выделяется минимальная мощность.
Ответ:
а) только А
б) только Б
в) и А, и Б
г) ни А, ни Б
Алгоритм решения
- Проверить истинность каждого из утверждений.
- Выбрать верный ответ.
Решение
Согласно первому утверждению, при коротком замыкании в цепи сила тока будет равна 6 А. Это действительно так, потому что при этом значении силы тока мощность равна нулю. А это значит, что сопротивление на внешней цепи было нулевым.
Согласно второму утверждению, при силе тока в цепи 3 А на реостате выделяется минимальная мощность. Это не так. На графике этой силе тока соответствует максимальная мощность.
Верно только первое утверждение «А».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.3k
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:
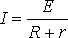 , (1)
, (1)
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
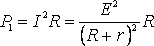 . (2)
. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®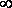 эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
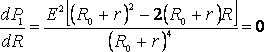 . (3)
. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
R0 = r. (4)
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи 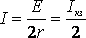 (5)
(5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
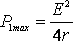 . (6)
. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
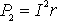 .
.  (7)
(7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
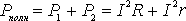 = I2(R+r) = IE (8)
= I2(R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен 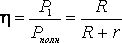 . (9)
. (9)
Из формулы (8) следует, что
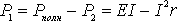 , (10)
, (10)
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 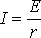 . Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
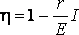 (11)
(11)
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.


Рис.1. I0 E/r
Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Рис. 2.
Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой  э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку  в нижней части экрана) и амперметр (кнопка
в нижней части экрана) и амперметр (кнопка  там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр
там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр  , измеряющий напряжение на нагрузке.
, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода  внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой  . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
Таблица 1. Исходные параметры электрической цепи
|
Номер варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Е, В |
10,0 |
9,5 |
9,0 |
8,5 |
8,0 |
8,5 |
9,0 |
9,5 |
|
r, Ом |
4,8 |
5,7 |
6,6 |
7,5 |
6,4 |
7,3 |
8,2 |
9,1 |
5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.
6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.
7. Вычислите по формулам (2), (7), (8), (9) Р1, Р2, Рполн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.
8. Постройте на одном листе миллиметровой бумаге графики зависимости P1 = f(R), P2 = f(R), Pполн=f(R), h = f (R) и U = f(R).
9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.
Таблица 2. Результаты измерений и расчётов
|
R, Ом |
2,0 |
2,5 |
3,0 |
… |
20 |
||
|
U, В |
|||||||
|
I, А |
|||||||
|
P1, Вт |
|||||||
|
P2, ВТ |
|||||||
|
Pполн, ВТ |
|||||||
|
h |
Вопросы и задания для самоконтроля
- Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
- Что такое ток короткого замыкания?
- Что такое полная мощность?
- Как вычисляется к.п.д. источника тока?
- Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
- Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
- К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
- Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
- Объясните явление.
- При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.
Тема: Мощность внешней цепи с ЭДС (Прочитано 17704 раз)
0 Пользователей и 1 Гость просматривают эту тему.
eirine
ЭДС аккумуляторной батареи E = 36 В, внутренне сопротивление r = 1 Ом. Внешняя цепь потребляет мощность N = 68 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь и ее сопротивление R.
« Последнее редактирование: 08 Декабря 2011, 18:52 от alsak »

Записан
Мощность во внешней цепи можно найти несколькими способами
[ N=I^{2} cdot R=left(frac{E}{R+r} right)^{2} cdot R, ; ; ; N=Icdot E-I^{2} cdot r. ]
Можно найти внешнее сопротивление R из первого уравнения, можно найти I — из второго. Воспользуемся вторым способом:
r⋅I2 – E⋅I + N = 0,
[ I=frac{Epm sqrt{E^{2} -4Ncdot r} }{2r}, ]
I1 = 34 A, I2 = 2 A.
Внешнее сопротивление R найдем из закона Ома для полной цепи:
[ I=frac{E}{R+r}, ; ; ; R=frac{E}{I} -r, ]
R1 = 0,059 Ом, R1 = 17 Ом.
Для нахождения напряжения U, под которым находится внешняя цепь, найдем из закона Ома для участка цепи:
U = I⋅R,
U1 = 2 В, U2 = 34 В.

Записан
Примеры решения задач
Задача
1. Определить
токи в ветвях данной цепи (рис. 11.4.).
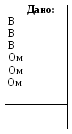

Решение
Рассчитаем
электрическую цепь с помощью правил
Кирхгофа.
1. Определим
количество узлов и ветвей в цепи (2 узла,
3 ветви).
2. Произвольно
расставим токи в ветвях.
3.
По первому закону Кирхгофа составим
![]() уравнение, где
уравнение, где![]()
– число узлов.
Составим
уравнение для узла А:
![]()
Токи
![]()
и ![]()
входят в узел, их берем со знаком плюс.
4. Произвольно
выбираем направление обхода контуров
(по часовой стрелке).
5.
Число независимых уравнений, составляемых
по второму правилу Кирхгофа, должно
быть меньше числа замкнутых контуров,
имеющихся в цепи. Для составления
уравнений первый контур можно выбирать
произвольно. Все следующие контуры
следует выбирать так, чтобы в каждый
новый контур входила хотя бы одна ветвь
цепи, не участвовавшая ни в одном из
ранее использованных контуров. Для
контура 1–2–А–В–1
![]() .
.
Токи
I1
и I2
совпадают с направлением обхода, поэтому
произведения
![]() и
и![]() берутся со знаком “плюс”. Направление
берутся со знаком “плюс”. Направление
действия![]() совпадает с направлением обхода, берется
совпадает с направлением обхода, берется
знак “плюс”. Направление действия![]() противоположно обходу, поэтому знак
противоположно обходу, поэтому знак
“минус”.
Для контура
1–2–3–4–1
![]()
После
подстановки известных числовых значений
получим систему уравнений:
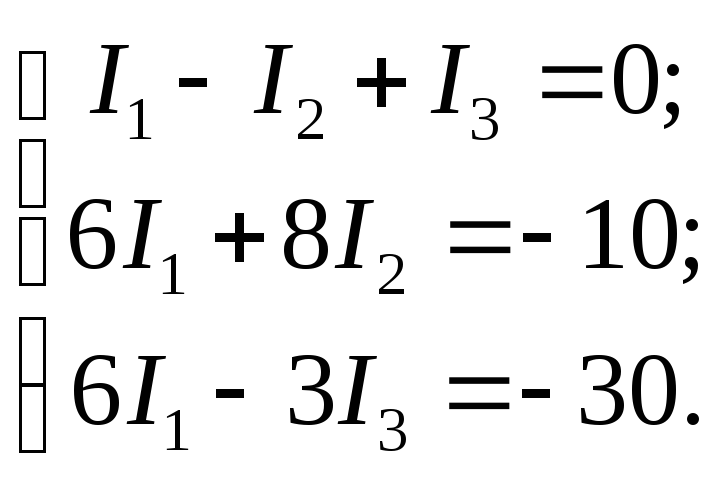
Решим
систему уравнений методом определителей:
![]() ;
;
![]() ;
;![]() .
.
Составим
и вычислим определитель системы :
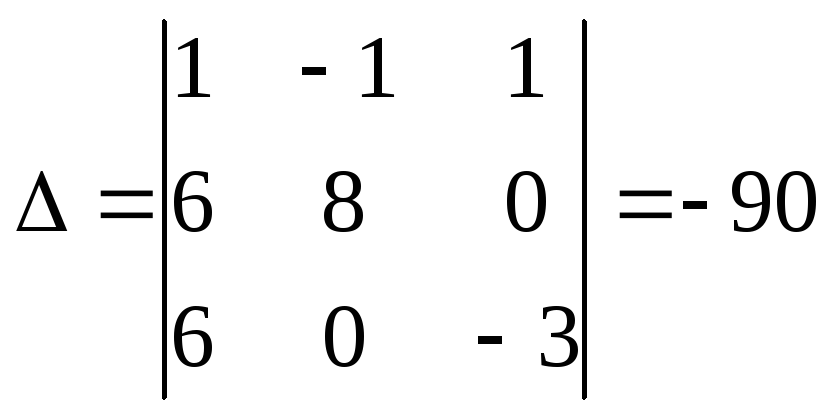 .
.
Составим
и вычислим определители 1,
2:
 ;
;
![]() А;
А;![]() А.
А.
 ;
;
![]() А.
А.
Ток
в первой ветви течет в направлении,
противоположном произвольно выбранному.
Е3
работает как генератор, а Е1
и Е2
являются потребителями.
Ответ:
![]() А;
А;![]() А;
А;![]() А.
А.
Задача
2: Определить
![]() в данной схеме (рис. 11.5).
в данной схеме (рис. 11.5).
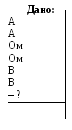

Решение
В
данной цепи три узла (а, с, в) и две ветви
(ас и св). Запишем закон Ома для каждой
ветви:
ас:
![]() ;
;
св:
![]() .
.
Полученную
систему уравнений решаем любым
алгебраическим методом и находим
![]()
Ответ:
![]() В.
В.
З адача
адача
2-а (резерв).
Найти показание амперметра (рис. 11.6).

Ответ:
![]() А.
А.
Задача
3. Определить
ток в цепи и потенциалы точек 2, 3, 4
относительно точки 1, потенциал которой
принять равным нулю. Построить
потенциальную диаграмму (рис. 11.7).
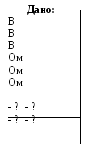
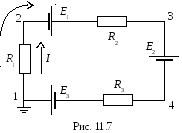
Решение
1.
Выберем произвольно направление тока
и обхода (лучше одинаковое) по часовой
стрелке.
2. Запишем закон
Ома для замкнутой цепи, учтя знаки ЭДС:
 .
.
3.
Запишем закон Ома для участков цепи и,
решая уравнения, вычислим потенциалы
точек 2, 3, 4:
1
– 2:
![]() В.
В.
2
– 3:
![]() В.
В.
3
– 4:
![]() В.
В.
Для
построения потенциальной диаграммы
выбираем оси координат, на которых в
масштабе откладываем сопротивление R
и потенциалы :

По
потенциальной диаграмме найдем
![]() В (рис. 11.8).
В (рис. 11.8).
Ответ:
![]() А;
А;![]() В;
В;![]() В;
В;![]() В.
В.
Задача
4. Как изменятся
показания приборов, если лампочка Л3
перегорит? Сопротивления лампочек
одинаковы (рис. 11.9). Исследование режима
работы цепи лучше оформить в виде
таблицы. Перед решением выяснить, как
включены лампочки, почему будут изменяться
показания приборов. Необходимо считать
E
= const,
r
= const.

Таблица 11.1
|
№ |
Было |
Стало |
Вывод |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
Ответ:
Внешнее сопротивление увеличивается,
ток в цепи уменьшается (показание
амперметра уменьшается), напряжение на
всей внешней цепи, измеряемое вольтметром
V,
увеличивается; на участках U1
уменьшается, U2
увеличивается.
Задача
5. Проволочный
куб составлен из проводников. Сопротивление
каждого проводника, составляющего ребро
куба, R1
= 1 Ом. Вычислить сопротивление этого
куба, если он включен в электрическую
цепь, как показано на рис. 11.10, а, б.


Решение
а) Найдем на кубе
точки равных потенциалов и соединим их
в узлы. Эквивалентная схема изображена
на рис. 11.11.

Общее
сопротивление
![]() .
.
Ответ:
![]() Ом.
Ом.
б) Относительно
точек А и В куб имеет плоскость симметрии.
Точки, лежащие на плоскости симметрии,
соединяем в узел. Эквивалентная схема
изображена на рис. 11.12.

![]() ;
;
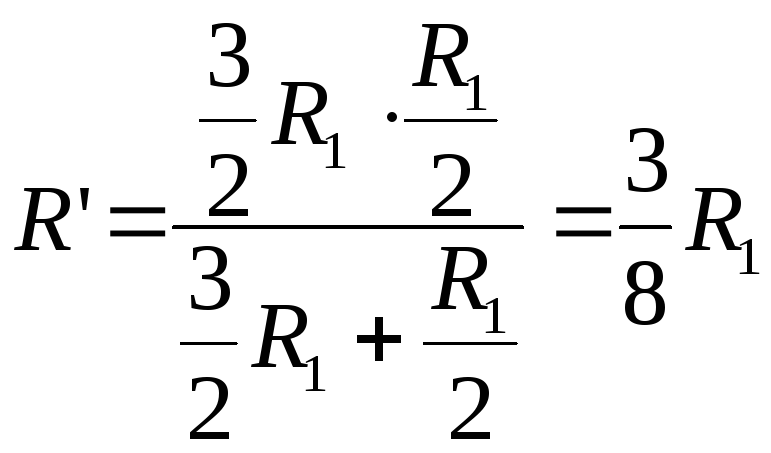 ;
;
![]() .
.
Ответ:
![]() Ом.
Ом.
Задачи
для самостоятельного решения
Задача
1. Две группы
из трех последовательно соединенных
элементов соединены параллельно. ЭДС
каждого элемента E
= 1,2 В, внутреннее сопротивление r
= 0,2 Ом. Полученная батарея замкнута на
внешнее сопротивление R
= 1,5 Ом. Найти силу тока во внешней цепи.
Ответ:
I
= 2 А.
Задача
2*.
В цепь, составленную из источника ЭДС
с внутренним сопротивлением r
= 1 Ом и сопротивления R
= 100 Ом, включается вольтметр, первый раз
– параллельно сопротивлению, второй –
последовательно с ним. Показания
вольтметра оказались одинаковыми. Найти
сопротивление вольтметра.
Ответ:
![]() Ом.
Ом.
Задача
3*.
Сила тока в проводнике равномерно
нарастает от I0=
0 до I
= 3 А за 10 с.
Определить заряд, прошедший в проводнике.
Ответ:
q
= 15 Кл.
Задача
4. Определить
плотность тока в железном проводнике
длиной
![]() м, если провод находится под напряжениемU
м, если провод находится под напряжениемU
= 6 В, (![]() Омм).
Омм).
Ответ:
![]() А/м2.
А/м2.
Задача
5. Напряжение
на шинах электростанции U
= 6600 В. Потребитель находится на расстоянии
l
= 10 км. Какого сечения нужно взять медный
провод для устройства двухпроводной
линии электропередачи, если сила тока
в линии I
= 20 А и потери напряжения в проводах не
превышают 3 %?
Ответ:
S
= 3,410-5
м2.
Задача
6. Катушка и
амперметр соединены последовательно
и присоединены к источнику тока. К
зажимам катушки присоединен вольтметр
сопротивлением
![]() Ом. Показания амперметраI
Ом. Показания амперметраI
= 0,5 А, вольтметра U
= 100 В. 1) Определить сопротивление катушки.
2) Сколько процентов от точного значения
сопротивления катушки составит ошибка,
если не учитывать сопротивления
вольтметра?
Ответ:
1) R
= 250 Ом; 2) 20 %
Задача
7. Две батареи
(E1
= 10 В, r1
= 1 Ом, E2
= 8 В, r2
= 2 Ом) и резистор сопротивлением R
= 6 Ом соединены, как показано на рис.
11.13. Найти силу тока в батареях и резисторе.
О твет:
твет:
I
= 6,4 A; 5,8 A; 0,6 A.
Задача
8.
К элементу
с Е
= 1,5 В присоединили катушку с сопротивлением
R
= 0,1 Ом. Амперметр показал силу тока I1
= 0,5 A.
Когда к элементу присоединили
последовательно еще один элемент с
такой же ЭДС, то сила тока в той же катушке
стала I2
= 0,4 A.
Определить внутреннее сопротивление
первого и второго элементов.
Ответ:
r1
= 2,9 Ом; r2
= 4,5 Ом.
Задача
9. Проволока
имеет сопротивление 36 Ом. Когда ее
разрезали на несколько равных частей
и соединили эти части параллельно, то
получилось сопротивление 1 Ом. На сколько
частей разрезали проволоку?
Ответ:
n
= 6.
Задача
10. К источнику
с ЭДС E
= 18 В и внутренним сопротивлением
![]() Ом подключены три одинаковых проводника
Ом подключены три одинаковых проводника
сопротивлением![]() Ом каждый, соединенных по схеме,
Ом каждый, соединенных по схеме,
изображенной на рис. 11.14. Сопротивлением
соединительных проводов АС и ВД можно
пренебречь. Определить силу тока,
текущего через каждое сопротивление.
О твет:
твет:
I
= 3 A.
Задача
11. Два элемента
(E1
= 1,2 В, r1
= 0,1 Ом, E2
= 0,9 В, r2
= 0,3 Ом) соединены одноименными полюсами.
Сопротивление соединительных проводов
R
= 0,2 Ом. Определить силу тока в цепи.
Ответ:
I
= 0,5 А.
Задача
12. Два
источника тока (E1
= 8 В, r1
= 2 Ом, E2
= 6 В, r2
= 1,5 Ом) и резистор R
= 10 Ом соединены, как показано на рис.
11.15. Вычислить силу тока, текущего через
резистор.
О твет:
твет:
I
= 0,63 A.
Задача
13. Определить
силу тока в сопротивлении R3
и напряжение на концах этого сопротивления,
если E1
= 4 В, E2
= 3 В, R1
= 2 Ом, R2
= 6 Ом, R3
= 1 Ом. Внутренним сопротивлением
источников тока пренебречь (рис. 11.16).
Ответ:
I3
= 0, U3
= 0.

Задача
14. Три батареи
с ЭДС E1
= 12 В, E2
= 5 В, E3
= 10 В и одинаковыми внутренними
сопротивлениями, равными 1 Ом, соединены
между собой одноименными полюсами.
Сопротивление соединительных проводов
ничтожно мало. Найти силу тока, текущего
через батареи.
Ответ:
I
= 3 A; 4 A; 1 A.
Задача
15.
Три источника
тока (E1
= 11 В, E2
= 4 В, E3
= 6 В) и три резистора (R1
= 5 Ом, R2
= 10 Ом, R3
= 2 Ом) соединены так, как показано на
рис. 11.17. Определить силу тока в резисторах.
Внутреннее сопротивление источников
пренебрежимо мало.
Ответ:
I
= 0,8 A; 0,3 A; 0,5 A.

Задача
16.
Три
сопротивления R1
= 5 Ом, R2
= 1 Ом, R3
= 3 Ом и источник тока E1
= 1,4 В соединены, как показано на рис.
11.18. Определить ЭДС источника тока,
который нужно включить в цепь между
точками А и В, чтобы в сопротивлении R3
шел ток силой I
= 1 A
в направлении, указанном стрелкой.
Сопротивлением источников тока
пренебречь.
Ответ:
E
= 3,6 В.

Задача
17. Сколько
витков нихромовой (
= 110–6
Омм)
проволоки диаметром 1 мм надо навить на
фарфоровый цилиндр радиусом 2,5 см, чтобы
получить печь сопротивлением 40 Ом? Какой
ток пойдет по проволоке при включении
печи в сеть с напряжением 220 В?
Ответ:
N
= 200 витков; I
= 5,5 A.
Задача
18. Сетка
состоит из одинаковых звеньев.
Сопротивление каждого звена R
= 1 Ом. Найти сопротивление между точками
А и В (рис. 11.19).
Ответ:
RАВ
= 1,5 Ом.

Задача
19*.
Зайти сопротивление между точками А и
В цепи при разомкнутом и замкнутом
ключе. Сопротивление каждой стороны и
диагонали квадрата R
= 1 Ом (рис. 11.20).
Ответ:
При разомкнутом ключе RАВ
=
![]() =
=
0,625 Ом; при замкнутом ключеRАВ
=
![]() = 0,5 Ом.
= 0,5 Ом.

Задача
20*.
Найти сопротивление между соседними
вершинами проволочного куба. Сопротивление
каждого из ребер куба R1
= 1 Ом.
Ответ:
![]() Ом.
Ом.
Задача
21. Найти
сопротивление между вершинами куба,
расположенными на диагонали одной из
его граней. Сопротивление каждого из
ребер куба R1
= 1 Ом.
Ответ:
![]() Ом.
Ом.
Задача
22*.
Провод АСВ изогнут так, что точки А, С и
В находятся на вершинах правильного
треугольника. К серединам сторон АС и
ВС подключена перемычка EF
из провода с вдвое меньшей площадью
сечения. К точкам А и В подано напряжение
U
= 3 В. Найти падение напряжения на перемычке
(рис. 11.21).
О твет:
твет:![]() В.
В.
Задача
23. Катушка
из медной проволоки (
= 1,710–8
Омм)
имеет сопротивление R
= 10,8 Ом. Масса проволоки 3,42 кг. Сколько
метров проволоки и какого диаметра
намотано на катушке?
Ответ:
l
= 500 м; d
= 1 мм.
Задача
24. Элемент,
амперметр и сопротивление включены
последовательно. Сопротивление сделано
из медной проволоки (![]() Омм)
Омм)
длиной 100 м и поперечным сечением 2 мм2,
сопротивление амперметра 0,05 Ом, амперметр
показывает 1,43 А. Если же взять сопротивление
из алюминиевой проволоки (![]() Омм)
Омм)
и длиной 57,3 м и поперечным сечением 1
мм2,
то амперметр покажет 1 А. Найти ЭДС
элемента и его внутреннее сопротивление.
Ответ:
E
= 2 В; r
= 0,5 м.
Задача
25. В схеме
ЭДС батареи E
= 100 В, R1
= 100 Ом, R2
= 200 Ом, R3
= 300 Ом. Какое напряжение покажет вольтметр,
если его сопротивление 2000 Ом? Сопротивлением
батареи и проводов пренебречь (рис.
11.22).
Ответ:
U
= 80 В.

Задача
26. ЭДС элемента
E
=1,6 В и внутреннее сопротивление r
= 0,5 Ом. Чему равен КПД элемента при силе
тока в 2,4 А?
Ответ:
КПД = 25 %.
Задача
27. Найти ЭДС
батареи (по схеме предыдущей задачи),
если R1
= R2
= R3
= 200 Ом. Вольтметр показывает 100 В, его
сопротивление 1000 Ом. Сопротивлением
батареи и проводов пренебречь (рис.
11.22).
Задача
28. Найти
показания амперметра и вольтметра в
схемах а, б, в (рис. 11.23). Сопротивление
вольтметра 1000 Ом, R1
= 400 Ом, R2
= 600 Ом, ЭДС батареи E
= 110 В. Сопротивлением батареи и амперметра
пренебречь.
Ответ:
а) I
= 0,57 А, U
= 110 В;
б)
I
= 0,09 А, U
= 53,2 В;
в)
I
= 0,142 А, U
= 53,2 В.

Задача
29. Два элемента
(E1
= E2
= 2 В; r1
= 1 Ом r2
= 2 Ом) соединены по схеме (рис. 11.24). Сила
тока, текущего через первый источник,
равна I1
= 1 А. Найти
остальные токи и внешнее сопротивление
R.
Ответ:
I2
= 0,5А; I3
= 1,5 А; R
=
![]() Ом.
Ом.

Задача
30. Решить
предыдущую задачу, если E1
= E2
= 4 В, r1
= r2
= 0,5 Ом, I1
= 2 А (рис. 11.24).
Ответ:
I2
= 2 А; I3
= 4 А; R
= 0,75 Ом.
Задача
31. Какую силу
тока показывает миллиамперметр в схеме,
если E1
= 2 В, E2
= 1 В, R1
= 1000 Ом, R2
= 500 Ом, R3
= 200 Ом, сопротивление миллиамперметра
RА
= 200 Ом (рис. 11.25).
О твет:
твет:
I
= 0,45 мА.
Задача
32. Решить
предыдущую задачу, если E1
= 1 В, E2
= 2 В,
R3
= 1500 Ом, RА
= 500 Ом и падение напряжения на сопротивлении
R2
U2
= 1 В (рис. 11.25).
Ответ:
I
= 1 мА.
Задача
33. Два элемента
с одинаковой ЭДС в 2 В и одинаковым
внутренним сопротивлением, равным 0,5
Ом, соединены с сопротивлениями R1
= 0,5 Ом, R2
= 1,5 Ом, как показано на рис. 11.16. Найти
токи в ветвях.
Ответ:
I
= 2,22 А; 0,44 А; 1,78 А.

Задача
34. Определите
общее сопротивление между точками А и
В, если R1
= 1 Ом, R2
= 3 Ом, R3
= R4
= R6
= 2 Ом, R5
= 4 Ом.
Ответ:
R
= 1,2 Ом.
Задача
35. Амперметр
показывает силу тока I
= 1,5 A.
Сила тока через сопротивление R1
равна I1
= 0,5 A.
Сопротивление R2
= 2 Ом, R3
= 6 Ом.
Определите сопротивление R1,
а также силу токов I2,
I3,
протекающих через сопротивления R2
и R3.
Сопротивления включены параллельно.
Ответ:
R1
=
3 Ом,
I2
=
0,75 A, I3
=
0,25 A.
Задача
36. По
алюминиевому проводу сечением 0,2 мм2
течет ток 0,2 А. Определите силу действующую
на отдельные свободные электроны со
стороны электрического поля. Удельное
сопротивление алюминия 26 нОмм.
Ответ:
F
= 4,1610-21
Н.
Задача
37. Определите
ток короткого замыкания источника ЭДС,
если при внешнем сопротивлении R1=
50 Ом ток в цепи I1=
0,2 А, а при R2=
110 Oм
– I2=0,1
А.
Ответ:
Iкз
= 1,2 А.
Задача
38. Два
источника ЭДС 2 В и 1,5 В и внутренними
сопротивления-ми 0,5 Ом и 0,4 Ом соответственно
включены параллельно сопротивлению R
= 2 Ом. Определите силу тока через это
сопротивление.
Ответ:
I
= 0,775 А.
Задача
39. Даны Е1=Е2
=Е3,
R1=
48 Oм,
R2
= 24 Oм,
падение напряжения U2
на
сопротивлении R2
равно 12 В. Пренебрегая внутренним
сопротивлением элементов, определите:
1) силу тока во всех участках цепи; 2)
сопротивле-ние R3.
Ответ:
1) I1
=
0,25
A,
I2
=
0,5
A,
I3
=
0,75
A;
2) R3
=
16
Ом
.
Соседние файлы в папке Часть 2
- #
- #
- #
- #
- #
- #
- #
Электрический ток
Мы выяснили, что подвижные носители зарядов в проводнике перемещаются под действием внешнего электрического поля, пока не выровняются потенциалы всех точек проводника. Однако если в двух точках проводника каким-то образом искусственно поддерживать различные потенциалы, то это поле будет обеспечивать непрерывное движение зарядов: положительных — от точек с большим потенциалом к точкам с меньшим потенциалом, а отрицательных — наоборот. Когда эта разность потенциалов не меняется со временем, то в проводнике устанавливается постоянный электрический ток.
Вспомним из курса физики некоторые сведения об электрическом токе.
Упорядоченное движение свободных зарядов в проводнике называется электрическим током проводимости, или электрическим током.
Основными условиями существования электрического тока являются:
- наличие свободных заряженных частиц;
- наличие источника тока, создает электрическое поле, действие которого приводит упорядоченное движение свободных заряженных частиц;
- замкнутость электрической цепи, которая обеспечивает циркуляцию свободных заряженных частиц.
В зависимости от величины удельного сопротивления, который вещества оказывают постоянному току, они делятся на проводники, полупроводники, диэлектрики.
В зависимости от среды различают особенности прохождения электрического тока, в частности в металлах, жидкостях и газах, где носителями тока могут быть свободные электроны, положительные и отрицательные ионы.
Полная электрическая цепь содержит источник тока и электроприборы, а также устройство для замыкания (размыкания) электрической цепи. За направление тока в цепи условно выбирают направление от положительного полюса источника тока к отрицательному (реальное движение носителей тока — электронов — происходит в обратном направлении).
Основными физическими величинами, характеризующими электрический ток, являются следующие:
Сила тока I — физическая величина, характеризующая скорость перераспределения электрического заряда в проводнике и определяется отношением заряда q, проходящий через любой сечение проводника за время t, к величине этого интервала времени, I=q/t. Единица силы тока — ампер, 1А =1Кл/сек.
Термин «сила тока» предложили задолго до установления научных положений электродинамики. Он несколько неудачный, поскольку никакого отношения к «силе» он не имеет.
Электрическое сопротивление R — это физическая величина, характеризующая свойство проводника противодействовать прохождению электрического тока. Единица электрического сопротивления — ом, 1 Ом.
Сопротивление проводника зависит от его физических параметров — длины l, площади поперечного сечения S и от удельного сопротивления вещества p, из которой он изготовлен: R = р*l/S.
И как мы знаем, образования тока в проводнике обуславлено наличием разности потенциалов ϕ 1 – ϕ 2 , которую еще называют напряжением.
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля, U = A/q. Единица напряжения — вольт, 1 В.
Электродвижущая сила
При подключении к полюсам источника проводник, благодаря наличию разности потенциалов, свободные электроны проводимости, не прекращая хаотического движения, под действием кулоновских сил начнут двигаться направлено — от конца проводника с более низким потенциалом к концу с высшим, то есть от отрицательного полюса источника тока к положительному. Но силы электрического поля не могут переместить электрические заряды между полюсами внутри источника, поскольку действуют на них в противоположном направлении. Поэтому внутри источника, кроме электрических сил F кл , действуют еще и сторонние силы F ст. Природа сторонних сил может быть различной: в химических элементах — это действие химических реакций, в фотоэлементах — действие солнечных лучей, электрогенераторах — изменение магнитного потока.
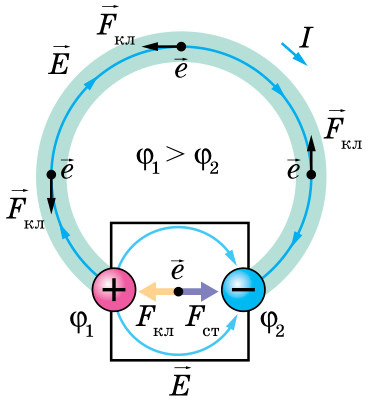
Сторонние силы перемещают отрицательные заряды от положительного полюса батареи к отрицательному и противодействуют электрическим силам, которые стремятся выровнять потенциалы на полюсах. Благодаря этому заряды циркулируют по замкнутому кругу, создавая ток. Участок круга, в которой заряды движутся под действием кулоновских сил, называют однородной, а ту, в которой носители заряда движутся под действием как кулоновских, так и сторонних сил, — неоднородной. Если соединить концы неоднородного участка, получим полный круг, в котором ту часть замкнутого круга, в которой заряды движутся под действием кулоновских сил (электростатической разности потенциалов), называют внешней, а ту, в которой носители заряда движутся под действием сторонних сил, — внутренней. Полюса источника тока разделяют внутренний и внешний участки цепи.
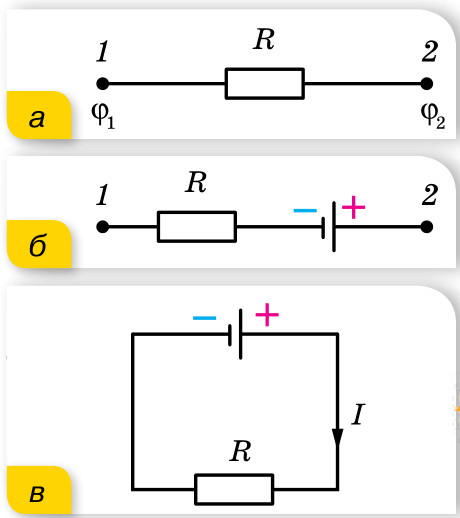
б — неоднородный участок; в — полный круг, содержащий внешнюю и внутреннюю части
Для перемещения зарядов сторонние силы выполняют соответствующую работу А. Чем больше заряд перемещается, тем больше работа выполняется. Иными словами, A ст ~ q или, используя знак равенства, A ст = εq, где ε — постоянный коэффициент пропорциональности, характеризующий соответствующий источник и называеющийся электродвижущей силой источника тока (сокращенно ЭДС).
Электродвижущая сила ε — это физическая величина, характеризующий энергию стороних сил источника тока и измеряется: работой сторонних сил (то есть сил не электростатического происхождения), выполненной для перемещения единичного позитивного электрического заряда, ε = A ст/q.
Единица электродвижущей силы — вольт, 1 В = 1 Дж/ 1Кл.
В результате разделения внутри источника положительных и отрицательных зарядов, источник приобретает запас потенциальной электрической энергии, которая тратится на выполнение работы по перемещению зарядов по всей окружности. Работа сторонних сил равна сумме работ, выполняемых по перемещению заряда на внутренней и внешней участках цепи.
В источниках тока постоянно происходит разделение положительных и отрицательных зарядов, которые сосредотачиваются на его полюсах, что вызывает появление электрического поля (стационарного). Свойства этого поля отличаются от электрического поля неподвижных зарядов, которое мы изучали в электростатике. В таблице 2 представлены сравнения свойств электрических полей подвижных и неподвижных зарядов.
| Электростатическое поле неподвижных зарядов | Стационарное электрическое поле движущихся зарядов |
| Линии напряженности являются незамкнутыми.
Работа поля по замкнутому контуру равна нулю |
Имеет замкнутые линии напряженности.
Работа поля по перемещению заряда вдоль замкнутой линии напряженности не равна нулю. Такое поле называют вихревым |
Закон Ома для полной цепи
Источник тока, как и любой проводник, имеет определенное сопротивление, который называют внутренним сопротивлением источника и обозначают r, в отличие от сопротивления внешней цепи R. Как известно из курса физики, по закону Ома, для участка цепи сила тока I на участке цепи прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению R этого участка, I=U/R. Формулу закона Ома записывают и в таком виде: U = IR, где произведение IR называют падением напряжения на данном участке цепи. Для участка, который не содержит источника тока, понятие напряжения и падения напряжения совпадают.
Согласно закону Ома, для внешней и внутренней участков цепи можно записать U вн = Ir, U вн = IR. Тогда ε = IR + Ir, то есть сумма падений напряжений на внешнем и внутреннем участках цепи равна ЭДС источника.
Соотношение, записанное в виде I = ε/R+r, называют законом Ома для полной цепи: сила тока в замкнутоq электрической цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Следовательно, сила тока в цепи зависит от трех величин, две из которых (ЭДС и внутреннее сопротивление) характеризуют источник, а третья зависит от самой цепи. Если пользоваться определенным источником электрической энергии, то ε и r можно считать постоянными величинами. Если менять сопротивление внешней цепи, то соответственно будет меняться сила тока I в цепи и падение напряжения IR на наружной части круга. С увеличением сопротивления внешней цепи сила тока уменьшается, а напряжение растет. Если R = ∞ (цепь разомкнута), то I = 0, падение напряжения внутри источника отсутствует, а напряжение на полюсах источника равна его ЭДС. На этом основывается метод измерения ЭДС источника. Вольтметр присоединяют к полюсам источника при разомкнутой внешней цепи. В этом случае вольтметр показывает падение напряжения IR на самом себе. А поскольку сопротивление вольтметра обычно очень большое, т.е R >> r, U = IR ≈ ε. Чем больше сопротивление вольтметра по сравнению с внутренним сопротивлением источника тока, то точнее будет измеренное значение ЭДС.
Работа и мощность электрического тока
Электрическое поле, создавая упорядоченное движение заряженных частиц в проводнике, выполняет работу, которую принято называть работой тока.
Работа электрического тока А — физическая величина, характеризующая: изменение электрической энергии тока — превращение ее в другие виды.
Единица работы электрического тока — джоуль, 1 Дж. В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.
Если рассматривать внешний участок электрической цепи, то работа тока определяется как А = qU = UIt, где q — заряд, прошедший через поперечное сечение проводника за время t, U — электрическое напряжение на участке цепи, I — сила тока.
Если на участке цепи, по которой проходит ток, не выполняется механическая работа и не происходят химические реакции, то результатом работы электрического тока будет только нагрев проводников. Нагретый проводник вследствие теплообмена отдает полученную энергию в окружающую среду. Согласно закону сохранения энергии, количество выделенной теплоты равна работе тока: Q = А и вычисляется по закону Джоуля — Ленца: количество теплоты Q, выделяемой за время t в проводнике с сопротивлением R во время прохождения по нему тока силой I, равна Q = I2Rt.
Воспользовавшись законом Ома I = U/R, математически можно получить и такие формулы закона Джоуля — Ленца: Q =U2t/R и Q = UIt. Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.
Мощность электрического тока Р — физическая величина, характеризующая способность электрического тока выполнять определенную работу и измеряется работой, выполненной в единицу времени, Р = A/t, здесь А — работа электрического тока, t — время, за которое эта работа выполнена. Мощность во внешнем участке электрической цепи можно определить по формулам Р = UI, Р = I2R, Р = U2/R, где U — электрическое напряжение, I — сила тока, R — электрическое сопротивление участка цепи. Единица мощности — ватт, 1 Вт = 1.
Если цепь состоит из нескольких потребителей, то при параллельном их соединения общая мощность тока во всей цепи равна сумме мощностей отдельных потребителей. Это стоит принять во внимание. В быту мы пользуемся мощными электрическими приборами. Если одновременно их включить, то общая мощность может превышать ту, на которую рассчитана электрическая сеть в помещении.
Выясним, в каком случае в электрической цепи выделяется максимальная мощность. Для этого запишем закон Ома для полной цепи в таком виде: ε = IR + Ir. Умножив обе части уравнения на I, получим: εI = I 2 R + I 2 r, где εI — полная мощность, которую развивает источник тока, I2R — мощность потребителей внешней участка цепи, I2г — мощность, которую потребляет внутренняя часть круга. Итак, потребляемая мощность внешней частью цепи, составляет: P = εI – I 2 r.
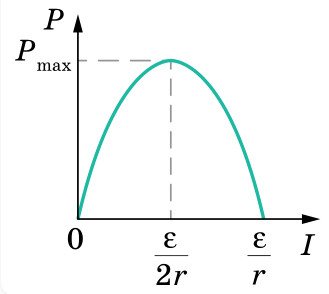
Графиком зависимости Р (I) является парабола, вершина которой имеет координаты {ε/2r;ε2/4r}. Из графика видно, что максимальная мощность потребляется во внешнем цепи при силе тока I = ε/2r.
Короткое замыкание
С уменьшением сопротивления внешней цепи, R -> 0, сила тока достигает максимального значения Iк.з. Этот случай называют коротким замыканием. Для источников тока, имеющих сравнительно малое внутреннее сопротивление (например, в свинцовых аккумуляторах r=0,1-0,001 Ом), сила тока короткого замыкания может достичь очень больших значений. Проводники могут расплавиться, а сам источник — выйти из строя. Особенно опасны короткие замыкания в осветительных сетях, питающихся от трансформаторных подстанций, ЭДС которых измеряется сотнями вольт. Сила тока короткого замыкания в них может достичь нескольких тысяч ампер.


