Как найти силу тока зная плотность тока

Лекция
5

2.1.Электрический ток. Сила и плотность тока. Уравнение непрерывности для плотности тока

Электрический
ток – всякое упорядоченное движение
электрических зарядов.
Электрический ток, который возникает
как упорядоченное движение свободных
зарядов под действием электрического
поля в проводящих средах, называется
током проводимости.

Кроме тока
проводимости существуют другие виды
тока. Если какое-то тело зарядить и
перемещать в пространстве, то в этом
случае электрические заряды будут
перемещаться вместе с макроскопическим
телом. Такой ток называют конвекционным
или переносным.

В случае тока в
вакууме микроскопические электрические
заряды движутся в пустоте независимо
от макроскопических тел (например,
потоки электронов в электрической
лампе).

Для существования
и появления тока необходимы следующие
условия:

–
наличие в данной среде свободных
носителей заряда, т.е. частиц, которые
могли бы упорядоченно перемещаться.

–
существование в данной среде внешнего
электрического поля, энергия которого
расходуется на упорядоченное перемещение
электрических зарядов.

–
источник энергии, пополняющий запас
энергии электрического поля.

За положительное
направление тока принято направление
упорядоченного движения положительных
электрических зарядов.

Сила
тока – это скалярная величина, равная
отношению заряда dq,
переносимого через рассматриваемую
поверхность dS
за малый промежуток времени, к величине
dt
этого промежутка:

.

Если
сила и направление тока не меняется во
времени, ток называется постоянным:
,

где q
–заряд, переносимый через рассматриваемую
поверхность за конечный интервал
времени t
.

Сила
тока в системе СИ измеряется в Амперах

.

Характеристикой
тока, отражающей его распределение по
поверхности, является плотность тока
.
Плотность тока – векторная величина,
направленная противоположно движению
электронов, и численно равная отношению
силы токачерез очень малый элемент поверхности,
нормальный к направлению движения
зарядов, к величине
площади этого элемента:

,
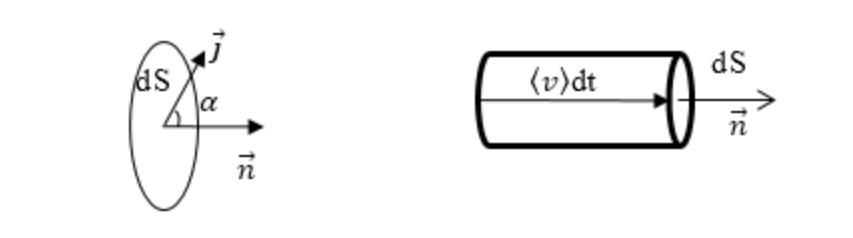
где
– орт вектора,
совпадающий с нормалью к поверхности.
Для произвольно ориентированного
элементаdS
имеем:
,
где
-угол
между направлением тока и нормалью кdS.

Для
постоянного тока
по всему поперечному сечениюS
однородного проводника, сила тока I=jS.

Зная
вектор
в каждой точке пространства, можно найти
силу тока через любую поверхность:
.
Таким образом, сила
тока есть поток вектора плотности тока
через поверхность S.

Электрический
ток может быть обусловлен движением
как положительных, так и

отрицательных
носителей. Перенос отрицательного
заряда в одном направлении эквивалентен
переносу такого же по величине
положительного заряда в противоположном
направлении.

Если
ток создается носителями обоих знаков,
и за время dt
через данную поверхность положительные
носители переносят заряд
в одном направлении, а отрицательные
– зарядв противоположном, то сила тока равна

.

Поле
вектора плотности тока можно изобразить
с помощью линий тока, это кривые,
касательные в каждой точке к которым
совпадают по направлению с вектором
.

Пусть
в единице объема содержится
положительных носителей и– отрицательных. Алгебраическая величина
зарядов носителей равна соответственнои.
Если под действием поля носители
приобретают средние скоростии,
то за единицу времени через единичную
площадку пройдетположительных носителей, которые
перенесут заряд,
отрицательные носители перенесут в
противоположном направлении заряд.

Тогда
плотность тока равна
,
или в векторной форме,
оба слагаемых имеют одинаковое направление
(скоростьнаправлена противоположно,дает знак минус, поэтомуимеет то же направление, что).
Произведение– плотность заряда положительных
носителей,–плотность заряда отрицательных
носителей, тогда.

Рассмотрим
некоторую среду, в которой течет ток.
Выберем воображаемую замкнутую
поверхность S.
Заряд, выходящий в единицу времени из
объема V,ограниченного
поверхностью S,
согласно закону сохранения заряда,
равен скорости убывания заряда q,
содержащегося в данном объеме (рис.2.1)

.

Н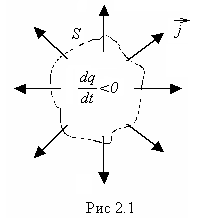о,
тогда.
Преобразуем это выражение по теореме
Остроградского-Гаусса, имеем.
Это равенство выполняется при произвольном
выборе объемаV,
следовательно, в каждой точке пространства
должно выполняться условие

.

Это
равенство получило название уравнения
непрерывности. Оно
выражает закон сохранения заряда.
Согласно этому уравнению, в точках,
которые являются источниками вектора
,
происходит убывание заряда.

В
случае стационарного тока объемная
плотность заряда
не зависит от времени, тогда уравнение
непрерывности имеет вид:

–в случае постоянного тока векторне имеет источников. Это означает, что
линии тока нигде не начинаются и нигде
не заканчиваются. Следовательно, линии
постоянного тока всегда замкнуты, и
число линий, входящих в замкнутую
поверхность, равно числу линий, выходящих
их поверхности,
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  08.03.2015550.91 Кб49.doc

• #
• #
• #
• #
• #
• #

В электродинамике — разделе учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел, важнейшим понятием является понятие элек­трического тока.

2.1. Электрический ток в проводниках. Направление электрического тока. Сила и плотность тока

Направленное движение электрических зарядов называется электрическим током. Носителями зарядов в зависимости от типа проводника могут быть электроны и ионы. В металлических проводниках – это свободные электроны, или электроны проводимости, в гальванических ваннах, т. е. в растворах электролитов, – положительные и отрицательные ионы. Тела или вещества, в которых можно создать электрический ток, называют проводниками электрического тока. Проводниками являются все металлы, водные растворы солей или кислот, ионизованные газы.

При движении свободных заряженных частиц происходит перенос заряда. Количественной характеристикой – силой $$ I$$ тока – принято считать скорость переноса заряда через любое поперечное сечение проводника, т. е. количество заряда, перемещённого через «контрольную поверхность», на которой осуществляется подсчёт пересёкшего её заряда, в единицу времени:

где `q` – заряд, прошедший через произвольное фиксированное поперечное сечение проводника за время от `0` до `t`. Если сила тока не изменяется со временем, ток называют постоянным. Единица измерения силы тока в системе СИ называется ампером (А) (в честь А.М. Ампера – французского учёного XIX века) и вводится через магнитное взаимодействие токов.

Один ампер есть сила такого тока, поддерживаемого в двух бесконечных (очень длинных) прямолинейных параллельных проводниках ничтожно малой площади поперечного сечения, расположенных на расстоянии `1`м в вакууме, при котором в расчёте на `1` метр длины проводника действует сила  `F=2*10^(-7) “Н”`.

Единица измерения силы тока ампер, наряду с метром, секундой, килограммом, является основной единицей системы СИ. Единица измерения заряда кулон (Кл) является производной и вводится в соответствии с (1): один кулон – это электрический заряд, проходящий через поперечное сечение проводника при силе тока $$ 1mathrm{A}$$ за $$ 1mathrm{c}$$, т. е. $$ 1mathrm{Кл}=1mathrm{A}·1mathrm{c}.$$

За направление электрического тока принимают направление, в котором движутся положительно заряженные носители тока.

Отношение силы `I` тока к площади `S` поперечного сечения проводника называется плотностью тока:

которая равна силе тока в расчёте на единицу площади поперечного сечения.

Сила тока I для тока, протекающего через некоторую площадь сечения проводника S эквивалентна производной заряда q по времени t и количественно характеризует электрический ток.

Таким образом выходит, что сила тока — это поток заряженных частиц через некоторую поверхность S.

Электрический ток является процессом движения как отрицательных, так и положительных зарядов.

Перенос заряда одного знака в определенную сторону равен переносу заряда, обладающего противоположным знаком, в обратном направлении. В ситуации, когда ток образуется зарядами и положительного, и отрицательного знаков (dq+ и dq−), справедливым будет заключение о том, что сила тока равна следующему выражению:

I=dq+dt+dq-dt.

В качестве положительного определяют направление движения положительных зарядов. Ток может быть постоянным, когда ни сила тока, ни его направление не претерпевают изменений с течением времени, или, наоборот, переменным. При условии постоянства, формула силы тока может выражаться в следующем виде:

I=q∆t,

где сила тока определена в качестве заряда, который пересекает некоторую поверхность S в единицу времени. В системе СИ роль основной единицы измерения силы тока играет Ампер (А).

1A=1 Кл1 с.

Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью

Выделим в проводнике, в котором протекает ток, малый объем dV случайной формы. С помощью следующего обозначения υ определим среднюю скорость движения носителей зарядов в проводнике. Пускай n0 представляет собой концентрацию носителей заряда. На поверхности проводника выберем пренебрежительно малую площадку dS, которая расположена ортогонально скорости υ (рис. 1).

Рисунок 1

Проиллюстрируем на поверхности площадки dS очень короткий прямой цилиндр, имеющий высоту υdt. Весь массив частиц, которые располагались внутри такого цилиндра за время dt пересекут плоскость dS и перенесут через нее, в направлении скорости υ, заряд, выражающийся в виде следующего выражения:

dq=n0qeυdSdt,

где qe=1,6·10-19 Кл является зарядом электрона, другими словами отдельной частицы или же носителя тока. Разделим приведенную формулу на dSdt и получим:

j=dqdSdt,

где j представляет собой модуль плотности электрического тока.

j=n0qeυ,

где j является модулем плотности электрического тока в проводнике, в котором заряд переносится электронами. В случае, если ток появляется как результат движения нескольких типов зарядов, то формула плотности тока может быть определена в виде следующего выражения:

j=∑niqiυii,

где i представляет собой носитель заряда. Плотность тока — это векторная величина. Снова обратим внимание на рисунок 1. Пускай n→ представляет собой единичный перпендикуляр к плоскости dS. В случае, если частицы, переносящие заряд, являются положительными, то переносимый ими заряд в направлении нормали больше нуля. В общем случае переносимый в единицу времени элементарный заряд может быть записана в следующем виде:

dqdt=j→n→dS=jndS.

Формула приведенная выше справедлива также в том случае, когда плоскость площадки dS неортогональная по отношению к вектору плотности тока. По той причине, что составляющая вектора j→, направленная под прямым углом к нормали, через сечение dS электричества не переносит. Исходя из всего вышесказанного, плотность тока в проводнике окончательно запишем, применяя формулу j=n0qeυ в таком виде:

j→=-n0qeυ→.

Таким образом, плотность тока эквивалентна количеству электричества, другими словами заряду, который протекает за одну секунду через единицу сечения проводника. В отношении однородного цилиндрического проводника справедливым будет записать, что:

j=IS∆t,

где S играет роль площади сечения проводника. Плотность постоянного тока равна по всей площади сечения проводника. Для двух разных сечений проводника (S1,S2) с постоянным током справедливо следующее равенство:

j1j2=S2S1.

Основываясь на законе Ома для плотности токов можно записать такое выражение:

j→=λE→,

где λ обозначает коэффициент удельной электропроводности. Определив плотность тока, мы имеем возможность выразить силу тока в следующем виде:

I=∫SjndS,

где интегрирование происходит по всей поверхности S любого сечения проводника. Единица плотности тока Aм2.

Линии тока

Линии, вдоль которых движутся заряженные частицы, носят название линий тока.

Направления движения положительных зарядов также определяются в качестве направлений линий тока. Изобразив линии тока, можно получить наглядное представление о движении электронов и ионов, которые формируют собой ток. Если внутри проводника выделить трубку с током, у которой боковая поверхность состоит из линий тока, то движущиеся заряженные частицы не будут пересекать боковую поверхность данной трубки. Такую трубка представляет собой так называемую трубку тока. К примеру, поверхность металлической проволоки в изоляторе будет определяться как труба тока.