Как найти силу трения действующую на автомобиль

Благодаря этой силе автомобили тормозят на светофоре, катер останавливается в воде, колесо буксует в яме. Как вы уже поняли, в этой статье мы будем разбираться, как решать задачи на силу трения.

Сила трения имеет электромагнитную природу. Это значит, что эта сила проявляется в результате взаимодействия частиц, из которых состоит вещество.

Хотите больше полезной и интересной информации по разным темам? Подписывайтесь на наш телеграм-канал.

Что нужно знать о силе трения, чтобы решать задачи

Трение – один из видов взаимодействия тел, которое возникает при их соприкосновении.

Сила трения всегда направлена в сторону, противоположную движению и по касательной к соприкасающимся поверхностям. Между твердыми телами возникает сухое трение, а при движении тел в жидкостях или газах говорят о вязком трении.

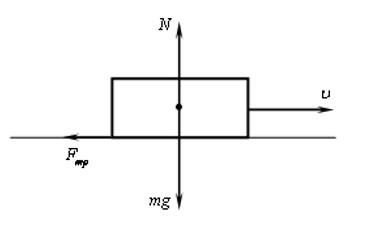
Природу этой силы мы уже установили. Помимо этого нужно знать, что бывают разные виды сил трения:

• трение покоя; 
• трение скольжения;
• трение качения (при перекатывании тел друг по другу);
• сопротивление среды (для движения в жидкости).

Вот пример на виды силы трения: брусок лежит на столе, и никто его на трогает. В этом случае действуют только сила тяжести и сила нормальной реакции опоры. Если мы начнем толкать брусок, но так сильно, чтобы его сдвинуть, на него будет действовать сила трения покоя, по третьему закону Ньютона равная внешней силе, приложенной к бруску. Сила трения покоя имеет предельное значение. Если внешняя сила будет больше этого значения, брусок начнет скользить по столу. В этом случае говорят о силе трения-скольжения. А вот и простейшая формула для силы трения:

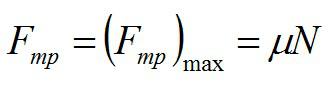
«Мю» – коэффициент трения скольжения. Это безразмерная величина, которая зависит от материалов взаимодействующих тел и от качества их поверхностей. Величина коэффициента трения не превышает единицы.

При решении простых физических задач силу трения скольжения часто принимают равной максимальной силе трения покоя.

Не забывайте также про нашу памятку и подборку полезных формул.

Вопросы по теме «Сила трения»

Вопрос 1. От чего зависит сила трения?

Ответ. Взглянем на формулу выше, и ответ придет сам. Сила трения зависит от свойств соприкасающихся тел, силы нормальной реакции опоры, скорости относительного движения тел.

Вопрос 2. Зависит ли сила трения от площади соприкасающихся поверхностей?

Ответ. Нет, площадь не влияет на силу трения.

Вопрос 3. Какими способами можно уменьшить или увеличить силу трения?

Ответ. Можно уменьшить коэффициент трения, сделав сухое трения вязким. Для увеличения силы трения необходимо увеличить давление на них.

Вопрос 4. Тело покоится на плоскости. Действует ли на него сила трения?

Ответ. Если на тело не действуют внешние силы, то сила трения покоя, по третьему закону Ньютона, равна нулю.

Вопрос 5. Какая из этих сил самая большая по модулю: сила трения покоя, сила трения качения или сила трения скольжения?

Ответ. Сила трения скольжения имеет самое большое значение.

Вопрос 6. Какие есть примеры полезного действия силы трения?

Ответ. Среди полезного использования силы трения можно выделить работу тормозов транспортных средств, добычу огня первобытными людьми.

Задачи на силу трения с решениями

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задача №1. Нахождение силы трения

Условие

Брусок массой 5 килограмм скользит по горизонтальной поверхности. Сила трения скольжения равна 20 Н. Найдите силу трения, если масса бруска уменьшится в два раза, а коэффициент трения останется неизменным. 

Решение

Применим формулы:

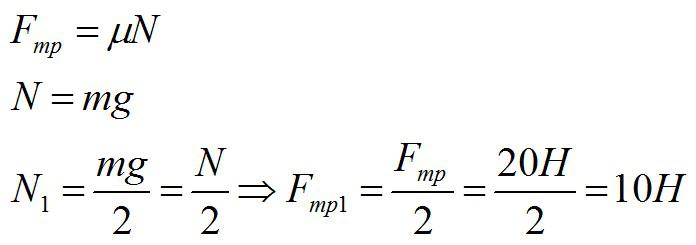
Ответ: 10 Н.

Задача №2. Нахождение коэффициента трения

Условие

Тело скользит по горизонтальной плоскости. Найти коэффициент трения, если сила трения равна 5 Н, а сила давления тела на плоскость – 20 Н.

Решение

Сила давления тела на плоскость равна силе нормальной реакции опоры. 

Ответ: 0,25

Задача №3. Нахождение силы трения и коэффициента трения

Условие

Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определите силу трения и коэффициент трения.

Решение

Сначала найдем ускорение, с которым движется лыжник. Затем по второму закону Ньютона найдем силу, которая действует на него:

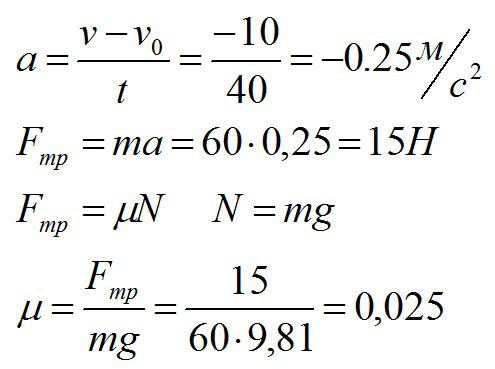
Ответ: 15 Н; 0,025.

Задача №4. Нахождение силы трения

Условие

Брусок массой 20 кг равномерно перемещается по горизонтальной поверхности под действием постоянной силы, направленной под углом 30° к поверхности и равной 75 Н. Каков коэффициент трения между бруском и плоскостью?

Решение

Сначала воспользуемся вторым законом Ньютона, учитывая, что ускорение равно нулю. Затем найдем проекции силы на вертикальную и горизонтальную оси:

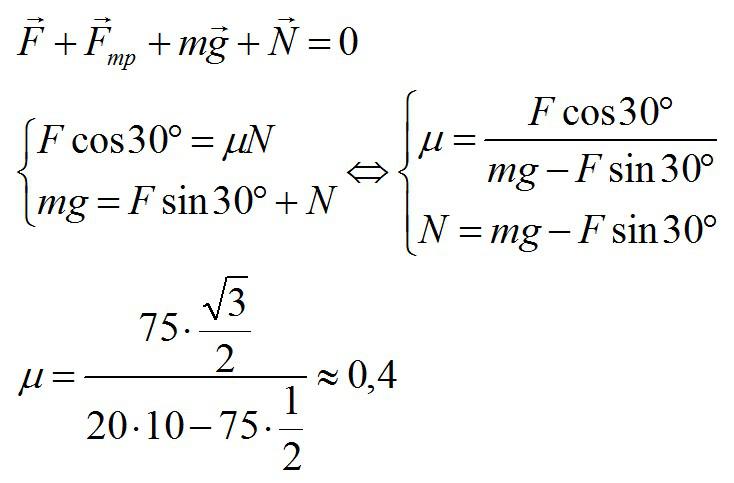
Ответ: 0,4

Задача №5. Нахождение силы трения покоя

Условие

Ящик массой 10 кг стоит на горизонтальном полу. Коэффициент трения между полом и ящиком равен 0,25. К ящику в горизонтальном направлении прикладывают силу 16 Н. Сдвинется ли он с места. Какова сила трения между ящиком и полом?

Решение

Вычислим максимальную силу трения покоя:

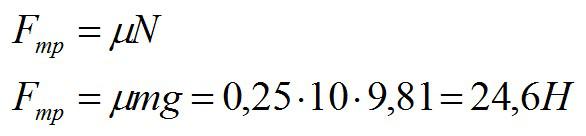
Так как приложенная сила по условию меньше, чем максимальная сила трения покоя, ящик останется стоять на месте. Сила трения между полом и ящиком, по третьему закону Ньютона, равна приложенной силе.

Ответ: 16 Н.

Нужна помощь в решении задач или других заданий? Обращайтесь за ней в профессиональный студенческий сервис.

1. Сила трения скольжения

Поставим опыт

Толкнем лежащий на столе брусок, сообщив ему некоторую начальную скорость. Мы увидим, что брусок скользит по столу и его скорость уменьшается до полной остановки (на рисунке 17.1 показаны последовательные положения бруска через равные промежутки времени). Как вы уже знаете из курса физики основной школы, тормозит брусок силы трения скольжения, действующая на него со стороны стола.

Силы трения скольжения действуют на каждое из соприкасающихся тел, когда они движутся друг относительно друга.

Эти силы действуют на каждое из соприкасающихся тел (рис. 17.2). Они равны по модулю и противоположны по направлению, потому что связаны третьим законом Ньютона.

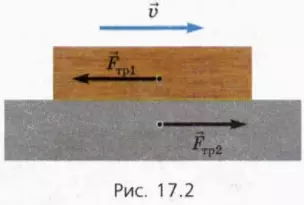
Когда брусок скользит по столу, мы не замечаем силу трения скольжения, действующую на стол со стороны бруска, потому что стол прикреплен к полу (или на стол со стороны пола действует довольно большая сила трения покоя, речь о которой пойдет далее).

Если же толкнуть брусок, лежащий на тележке, то под действием силы трения скольжения, действующей на тележку со стороны бруска, тележка станет двигаться с ускорением, а скорость бруска относительно тележки будет уменьшаться.

? 1. Во сколько раз ускорение бруска относительно стола в этом опыте больше, чем ускорение тележки относительно стола, если масса бруска 200 г, а масса тележки 600 г? Трением между тележкой и столом можно пренебречь.

Силы трения скольжения направлены вдоль поверхности соприкосновения тел. Действующая на каждое тело сила трения направлена противоположно скорости этого тела относительно другого тела.

Силы трения скольжения обусловлены главным образом зацеплением и разрушением неровностей соприкасающихся тел (эти неровности на рисунке 17.3 для наглядности преувеличены). Поэтому обычно чем более гладкие поверхности соприкасающихся тел, тем меньше силы трения между ними.

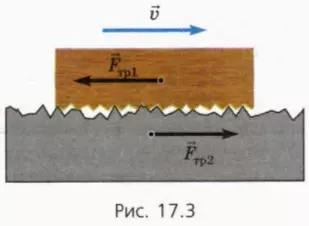
Однако если сделать соприкасающиеся поверхности очень гладкими (например, отшлифовать их), то сила трения скольжения может увеличиться вследствие действия сил межмолекулярного притяжения.

Выясним, от чего зависит сила трения скольжения.

От чего зависит сила трения скольжения?

Поставим опыт
Будем с помощью динамометра тянуть брусок по столу с постоянной скоростью (рис. 17.4, а), прикладывая к нему горизонтально направленную силу _упр.

При движении с постоянной скоростью ускорение бруска равно нулю. Следовательно, силу трения скольжения, действующую на брусок со стороны стола, уравновешивает сила упругости, действующая на брусок со стороны динамометра. Значит, эти силы равны по модулю, то есть динамометр показывает модуль силы трения.

Повторим опыт, положив на брусок другой такой же брусок (рис. 17.4, б). Мы увидим, что сила трения скольжения увеличилась в 2 раза. Заметим теперь, что в этом опыте (по сравнению с опытом с одним бруском) сила нормальной реакции тоже увеличилась в 2 раза.

Изменяя силу нормальной реакции, можно убедиться, что модуль силы трения скольжения Fтр пропорционален модулю силы нормальной реакции N:

F_тр.ск = μN.     (1)

Как показывает опыт, сила трения скольжения практически не зависит от относительной скорости движения соприкасающихся тел и от площади их соприкосновения.

Коэффициент пропорциональности μ называют коэффициентом трения. Его определяют из опыта (см. лабораторную работу 4). Он зависит от материала и качества обработки соприкасающихся поверхностей. На форзаце задачника (под обложкой) приведены приближенные значения коэффициента трения для некоторых видов поверхностей.

Коэффициент трения шин по мокрому асфальту или по льду в несколько роз меньше коэффициента трения шин по сухому асфальту. Поэтому тормозной путь автомобиля значительно увеличивается во время дождя или гололеда. О скользкой дороге водителей предупреждает дорожный знак (рис. 17.5).

? 2. Тело массой m движется по горизонтальной поверхности. Коэффициент трения между телом и поверхностью μ.
а) Чему равна сила трения скольжения?
б) С каким по модулю ускорением движется тело, если на него действуют только сила тяжести, сила нормальной реакции и сила трения скольжения?

? 3. Лежащему на столе бруску сообщили скорость 2 м/с, и он прошел до остановки 1 м (тормозной путь). Чему равен коэффициент трения между бруском и столом?

? 4. Можно приближенно считать, что на автомобиль при торможении действует сила трения скольжения. Оцените, чему равен тормозной путь автомобиля на сухом асфальте и на льду при начальной скорости 60 км/ч; 120 км/ч. Сравните найденные значения с длиной классной комнаты.

Полученные ответы удивят вас. Наверное, вы станете осторожнее на дороге во время дождя и особенно гололеда.

2. Сила трения покоя

Поставим опыт
Попробуйте сдвинуть с места шкаф (рис. 17.6). Он будет оставаться в покое, даже если прикладывать к нему довольно большую силу.

Какая же сила уравновешивает горизонтально направленную силу, приложенную вами к шкафу? Это сила трения покоя, действующая на шкаф со стороны пола.

Силы трения покоя возникают при попытке сдвинуть одно из соприкасающихся тел относительно другого в том случае, когда тела остаются в покое друг относительно друга. Эти силы препятствуют относительному движению тел.

? 5. Действует ли сила трения покоя на пол со стороны шкафа (рис. 17.6)?

Причины возникновения силы трения покоя сходны с причинами возникновения силы трения скольжения: наличие неровностей на соприкасающихся поверхностях тел и действие сил межмолекулярного притяжения.

Будем постепенно увеличивать приложенную к шкафу горизонтальную силу. При достижении некоторого ее значения шкаф сдвинется с места н начнет скользить по полу. Следовательно, модуль силы трения покоя Fтр.пок не превышает некоторого предельного значения, называемого максимальной силой трения покоя.

Опыт показывает, что максимальная сила трения покоя немного больше силы трения скольжения. Однако для упрощения решения школьных задач принимают, что максимальная сила трения покоя равна силе трения скольжения:

F_тр.пок ≤ μN.      (2)

Если тело покоится, то сила трения покоя _тр.пок уравновешивает силу , направленную вдоль поверхности соприкосновения тел и стремящуюся сдвинуть тело.
Следовательно, в этом случае

F_тр.пок = F.     (3)

Обратите внимание: сила трения покоя удовлетворяет двум соотношениям – неравенству (4) и равенству (5). Из них следует неравенство для силы , которая не может сдвинуть тело:

F ≤ μN.     (4)

Если же F > μN, то тело начнет скользить, и на него будет действовать сала трения скольжения. В таком случае

F_тр = F_тр.ск = μN.

Соотношения (3) и (5) иллюстрирует график зависимости силы трения Fтр от приложенной к телу силы F (рис. 17.7).

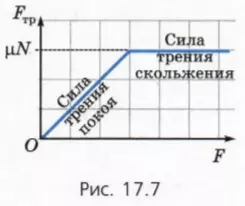
? 6. К лежащему на столе бруску массой 1 кг прикладывают горизонтальную силу, равную по модулю F. Коэффициент трения между бруском и столом равен 0,3. Чему равна действующая на брусок со стороны стола сила трения, если F = 2 Н? F = 5 Н?

? 7. Тягач тянет по горизонтали связку бревен массой 10 т с силой 40 кН. Чему равно ускорение связки, если коэффициент трения между бревнами и дорогой равен 0,3? 0,5?

? 8. Находящийся на столе брусок массой 1 кг тянут горизонтальной пружиной жесткостью 100 Н/м. Коэффициент трения 0,3. Каково удлинение x пружины, если брусок покоится? движется со скоростью 0,5 м/с?

Может ли сила трение быть движущей силой?

Делая шаг, человек толкает дорогу назад, действуя на нее силой трения покоя _тр1: ведь подошва во время толчка покоится относительно дороги (на это иногда указывает четкий отпечаток подошвы) (рис. 17.8, а). Согласно третьему закону Ньютона, со стороны дороги на человека действует такая же по модулю сила трения покоя _тр2, направленная вперед.

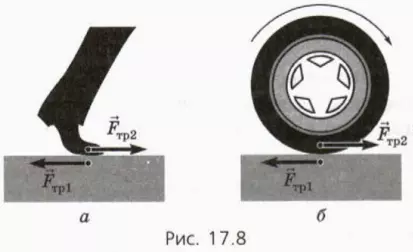
Сила трения покоя разгоняет и автомобиль (рис. 17.8, б). Когда колесо катится без проскальзывания, его нижняя точка покоится относительно дороги. Ведущее колесо автомобиля (приводимое во вращение двигателем) толкает дорогу назад, действуя на нее силой трения покоя _тр1. Согласно третьему закону Ньютона, дорога при атом толкает колесо (а вместе с ним и автомобиль) вперед силой трения покоя _тр2. Именно эту силу и называют часто силой тяги.

? 9. С какой целью локомотивы (электровозы и тепловозы) делают очень массивными?

? 10. Коэффициент трения между шинами ведущих колес автомобиля и дорогой равен 0,5. Считайте, что сопротивлением воздуха можно пренебречь.
а) С каким максимально возможным ускорением может двигаться автомобиль, если все его колеса – ведущие?
б) Увеличилось бы или уменьшилось максимально возможное ускорение автомобиля, если ведущими были бы только передние или только задние колеса? Обоснуйте свой ответ.

Подсказки. Ускорение автомобиля обусловлено действием силы трения покоя со стороны дороги.

Дополнительные вопросы и задания

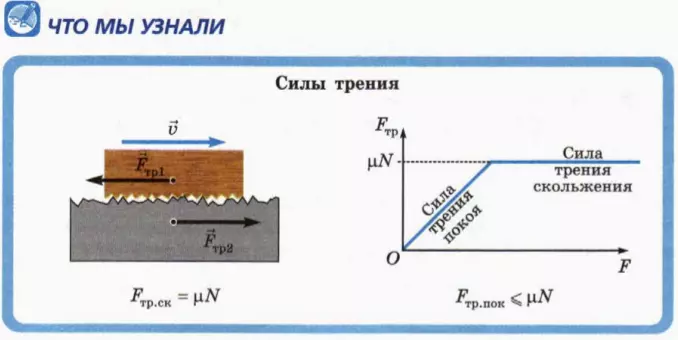
11. На рисунке 17.9 приведены графики зависимости силы трения скольжения от силы нормальной реакции при движении по столу трех разных брусков. Между каким бруском и столом коэффициент трения наибольший? Чему он равен?

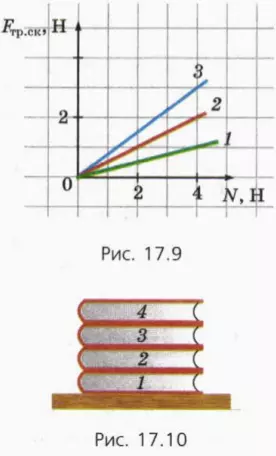
12. На столе лежит стопка из четырех одинаковых книг массой 500 г каждая (рис. 17.10). Коэффициент трения между обложками книг равен 0,4. Какую горизонтально направленную силу надо приложить, чтобы, придерживая остальные книги:
а) сдвинуть книгу 4?
б) сдвинуть книги 3 и 4 вместе?
в) вытащить книгу 3?
г) вытащить книгу 2?

13. Оцените, до какой скорости может разогнаться за 2 с автомобиль на мокром асфальте. Все его колеса ведущие.

2017-12-15   

Как направлена сила трения, действующая на ведущие колеса автомобиля, при разгоне (а), торможении (б), повороте (в)? Равна ли эта сила своему максимальному значению $mu N$ ($mu$ – коэффициент трения, $N$ – сила реакции полотна дороги), и если да, то в каких ситуациях? А в каких ситуациях нет? Хорошо это, или плохо, если сила трения достигает своего максимального значения? Почему? Какой автомобиль может развивать на дороге большую мощность – передне- или заднеприводный – при одинаковой мощности мотора и почему? Считать, что масса автомобиля распределена равномерно, и его центр тяжести находится посередине.

Решение:

Обсудим сначала вопрос о роли силы трения в движении машины. Представим себе, что водитель машины, стоящей на гладком-гладком льду (сила трения между колесами и льдом отсутствует), нажимает на педаль газа. Что будет происходить? Ясно, что машина ехать не будет: колеса будут вращаться, но будут пробуксовывать относительно льда – ведь трения-то нет. Причем это будет происходить независимо от мощности двигателя. А это значит, что для того, чтобы мощность двигателя использовать, нужно трение – без него машина не поедет.

Что же происходит, когда сила трения есть. Пусть сначала она очень маленькая, а водитель стоящей машины снова нажимает на педаль газа? Колеса (речь сейчас идет о ведущих колесах автомобиля, допустим это передние колеса) проскальзывают относительно поверхности (трение – маленькое), вращаясь так, как показано на рисунке, но при этом возникает сила трения, действующая со стороны дороги на колеса, направленная вперед по ходу движения машины. Она и толкает машину вперед.

Если сила трения большая, то при плавном нажатии на педаль газа колеса начинают вращаться, и как бы отталкиваются от шероховатостей дороги, используя силу трения, которая направлена вперед. При этом колеса не проскальзывают, а катятся по дороге, так, что нижняя точка колеса не перемещается относительно полотна. Иногда и при большом трении колеса пробуксовывают. Наверняка, вы сталкивались с ситуацией, когда какой-нибудь «сумасшедший водитель» так трогается при включении зеленого сигнала светофора, что колеса «визжат», а на дороге остается черный след из-за скольжения резины по асфальту. Итак, в экстренной ситуации (при резком торможении или трогании с побуксовкой) колеса скользят относительно дороги, в обычных случаях (когда на дороге не остается черного следа от стирающихся покрышек) колесо не скользит, а только катится по дороге.

Итак, если машина едет равномерно, то колеса не скользят по дороге, а катятся по ней так, что нижняя точка колеса покоится (а не проскальзывает) относительно дороги. Как в этом случае направлена сила трения? Сказать, что противоположно скорости машины – неверно, ведь говоря так про силу трения, подразумевают случай скольжения тела относительно поверхности, а сейчас у нас скольжения колес относительно дороги нет. Сила трения в этом случае может быть направлена как угодно, и мы сами определяем ее направление. И вот как это происходит.

Представим себе, что нет никаких препятствующих движению машины факторов. Тогда машина движется по инерции, колеса вращаются по инерции, причем угловая скорость вращения колес связана со скоростью движения машины. Установим эту связь. Пусть колесо движется со скоростью $v$ и вращается так, что нижняя точка колеса не проскальзывает относительно дороги. Перейдем в систему отсчета, связанную с центром колеса. В ней колесо как целое не движется, а только вращается, а земля движется назад со скоростью $v$. Но поскольку колесо не проскальзывает относительно земли, то его нижняя точка имеет такую же скорость как земля. А значит, и все точки поверхности колеса вращаются относительно центра со скоростью $v$ и, следовательно, имеют угловую скорость $omega = v / R$, где R – радиус колеса. Переходя теперь назад в систему отсчета, связанную с землей, заключаем, что при отсутствии проскальзывания между нижней точкой колеса и дорогой угловая скорость колеса $omega = v / R$, а все точки поверхности имеют разные скорости относительно земли: например, нижняя точка – нулевую, верхняя $2v$ и т. д.

А пусть водитель при таком движении машины нажимает на педаль газа. Он заставляет колесо вращаться быстрее, чем нужно при данной скорости машины. Колесо стремится проскользнуть назад, возникает сила трения, направленная вперед, которая и разгоняет машину (машина как бы отталкивается от шероховатостей дороги, используя силу трения). Если водитель нажимает на педаль тормоза, колесо стремится вращаться медленнее, чем нужно при данной скорости машины. Возникает сила трения, направленная назад, которая тормозит машину. Если водитель поворачивает колеса машины, возникает сила трения, направленная в сторону поворота, которая машину поворачивает. Таким образом, управление машиной – разгоном, торможением, поворотом – основано на правильном использовании силы трения, причем, конечно, подавляющее большинство водителей об этом даже не догадываются.

Ответим теперь на вопрос: равна ли эта сила своему максимальному значению? Вообще говоря, нет, поскольку нет скольжения колеса относительно дороги, а сила трения равна максимальному значению при скольжении. В покое сила трения может принимать любые значения от нуля до максимального $mu N$, где $mu$ – коэффициент трения; $N$ – сила реакции опоры. Поэтому если мы разгоняемся (сила трения направлена вперед), но хотим увеличить темп разгона, мы сильнее нажимаем на педаль газа, и увеличиваем силу трения. Аналогично, если мы тормозим (сила трения направлена назад), но хотим увеличить степень торможения, мы сильнее нажимаем на тормоз и увеличиваем силу трения. Но ясно, что ее можно увеличить и в том и в другом случае, если она не была максимальной! Таким образом, для управления машиной сила трения не должна равняться максимальному значению, и эту разность мы используем для совершения тех или иных маневров. И любой водитель (даже если он ничего не знает про силу трения, а таких, конечно, подавляющее большинство) интуитивно чувствует, есть ли у него резерв силы трения, «далеко» ли машина от пробуксовки, и есть ли возможность ей управлять.

Тем не менее, есть одна ситуация, когда сила трения равна своему максимальному значению. Эта ситуация называется заносом. Пусть водитель резко затормозил на скользкой дороге. Машина начинает скользить по дороге, это состояние движения и называется заносом. В этом случае сила трения направлена противоположно скорости (назад) и равна своему максимальному значению. Это ситуация очень опасна, ведь машина АБСОЛЮТНО неуправляема. Мы не можем повернуть (хоть как-то, хоть чуть-чуть), ведь для поворота нам нужна сила трения, направленная в сторону поворота, а в нашем распоряжении ее нет – сила трения максимальна и направлена назад. Мы не можем увеличить скорость торможения (невозможно увеличить силу трения – она и так максимальна), не можем (даже если бы мы захотели этого в такой ситуации) ускориться. Мы не можем ничего! Ситуация осложняется еще и тем, что в состоянии заноса машину никто не «держит» на дороге. Почему машина в обычных условиях не съезжает в кювет, ведь полотно дороги всегда делается покатым к обочинам, чтобы стекала вода? Ее держит сила трения, а вот если машина скользит (занос) сила трения направлена противоположно скорости и никак иначе. Поэтому любое «боковое» возмущение – покатость дороги, небольшой камень под одним из колес – могут развернуть или сбросить машину на обочину. Никогда не допускайте заноса1.

Теперь сравним мощность, которую могут развивать на дороге передне- и заднеприводной автомобили с одинаковым мотором. Очевидно, что мощность, которую может развивать автомобиль на дороге, зависит не только от его двигателя, но и от того, как автомобиль «использует» силу трения. Действительно, в отсутствие силы трения автомобиль стоял бы на месте (с вращающимися колесами) независимо от мощности двигателя (вращающего эти колеса). Докажем, что заднеприводные автомобили мощнее переднеприводных при одинаковой мощности мотора и оценим отношение мощностей, которые может развивать двигатель, разгоняя машину на дороге (при условии, что мощность самого двигателя может быть очень большой).

Разгоняет автомобиль сила трения, действующая на ведущие колеса, а она не может превышать значения $mu N$ ($N$ – сила реакции). Поэтому чем больше сила реакции, тем больших значений может достигнуть разгоняющая сила трения (а нажатие на педаль газа в ситуации, когда сила трения достигла максимума, приведет только к проскальзыванию и к заносу, но не к увеличению мощности, которую развивает двигатель). Найдем силы реакции для задних и передних колес машины. Силы, действующие на машину при разгоне, показаны на рисунках (на правом – для заднеприводной, на левом – для переднеприводной). На машину действуют: сила тяжести, силы реакции и сила трения. Поскольку машина движется поступательно, сумма моментов всех сил относительно ее центра тяжести равна нулю. Поэтому, если центр тяжести машины находится точно посередине машины, расстояние между задними и передними колесами $l$, а высота центра тяжести над дорогой $h$, условие равенства нулю суммы моментов относительно центра тяжести дает (при условии, что машина движется, развивая максимальную мощность на максимуме силы трения):

переднеприводная машина

$N_{1} frac{l}{2} = N_{2} frac{l}{2} + F_{тр} h = N_{2} frac{l}{2} + mu N_{2} h$, (1)

заднеприводная машина

$N_{1} frac{l}{2} = N_{2} frac{l}{2} + F_{тр} h = N_{2} frac{l}{2} + mu N_{1}h$, (2)

где $mu$ – коэффициент трения. Учитывая, что и в том и в другом случае $N_{1} + N_{2} = mg$, из (1) найдем силу реакции для передних колес в случае переднеприводного автомобиля

$N_{2}^{пп} = frac{mgl/2}{l + mu h}$ (3)

и из (2) силу реакции задних колес в случае заднего привода

$N_{1}^{зп} = frac{mgl/2}{l – mu h}$ (4)

(здесь (пп) и (зп) – передний и задний привод). Отсюда находим отношение сил трения, разгоняющих передне- и заднеприводную машину, и, следовательно, отношение мощностей, которые может развивать на дороге их двигатель

$frac{P^{(пп)}}{P^{зп}} = frac{l – mu h}{l + mu h}$. (5)

Для значений $l = 3 м, h = 0,5 м$ и $mu = 0,5$ имеем из (5)

$frac{P^{(пп)}}{P^{(зп)}} = 0,85$.