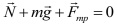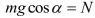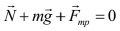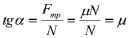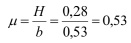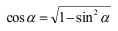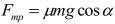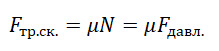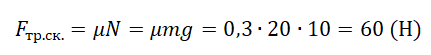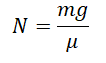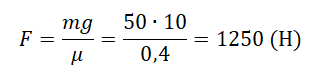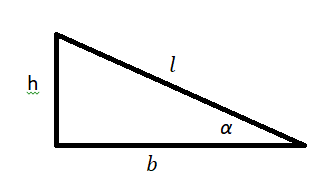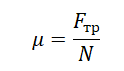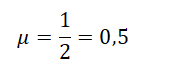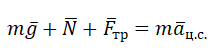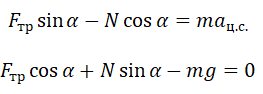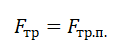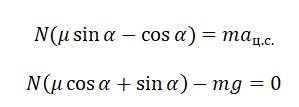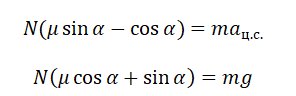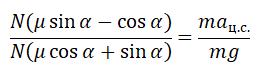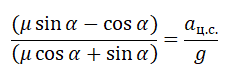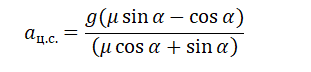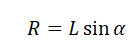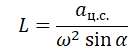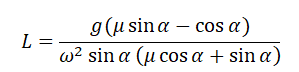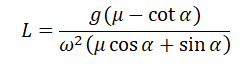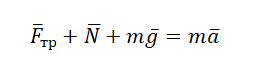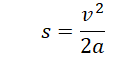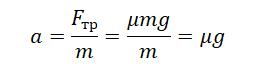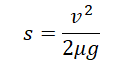- Авторы
- Научный руководитель
- Файлы
- Литература
Новосадов Д.А.
1
1 г. Димитровград, МАОУ «СШ №19 им. И. П. Мытарева г. Димитровграда Ульяновской области», 10 «Б» класс
Хайруллова Е.В. (Димитровград, МАОУ «СШ №19 им. И. П. Мытарева г. Димитровграда Ульяновской области»)
Нехожина Е.П. (Димитровград, МАОУ «СШ №19 им. И. П. Мытарева г. Димитровграда Ульяновской области»)
1. Касьянов В.А. Физика 10 класс. Углубленный уровень, Москва, «Дрофа», 2018 год.
2. Как найти силу трения скольжения. Статья. https://www.kakprosto.ru/kak-133127-kak-nayti-silu-treniya-skolzheniya
3. Мякишев Г. Я., Буховцев Б. Б., Сотский Н.Н. Физика 10 класс. Учебник для общеобразовательных учреждений, Москва, «Просвещение», 2011 год.
4. Сила трения. Статья. http://fizikatyt.ru/2016/07/14/%D1%81%D0%B8%D0%BB%D0%B0-%D1%82%D1%80%D0%B5%D0%BD%D0%B8%D1%8F/
5. Сила трения. Виды трения. Интернет – урок. https://interneturok.ru/physics/10-klass/bsily-v-mehanikeb/sila-treniya-vidy-treniya
6. Трение. Статья http://class-fizika.narod.ru/7_tren.htm
7. Трение. Материал из Википедии. https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B5%D0%BD%D0%B8%D0%B5
Вычислить силу трения можно по формуле:
Fтр = Fсдвиг, если тело покоится.
Из формулы видно, что сила трения вычисляется по-разному в случае, если тело покоится и в случае, если тело движется. На первую часть формулы, которая относится к силе трения покоя, в школьном курсе нет задач, а в олимпиадных задачах и задачах ЕГЭ эта формула применяется. Поэтому для выпускников актуально не просто запомнить формулу, а научиться ее применять. Для ее применения необходимо понять формулу и доказать ее истинность.
Целью работы является изучение силы трения и создание компьютерной модели для вычисления силы трения на наклонной плоскости. Для достижения этой цели поставлены следующие задачи:
1. Изучить силу трения, возникающую при взаимодействии поверхностей тела и наклонной плоскости при разных углах ее наклона.
2. Провести эксперименты, подтверждающие изученные закономерности.
3. На основе результатов экспериментов создать математическую и компьютерную модель для изучения силы трения.
Проблема исследования состоит в доказательстве формулы для силы трения. Объектом исследования является сила трения при движении тела по наклонной плоскости. Предметом исследования значение силы трения при разных углах наклона плоскости к горизонту. Продуктом работы является компьютерная модель для изучения силы трения между телом и наклонной плоскостью.
Формула для вычисления силы трения хорошо известна и изучается на уроках физики. Но эта формула не доказывалась, ни на уроке, ни в учебнике. В своей работе я привожу доказательство истинности формулы для вычисления силы трения на примере ее изучения в случае, когда сила возникает между телом и наклонной плоскостью. В этом и состоит мой вклад в изучаемый вопрос и новизна в подходе к изучению силы трения.
В ходе работы использовались следующие методы исследования:
• Теоретические (изучение, анализ, обобщение литературы).
• Эмпирические (наблюдения, беседы, измерения).
• Интерпретационные (количественная и качественная обработка результатов).
Литература, которую я использовал при изучении вопроса, является учебной. Это учебники физики для 7-го и 10-го классов различных авторов и открытые источники информации в сети интернет.
Основная часть
1. Виды силы трения
Сила трения – это сила, возникающая при движении или попытке движения одного тела по поверхности другого, направленная вдоль поверхности в сторону, противоположную движению или попытке движения. Причиной возникновения силы трения является сила притяжения между атомами веществ, находящихся на минимальном расстоянии друг от друга, т. е. на микроскопических выступах поверхностей. Суммарная сила притяжения атомов соприкасающихся тел столь значительна, что под действием внешней силы, приложенной к телу, тело остается в покое. Это означает, что на тело действует сила, равная по модулю внешней силе, но противоположно направленная. Это сила является силой трения покоя. Когда приложенная сила достигает максимального значения, достаточного для разрыва связей между выступами, тело начинает скользить. При этом сила трения скольжения остается постоянной, несколько меньше силы трения покоя.
2. Трение покоя у бруска находящегося в покое на наклонной плоскости
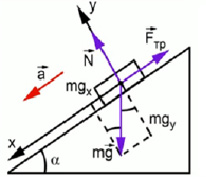
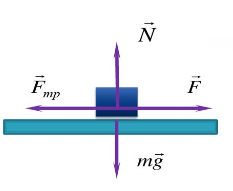
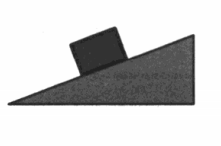
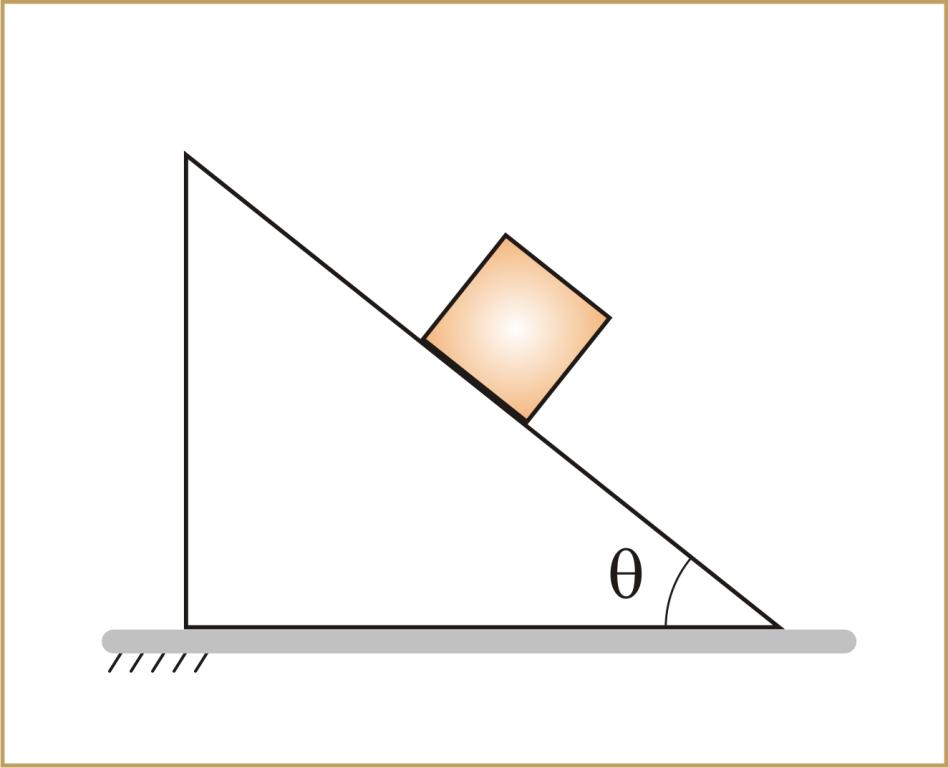
Рассмотрим ситуацию, когда деревянный брусок покоится на наклонной плоскости. На него действуют силы: тяжести, трения и реакции опоры. Покажем силы на чертеже и выберем оси координат (рис.1)
Рис.1.
Запишем первый закон Ньютона для нашего тела.
Спроецируем закон на выбранные оси ОХ и ОY. Учитывая, что угол альфа- угол между силой тяжести и перпендикуляром, на ось Х, получаем:
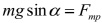
Значит силу трения можно найти из уравнения (1)
Учитывая, что синус угла можно найти как отношение высоты наклонной плоскости к ее длине, а масса бруска, равна 145 г, можно вычислить значения силы трения при разных углах наклона плоскости. Выполнив измерения и вычисления, получил данные, представленные в приложении 1.
Анализируя полученные данные, приходим к выводу, что при увеличении угла наклона сила трения всегда увеличивается. Но трение не может все время увеличиваться, так как в этом случае тело не будет скатываться с наклонной плоскости, а это противоречит реальности. Действительно, при угле наклона плоскости к горизонту α=90 0, тело падает под действием силы тяжести и сила трения отсутствует. Значит, существует максимальное значение силы трения для тела при изменении угла наклона плоскости от 0 0 до 90 0. Это значение соответствует ситуации равномерного скатывания тела с наклонной плоскости.
3. Трение скольжения бруска равномерно скатывающегося с наклонной плоскости
Для этой ситуации так же запишем первый закон Ньютона, так как при движении бруска ускорения нет.
Используя рис. 1, проецируем силы, действующие на брусок, на оси ОХ и ОY. Получаем, что
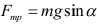
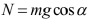
Поделив уравнение (3) на уравнение (4), получаем:
Но тангенс угла наклона можно вычислить как отношение высоты наклонной плоскости к ее длине основания. Следовательно, максимальный коэффициент трения можно вычислить тоже через отношение высоты наклонной плоскости к ее длине основания. Рассчитаем значение коэффициента силы трения при ее максимальном значении.
Брусок спускается без ускорения при высоте наклонной плоскости 28 см и ее основании 53 см. Тогда коэффициент трения равен 0,53, а максимальная сила трения 0,67 Н
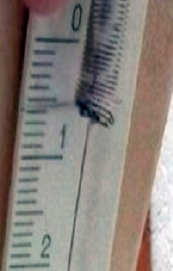
Проверим это с помощью динамометра. Значение трения получилось близкое к расчетному 0,67 Н, как видно на рисунке 2.
Рис.2.
4. Трение скольжения бруска скатывающегося с ускорением наклонной плоскости
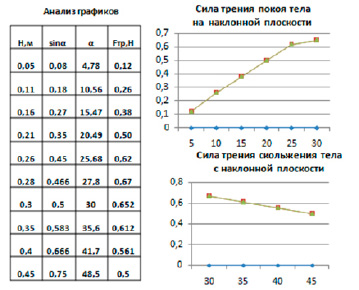
При дальнейшем увеличении угла наклона плоскости, сила трения начинает уменьшаться. Приложение 3 и Приложение 4. Выясним, почему это происходит. При увеличении угла, всегда уменьшается значение его косинуса.
А от косинуса зависит «игрековая» проекция силы тяжести, которая равна силе реакции опоры. Найдем отношение силы трения к значению косинуса угла. Это отношение остается неизменным и равно 0,75313. В эксперименте не меняется значение массы скатывающегося тела и материал трущихся поверхностей. Предположим, что это отношение и есть произведение коэффициента трения, массы тела и ускорения свободного падения. Вычисляя произведение, мы получаем такое же значение.
Следовательно, сила трения скольжения вычисляется действительно по формуле произведение коэффициента трения и силы реакции опоры.
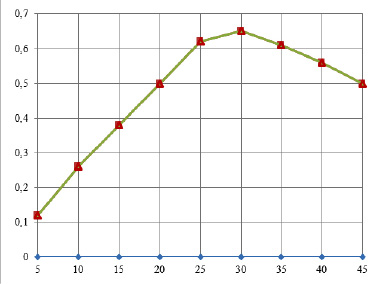
По результатам своих исследований я построил график зависимости силы трения от угла наклона плоскости. (рис.3.)
Рис.3.
5. Анализ зависимости силы трения тела на наклонной плоскости от угла наклона плоскости к горизонту
Анализируя график зависимости силы трения бруска от угла наклона плоскости к горизонту (Приложение 5) , видно, что в случае покоя тела сила трения равна сдвигающей силе. Так как сдвигающей силой на наклонной плоскости являлась иксовая проекция силы тяжести, которая увеличивалась при увеличении угла наклона, то и увеличивалась сила трения покоя.
В случае движения тела по плоскости сила трения уменьшается, так как уменьшается игрековая проекция силы тяжести. А сила трения вычисляется как произведение коэффициента трения на силу реакции опоры. (рис.3) Формула силы трения доказана.
Fтр = Fсдвиг, если тело покоится
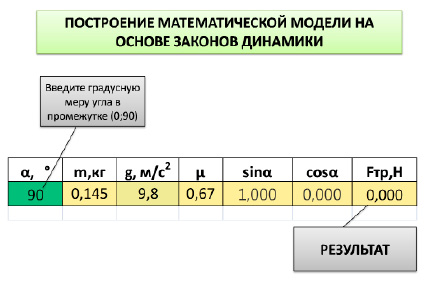
6. Компьютерная модель для изучения силы трения на наклонной плоскости
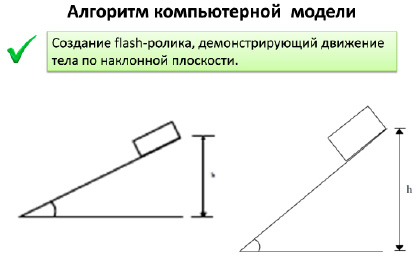
Изучив законы динамики, мной была построена компьютерная модель для изучения силы трения тела на наклонной плоскости с помощью программы Microsoft Office Excel 2007. Данная математическая модель автоматически просчитывает силу трения для произвольных углов. Ее интерфейс показан в приложении 7. Так же был создан флеш – ролик, демонстрирующий движение тела по наклонной плоскости. Для создания анимированных роликов использовался Adobe Flash cs6. (приложение 8) Для создания презентации применялся Microsoft PowerPoint 2007.
Для проведения эксперимента мне потребовалось оборудование:
Деревянная наклонная плоскость произвольной длины, линейка или рулетка, небольшой деревянный брусок, динамометр. (приложение 9)
Приложение 1
Таблица 1
Значения силы трения покоя бруска на наклонной плоскости при разных углах наклона плоскости к горизонту
|
H, м |
L, м |
sinα |
M, кг |
Fтр, Н |
|
0,05 |
0,6 |
0,08 |
0,145 |
0,12 |
|
0,11 |
0,6 |
0,18 |
0,145 |
0,26 |
|
0,16 |
0,6 |
0,27 |
0,145 |
0,38 |
|
0,21 |
0,6 |
0,36 |
0,145 |
0,50 |
|
0,26 |
0,6 |
0,45 |
0,145 |
0,62 |
|
0,3 |
0,6 |
0,5 |
0,145 |
0,71 |
Приложение 2
Фотографии экспериментов по определению максимального коэффициента трения при равномерном скатывании бруска с наклонной плоскости
Приложение 3
Фотографии экспериментов по определению коэффициента трения при равноускоренном скатывании бруска с наклонной плоскости
Приложение 4
Значения силы трения скольжения бруска по наклонной плоскости при разных углах наклона плоскости к горизонту
|
H,м |
L,м |
sinα |
α, 0 |
Fтр, Н |
|
0,28 |
0,6 |
0,466 |
27,8 |
0,67 |
|
0,3 |
0,6 |
0,5 |
30 |
0,652 |
|
0,35 |
0,6 |
0,583 |
35,6 |
0,612 |
|
0,4 |
0,6 |
0,666 |
41,7 |
0,561 |
|
0,45 |
0,6 |
0,75 |
48,5 |
0,5 |
Приложение 5
Расчет отношения силы трения скольжения к косинусу угла наклона плоскости к горизонту
|
sinα |
cosα |
Fтр/cosα |
|
0,466 |
0,884 |
0,75313 |
|
0,5 |
0,866 |
0,75313 |
|
0,583 |
0,813 |
0,75313 |
|
0,666 |
0,746 |
0,75313 |
|
0,75 |
0,661 |
0,75313 |
Приложение 6
Зависимость силы трения тела на наклонной плоскости в зависимости от угла наклона плоскости к горизонту
Приложение 7
Интерфейс электронной модели для изучения силы трения
Приложение 8
Интерфейс флеш–ролика, демонстрирующего движение тела по наклонной плоскости
Приложение 9
Оборудование для изучения силы трения тела на наклонной плоскости
Заключение
Работая над проектом, я получил следующие результаты:
1. Доказал экспериментально формулу для вычисления силы трения;
2. Выяснил наилучшие условия постановки эксперимента;
3. Экспериментальным и теоретическим путями определил коэффициент трения скольжения тела дерева по дереву;
4. Создал компьютерную модель движения тела по наклонной плоскости для изучения силы трения.
Данную модель можно применить на уроках физики при изучении силы трения и на уроках лабораторного практикума при исследовании силы трения в различных ситуациях.
Библиографическая ссылка
Новосадов Д.А. ИЗУЧЕНИЕ СИЛЫ ТРЕНИЯ И СОЗДАНИЕ КОМПЬЮТЕРНОЙ МОДЕЛИ ДЛЯ РАСЧЕТА СИЛЫ ТРЕНИЯ НА НАКЛОННОЙ ПЛОСКОСТИ // Международный школьный научный вестник. – 2018. – № 5-5.
;
URL: https://school-herald.ru/ru/article/view?id=752 (дата обращения: 20.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
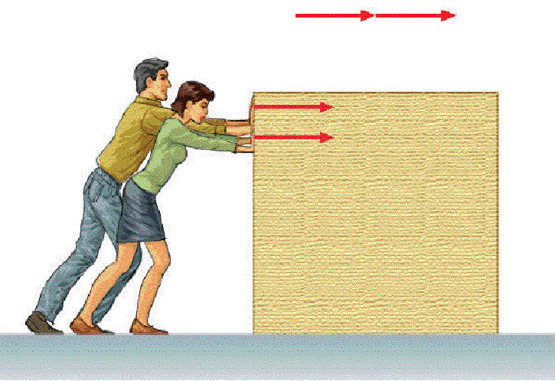
Физика > Решение проблем с трением и наклонами
Совмещение движения на наклоне с трением, располагает такими понятиями как равновесие и контактная сила.
Задача обучения
- Рассчитать силу трения на уклоне.
Основные пункты
- Движению на уклоне сопротивляется трение.
- Сила трения зависит от угла наклона. Ff = μmgcos(θ) – максимальная сила трения при наклоне.
- Если сила трения больше или равна силам в направлении движения, то чистая сила приравнивается к нулю, а объект пребывает в равновесии.
Термины
- Трение – сила, сопротивляющаяся относительному движению и склонности к такому движению у двух тел, пребывающих в контакте.
- Равновесие – пребывание тела в состоянии покоя или равномерном движении, где силы приравниваются к нулю.
Контактная сила на уклоне
Наклонная плоскость располагает двумя контактными поверхностями. На одной размещается объект, а вторая – основа, контактирующая с поверхностью под ней. Поэтому движение объекта может зависеть от перемещения наклонной плоскости.
Блок и наклонная система, отображающие действующие силы
Вычисление силы трения на угле наклона отличается о того, где объект пребывает на поверхности того же уровня. Сила трения зависит от коэффициента трения и нормальной силы: Ff = μFn. Когда наклон обладает углом θ, нормальная сила – Fn = mgcos(θ).
Сила трения оказывает сопротивление движению. Если блок подталкивать вверх, то сила трения будет указывать вниз. Если блок сбрасывать, то сила трения укажет вверх.
Равновесие сил на уклоне
Когда другие силы не действуют, только гравитация и трение противостоят склонности объекта скользить вниз. Если сила трения равна гравитации, то объект не будет скользить. Когда силы приравниваются нулю, блок пребывает в равновесии.
Гравитационная сила вниз по склону отображается как mgsin(θ). Θ – угол, создаваемый наклоном с горизонтальной поверхностью. Для того, чтобы поместить объект в равновесие, максимальная сила трения Ff = μmgcos(θ) должна превосходить или приравниваться к FG = mgsin(θ). Сила трения не способна превысить действующие на нее силы и выступает только противовесом движению.
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
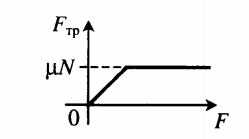
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
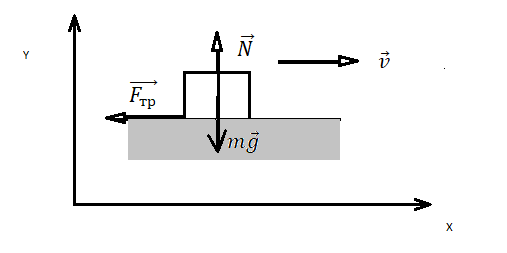
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
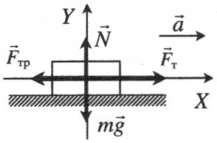 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
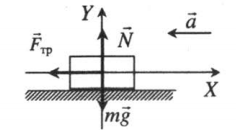 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
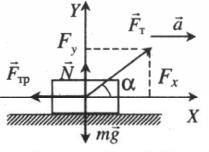 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
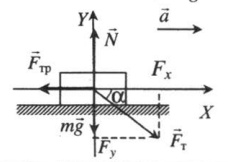 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
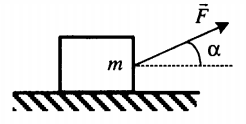
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
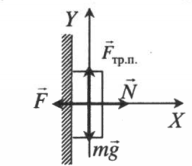 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
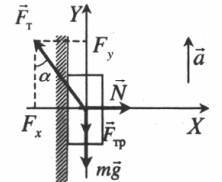 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
Следовательно:
Движение тела по наклонной плоскости
Движение вниз без трения |
|
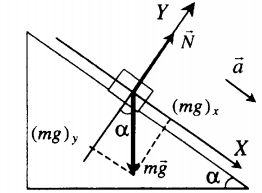 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
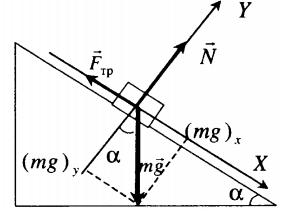 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
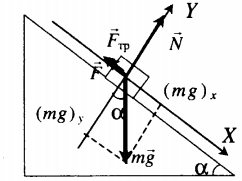 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
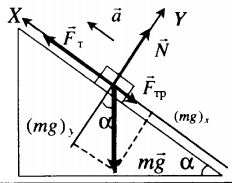 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
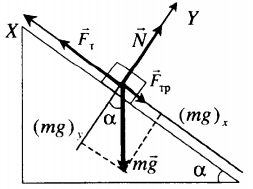 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
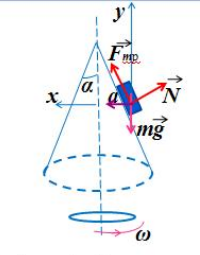
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
Выразим ускорение через проекцию сил на ось ОХ:
Подставим найденное ускорение в формулу тормозного пути и получим:
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.4k
Динамика и кинематика – это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.
Основная формула динамики
Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:
F¯ = m*a¯
Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.
В случае движения вращения второй закон Ньютона записывается в виде:
M = I*α
Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.
Формулы кинематики
Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:
a = Δv/Δt;
v = v0 ± a*t;
S = v0*t ± a*t2/2
Здесь v0 – значение начальной скорости тела, S – пройденный за время t путь вдоль прямолинейной траектории. Знак “+” следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак “-“. Это важный момент.
Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:
α = Δω/Δt;
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2
Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.
Линейные и угловые характеристики друг с другом связаны формулами:
a = α*r;
v = ω*r
Здесь r – радиус вращения.
Движение по наклонной плоскости: силы
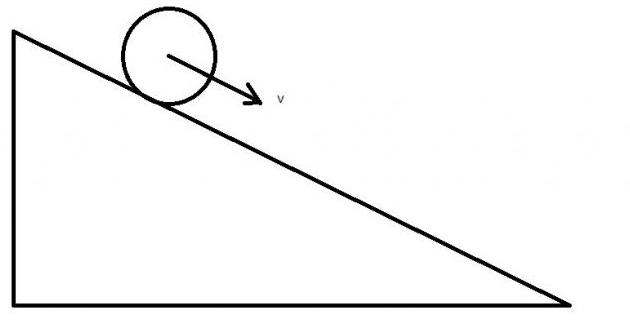
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.
Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:
- тяжести;
- реакции опоры;
- трения качения и/или скольжения;
- натяжение нити;
- сила внешней тяги.
Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.
Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.
Методика решения
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.
Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:
Ff = µ*N
Где N – реакция опоры, µ – коэффициент трения, не имеющий размерности.
Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:
F = m*g*sin(φ) – µ*m*g*cos(φ) = m*g*(sin(φ) – µ*cos(φ)) = m*a
Здесь φ – это угол наклона плоскости к горизонту.
Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.
В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:
F = m*g*sin(φ) – Fr = m*a
Где Fr – сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, Fr создает следующий момент:
M = Fr*r = I*α
Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.
Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.
Задача на движение бруска по наклонной плоскости
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.
Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:
m*g*(sin(φ) – µ*cos(φ)) = m*a =>
a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с2
Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:
S = a*t2/2
Откуда следует выразить время, и подставить известные значения:
t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с
Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.
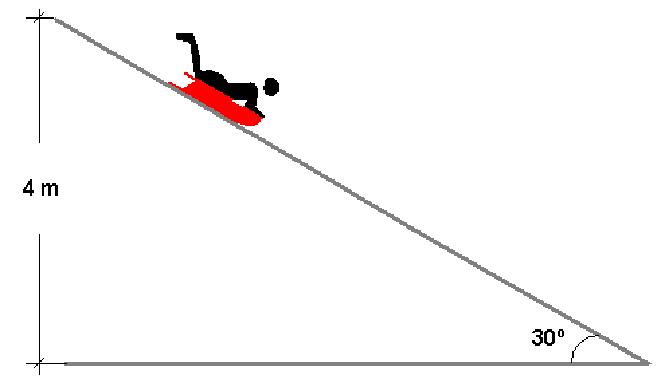
Задача со скатывающимся по плоскости цилиндром
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.
Запишем соответствующие уравнения:
m*g*sin(φ) – Fr = m*a;
Fr*r = I*α = I*a/r
Момент инерции I цилиндра вычисляется по формуле:
I = 1/2*m*r2
Подставим это значение во вторую формулу, выразим из нее силу трения Fr и заменим полученным выражением ее в первом уравнении, имеем:
Fr*r = 1/2*m*r2*a/r = >
Fr = 1/2*m*a;
m*g*sin(φ) – 1/2*m*a = m*a =>
a = 2/3*g*sin(φ)
Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.
Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:
S = a*t2/2 =>
t = √(2*S/a)
Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:
v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))
Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.