Каждый из нас знаком с проявлением силы трения. Действительно, любое движение в повседневной жизни, будь то ходьба человека или перемещение транспортного средства, невозможно без участия этой силы. В физике принято изучать три вида сил трения. В данной статье рассмотрим один из них, разберемся, что собой представляет трение покоя.
Брусок на горизонтальной поверхности

Прежде чем переходить к ответам на вопросы, что такое сила трения покоя и чему равна она, рассмотрим простой случай с бруском, который лежит на горизонтальной поверхности.
Проанализируем, какие силы действуют на брусок. Во-первых, это вес самого предмета. Обозначим его буквой P. Он направлен вертикально вниз. Во-вторых, это реакция опоры N. Она направлена вертикально вверх. Второй закон Ньютона для рассматриваемого случая запишется в таком виде:
m*a = P – N.
Знак минус здесь отражает противоположные направления векторов веса и реакции опоры. Поскольку брусок покоится, то величина a равна нулю. Последнее означает, что:
P – N = 0 =>
P = N.
Реакция опоры уравновешивает вес тела и равна ему по абсолютной величине.
Действующая внешняя сила на брусок на горизонтальной поверхности

Теперь к описанной выше ситуации добавим еще одну действующую силу. Предположим, что человек начал толкать брусок вдоль горизонтальной поверхности. Обозначим эту силу буквой F. Можно заметить удивительную ситуацию: если сила F невелика, то несмотря на ее действие, брусок продолжает покоиться на поверхности. Вес тела и реакция опоры направлены перпендикулярно поверхности, поэтому их горизонтальные проекции равны нулю. Иными словами, силы P и N не могут оказать никакого противодействия величине F. В таком случае, почему брусок остается в состоянии покоя и не движется?
Очевидно, что должна существовать сила, которая направлена против силы F. Этой силой является трение покоя. Она направлена против F вдоль горизонтальной поверхности. Действует она в области контакта нижней грани бруска и поверхности. Обозначим ее символом Ft. Закон Ньютона для горизонтальной проекции запишется в виде:
F = Ft.
Таким образом, модуль силы трения покоя всегда равен абсолютной величине внешних сил, действующих вдоль горизонтальной поверхности.
Начало движения бруска
Чтобы записать формулу трения покоя, продолжим начатый в предыдущих пунктах статьи эксперимент. Будем увеличивать абсолютное значение внешней силы F. Брусок какое-то время еще будет оставаться в покое, но наступит момент, когда он начнет двигаться. В этот момент сила трения покоя приобретет максимальное значение.
Чтобы найти это максимальное значение, возьмем еще один точно такой же брусок, как и первый, и положим его сверху. Площадь контакта бруска с поверхностью не изменилась, однако его вес увеличился вдвое. Экспериментально было установлено, что сила F отрыва бруска от поверхности также увеличилась вдвое. Этот факт позволил записать следующую формулу трения покоя:
Ft = µs*P.
То есть максимальная величина силы трения оказывается пропорциональной весу тела P, где в качестве коэффициента пропорциональности выступает параметр µs. Величина µs называется коэффициентом трения покоя.
Поскольку вес тела в проведенном эксперименте равен силе реакции опоры N, то формулу для Ft можно переписать так:
Ft = µs*N.
В отличие от предыдущего, это выражение можно использовать всегда, даже когда тело находится на наклонной плоскости. Модуль силы трения покоя прямо пропорционален силе реакции опоры, с которой поверхность действует на тело.
Физические причины возникновения силы Ft
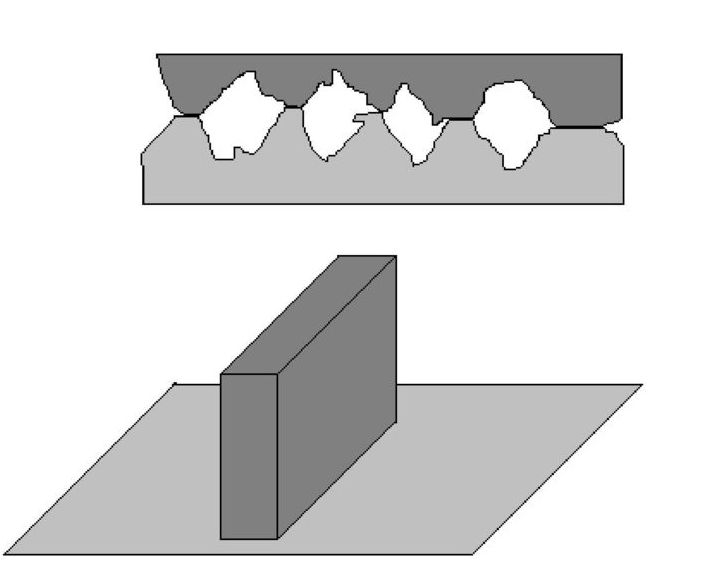
Вопрос, почему появляется трение покоя, является сложным и требует рассмотрения контакта между телами на микроскопическом и атомарном уровне.
В общем случае можно назвать две физические причины возникновения силы Ft:
- Механическое взаимодействие между пиками и впадинами.
- Физико-химическое взаимодействие между атомами и молекулами тел.
Насколько бы гладкой ни была любая поверхность, она обладает неровностями и неоднородностями. Грубо эти неоднородности можно представить в виде микроскопических пиков и впадин. Когда пик одного тела попадает во впадину другого тела, то происходит механическое сцепление между этими телами. Огромное число микроскопических сцепок является одной из причин появления трения покоя.
Вторая причина заключается в физико-химическом взаимодействии между молекулами или атомами, из которых состоят тела. Известно, когда два нейтральных атома приближаются друг к другу, то между ними могут возникать некоторые электрохимические взаимодействия, например, диполь-дипольные или ван-дер-ваальсовые. В момент начала движения брусок вынужден преодолевать эти взаимодействия, чтобы оторваться от поверхности.
Особенности силы Ft

Выше уже было отмечено, чему равна сила трения покоя максимальная, а также указано ее направление действия. Здесь перечислим другие характеристики величины Ft.
Трение покоя не зависит от площади контакта. Она определяется исключительно реакцией опоры. Чем больше площадь контакта, тем меньше деформация микроскопических пиков и впадин, однако тем больше их количество. Этот интуитивный факт объясняет, почему максимальная величина Ft не изменится, если брусок перевернуть на грань с меньшей площадью.
Трение покоя и трение скольжения имеют одну и ту же природу, описываются одинаковыми формулами, однако вторая всегда меньше, чем первая. Трение скольжения появляется, когда брусок начинает движение по поверхности.
Сила Ft в большинстве случаев является неизвестной величиной. Формула, которая приведена выше для нее, соответствует максимальному значению Ft в момент начала движения бруска. Чтобы яснее понять названный факт, ниже приведен график зависимости силы Ft от внешнего воздействия F.
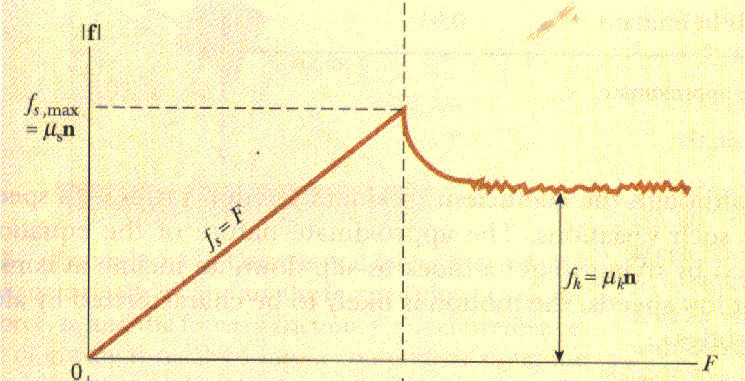
Видно, что с возрастанием F трение покоя растет линейно, достигает максимума, а затем уменьшается, когда тело начинает движение. Во время движения говорить о силе Ft уже нельзя, поскольку ее заменяет трение скольжения.
Наконец, последней важной особенностью силы Ft является то, что она не зависит от скорости перемещения (при относительных больших скоростях Ft уменьшается).
Коэффициент трения µs

Так как в формуле для модуля силы трения фигурирует величина µs, следует сказать о ней несколько слов.
Коэффициент трения µs является уникальной характеристикой двух поверхностей. Он не зависит от веса тела, его определяют экспериментально. Например, для пары дерево-дерево он изменяется от 0,25 до 0,5 в зависимости от типа дерева и качества обработки поверхности трущихся тел. Для смазанной воском деревянной поверхности на мокром снегу µs = 0,14, а для человеческих суставов этот коэффициент принимает весьма низкие значения (≈0,01).
Какое бы значение ни имел µs для рассматриваемой пары материалов, аналогичный коэффициент трения скольжения µk будет всегда меньше. Например, при скольжении дерева по дереву он равен 0,2, а для суставов человека не превышает величины 0,003.
Далее рассмотрим решение двух физических задач, в которых применим полученные знания.
Брусок на наклонной поверхности: расчет силы Ft
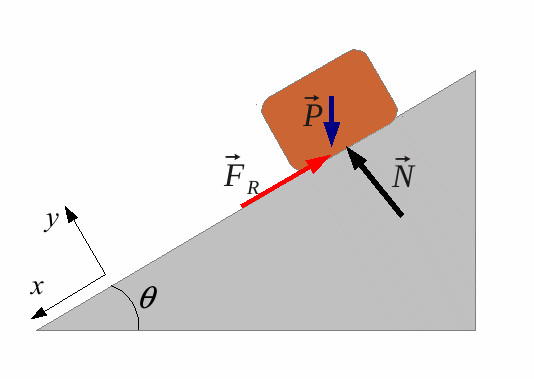
Первая задача является достаточно простой. Предположим, что на деревянной поверхности лежит брусок из дерева. Его масса равна 1,5 кг. Поверхность наклонена под углом 15o к горизонту. Необходимо определить силу трения покоя, если известно, что брусок не движется.
Подвох этой задачи заключается в том, что многие начинают вычислять реакцию опоры, а затем, используя справочные данные для коэффициента трения µs, пользуются приведенной выше формулой для определения максимального значения Ft. Однако в данном случае Ft не является максимальной. Ее модуль равен лишь внешней силе, которая стремится сдвинуть брусок с места вниз по плоскости. Эта сила равна:
F = m*g*sin(α).
Тогда сила трения Ft будет равна величине F. Подставляя данные в равенство, получаем ответ: сила трения покоя на наклонной плоскости Ft = 3,81 ньютона.
Брусок на наклонной поверхности: расчет максимального угла наклона
Теперь решим такую задачу: деревянный брусок находится на деревянной наклонной плоскости. Полагая коэффициент трения равным 0,4, необходимо найти максимальный угол наклона α плоскости к горизонту, при котором брусок начнет скользить.
Скольжение начнется, когда проекция веса тела на плоскость станет равной максимальной силе трения покоя. Запишем соответствующее условие:
F = Ft =>
m*g*sin(α) = µs*m*g*cos(α) =>
tg(α) = µs =>
α = arctg(µs).
Подставляя в последнее уравнение значение µs = 0,4, получаем α = 21,8o.
| Условие возникновения | Действует между телами, покоящимися относительно друг друга | ||
| Физическая природа силы | Электромагнитная природа обусловлена взаимодействием атомов или молекул элементов поверхностей взаимодействующих тел | ||
| Направление силы |
|
||
|
Формула |
|
||
| Особенности | Значение коэффициента трения (mu) определяется структурой трущихся поверхностей | ||
| Границы применимости | При точных расчётах учитывают, что значение предельной силы трения покоя больше значения, определяемого формулой ((1)) |
2. Сила трения скольжения
| Условие возникновения | Относительное перемещение контактирующих тел | ||
| Физическая природа силы | Электромагнитная природа обусловлена атомно-молекулярным взаимодействием контактирующих поверхностей | ||
| Направление силы |
|
||
|
Формула (закон Кулона — Амонтона) |
|
||
| Особенности | Значение коэффициента трения (mu) определяется структурой трущихся поверхностей | ||
| Границы применимости | Формула ((2)) справедлива при небольших значениях относительной скорости тел |
| Условие возникновения | Относительное перемещение тел, сопровождающееся их вращением | ||
| Природа силы | Электромагнитная природа обусловлена деформацией поверхностей взаимодействующих тел и межмолекулярным взаимодействием поверхностей взаимодействующих тел | ||
| Направление силы |
|
||
| Формула |
(F_{тр}=frac{f}{R} · Mg), где (f) — коэффициент трения качения, ([f]=м) |
||
| Особенности | Значение коэффициента трения качения (f) существенно меньше коэффициента трения скольжения (mu) | ||
| Границы применимости | Скорости качения существенно меньше скорости деформации взаимодействующих поверхностей |
Источники:
Рис. 1. Направление силы трения покоя. © ЯКласс.
Рис. 2. Изображение графика зависимости силы трения покоя от внешней силы. © ЯКласс.
Рис. 3. Направление силы трения скольжения. © ЯКласс.
Рис. 4. Изображение графика зависимости силы трения скольжения от внешней силы. © ЯКласс.
Рис. 5. Направление сил трения качения и полной реакции. © ЯКласс.
Из-за чего возникает сила трения? Она возникает в результате движения одно тела по поверхности другого тела.
Причины возникновения силы трения:
- Все тела имеют шероховатости. Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения.
- Между атомами и молекулами поверхностей тел действуют электромагнитные силы притяжения и отталкивания. Таким образом, сила трения имеет электромагнитную природу.
Существуют следующие виды сухого трения:
Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки. Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения.
1. Сила трения покоя.
Этот вид силы трения возникает в ситуации возможного движения тела по поверхности другого тела. Эта сила направлена против направления возможного движения. Сила трения покоя может принимать любые значения в диапазоне от нуля до своего максимального предельного значения, после которого она переходит в силу трения скольжения. То есть сила трения покоя действует пока тело стоит на месте.
Важно: При решении стандартных физических задач принимается, что максимальная сила трения покоя равна силе трения скольжения и рассчитывается по формуле Fтр = μN, где N – сила реакции опоры;
μ – коэффициент трения.
Коэффициент трения – это безразмерная величина. Он зависит от свойств соприкасающихся поверхностей и не зависит от силы давления (соответственно, и от силы реакции опоры, так как это силы, описываемые третьим законом Ньютона) и от площади соприкасающихся поверхностей.
Обычная ситуация: на кухне имеется холодильник, его нужно переставить на другое место.
Когда никто не пытается двигать холодильник, стоящий на горизонтальном полу, трения между ним и полом нет. Но как только его начинают толкать, коварная сила трения покоя тут же возникает и полностью компенсирует усилие. Причина её возникновения — те самые неровности соприкасающихся поверхностей, которые деформируясь, препятствуют движению холодильника. Поднатужились, увеличили силу, приложенную к холодильнику, но он не поддался и остался на месте. Это означает, что сила трения покоя возрастает вместе с увеличением внешнего воздействия, оставаясь равной по модулю приложенной силе, ведь увеличиваются деформации неровностей.
Пока силы равны, холодильник остаётся на месте.
Сила трения, которая действует между поверхностями покоящихся тел и препятствует возникновению движения, называется силой трения покоя.
2. Сила трения скольжения
Что же делать с холодильником и можно ли победить силу трения покоя? Не будет же она расти до бесконечности? Зовём на помощь друга, и вдвоём уже удаётся передвинуть холодильник. Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:
Теперь на движущийся холодильник действует сила трения скольжения. Она возникает при относительном движении контактирующих твёрдых тел.
Итак, сила трения покоя может меняться от нуля до некоторого максимального значения — Fтр. пок. макс И если приложенная сила больше, чем Fтр. пок. макс, то у холодильника появляется шанс сдвинуться с места.
Теперь, после начала движения, можно прекратить наращивать усилие и ещё одного друга можно не звать. Чтобы холодильник продолжал двигаться равномерно, достаточно прикладывать силу, равную силе трения скольжения:
Чтобы понять, как измеряется сила трения, нужно понять, какие факторы влияют на величину силы трения. Почему так трудно двигать холодильник?
Самое очевидное — его масса играет первостепенную роль. Можно вытащить из него все продукты и тем самым уменьшить его массу, и, следовательно, силу давления холодильника на опору (пол). Пустой холодильник сдвинуть с места гораздо легче! Следовательно, чем меньше сила нормального давления тела на поверхность опоры, тем меньше и сила трения. Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.
Сила реакции опоры обозначается N. Можно сделать вывод
Второй фактор, влияющий на величину силы трения, — материал и степень обработки соприкасающихся поверхностей. Так, двигать холодильник по бетонному полу гораздо тяжелее, чем по ламинату. Зависимость силы трения от рода и качества обработки материала обеих соприкасающихся поверхностей выражают через коэффициент трения.
Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.
Он чаще всего попадает в интервал от нуля до единицы, не имеет размерности и определяется экспериментально.
Можно предположить, что сила трения зависит также от площади соприкасающихся поверхностей. Однако, положив холодильник набок, мы не облегчим себе задачу.
Ещё Леонардо да Винчи экспериментально доказал, что сила трения не зависит от площади соприкасающихся поверхностей при прочих равных условиях.
Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.
Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:
Рассмотрим пример в виде задачи
Брусок массой m покоится на плоскости, наклонённой под углом α к горизонту. Коэффициент трения между бруском и плоскостью равен μ. Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ:
А) модуль силы нормальной реакции плоскости
Б) модуль силы трения
ФОРМУЛЫ:
1) mgsinα
2) μmgsinα
3) mgcosα
4) μmgcosα
Cделаем рисунок к задаче:
Для решение задачи нам потребуется проецировать на оси нашей системы координат второй закон Ньютона
Как мы только что увидели, сила трения покоя может быть больше силы трения скольжения для одного и того же угла наклона. В большей степени это зависит от угла наклона плоскости и значения коэффициента трения скольжения.
Однако, здесь есть подвох (!). Тело всё таки не двигается, поэтому никакой речи о силе трения скольжения идти не может, согласны?
Для обеспечения покоя бруска сила трения покоя должна возрастать с увеличением угла α . Но мы знаем, что она не может быть больше максимального значения – силы трения скольжения:
Поэтому ясно, что существует предельный угол αпр наклона плоскости, при котором покой бруска станет невозможным, начнется соскальзывание. Значение этого угла мы нашли из условия, что сила трения покоя становится максимальной. Если угол наклонной плоскости будет равен углу трения (предельному углу), то тело будет либо равномерно скользить вниз под действие собственной силы тяжести, либо покоиться.
Видно, что предельный угол не зависит от массы бруска. Последнее соотношение позволяет на практике определить значение коэффициента трения с помощью изменения угла наклона плоскости для исследуемых предметов. К примеру, мы можем определить коэффициент трения дерева об дерево, если на деревянную доску положим деревянный брусок, а потом будем поднимать доску и фиксировать тот угол, при котором брусок начинает соскальзывать с доски. Тангенс этого угла как раз таки и будет определять коэффициент трения для этих материалов.
Неплохое дополнение по теме вы можете почитать: ЗДЕСЬ.
3. Сила трения качения
Ещё древние строители заметили, что если тяжёлый предмет водрузить на колёсики, то сдвинуть с места и затем катить его будет гораздо легче, чем тянуть волоком. Вот бы пригодилась эта древняя мудрость, когда мы тянули холодильник! Однако всё равно нужно толкать или тянуть тело, чтобы оно не остановилось. Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Причина трения качения — деформация катка и опорной поверхности. Сила трения качения может быть в сотни раз меньше силы трения скольжения при той же силе давления на поверхность. Примерами уменьшения силы трения за счёт подмены трения скольжения на трение качения служат такие приспособления, как подшипники, колёсики у чемоданов и сумок, ролики на прокатных станах.
Вязкое трение
Вязкое возникает при движении твёрдого тела в жидкости или газе. Оно препятствует движению лодки, которая скользит по реке, или воздействует на летящий самолёт со стороны воздуха. Интересная особенность вязкого трения в том, что отсутствует трение покоя. Попробуйте сдвинуть пальцем лежащий на земле деревянный брус и проделайте тот же эксперимент, опустив брус на воду. Чтобы сдвинуть брус с места в воде, будет достаточно сколь угодно малой силы. Однако по мере роста скорости силы вязкого трения сильно увеличиваются.
Спасибо, что дочитали до конца 🙂 Если вам нравятся такие разборы, и вы хотите видеть их чаще, то оставьте обратную связь (лайки, комментарии, ваши мысли).
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Physics.Math.Code (Дзен)
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Сила трения покоя


4.2
Средняя оценка: 4.2
Всего получено оценок: 67.
4.2
Средняя оценка: 4.2
Всего получено оценок: 67.
Определение силы трения покоя, возникающей между соприкасающимися телами – прикладная задача большой важности. Причина проста: трение играет важную роль для человека.
Трение сцепления
Всякие неподвижные тела, соприкасаясь, воздействуют друг на друга. Одной из возникающих сил является сила трение покоя (сцепления), которая обусловлена шероховатостью поверхностей.
Ее легко обнаружить, если попытаться перемещать одно из тел относительно другого. Для того, чтобы началось движение, необходимо преодолеть предельную силу сцепления. Направлена сила против внешнего воздействия вдоль поверхности соприкосновения.
В том случае, если между телами есть некая промежуточная жидкая среда трение называют вязким. Жидкость уменьшает предельное значение силы трения покоя.
Опытным путем легко убедиться, что чем больше масса тела, тем тяжелее сдвинуть его. Влияет так же и степень шероховатости поверхности, а также угол ее наклона. В гору тянуть тяжелее, чем с горы. Также легко проверить, что независимо от того, большей гранью или меньше лежит тело, сила трения не меняется.
Тогда формулу для модуля предельной силы трения покоя можно записать так:
$$F_{тр} = C cdot m$$,
где C – некий коэффициент пропорциональности.
Кулоном было установлено, что сила трения покоя зависит не столько от массы, сколько от того, как сильно тела прижимаются друг от друга. Поэтому он записал расчетную формулу следующим образом:
$$F_{тр} = C cdot N$$,
где N – сила реакции опоры, а C – безразмерный параметр, учитывающий характер поверхности. Эта формула силы трения покоя наиболее общая. Для случаев, когда поверхность наклонная, нужно брать проекцию N на ось у. Также по этой формуле рассчитывают трение скольжения, зависимостью которой от скорости движения в практических задачах пренебрегают.
Сила трения не всегда играет негативную роль. За счет нее человек двигается, за счет нее работают передаточные механизмы, благодаря ей автомобиль не вылетает в кювет при повороте.
Коэффициент трения покоя
Параметр, который учитывает характер поверхности трения, назвали коэффициентом трения покоя. Он находится для различных материалов экспериментальным путем. Также для него существует специальное обозначение – $mu$.
Между точильным камнем и металлом коэффициент трения равен примерно 0,9. Для заточенной стали и льда – около 0,02. Из этого становится понятно, почему конькобежец скользит, а точильный камень стачивает металл.
Задачи
- Найти коэффициент трения покоя, если брусок находится в состоянии покоя на наклонной поверхности. Угол наклона – 30˚.
Решение
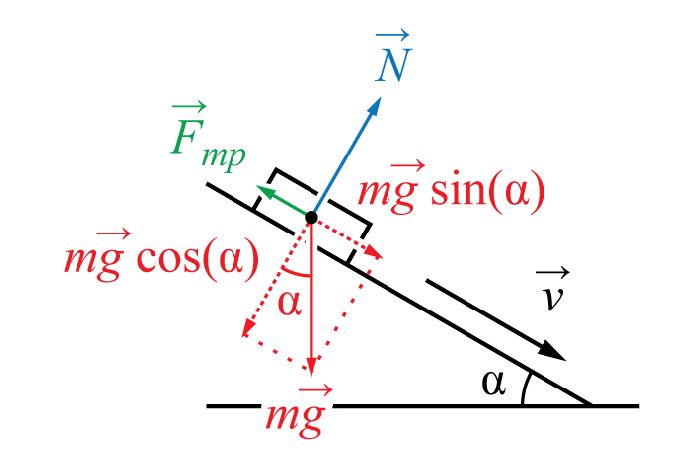
Запишем второй закон Ньютона в векторной форме:
$vec F_{тр} = m vec g + vec N$
И в проекциях на оси:
$N = mg cdot cos alpha$
$mu N = mg cdot sin alpha$
Тогда:
$mu = tg alpha = 0,57$
- Какую минимальную силу необходимо приложить к блоку массой 100 кг, чтобы поднять его по наклонной поверхности. Коэффициент трения – 0,3, угол наклона – 30˚.
Решение
Запишем второй закон Ньютона в векторной форме:
$vec F = m vec g + vec F_{тр} + vec N$
И в проекциях на оси:
$N = mg cdot cos alpha$ – на Оу.
$F = mg cdot sin alpha + mu N$ – на Ох.
Тогда, учитывая выражение для N, рассчитаем силу:
$F = mg cdot (sin alpha + mu cos alpha) = 100 cdot 10 cdot (0,5 + 0,3 cdot 0,87) = 761 Н$

Что мы узнали?
В ходе урока установили природу сил трения, а также разобрались с тем, от чего она зависит. Рассмотрели расчетную формулу и компоненты, входящие в нее, ввели определение коэффициента трения покоя. Для закрепления пройденного материала решили две задачи.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 67.
А какая ваша оценка?
Тре́ние — физическое явление
соприкасающихся тел при их относительном смещении в плоскости касания (внешнее трение) либо при относительном смещении параллельных слоёв жидкости, газа или деформируемого твёрдого тела (внутреннее трение, или вязкость). Далее в этой статье под трением понимается лишь внешнее трение. Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.
Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии. В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз[ссылка 1].
Сила трения[править | править код]
Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. Причиной возникновения трения является шероховатость трущихся поверхностей и взаимодействие молекул этих поверхностей. Сила трения зависит от материала трущихся поверхностей и от того, насколько сильно эти поверхности прижаты друг к другу. В простейших моделях трения (закон Кулона для трения) считается, что сила трения прямо пропорциональна силе нормальной реакции между трущимися поверхностями. В целом же, в связи со сложностью физико-химических процессов, протекающих в зоне взаимодействия трущихся тел, процессы трения принципиально не поддаются описанию с помощью простых моделей классической механики.
Разновидности силы трения[править | править код]
При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на:
- Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
- Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.
- Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
- Трение кручения — момент силы, возникающий между двумя контактирующими телами при вращении одного из них относительно другого и направленный против вращения. Определяется формулой:
, где
— нормальное давление,
— коэффициент трения кручения, имеющий размерность длины[1].
Характер фрикционного взаимодействия[править | править код]
В физике взаимодействие трения принято разделять на:
- сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твёрдыми смазочными материалами) — очень редко встречающийся на практике случай, характерная отличительная черта сухого трения — наличие значительной силы трения покоя;
- граничное, когда в области контакта могут содержаться слои и участки различной природы (оксидные плёнки, жидкость и так далее) — наиболее распространённый случай при трении скольжения;
- смешанное, когда область контакта содержит участки сухого и жидкостного трения;
- жидкостное (вязкое), при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды;
- эластогидродинамическое (вязкоупругое), когда решающее значение имеет внутреннее трение в смазывающем материале, возникает при увеличении относительных скоростей перемещения.
Сила реакции опоры[править | править код]

Сила нормальной реакции определяется как результирующая сила, сжимающая две параллельные поверхности вместе, а её направление перпендикулярно этим поверхностям. В простом случае, когда масса лежит на горизонтальной поверхности, единственной составляющей нормальной силы является сила тяжести, где 



Коэффициент трения — это эмпирическое (экспериментально измеренное) структурное свойство, которое зависит только от различных аспектов контактирующих материалов, таких как шероховатость поверхности. Коэффициент трения не зависит от массы или объёма. Например, большой алюминиевый блок имеет тот же коэффициент трения, что и маленький алюминиевый блок. Однако величина самой силы трения зависит от силы реакции опоры и, следовательно, от массы блока.
В зависимости от ситуации расчёт нормальной силы 








Если объект находится на наклонной поверхности, например на наклонной плоскости, нормальная (к поверхности) сила тяжести меньше, чем 
В общем, процесс решения любой статической задачи с трением состоит в том, чтобы рассматривать соприкасающиеся поверхности предварительно как неподвижные, чтобы можно было рассчитать соответствующую тангенциальную силу реакции между ними. Если эта сила реакции удовлетворяет 

Коэффициент трения[править | править код]
Коэффициент трения, часто обозначаемый греческой буквой µ, представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения. Коэффициент трения зависит от используемых материалов; например, лёд имеет низкий коэффициент трения о сталь, а резина — высокий коэффициент трения при скольжении по дорожному покрытию. Коэффициенты трения находятся в диапазоне от почти нуля до значений больше единицы. Трение между металлическими поверхностями больше между двумя поверхностями из одинаковых металлов, чем между двумя поверхностями из разных металлов — следовательно, латунь будет иметь более высокий коэффициент трения при движении по латуни, но меньше при движении по стали или алюминию[2].
Для поверхностей в состоянии покоя относительно друг друга 

Для поверхностей, находящихся в относительном движении 


Артур Морин ввёл этот термин и продемонстрировал полезность коэффициента трения[4]. Коэффициент трения — это эмпирическая величина — его нужно измерить экспериментально и он не может быть определён путём расчётов[5]. Более грубые поверхности обычно имеют более высокие эффективные значения коэффициента трения. Как статические, так и кинетические коэффициенты трения зависят от пары контактирующих поверхностей; для данной пары поверхностей коэффициент трения покоя обычно больше, чем коэффициент кинетического трения; в некоторых наборах два коэффициента равны, например, тефлон на тефлоне.
Большинство сухих материалов имеют значения коэффициента трения от 0,3 до 0,6. Значения вне этого диапазона встречаются реже, но тефлон, например, может иметь коэффициент всего 0,04. Нулевое значение означало бы отсутствие трения, ненаблюдаемое свойство. Резина при контакте с другими поверхностями может иметь коэффициент трения от 1 до 2. Иногда утверждают, что μ всегда <1, но это неверно. В то время как в большинстве соответствующих приложений μ <1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше, чем нормальное усилие поверхности на объект. Например, поверхности, покрытые силиконовым каучуком или акриловым каучуком, имеют коэффициент трения, который может быть значительно больше 1.
Хотя часто утверждается, что коэффициент трения является «материальным свойством», его лучше классифицировать как «системное свойство». В отличие от истинных свойств материала (таких как проводимость, диэлектрическая проницаемость, предел текучести), коэффициент трения для любых двух материалов зависит от системных переменных, таких как температура, скорость, атмосфера, а также от того, что сейчас обычно называют временем старения и разрушения; а также от геометрических свойств границы раздела материалов, а именно структуры их поверхностей[3]. Например, медный штифт, скользящий по толстой медной пластине, может иметь коэффициент трения, который изменяется от 0,6 при низких скоростях (скольжение металла по металлу) до менее 0,2 при высоких скоростях, когда поверхность меди начинает плавиться из-за нагрева от трения. Последняя скорость, конечно, не определяет коэффициента трения однозначно; если диаметр штифта увеличивается так, что нагрев от трения быстро устраняется, температура падает, и штифт остаётся твердым, а коэффициент трения повышается до значения, наблюдаемого при испытании на «низкой скорости».
При определённых условиях некоторые материалы имеют очень низкие коэффициенты трения. Примером является (высокоупорядоченный пиролитический) графит, который может иметь коэффициент трения ниже 0,01[6]. Этот режим сверхнизкого трения называется сверхсмазкой.
Статическое трение[править | править код]
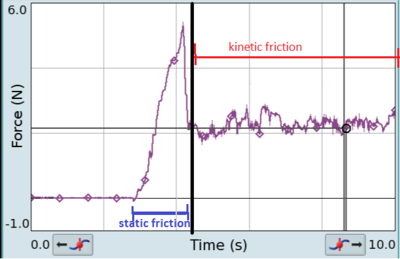
Когда масса неподвижна, то объект испытывает статическое трение. Трение увеличивается по мере увеличения приложенной силы, пока блок не переместится. После того, как блок начнёт перемещение, он испытывает кинетическое трение, которое меньше максимального статического трения.
Статическое трение — это трение между двумя или более твёрдыми объектами, которые не движутся относительно друг друга. Например, статическое трение может предотвратить скольжение объекта по наклонной поверхности. Коэффициент статического трения, обычно обозначаемый как μs, обычно выше, чем коэффициент кинетического трения. Считается, что статическое трение возникает в результате особенностей шероховатости поверхности на различных масштабах длины на твёрдых поверхностях. Эти особенности, известные как неровности, присутствуют вплоть до наноразмеров и приводят к тому, что настоящий контакт твёрдого тела с твёрдым телом существует только в ограниченном количестве точек, составляющих лишь часть видимой или номинальной площади контакта[7]. Линейность между приложенной нагрузкой и истинной площадью контакта, возникающая из-за деформации неровностей, приводит к линейности между статической силой трения и нормальной силой, обнаруживаемой для типичного трения Амонтона — Кулона[8].
Сила статического трения должна быть преодолена приложенной силой, прежде чем объект сможет двигаться. Максимально возможная сила трения между двумя поверхностями до начала скольжения является произведением коэффициента трения покоя и нормальной силы: 



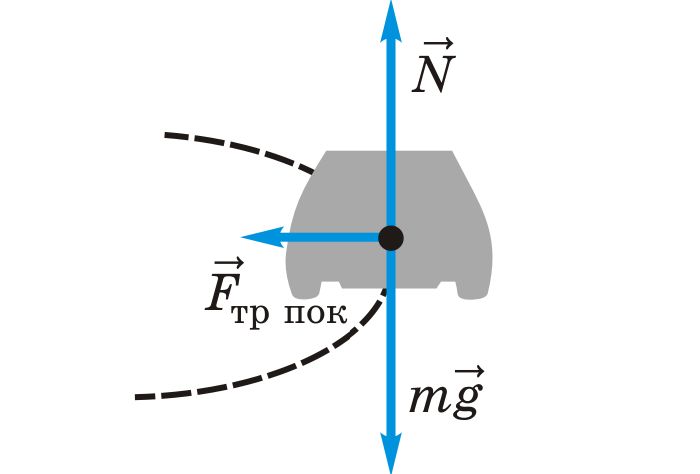
Примером статического трения может служить сила, препятствующая скольжению автомобильного колеса при качении по земле. Несмотря на то, что колесо находится в движении, участок шины, контактирующий с землёй, неподвижен относительно земли, поэтому это статическое, а не кинетическое трение.
Максимальное значение статического трения иногда называют ограничивающим трением[10], хотя этот термин не используется повсеместно[11].
Кинетическое трение[править | править код]
Кинетическое трение, также известное как трение скольжения, возникает, когда два объекта движутся относительно друг друга и трутся друг о друга (как салазки по земле). Коэффициент кинетического трения обычно обозначается как μk и обычно меньше коэффициента трения покоя для тех же материалов[12][13]. Однако Ричард Фейнман отмечает, что «с сухими металлами очень трудно показать какое-либо различие»[14]. Сила трения между двумя поверхностями после начала скольжения является произведением коэффициента кинетического трения и силы реакции опоры: 
Новые модели показывают, насколько кинетическое трение может быть больше, чем трение покоя. Кинетическое трение, во многих случаях, в первую очередь вызвано химической связью между поверхностями, а не переплетёнными неровностями[16]; однако во многих других случаях эффекты шероховатости являются доминирующими, например, при трении резины о дорогу. Шероховатость поверхности и площадь контакта влияют на кинетическое трение для микро- и наноразмерных объектов, где силы рапределённые по площади поверхности преобладают над силами инерции[17].
Происхождение кинетического трения в наномасштабе можно объяснить термодинамикой[18]. При скольжении новая поверхность образуется в задней части скользящего истинного контакта, а существующая поверхность исчезает в передней части. Поскольку все поверхности включают в себя термодинамическую поверхностную энергию, работа должна быть затрачена на создание новой поверхности, а энергия выделяется в виде тепла при удалении поверхности. Таким образом, требуется сила, чтобы переместить заднюю часть контакта, и тепло трения выделяется спереди.

Угол трения θ, когда блок только начинает скользить.
Угол трения[править | править код]
Для некоторых приложений более полезно определять статическое трение в терминах максимального угла, перед которым один из элементов начнёт скользить. Он называется углом трения и определяется как:
где θ — угол от горизонтали, а μs — статический коэффициент трения между телами[19]. Эту формулу также можно использовать для расчета μs на основе эмпирических измерений угла трения.
Трение на атомном уровне[править | править код]
Определение сил, необходимых для перемещения атомов друг мимо друга, является сложной задачей при разработке наномашин. В 2008 году учёные впервые смогли переместить отдельный атом по поверхности и измерить необходимые силы. Используя сверхвысокий вакуум и почти низкую температуру (5 К), при помощи модифицированного атомно-силового микроскопа перемещались атомы кобальта и молекулы монооксида углерода по поверхности меди и платины[20].
Закон Амонтона — Кулона[править | править код]
Основной характеристикой трения является коэффициент трения 
В простейших случаях сила трения 

| Пары материалов |  покоя покоя |
 скольжения скольжения
|
|---|---|---|
| Сталь-Сталь | 0,5—0,8[21] | 0,15—0,18 |
| Резина-Сухой асфальт | 0,95—1 | 0,5—0,8 |
| Резина-Влажный асфальт | 0,25—0,75 | |
| Лёд-Лёд | 0,05—0,1 | 0,028 |
| Резина-Лёд | 0,3 | 0,15—0,25 |
| Стекло-Стекло | 0,9 | 0,7 |
| Нейлон-Нейлон | 0,15—0,25 | |
| Полистирол-Полистирол | 0,5 | |
| Плексиглас, оргстекло | 0,8 |
Закон Амонтона — Кулона с учётом адгезии[править | править код]
Для большинства пар материалов значение коэффициента трения 


Прикладное значение[править | править код]
Трение в механизмах и машинах[править | править код]
В большинстве традиционных механизмов (ДВС, автомобили, зубчатые шестерни и пр.) трение играет отрицательную роль, уменьшая КПД механизма. Для уменьшения силы трения используются различные натуральные и синтетические масла и смазки. В современных механизмах для этой цели используется также напыление покрытий (тонких плёнок) на детали. С миниатюризацией механизмов и созданием микроэлектромеханических систем (МЭМС) и наноэлектромеханических систем (НЭМС) величина трения по сравнению с действующими в механизме силами увеличивается и становится весьма значительной 
Сцепление с поверхностью[править | править код]
Наличие трения обеспечивает возможность перемещаться по поверхности. Так, при ходьбе именно за счёт трения происходит сцепление подошвы с полом, в результате чего происходит отталкивание от пола и движение вперёд. Точно так же обеспечивается сцепление колёс автомобиля (мотоцикла) с поверхностью дороги. В частности, для улучшения этого сцепления разрабатываются новые формы и специальные типы резины для покрышек, а на гоночные болиды устанавливаются антикрылья, сильнее прижимающие машину к трассе.
Трение внутри материалов[править | править код]
История[править | править код]
Греки, в том числе Аристотель, Витрувий и Плиний Старший интересовались причиной и снижением трения[22]. Они знали о различиях между статическим и кинетическим трением, а Фемистий утверждал в 350 году, что «легче продолжать движение движущегося тела, чем перемещать тело в состоянии покоя»[22][23][24][25].
Классические законы трения скольжения были открыты Леонардо да Винчи в 1493 году, который был пионером в области трибологии, но законы, задокументированные в его записных книжках, не были опубликованы и остались неизвестными[4][26][27][28][29][30]. Эти законы были переоткрыты Гийомом Амонтоном в 1699 году[31] и стали известны как три закона Амонтона сухого трения. Амонтон представлял природу трения с точки зрения неровностей поверхности и силы, необходимой для увеличения веса, прижимающего поверхности друг к другу. Эта точка зрения была развита Бернаром Форестом де Белидором[32] и Леонардом Эйлером в 1750 году, которые вывели угол естественного откоса груза на наклонной плоскости и впервые различили статическое и кинетическое трение[33]. Иоанн Теофил Дезагюлье в 1734 году первым осознал роль адгезии в трении[34]. Эти микроскопические силы заставляют поверхности слипаться; и он предположил, что трение — это сила, необходимая для разрыва прилегающих поверхностей.
Понимание трения в дальнейшем развил Шарль-Огюстен де Кулон (1785)[31]. Кулон исследовал влияние четырёх основных факторов, влияющих на трение: природы контактирующих материалов и покрытия их поверхностей; протяженность площади поверхности; нормальное давление (или нагрузка); и продолжительность контакта поверхностей (время покоя)[4]. Кулон также рассмотрел влияние скорости скольжения, температуры и влажности, чтобы выбрать между различными икорктическими объяснениями природы трения. Различие между статическим и кинетическим трением появляется в законе трения Кулона, хотя это различие уже было замечено Иоганном Андреасом фон Зегнером в 1758 году[4]. Эффект времени покоя объяснил Питер ван Мушенбрук в 1762 году путём рассмотрения поверхностей волокнистых материалов со сцепляющимися вместе волокнами, что занимает конечное время, в течение которого увеличивается трение.
Джон Лесли (1766—1832) отметил слабость взглядов Амонтона и Кулона: если трение возникает из-за того, что груз поднимается по наклонной плоскости последовательных выступов, то почему тогда оно не уравновешивается движением вниз по противоположному склону? Лесли столь же скептически относился к роли адгезии, предложенной Дезагюлье, которая в целом должна приводить как к ускорению, так и к замедлению движения[4]. По мнению Лесли, трение следует рассматривать как зависящий от времени процесс уплощения, сдавливания неровностей, что создаёт новые препятствия в тех люластях, что раньше было полостями.
Артур-Жюль Морен (1833) разработал концепцию трения скольжения по сравнению с трением качения. Осборн Рейнольдс (1866) вывел уравнение вязкого течения. Это завершило классическую эмпирическую модель трения (статического, кинетического и жидкостного), обычно используемую сегодня в технике[26]. В 1877 году Флеминг Дженкин и Джеймс А. Юинг исследовали непрерывность статического и кинетического трения[35].
В центре внимания исследований в 20 веке стало понимание физических механизмов трения. Франк Филип Боуден и Дэвид Табор (1950) показали, что на микроскопическом уровне фактическая площадь контакта между поверхностями составляет очень небольшую часть видимой площади[27]. Эта фактическая площадь контакта, вызванная неровностями, увеличивается по мере увеличения давлением. Развитие атомно-силового микроскопа (1986) позволило учёным изучить трение в атомном масштабе[26] показав, что на этом масштабе сухое трение — это продукт межповерхностного сдвигового напряжения и площади контакта. Эти два открытия объясняют первый закон Амонтона; макроскопическая пропорциональность между нормальной силой и статической силой трения между сухими поверхностями.
Журналы[править | править код]
- Трение, Износ, Смазка, журнал о трении.
- Трение и Износ, журнал о трении издаётся Национальной Академией Наук Беларуси с 1980 г.
- Journal of Tribology Архивная копия от 16 января 2013 на Wayback Machine, международный журнал о трении.
- Wear, международный журнал о трении и износе.
- Таблицы коэффициентов трения, численные значения коэффициентов трения.
Литература[править | править код]
- Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 1. Трение в машинах. Теория, расчет и конструкция подшипников и подпятников скольжения. Машгиз. М.-Л. — 1947. 256 с.
- Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 2. Износ материалов. Классификация видов износа, методов и машин для лабораторного испытания материалов на износ машины и производственные на них исследования. Машгиз. М.-Л. — 1947. 220 с.
- Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 3. Износ машин. Износ машин и деталей и способы борьбы с их износом. Машгиз. М.-Л. — 1947. 164 с.
- Зайцев А. К., А. Кононов Максимович Основы учения о трении, износе и смазке машин. Часть 4. Смазка машин. Машгиз. М.-Л. — 1948. 279 с.
- Archbutt L., Deeley R.M. Lubrication and Lubicants. London. — 1927
- Арчбютт Л., Дилей Р. М. Трение, смазка и смазочные материалы. Руководство по теории и практике смазки и по методам испытания смазочных материалов. Госгоргеолнефтиздат. — Л. — 1934. — 703 с.
- 2-е изд., перераб. и доп. — М.-Л.: Гостоптехиздат. — 1940. — 824 с.
- Дерягин Б. В. Что такое трение? М.: Изд. АН СССР, 1963.
- Основы теории систем с трением/ А. П. Иванов. — М.-Ижевск: НИЦ «РХД», ИКИ, 2011. 304 с. (Предисловие автора, обнарод. в качестве анонса к книге // Нелинейная динамика, 2010. Т 6, № 4. С. 913—916).
- Крагельский И. В., Щедров В. С. Развитие науки о трении. Сухое трение. М.: Изд. АН СССР, 1956.
- Фролов, К. В. (ред.) Современная трибология: Итоги и перспективы. ЛКИ, 2008.
- Bowden F. P., Tabor D. The Friction and Lubrication of Solids. Oxford University Press, 2001.
- Persson Bo N. J.: Sliding Friction. Physical Principles and Applications. Springer, 2002.
- Popov V. L. Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer, 2009.
- Rabinowicz E. Friction and Wear of Materials. Wiley-Interscience, 1995.
Примечания[править | править код]
- На русском
- ↑ Ерин Ю. Сверхпроводимость уменьшает силу трения. Элементы.ру (15 февраля 2011). Дата обращения: 26 февраля 2011. Архивировано 22 августа 2011 года.
- На других языках
- ↑ Зиновьев В. А. Краткий технический справочник. Том 1. — М.: Государственное издательство технико-теоретической литературы, 1949. — С. 296
- ↑ Air Brake Association. The Principles and Design of Foundation Brake Rigging. — Air brake association, 1921. — P. 5. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ 1 2 Hanaor, D. (2016). “Static friction at fractal interfaces”. Tribology International. 93: 229—238. arXiv:2106.01473. DOI:10.1016/j.triboint.2015.09.016.
- ↑ 1 2 3 4 5 Dowson, Duncan. History of Tribology. — 2nd. — Professional Engineering Publishing, 1997. — ISBN 978-1-86058-070-3.
- ↑ Valentin L. Popov (17 Jan 2014). “Generalized law of friction between elastomers and differently shaped rough bodies”. Sci. Rep. 4. DOI:10.1038/srep03750. PMID 24435002.
- ↑ Dienwiebel, Martin (2004). “Superlubricity of Graphite” (PDF). Phys. Rev. Lett. 92 (12). Bibcode:2004PhRvL..92l6101D. DOI:10.1103/PhysRevLett.92.126101. PMID 15089689. Архивировано (PDF) из оригинала 2011-09-17. Дата обращения 2021-09-18.
- ↑ multi-scale origins of static friction Архивная копия от 18 сентября 2021 на Wayback Machine 2016
- ↑ Greenwood J.A. and JB Williamson (1966). “Contact of nominally flat surfaces”. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 295 (1442).
- ↑ Nakano, K. (2020-12-10). “Dynamic stiction without static friction: The role of friction vector rotation”. Physical Review E. 102 (6): 063001. DOI:10.1103/PhysRevE.102.063001.
- ↑ Bhavikatti, S. S. Engineering Mechanics / S. S. Bhavikatti, K. G. Rajashekarappa. — New Age International, 1994. — P. 112. — ISBN 978-81-224-0617-7. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ Beer, Ferdinand P. Vector Mechanics for Engineers / Ferdinand P. Beer, Johnston. — McGraw-Hill, 1996. — P. 397. — ISBN 978-0-07-297688-5.
- ↑ Sheppard, Sheri. Statics: Analysis and Design of Systems in Equilibrium / Sheppard, Sheri, Tongue, Benson H., Anagnos, Thalia. — Wiley and Sons, 2005. — ISBN 978-0-471-37299-8.
- ↑
Meriam, James L. Engineering Mechanics: Statics / Meriam, James L., Kraige, L. Glenn, Palm, William John. — Wiley and Sons, 2002. — ISBN 978-0-471-40646-4. - ↑ Feynman, Richard P. The Feynman Lectures on Physics, Vol. I, p. 12–5. Addison-Wesley. Дата обращения: 16 октября 2009. Архивировано 10 марта 2021 года.
- ↑ Beatty. Recurring science misconceptions in K-6 textbooks. Дата обращения: 8 июня 2007. Архивировано 7 июня 2011 года.
- ↑ Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ Makkonen, L (2012). “A thermodynamic model of sliding friction”. AIP Advances. 2 (1). Bibcode:2012AIPA….2a2179M. DOI:10.1063/1.3699027.
- ↑ Nichols, Edward Leamington. The Elements of Physics / Edward Leamington Nichols, William Suddards Franklin. — Macmillan, 1898. — Vol. 1. — P. 101. Архивная копия от 1 августа 2020 на Wayback Machine
- ↑ Ternes, Markus (2008-02-22). “The Force Needed to Move an Atom on a Surface” (PDF). Science. 319 (5866): 1066—1069. Bibcode:2008Sci…319.1066T. DOI:10.1126/science.1150288. PMID 18292336. Архивировано (PDF) из оригинала 2021-08-17. Дата обращения 2021-09-18.
- ↑ Friction theory and coefficients of friction for some common materials and materials combinations. Дата обращения: 1 января 2015. Архивировано 3 декабря 2013 года.
- ↑ 1 2 Chatterjee, Sudipta (2008). Tribological Properties of Pseudo-elastic Nickel-titanium (Thesis). University of California. pp. 11—12. ISBN 9780549844372 – via ProQuest.
Classical Greek philosophers like Aristotle, Pliny the Elder and Vitruvius wrote about the existence of friction, the effect of lubricants and the advantages of metal bearings around 350 B.C.
- ↑ Fishbane, Paul M. Physics for Scientists and Engineers / Paul M. Fishbane, Stephen Gasiorowicz, Stephen T. Thornton. — Extended. — Englewood Cliffs, New Jersey : Prentice Hall, 1993. — Vol. I. — P. 135. — «Themistius first stated around 350 B.C. that kinetic friction is weaker than the maximum value of static friction.». — ISBN 978-0-13-663246-7.
- ↑ Hecht, Eugene. Physics: Algebra/Trig. — 3rd. — Cengage Learning, 2003. — ISBN 9780534377298.
- ↑ Sambursky, Samuel. The Physical World of Late Antiquity. — Princeton University Press. — ISBN 9781400858989.
- ↑ 1 2 3 Armstrong-Hélouvry, Brian. Control of machines with friction. — USA : Springer, 1991. — P. 10. — ISBN 978-0-7923-9133-3. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ 1 2 van Beek. History of Science Friction. tribology-abc.com. Дата обращения: 24 марта 2011. Архивировано 7 августа 2011 года.
- ↑ Hutchings, Ian M. (2016). “Leonardo da Vinci’s studies of friction” (PDF). Wear. 360–361: 51—66. DOI:10.1016/j.wear.2016.04.019. Архивировано (PDF) из оригинала 2021-08-31. Дата обращения 2021-09-18.
- ↑ Hutchings, Ian M. (2016-08-15). “Leonardo da Vinci’s studies of friction”. Wear. 360–361: 51—66. DOI:10.1016/j.wear.2016.04.019. Архивировано из оригинала 2021-09-18. Дата обращения 2021-09-18.
- ↑ Kirk. Study reveals Leonardo da Vinci’s ‘irrelevant’ scribbles mark the spot where he first recorded the laws of friction. phys.org (22 июля 2016). Дата обращения: 26 июля 2016. Архивировано 25 июля 2016 года.
- ↑ 1 2 Popova, Elena (2015-06-01). “The research works of Coulomb and Amontons and generalized laws of friction”. Friction [англ.]. 3 (2): 183—190. DOI:10.1007/s40544-015-0074-6.
- ↑ Forest de Bélidor, Bernard. «Richtige Grund-Sätze der Friction-Berechnung Архивная копия от 27 апреля 2021 на Wayback Machine» («Correct Basics of Friction Calculation»), 1737, (in German)
- ↑ Leonhard Euler. Friction Module. Nano World. Дата обращения: 25 марта 2011. Архивировано 7 мая 2011 года.
- ↑ Goedecke, Andreas. Transient Effects in Friction: Fractal Asperity Creep. — Springer Science and Business Media, 2014. — P. 3. — ISBN 978-3709115060. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ Fleeming Jenkin & James Alfred Ewing (1877) «On Friction between Surfaces moving at Low Speeds Архивная копия от 18 сентября 2021 на Wayback Machine», Philosophical Magazine Series 5, volume 4, pp 308-10; link from Biodiversity Heritage Library








