| Условие возникновения | Действует между телами, покоящимися относительно друг друга | ||
| Физическая природа силы | Электромагнитная природа обусловлена взаимодействием атомов или молекул элементов поверхностей взаимодействующих тел | ||
| Направление силы |
|
||
|
Формула |
|
||
| Особенности | Значение коэффициента трения (mu) определяется структурой трущихся поверхностей | ||
| Границы применимости | При точных расчётах учитывают, что значение предельной силы трения покоя больше значения, определяемого формулой ((1)) |
2. Сила трения скольжения
| Условие возникновения | Относительное перемещение контактирующих тел | ||
| Физическая природа силы | Электромагнитная природа обусловлена атомно-молекулярным взаимодействием контактирующих поверхностей | ||
| Направление силы |
|
||
|
Формула (закон Кулона — Амонтона) |
|
||
| Особенности | Значение коэффициента трения (mu) определяется структурой трущихся поверхностей | ||
| Границы применимости | Формула ((2)) справедлива при небольших значениях относительной скорости тел |
| Условие возникновения | Относительное перемещение тел, сопровождающееся их вращением | ||
| Природа силы | Электромагнитная природа обусловлена деформацией поверхностей взаимодействующих тел и межмолекулярным взаимодействием поверхностей взаимодействующих тел | ||
| Направление силы |
|
||
| Формула |
(F_{тр}=frac{f}{R} · Mg), где (f) — коэффициент трения качения, ([f]=м) |
||
| Особенности | Значение коэффициента трения качения (f) существенно меньше коэффициента трения скольжения (mu) | ||
| Границы применимости | Скорости качения существенно меньше скорости деформации взаимодействующих поверхностей |
Источники:
Рис. 1. Направление силы трения покоя. © ЯКласс.
Рис. 2. Изображение графика зависимости силы трения покоя от внешней силы. © ЯКласс.
Рис. 3. Направление силы трения скольжения. © ЯКласс.
Рис. 4. Изображение графика зависимости силы трения скольжения от внешней силы. © ЯКласс.
Рис. 5. Направление сил трения качения и полной реакции. © ЯКласс.
К бруску массой 10 кг, находящемуся на горизонтальной поверхности, приложена сила. Учитывая, что коэффициент трения равен 0,7, определите:
- силу трения для случая, если F = 50 Н и направлена горизонтально;
- силу трения для случая, если F = 80 Н и направлена горизонтально;
- построить график зависимости ускорения бруска от горизонтально приложенной силы;
- с какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать брусок?
Решение:
1. Определим максимальную силу трения покоя. Она будет равна:
μmg = 0,7×10×10 = 70 (H).
Приложенной силы будет недостаточно для того, чтобы сдвинуть тело. По третьему закону Ньютона F = Fmp = 50 H.
2. В случае приложенной силы F = 80 Н тело приобретает ускорение, равное:
3. Для построения зависимости a(F) воспользуемся функцией:
| a = | F − Fmp | = | F − μmg | = | F | − μg. (1) |
| m | m | m |
Из уравнения (1) можно сделать вывод, что зависимость ускорения от горизонтально приложенной силы линейная.
При F = 0 a = −μg, а при a = 0 F = μmg. Построим график зависимости a(F), см. рисунок.
4. Запишем уравнение движения санок в проекциях на горизонтальное и вертикальное направления:
и
где α — угол между веревкой и горизонтом, а сила трения равна Fmp = μN. Из записанных уравнений найдем силу натяжения веревки:
| F = | μmg | . (2) |
| cos α + μ • sin α |
Ее значение зависит от угла α. Проанализируем эту зависимость. Тело будет двигаться равномерно, если горизонтальная составляющая силы натяжения веревки Fcos α равна силе трения Fmp. Поэтому для обеспечения минимальной силы F веревку, казалось бы, надо тянуть горизонтально, т. е. под углом α = 0°. Но с другой стороны, желательно, чтобы угол α был побольше, так как в этом случае за счет увеличения вертикальной составляющей Fsin α, стремящейся приподнять санки, уменьшается их давление на опору, и соответственно уменьшается сила трения.
Таким образом, на результат влияют два конкурирующих фактора. Для выяснения, при каких α превалирует первый из них, а при каких — второй, представим зависимость F = F(α) в виде графика. Из него видно, что исследуемая функция при α = αо имеет минимум. Для нахождения значений αо и Fmin воспользуемся аналитическим методом. Функция (2) минимальна, когда знаменатель максимален. Обозначим знаменатель буквой y. Найдем производную y’ по α и приравняем ее к нулю:
y’ = −sin α + μ cos α = 0.
Отсюда, обозначив соответствующий угол как αо, получим:
и
Тогда:
| Fmin = | μmg | . |
| cos αo + μsin αo |
Используя тригонометрические соотношения и предыдущее равенство, найдем:
| cos αo = | 1 | = | 1 | , |
| √(tg2αo + 1) | √(μ2 + 1) |
| sin αo = | tg αo | = | μ | . |
| √(tg2αo + 1) | √(μ2 + 1) |
Следовательно:
| Fmin= | μmg | = 56 H. |
| √(μ2 + 1) |
Далее: зависимость потока воды от температуры [тема: графическое решение задач по физике]
Каждый из нас знаком с проявлением силы трения. Действительно, любое движение в повседневной жизни, будь то ходьба человека или перемещение транспортного средства, невозможно без участия этой силы. В физике принято изучать три вида сил трения. В данной статье рассмотрим один из них, разберемся, что собой представляет трение покоя.
Брусок на горизонтальной поверхности
Прежде чем переходить к ответам на вопросы, что такое сила трения покоя и чему равна она, рассмотрим простой случай с бруском, который лежит на горизонтальной поверхности.
Проанализируем, какие силы действуют на брусок. Во-первых, это вес самого предмета. Обозначим его буквой P. Он направлен вертикально вниз. Во-вторых, это реакция опоры N. Она направлена вертикально вверх. Второй закон Ньютона для рассматриваемого случая запишется в таком виде:
m*a = P – N.
Знак минус здесь отражает противоположные направления векторов веса и реакции опоры. Поскольку брусок покоится, то величина a равна нулю. Последнее означает, что:
P – N = 0 =>
P = N.
Реакция опоры уравновешивает вес тела и равна ему по абсолютной величине.
Действующая внешняя сила на брусок на горизонтальной поверхности
Теперь к описанной выше ситуации добавим еще одну действующую силу. Предположим, что человек начал толкать брусок вдоль горизонтальной поверхности. Обозначим эту силу буквой F. Можно заметить удивительную ситуацию: если сила F невелика, то несмотря на ее действие, брусок продолжает покоиться на поверхности. Вес тела и реакция опоры направлены перпендикулярно поверхности, поэтому их горизонтальные проекции равны нулю. Иными словами, силы P и N не могут оказать никакого противодействия величине F. В таком случае, почему брусок остается в состоянии покоя и не движется?
Очевидно, что должна существовать сила, которая направлена против силы F. Этой силой является трение покоя. Она направлена против F вдоль горизонтальной поверхности. Действует она в области контакта нижней грани бруска и поверхности. Обозначим ее символом Ft. Закон Ньютона для горизонтальной проекции запишется в виде:
F = Ft.
Таким образом, модуль силы трения покоя всегда равен абсолютной величине внешних сил, действующих вдоль горизонтальной поверхности.
Начало движения бруска
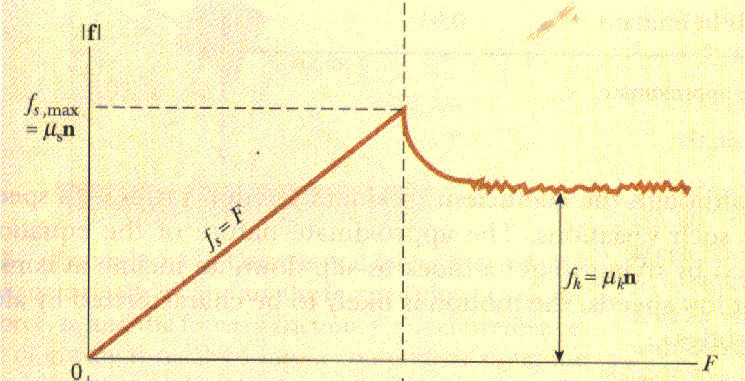
Чтобы записать формулу трения покоя, продолжим начатый в предыдущих пунктах статьи эксперимент. Будем увеличивать абсолютное значение внешней силы F. Брусок какое-то время еще будет оставаться в покое, но наступит момент, когда он начнет двигаться. В этот момент сила трения покоя приобретет максимальное значение.
Чтобы найти это максимальное значение, возьмем еще один точно такой же брусок, как и первый, и положим его сверху. Площадь контакта бруска с поверхностью не изменилась, однако его вес увеличился вдвое. Экспериментально было установлено, что сила F отрыва бруска от поверхности также увеличилась вдвое. Этот факт позволил записать следующую формулу трения покоя:
Ft = µs*P.
То есть максимальная величина силы трения оказывается пропорциональной весу тела P, где в качестве коэффициента пропорциональности выступает параметр µs. Величина µs называется коэффициентом трения покоя.
Поскольку вес тела в проведенном эксперименте равен силе реакции опоры N, то формулу для Ft можно переписать так:
Ft = µs*N.
В отличие от предыдущего, это выражение можно использовать всегда, даже когда тело находится на наклонной плоскости. Модуль силы трения покоя прямо пропорционален силе реакции опоры, с которой поверхность действует на тело.
Физические причины возникновения силы Ft
Вопрос, почему появляется трение покоя, является сложным и требует рассмотрения контакта между телами на микроскопическом и атомарном уровне.
В общем случае можно назвать две физические причины возникновения силы Ft:
- Механическое взаимодействие между пиками и впадинами.
- Физико-химическое взаимодействие между атомами и молекулами тел.
Насколько бы гладкой ни была любая поверхность, она обладает неровностями и неоднородностями. Грубо эти неоднородности можно представить в виде микроскопических пиков и впадин. Когда пик одного тела попадает во впадину другого тела, то происходит механическое сцепление между этими телами. Огромное число микроскопических сцепок является одной из причин появления трения покоя.
Вторая причина заключается в физико-химическом взаимодействии между молекулами или атомами, из которых состоят тела. Известно, когда два нейтральных атома приближаются друг к другу, то между ними могут возникать некоторые электрохимические взаимодействия, например, диполь-дипольные или ван-дер-ваальсовые. В момент начала движения брусок вынужден преодолевать эти взаимодействия, чтобы оторваться от поверхности.
Особенности силы Ft
Выше уже было отмечено, чему равна сила трения покоя максимальная, а также указано ее направление действия. Здесь перечислим другие характеристики величины Ft.
Трение покоя не зависит от площади контакта. Она определяется исключительно реакцией опоры. Чем больше площадь контакта, тем меньше деформация микроскопических пиков и впадин, однако тем больше их количество. Этот интуитивный факт объясняет, почему максимальная величина Ft не изменится, если брусок перевернуть на грань с меньшей площадью.
Трение покоя и трение скольжения имеют одну и ту же природу, описываются одинаковыми формулами, однако вторая всегда меньше, чем первая. Трение скольжения появляется, когда брусок начинает движение по поверхности.
Сила Ft в большинстве случаев является неизвестной величиной. Формула, которая приведена выше для нее, соответствует максимальному значению Ft в момент начала движения бруска. Чтобы яснее понять названный факт, ниже приведен график зависимости силы Ft от внешнего воздействия F.
Видно, что с возрастанием F трение покоя растет линейно, достигает максимума, а затем уменьшается, когда тело начинает движение. Во время движения говорить о силе Ft уже нельзя, поскольку ее заменяет трение скольжения.
Наконец, последней важной особенностью силы Ft является то, что она не зависит от скорости перемещения (при относительных больших скоростях Ft уменьшается).
Коэффициент трения µs
Так как в формуле для модуля силы трения фигурирует величина µs, следует сказать о ней несколько слов.
Коэффициент трения µs является уникальной характеристикой двух поверхностей. Он не зависит от веса тела, его определяют экспериментально. Например, для пары дерево-дерево он изменяется от 0,25 до 0,5 в зависимости от типа дерева и качества обработки поверхности трущихся тел. Для смазанной воском деревянной поверхности на мокром снегу µs = 0,14, а для человеческих суставов этот коэффициент принимает весьма низкие значения (≈0,01).
Какое бы значение ни имел µs для рассматриваемой пары материалов, аналогичный коэффициент трения скольжения µk будет всегда меньше. Например, при скольжении дерева по дереву он равен 0,2, а для суставов человека не превышает величины 0,003.
Далее рассмотрим решение двух физических задач, в которых применим полученные знания.
Брусок на наклонной поверхности: расчет силы Ft
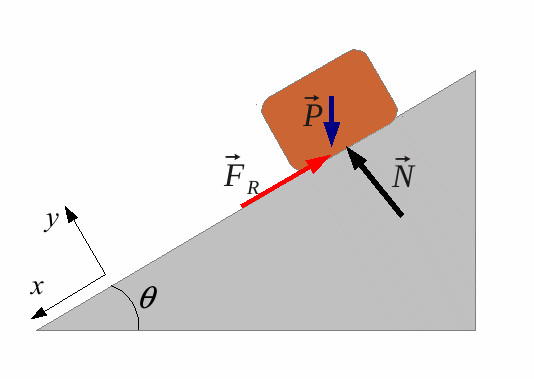
Первая задача является достаточно простой. Предположим, что на деревянной поверхности лежит брусок из дерева. Его масса равна 1,5 кг. Поверхность наклонена под углом 15o к горизонту. Необходимо определить силу трения покоя, если известно, что брусок не движется.
Подвох этой задачи заключается в том, что многие начинают вычислять реакцию опоры, а затем, используя справочные данные для коэффициента трения µs, пользуются приведенной выше формулой для определения максимального значения Ft. Однако в данном случае Ft не является максимальной. Ее модуль равен лишь внешней силе, которая стремится сдвинуть брусок с места вниз по плоскости. Эта сила равна:
F = m*g*sin(α).
Тогда сила трения Ft будет равна величине F. Подставляя данные в равенство, получаем ответ: сила трения покоя на наклонной плоскости Ft = 3,81 ньютона.
Брусок на наклонной поверхности: расчет максимального угла наклона
Теперь решим такую задачу: деревянный брусок находится на деревянной наклонной плоскости. Полагая коэффициент трения равным 0,4, необходимо найти максимальный угол наклона α плоскости к горизонту, при котором брусок начнет скользить.
Скольжение начнется, когда проекция веса тела на плоскость станет равной максимальной силе трения покоя. Запишем соответствующее условие:
F = Ft =>
m*g*sin(α) = µs*m*g*cos(α) =>
tg(α) = µs =>
α = arctg(µs).
Подставляя в последнее уравнение значение µs = 0,4, получаем α = 21,8o.
